Next Article in Journal
Antarctic Sea Ice Proxies from Marine and Ice Core Archives Suitable for Reconstructing Sea Ice over the Past 2000 Years
Previous Article in Journal
An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 9
Issue 12
10.3390/geosciences9120505
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Water, Hydrous Melting, and Teleseismic Signature of the Mantle Transition Zone

by
Ilya Fomin
1,* and
Christian Schiffer
2
1
Department of Earth and Environmental Sciences, Macquarie University, 12 Wally’s Walk, Sydney, NSW 2109, Australia
2
Department of Earth Sciences, Uppsala University, Villavägen 16, 75236 Uppsala, Sweden
*
Author to whom correspondence should be addressed.
Geosciences 2019, 9(12), 505; https://doi.org/10.3390/geosciences9120505
Submission received: 2 October 2019 / Revised: 27 November 2019 / Accepted: 29 November 2019 / Published: 4 December 2019
(This article belongs to the Section Geophysics)
Browse Figures
Versions Notes

Abstract

:
Recent geophysical and petrological observations indicate the presence of water and hydrous melts in and around the mantle transition zone (MTZ), for example, prominent low-velocity zones detected by seismological methods. Experimental data and computational predictions describe the influence of water on elastic properties of mantle minerals. Using thermodynamic relationships and published databases, we calculated seismic velocities and densities of mantle rocks in and around the MTZ in the presence of water for a plausible range of mantle potential temperatures. We then computed synthetic receiver functions to explore the influence of different water distribution patterns on the teleseismic signature. The results may improve our understanding and interpretation of seismic observations of the MTZ.

1. Introduction

Three major phase transitions define the mantle transition zone (MTZ) between the upper mantle and lower mantle: olivine transforms to wadsleyite at ~410 km, wadsleyite to ringwoodite at ~520 km, which then breaks down into bridgmanite, and periclase at ~660 km (e.g., [1]). The exact depths of these transitions (in the following referred to as “410”, “520”, and “660”, respectively) vary with temperature, pressure, chemical composition, and volatile content in rocks. Phase changes may cause strong seismic velocity discontinuities, which can be imaged using different seismological methods (e.g., [2,3,4,5]). The MTZ can act as a strong thermomechanical boundary between the upper and lower mantle, possibly impeding mass exchange between the upper and lower mantle (subduction and upwelling). Mapping of the actual depths of phase transitions is essential in order to understand the geodynamics of the Earth (e.g., [6,7]).
For decades, olivine with spinel structure has been recognised as a potential water-carrying mineral in the Earth’s mantle [1,8,9,10,11]. The ability of the MTZ to capture, store and release water may be a crucial aspect of the global water budget/cycle, mantle dynamics, and plate tectonics [12,13,14,15]. Reference [16] described the peridotite-water system and proposed hydration of the MTZ by dehydration of subducting slabs which has been supported by other studies (e.g., [17]). The finding of a water-rich ringwoodite inclusion in diamond was direct evidence for the presence of water in the mantle [18,19] and proposed the presence of water in the MTZ to explain the electrical conductivity of mantle rocks; however, this interpretation is debated (e.g., [20]). Reference [21] interpreted high seismic attenuation anomalies in the MTZ beneath the North Atlantic as evidence for water-rich rocks. A similar study proposed a 20–35 km thick layer with up to 700 ppm of water, close to the 410 [22,23], used water-bearing nominally anhydrous minerals (NAMs) for thermodynamic modelling to explain observed seismological data. Reference [24] argues that a nearly water-saturated MTZ is required to explain estimated viscosities of MTZ minerals.
The presence of water alters the depths of phase transitions and elastic moduli of solid rocks and affects the seismic velocity structure (e.g., [25]). It also reduces rock solidi to values potentially well-below the mantle adiabat (e.g., [1,26]). Hydrated mantle-derived melts observed in specific geodynamic settings, such as atop stagnated slabs [27] or in hotspots [28], require sufficient amounts of water to be stored in or to be transported into the MTZ. Melts have a major influence on seismic velocities [29] and may form prominent seismic signals. Reference [30] presented a conceptual model of a hydrous MTZ overlain by a melt layer based on the fact that, at ~8 GPa, dry silicate melt is denser than the solid upper mantle but is less dense than MTZ lithologies which is supported by modern experimental [31] and computational studies [32].
P-receiver functions (RFs) are a common method to image discontinuities in the crust and upper to mid-mantle including the MTZ (e.g., [2,3,4,5]). Some authors attribute negative peaks in P-RFs observed in the upper and mid-mantle across the globe to the presence of water and hydrous melting (e.g., [23,33,34,35,36,37]).
In this contribution, we parameterised the elastic properties of hydrous solid phases and melt in the MTZ region in a forward model of seismic properties and produced P-RFs for different thermal and hydrous anomalies. The synthetic RF signatures may provide a guideline for the interpretation of the effects of water on observed RFs in the MTZ.

2. Petrological-Geophysical Modelling Approach

A MATLAB script parametrises a rectangular section of the Earth from the surface to the depth of 700 km as a 2D domain of 1 km × 1 km cells. Each cell stored the chemical composition, pressure, and temperature used to calculate the physical properties of the rocks. A forward model computed synthetic RFs for a given one-dimensional velocity structure.

2.1. Chemical Composition and Proportion of Phases

The upper mantle and MTZ in our model had pyrolitic composition with 60 vol.% of olivine or its polymorph, 25 vol.% of pyroxene (in the upper mantle above the MTZ only), and 15 vol.% of garnet [38,39,40]. The iron end-member comprised 11 mol.% of olivine and pyroxene and 15 mol.% of garnet. The uppermost part of the lower mantle consisted of periclase with 27 mol.% of FeO and equal amounts of bridgmanite and majoritic garnet with 11 mol.% FeO. This data agreed with recent density functional theory (DFT) calculations in Reference [41] that predicted 20–35 mol.% of FeO in periclase and 4–7 mol.% FeO in bridgmanite. The fraction of bridgmanite in the lower mantle was around 68 mol.% (including calcium endmember, [42]). We did not include any hydrous phases in our simulations, because a proper estimate of their content and influence on the rock properties required an extensive thermodynamic framework and was beyond the scope of current paper.

2.2. Elastic Constants

We used physical parameters (i.e., molar volume M, isothermal bulk modulus KT0, isothermal bulk modulus pressure derivative KT’, shear modulus G, shear modulus pressure derivative G’) for olivine, pyroxene, and periclase from a self-consistent thermodynamic database [43]. More recent publications (e.g., [44,45,46,47]) confirm those values within several percent of uncertainty. We used more recent data for garnet [48] and bridgmanite [49]. Properties of solid solutions depended linearly on their composition, which is supported by experimental data (e.g., [46,47]). Bulk properties of rocks were averaged with Voigt–Reuss–Hill means [50].
The seismic velocity model accounted for thermal derivatives of the shear moduli for olivine [51], wadsleyite [52,53], and ringwoodite [54] as well as garnet and pyroxene [55]. Bulk moduli followed an Arrhenius-type dependency on temperature (e.g., [55,56]).
There are only few estimates of thermal expansion coefficients for relevant minerals under mantle conditions, for example: 12.8 × 10−5 1/K for olivine [57], 8.9 × 10−5 1/K for ringwoodite [58], 5.7 × 10−5 1/K for periclase [59], and 4.0 × 10−5 1/K for bridgmanite [60]. Thermal expansion coefficients of bulk mantle lithologies are better constrained: 3.45 × 10−5 1/K for lithospheric mantle [61]; 2.5 × 10−5–4.0 × 10−5 1/K [62] and 2.5 × 10−5–3.4 × 10−5 1/K [63] for sub-lithospheric upper mantle; 2.4 × 10−5–2.7 × 10−5 1/K [62] and 2.1 × 10−5–2.9 × 10−5 1/K [63] in the MTZ; 3.0 × 10−5 1/K [62] and 2.1 × 10−5–2.4 × 10−5 1/K [63] for the uppermost lower mantle. We used the values found in Reference [63].

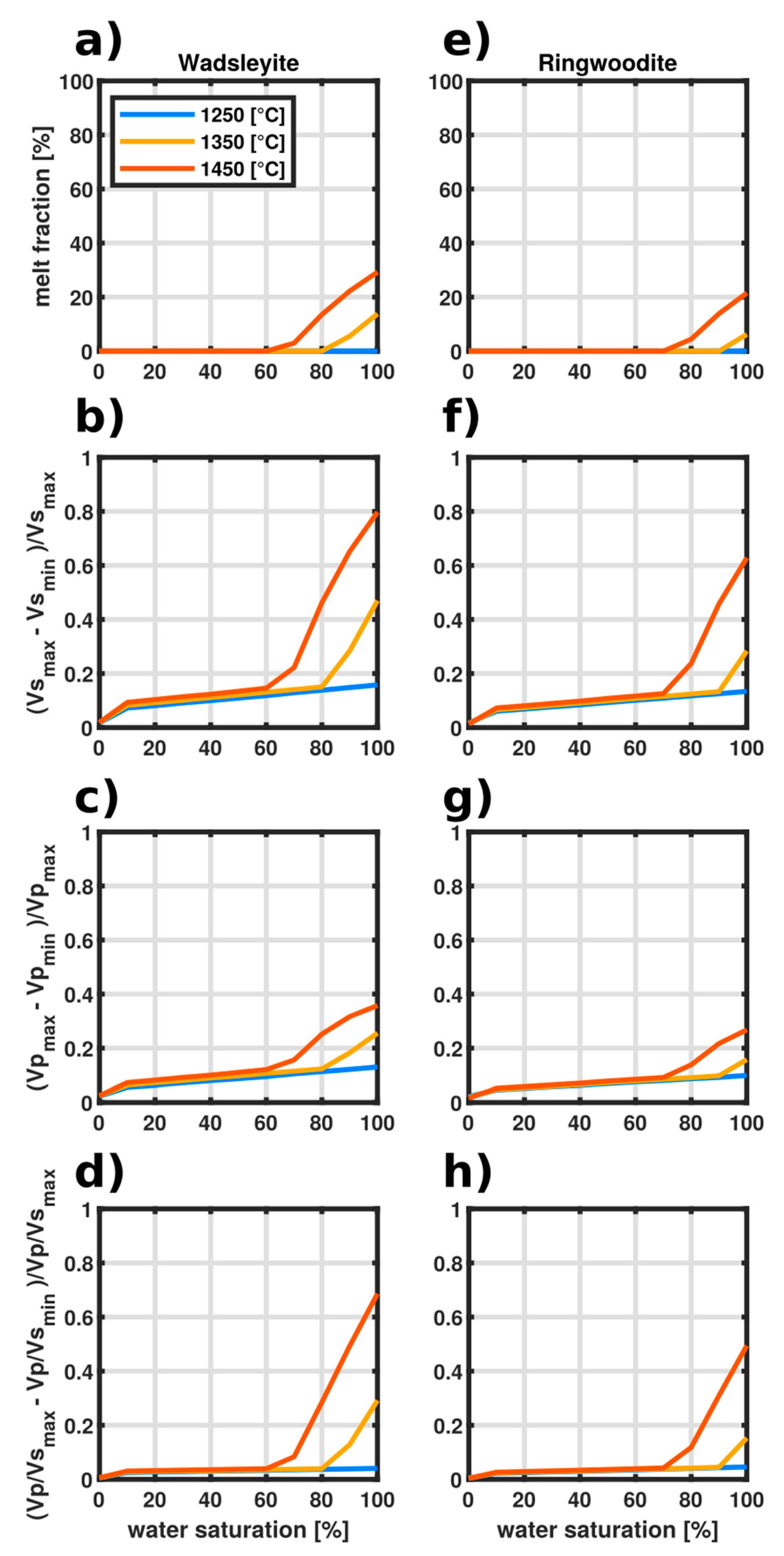
2.3. Water Saturation and Considered Mineral Phases

The model involved only nominally anhydrous minerals (NAMs) which is a common assumption for the mantle far away from subducting slabs, likely the main modern source of water influx to the mantle (e.g., [12]). The upper limits of water content in NAMs are well-studied, and these estimates are consistent. Olivine can carry a few thousands of ppm of water, garnet can hold hundreds of ppm (except hydrated species), pyroxene may contain up to 700 ppm of water, and omphacite up to 2000 ppm [64]. High-pressure olivine polymorphs can bear much more water, up to 1.5 wt.% for wadsleyite and 1.7 wt.% for ringwoodite [65].
The reduction of elastic moduli with increasing water content is usually assumed to be linear. The derivatives ∂KS/∂CH2O and ∂G/∂CH2O are studied for olivine and its polymorphs, but measurements for pyroxene and garnet are still sparse. Therefore, we considered the effects of water content only for olivine and its polymorphs which can also hold much more water than other NAMs. We included a linear correction for iron content [66]. Experiments compared to ab initio estimates (Table 1) predicted lower elastic moduli reduction for olivine and higher reduction for wadsleyite and ringwoodite.

2.4. Thermal Profile

The mantle thermal (and pressure) profile determines phase stability, density, and chemical composition of coexisting minerals. Higher mantle potential temperatures (Tp) lead to a reduction of seismic velocities due to the decreasing elastic moduli (VP: 0.75 ± 0.15%, VS: 1.3 ± 0.30% per 100 °C, [68]). Independent estimates of the Tp were derived from petrological analyses of mantle-derived rocks and depend on the presence of volatiles and the primary melt composition. Fluid-bearing conditions result in a Tp range of 1335–1355 °C and up to 1430 °C for dry depleted rocks [69]. However, newer studies propose a much wider temperature range of 1280–1400 °C for “ambient mantle” (e.g., [70,71]). Estimates of the adiabatic gradient in the mantle are very consistent at approximately 0.4–0.5 K/km for the upper mantle and 0.3 K/km in the lower mantle [62]. We computed models for a range of mantle potential temperatures (1250 °C “cold”, 1350 °C “medium”, 1450 °C “hot”) and a temperature gradient of 0.4 °C/km.

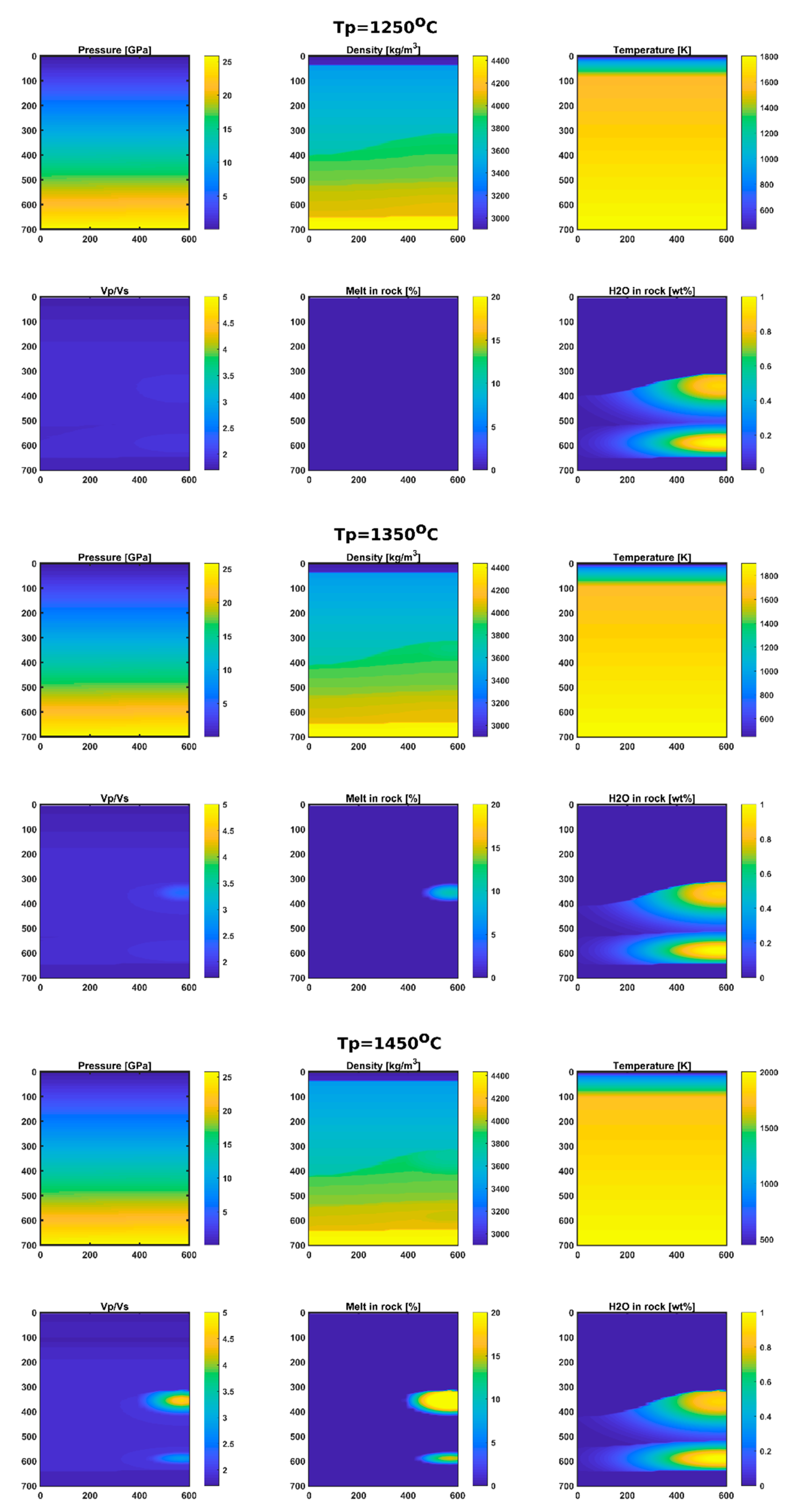
2.5. Water Distribution Patterns

We tested two general patterns of water distribution. The first one (“linear”) assumed a linearly increasing water content in the MTZ in a lateral direction. The second one (“Gaussian”) comprised a 2D Gaussian water distribution centred at a 410 km depth and/or at a 575 km depth which resulted in two approximately ellipsoid hydration anomalies with lateral and vertical variations in water content. Three values of maximum water content in the different anomalies were defined at 0% (“dry”), 50% (“intermediate”) or 100% (“wet”) of the saturation level for a given phase. We tested different combinations of saturation levels in the upper and lower MTZ (wadsleyite and ringwoodite bearing layers): 0–0%, 0–50%, 50–0%, 50–50%, 100–0%, 0–100%, and 100–100% (each in percent with regards to the maximum saturation level) for each distribution pattern (linear and Gaussian).

2.6. Domain Calculation

The mantle phase diagram includes stability fields for olivine, wadsleyite, ringwoodite, and oxides. The reference Clapeyron slopes and pressures of phase transitions adjust to the given water content [1,25], temperature [72], and iron content [73]. The depth of each phase transition was estimated individually in each rock column. We used the third-order Birch–Murnaghan equation with the Mie–Grüneisen approach to compute the elastic moduli and densities under lithostatic pressure (derived from the weight of overlying rocks) and the Adams–Williamson equations to calculate seismic velocities [55].
We used a reference melting diagram from Reference [1]. Temperatures of liquidus and solidus decrease linearly from dry to wet conditions with increasing water content [26]. The melt fraction also increases linearly between solidus and liquidus [74]. We used parameters from Reference [31] for the equation of state, which allows to derive the bulk modulus of a melt-bearing rock by the Biot–Gassmann equation (e.g., [75]). Due to the high melt fractions that we obtained in our simulations (up to 30%), we also altered the shear modulus value using a relationship from Reference [76], in which we assumed a shear modulus of 0 for the melt fraction.

2.7. Seismic Velocity Reduction Due to the Attenuation

Seismic attenuation depends on the grain size, mechanism of dislocations, temperature, pressure, and rock properties (e.g., [77]). The exact mechanisms and magnitudes of seismic attenuation are still poorly known (e.g., [78]). However, a first-order estimate for the influence of seismic attenuation on the synthetic RFs is an important step to make comparisons to natural data.
Generally, seismic attenuation may be divided into three components: a “dry” value, a correction for the presence of water, and a correction for the presence of melt. We used a parameterisation summarised in Reference [78] for the “dry” component which resulted in an up to 0.5% decrease in the seismic wave amplitude (e.g., [14]). Reference [77] presented an approach to quantify the influence of water on seismic attenuation which we used to correct the value of “dry” seismic attenuation. If melt existed in the rock, we used attenuation values provided by Reference [79]. The decrease in seismic energy in this case reached values up to several percent depending on the actual melt fraction.

2.8. Receiver Function Modelling

P-receiver functions (RFs) are deconvolved waveforms of converted P-to-S phases from teleseismic earthquakes and a common tool to image seismic discontinuities, traditionally in the crust and upper mantle (e.g., [80,81,82,83]). The P-to-S conversions become visible as pulses at the delay time of the converted S-wave after the arrival of the primary P-wave, which is dependent on the overlying S and P wave velocity structure and ray parameter of the earthquake wave [84].
From the derived Vp, Vs, and density structure, we computed synthetic RFs using a 1D wavefield to calculate the surface response to an incoming plane wave [85]. Subsequent water-level deconvolution with a Gaussian factor of 1 isolates the RF waveforms (e.g., [80,86]). Although lithospheric layering was included in the thermal-petrological modelling, the evoked lithospheric seismic discontinuities were disregarded in this step to avoid multiples that may compromise the MTZ signals, although these can be assumed to only cause minimal interference [7]. Since the true velocity structure was known, we are able to perfectly back-migrate the signals to their true conversion depth.

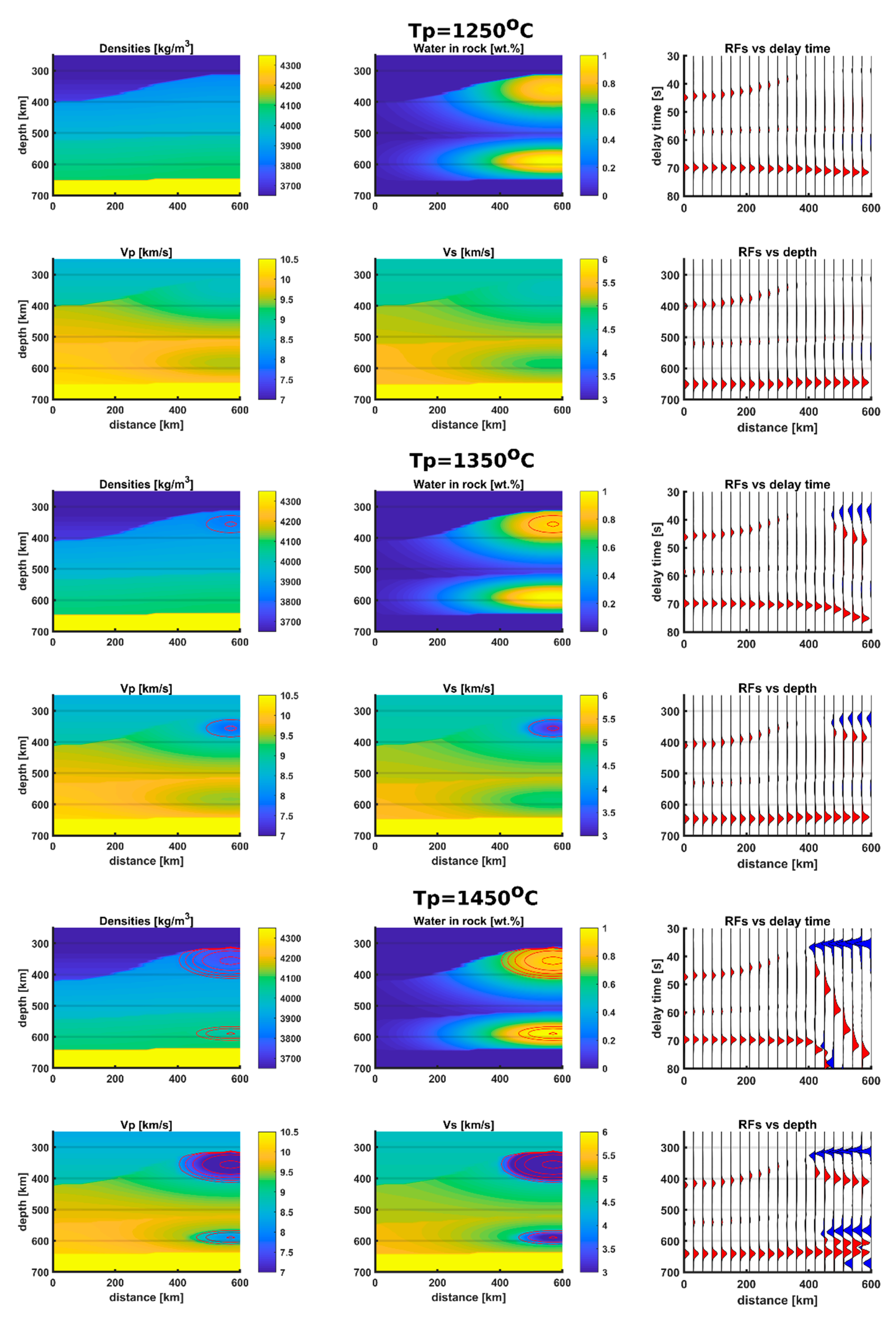
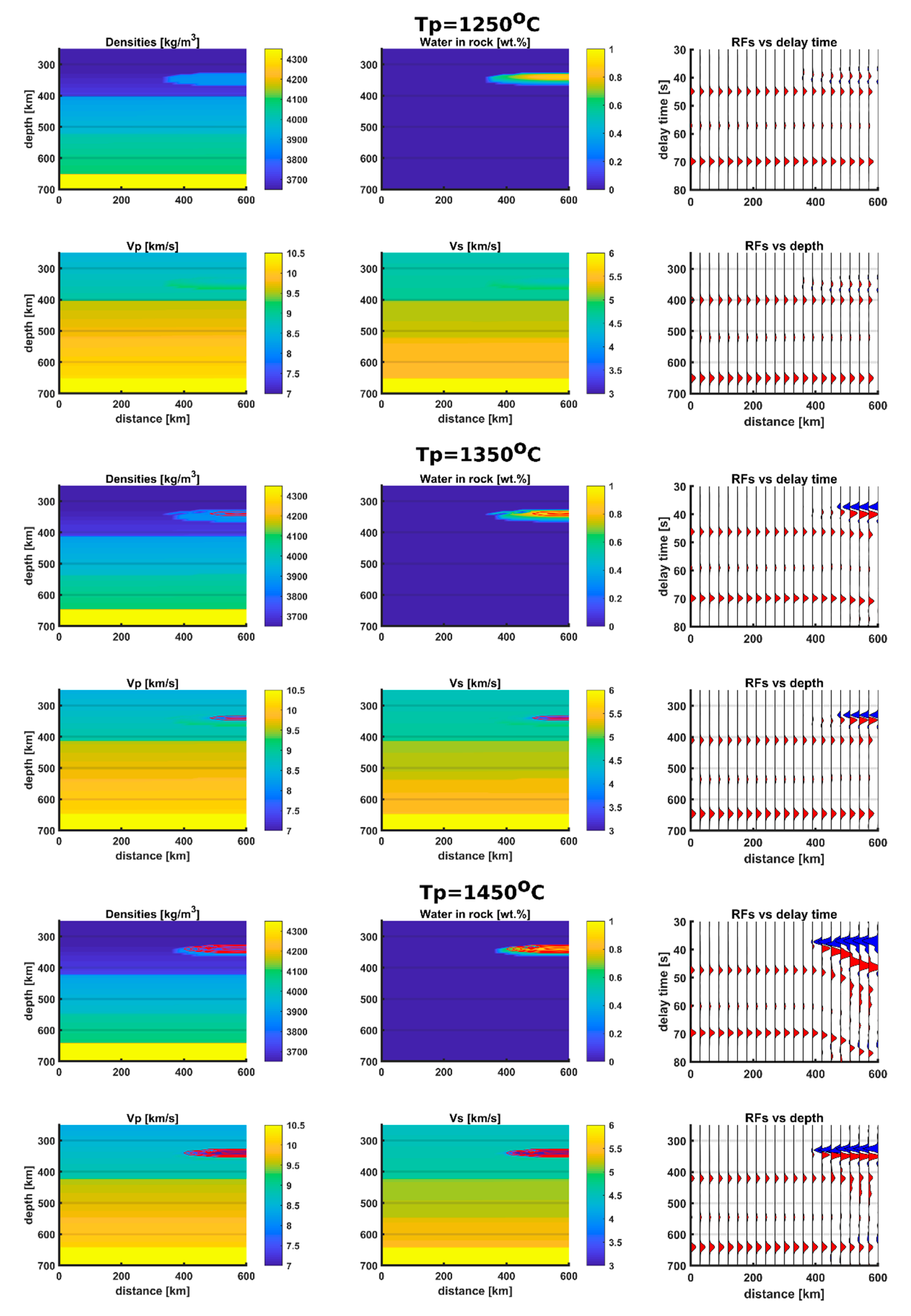
3. Results

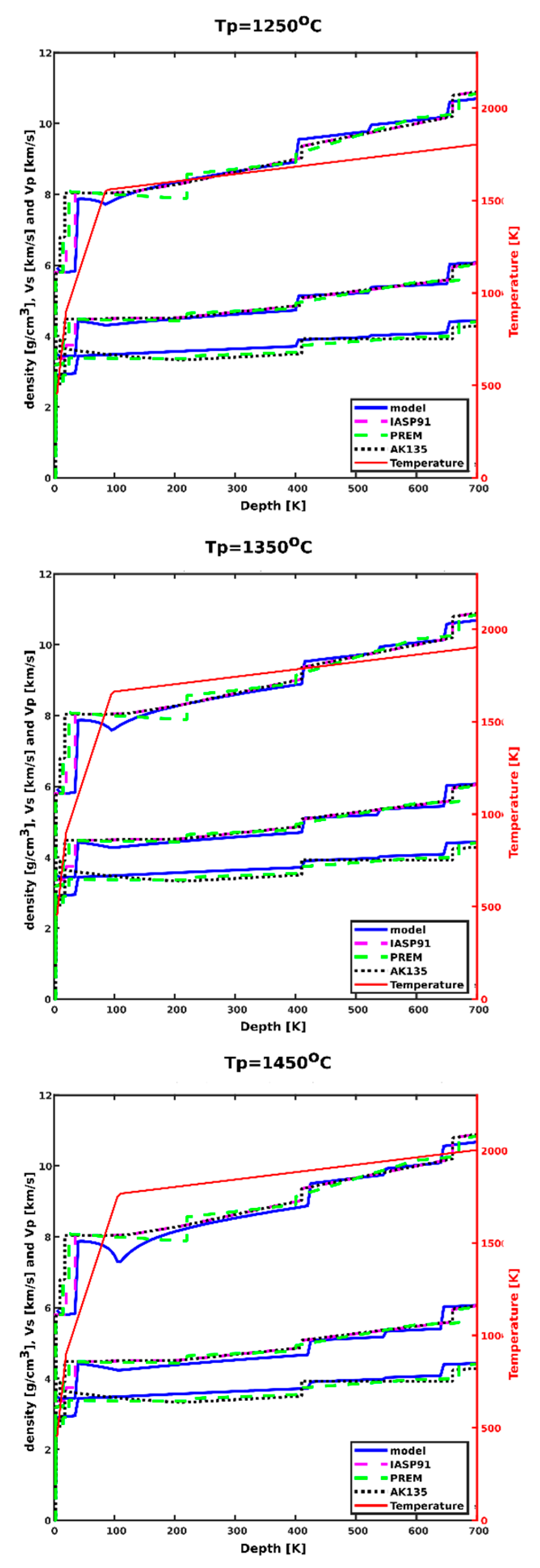
3.1. Phase Equilibria

The depths of the MTZ-phase transitions computed for a dry system (405, 525 and 655 km, Figure 1 and Figure S1) were close to the reference levels of 410, 520, and 660 km. These depths changed considerably under wet conditions: the depth of the olivine–wadsleyite transition (410) shifts to a depth of 300 km, and the depth of wadsleyite–ringwoodite transition (520) moves to 450 km. This behaviour follows the general principle that the presence of a specific component (water) increases the stability field of a phase that effectively dissolves it. A lack of experimental data did not allow us to constrain the behaviour of the lower–upper mantle boundary.
Figure 2 summarises the changes in physical properties in response to temperature and water content. No melt forms under the cold 1250 °C geotherm, even if the rock column is fully water-saturated (Figure 2a,e). For the medium 1350 °C geotherm melting is only observed in almost water-saturated rocks (more than 80% for wadsleyite and 90% for ringwoodite). The melt fraction reaches 14% and 7%, respectively. Melting starts at much lower water saturation levels in a hot 1450 °C geotherm (≥60% for wadsleyite and ≥70% for ringwoodite). The melt fraction reaches 30% for water-saturated wadsleyite and 21% for water-saturated ringwoodite.

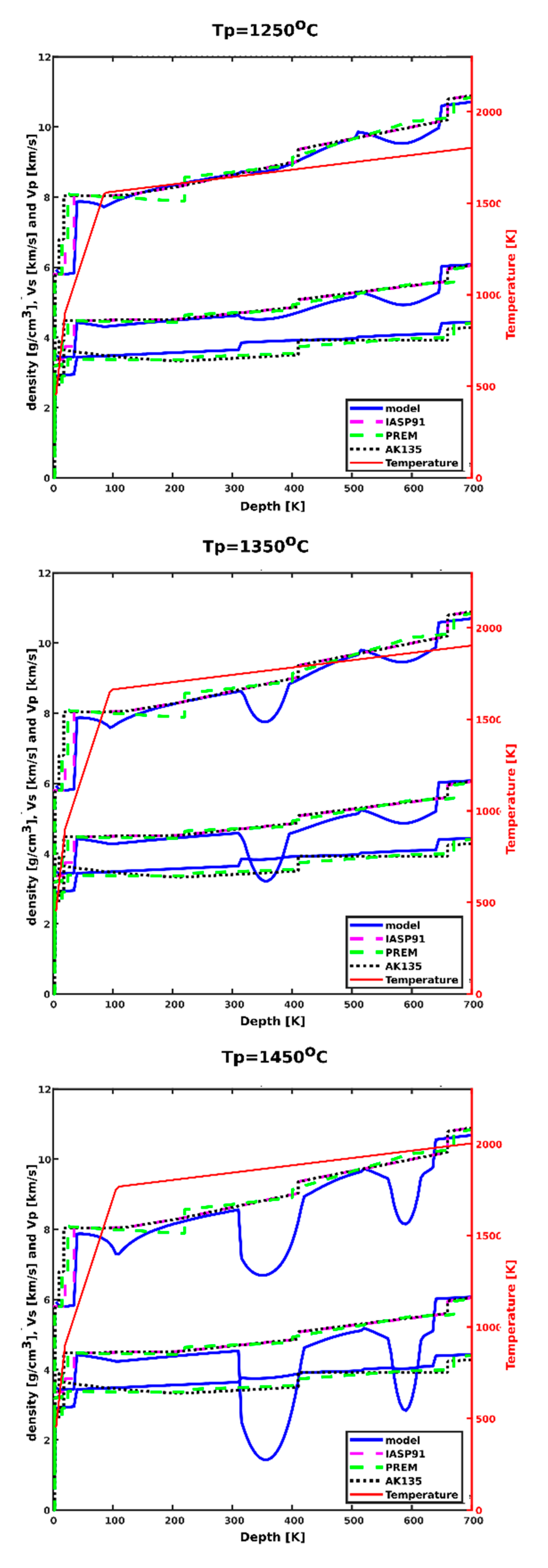
3.2. Velocity Models

Variations in the MTZ thickness due to the water content and temperature did not allow to compare the different models directly in the spatial domain. We therefore computed a relative velocity change ((Vmax − Vmin)/Vmax) for each MTZ layer and every model. This relative velocity reduction in dry systems was less than 2% for Vs and 2.5% for Vp, both in the lower and upper MTZ layers and for all the studied geotherms (Figure 2b,c,f,g).
Even small amounts of water are enough to substantially alter the velocity structure: 10% of water saturation reduces Vs by 6%–10% and Vp by 4.5%–7.5%. Further addition of water decreases seismic velocities linearly up to 10%–15% (Vs) and 7.5%–12% (Vp) dependent on mantle potential temperature. The reduction of seismic velocities is larger for wadsleyite-bearing rocks compared to ringwoodite-bearing rocks: 17%–20% larger for Vs and 22%–32% for Vp at 1250 °C, 21%–26% for Vs and 30%–35% for Vp at 1350 °C, and 35%–45% for Vs and 40%–50% for Vp at 1450 °C.
The presence of melt reduces the shear moduli of rocks drastically. Our parameterisation for the shear modulus [76] and bulk modulus (Biot–Gassmann) resulted in a non-linear velocity reduction with increasing melt fraction and temperature (Figure 2). The Vs was reduced by up to 80% and Vp by up to 34% in the wadsleyite-bearing rocks (for a 1450 °C geotherm and 100% water saturation). In the same conditions, ringwoodite-bearing rocks showed a 65% reduction for Vs and 26% for Vp. The seismic attenuation parameterisation predicted an additional velocity reduction which reached ~10% of Vp and ~7% Vs under wet and hot conditions.

3.3. Receiver Functions

Receiver functions in the MTZ region are usually free of large-amplitude lithospheric multiples and, thus, observed peaks corresponded solely to velocity discontinuities within the MTZ itself. Here, we completely removed lithospheric multiples. As discussed above, both temperature and water content change the depth of the MTZ-phase transitions and both quantities can enhance or reduce existing seismic discontinuities or add new ones.
We performed a number of simulations to explore the influence of different water distribution profiles (linear and Gaussian), mantle potential temperature (1250 °C “cold”, 1350 °C “medium”, 1450 °C “hot”), and water content in MTZ olivine polymorphs (“dry”, “intermediate”, and “wet” cases). As a reference example illustrated in the main text, we focused on the Gaussian water anomaly distribution, both in the upper and lower MTZ reaching up to 100% water saturation. The corresponding figures of this example are shown in the main text (Figure 3, Figure 4, Figure 5 and Figure 6). We also describe the corresponding linear model in the text, but figures are shown only in the Supplementary Materials. The other tested models are also documented in the Supplementary Materials investigating potential mantle temperatures.
The results discussed are entirely based on this small set of defined models to illustrate the general problem and behaviour of water in the MTZ and its teleseismic signature. Any combination and geometry could, in theory, be tested and would result in a unique model and receiver function signal.

3.3.1. General Observations

The water-induced reduction of elastic moduli was proportional to the absolute amount of water. Therefore, only MTZ-lithologies were strongly affected by the addition of water, because the water-storing capacity of the upper mantle (above the MTZ) and lower mantle main rock-forming minerals is very low. The amplitude of the 410 was generally reduced if water was present in the upper MTZ and that of the 660 was increased if water was present in the lower MTZ. In some cases (high water content and temperature), we created pronounced low-velocity zones which was only the case when melts were formed (from approximately 70% water saturation for 1450 °C or and 90% for 1350 °C, Figure 2a,e). Therefore, no model with an intermediate water content showed occurrence of melt and visible low-velocity zones.

3.3.2. Gaussian Distribution Models

Models with Gaussian water anomalies (Figure 3 and Figure 4, Figures S2–S7) exhibited much weaker discontinuities compared to the linear models presented hereafter, due to the smooth vertical gradient in the water content, an inherent feature of the Gaussian model parameterisation, compared to the abrupt changes exhibited in the linear models. There were no melt formed in the dry and intermediate cases as well as under wet conditions and cold geotherm.
In the presence of water in the upper MTZ (intermediate and wet setups), the 410 discontinuity appeared shallower and the corresponding RF-amplitude weaker (Figure 3 and Figure 4, Figures S2–S5). High water content may reduce the MTZ seismic velocities to values similar to the overlying upper mantle, so that the seismic 410 discontinuity vanishes. The effects on the 520 discontinuity were usually much less pronounced, because the centre of the Gaussian water anomalies were placed closer to the 410, and, logically, the water anomaly at the 520 km depth was at the lower end of the Gaussian distribution and weaker.
In the case of a hydrous lower MTZ (Figure 3 and Figure 4, Figures S2, S3, S6, and S7), which is generally thinner than the upper MTZ, the shallowing of the 520 appeared to be less affected by the addition of water; however, the weak, positive 520 peak also disappeared with increasing water content and an associated velocity reduction in the lower MTZ. Whilst no negative peaks were observed in the upper MTZ for cases without melt (intermediate water anomalies and/or cold geotherms), in the lower MTZ, weak but clearly negative conversions were produced just below the actual 520. This was due to the relatively sharp increase of water saturation, even in cases of a cold geotherm and intermediate water saturation.
As soon as the first melts were generated (see Figure 2 for an overview), Vp and Vs were extremely reduced and the Vp–Vs ratios increased, resulting in low-velocity “melt pockets” both in the upper and lower MTZ. These melt pockets were clearly visible in the RFs, marked by high-amplitude negative conversions at the top and high-amplitude positive conversions at the bottom of the area of partial melt (Figure 5, Figures S2, S4, and S6). In the case of the lower MTZ, the 660 appeared as a double-peak, the shallower one coinciding with the lower limit of the melt pocket and the deeper with the actual lower–upper mantle boundary.

3.3.3. Linear Distribution Models

The other set of models included a homogeneous water anomaly across the entire vertical column of the upper and/or lower MTZ, i.e., simulating the case in which the entire vertical MTZ-layers were saturated with the same amount of water (Figures S8–S13). The water content increased from zero at the left model bound to the maximum water content of 50% or 100% and the right model bound. In the linear model setup, it was possible to observe the impact of pressure versus temperature on melting more systematically. More melt was produced at shallower depths (lower pressure) than at greater depths (higher pressure) with the same water concentration, although the temperature was lower (Figures S8, S10, and S12). In this specific model setup, the distribution of melt appeared like an “inverted” (upward opening) triangle.
In contrast to the Gaussian models, the linear water distribution models preserve the seismic discontinuities exactly at the depth of the actual phase transitions, as these also form the boundaries between hydrated and non-hydrated layers. The signal of the 410 generally weakens due to the reduction of seismic velocities with increasing water contents. When only the lower MTZ carried water, we observed that the 520 amplitude decreased and could even become negative for high amounts of water, also for models without melt generation (Figures S12 and S13). This amplitude reversal was obviously amplified in the presence of melt (Figure S12). The 660 amplitude increased with increasing water content in the lower MTZ, but the difference was not extremely clear, even when melt was generated. When both the upper and lower MTZ had the same level of water saturation, we observed that the 520 discontinuity remained largely unchanged.
A wet upper MTZ exhibited a small negative conversion under the cold conditions (1250 °C geotherm), corresponding to a weak low-velocity zone. Intensive melting under higher temperatures (1350 °C and 1450 °C geotherms) in the upper MTZ resulted in a prompt and abrupt high-amplitude negative conversion at the 410, which was now at shallower depth, clearly visible in the RFs (Figures S8 and S10). Similarly, high water content in the lower MTZ at high temperatures causes an immediate and high-amplitude negative conversion at the 520, which now almost reached the same depth as the 410. However, we deemed models with 100% water saturation throughout the entire layers of the vertical MTZ column as rather unrealistic.

3.3.4. Velocity Pull-Down and Depth Conversion

We observed that, in cases with high water content and hot geotherms, both for upper and/or lower MTZ layers, the RF conversion appeared to be interfering with spurious negative conversions that did not seem to belong to any primary phase (Figures S8, S10, and S12). Conversions beneath a water/melt anomaly with reduced seismic velocities arrived later. This delay became particularly large when the melt was produced and Vp/Vs increased. For moderate low-velocity anomalies, the conversions arrived still within the shown delay time limit (80 s). For the more extreme (and perhaps less realistic) cases with melt in one of the entire MTZ rock columns (e.g., linear model, 1450 °C geotherm, 100% water saturation, Figure S8), the conversions arrived extremely late (up to 150 s compared to approximately 67 s for the dry case) and interacted with multiple conversions of MTZ discontinuities above the melt layers such as the 410. This theoretical situation is perhaps rather unlikely, as it requires fully water-saturated layers of the MTZ. However, the general problem remains that substantial water/melt and corresponding velocity anomalies may result in extremely delayed conversion times compared to the dry case. These large delay times also carry an opportunity for identifying water in the MTZ and hydrous melts, as the amount of water can be modelled in order to fit observed delay time anomalies in RFs if the data are good enough.
In this study, the RFs were perfectly depth-converted, as we know the exact velocity model, so that the true model depths are recovered. However, in reality, it requires an accurate a priori velocity model (Vp and Vs) from other sources to place the conversion at the right depth and place. At MTZ depths, the size of such melt pockets may be easily below resolution of common tomographic techniques which are usually used to perform depth conversions. The resulting, usually over hundreds of km, smoothed models used for depth conversions may therefore result in large depth errors.

4. Discussion

Our model did not include full thermodynamic calculations (Gibbs minimisation) and was therefore limited to the phase diagrams from the published literature. However, it predicted all main MTZ phase transitions (Figure 1) within 5 km from the reference depths at 410 km (olivine–wadsleyite), 520 km (wadsleyite–ringwoodite), and 660 km (ringwoodite–bridgmanite) at ambient mantle temperatures. This approach is simplistic, because it does not include zones where two mineral phases may coexist (e.g., olivine and wadsleyite). Experiments showed that phase transitions may occur over the intervals of 4–8 km [87] to 7–13 km [58], which is below the vertical seismic resolution at these depths (e.g., [7,88]). Transformations between olivine polymorphs are fast (tens of hours), so that metastability effects might be minor [89] and negligible for our simulations.
Seismic velocities computed with our code for dry conditions fit the reference Earth models (PREM [90] and ak135-F [91]) within 1%–3% and reproduce the most prominent features such as depths of the 410 and 660 discontinuities (Figure 1). We parameterised the shifts of phase transitions after [72], but we did not include water partitioning between liquid and solid phases nor between the two coexisting olivine polymorphs fields described in this paper. Therefore, our simple calculations tended to overestimate the depths shift of phase transitions in the wet systems.
We presented models of water and hydrous melt anomalies within the MTZ. Indeed, some seismological studies (RFs and precursors) did show signals indicative of low-velocity zones within the MTZ, usually in the lower MTZ (e.g., [37,92,93,94,95,96,97,98,99]). These anomalies can, in principle, be “reproduced” by our code when placing a water-melt anomaly of the right shape and amplitude at the observed depths.
The influence of melt is a challenging problem since its amount reaches 30% for 100% water saturation for a 1450 °C geotherm. That is close to the minimum values (30%–50% of liquid) of the rheological transition from brittle to viscous behaviour in crystal mushes [100,101]. Therefore, shear moduli and seismic velocities should be sufficiently reduced. The values that we obtained were generally consistent with the results developed by other studies using the Gassmann approach (e.g., [102]). However, our simulations did not include migration and accumulation of melts. This missing element is likely to be a significant factor altering chemical compositions and the thermal and velocity structure in and around the MTZ.
Some studies propose a zone of neutral buoyancy of peridotitic melt above the MTZ (e.g., [31,32]) and a number of MTZ-targeted RF and precursor surveys observe prominent low-velocity zones above the 410 boundary which might correspond to melt ponded at this depth (e.g., [5,33,35,98,99,103,104,105,106,107,108,109]).
The presence of water expands the stability regions of water-bearing phases such as wadsleyite in the upper mantle. If a relatively small and isolated water-bearing anomaly is located above the 410 discontinuity entirely surrounded by dry mantle pyrolite, a rock “enclave” or “lens” with wadsleyite-bearing lithology may form in the upper mantle. The developed algorithm predicts water-rich lenses well above the MTZ (Figure 6). Such lenses can maintain wadsleyite-bearing lithologies at depths as shallow as 350 km (in the most extreme case) and may contain melt depending on the actual mantle temperature (Supplementary Materials Figure S14). They result in very prominent low-velocity RF signatures. This case may therefore be relevant to the nature of ultra-low zones shown in aforementioned papers. The long-term stability and formation mechanisms of such lenses in nature are beyond the scope of this paper and require a detailed self-consistent thermodynamic modelling.
The vertical seismic resolution in the MTZ region is typically of several tens of kilometres, the horizontal resolution is of the order of hundreds of kilometres (Fresnel zone); hence, imaging below this scale is not possible. Nevertheless, water- and melt-anomalies may occur at a much smaller scale than assumed in this study which will consequently not be detectable by many seismological techniques. Instead, we assumed large-scale anomalies varying over large wavelengths. Water and melts will more likely distribute in heterogeneous small-scale systems and not homogeneously within a large area. For example, using full waveform scattering imaging, reference [99] showed that the MTZ beneath the US is characterised by a small-scale (<100 km horizontal) low-velocity heterogeneity that possibly represents bodies of subducted, hydrated harzburgite, either in the form of isolated blobs or small-scale density instabilities. The important issue is that these anomalies are too small to be detected by tomographic methods but require high-resolution imaging techniques such as the one proposed by the authors. In many teleseismic images of the MTZ region, these would appear simply as smoothed large-scale bodies with approximately average properties distributed within the target area.

5. Conclusions

We provide a practical and computationally fast tool to produce seismic models of water-bearing lithologies and hydrous melts in and around the MTZ that can be used to investigate the resulting RF images. Our setup with pyrolithic lithology without water exhibits phase transitions close to the well-known 410, 520, and 660 discontinuities. Water expands stability fields of the water-carrying lithologies by several tens of kilometres.
The model predicts melting in regions with high mantle potential temperature and sufficient amounts of water. Melt-bearing anomalies placed at the depths of observed low-velocity zones produce synthetic RF signatures similar to observations. According to our model, hydrous melting is a necessity to explain clear low-velocity zones observed RFs and precursors. The presence of water only, without the occurrence of melts, merely results in amplitude changes of the 410 or 520 discontinuities, but the corresponding velocity reduction is not enough to produce noticeable negative conversions.
This paper may provide a reference for understanding the origin and nature of hydrous anomalies and interpreting seismological images of the MTZ. However, our tool relies on extremely simple parameterisations and approximations, so a more complex and detailed framework is needed for seismological studies and solution of inversion problems.

Supplementary Materials

The following are available online at https://www.mdpi.com/2076-3263/9/12/505/s1, Figure S1: S1: 0% H2O Wadsleyite, 0% H2O Ringwoodite., Figure S2: 100% H2O Wadsleyite, 100% H2O Ringwoodite, “gaussian”, Figure S3: 50% H2O Wadsleyite, 50% H2O Ringwoodite, “gaussian”, Figure S4: 100% H2O Wadsleyite, 0% H2O Ringwoodite, “gaussian”, Figure S5: 50% H2O Wadsleyite, 0% H2O Ringwoodite, “gaussian”, Figure S6: 0% H2O Wadsleyite, 1000% H2O Ringwoodite, “gaussian”, Figure S7: 0% H2O Wadsleyite, 50% H2O Ringwoodite, “gaussian”, Figure S8: 100% H2O Wadsleyite, 100% H2O Ringwoodite, linear, Figure S9: 50% H2O Wadsleyite, 50% H2O Ringwoodite, linear, Figure S10: 100% H2O Wadsleyite, 0% H2O Ringwoodite, linear, Figure S11: 50% H2O Wadsleyite, 0% H2O Ringwoodite, linear, Figure S12: 0% H2O Wadsleyite, 100% H2O Ringwoodite, linear, Figure S13: 0% H2O Wadsleyite, 50% H2O Ringwoodite, linear, Figure S14: S14: Upper mantle “water lens” with maximum water-saturation of 100%.

Author Contributions

I.F. contributed more to the general framework of the developed script and its thermodynamic part, while C.S. worked mostly on its seismic part. The authors contributed nearly equally to the discussion of the results and writing of the paper.

Funding

This research received no external funding.

Acknowledgments

The authors thank three anonymous reviewers for useful and constructive comments. This paper was inspired by a student project performed during a PhD intensive course “Deep Earth Systems” at the Department of Geoscience, Aarhus University. Thanks to A. Saukko and P. Edwards for discussions during and after the course.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Litasov, K.D.; Ohtani, E. Effect of water on the phase relations in Earth’s mantle and deep water cycle. Geol. Soc. Am. Spec. Pap. 2007, 421, 115–156. [Google Scholar] [CrossRef]
  2. Andrews, J.; Deuss, A. Detailed nature of the 660km region of the mantle from global receiver function data. J. Geophys. Res. Solid Earth 2008, 113, B06304. [Google Scholar] [CrossRef]
  3. Lawrence, J.F.; Shearer, P.M. A global study of transition zone thickness using receiver functions. J. Geophys. Res. Solid Earth 2006, 111, B06307. [Google Scholar] [CrossRef] [Green Version]
  4. Stammler, K.; Kind, R.; Petersen, N.; Korsarev, G.; Vinnik, L.; Qiyuan, L. The upper mantle discontinuities: Correlated or anticorrelated? Geophys. Res. Lett. 1992, 15, 1563–1566. [Google Scholar] [CrossRef]
  5. Vinnik, L.; Kosarev, G.; Petersen, N. Mantle transition zone beneath Eurasia. Geophys. Res. Let. 1996, 23, 1485–1488. [Google Scholar] [CrossRef]
  6. Cottaar, S.; Deuss, A. Large-scale mantle discontinuity topography beneath Europe: Signature of akimotoite in subducting slabs. J. Geophys. Res. Solid Earth 2006, 121, 279–292. [Google Scholar] [CrossRef] [Green Version]
  7. Nagel, T.; Duesterhoeft, N.; Schiffer, C. Garnet-controlled very low velocities in the lower transition zone at sites of mantle upwelling. Terra Nova 2018, 30, 333–340. [Google Scholar] [CrossRef]
  8. Bell, D.R.; Rossman, G.R. Water in Earth’s mantle: The role of nominally anhydrous minerals. Science 1992, 255, 1391–1397. [Google Scholar] [CrossRef]
  9. Inoue, T.; Yurimoto, H.; Kudoh, Y. Hydrous modified spinel, Mg1.75SiH0.5O4: A new water reservoir in the mantle transition region. Geophys. Res. Lett. 1995, 22, 117–120. [Google Scholar] [CrossRef]
  10. Kohlstedt, D.L.; Keppler, K.; Rubie, D.C. Solubility of water in the α, β and γ phases of (Mg,Fe)2SiO4. Contrib. Mineral Petrol. 1996, 123, 345–357. [Google Scholar] [CrossRef]
  11. Bolfan-Casanova, N. Water in the Earth’s mantle. Mineral. Mag. 2005, 69, 229–257. [Google Scholar] [CrossRef]
  12. Thompson, A.B. Water in the Earth’s upper mantle. Nature 1992, 358, 295–302. [Google Scholar] [CrossRef]
  13. Richard, G.C.; Bercovici, D. Water-induced convection in the Earth’s mantle transition zone. J. Geophys. Res. Solid Earth 2009, 114, B01205. [Google Scholar] [CrossRef] [Green Version]
  14. Karato, S. Water distribution across the mantle transition zone and its implications for global material circulation. Earth Planet Sci. Lett. 2011, 301, 413–423. [Google Scholar] [CrossRef]
  15. Peslier, A.H.; Schönbächler, M.; Busemann, H.; Karato, S.-I. Water in the Earth’s Interior: Distribution and Origin. Space Sci. Rev. 2017, 21, 743–810. [Google Scholar] [CrossRef]
  16. Ohtani, E.; Litasov, K.; Hosoya, T.; Kubo, T.; Kondo, T. Water transport into the deep mantle and formation of a hydrous transition zone. Phys. Earth Planet Inter. 2004, 255–269. [Google Scholar] [CrossRef]
  17. Maruyama, S.; Okamoto, K. Water transportation from the subducting slab into the mantle transition zone. Gondwana. Res. 2007, 11, 148–165. [Google Scholar] [CrossRef]
  18. Pearson, D.G.; Brenker, F.E.; Nestola, F.; McNeill, J.; Nasdala, L.; Hutchison, M.T.; Matveev, S.; Mather, K.; Silversmit, G.; Schmitz, S.; et al. Hydrous mantle transition zone indicated by ringwoodite included within diamond. Nature 2014, 507, 221–224. [Google Scholar] [CrossRef]
  19. Huang, X.; Xu, Y.; Karato, S. Water content in the transition zone from electrical conductivity of wadsleyite and ringwoodite. Nature 2005, 434, 746–749. [Google Scholar] [CrossRef]
  20. Yoshino, T.; Nishi, M.; Matsuzakia, T.; Yamazaki, D.; Katsura, T. Electrical conductivity of majorite garnet and its implications for electrical structure in the mantle transition zone. Phys. Earth Planet Inter. 2008, 170, 193–200. [Google Scholar] [CrossRef]
  21. Zhu, H.; Bozdağ, E.; Duffy, T.S.; Tromp, J. Seismic attenuation beneath Europe and the North Atlantic: Implications for water in the mantle. Earth Planet Sci. Let. 2013, 381, 1–11. [Google Scholar] [CrossRef]
  22. Van der Meijde, M.; Marone, F.; Giardini, D.; van der Lee, S. Seismic evidence for water deep in Earth’s upper mantle. Science 2003, 300, 1556–1558. [Google Scholar] [CrossRef] [PubMed]
  23. Thio, V.; Cobden, L.; Trampert, J. Seismic signature of a hydrous mantle transition zone. Phys. Earth Planet Inter. 2016, 250, 46–63. [Google Scholar] [CrossRef] [Green Version]
  24. Fei, H.; Yamazaki, D.; Sakurai, M.; Miyajima, N.; Ohfuji, H.; Katsura, T.; Yamamoto, T. A nearly water-saturated mantle transition zone inferred from mineral viscosity. Sci. Adv. 2017, 3, e1603024. [Google Scholar] [CrossRef] [Green Version]
  25. Frost, D.J.; Dolejš, D. Experimental determination of the effect of H2O on the 410-km seismic discontinuity. Earth Planet Sci. Let. 2007, 256, 182–195. [Google Scholar] [CrossRef]
  26. Kawamoto, T. Hydrous phase stability and partial melt chemistry in H2O-saturated KLB-1 peridotite up to the uppermost lower mantle conditions. Phys. Earth Planet. Inter. 2004, 143, 387–395. [Google Scholar] [CrossRef]
  27. Sakuyama, T.; Tian, W.; Kimura, J.-I.; Fukao, Y.; Hirahara, Y.; Takahashi, T.; Senda, R.; Chang, Q.; Miyazaki, T.; Obayashi, M.; et al. Melting of dehydrated oceanic crust from the stagnant slab and of the hydrated mantle transition zone: Constraints from Cenozoic alkaline basalts in eastern China. Chem. Geol. 2013, 359, 32–48. [Google Scholar] [CrossRef]
  28. Wallace, P.J. Water and partial melting in mantle plumes: Inferences from the dissolved H2O concentrations of Hawaiian basaltic magmas. Geophys. Res. Let. 1998, 25, 3639–3642. [Google Scholar] [CrossRef]
  29. Watanabe, T. Effects of water and melt on seismic velocities and their application to characterization of seismic reflectors. Geophys. Res. Let. 1993, 20, 2933–2936. [Google Scholar] [CrossRef]
  30. Bercovici, D.; Karato, S. Whole-mantle convection and the transition-zone water filter. Nature 2003, 425, 39–44. [Google Scholar] [CrossRef]
  31. Sakamaki, T.; Ohtani, E.; Urakawa, S.; Suzuki, A.; Katayama, Y. Measurement of hydrous peridotite magma density at high pressure using the X-ray absorption method. Earth Planet Sci. Let. 2009, 287, 293–297. [Google Scholar] [CrossRef]
  32. Bajgain, S.; Ghosh, D.B.; Karki, B.B. Structure and density of basaltic melts at mantle conditions from first-principles simulations. Nat. Comm. 2015, 6, 8578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  33. Schaeffer, A.J.; Bostock, M.G. A low-velocity zone atop the transition zone in northwestern Canada. J. Geophys. Res. Solid Earth 2010, 115, B06302. [Google Scholar] [CrossRef] [Green Version]
  34. Schmandt, B.; Jacobsen, S.D.; Becker, T.W.; Liu, Z.; Dueker, K.G. Dehydration melting at the top of the lower mantle. Science 2014, 344, 1265–1268. [Google Scholar] [CrossRef] [PubMed]
  35. Vinnik, L.; Farra, V. Low S velocity atop the 410-km discontinuity and mantle plumes. Earth Planet Sci. Let. 2007, 262, 398–412. [Google Scholar] [CrossRef]
  36. Liu, Z.; Park, J.; Karato, S.-I. Seismological detection of low-velocity anomalies surrounding the mantle transition zone in Japan subduction zone. Geophys. Res. Let. 2016, 43, 2480–2487. [Google Scholar] [CrossRef] [Green Version]
  37. Thompson, D.A.; Hammond, J.O.S.; Kendall, J.-M.; Stuart, G.W.; Helffrich, G.R.; Keir, D.; Ayele, A.; Goitom, B. Hydrous upwelling across the mantle transition zone beneath the Afar Triple Junction. Geochem. Geophys. 2015, 16, 834–846. [Google Scholar] [CrossRef] [Green Version]
  38. Irifune, T.; Isshiki, M. Iron partitioning in a pyrolite mantle and the nature of the 410-km seismic discontinuity. Nature 1998, 392, 702–705. [Google Scholar] [CrossRef]
  39. Stixrude, L.; Lithgow-Bertelloni, C. Influence of phase transformations on lateral heterogeneity and dynamics in Earth’s mantle. Earth Planet Sci. Let. 2007, 263, 45–55. [Google Scholar] [CrossRef]
  40. Kaminsky, F. Mineralogy of the lower mantle: A review of super-deep mineral inclusions in diamond. Earth Sci. Rev. 2012, 110, 127–147. [Google Scholar] [CrossRef]
  41. Muir, J.M.; Brodholt, J.P. Ferrous iron partitioning in the lower mantle. Phys. Earth Planet Inter. 2016, 257, 12–17. [Google Scholar] [CrossRef] [Green Version]
  42. Mattern, E.; Matas, J.; Ricard, Y.; Bass, J. Lower mantle composition and temperature from mineral physics and thermodynamic modelling. Geophys. J. Int. 2005, 160, 973–990. [Google Scholar] [CrossRef]
  43. Stixrude, L.; Lithgow-Bertelloni, C. Thermodynamics of mantle minerals II. Phase equilibria. Geophys. J. Int. 2011, 184, 1180–1213. [Google Scholar] [CrossRef]
  44. Holland, T.J.B.; Hudson, N.F.C.; Powell, R.; Harte, B. New Thermodynamic models and calculated phase equilibria in ncfmas for basic and ultrabasic compositions through the transition zone into the uppermost lower mantle. J. Petrol. 2013, 54, 1901–1920. [Google Scholar] [CrossRef]
  45. Sakai, T.; Dekura, H.; Hirao, N. Experimental and theoretical thermal equations of state of MgSiO3 post-perovskite at multi-megabar pressures. Sci. Rep. 2016, 6, 22652. [Google Scholar] [CrossRef]
  46. Núñez-Valdez, M.; Wu, Z.; Yu, Y.G.; Wentzcovitch, R.M. Thermal elasticity of (FexMg(1-x))2SiO4 olivine and wadsleyite. Geophys. Res. Let. 2013, 40, 290–294. [Google Scholar] [CrossRef]
  47. Liu, X.; Xiong, Z.; Chang, L.; He, Q.; Wang, F.; Shieh, S.R.; Wu, C.; Li, B.; Zhang, L. Anhydrous ringwoodites in the mantle transition zone: Their bulk modulus, solid solution behavior, compositional variation, and sound velocity feature. Solid Earth Sci. 2016, 1, 28–47. [Google Scholar] [CrossRef] [Green Version]
  48. Erba, A.; Mahmoud, A.; Orlando, R.; Dovesi, R. Elastic properties of six silicate garnet end members from accurate ab initio simulations. Phys. Chem. Miner. 2014, 41, 151–160. [Google Scholar] [CrossRef]
  49. Wolf, A.S.; Jackson, J.M.; Dera, P.; Prakapenka, V.B. The thermal equation of state of (Mg, Fe)SiO3 bridgmanite (perovskite) and implications for lower mantle structures. J. Geophys. Res. Solid Earth 2015, 120, 7460–7489. [Google Scholar] [CrossRef] [Green Version]
  50. Watt, J.P.; Davies, G.F.; O’Connell, R.J. The elastic properties of composite materials. Rev. Geophys. 1976, 14, 541–563. [Google Scholar] [CrossRef]
  51. Mao, Z.; Fan, D.; Lin, J.; Yang, J.; Tkachev, S.N.; Zhuravlev, K.; Prakapenka, V.B. Elasticity of single-crystal olivine at high pressures and temperatures. Earth Planet Sci. Let. 2015, 426, 204–215. [Google Scholar] [CrossRef] [Green Version]
  52. Mayama, N.; Suzuki, I.; Saito, T.; Ohno, I.; Katsura, T.; Yoneda, A. Temperature dependence of elastic moduli of β-(Mg,Fe)2SiO4. Geophys. Res. Let. 2004, 31, L04612. [Google Scholar] [CrossRef] [Green Version]
  53. Isaak, D.G.; Gwanmesia, G.D.; Falde, D.; Davis, M.G.; Triplett, R.S.; Wang, L. The elastic properties of β-Mg2SiO4 from 295 to 660 K and implications on the composition of Earth’s upper mantle. Phys. Earth Planet Inter. 2007, 162, 22–31. [Google Scholar] [CrossRef]
  54. Mayama, N.; Suzuki, I.; Saito, T.; Ohno, I.; Katsura, T.; Yoneda, A. Temperature dependence of the elastic moduli of ringwoodite. Phys. Earth Planet Inter. 2005, 148, 353–359. [Google Scholar] [CrossRef]
  55. Bina, C.R.; Helffrich, G.R. Calculation of elastic properties from thermodynamic equation of state principles. Ann. Rev. Earth Planet Sci. 1992, 20, 527–552. [Google Scholar] [CrossRef]
  56. Vacher, P.; Mocquet, A.; Sotin, C. Computation of seismic profiles from mineral physics: the importance of the non-olivine components for explaining the 660 km depth discontinuity. Phys. Earth Planet. Inter. 1998, 106, 275–298. [Google Scholar] [CrossRef]
  57. Katsura, T.; Shatskiy, A.; Geeth, M.A.; Manthilake, M.; Zhai, S.; Fukui, H.; Yamazaki, D.; Matsuzaki, T.; Yoneda, A.; Ito, E.; et al. Thermal expansion of forsterite at high pressures determined by in situ X-ray diffraction: The adiabatic geotherm in the upper mantle. Phys. Earth Planet. Inter. 2009, 174, 86–92. [Google Scholar] [CrossRef]
  58. Katsura, T.; Yamada, H.; Nishikawa, O.; Song, M.; Kubo, A.; Shinmei, T.; Yokoshi, S.; Aizawa, Y.; Yoshino, T.; Walter, M.J.; et al. Olivine-wadsleyite transition in the system (Mg,Fe)2SiO4. J. Geophys. Res. Solid Earth 2004, 109, B02209. [Google Scholar] [CrossRef]
  59. Chopelas, A.; Boehler, R. Thermal expansivity in the lower mantle. Geophys Res. Let 1992, 19, 1983–1986. [Google Scholar] [CrossRef]
  60. Knittle, E.; Jeanloz, R.; Smith, G.L. Thermal expansion of silicate perovskite and stratification of the Earth’s mantle. Nature 1986, 319, 214–216. [Google Scholar] [CrossRef]
  61. Afonso, J.C.; Ranalli, G.; Fernandez, M. Thermal expansivity and elastic properties of the lithospheric mantle: results from mineral physics of composites. Phys. Earth Planet. Inter. 2005, 149, 279–306. [Google Scholar] [CrossRef]
  62. Katsura, T.; Yoneda, A.; Yamazaki, D.; Yoshino, T.; Ito, E. Adiabatic temperature profile in the mantle. Phys. Earth Planet. Inter. 2010, 183, 212–218. [Google Scholar] [CrossRef]
  63. Stacey, F.D.; Davis, P.M. Physics of the Earth, 4th ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 348–360. [Google Scholar] [CrossRef]
  64. Jacobsen, S. Effect of water on the equation of state of nominally anhydrous minerals. Rev. Mineral. Geochem. 2009, 62, 321–342. [Google Scholar] [CrossRef]
  65. Wood, B.J.; Corgne, A. Mineralogy of the Earth: Trace Elements and Hydrogen in the Earth’s Transition Zone and Lower Mantle. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 61–84. [Google Scholar] [CrossRef]
  66. Liu, W.; Tian, L.; Zhao, J.; Liu, H.; Liu, L.; Du, J. Water effect on high-pressure elasticity of olivine, wadsleyite and ringwoodite in Mg2SiO4 by first-principles. Int J. Mod. Phys. B 2012, 26, 1250106. [Google Scholar] [CrossRef]
  67. Mao, Z.; Li, X.Y. Effect of hydration on the elasticity of mantle minerals and its geophysical implications. Sci. China Earth Sci. 2016, 59, 873–888. [Google Scholar] [CrossRef]
  68. Cammarano, F.; Goes, S.; Vacher, P.; Giardini, D. Inferring upper-mantle temperatures from seismic velocities. Phys. Earth Planet. Inter. 2003, 138, 197–222. [Google Scholar] [CrossRef]
  69. Green, D.H.; Falloon, T.J. Primary magmas at mid-ocean ridges, hotspots, and other intraplate settings: Constraints on mantle potential temperature. Geol. Soc. Am. Spec. Pap. 2005, 388, 217–247. [Google Scholar] [CrossRef]
  70. Herzberg, C.; Asimow, P.D.; Arndt, N.; Niu, Y.; Lesher, C.M.; Fitton, J.G.; Cheadle, M.J.; Saunders, A.D. Temperatures in ambient mantle and plumes: Constraints from basalts, picrites, and komatiites. Geochem. Geophys. 2007, 8, Q02006. [Google Scholar] [CrossRef]
  71. Herzberg, C. Basalts as temperature probes of Earth’s mantle. Geology 2011, 39, 1179–1180. [Google Scholar] [CrossRef] [Green Version]
  72. Fei, Y.; Bertka, C.M. Phase transitions in the Earth’s mantle and mantle mineralogy. In Mantle Petrology: Field Observations and High-Pressure Experimentation: A Tribute to F. R. Boyd; Fei, Y., Bertka, C.M., Mysen, B.O., Eds.; Geochemical Society: Washington, DC, USA, 1999; pp. 189–208. [Google Scholar]
  73. Mrosko, M.; Koch-Müller, M.; McCammon, C.; Rhede, D.; Smyth, J.R.; Wirth, R. Water, iron, redox environment: effects on the wadsleyite-ringwoodite phase transition. Contrib. Mineral. Petrol. 2015, 170, 9. [Google Scholar] [CrossRef]
  74. Hirschmann, M.M. Mantle solidus: Experimental constraints and the effects of peridotite composition. Geochem. Geophys. 2000, 1, 2000GC000070. [Google Scholar] [CrossRef]
  75. Saxena, N. Exact results for generalized Biot–Gassmann equations for rocks that change in pore shape and grain geometry. Geophys. J. Int. 2015, 203, 1575–1586. [Google Scholar] [CrossRef]
  76. Kováčik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci Lett 2001, 20, 1953–1955. [Google Scholar] [CrossRef]
  77. Cammarano, F.; Romanowicz, B. Radial profiles of seismic attenuation in the upper mantle based on physical models. Geophys. J. Int. 2008, 175, 116–134. [Google Scholar] [CrossRef] [Green Version]
  78. Artemieva, I.M.; Billien, M.; Leveque, J.-J.; Mooney, W.D. Shear wave velocity, seismic attenuation, and thermal structure of the continental upper mantle. Geophys. J. Int. 2004, 157, 607–628. [Google Scholar] [CrossRef] [Green Version]
  79. Chantel, J.; Manthilake, G.; Andrault, D.; Novella, D.; Yu, T.; Wang, Y. Experimental evidence supports mantle partial melting in the asthenosphere. Sci. Adv. 2016, 2, e1600246. [Google Scholar] [CrossRef] [Green Version]
  80. Langston, C.A. Structure under Mount Rainier, Washington, inferred from teleseismic body waves. J. Geophys. Res. 1979, 84, 4749–4762. [Google Scholar] [CrossRef] [Green Version]
  81. Vinnik, L.P. Detection of waves converted from P to SV in the mantle. Phys. Earth Planet. Inter. 1977, 15, 39–45. [Google Scholar] [CrossRef]
  82. Ammon, C.J. The isolation of receiver effects from teleseismic P waveforms. Bull. Seism. Soc. Am. 1991, 81, 2504–2510. [Google Scholar]
  83. Kind, R.; Kosarev, G.L.; Petersen, N.V. Receiver functions at the stations of the German Regional Seismic Network (GRSN). Geophys. J. Int. 1995, 121, 191–202. [Google Scholar] [CrossRef] [Green Version]
  84. Zhu, L.; Kanamori, H. Moho depth variation in southern California from teleseismic receiver functions. J. Geophys. Res. 2000, 105, 2969–2980. [Google Scholar] [CrossRef] [Green Version]
  85. Kennett, B.L.N. Seismic Wave Propagation in Stratified Media; Cambridge University Press: Cambridge, UK, 1983; p. 342. [Google Scholar]
  86. Clayton, R.W.; Wiggins, R.A. Source shape estimation and deconvolution of teleseismic bodywaves. Geophys J. Royal Astron. Soc. 1976, 47, 151–177. [Google Scholar] [CrossRef] [Green Version]
  87. Stixrude, L. Structure and sharpness of phase transitions and mantle discontinuities. J. Geophys Res. Solid Earth 1997, 102, 14835–14852. [Google Scholar] [CrossRef]
  88. Tauzin, B.; Ricard, Y. Seismically deduced thermodynamics phase diagrams for the mantle transition zone. Earth Planet. Sci. Let. 2014, 401, 337–346. [Google Scholar] [CrossRef]
  89. Kerschhofer, L.; Dupas, C.; Liu, M.; Sharp, T.G.; Durham, W.B.; Rubie, D.C. Polymorphic transformations between olivine, wadsleyite and ringwoodite: mechanisms of intracrystalline nucleation and the role of elastic strain. Mineral. Mag. 1998, 62, 617–638. [Google Scholar] [CrossRef]
  90. Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
  91. Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the earth from travel times. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
  92. Vinnik, L.; Farra, V. S velocity reversal in the mantle transition zone. Geophys. Res. Let. 2006, 33, L18316. [Google Scholar] [CrossRef] [Green Version]
  93. Vinnik, L.P.; Foulger, G.R.; Du, Z. Seismic boundaries in the mantle beneath Iceland: a new constraint on temperature. Geophys. J. Int. 2005, 160, 533–538. [Google Scholar] [CrossRef] [Green Version]
  94. Blum, J.; Shen, Y. Thermal, hydrous, and mechanical states of the mantle transition zone beneath southern Africa. Earth Planet Sci. Let. 2004, 217, 367–378. [Google Scholar] [CrossRef]
  95. Shen, X.; Yuan, X.; Li, X. A ubiquitous low-velocity layer at the base of the mantle transition zone. Geophys. Res. Let. 2014, 41, 836–842. [Google Scholar] [CrossRef] [Green Version]
  96. Eagar, K.C.; Fouch, M.J.; James, D.E. Receiver function imaging of upper mantle complexity beneath the Pacific Northwest, United States. Earth Planet. Sci. Let. 2010, 297, 141–153. [Google Scholar] [CrossRef]
  97. Bonatto, L.; Schimmel, M.; Gallart, J.; Morales, J. Studying the 410-km and 660-km discontinuities beneath Spain and Morocco through detection of P-to-S conversions. Geophys J. Int. 2013, 194, 920–935. [Google Scholar] [CrossRef] [Green Version]
  98. Zhang, Z.; Dueker, K.G.; Huang, H.-H. Ps mantle transition zone imaging beneath the Colorado Rocky Mountains: Evidence for an upwelling hydrous mantle. Earth Planet. Sci. Let. 2018, 492, 197–205. [Google Scholar] [CrossRef]
  99. Wang, Y.; Pavlis, G.L.; Li, M. Heterogeneous distribution of water in the mantle transition zone inferred from wavefield imaging. Earth Planet. Sci. Let. 2019, 505, 42–50. [Google Scholar] [CrossRef]
  100. Vigneresse, J.L.; Barbey, P.; Cuney, M. Rheological Transitions during partial melting and crystallization with application to felsic magma segregation and transfer. J. Petrol. 1996, 37, 1579–1600. [Google Scholar] [CrossRef]
  101. Petford, N. Rheology of granitic magmas during ascent and emplacement. Ann. Rev. Earth Planet. Sci. 2003, 31, 399–427. [Google Scholar] [CrossRef] [Green Version]
  102. Russell, B. A Gassmann-consistent rock physics template. CSEG Recorder 2013, 38, 22–30. [Google Scholar]
  103. Revenaugh, J.; Sipkin, S.A. Seismic evidence for silicate melt atop the 410-km mantle discontinuity. Nature 1994, 369, 474–476. [Google Scholar] [CrossRef]
  104. Fee, D.; Dueker, K. Mantle transition zone topography and structure beneath the Yellowstone hotspot. Geophys Res. Let. 2004, 31, L18603. [Google Scholar] [CrossRef] [Green Version]
  105. Song, T.R.A.; Helmberger, D.V.; Grand, S.P. Low-velocity zone atop the 410-km seismic discontinuity in the northwestern United States. Nature 2004, 427, 530–533. [Google Scholar] [CrossRef] [PubMed]
  106. Jasbinsek, J.; Dueker, K. Ubiquitous low-velocity layer atop the 410-km discontinuity in the northern Rocky Mountains. Geochem. Geophys. 2007, 8, Q10004. [Google Scholar] [CrossRef] [Green Version]
  107. Courtier, A.M.; Revenaugh, J. Deep upper-mantle melting beneath the Tasman and Coral Seas detected with multiple ScS reverberations. Earth Planet. Sci. Let. 2007, 259, 66–76. [Google Scholar] [CrossRef]
  108. Schmandt, B.; Dueker, K.G.; Hansen, S.M.; Jasbinsek, J.J.; Zhang, Z. A sporadic low-velocity layer atop the western US mantle transition zone and short-wavelength variations in transition zone discontinuities. Geochem. Geophys. 2011, 12, Q08014. [Google Scholar] [CrossRef] [Green Version]
  109. Tauzin, B.; Debayle, E.; Wittlinger, G. Seismic evidence for a global low-velocity layer within the Earth’s upper mantle. Nat. Geosci. 2010, 3, 718–721. [Google Scholar] [CrossRef]
Geosciences 09 00505 g001 550
Figure 1. 1D geotherms (red) and density/velocity depth models (all blue) for the reference model (no water content) for the three potential temperatures (1250 °C, 1350 °C, 1450 °C) in comparison to global reference models AK135 (black, dotted), IASP91 (magenta, dashed), and PREM (green, dashed).
Figure 1. 1D geotherms (red) and density/velocity depth models (all blue) for the reference model (no water content) for the three potential temperatures (1250 °C, 1350 °C, 1450 °C) in comparison to global reference models AK135 (black, dotted), IASP91 (magenta, dashed), and PREM (green, dashed).
Geosciences 09 00505 g001
Geosciences 09 00505 g002 550
Figure 2. The effect of water and temperature on the melt fraction (%) (a,e), relative S-wave velocity change (b,f), relative P-wave velocity change (c,g), and relative Vp/Vs ratio change (d,h) for wadsleyite (a–d) and ringwoodite (e–h). The relative changes in Vp, Vs, and Vp/Vs display the difference between the maximum and minimum value, normalised by the maximum ((Vmax − Vmin)/Vmax). A constant, low-gradient linear increase of this relative change was observed where no melt is present, which seems almost temperature independent. After the appearance of the first melt, the gradients increased significantly, while the gradients were still similar relative to the onset of melting.
Figure 2. The effect of water and temperature on the melt fraction (%) (a,e), relative S-wave velocity change (b,f), relative P-wave velocity change (c,g), and relative Vp/Vs ratio change (d,h) for wadsleyite (a–d) and ringwoodite (e–h). The relative changes in Vp, Vs, and Vp/Vs display the difference between the maximum and minimum value, normalised by the maximum ((Vmax − Vmin)/Vmax). A constant, low-gradient linear increase of this relative change was observed where no melt is present, which seems almost temperature independent. After the appearance of the first melt, the gradients increased significantly, while the gradients were still similar relative to the onset of melting.
Geosciences 09 00505 g002
Geosciences 09 00505 g003 550
Figure 3. 1D geotherms (red) and density–velocity models (all blue) cutting through a Gaussian anomaly model (water-saturated case) for the three potential temperatures (1250 °C, 1350 °C, 1450 °C) in comparison to global reference models AK135 (black, dotted), IASP91 (magenta, dashed), and PREM (green, dashed).
Figure 3. 1D geotherms (red) and density–velocity models (all blue) cutting through a Gaussian anomaly model (water-saturated case) for the three potential temperatures (1250 °C, 1350 °C, 1450 °C) in comparison to global reference models AK135 (black, dotted), IASP91 (magenta, dashed), and PREM (green, dashed).
Geosciences 09 00505 g003
Geosciences 09 00505 g004 550
Figure 4. Model domains for three different mantle potential temperatures (Tp = 1250 °C, 1350 °C, and 1450 °C). Each panel shows the potential pressure, density, temperature, Vp/Vs ratios, melt fraction, and water content of the model.
Figure 4. Model domains for three different mantle potential temperatures (Tp = 1250 °C, 1350 °C, and 1450 °C). Each panel shows the potential pressure, density, temperature, Vp/Vs ratios, melt fraction, and water content of the model.
Geosciences 09 00505 g004
Geosciences 09 00505 g005 550
Figure 5. Model domains for three different temperatures (Tp = 1250 °C, 1350 °C, and 1450 °C) and synthetic receiver function results. Each panel shows the densities, water content, Vp and Vs, and receiver functions for the respective 1D column in the delay time and depth. Red contours represent 5% steps of melt fraction (the outer one represents 5% and inward increasing). A comparison between delay time and depth-converted receiver functions illustrates the velocity pulldown caused by the low-velocity zone leading to very long delay times of discontinuities below a pronounced low-velocity zone.
Figure 5. Model domains for three different temperatures (Tp = 1250 °C, 1350 °C, and 1450 °C) and synthetic receiver function results. Each panel shows the densities, water content, Vp and Vs, and receiver functions for the respective 1D column in the delay time and depth. Red contours represent 5% steps of melt fraction (the outer one represents 5% and inward increasing). A comparison between delay time and depth-converted receiver functions illustrates the velocity pulldown caused by the low-velocity zone leading to very long delay times of discontinuities below a pronounced low-velocity zone.
Geosciences 09 00505 g005
Geosciences 09 00505 g006 550
Figure 6. Same as in Figure 5 for a model setup with an isolated water lens in the lowermost asthenospheric upper mantle. High water content allows wadsleyite-bearing lithology to form instead of olivine and also promotes melting. The area of melting is shifted to the top of the lens due to the lithostatic pressure gradient within the lens. Such types of structures cause drastic changes in RF patterns.
Figure 6. Same as in Figure 5 for a model setup with an isolated water lens in the lowermost asthenospheric upper mantle. High water content allows wadsleyite-bearing lithology to form instead of olivine and also promotes melting. The area of melting is shifted to the top of the lens due to the lithostatic pressure gradient within the lens. Such types of structures cause drastic changes in RF patterns.
Geosciences 09 00505 g006
Table
Table 1. First-principle ab initio [66] and a comprehensive summary of experimental [67] estimates of the influence of water content (per wt.%) on the elastic moduli. CFe = Fe/(Fe + Mg) in mol.%.
Table 1. First-principle ab initio [66] and a comprehensive summary of experimental [67] estimates of the influence of water content (per wt.%) on the elastic moduli. CFe = Fe/(Fe + Mg) in mol.%.
MethodComputationExperiments
PhaseOlvWadRinOlvWadRin
KS0−6.1−8.4−8.5−3.8–0.4CFe−12.4–0.5CFe−11.8
G−3.7−6.0−7.4−2.2–0.52CFe−9.7–0.5CFe−5.6–0.9CFe

Share and Cite

MDPI and ACS Style

Fomin, I.; Schiffer, C. Water, Hydrous Melting, and Teleseismic Signature of the Mantle Transition Zone. Geosciences 2019, 9, 505. https://doi.org/10.3390/geosciences9120505

AMA Style

Fomin I, Schiffer C. Water, Hydrous Melting, and Teleseismic Signature of the Mantle Transition Zone. Geosciences. 2019; 9(12):505. https://doi.org/10.3390/geosciences9120505

Chicago/Turabian Style

Fomin, Ilya, and Christian Schiffer. 2019. "Water, Hydrous Melting, and Teleseismic Signature of the Mantle Transition Zone" Geosciences 9, no. 12: 505. https://doi.org/10.3390/geosciences9120505

APA Style

Fomin, I., & Schiffer, C. (2019). Water, Hydrous Melting, and Teleseismic Signature of the Mantle Transition Zone. Geosciences, 9(12), 505. https://doi.org/10.3390/geosciences9120505

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop