An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design
Abstract
1. Introduction
2. Current Practices in Rock Engineering Design
2.1. Empirical Design
2.1.1. Empirical Support Recommendation—Rock Mass Rating
- Strength of intact rock
- Rock Quality Designation (RQD) [11]
- Spacing of joints
- Condition of joints
- Groundwater conditions
2.1.2. Empirical Support Recommendation—Q Tunnelling Index
- RQD = Rock Quality Designation [11]
- Jn = Number of joint/fracture sets
- Jr = Roughness of most unfavourable joints
- Ja = Alteration or infilling of joints
- Jw = Water inflow
- SRF = Stress reduction factor, quantifies stress conditions
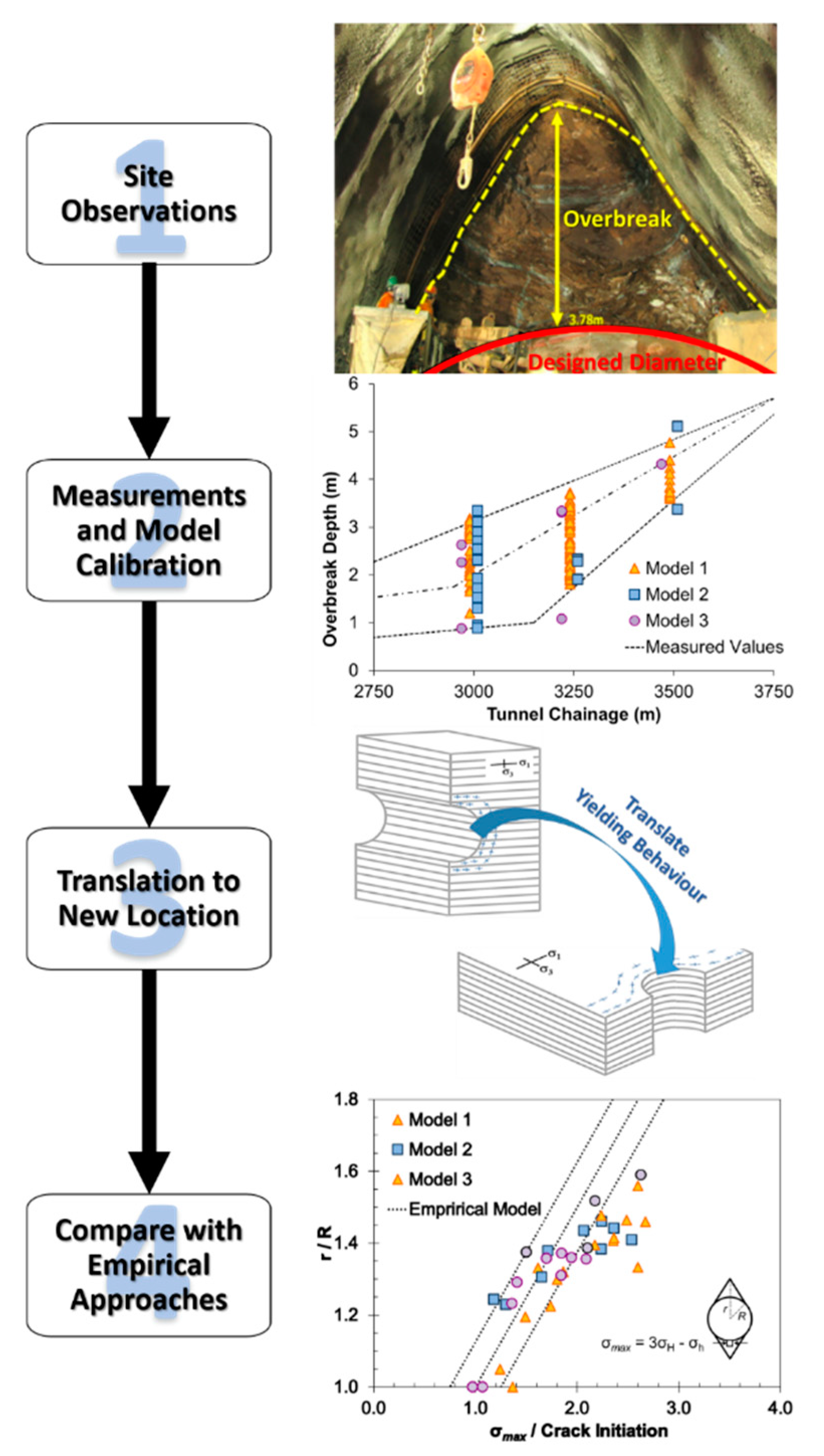
2.2. Numerical Methods
- Site observations
- Measurements and model calibration
- Conceptual translation of the calibrated behaviour to the new site location
- Comparison with empirical approaches [14] to validate the new design.
- Continuum methods—finite element modelling (FEM), finite difference modelling (FDM), boundary element modelling (BEM).
- Discrete methods—discrete element modelling (DEM), discrete fracture network (DFN) modelling.
- Hybrid continuum/discrete methods.
2.2.1. Continuum Methods
2.2.2. Discrete Methods
2.2.3. Hybrid Continuum/Discrete Methods
2.3. Discussion of Current Practices
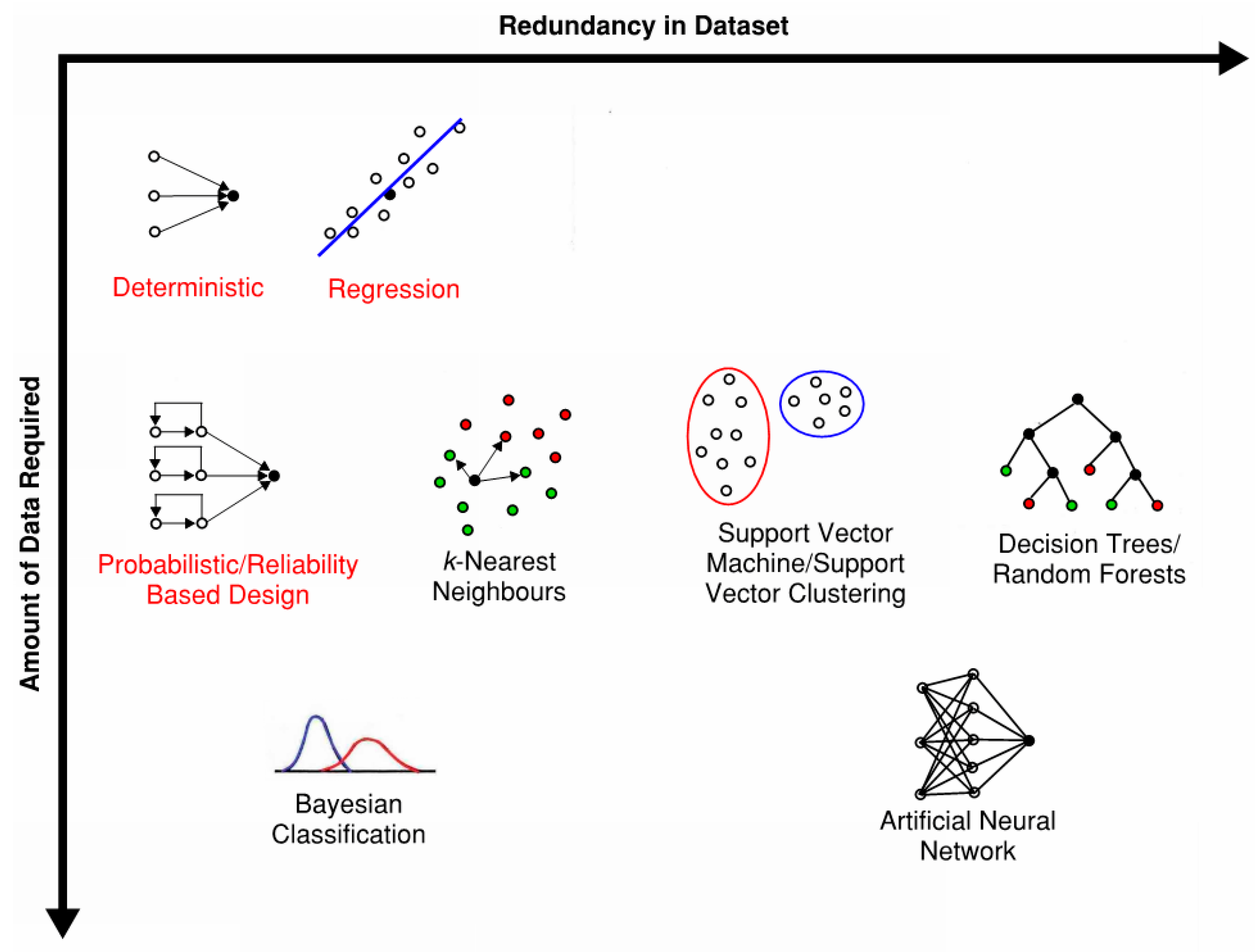
3. Review of Machine Learning Algorithms
- Supervised learning: data is labelled, i.e., the training samples contain inputs with a corresponding output
- Unsupervised learning: data is unlabeled, i.e., the training samples do not have an associated output
- Semi-supervised learning: a mixture of labelled and unlabeled data
- Reinforcement learning: no data; the algorithm maps situations to actions to maximize a reward [59]
3.1. Categorical Prediction Models
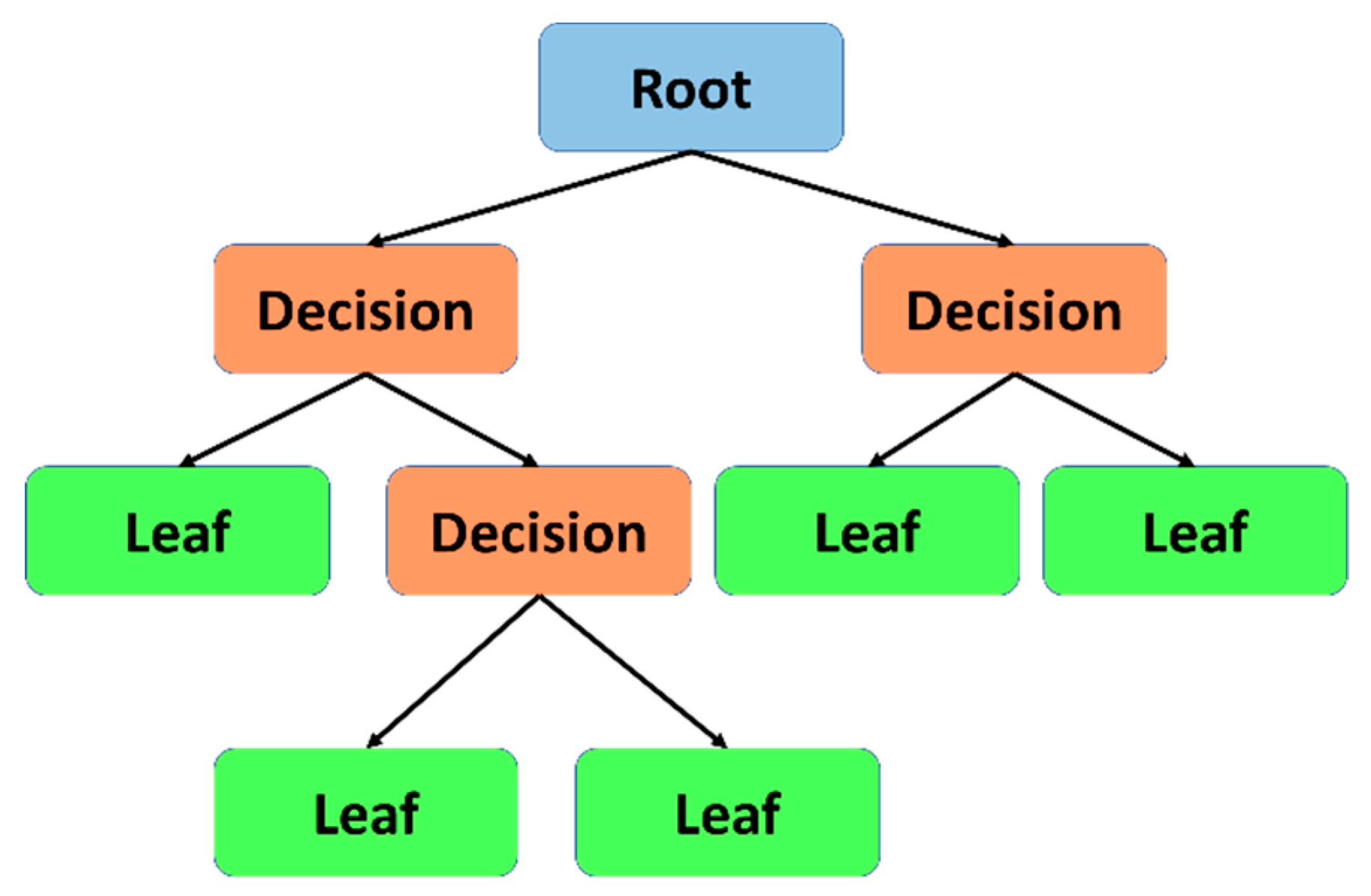
3.1.1. Decision Trees
3.1.2. Naïve Bayesian Classification
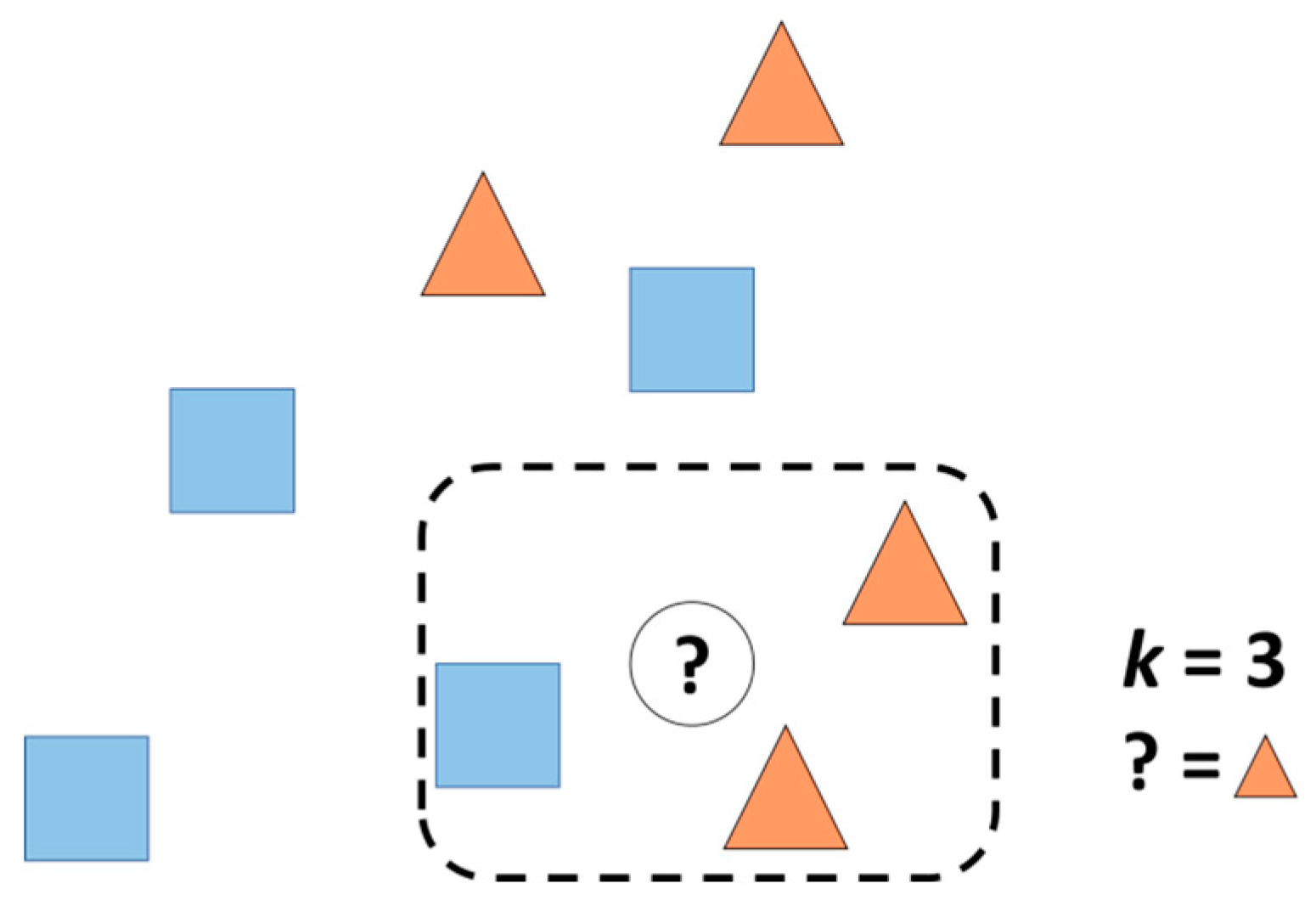
3.1.3. k-Nearest Neighbours Classification
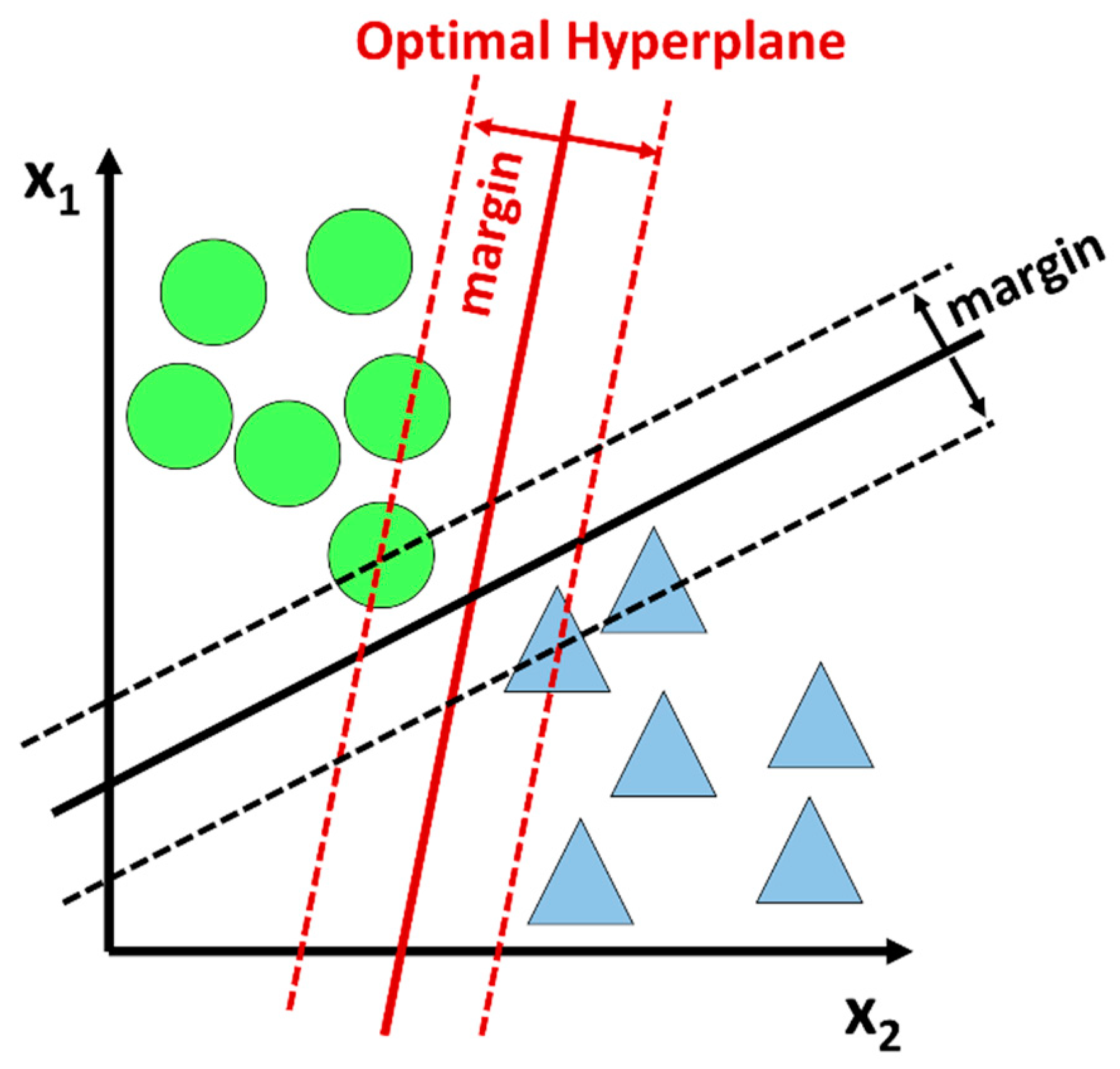
3.1.4. Support Vector Machine
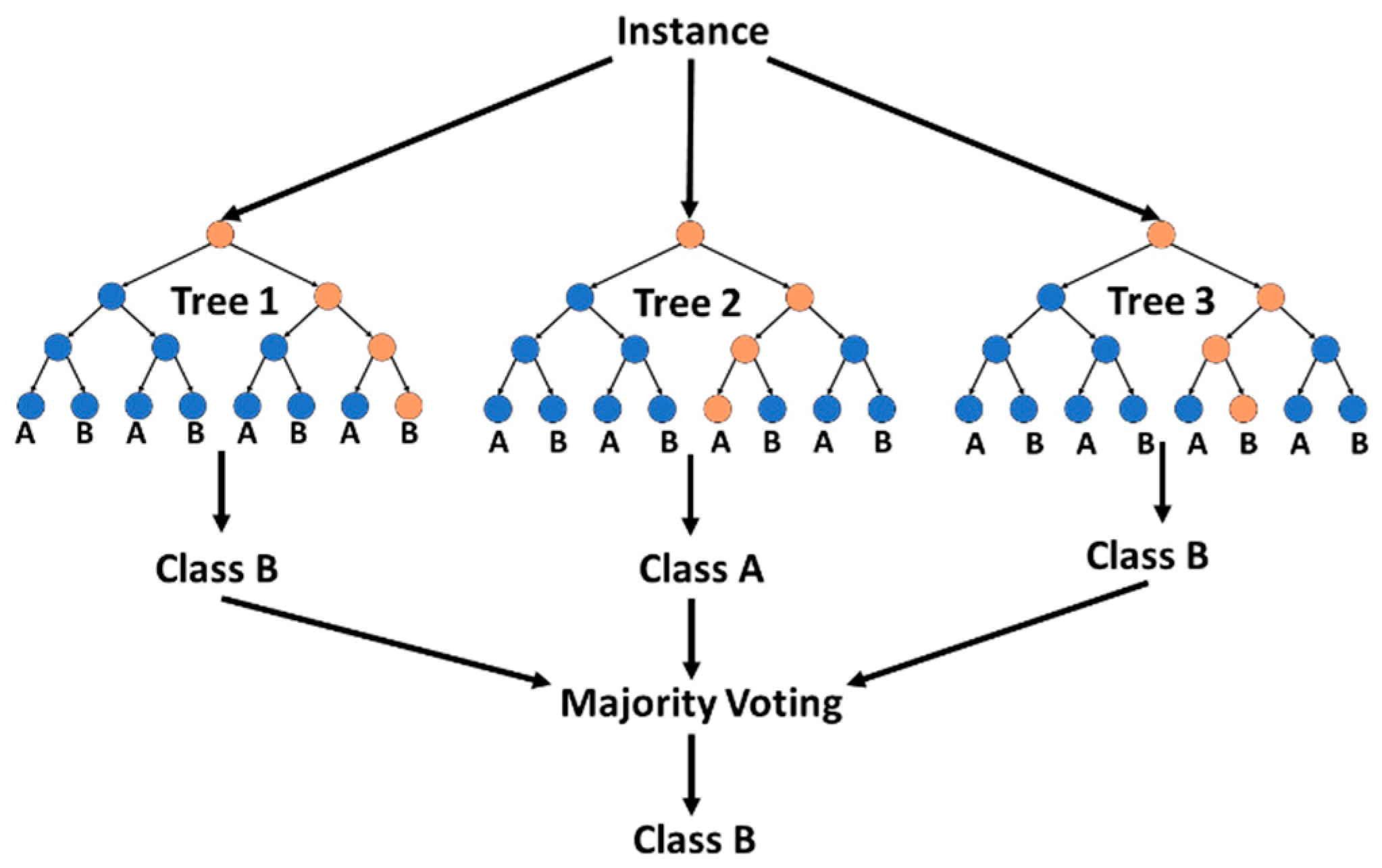
3.1.5. Random Forests
3.2. Numerical Prediction Models
3.2.1. Support Vector Clustering
3.2.2. k-Nearest Neighbours Regression
3.2.3. Artificial Neural Networks
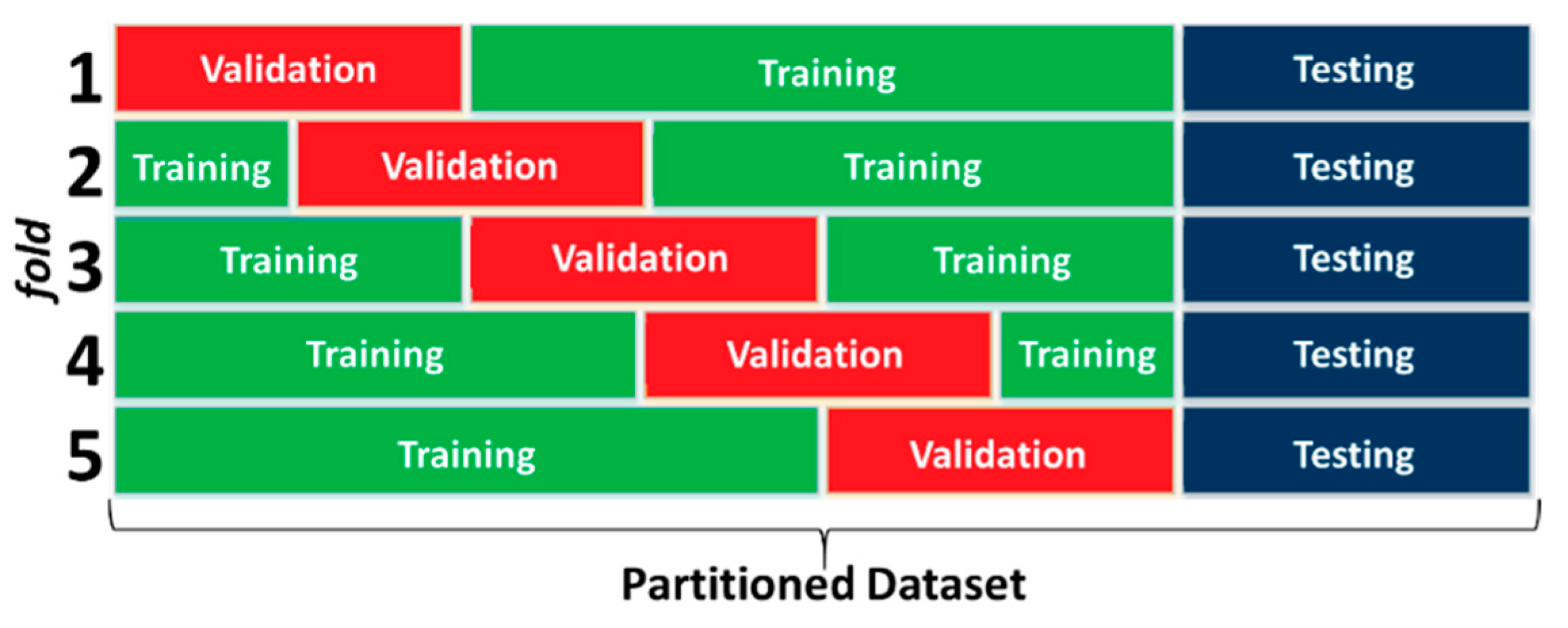
4. Discussion of Machine Learning for Rock Engineering Design
- Random data division
- Data division ensuring statistical consistency within subsets
- Data division using self-organising maps
- Data division using fuzzy logic methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoek, E. Rock Mechanics-an Introduction for the Practical Engineer. Min. Mag. 1966, 1–67. [Google Scholar]
- Mitchell, T.M. Chapter 1: What Is Machine Learning? In Machine Learning: Hands-on for Developers and Technical Professionals; John Wiley & Sons, Inc.: Indianapolis, IN, USA, 2015. [Google Scholar]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.W.; Mount, N.J.; See, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two Decades of Anarchy? Emerging Themes and Outstanding Challenges for Neural Network River Forecasting. Prog. Phys. Geogr. 2012. [Google Scholar] [CrossRef]
- PDAC. Concepts and Application of Machine Learning to Mining Geoscience: A Practical Course; PDAC: Toronto, ON, Canada, 2019. [Google Scholar]
- Karpatne, A.; Atluri, G.; Faghmous, J.; Steinback, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theroy-Guided Data Science: A New Paradigm for Scientific Discovery from Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Mcgaughey, W.J.; Geoscience, M. Data-Driven Geotechnical Hazard Assessment: Practice and Pitfalls. In Proceedings of the First International Conference on Mining Geomechanical Risk, Perth, Western Australia, 9–11 April 2019; pp. 219–232. [Google Scholar]
- LimiteStateInc. Eucocode 7 Design Approach 1: Basic Procedure. Available online: http://www.limitstate.com/geo/eurocode7 (accessed on 7 October 2019).
- Bieniawski, Z.T. Classification of Rock Masses for Engineering: The RMR System and Future Trends. In Chapter 22 in Comprehensive Rock Engineering; Elsevier: Amsterdam, The Netherlands, 1993; pp. 553–573. [Google Scholar]
- Barton, N.R.; Lien, R.; Lunde, J. Engineering Classification of Rock Masses for the Design of Tunnel Support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Barton, N.R.; Bieniawski, Z.T. RMR and Q-Setting Records Straight; Tunnels & Tunnelling International; Progressive Media Markets Ltd.: London, UK, 2008; pp. 26–29. [Google Scholar]
- Deere, D.U. Technical Description of Rock Cores for Engineering Purposes. Rock Mech. Eng. Geol. 1963, 1, 16–22. [Google Scholar]
- Jing, L.; Hudson, J.A. Numerical Methods in Rock Mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Perras, M.A.; Wannenmacher, H.; Diederichs, M.S. Underground Excavation Behaviour of the Queenston Formation: Tunnel Back Analysis for Application to Shaft Damage Dimension Prediction. Rock Mech. Rock Eng. 2015. [Google Scholar] [CrossRef]
- Diederichs, M.S. The 2003 Canadian Geotechnical Colloquium: Mechanistic Interpretation and Practical Application of Damage and Spalling Prediction Criteria for Deep Tunnelling. Can. Geotech. J. 2007, 44, 1082–1116. [Google Scholar] [CrossRef]
- Perras, M.; Diederichs, M.S. Predicting Excavation Damage Zone Depths in Brittle Rocks. J. Rock Mech. Geotech. Eng. 2016, 8, 60–74. [Google Scholar] [CrossRef]
- Perras, M. Tunnelling in Horizontally Laminated Ground: The Influence of Lamination Thickness on Anisotropic Behaviour and Practical Observations from the Niagara Tunnel Project. Master’s Thesis, Queen’s University, Kingston, ON, Canada, 2009. [Google Scholar]
- ITASCA Consulting Group Inc. FLAC 8 Basics, 1st ed.; ITASCA Consulting Group Inc.: Minneapolis, MN, USA, 2015. [Google Scholar]
- NWMO. Geosynthesis, Technical Report DGR-TR-2011-11; NWMO: Toronto, ON, Canada, 2011. [Google Scholar]
- Jing, L.; Stephansson, O. Constitutive Models of Rock Fractures and Rock Masses-the Basics. In Developments in Geotechnical Engineering; Elsevier B. V.: Amsterdam, The Netherlands, 2007; Volume 85, pp. 47–109. [Google Scholar] [CrossRef]
- Garza-Cruz, T.; Pierce, M.; Kaiser, P.K. Use of 3DEC to Study Spalling and Deformation Associated with Tunnneling at Depth. In Deep Mining 2014, Proceedings of the 7th International Conference on Deep and High Stress Mining, Sudbury, ON, Canada, 14–18 September 2014; Australian Centre for Geomechanics: Crawley, Australia, 2014; pp. 421–436. [Google Scholar]
- Hoek, E.; Grabinsky, M.W.; Diederichs, M.S. Numerical Modelling for Underground Excavation Design. Trans. Inst. Min. Met. Sect. A Min. Ind. 1990, 100, 22–30. [Google Scholar]
- Rocscience. RS2; Rocscience: Toronto, ON, Cananda, 2019. [Google Scholar]
- GEO-SLOPE. GeoStudio; GEO-SLOPE: Calgary, AB, Canada, 2016. [Google Scholar]
- Bentley. Plaxis 2D; Bentley: Exton, PA, USA, 2019. [Google Scholar]
- Dassault Systems. ABAQUS; Dassault Systems: Vélizy-Villacoublay, France, 2019. [Google Scholar]
- Geraili Mikola, R. Adonis. Available online: https://geotechpedia.com/Software/Show/1015/ADONIS (accessed on 18 October 2019).
- UCRegents. OpenSees; UCRegents: San Francisco, CA, USA, 2006. [Google Scholar]
- EDF. Code_Aster; EDF: Paris, France, 2019. [Google Scholar]
- Laforce, T. PE281 Boundary Element Method; Stanford University: Stanford, CA, USA, 2006; pp. 1–12. [Google Scholar]
- Roscience Inc. Examine2D; Roscience Inc.: Toronto, ON, Canada, 2019. [Google Scholar]
- Map3D. Map3D. 2019. Available online: https://www.map3d.com/ (accessed on 20 October 2019).
- Wieleba, P.; Sikora, J. Open Source BEM Library. Adv. Eng. Softw. 2009, 40, 564–569. [Google Scholar] [CrossRef]
- Lisjak, A.; Tatone, B.S.A.; Grasselli, G.; Vietor, T. Numerical Modelling of the Anisotropic Mechanical Behaviour of Opalinus Clay at the Laboratory-Scale Using FEM/DEM. Rock Mech. Rock Eng. 2014, 47, 187–206. [Google Scholar] [CrossRef]
- ITASCA Consulting Group Inc. UDEC Manual; ITASCA Consulting Group Inc.: Minneapolis, MN, USA, 1992. [Google Scholar]
- ITASCA Consulting Group Inc. PFC; ITASCA Consulting Group Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
- ITASCA Consulting Group Inc. 3DEC Manual; ITASCA Consulting Group Inc.: Minneapolis, MN, USA, 1994. [Google Scholar]
- ITASCA Consulting Group Inc. PFC3D; ITASCA Consulting Group Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
- Šmilauer, V. Yade User’s Manual. Available online: https://yade-dem.org/doc/user.html (accessed on 18 October 2019).
- Sandia National Labs; Temple University. LAMMPS. 2019. Available online: https://lammps.sandia.gov/ (accessed on 18 October 2019).
- Golder Associates Inc. FracMan Geotechnical Edition; Golder Associates Inc.: Toronto, ON, Canada, 2019. [Google Scholar]
- Miraco Mining Innovation. MoFrac; Miraco Mining Innovation: Sudbury, ON, Canada, 2019. [Google Scholar]
- Alghalandis Computing. ADFNE. 2019. Available online: https://alghalandis.net/products/adfne/ (accessed on 18 October 2019).
- Varadarajan, A.; Sharma, K.G.; Singh, R.K. Some Aspect of Coupled FEBEM Analysis of Underground Openings. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 557–571. [Google Scholar] [CrossRef]
- Lorig, L.J.; Brady, B.H.G.; Cundall, P.A. Hybrid Distinct Element-Boundary Element Analysis of Jointed Rock. Int. J. Rock Mech. Min. Sci. 1986, 23, 303–312. [Google Scholar] [CrossRef]
- Pan, X.D.; Reed, M.B. A Coupled Distinct Element-Finite Element Method for Large Deformation Analysis of Rock Masses. Int. J. Rock Mech. Min. Sci. 1991, 28, 93–99. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Cottrell, B.E.; Grasselli, G. An Example of Realistic Modelling of Rock Dynamics Problems: FEM/DEM Simulation of Dynamic Brazilian Test on Barre Granite. Rock Mech. Rock Eng. 2010, 43, 707–716. [Google Scholar] [CrossRef]
- Li, X.; Kim, E.; Walton, G. A Study of Rock Pillar Behaviors in Laboratory and In-Situ Scales Using Combined Finite-Discrete Element Method Models. Int. J. Rock Mech. Min. Sci. 2019, 118, 21–32. [Google Scholar] [CrossRef]
- Geomechanica. Irazu; Geomechanica: Toronto, ON, Canada, 2019. [Google Scholar]
- Knight, E.E.; Rougier, E.; Lei, Z.; Munjiza, A. Hybrid Optimization Software Suite; Los Alamos National Laboratory: Los Alamos, NM, USA, 2014. [Google Scholar]
- Rockfield. Elfen. Available online: https://www.rockfieldglobal.com/ (accessed on 24 November 2019).
- Grasselli’s Geomechanics Group. Y-GEO; Grasselli’s Geomechanics Group: Toronto, ON, Canada, 2019. [Google Scholar]
- Sklavounos, P.; Sakellariou, M. Intelligent Classification of Rock Masses. In WIT Transactions on Information and Communication Technologies; WIT Press: Billerica, MA, USA, 1995; Volume 8. [Google Scholar]
- Singh, V.K.; Singh, D.; Singh, T.N. Prediction of Strength Properties of Some Schistose Rocks from Petrographic Properties Using Artificial Neural Networks. Int. J. Rock Mech. Min. Sci. 2001. [Google Scholar] [CrossRef]
- Millar, D.; Clarici, E. Investigation of Back-Propagation Artificial Neural Networks in Modelling the Stress-Strain Behaviour of Sandstone Rock. Genet. Sel. Evol. 2002, 47, 3326–3331. [Google Scholar] [CrossRef]
- Mahdevari, S.; Torabi, S.R. Prediction of Tunnel Convergence Using Artificial Neural Networks. Tunn. Undergr. Space Technol. 2012, 28, 218–228. [Google Scholar] [CrossRef]
- Afraei, S.; Shahriar, K.; Madani, S.H. Developing Intelligent Classification Models for Rock Burst Prediction after Recognizing Significant Predictor Variables, Section 1: Literature Review and Data Preprocessing Procedure. Tunn. Undergr. Space Technol. 2019. [Google Scholar] [CrossRef]
- Ferentinou, M.; Fakir, M. Integrating Rock Engineering Systems Device and Artificial Neural Networks to Predict Stability Conditions in an Open Pit. Eng. Geol. 2018, 246, 293–309. [Google Scholar] [CrossRef]
- Mohammed, M.; Khan, M.; Bashier, E.; Bashier, M. Chapter 1 Introduction to Machine Learning. In Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2016; pp. 1–34. [Google Scholar] [CrossRef]
- Marsland, S. Machine Learning: An Algorithmic Perspective; Chapman and Hall: New York, NY, USA, 2009. [Google Scholar]
- Mohammed, M.; Khan, M.; Bashier, E.; Bashier, M. Chapter 2 Decision Trees. In Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2016; pp. 1–204. [Google Scholar] [CrossRef]
- Einstein, H.H.; Labreche, D.A.; Markow, M.J.; Baecher, G.B. Decision Analysis Applied to Rock Tunnel Exploration. Eng. Geol. 1978, 12, 143–161. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Lingga, B. Rockburst Prediction in Kimberlite Using Decision Tree with Incomplete Data. J. Sustain. Min. 2018, 17, 158–165. [Google Scholar] [CrossRef]
- Khan, M.; Bashier, E.; Bashier, M. Chapter 4 Naïve Bayesian Classification. In Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Araghinejad, S. Chapter 5: Artificial Neural Networks. In Data-Driven Modeling: Using MATLAB ® in Water Resources and Environmental Engineering; Springer: Berlin, Germany, 2014; Volume 67. [Google Scholar] [CrossRef]
- Ribeiro e Sousa, L.; Miranda, T.; Leal e Sousa, R.; Tinoco, J. The Use of Data Mining Techniques in Rockburst Risk Assessment. Engineering 2017, 3, 552–558. [Google Scholar] [CrossRef]
- Khan, M.; Bashier, E.; Bashier, M. Chapter 5 The k -Nearest Neighbors Classifiers. In Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cracknell, M.J.; Reading, A.M. Geological Mapping Using Remote Sensing Data: A Comparison of Five Machine Learning Algorithms, Their Response to Variations in the Spatial Distribution of Training Data and the Use of Explicit Spatial Information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Khan, M.; Bashier, E.; Bashier, M. Chapter 8 Support Vector Machine. In Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Sun, Y.; Feng, X.; Yang, L. Predicting Tunnel Squeezing Using Multiclass Support Vector Machines. Adv. Civ. Eng. 2018, 2018, 17–20. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Du, X.; Tang, X. Prediction of Open Stope Hangingwall Stability Using Random Forests. Nat. Hazards 2018, 92, 1179–1197. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Horn, D.; Siegelmann, H.; Vapnik, V. Support Vector Clustering. J. Mach. Learn. Res. 2001, 2, 125–137. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Soleimani, S.; Loáiciga, H.A. Modeling Water-Quality Parameters Using Genetic Algorithm-Least Squares Support Vector Regression and Genetic Programming. J. Environ. Eng. 2017, 143, 1–10. [Google Scholar] [CrossRef]
- Jing, L.; Stephansson, O. Chapter 4 Fluid Flow and Coupled Hydro-Mechanical Behavior of Rock Fractures. In Developments in Geotechnical Engineering; Elsevier B. V.: Amsterdam, The Netherlands, 2007; Volume 85, pp. 111–144. [Google Scholar] [CrossRef]
- Abbasi, M.; El Hanandeh, A. Forecasting Municipal Solid Waste Generation Using Artificial Intelligence Modelling Approaches. Waste Manag. 2016, 56, 13–22. [Google Scholar] [CrossRef]
- Khan, M.; Bashier, E.; Bashier, M. Chapter 6 Neural Networks. In Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bell, J. Chapter 5: Artificial Neural Networks. In Machine Learning: Hands-on for Developers and Technical Professionals; John Wiley & Sons, Inc.: Indianapolis, IN, USA, 2015. [Google Scholar]
- Trivedi, R.; Singh, T.N.; Mudgal, K.; Gupta, N. Application of Artificial Neural Network for Blast Performance Evaluation. Int. J. Res. Eng. Technol. 2015, 3, 564–574. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C. Optimising Fuzzy Neural Network Architecture for Dissolved Oxygen Prediction and Risk Analysis. Water 2017, 9. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C. Dissolved Oxygen Prediction Using a Possibility Theory Based Fuzzy Neural Network. Hydrol. Earth Syst. Sci. 2016, 20, 2267–2293. [Google Scholar] [CrossRef]
- Khan, U.T.; He, J.; Valeo, C. River Flood Prediction Using Fuzzy Neural Networks: An Investigation on Automated Network Architecture. Water Sci. Technol. 2018, 2017, 238–247. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Deng, Y.; Sadiq, R.; Jiang, W.; Tesfamariam, S. Risk Analysis in a Linguistic Environment: A Fuzzy Evidential Reasoning-Based Approach. Expert Syst. Appl. 2011, 38, 15438–15446. [Google Scholar] [CrossRef]
- Song, Z.; Jiang, A.; Jiang, Z. Back Analysis of Geomechanical Parameters Using Hybrid Algorithm Based on Difference Evolution and Extreme Learning Machine. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Ching, J.; Phoon, K.; Li, K.; Weng, M. Multivariate Probability Distribution for Some Intact Rock Properties. Can. Geotech. J. 2019, 18, 1–18. [Google Scholar] [CrossRef]
- Kumar, M.; Samui, P.; Naithani, A.K. Determination of Uniaxial Compressive Strength and Modulus of Elasticity of Travertine Using Machine Learning Techniques. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–15. [Google Scholar]
- Fakir, M.; Ferentinou, M. A Holistic Open Pit Mine Slope Stability Index Using Artificial Neural Networks; ISRM: Lisbon, Portugal, 2017; Volume 2017. [Google Scholar]
- Kumar, M.; Samui, P. Analysis of Epimetamorphic Rock Slopes Using Soft Computing. J. Shanghai Jiaotong Univ. 2014, 19, 274–278. [Google Scholar] [CrossRef]
- Hibert, C.; Provost, F.; Malet, J.P.; Maggi, A.; Stumpf, A.; Ferrazzini, V. Automatic Identification of Rockfalls and Volcano-Tectonic Earthquakes at the Piton de La Fournaise Volcano Using a Random Forest Algorithm. J. Volcanol. Geotherm. Res. 2017, 340, 130–142. [Google Scholar] [CrossRef]
- Mayr, A.; Rutzinger, M.; Geitner, C. Multitemporal Analysis of Objects in 3D Point Clouds for Landslide Monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 691–697. [Google Scholar] [CrossRef]
- Janeras, M.; Jara, J.A.; Royán, M.J.; Vilaplana, J.M.; Aguasca, A.; Fàbregas, X.; Gili, J.A.; Buxó, P. Multi-Technique Approach to Rockfall Monitoring in the Montserrat Massif (Catalonia, NE Spain). Eng. Geol. 2017, 219, 4–20. [Google Scholar] [CrossRef]
- Weidner, L.; Walton, G.; Kromer, R. Classification Methods for Point Clouds in Rock Slope Monitoring: A Novel Machine Learning Approach and Comparative Analysis. Eng. Geol. 2019, 263. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Chen, J.; Zhu, H. Automatic Characterization of Rock Mass Discontinuities Using 3D Point Clouds. Eng. Geol. 2019, 259, 105131. [Google Scholar] [CrossRef]
- Bizjak, K.F.; Petkovšek, B. Displacement Analysis of Tunnel Support in Soft Rock around a Shallow Highway Tunnel at Golovec. Eng. Geol. 2004, 75, 89–106. [Google Scholar] [CrossRef]
- Santos, O.J.; Celestino, T.B. Artificial Neural Networks Analysis of São Paulo Subway Tunnel Settlement Data. Tunn. Undergr. Space Technol. 2008. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Fahimifar, A.; Ghaleini, E.N.; Momenzadeh, M.; Armaghani, D.J. Development of a New Hybrid ANN for Solving a Geotechnical Problem Related to Tunnel Boring Machine Performance. Eng. Comput. 2019. [Google Scholar] [CrossRef]
- Leu, S.S.; Chen, C.N.; Chang, S.L. Data Mining for Tunnel Support Stability: Neural Network Approach. Autom. Constr. 2001, 10, 429–441. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Y. A Fast Detection Method via Region-Based Fully Convolutional Neural Networks for Shield Tunnel Lining Defects. Comput. Civ. Infrastruct. Eng. 2018. [Google Scholar] [CrossRef]
- Dong, L.J.; Li, X.B.; Peng, K. Prediction of Rockburst Classification Using Random Forest. Trans. Nonferrous Met. Soc. China 2013, 23, 472–477. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Shi, X. Long-Term Prediction Model of Rockburst in Underground Openings Using Heuristic Algorithms and Support Vector Machines. Saf. Sci. 2012, 50, 629–644. [Google Scholar] [CrossRef]
- Liu, K.; Liu, B. Optimization of Smooth Blasting Parameters for Mountain Tunnel Construction with Specified Control Indices Based on a GA and ISVR Coupling Algorithm. Tunn. Undergr. Space Technol. 2017. [Google Scholar] [CrossRef]
- Vallejos, J.A.; McKinnon, S.D. Logistic Regression and Neural Network Classification of Seismic Records. Int. J. Rock Mech. Min. Sci. 2013, 62, 86–95. [Google Scholar] [CrossRef]
- Dong, L.; Li, X.; Xu, M.; Li, Q. Comparisons of Random Forest and Support Vector Machine for Predicting Blasting Vibration Characteristic Parameters. Procedia Eng. 2011, 26, 1772–1781. [Google Scholar] [CrossRef]
- Paraskevopoulou, C.; Diederichs, M. Analysis of Time-Dependent Deformation in Tunnels Using the Convergence-Confinement Method. Tunn. Undergr. Space Technol. 2018. [Google Scholar] [CrossRef]
- Spence, E. CO Summer School Central: Introduction to Neural Networks with Python I; CO Summer School Central: Toronto, ON, Canada, 2018. [Google Scholar]
- Mandic, D.; Chambers, J. Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures, and Stability; John Wiley & Sons, Inc.: Indianapolis, IN, USA, 2001. [Google Scholar]
- Solomatine, D.P.; Ostfeld, A. Data-Driven Modelling: Some Past Experiences and New Approaches. J. Hydroinform. 2007, 10, 3–22. [Google Scholar] [CrossRef]
- Martins, F.F.; Miranda, T.F.S. Prediction of Hard Rock TBM Penetration Rate Based on Data Mining Techniques. In Proceedings of the 18th international Conference on Soil Mechanics and Geotechnical Engineering; Presses des Ponts: Paris, France, 2013; pp. 1751–1754. [Google Scholar]
- Snieder, E.; Shakir, R.; Khan, U.T. A Comprehensive Comparison of Four Input Variable Selection Methods for Artificial Neural Network Flow Forecasting Models. J. Hydrol. 2019, 124299. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods Used for the Development of Neural Networks for the Prediction of Water Resource Variables in River Systems: Current Status and Future Directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural Networks for the Prediction and Forecasting of Water Resources Variables: A Review of Modelling Issues and Applications. Environ. Model. Softw. 2000. [Google Scholar] [CrossRef]
- May, R.J.; Maier, H.R.; Dandy, G.C. Data Splitting for Artificial Neural Networks Using SOM-Based Stratified Sampling. Neural Netw. 2010, 23, 283–294. [Google Scholar] [CrossRef]
- Shu, C.; Burn, D.H. Artificial Neural Network Ensembles and Their Application in Pooled Flood Frequency Analysis. Water Resour. Res. 2004, 40, 1–10. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Data Division for Developing Neural Networks Applied to Geotechnical Engineering. J. Comput. Civ. Eng. 2004, 18, 105–114. [Google Scholar] [CrossRef]
- Daszykowski, M.; Walczak, B.; Massart, D.L. Representative Subset Selection. Anal. Chim. Acta 2002, 468, 91–103. [Google Scholar] [CrossRef]
- Xie, Q.; Peng, K. Space-Time Distribution Laws of Tunnel Excavation Damaged Zones (EDZs) in Deep Mines and EDZ Prediction Modeling by Random Forest Regression. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Chou, J.S.; Thedja, J.P.P. Metaheuristic Optimization within Machine Learning-Based Classification System for Early Warnings Related to Geotechnical Problems. Autom. Constr. 2016, 68, 65–80. [Google Scholar] [CrossRef]

| Rock Engineering Problem | MLAs | Opportunities |
|---|---|---|
| Rock mass properties | Categorical ANNs [52,83,84] | • Backwards predict rock mass properties based on observed site conditions • Predict rock mass scale properties based on lab-scale properties and rock mass behaviour |
| Laboratory testing and constitutive behaviour | Numerical ANNs [54,85] SVM [85] | • Use geology and peak Unconfined Compressive Strength to predict crack initiation and crack damage thresholds • Use laboratory tests and field observations to predict constitutive behaviour • Use rock mass scale classification (e.g., Q, RMR) to predict lab-scale properties |
| Slope stability | Categorical ANNs [57,86] SVM [87] RF [88,89] Clustering [90] | • Predict slope movements based on geometry, piezometers, inclinometer data, etc. • Predict volume of structurally controlled failure based on mapped discontinuities |
| Point cloud analysis | RF [91] kNN [92] | • Use successive tunnel scans to get volume differences and predict time-dependent deformations |
| Tunnel performance | Numerical ANNs [55,93,94,95] Categorical ANNS [96,97] SVM [69] RF [61,70] | • Predict stress/strain fields for input into numerical models • Use preliminary/incomplete field mapping to prediction rock mass classification (e.g., Q, RMR) • Predict tunnel support class based on rock mass classification (e.g., Q, RMR) • Predict rock support performance-based on geology, excavation method, environmental conditions, etc. • Use microseismic monitoring arrays to predict rock mass deformation as excavation is developed |
| Rock bursts | Categorical ANNs [65] Naïve Bayesian classifiers [65] kNN [65] RF [98] SVM [65,99] Decision Trees [62] | • Predict magnitude and location of events using 3D excavation geometry, time-series seismic events, mapped geology, etc. • Use previous rockburst events, geology, etc. to predict magnitude of failed material and performance of rock support • Use mapped rock classification (e.g., Q, RMR) to predict probability of rockburst |
| Blasting | Categorical ANNs [100,101] Numerical ANNS [100] SVM [99,102] RF [102] | • Use blast parameters and damage extent to predict optimum parameters for future blasts • Predict blast parameters using mapped rock classification (e.g., Q, RMR) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morgenroth, J.; Khan, U.T.; Perras, M.A. An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design. Geosciences 2019, 9, 504. https://doi.org/10.3390/geosciences9120504
Morgenroth J, Khan UT, Perras MA. An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design. Geosciences. 2019; 9(12):504. https://doi.org/10.3390/geosciences9120504
Chicago/Turabian StyleMorgenroth, Josephine, Usman T. Khan, and Matthew A. Perras. 2019. "An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design" Geosciences 9, no. 12: 504. https://doi.org/10.3390/geosciences9120504
APA StyleMorgenroth, J., Khan, U. T., & Perras, M. A. (2019). An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design. Geosciences, 9(12), 504. https://doi.org/10.3390/geosciences9120504





