Evaluation of The Seismic Hazard in The Marmara Region (Turkey) Based on Updated Databases
Abstract
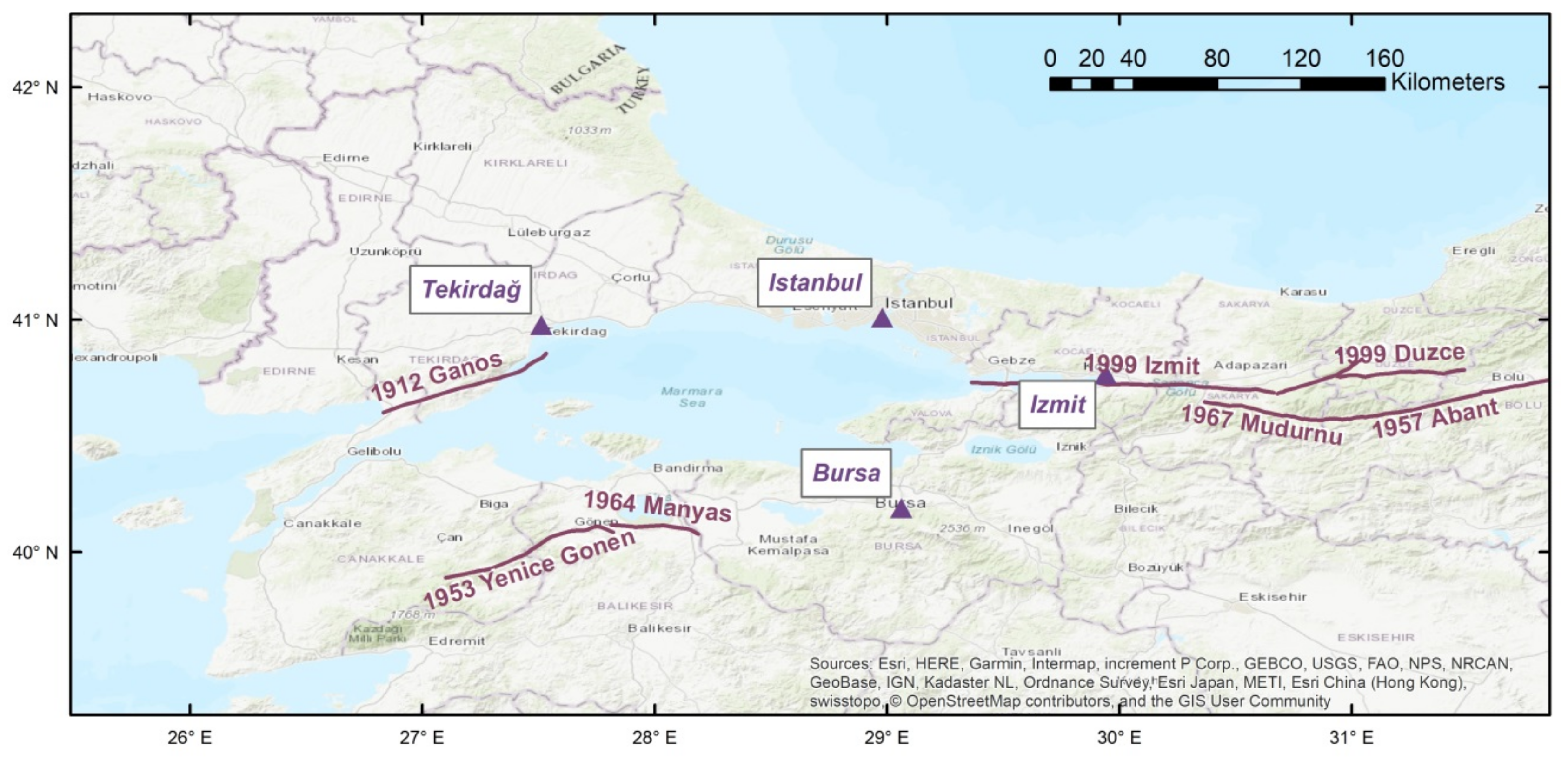
1. Introduction
2. Review of Previous Efforts
3. Data Set
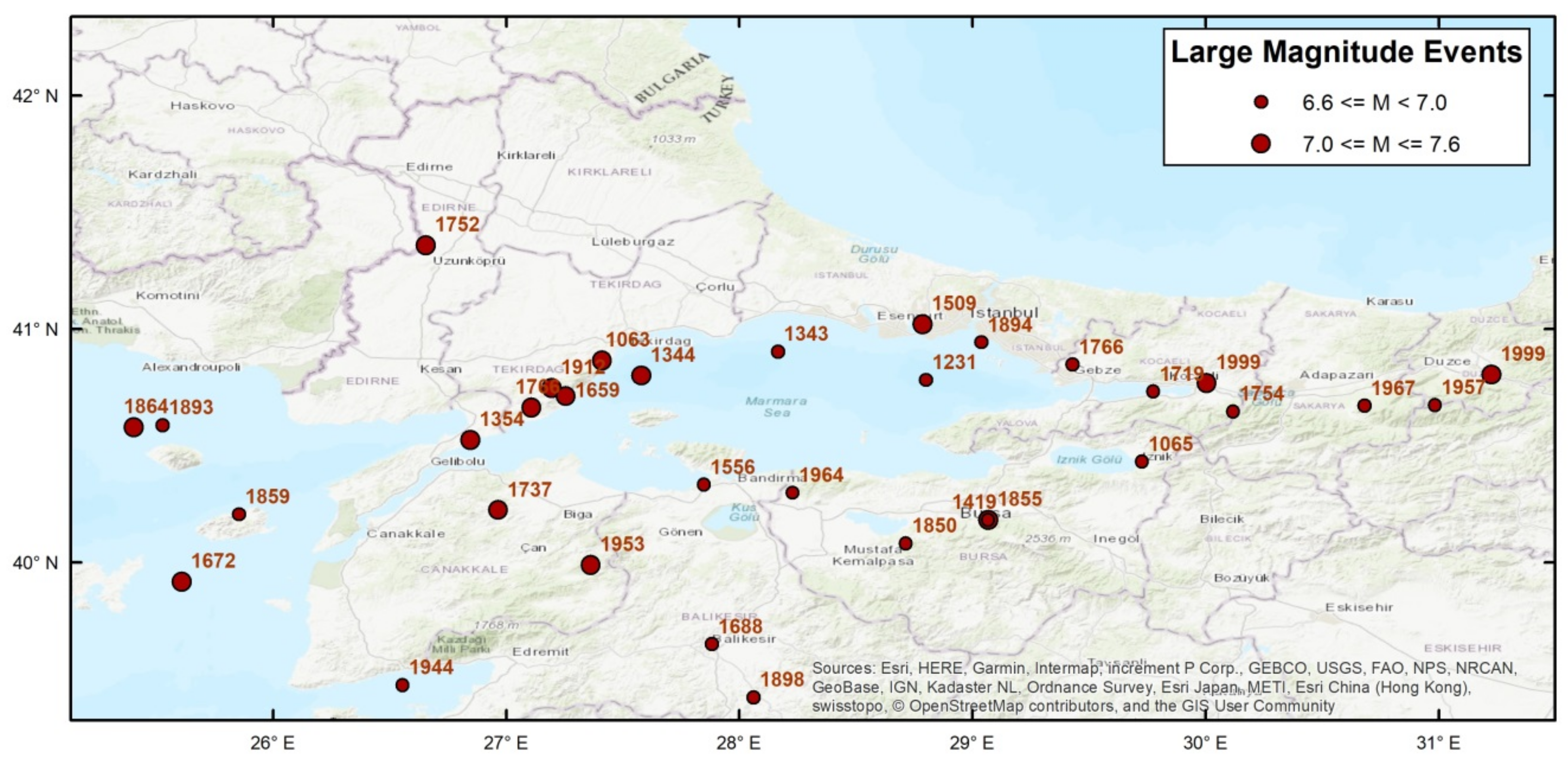
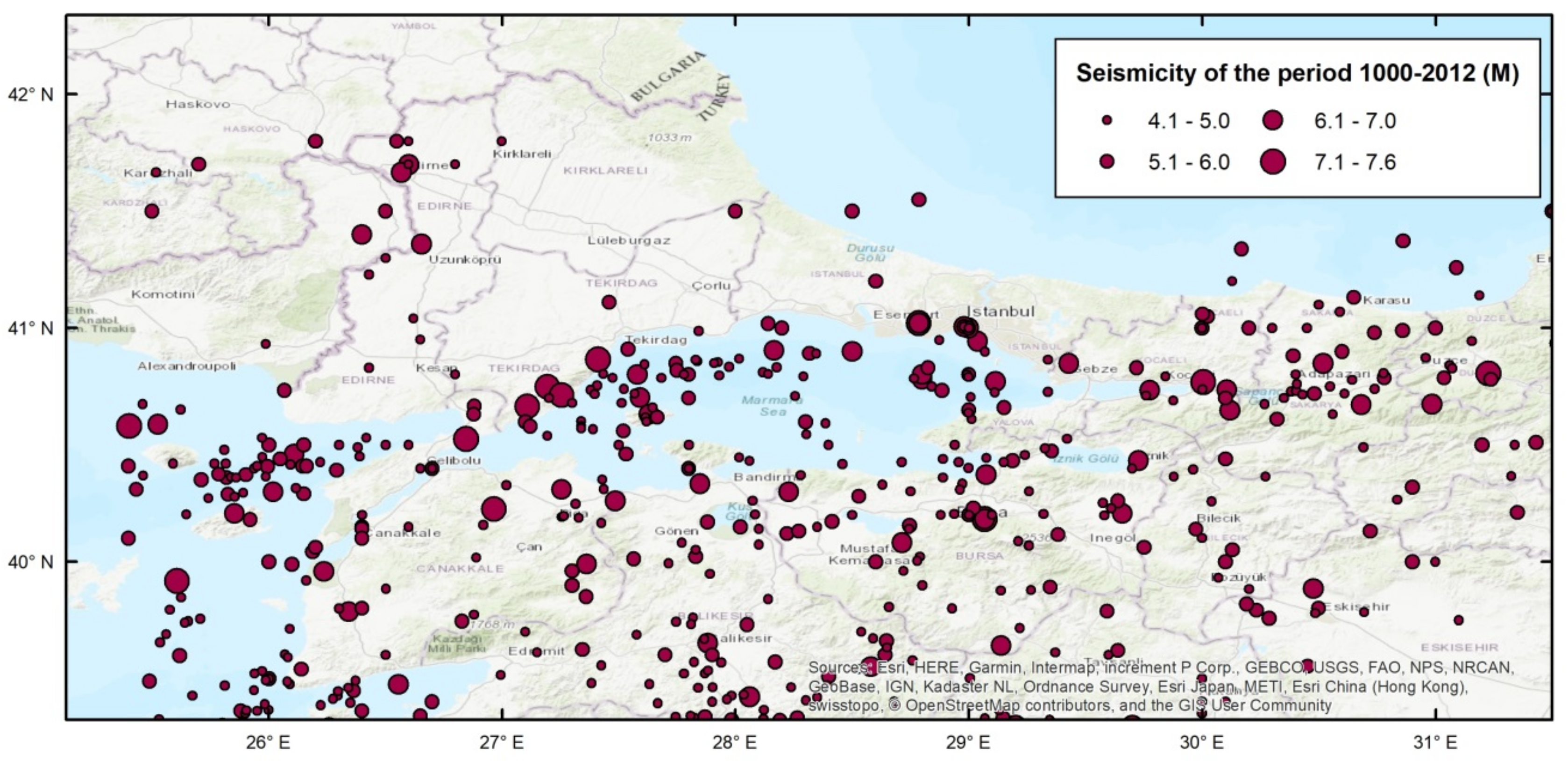
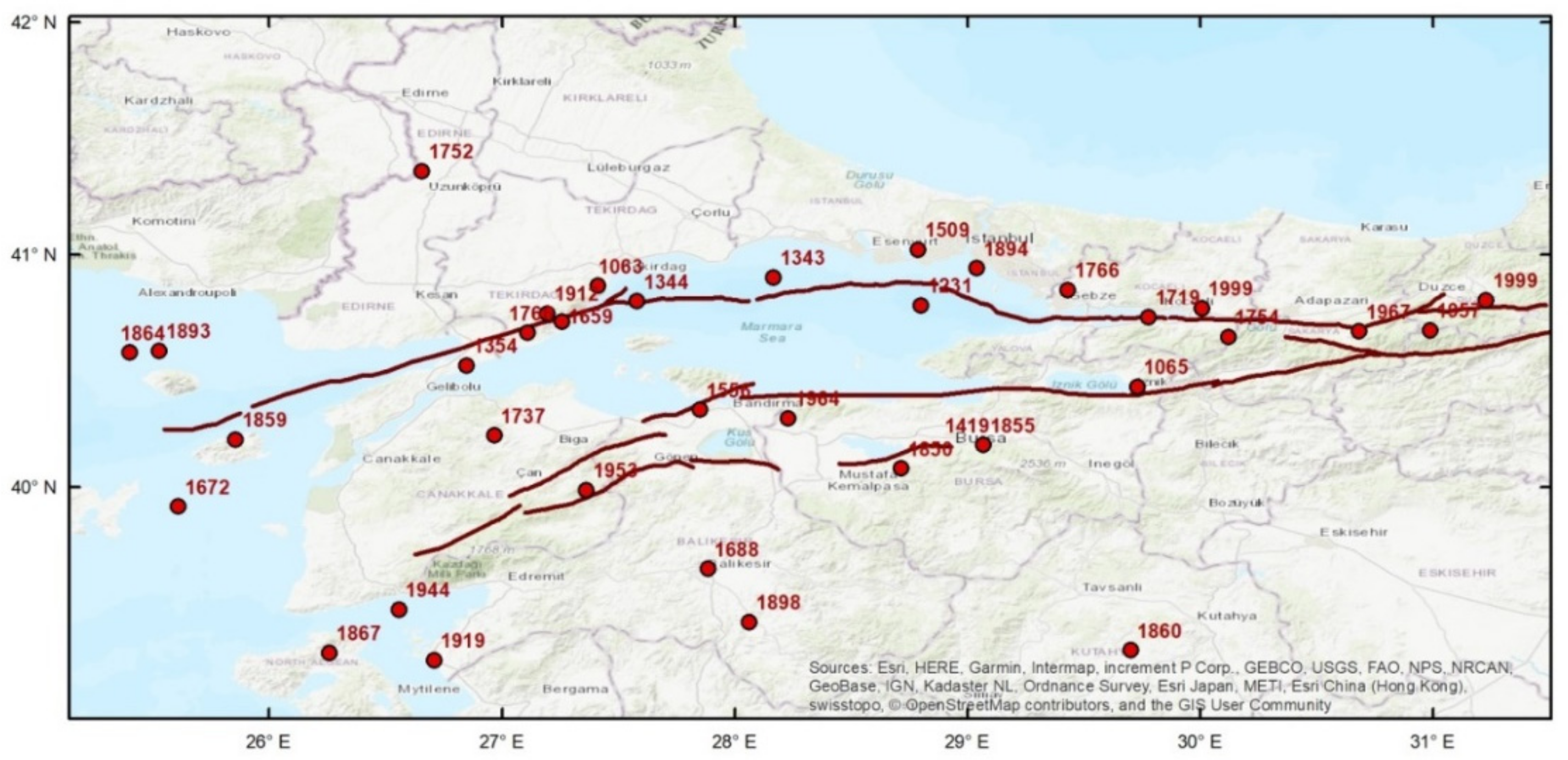
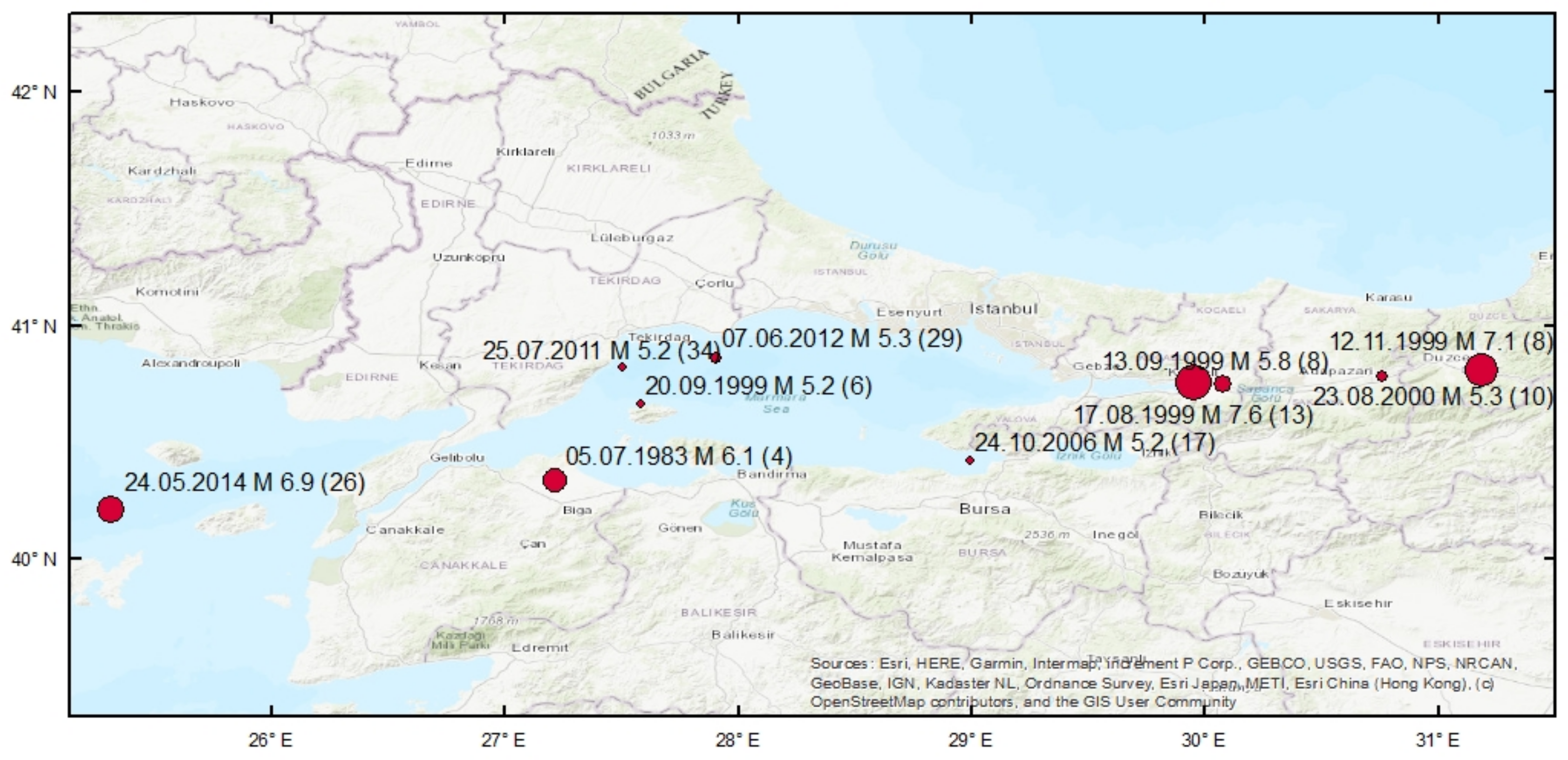
3.1. Earthquake Catalogue
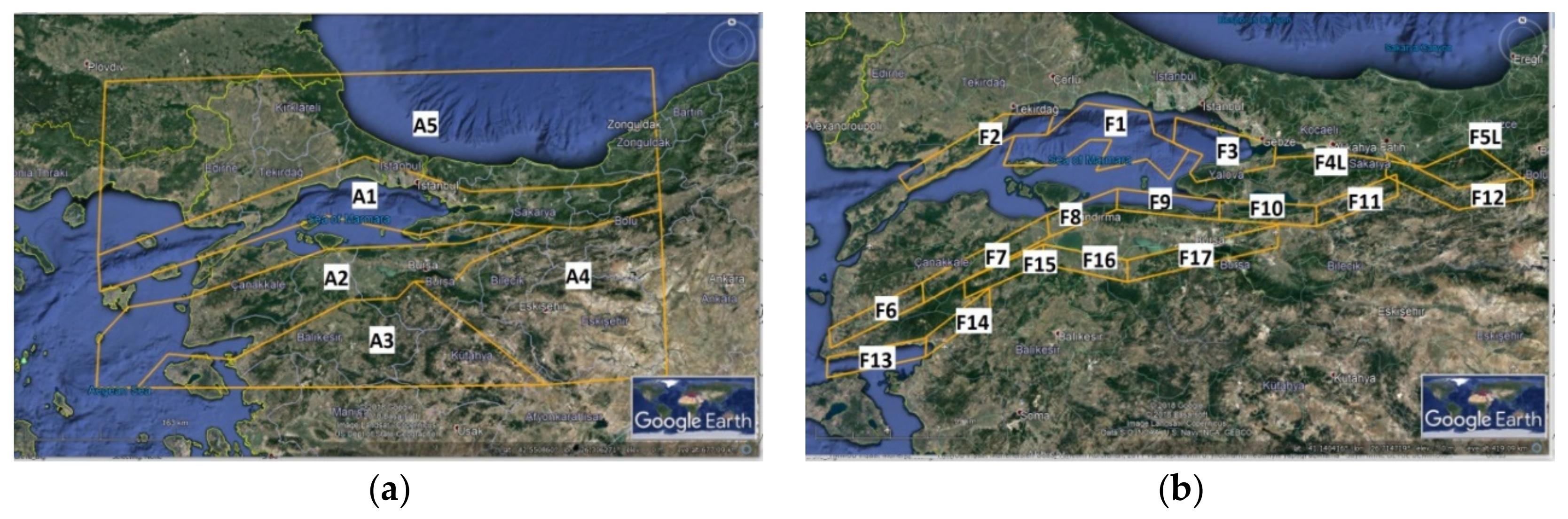
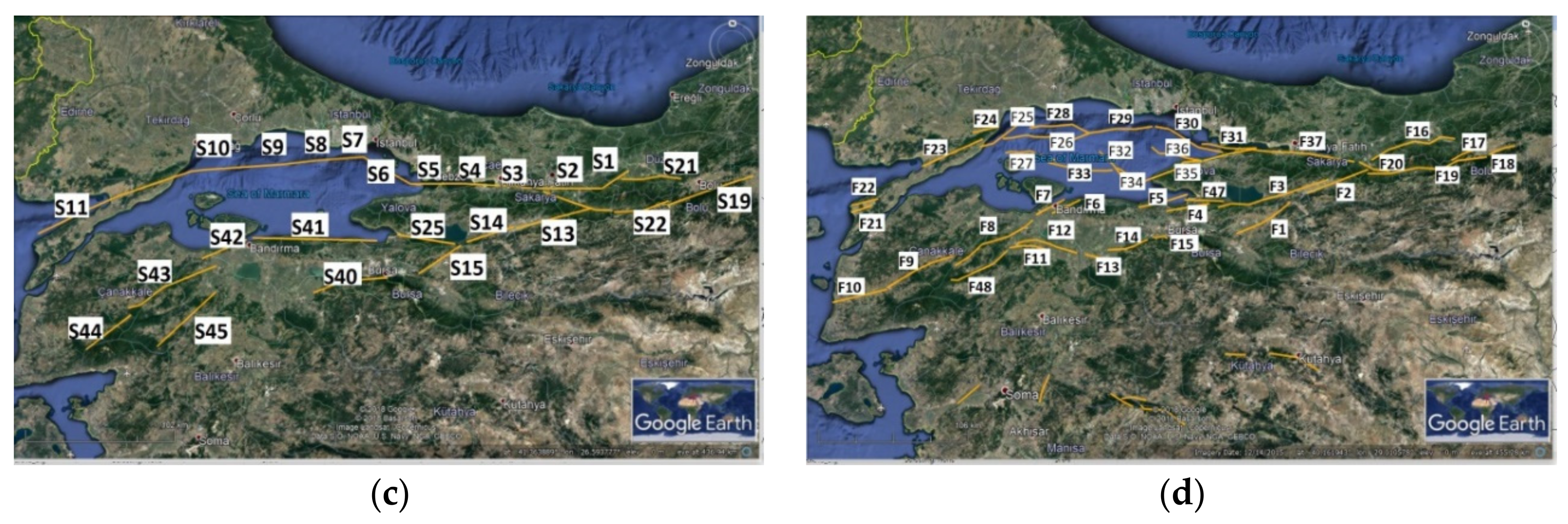
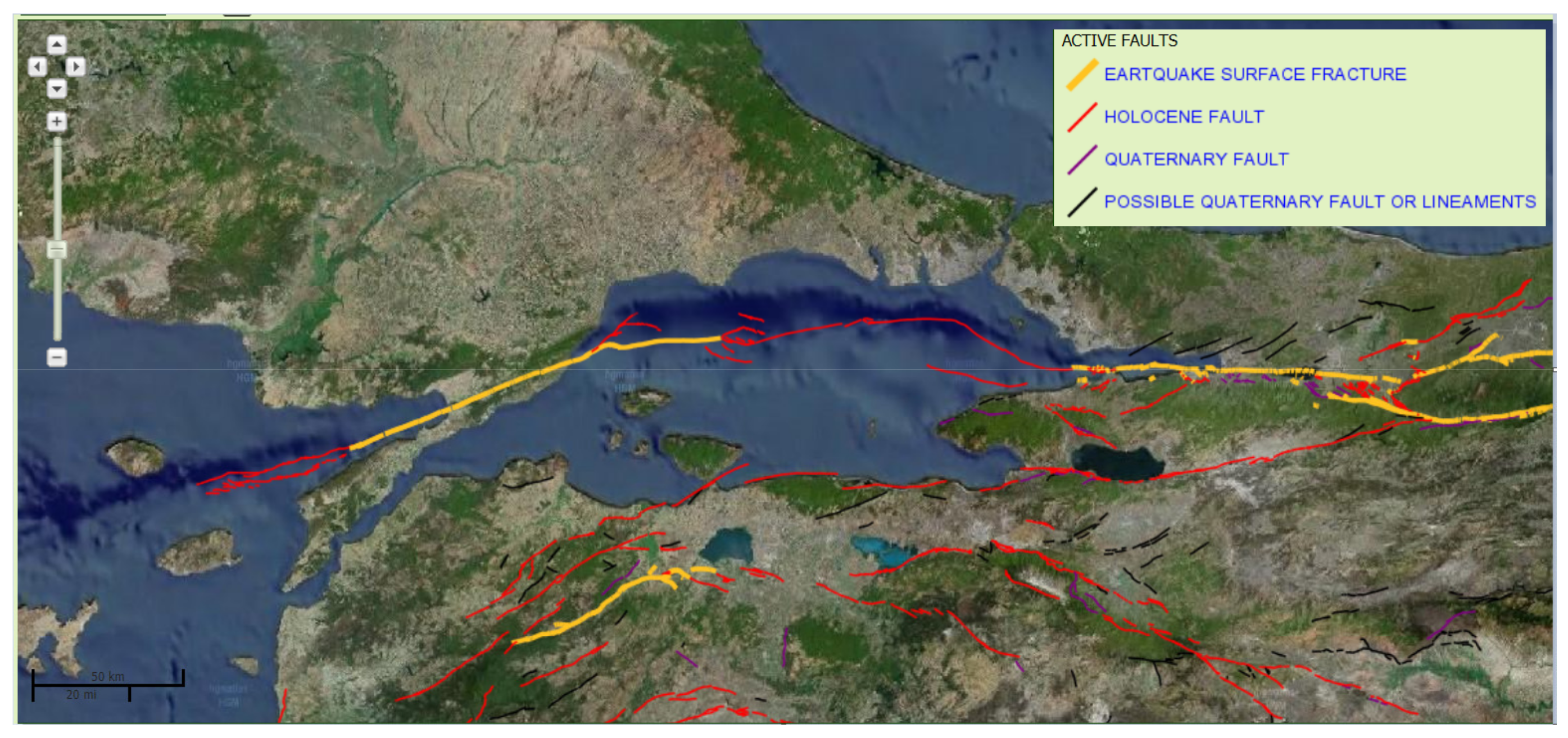
3.2. Fault Database
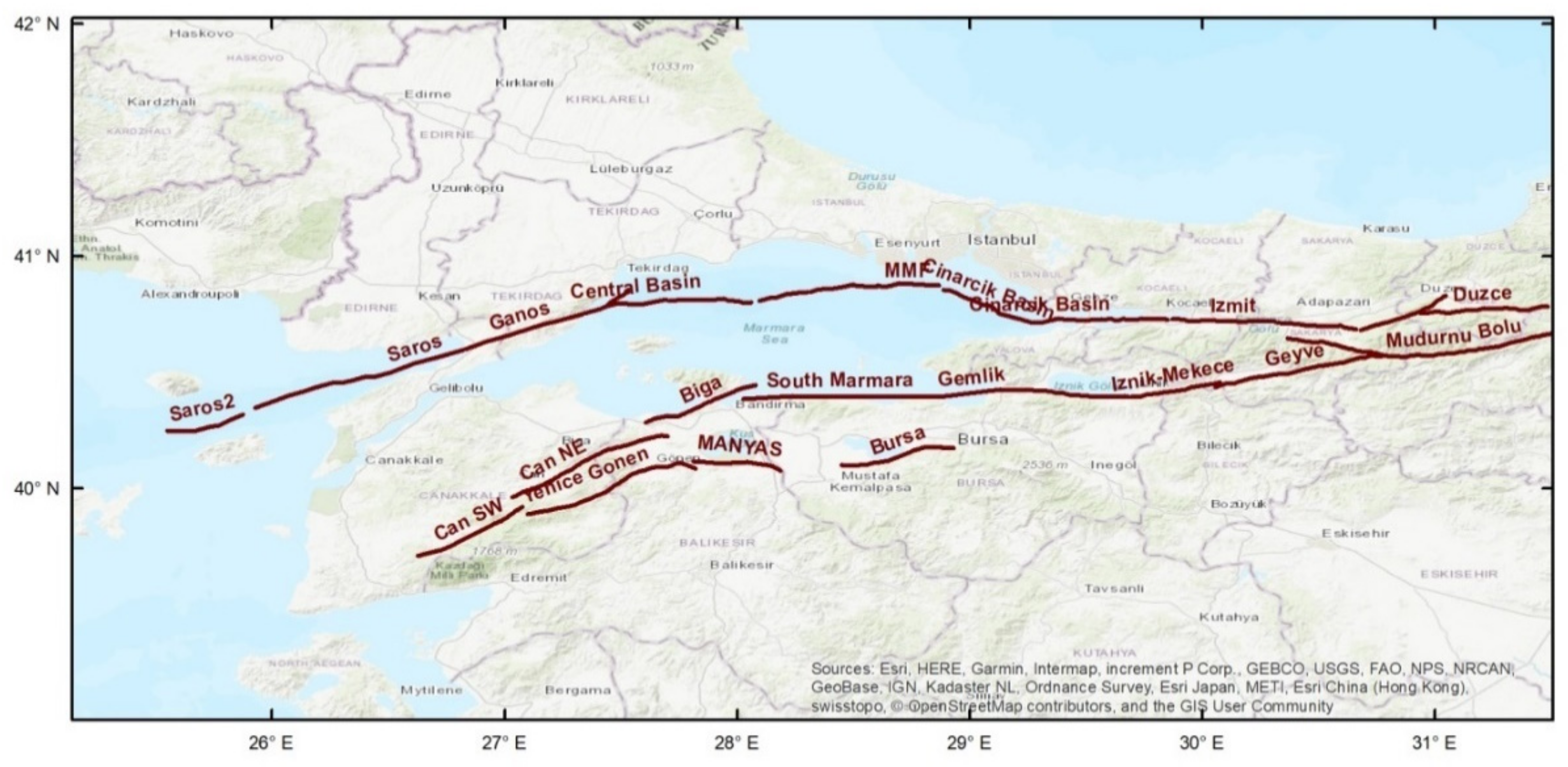
3.3. The Fault Source Model
4. Probabilistic Seismic Hazard Model and Methodology
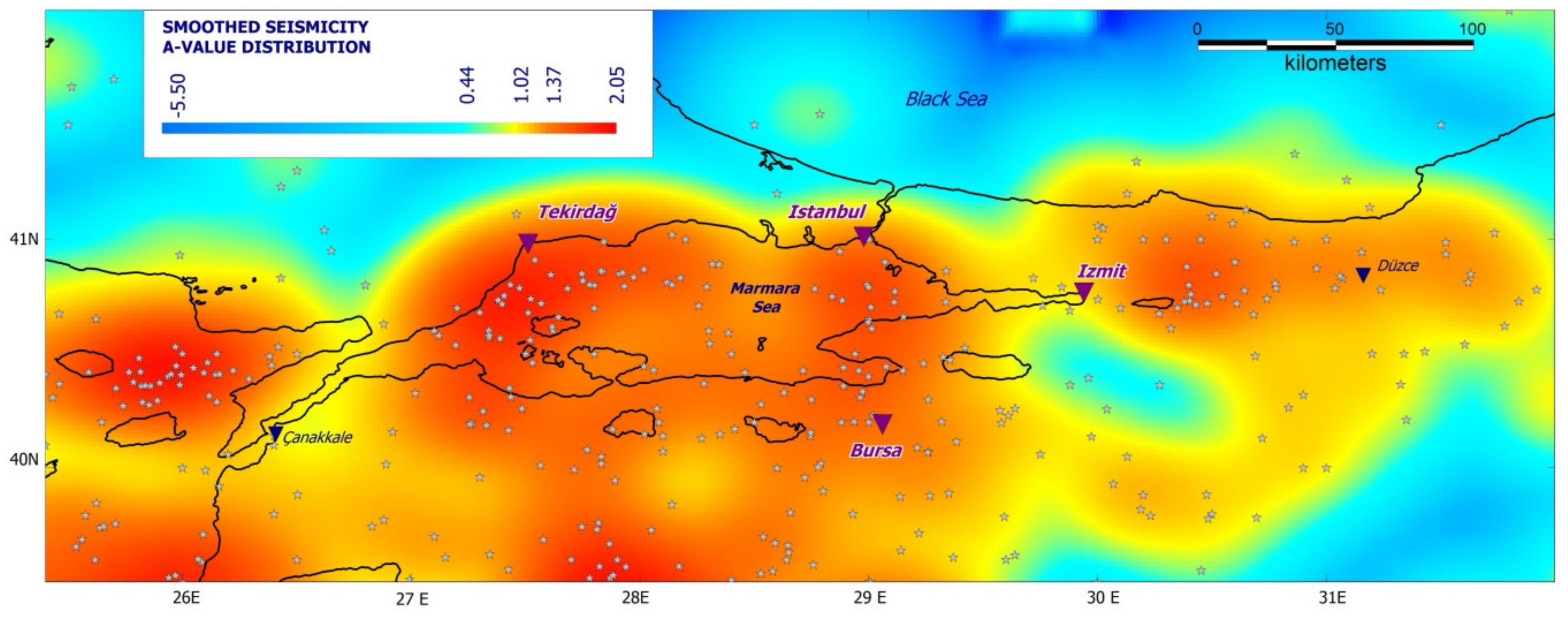
4.1. Seismicity-based Source Model
4.2. Fault-based Source Models
4.2.1. Earthquake Rupture Forecast (ERF) Model: Poisson Approach
4.2.2. ERF Model: Time Dependent Approach
5. Computation of The Seismic Hazard
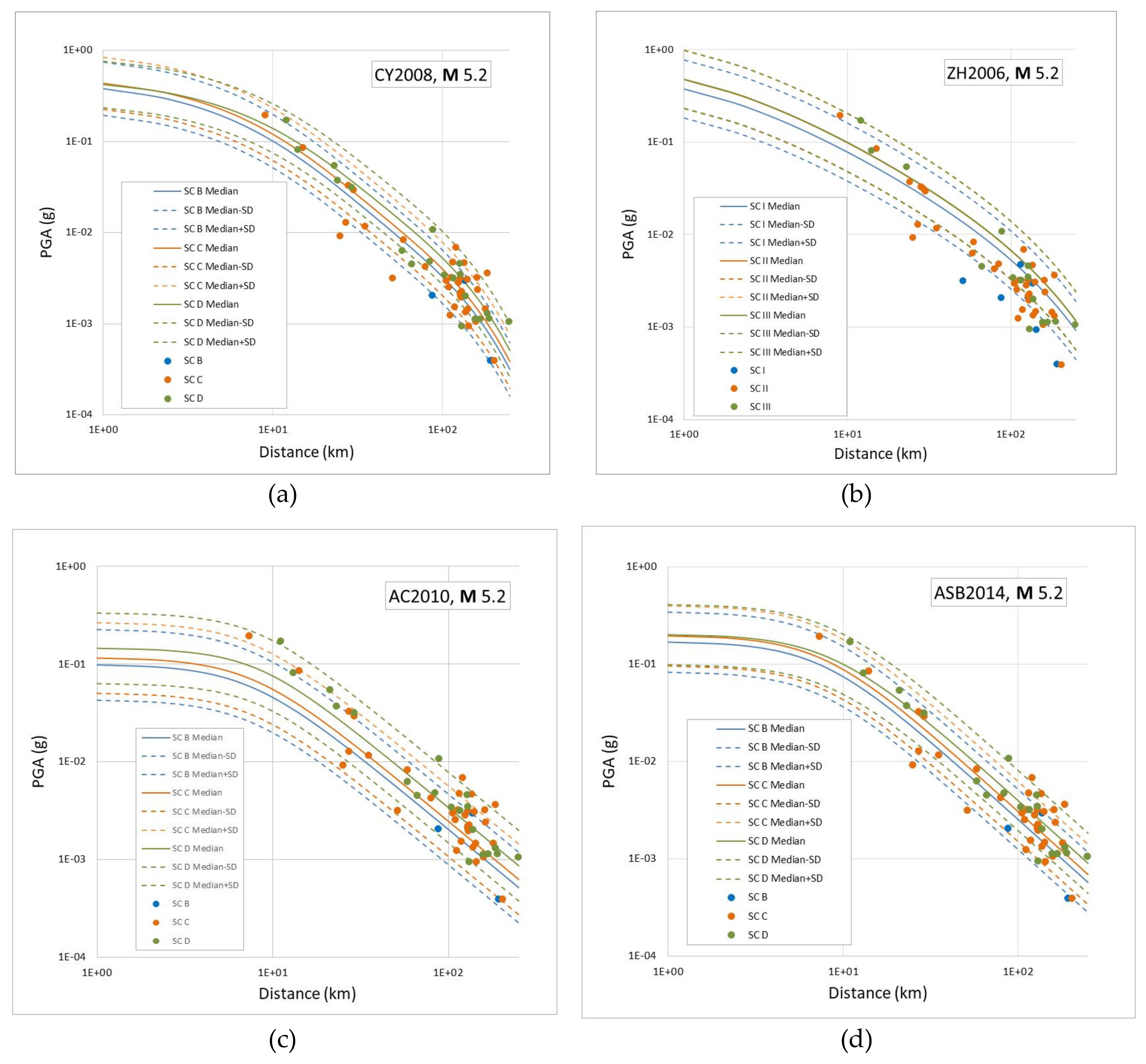
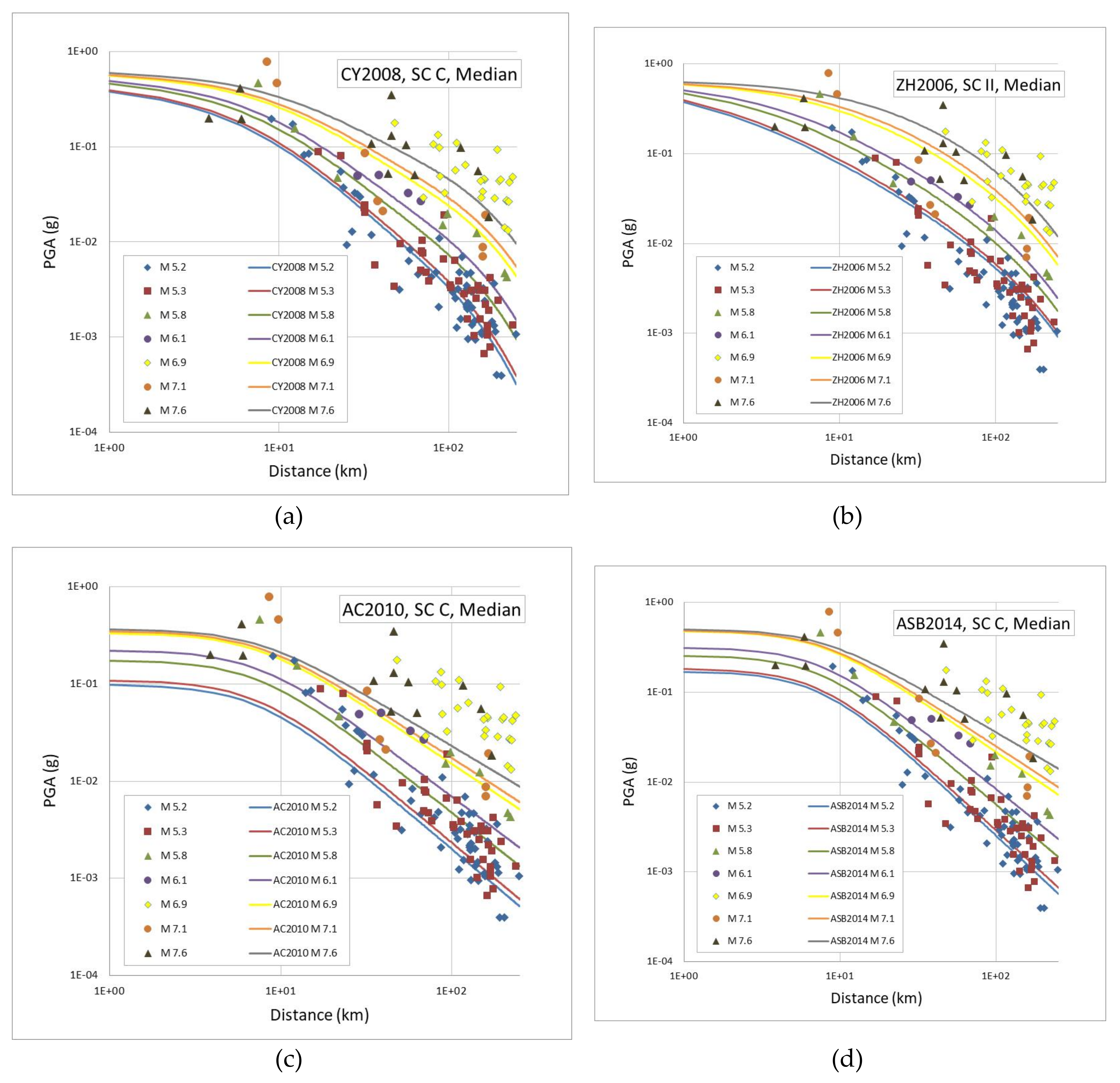
5.1. Ground Motion Characterisation and Logic Tree
5.2. Computation of The Seismic Hazard
6. Results
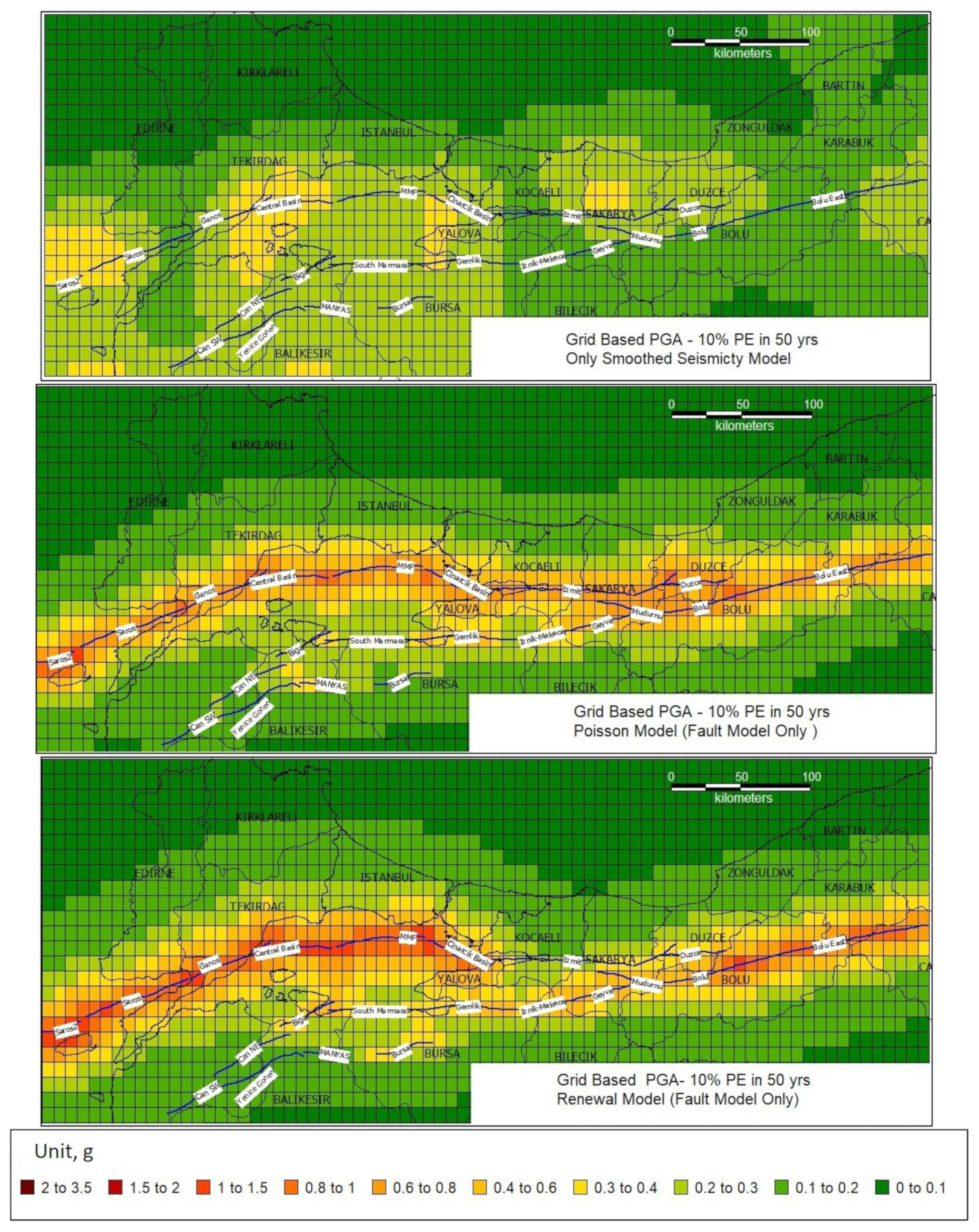
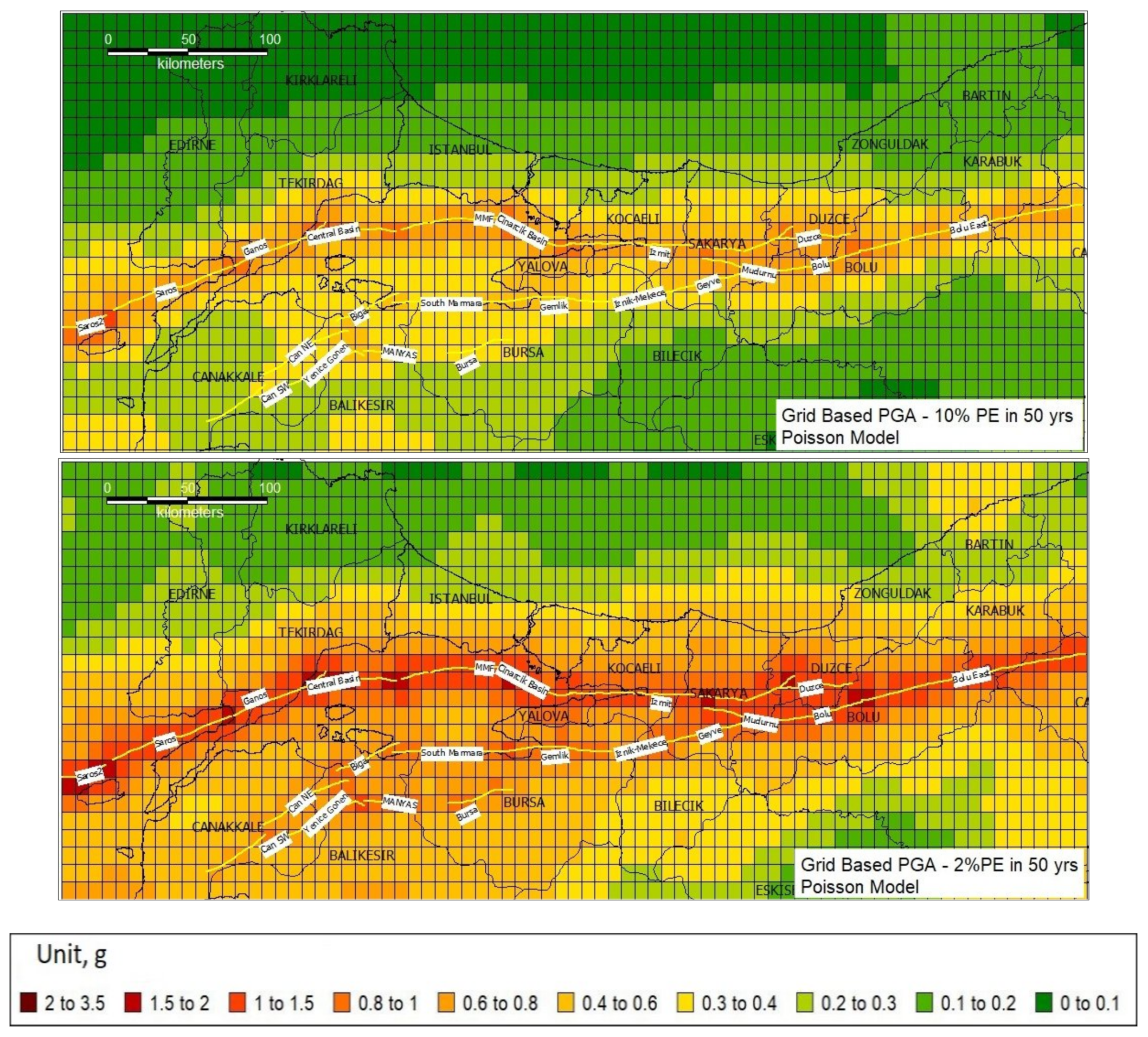
6.1. Hazard Maps for Selected Ground Motion Intensity Measures
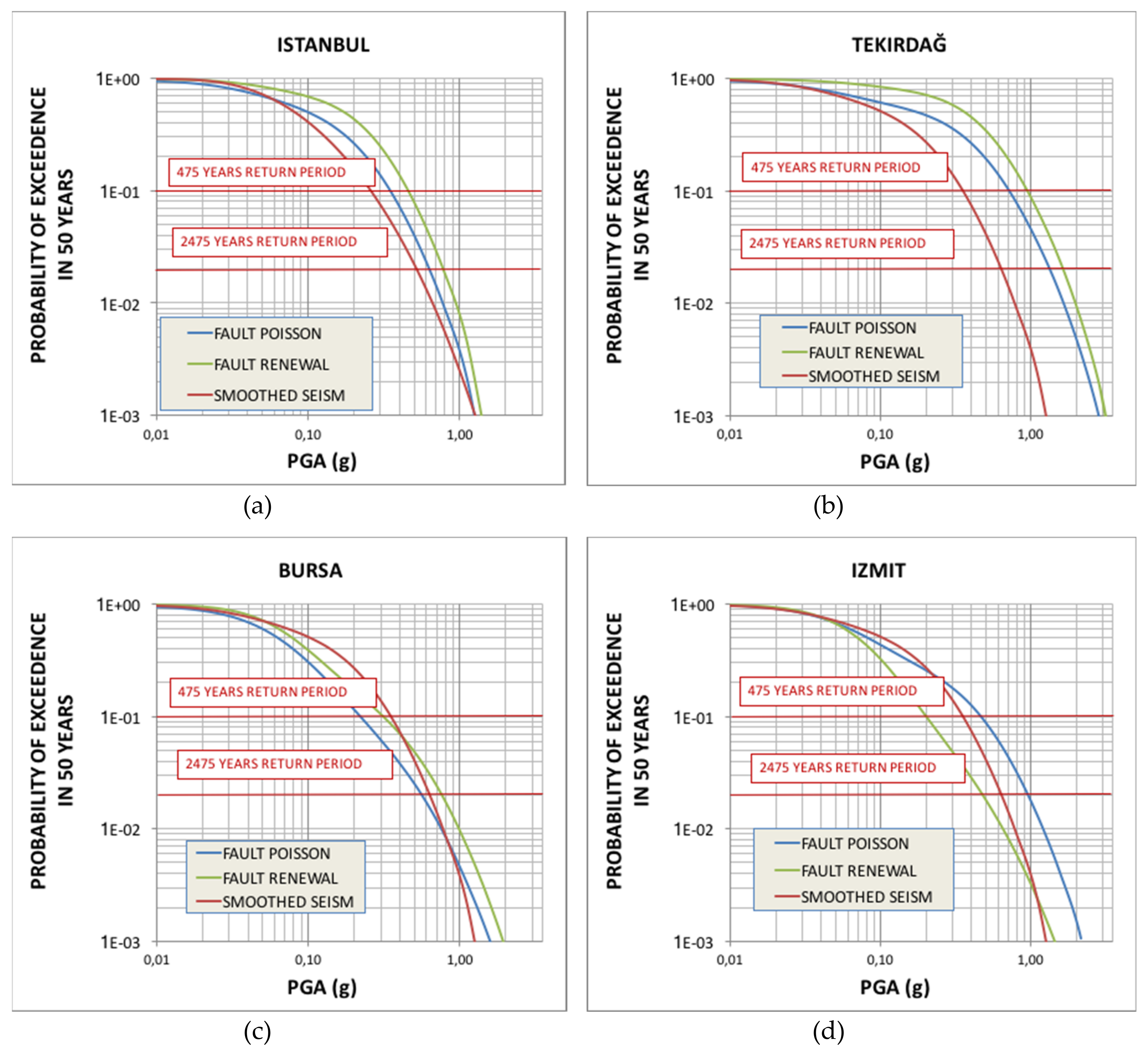
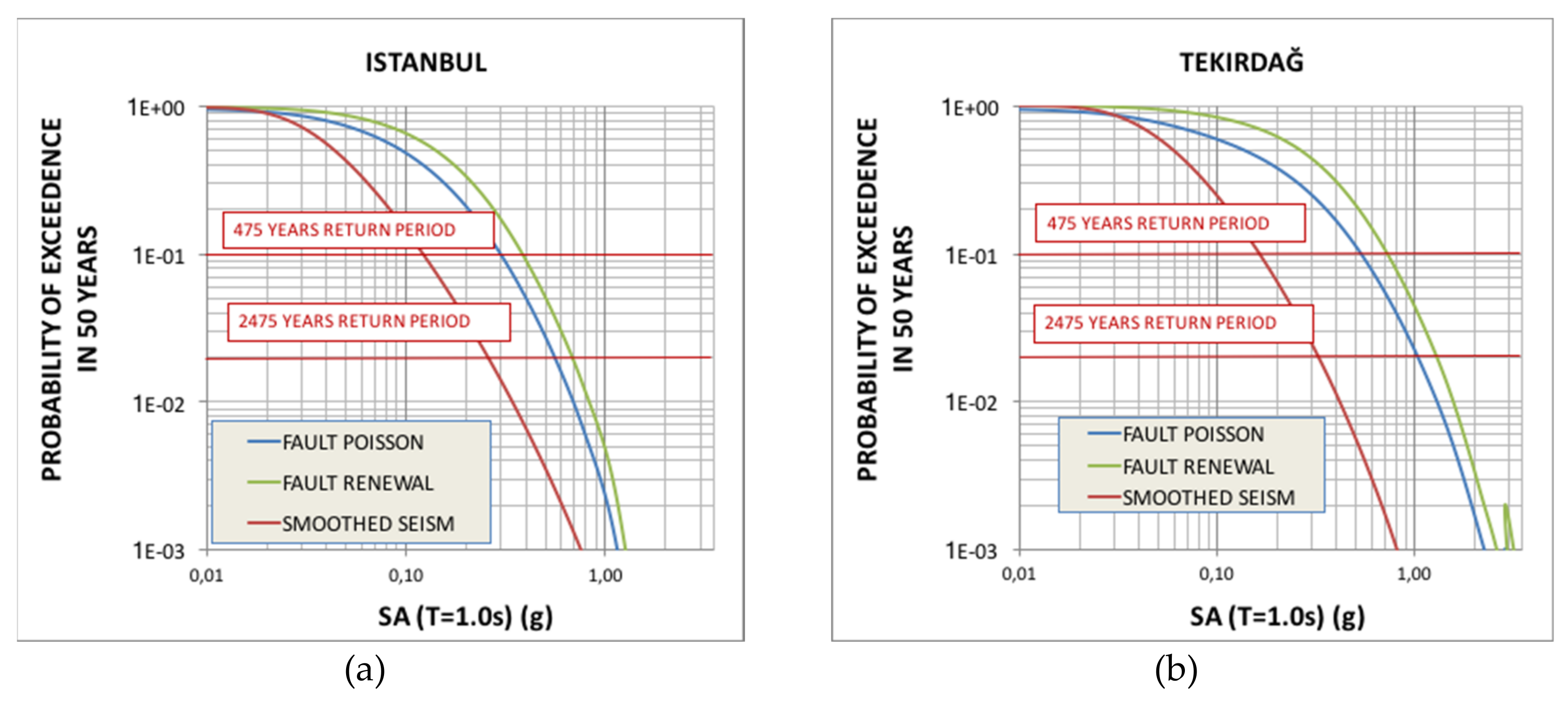
6.2. Hazard Curves for Selected Sites
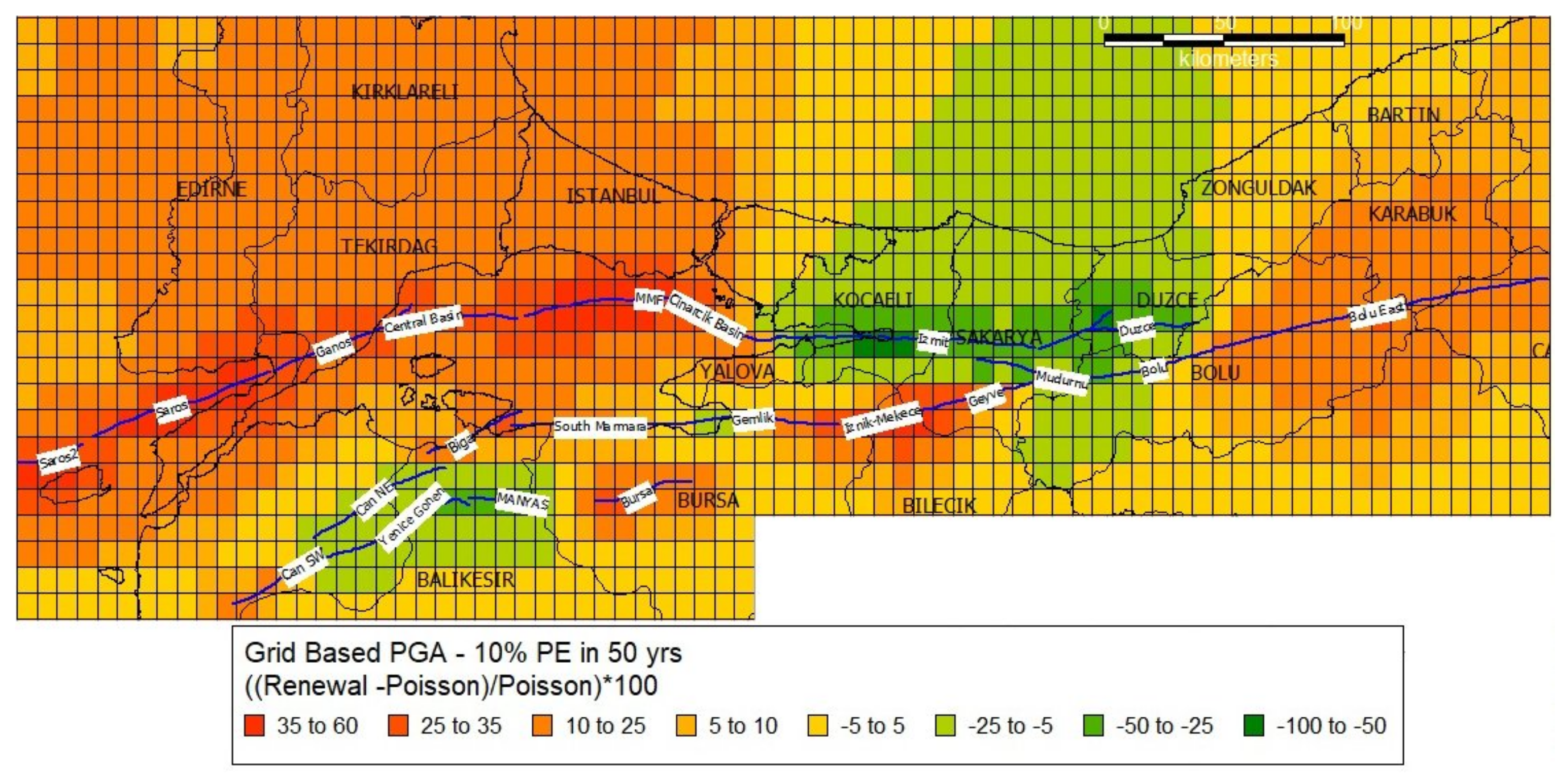
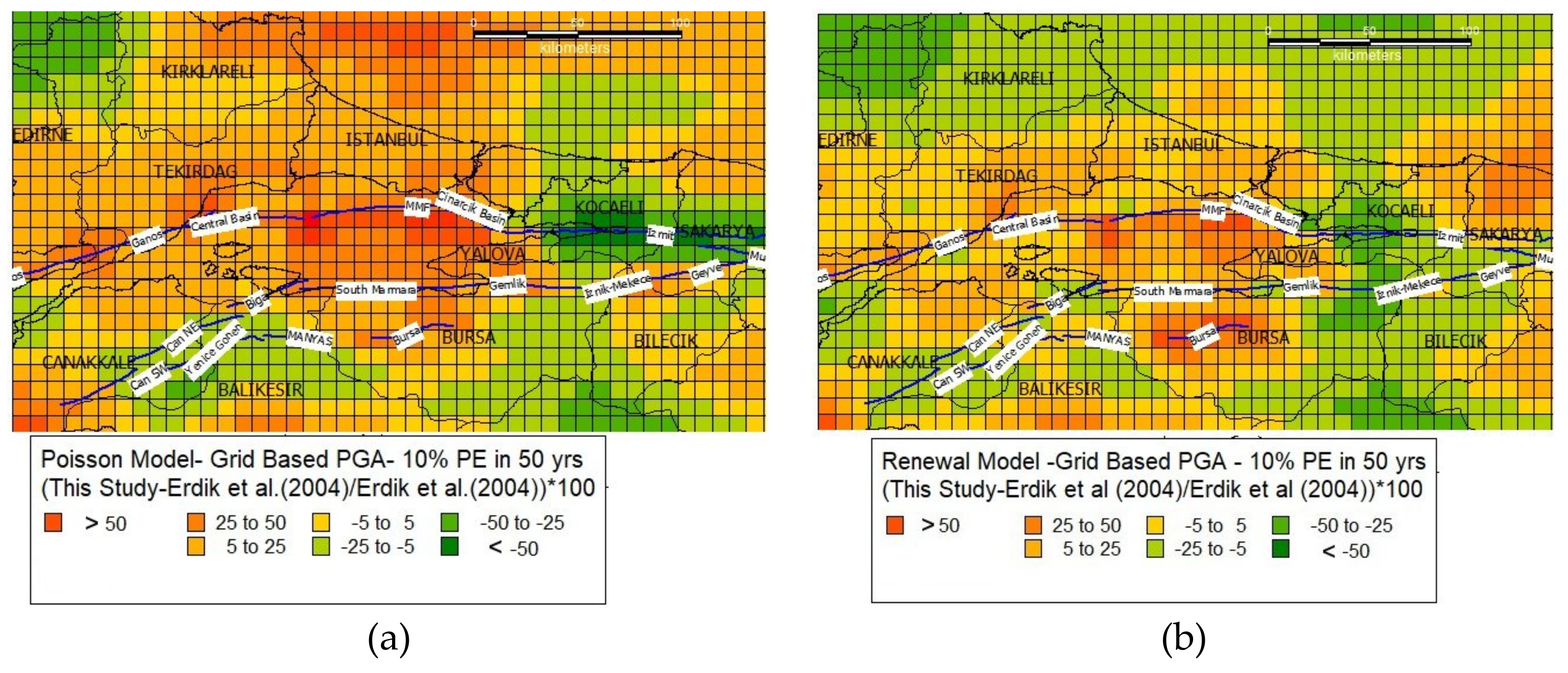
6.3. Discussion of the Results and Comparisons with Other Studies
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Parsons, T.; Toda, S.; Stein, R.S.; Barka, A.; Dietrich, J.H. Heightened odds of large earthquakes near Istanbul: An interaction-based probability calculation. Science 2000, 288, 661–665. [Google Scholar] [CrossRef]
- Parsons, T. Recalculated probability of M ≥ 7 earthquakes beneath the Sea of Marmara, Turkey. J. Geophys. Res. 2004, 109, B05304. [Google Scholar] [CrossRef]
- Murru, M.; Akinci, A.; Falcone, G.; Pucci, S.; Console, R.; Parsons, T. M ≥ 7 earthquake rupture forecast and time-dependent probability for the Sea of Marmara region, Turkey. J. Geophys. Res. 2016, 121, 2679–2707. [Google Scholar] [CrossRef]
- Hubert-Ferrari, A.; Barka, A.; Jaques, E.; Nalbant, S.S.; Meyer, B.; Armijo, R.; Tapponnier, P.; King, G.C.P. Seismic hazard in the Marmara Sea region following the 17 August 1999 Izmit earthquake. Nature 2000, 404, 269–273. [Google Scholar] [CrossRef]
- Armijo, R.; Pondard, N.; Meyer, B.; Uçarkuş, G.; Mercier de Le’pinay, B.; Malavieille, J.; Dominguez, S.; Gustcher, M.; Schmidt, S.; Beck, C.; et al. Submarine fault scarps in the Sea of Marmara pull-apart (North Anatolian Fault): Ιmplications for seismic hazard in Ιstanbul. Geochem. Geophys. Geosyst. 2005, 6, Q06009. [Google Scholar] [CrossRef]
- Pondard, N.; Armijo, R.; King, G.C.P.; Meyer, B.; Flerit, F. Fault interactins in the Sea of Marmara pull-apart (North Anatolian fault): Earthquake clustering and propagating earthquake sequences. Geophys. J. Int. 2007, 171, 1185–1197. [Google Scholar] [CrossRef]
- Bohnhoff, M.; Bulut, F.; Dresen, G.; Malin, P.E.; Eken, Y.; Aktar, M. An earthquake gap south of Istanbul. Nat. Commun. 2013, 4, 1999. [Google Scholar] [CrossRef]
- Atakan, K.; Ojeda, A.; Meghraoui, M.; Barka, A.; Erdik, M.; Bodare, A. Seismic Hazard in Istanbul following the 17 August 1999 Izmit and 12 November 1999 Düzce earthquakes. Bull. Seismol. Soc. Am. 2002, 92, 466–482. [Google Scholar] [CrossRef]
- Erdik, M.; Demircioğlu, M.; Şeşetyan, K.; Durukal, E.; Siyahi, B. Earthquake hazard in Marmara region, Turkey. Soil Dyn. Earthq. Eng. 2004, 24, 605–631. [Google Scholar] [CrossRef]
- Kalkan, E.; Gülkan, P.; Yılmaz, N.; Çelebi, M. Re-examination of probabilistic seismic hazard in the Marmara Sea region. Bull. Seismol. Soc. Am. 2009, 99, 2127–2146. [Google Scholar] [CrossRef]
- Gulerce, Z.; Ocak, S. Probabilistic seismic hazard assessment of Eastern Marmara Region. Bull. Earthq. Eng. 2013, 11, 1259–1277. [Google Scholar] [CrossRef]
- Sørensen, M.B.; Pulido, N.; Atakan, K. Sensitivity of ground motion simulations to earthquake source parameters: A case study for Istanbul, Turkey. Bull. Seismol. Soc. Am. 2007, 97, 881–900. [Google Scholar] [CrossRef]
- Ansal, A.; Akinci, A.; Cultrera, G.; Erdik, M.; Pessina, V.; Tuzce, G.; Ameri, G. Loss estimation in Istanbul based on deterministic earthquake scenarios in the Marmara Sea region, Turkey. Soil Dyn. Earth. Eng. 2009, 29, 699–709. [Google Scholar] [CrossRef]
- Mert, A.; Fahjan, Y.M.; Hutchings, L.J.; Pınar, A. Physically based probabilistic seismic hazard analysis using broadband ground motion simulation: A case study for the Prince Islands Fault, Marmara Sea. Earth Planets Space 2016, 68, 146. [Google Scholar] [CrossRef]
- Akinci, A.; Aochi, H.; Herrero, A.; Pischiutta, M.; Karanikas, D. Physics-Based Broadband Ground-Motion Simulations for Probable Mw ≥7.0 Earthquakes in the Marmara Sea Region (Turkey). Bull. Seismol. Soc. Am. 2017, 107, 1307–1323. [Google Scholar] [CrossRef]
- Spagnuolo, E.; Akinci, A.; Herrero, A.; Pucci, S. Implementing the effect of the rupture directivity on PSHA for the city of Istanbul, Turkey. Bull. Seismol. Soc. Am. 2016, 106. [Google Scholar] [CrossRef]
- Akinci, A.; Galadini, F.; Pantosti, D.; Petersen, M.; Malagnini, L.; Perkins, D. Effect of Time Dependence on Probabilistic Seismic-Hazard Maps and Deaggregation for the Central Apennines, Italy. Bull. Seism. Soc. Am. 2009, 99, 585–610. [Google Scholar] [CrossRef]
- Akinci, A.; Vannoli, P.; Falcone, G.; Taroni, M.; Tiberti, M.M.; Murru, M.; Burrato, P.; Mariucci, M.T. When time and faults matter: Towards a time-dependent probabilistic SHA in Calabria, Italy. Bull. Earthq. Eng. 2017, 15, 2497–2524. [Google Scholar] [CrossRef]
- Pagani, M.; Monelli, D.; Weatherill, G.; Danciu, L.; Crowley, H.; Silva, V.; Henshaw, P.; Butler, L.; Nastasi, M.; Panzeri, L.; et al. OpenQuake Engine: An open hazard (and risk) software for the Global Earthquake Model. Seismol. Res. Lett. 2014, 85, 692–702. [Google Scholar] [CrossRef]
- Erdik, M.; Biro, Y.; Onur, T.; Sesetyan, K.; Birgoren, G. Assessment of earthquake hazard in Turkey and neighboring regions. Ann. Geofis. 1999, 42, 1125–1138. [Google Scholar]
- Youngs, R.R.; Coppersmith, K.J. Implications of fault slip rates and earthquake recurrence models to probabilistic seismic hazard estimates. Bull. Seismol. Soc. Am. 1985, 75, 939–964. [Google Scholar] [CrossRef]
- Ambraseys, N.N.; Simpson, K.A.; Bommer, J.J. Prediction of Horizontal Response Spectra in Europe. Earthq. Eng. Struct. Dyn. 1996, 25, 371–400. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B.; Fumal, T.E. Equations for estimating horizontal response spectra and peak acceleration from Western North American earthquakes: A summary of recent work. Seismol. Res. Lett. 1997, 68, 128–153. [Google Scholar] [CrossRef]
- Campbell, K.W. Empirical Near-Source Attenuation Relationships for Horizontal and Vertical Components of Peak Ground Acceleration, Peak Ground Velocity, and Pseudo-Absolute Acceleration Response Spectra. Seismol. Res. Lett. 1997, 68, 154–179. [Google Scholar] [CrossRef]
- Sadigh, K.; Chang, C.Y.; Egan, J.A.; Makdisi, F.; Youngs, R.R. Attenuation Relationships for Shallow Crustal Earthquakes Based on California Strong Motion Data. Seismol. Res. Lett. 1997, 68, 180–189. [Google Scholar] [CrossRef]
- Boore, D.M.; Atkinson, G.A. Ground motion prediction equations for the average horizontal component of PGA, PGV, PGD, and 5% damped PSA art spectral periods between 0.01 s and 10.0 s. Earthq. Spectra 2008, 24, 99–138. [Google Scholar] [CrossRef]
- Campbell, K.W.; Bozorgnia, Y. NGA ground motion model for the geometric mean horizontal component of PGA, PGV, PGD and 5% damped linear elastic response spectra for periods ranging from 0.01 to 10 s. Earthq. Spectra 2008, 24, 139–171. [Google Scholar] [CrossRef]
- Chiou, B.S.J.; Youngs, R.R. An NGA model for the average horizontal component of peak ground motion and response spectra. Earthq. Spectra 2008, 24, 173–215. [Google Scholar] [CrossRef]
- Kalkan, E.; Gülkan, P. Site-dependent spectra derived from ground motion records in Turkey. Earthq. Spectra 2004, 20, 1111–1138. [Google Scholar] [CrossRef]
- Abrahamson, N.A.; Silva, W.J. Summary of the Abrahamson & Silva NGA ground-motion relations. Earthq. Spectra 2008, 24, 67–97. [Google Scholar]
- Idriss, I.M. An NGA empirical model for estimating the horizontal spectral values generated by shallow crustal earthquakes. Earthq. Spectra 2008, 24, 217–242. [Google Scholar] [CrossRef]
- Stucchi, M.; Rovida, A.; Gomez Capera, A.A.; Alexandre, P.; Camelbeeck, T.; Demircioglu, M.B.; Gasperini, P.; Kouskouna, V.; Musson, R.M.W.; Radulian, M.; et al. The SHARE European Earthquake Catalogue (SHEEC) 1000–1899. J. Seismol. 2012, 17, 523–544. [Google Scholar] [CrossRef]
- Albini, P.; Musson, R.M.W.; Gomez Capera, A.A.; Locati, M.; Rovida, A.; Stucchi, M.; Viganò, D. Global Historical Earthquake Archive and Catalogue (1000–1903); GEM Foundation: Pavia, Italy, 2013. [Google Scholar]
- Albini, P.; Musson, R.M.W.; Rovida, A.; Locati, M.; Gomez Capera, A.A.; Viganò, D. The Global Earthquake History. Earthq. Spectra 2014, 30, 607–624. [Google Scholar] [CrossRef]
- Storchak, D.A.; Di Giacomo, D.; Bondar, I.; Engdahl, E.R.; Harris, J.; Lee, W.H.; Villaseñor, A.; Bormann, P. Public release of the ISC-GEM global instrumental earthquake catalogue (1900–2009). Seismol. Res. Lett. 2013, 84, 10–815. [Google Scholar] [CrossRef]
- Kadirioğlu, F.T.; Kartal, R.F.; Kılıç, T.; Kalafat, D.; Duman, T.Y.; Azak, T.E.; Özalp, S.; Emre, Ö. An improved earthquake catalogue (M ≥ 4.0) for Turkey and its near vicinity (1900–2012). Bull. Earthq. Eng. 2016, 16. [Google Scholar] [CrossRef]
- Guidoboni, E.; Comastri, A. Catalogue of Earthquakes and Tsunamis in the Mediterranean Area from the 11th to the 15th Century; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2005. [Google Scholar]
- Ambraseys, N. Earthquakes in the Mediterranean and Middle East: A Multidisciplinary Study of Seismicity up to 1900; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gardner, J.K.; Knopoff, L. Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian? Bull. Seismol. Soc. Am. 1974, 64, 1363–1367. [Google Scholar]
- Barka, A.A. Slip distribution along the North Anatolian fault associated with the large earthquakes of the period 1939 to 1967. Bull. Seismol. Soc. Am. 1996, 86, 238–1254. [Google Scholar]
- Wong, H.K.; Lüdmann, T.; Uluğ, A.; Görür, N. The Sea of Marmara: A plate boundary sea in an escape tectonic regime. Tectonophysics 1995, 244, 231–250. [Google Scholar] [CrossRef]
- Armijo, R.; Meyer, B.; Hubert, A.; Barka, A. Westwards propagation of the North Anatolian fault into the northern Aegean: Timing and kinematics. Geology 1999, 27, 267–270. [Google Scholar] [CrossRef]
- Armijo, R.; Meyer, B.; Navarro, S.; King, G.; Barka, A. Asymmetric slip partitioning in the Sea of Marmara pull-apart: A clue to propagation processes of the North Anatolian fault? Terra Nova 2002, 14, 80–86. [Google Scholar] [CrossRef]
- Okay, A.; Demirbağ, E.; Kurt, H.; Okay, N.; Kuşcu, I. An active, deep marine strike-slip basin along the North Anatolian fault in Turkey. Tectonics 1999, 18, 129–147. [Google Scholar] [CrossRef]
- Le Pichon, X.; Şengör, A.M.C.; Demirbağ, E.; Rangin, C.; İmren, C.; Armijo, R.; Görür, N.; Çağatay, N.; Mercier de Lepinay, B.; Meyer, B.; et al. The active Main Marmara fault. Earth Planet. Sci. Lett. 2001, 192, 595–616. [Google Scholar] [CrossRef]
- Yaltırak, C. Tectonic evaluation of Marmara Sea and its surroundings. Mar. Geol. 2002, 3175, 1–37. [Google Scholar] [CrossRef]
- McNeill, L.C.; Mille, A.; Minshull, T.A.; Bull, J.M.; Kenyon, N.H.; Ivanov, M. Extension of the North Anatolian fault into the North Aegean trough: Evidence for transtension, strain partitioning, and analogues for Sea of Marmara basin models. Tectonics 2004, 23. [Google Scholar] [CrossRef]
- Barka, A.; Kadinsky-Cade, K. Strike-slip fault geometry in Turkey and its influence on earthquake activity. Tectonics 1988, 7, 663–684. [Google Scholar] [CrossRef]
- Emre, Ö.; Duman, T.Y.; Özalp, S.; Elmacı, H.; Olgun, Ş.; Şaroğlu, Ş. Active fault map of Turkey with explanatory text. Available online: http://www.mta.gov.tr/eng/maps/active-fault-1250000 (accessed on 14 November 2019).
- Hergert, T.; Heidbach, O. Slip-rate variability and distributed deformation in the Marmara Sea fault system. Nat. Geosci. 2010, 3, 132–135. [Google Scholar] [CrossRef]
- Aksu, A.E.; Calon, T.J.; Hiscott, R.N.; Yasar, D. Anatomy of the North Anatolian fault zone in the Marmara Sea, western Turkey: Extensional basins above a continental transform. GSA Today 2000, 6, 3–7. [Google Scholar]
- Imren, C.; Le Pichon, X.; Rangin, C.; Demirbag, E.; Ecevitoglu, B.; Görür, N. The North Anatolian fault within the Sea of Marmara: A new interpretation based on multi-channel seismic and multi-beam bathymetry data. Earth Planet. Sci. Lett. 2001, 186, 143–158. [Google Scholar] [CrossRef]
- Ergintav, S.; Reilinger, R.E.; Çakmak, R.; Floyd, M.; Cakir, Z.; Doğan, U.; King, R.W.; McClusky, S.; Özener, H. Istanbul’s earthquake hot spots: Geodetic constraints on strain accumulation along faults in the Marmara seismic gap. Geophys. Res. Lett. 2014, 41, 5783–5788. [Google Scholar] [CrossRef]
- Meade, B.; Hager, B.; McClusky, S.; Reilinger, R.E.; Ergintav, S.; Lenk, O.; Barka, A.; Özener, H. Estimates of seismic potential in the Marmara Sea region from block models of secular deformation constrained by global positioning system measurements. Bull. Seismol. Soc. Am. 2002, 92, 208–215. [Google Scholar] [CrossRef]
- Selim, H.H.; Tüysüz, O.; Karakas, A.; Tas, K.O. Morphotectonic evidence from € the southern branch of the North Anatolian Fault (NAF) and basins of the south Marmara sub-region, NW Turkey. Quat. Int. 2013, 292, 176–192. [Google Scholar] [CrossRef]
- Straub, C.; Kahle, H.G.; Schindler, C. GPS and geological estimates of the tectonic activity in the Marmara Sea region, NW Anatolia. J. Geophys. Res. 1997, 102, 27587–27601. [Google Scholar] [CrossRef]
- Frankel, A. Mapping seismic hazard in the Central and Eastern United States. Seismol. Res. Lett. 1995, 66, 8–21. [Google Scholar] [CrossRef]
- Akinci, A. HAZGRIDX: Earthquake Forecasting Model for ML ≥ 5.0 Earthquakes in Italy Based on Spatially Smoothed Seismicity. Ann. Geophys. 2010, 53, 51–61. [Google Scholar] [CrossRef]
- Schwartz, D.P.; Coppersmith, K.J. Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas fault zones. J. Geophys. Res. 1984, 89, 5681–5698. [Google Scholar] [CrossRef]
- Field, E.H.; Jackson, D.D.; Dolan, J.F. A mutually consistent seismic-hazard source model for Southern California. Bull. Seismol. Soc. Am. 1999, 89, 559–578. [Google Scholar]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1949, 34, 185–188. [Google Scholar]
- Weichert, D.H. Estimation of the earthquake recurrence parameters for unequal observation periods for different magnitudes. Bull. Seismol. Soc. Am. 1980, 70, 1337–1346. [Google Scholar]
- Wells, D.L.; Coppersmith, K.J. Empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Hanks, T.C.; Kanamori, H.A. Moment Magnitude Scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Matthews, M.V.; Ellsworth, W.L.; Reasenberg, P.A. A Brownian model for recurrent earthquakes. Bull. Seismol. Soc. Am. 2002, 92, 2233–2250. [Google Scholar] [CrossRef]
- Ellsworth, W.L.; Matthews, M.V.; Nadeau, R.M.; Nishenko, S.P.; Reasenberg, P.A.; Simpson, R.W. A physically based earthquake recurrence model for estimation of long-term earthquake probabilities. US Geol. Surv. Open File Rep. 1999, 522, 23. [Google Scholar]
- Wu, S.C.; Cornell, C.A.; Winterstein, S.R. A hybrid recurrence model and its implication on seismic hazard results. Bull. Seismol. Soc. Am. 1995, 85, 1–16. [Google Scholar]
- Working Group Calif. Earthquake Probabilities (WGCEP) Seismic hazards in southern California: Probable earthquakes, 1994–2014. Bull. Seismol. Soc. Am. 1995, 85, 379–439. [Google Scholar]
- Reiter, L. Earthquake Hazard Analysis: Issues and Insights; Columbia University Press: New York, NY, USA, 1990. [Google Scholar]
- Akkar, S.; Kale, Ö.; Yakut, A.; Çeken, U. Ground-motion characterization for the probabilistic seismic hazard assessment in Turkey. Bull. Earthq. Eng. 2018, 16, 3439–3463. [Google Scholar] [CrossRef]
- Akkar, S.; Eroğlu Azak, T.; Çan, T.; Çeken, U.; Demircioğlu Tümsa, M.B.; Duman, T.Y.; Erdik, Ö.M.; Ergintav, S.; Kadirioğlu, F.T.; Kalafat, D.; et al. Evolution of seismic hazard maps in Turkey. Bull. Earthq. Eng. 2018, 16, 3197–3228. [Google Scholar] [CrossRef]
- Şeşetyan, K.; Demircioğlu, M.B.; Duman, T.; Çan, T.; Tekin, S.; Eroğlu, T.; Zulfikar Fercan, Ö. A probabilistic seismic hazard assessment for the Turkish territory—Part I: The area source model. Bull. Earthq. Eng. 2018, 16, 3367–3397. [Google Scholar] [CrossRef]
- Demircioglu, M.B.; Sesetyan, K.; Duman, T.Y.; Çan, T.; Tekin, S.; Ergintav, S. A probabilistic seismic hazard assessment for the Turkish territory: Part II—Fault source and background seismicity model. Bull. Earthq. Eng. 2018, 16, 3399–3438. [Google Scholar] [CrossRef]
- Akkar, S.; Cağnan, Z. A Local Ground-Motion Predictive Model for Turkey, and Its Comparison with Other Regional and Global Ground-Motion Models. Bull. Seismol. Soc. Am. 2010, 100, 2978–2995. [Google Scholar] [CrossRef]
- Akkar, S.; Sandıkkaya, M.A.; Bommer, J.J. Empirical ground-motion models for point-and extended-source crustal earthquake scenarios in Europe and the Middle East. Bull. Earthq. Eng. 2014, 12, 359–387. [Google Scholar] [CrossRef]
- Zhao, J.X.; Zhang, J.; Asano, A.; Ohno, Y.; Oouchi, T.; Takahashi, T.; Ogawa, H.; Irikura, K.; Thio, H.K.; Somerville, P.G.; et al. Attenuation relations of strong ground motion in Japan using site classification based on predominant period. Bull. Seismol. Soc. Am. 2006, 96, 898–913. [Google Scholar] [CrossRef]

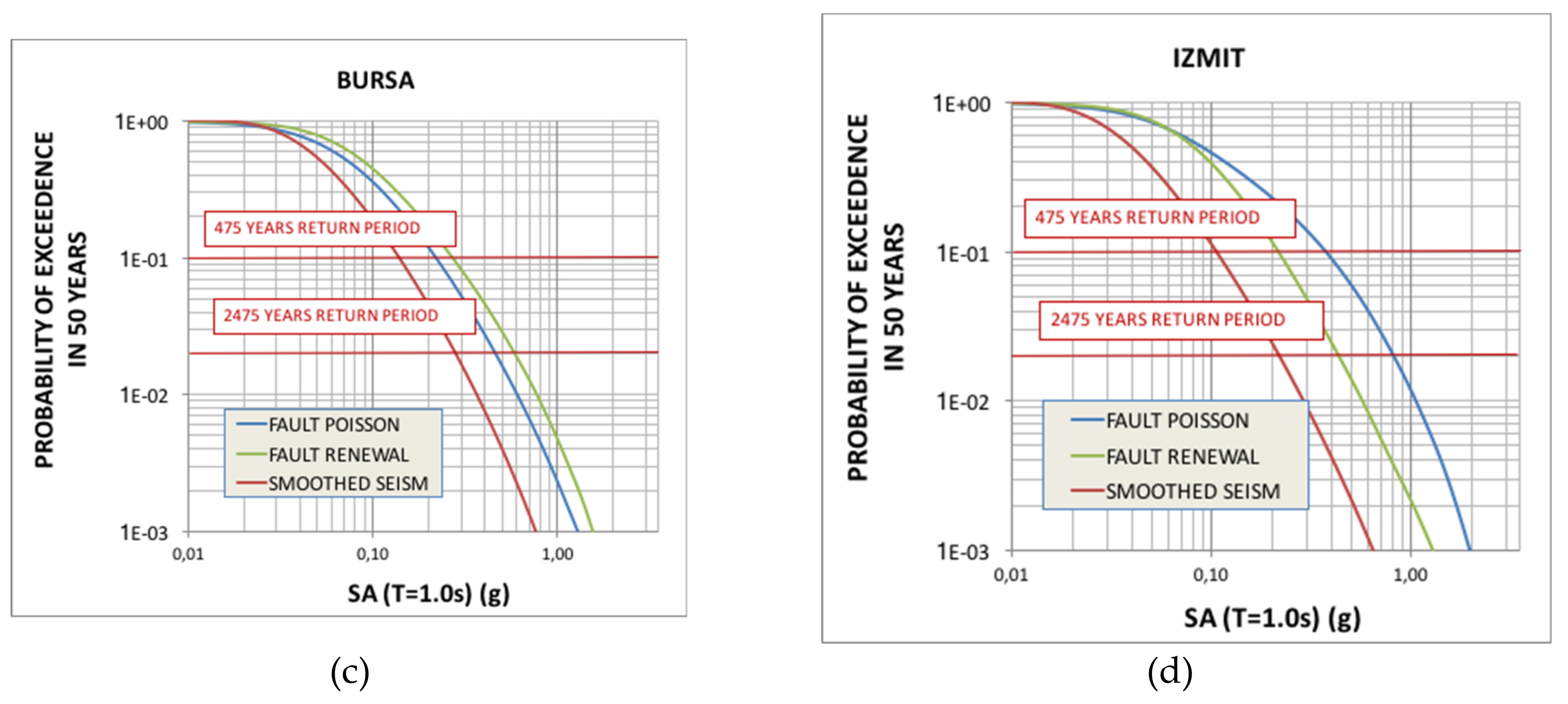
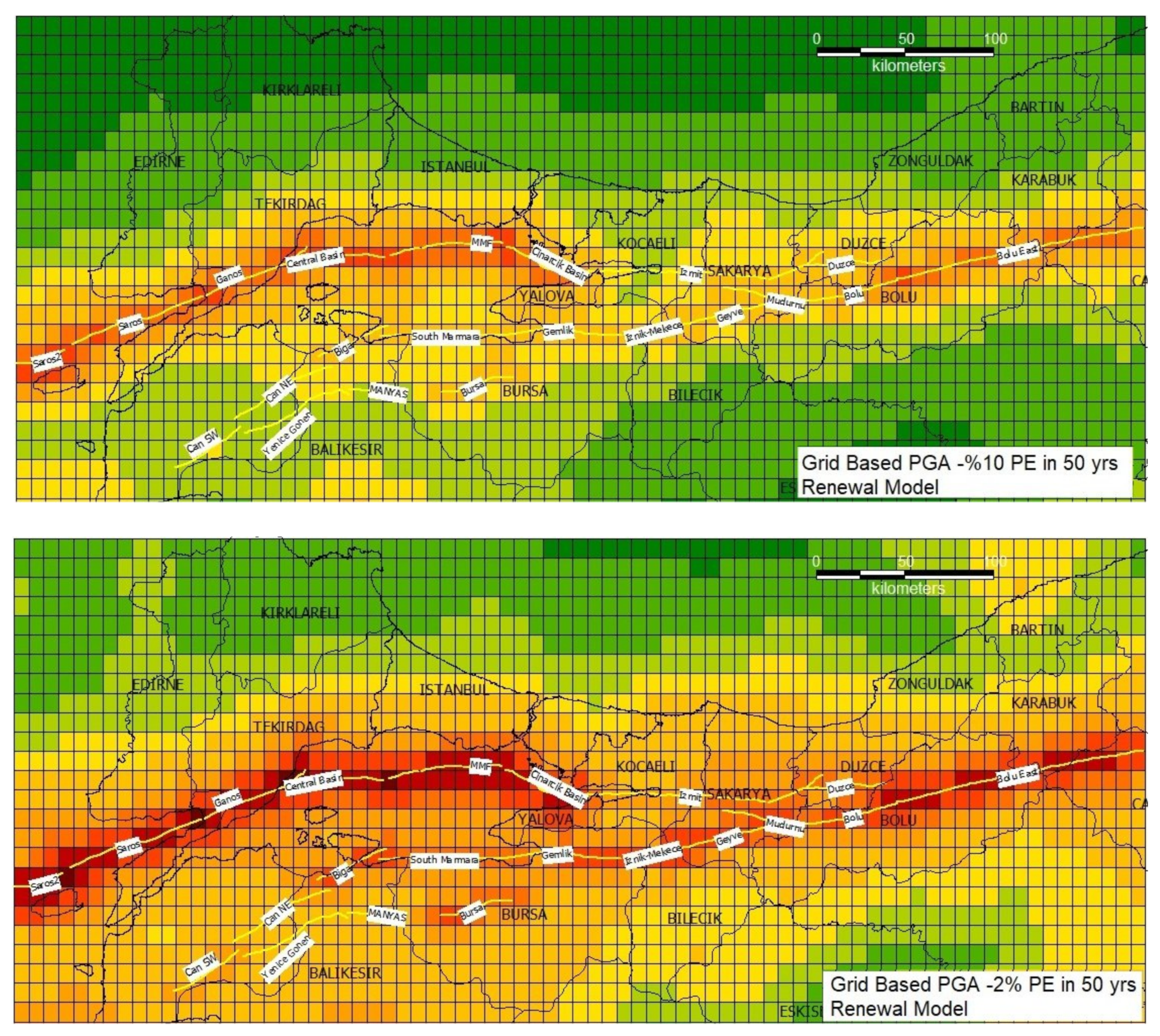
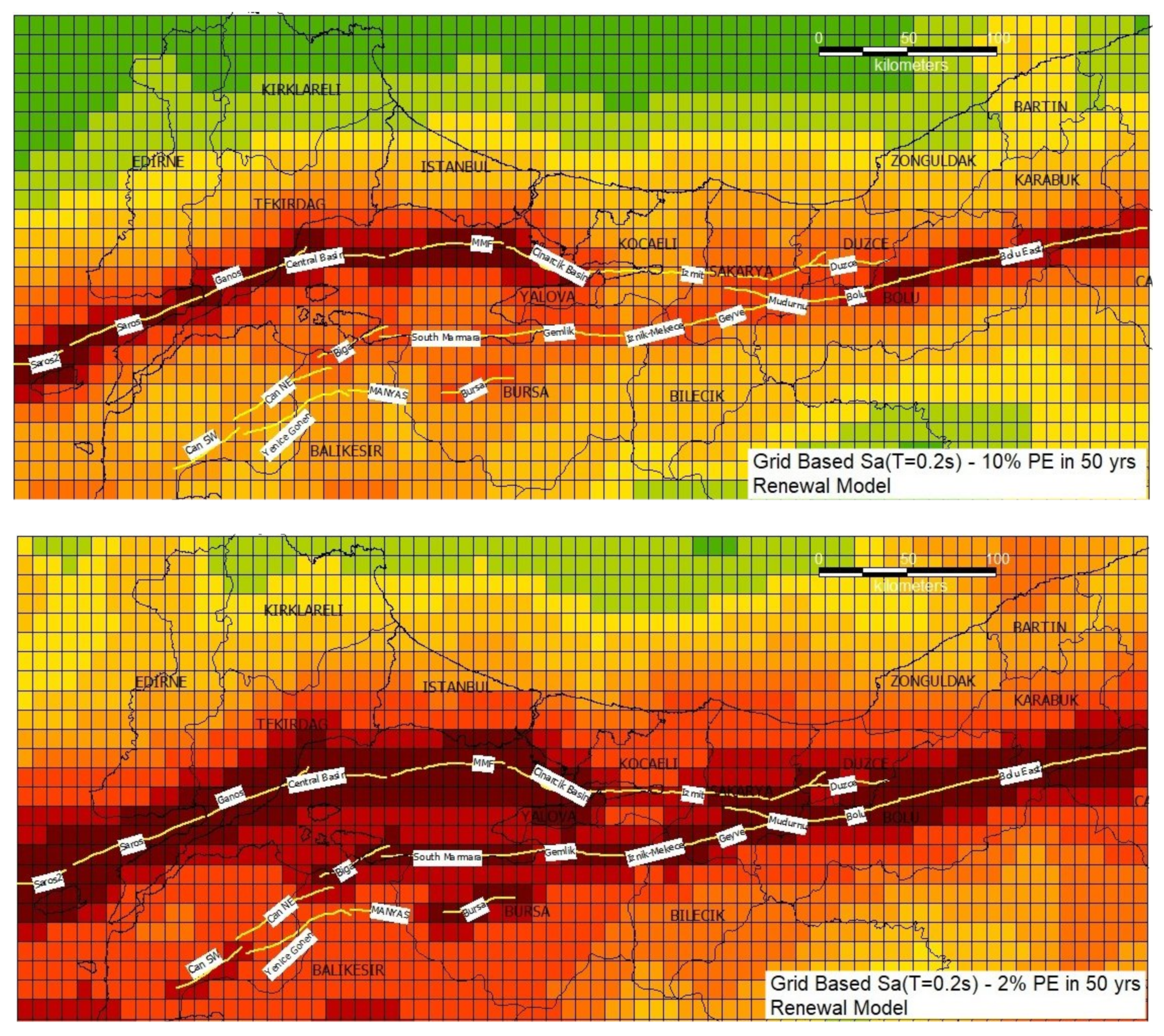
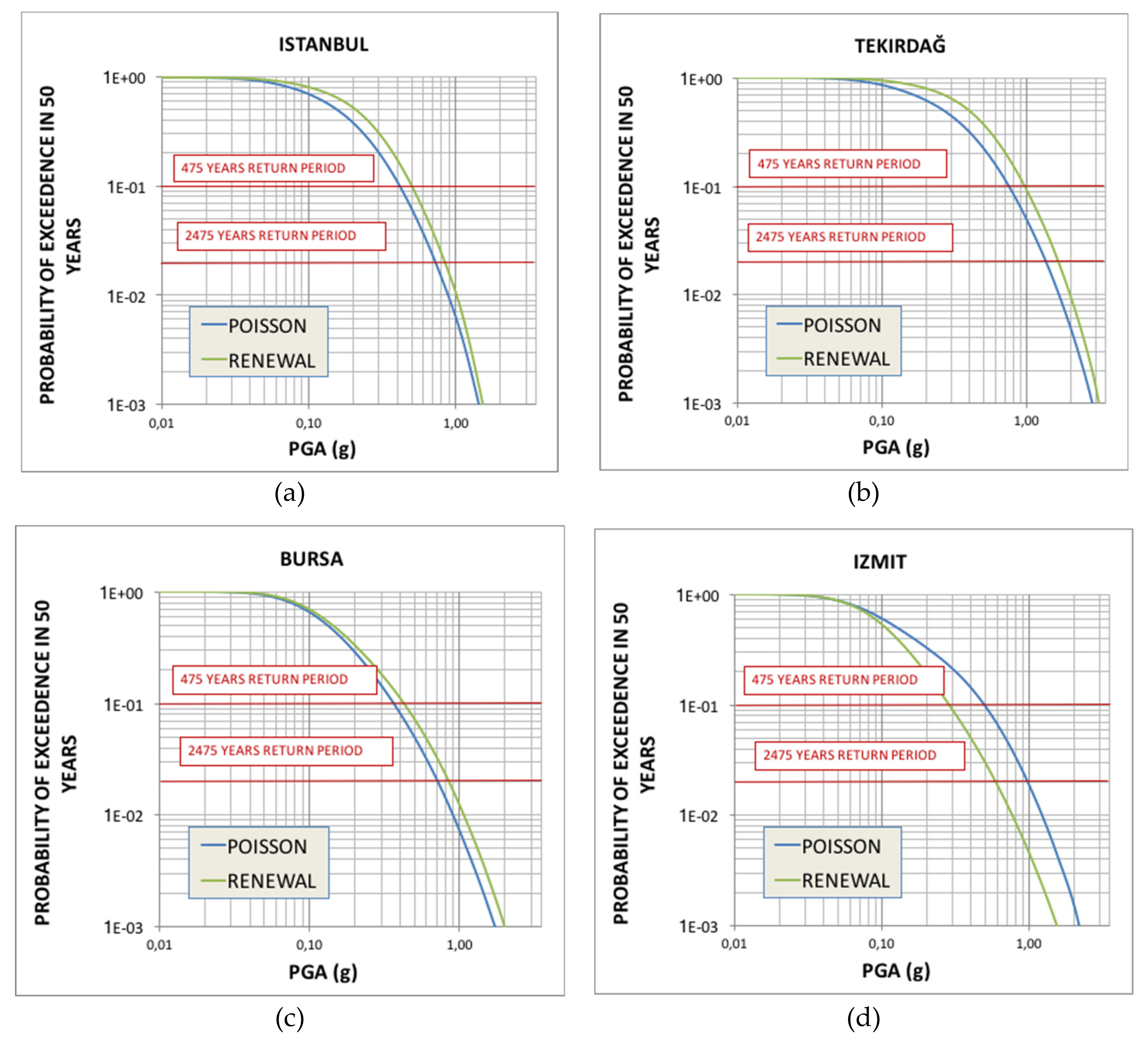
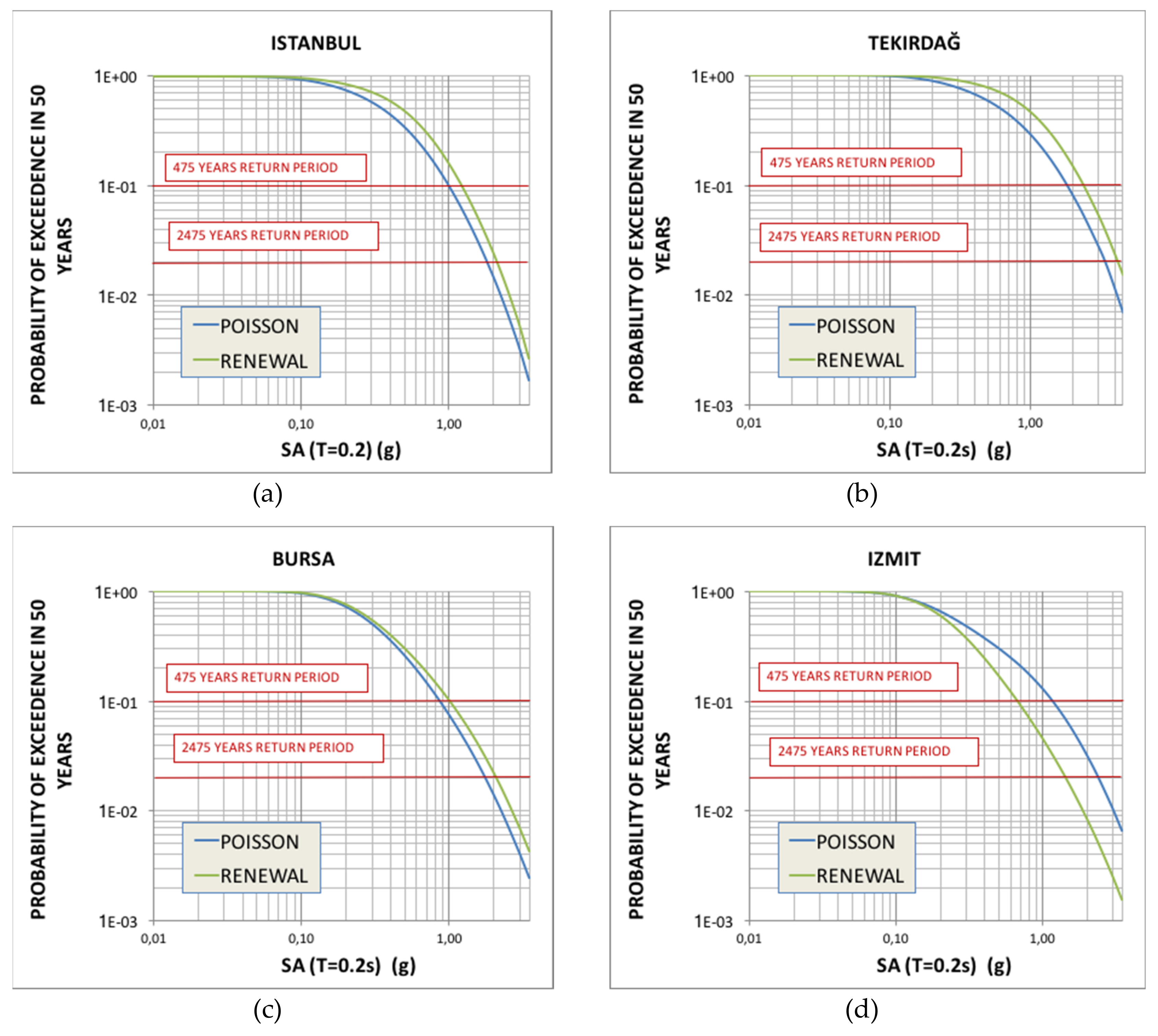

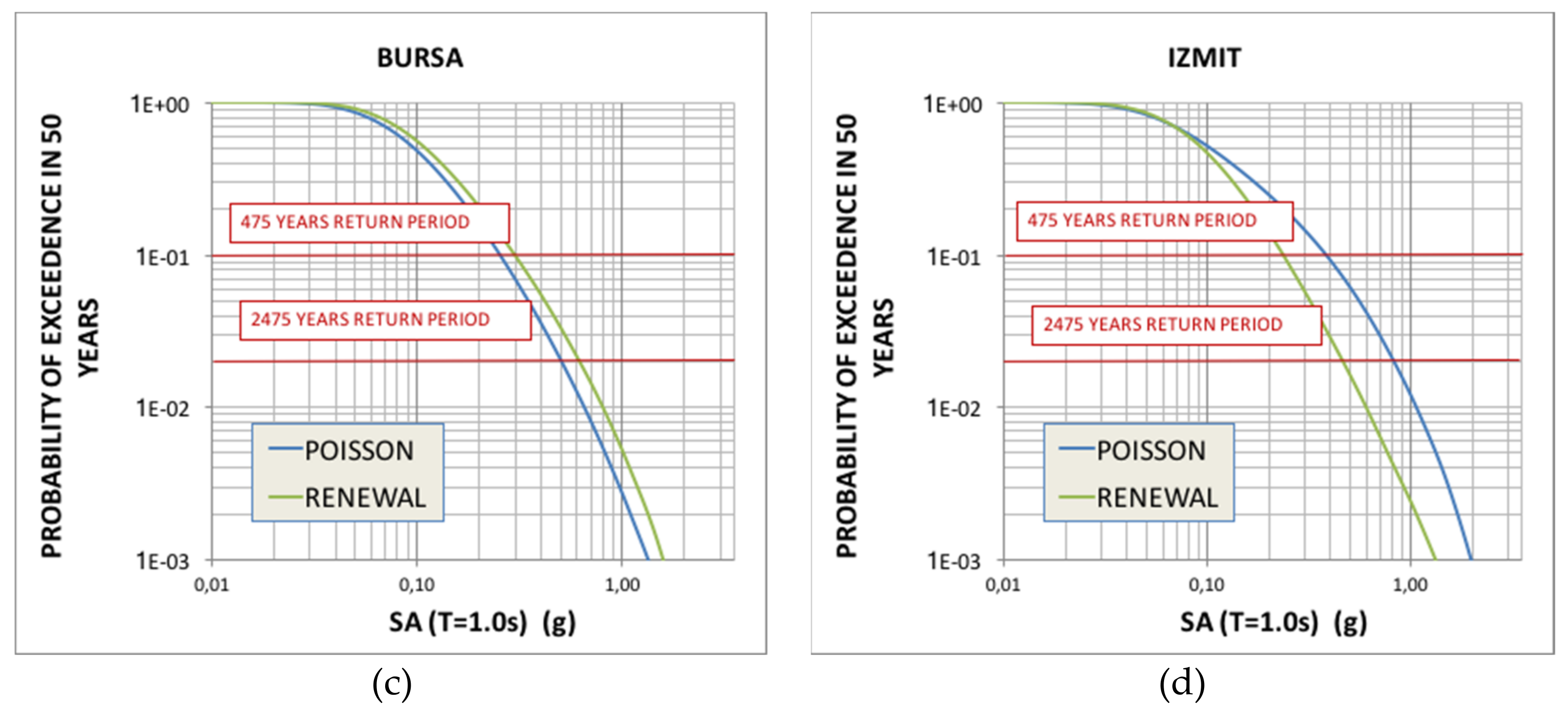

| PGA 475 years | ||||
|---|---|---|---|---|
| Time Dependent Model | Poisson Model | |||
| Model | Istanbul | İzmit | İstanbul | İzmit |
| Atakan et al. [8] | Between 0.20–0.26 | - | - | |
| Erdik et al. [9] | 0.45g | 0.35g | 0.37g | 0.77g |
| Kalkan and Gülkan [10] | Between 0.30–0.40g | Between 0.40–0.60g | - | - |
| Gülerce and Ocak [11] | - | - | - | 0.70g |
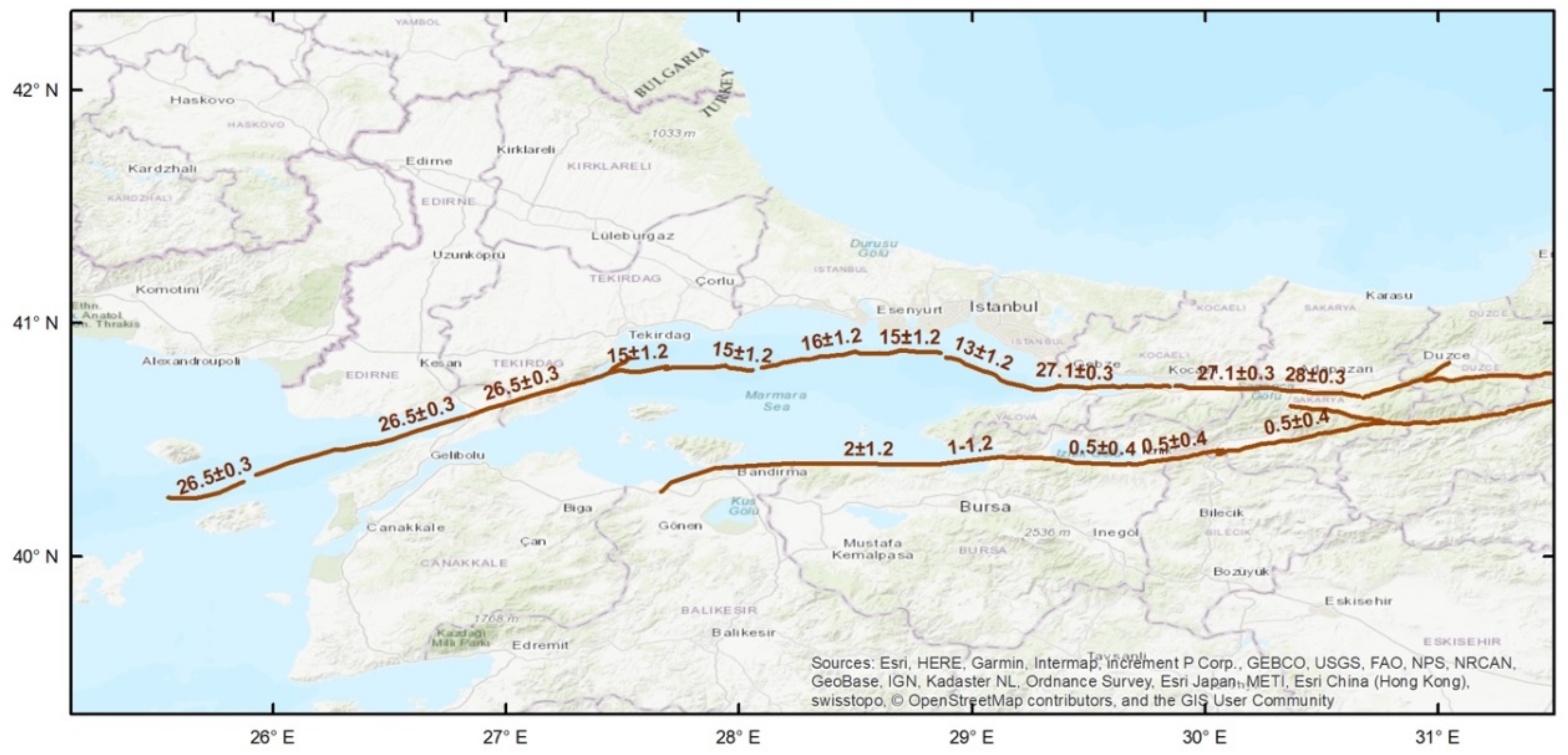
| Segment Name | Length (km) | Width (km) | Dip Angle | Slip Rate (mm/yr) | Fault Type | Associated Historical Events |
|---|---|---|---|---|---|---|
| Eastern Marmara Segments | ||||||
| Bolu East | 145 | 15 | 87.5 | 23.5 | SSF | 1668, 1944 |
| Bolu | 37 | 15 | 90 | 10 | SSF | 1957 |
| Mudurnu | 67 | 15 | 87.5 | 10 | SSF | 1967 |
| Duzce | 47 | 15 | 87.5 | 15 | SSF | 1999 |
| Northern Branch Segments | ||||||
| Izmit | 144 | 15 | 87.5 | 20 | SSF | 1719, 1999 |
| Cinarcik Basin | 46 | 15 | 70 | 14 | NSSF | 1231, 1754, 1894 |
| MMF | 66 | 15 | 87.5 | 18 | SSF | 1509, 1766 |
| Central Basin | 54 | 15 | 85 | 18 | NSSF | 1343 |
| Ganos | 66 | 15 | 82.5 | 19 | SSF | 1063, 1354, 1766, 1912 |
| Saros | 81 | 15 | 85 | 20 | SSF | 1859 |
| Saros2 | 29 | 15 | 70 | 20 | SSF | 1912 |
| Central and Southern Branch Segments | ||||||
| Geyve | 63 | 15 | 87.5 | 5 | SSF | 1296 |
| Iznik-Mekece | 63 | 15 | 87.5 | 4 | SSF | 1419 |
| Gemlik | 41 | 15 | 87.5 | 4 | SSF | 1855 |
| South Marmara | 71 | 15 | 87.5 | 3 | SSF | 1556 |
| Biga | 45 | 15 | 87.5 | 3 | SSF | 123 |
| Can NE | 65 | 15 | 87.5 | 2 | SSF | 1737 |
| Can SW | 46 | 15 | 87.5 | 2 | SSF | - |
| Bursa | 43 | 15 | 87.5 | 3.5 | SSF | 1143 |
| Manyas | 33 | 15 | 87.5 | 3 | SSF | 1964 |
| Yenice-Gonen | 68 | 15 | 87.5 | 2 | SSF | 1953 |
| Segment Name | Area L (km) × W (km) | Characteristic Magnitude | Slip Rate (mm/yr) | Fault Type | Return Period (yr) | Annual Rate (Poisson) |
|---|---|---|---|---|---|---|
| Bolu East | 145 × 15 | 7.5 | 23.5 | SSF | 130 | 0.00769 |
| Bolu | 37 × 15 | 6.9 | 10 | SSF | 150 | 0.00667 |
| Mudurnu | 67 × 15 | 7.2 | 10 | SSF | 235 | 0.00426 |
| Duzce | 47 × 15 | 7.1 | 15 | SSF | 160 | 0.00625 |
| Izmit | 144 × 15 | 7.5 | 20 | SSF | 155 | 0.00645 |
| Cinarcik Basin | 46 × 15 | 7.1 | 14 | NSSF | 175 | 0.00571 |
| MMF | 66 × 15 | 7.2 | 18 | SSF | 130 | 0.00769 |
| Central Basin | 54 × 15 | 7.1 | 18 | NSSF | 115 | 0.0087 |
| Ganos | 66 × 15 | 7.2 | 19 | SSF | 125 | 0.008 |
| Saros | 81 × 15 | 7.3 | 20 | SSF | 140 | 0.00714 |
| Saros2 | 29 × 15 | 6.8 | 20 | SSF | 70 | 0.01429 |
| Geyve | 63 × 15 | 7.2 | 5 | SSF | 500 | 0.002 |
| Iznik- Mekece | 63 × 15 | 7.2 | 4 | SSF | 625 | 0.0016 |
| Gemlik | 41 × 15 | 7 | 4 | SSF | 480 | 0.00208 |
| South Marmara | 71 × 15 | 7.2 | 3 | SSF | 750 | 0.00133 |
| Biga | 45 × 15 | 7.1 | 3 | SSF | 825 | 0.00121 |
| Can NE | 65 × 15 | 7.2 | 2 | SSF | 1200 | 0.00083 |
| Can SW | 46 × 15 | 7.1 | 2 | SSF | 1200 | 0.00083 |
| Bursa | 43 × 15 | 7.1 | 3.5 | SSF | 740 | 0.00135 |
| Manyas | 33 × 15 | 6.9 | 3 | SSF | 565 | 0.00177 |
| Yenice- Gonen | 68 × 15 | 7.2 | 2 | SSF | 1150 | 0.00087 |
| Segment Name | Annual Rate (Poisson Model) | Last Characteristic Event | Time Since Last Characteristic Event | 50 Year Conditional Probability (Renewal) | Annual Rate (Renewal Model) |
|---|---|---|---|---|---|
| Bolu East | 0.00769 | 1944 | 71 | 0.45299 | 0.01207 |
| Bolu | 0.00667 | 1957 | 58 | 0.3042 | 0.00725 |
| Mudurnu | 0.00426 | 1967 | 48 | 0.05209 | 0.00107 |
| Duzce | 0.00625 | 1999 | 16 | 0.04992 | 0.00102 |
| Izmit | 0.00645 | 1999 | 16 | 0.05769 | 0.00119 |
| Cinarcik Basin | 0.00571 | 1894 | 121 | 0.39448 | 0.01003 |
| MMF | 0.00769 | 1766 | 249 | 0.58186 | 0.01744 |
| Central Basin | 0.0087 | 1343 | 672 | 0.58835 | 0.01775 |
| Ganos | 0.008 | 1912 | 103 | 0.54558 | 0.01577 |
| Saros | 0.00714 | 1859 | 156 | 0.53494 | 0.01531 |
| Saros2 | 0.01429 | 1912 | 103 | 0.79969 | 0.03216 |
| Geyve | 0.002 | 1296 | 719 | 0.19793 | 0.00441 |
| Iznik- Mekece | 0.0016 | 1419 | 596 | 0.14505 | 0.00313 |
| Gemlik | 0.00208 | 1855 | 160 | 0.04967 | 0.00102 |
| South Marmara | 0.00133 | 1556 | 459 | 0.0886 | 0.00186 |
| Biga | 0.00121 | 123 | 1892 | 0.12705 | 0.00272 |
| Can NE | 0.00083 | 1737 | 278 | 0.00326 | 0.00007 |
| Can SW | 0.00083 | - | 1000 | 0.07225 | 0.0015 |
| Bursa | 0.00135 | 1143 | 872 | 0.13294 | 0.00285 |
| Manyas | 0.00177 | 1964 | 51 | 0.00005 | 0 |
| Yenice- Gonen | 0.00087 | 1953 | 62 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şeşetyan, K.; Demircioğlu Tümsa, M.B.; Akinci, A. Evaluation of The Seismic Hazard in The Marmara Region (Turkey) Based on Updated Databases. Geosciences 2019, 9, 489. https://doi.org/10.3390/geosciences9120489
Şeşetyan K, Demircioğlu Tümsa MB, Akinci A. Evaluation of The Seismic Hazard in The Marmara Region (Turkey) Based on Updated Databases. Geosciences. 2019; 9(12):489. https://doi.org/10.3390/geosciences9120489
Chicago/Turabian StyleŞeşetyan, Karin, Mine Betül Demircioğlu Tümsa, and Aybige Akinci. 2019. "Evaluation of The Seismic Hazard in The Marmara Region (Turkey) Based on Updated Databases" Geosciences 9, no. 12: 489. https://doi.org/10.3390/geosciences9120489
APA StyleŞeşetyan, K., Demircioğlu Tümsa, M. B., & Akinci, A. (2019). Evaluation of The Seismic Hazard in The Marmara Region (Turkey) Based on Updated Databases. Geosciences, 9(12), 489. https://doi.org/10.3390/geosciences9120489




