Abstract
Pounding between adjacent buildings during ground motion may result in structural damage or lead to total destruction of structures. The research on the phenomenon has recently been much advanced; however, the analyses have been carried out only for concrete, steel, and masonry structures, while pounding between wooden buildings has not been studied so far. The aim of this paper is to show the results of detailed non-linear seismic analysis of inter-story pounding between the wood-framed buildings modelled by using the finite element method. Firstly, the modal analysis of the structures was conducted. Then, the detailed non-linear analysis of earthquake-induced collisions between two wood-framed buildings of different heights was carried out. The results of the analysis indicate that the behavior of both structures in the longitudinal as well as in the transverse direction is significantly influenced by interactions. The response of the taller building is increased in both directions. On the other hand, the response of the lower building is decreased in the longitudinal direction, while it is increased in the transverse one. The results of the study presented in the paper indicate that, due to deformability of buildings made of wood, structural interactions may change their responses much more, as compared to steel, reinforced concrete, or masonry structures.
1. Introduction
During devastating ground motion, interactions between neighboring, insufficiently separated buildings, or bridge segments, have often been observed [1,2]. Past and recent investigations have confirmed that this phenomenon may result in substantial damage of colliding structures and even lead to their total collapse. For example, significant pounding-involved damage between neighboring parts of school buildings was observed after the Athens earthquake of 1999 [3]. During the Kocaeli (Izmit) earthquake of 1999, structural collisions resulted in substantial damage at points of contact. During the Mexico City earthquake of 1985, significant structural damage of buildings resulted from structural interactions [4]. Pounding damage was also observed after other ground motion (see [5] for more details).
A major reason of pounding between neighboring buildings is related to the differences in dynamic characteristics of the structures. These differences lead to the out-of-phase vibrations and finally to interactions during the time of ground motion [6,7,8,9]. Pounding between adjacent buildings has been investigated for more than three decades applying different models of structures. The basic research on pounding between insufficiently separated buildings in series was carried out by Anagnostopoulos [10] by using single degree-of-freedom systems. Further studies were conducted applying discrete multi degree-of-freedom models assuming that the mass of each story is lumped at floor level. The analyses were carried out for buildings with different properties, including differences in mass, stiffness, and heights (see, for example [11,12,13,14,15,16,17]).
The Finite Element Method (FEM) has also been used in recent years to conduct more detailed non-linear analyses of interactions between adjacent buildings during ground motion [18,19,20,21,22,23,24]. In particular, non-linear strain rate investigation on earthquake-induced collisions between two steel buildings with different number of stories was conducted in [18]. Jameel et al. [19] focused their FEM analysis on earthquake-induced pounding between two neighboring multi-story reinforced concrete frame structures with different heights. Favvata et al. [20] presented a broad seismic analysis between a reinforced concrete structure and a steel frame structure. The results of the study, presented in terms of displacements, ductility requirements, flexural demands, and shear demands, showed that interactions can be dangerous to both structures. The influence of masonry infill panels on earthquake-induced pounding-involved response of adjacent steel frame buildings in series was also numerically studied in [21] for three different configurations of structures. Bi et al. [22] studied collisions between a symmetric rectangular-shaped building and an asymmetric L-shaped building by using the explicit finite element code. They underlined that for the asymmetric buildings subjected to earthquake loading, torsional vibration modes of the structures are excited, which in turn may significantly change the structural responses. Hughes et al. [23] presented a three-dimensional finite element model of the experimental system used to study earthquake-induced structural pounding. The results of the experiment were compared with the results of numerical simulations using the FEM. In addition, different levels of complexity were tested for the finite element model to investigate the influence of pounding on structural response. The analysis on the influence of soil-structure interaction on seismic pounding between steel-frame buildings considering the effect of infill panels was also conducted [24].
Although the research on structural interactions during ground motion has recently been advanced significantly, analyses have been carried out only for concrete, steel, and masonry structures, while collisions between wooden buildings have not been studied so far. Moreover, most of the analyses have been focused on slab-to-slab interactions, whereas slab-to-column collisions can be much more dangerous (see [25,26]). Additionally, many investigations have been conducted using very simplified lumped mass models of structures. Therefore, the aim of this paper is to show the results of detailed non-linear seismic analysis of inter-story pounding between wood-framed buildings modelled by using the FEM.
2. Materials and Methods
2.1. Numerical Analysis of Interactions between Wood-Framed Buildings
2.1.1. Subject of the Analysis
The numerical study was focused on interactions between two wood-framed buildings under earthquake excitation. The first of them, a taller one (building A) is a seven-story structure with total dimensions equal to 30 m (width), 33 m (length), and 25 m (height). The longitudinal cross section of the structure is shown in Figure 1. The plans of its ground floor and the first floor are presented in Figure 2, while the plan of the upper floors (typical story layout) is shown in Figure 3. The second building, a lower one (building B) is a four-story structure with the plan of each floor identical to the plan of upper floors of building A (see Figure 3). Its height is equal to 14.5 m, while the width and length are 25 and 29 m, respectively. The longitudinal cross section of building B is shown in Figure 4. The details concerning layout and dimensions of all elements of both buildings were based on a construction project (as presented in Figure 1, Figure 2, Figure 3 and Figure 4) made available by MGA Michael Green Architecture.
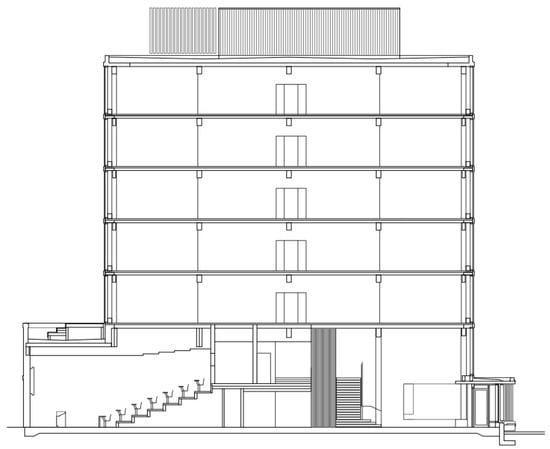
Figure 1.
Longitudinal cross section of building A.
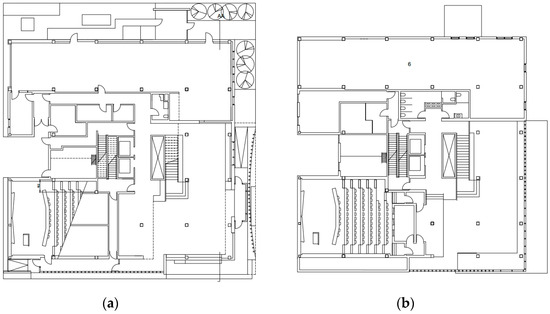
Figure 2.
Plans of building A: (a) ground floor; (b) first floor.
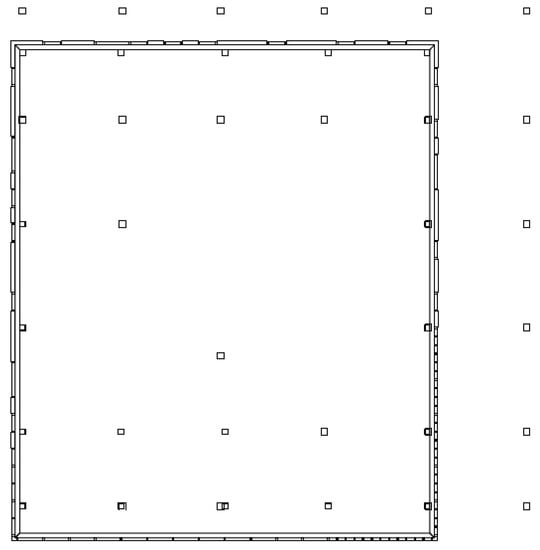
Figure 3.
Plan of upper floors of building A and all floors of building B.
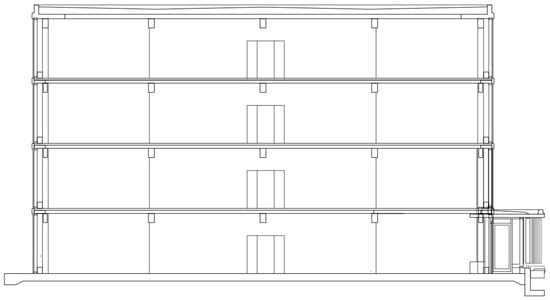
Figure 4.
Longitudinal cross section of building B.
In the case of both buildings, different floor plans along the height introduce irregularities due to different column and beam layout. The layout in building B is the same as for the last two stories of building A. Both wood-framed buildings were constructed using columns and girders made of coniferous wood C27 in accordance with the standard [27] with solid cross-sections. This class of wood, as a material, is described by the following parameters: Young modulus , shear modulus , Poisson’s ratio and mass density . Slabs were constructed of GL24H laminated wood with a thickness of 0.18 m and mass density equal to , according to standards [28,29]. Columns of the ground and first floor of building were made from solid wood with a square cross section of 0.38 × 0.38 m, while in the case of upper floors of building A and all floors of building B, smaller sections were used, i.e., 0.30 × 0.30 m. Most of the girders (horizontal beams) were made from solid wood of a cross section: 0.22 (width) × 0.50 m (height), only those above the openings in slabs of the first floor of building A were made using the increased cross-sections, i.e., 0.36 (width) × 1.24 m (height). Girders above caravans protruding beyond the outline of the ground floor and the first floor of building A were made from solid wood with the transverse dimensions of 0.30 (width) × 0.58 m (height). The mass distribution in building A is as follows: ground floor—90,512 kg, first floor—95,266 kg, second and third floor—62,841 kg, fourth to sixth floor—62,840 kg. For building B, the mass is the same for all floors and it is equal to 62,840 kg.
2.1.2. Model of Wood
In the numerical analysis, a linear model of wood was applied (see also [30,31]). The material is described by the properties summarized in Table 1.

Table 1.
Wood material properties used in the numerical study according to [27,29].
2.1.3. FE Models of Wood-Framed Buildings
Based on the project description of the wood-framed buildings A and B presented in Section 2.1.1, two numerical models were generated using the commercial software RFEM Dlubal [32] (see Figure 5). Columns and girders were modelled as two-node beam-column elements, while in the case of wooden slabs, shell elements were used. The connections between columns and beams were assumed to be rigid and the incorporation of their flexibility was not considered in the present study. The total number of beam-column elements and shell elements, used in the model of two buildings, is equal to 859 and 13, respectively. Ground conditions for a number of different locations were estimated using Geomap [33]. Geo Plus module for geodetic calculations was used and data transmission from field recorders was conducted so as to collect the necessary data to take into account the soil-structure interaction in the numerical analysis. However, in this paper, due to limitation of the space, only a general solution is presented without differentiating ground conditions and considering only the case when the soil is relatively stiff. In this case, all 56 structural supports of the numerical model were fixed for all displacements and rotations. It should be underlined that the size of finite elements used in the mesh was optimized from the point of view of accuracy of the results and computational time. It was confirmed that the application of the finer mesh nearly does not influence the results obtained since the difference was found to be lower than 2%, while the increase in the computational time is substantial. The Rayleigh damping was applied in the analysis. Based on the preliminarily estimated values of the natural frequencies of buildings A and B, the Rayleigh damping coefficients were obtained according to the procedure described in [34]. It was assumed that the damping ratio is equal to 5%, as suggested by Chopra [34] for wooden structures with relatively rigid connections. In the case of building A, these coefficients were calculated as equal to α = 0.35; β = 0.007, and for building B, the following values were obtained: α = 0.37; β = 0.006.
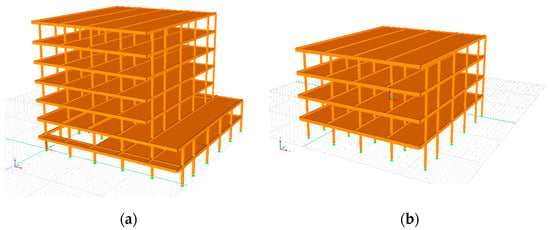
Figure 5.
FE model of buildings: (a) model of building A; (b) model of building B.
The material characteristics described in Section 2.1.2 were applied in the numerical model. Details of the geometric properties were specified following the descriptions from Section 2.1.1.
3. Results
3.1. Modal Analysis of Two Wood-Framed Buildings
The first stage of the numerical investigation was devoted to the modal analysis of two wood-framed buildings. The aim of the analysis was to determine the modes of free vibrations and the corresponding natural frequencies. The first four mode shapes for building A and building B are shown in Figure 6 and Figure 7, respectively. The values of natural frequencies corresponding to first four modes of free vibrations estimated for both structures are summarized in Table 2.
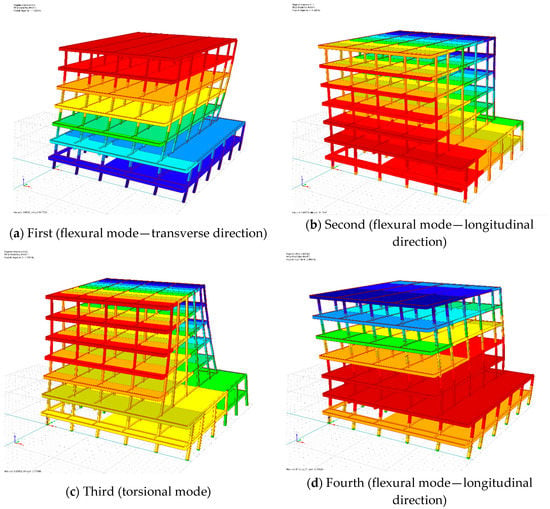
Figure 6.
Modes of free vibrations for building A.
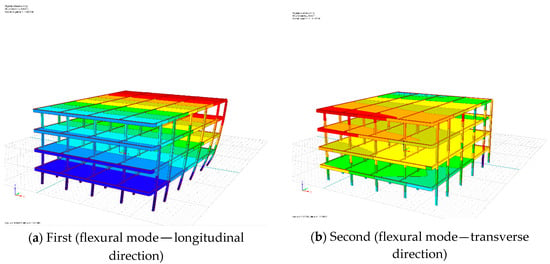
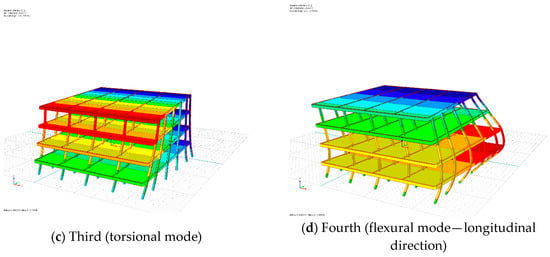
Figure 7.
Modes of free vibrations for building B.

Table 2.
Natural frequencies determined for models of buildings.
It can be seen from Figure 6 and Figure 7 that the floors of two buildings are almost rigid (their stiffness is relatively large) and the deformations are mainly observed in columns which are much more flexible elements. The natural frequencies of both buildings received from the modal analysis (Table 2) have been found to be consistent with the values obtained from the construction project. That confirms to some extent the accuracy of the numerical models created, even though a number of simplifications were introduced so as to reduce the computational time. Being aware of these simplifications, the verified models were used in the next stage of the study focused on pounding-involved response of two buildings during earthquakes. The results obtained from the analysis can be considered general, giving the outlook for the considered problem.
3.2. Collisions between Two Wood-Framed Buildings
The second stage of the numerical investigation was devoted to studying the pounding-involved response of two wood-framed buildings under seismic excitation. In the analysis, the initial gap of 0.1 m was applied between buildings A and B. It should be explained that such size of in-between gap can be observed in densely populated cities where buildings are constructed very closely one to another due to high prices of land. It can also concern cases when the neighboring structures belong to the same owner and they are used for the same purposes (see [35] for example). In the arrangement of structures considered in the study (see Figure 8), interaction between the wooden girders of the taller building A and the columns of the lower building B took place. Collisions were modelled by special gap-friction elements which were activated in the case of contact (see [18] for details). The change from one state to another made the analysis geometrically non-linear.
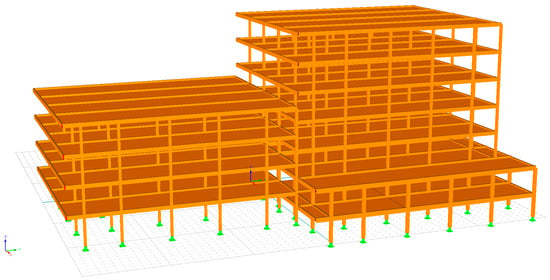
Figure 8.
FE model of two interacting wood-framed buildings.
The detailed non-linear FEM analysis was carried out for different earthquake records. The most representative results, obtained for the Loma Prieta earthquake (17.10.1989), are presented in this paper. In the analysis, the NS and EW components of the earthquake were applied in the longitudinal and transverse directions, respectively. The structural response was obtained applying the time-stepping explicit central difference method (see [34]). The time step of Δt = 0.002 s was found to be small enough to satisfy the conditions of numerical stability and accuracy during collisions between wood-framed buildings. Therefore, this time step was applied in the non-linear seismic analysis.
The representative nodes for both analyzed structures, including the top locations and points of contact (see Figure 9), were chosen, and the earthquake-induced structural responses with and without pounding were determined for them. Due to the limitation of the space, the examples of the responses obtained for the nodes no. N360, N364, N195, N199 (building A) and N401, N405, N426, N430 (building B) are shown in this paper.
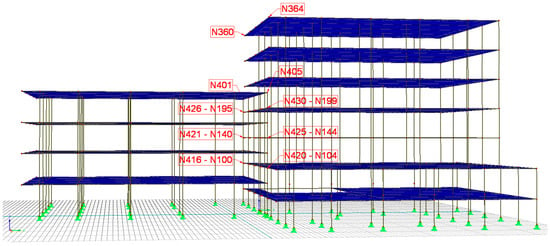
Figure 9.
The arrangement of representative nodes.
3.2.1. Response in the Longitudinal Direction
The examples of the results of the dynamic analysis in the longitudinal direction are shown in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, in which a comparison between the structural displacement responses with pounding and without pounding (large separation gap) is illustrated.
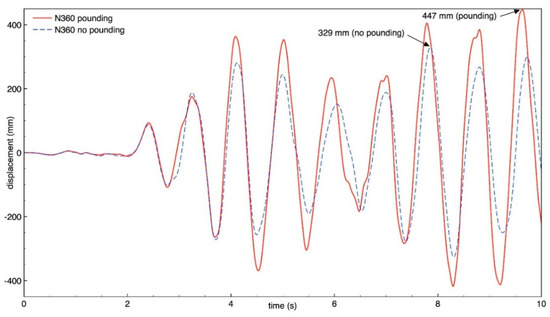
Figure 10.
Longitudinal response of building A (node N360) with and without pounding.
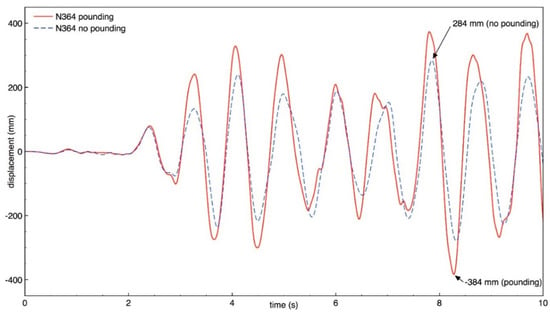
Figure 11.
Longitudinal response of building A (node N364) with and without pounding.
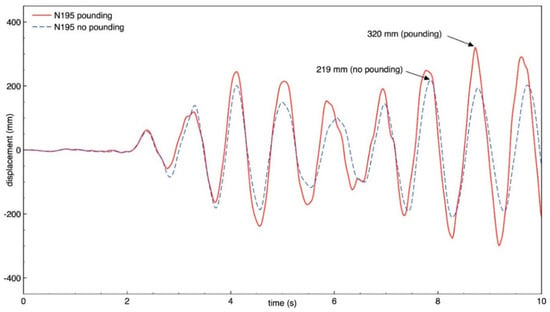
Figure 12.
Longitudinal response of building A (node N195) with and without pounding.
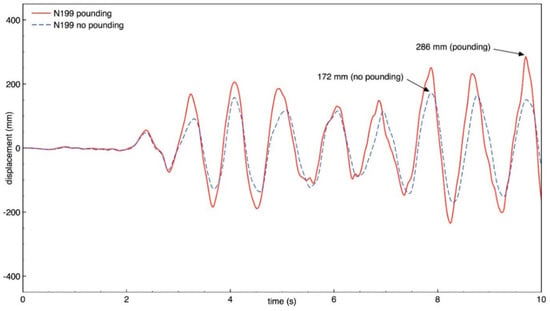
Figure 13.
Longitudinal response of building A (node N199) with and without pounding.
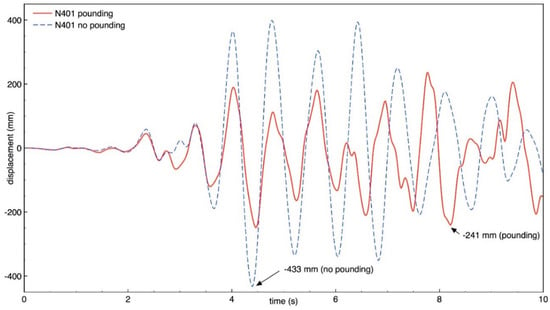
Figure 14.
Longitudinal response of building B (node N401) with and without pounding.
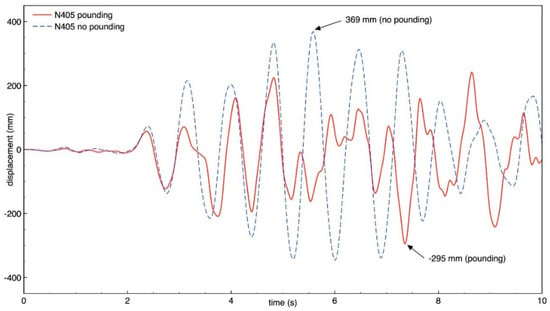
Figure 15.
Longitudinal response of building B (node N405) with and without pounding.
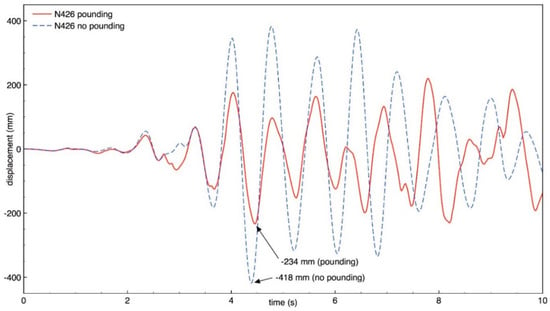
Figure 16.
Longitudinal response of building B (node N426) with and without pounding.
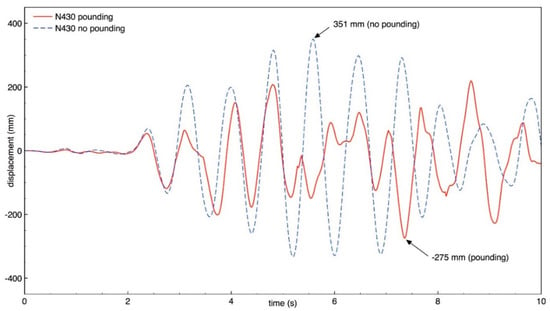
Figure 17.
Longitudinal response of building B (node N430) with and without pounding.
The results of the study indicate that the behavior of both buildings in the longitudinal direction is significantly influenced by earthquake-induced structural pounding. It can be seen from Figure 10, Figure 11, Figure 12 and Figure 13 that the response of building A (the taller one) is increased due to collisions and the increase in the peak displacement is as large as 35.9%, 35.2%, 46.1%, 66.3% for nodes N360, N364, N195, and N199, respectively. On the other hand, Figure 14, Figure 15, Figure 16 and Figure 17 show that the response of building B (the lower one) in the longitudinal direction significantly decreases due to structural interactions. In the case of this structure, a change in the peak displacement during the analyzed earthquake is equal to 44.3%, 20.1%, 44.0%, and 21.7% for nodes N401, N405, N426, and N430, respectively. Moreover, by comparing the displacement time histories for buildings without pounding in Figure 13 and Figure 17, it can be observed that a gap greater than 0.476 m would be required in order to prevent structural pounding during the Loma Prieta earthquake.
3.2.2. Response in the Transverse Direction
The displacement responses of both structures in the transverse direction, with pounding and without pounding (large separation gap), for eight representative nodes are presented in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25.
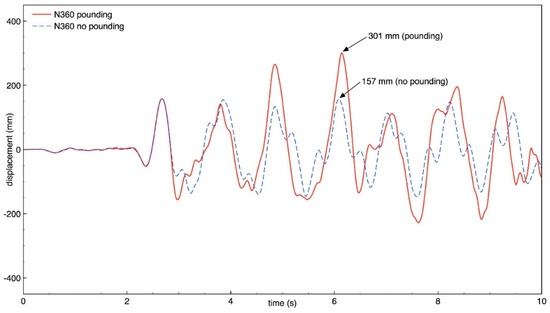
Figure 18.
Transverse response of building A (node N360) with and without pounding.
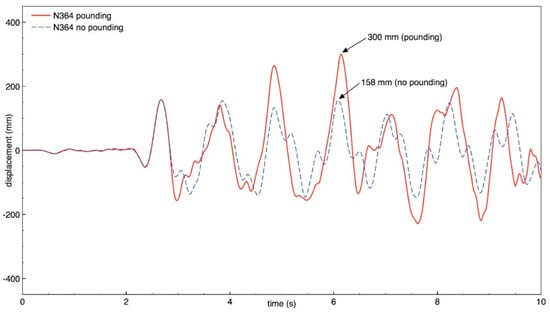
Figure 19.
Transverse response of building A (node N364) with and without pounding.
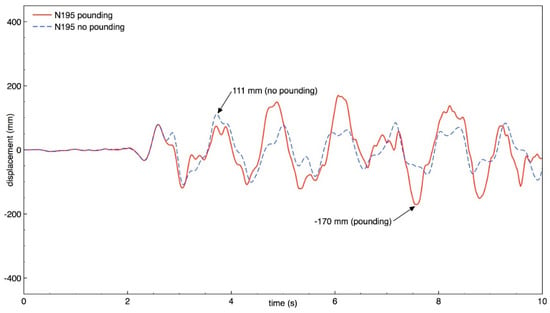
Figure 20.
Transverse response of building A (node N195) with and without pounding.
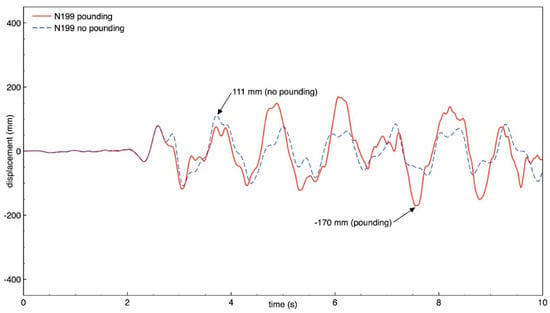
Figure 21.
Transverse response of building A (node N199) with and without pounding.
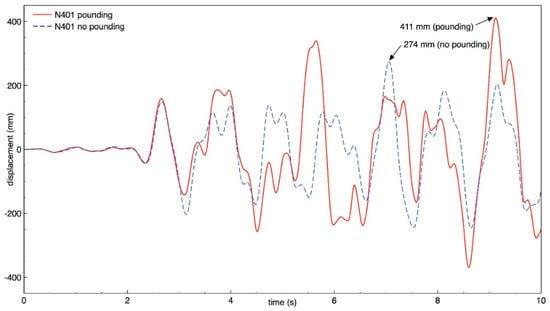
Figure 22.
Transverse response of building B (node N401) with and without pounding.
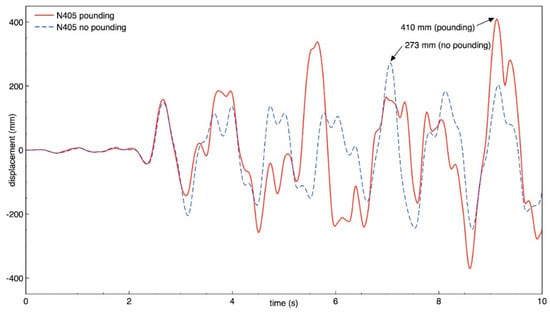
Figure 23.
Transverse response of building B (node N405) with and without pounding.
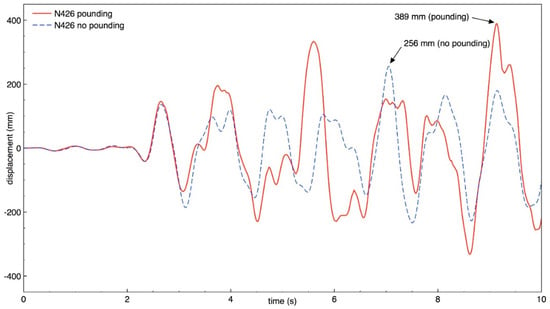
Figure 24.
Transverse response of building B (node N426) with and without pounding.
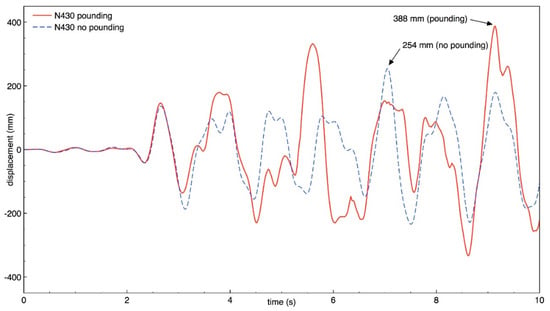
Figure 25.
Transverse response of building B (node N430) with and without pounding.
The results of the study show that also the behavior of both buildings in the transverse direction is significantly influenced by structural pounding during ground motion, similarly as was observed for the longitudinal direction. It can be seen from Figure 18, Figure 19, Figure 20 and Figure 21 that the response of building A (the taller one) is increased due to collisions and the increase in the peak displacement is as large as 91.7%, 89.9%, 53.2%, 53.2% for nodes N360, N364, N195, and N199, respectively. Figure 22, Figure 23, Figure 24 and Figure 25 indicate that also the transverse response of building B (the lower one) significantly increases due to structural interactions. In the case of this structure, a change in the peak displacement during the analyzed ground motion is equal to 50.0%, 50.2%, 52.0% and 52.8% for nodes N401, N405, N426, and N430, respectively.
4. Concluding Remarks
The inter-story pounding between wood-framed buildings during ground motion was analyzed in the paper using the FEM. Firstly, the modal analysis of the structures was conducted. Then, the detailed non-linear seismic analysis of interactions between two wood-framed buildings of different heights was carried out.
The results of the modal analysis show that the natural frequencies of both buildings are consistent with the values obtained from the construction project somehow confirming the accuracy of the numerical model models created. The results of the detailed non-linear analysis of earthquake-induced pounding between two wood-framed buildings indicate that the behavior of both structures in the longitudinal as well as in the transverse direction is significantly influenced by interactions. The response of the taller building is increased in both directions. On the other hand, the response of the lower building is decreased in the longitudinal direction, while it is increased in the transverse one.
A number of simplifications were introduced in the numerical models of both wood-framed buildings so as to reduce the computational time. That concerns, for example, the nonlinearity of wood, which was not considered in the models, although it might have an important influence on the structural response during the earthquake. Being aware of these simplifications, the verified models were used in the study so as to determine the pounding-involved response of two wood-frame buildings under seismic excitation. The results obtained from the analysis can be considered general, giving the outlook of the considered problem. These results clearly indicate that the pounding-involved behavior of the wooden buildings can be substantially different compared to the behavior of other types of structures exposed to earthquake-induced interactions (compared with [18,36], for example). Due to deformability of buildings made of wood, structural interactions may change their responses much more, as compared to steel, reinforced concrete, or masonry structures. The study described in this paper indicates that the peak displacement response of wooden buildings can be increased as the result of collisions by more than 90%. Meanwhile, the results of the study focused on earthquake-induced pounding between three-story and four-story steel buildings indicate that their peak response has decreased by 53% [18]. Additionally, the analysis conducted for interactions between two six-story reinforced concrete buildings shows that the peak displacement response of these structures has increased by 51% due to earthquake-induced collisions [36]. Further studies on pounding between wooden buildings are needed, following this first paper on the topic, so as to fully identify how dangerous it can be in different structural configurations.
It was assumed in the numerical models of both buildings that the connections between columns and beams are rigid and the incorporation of their flexibility was not considered in the analysis. Such an assumption is reasonable in the case of some types of connections, for example when wooden elements are tightly connected with appropriate glue [37]. In the case of other techniques, connections might be more flexible, and this effect is outside the scope of the present paper. Therefore, further investigations are required so as to take into account the flexibility of the connections in the numerical analysis focused on the pounding-involved response of wood-frame buildings under earthquake excitation.
Author Contributions
Conceptualization, W.M., M.S., N.L., A.J.-G. and R.J.; methodology, W.M. and R.J.; software, W.M. and M.S.; validation, M.S.; formal analysis, W.M., M.S., N.L. and R.J.; resources, N.L. and A.J.-G.; writing—original draft preparation, W.M., N.L. and A.J.-G.; writing—review and editing, A.J.-G. and R.J.; supervision, R.J.
Funding
This research received no external funding.
Acknowledgments
The project was supported by the MGA Michael Green Architecture that provided the input data for modelling.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Jankowski, R. Pounding between superstructure segments in multi-supported elevated bridge with three-span continuous deck under 3D non-uniform earthquake excitation. J. Earthq. Tsunami 2015, 9, 1550012. [Google Scholar] [CrossRef]
- Vasiliadis, L.; Elenas, A. Performance of school buildings during the Athens earthquake of September 7 1999. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002; Volume 264. [Google Scholar]
- Rosenblueth, E.; Meli, R. The 1985 earthquake: Causes and effects in Mexico City. Concr. Int. 1986, 8, 23–24. [Google Scholar]
- Anagnostopoulos, S.A. Earthquake induced pounding: State of the art. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; pp. 897–905. [Google Scholar]
- Miari, M.; Choong, K.K.; Jankowski, R. Seismic pounding between adjacent buildings: Identification of parameters, soil interaction issues and mitigation measures. Soil Dyn. Earthq. Eng. 2019, 121, 135–150. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Effective formula for impact damping ratio for simulation of earthquake-induced structural pounding. Geosciences 2019, 9, 347. [Google Scholar] [CrossRef]
- Bamer, F.; Markert, B. A nonlinear visco-elastoplastic model for structural pounding. Earthq. Eng. Struct. Dyn. 2018, 47, 2490–2495. [Google Scholar]
- Komodromos, P.; Polycarpou, P.C.; Papaloizou, L.; Phocas, M.C. Response of seismically isolated buildings considering poundings. Earthq. Eng. Struct. Dyn. 2007, 36, 1605–1622. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A. Pounding of building in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A.; Spiliopoulus, K.V. An investigation of earthquake induced pounding between adjacent buildings. Earthq. Eng. Struct. Dyn. 1992, 21, 289–302. [Google Scholar] [CrossRef]
- Maison, B.F.; Kasai, K. Dynamics of pounding when two buildings collide. Earthq. Eng. Struct. Dyn. 1992, 21, 771–786. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Favvata, M.J. Earthquake-induced interaction between adjacent reinforced concrete structures with non-equal heights. Earthq. Eng. Struct. Dyn. 2005, 34, 1–20. [Google Scholar] [CrossRef]
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef]
- Komodromos, P.; Polycarpou, P. On the numerical simulation of impact for the investigation of earthquake-induced pounding of building. In Proceedings of the Tenth International Conference on Computational Structures Technology, Stirlingshire, UK, 16 September 2010. [Google Scholar]
- Polycarpou, P.C.; Komodromos, P. Earthquake-induced poundings of a seismically isolated building with adjacent structures. Eng. Struct. 2010, 32, 1937–1951. [Google Scholar] [CrossRef]
- Crozet, V.; Politopoulos, I.; Chaudat, T. Shake table tests of structures subject to pounding. Earthq. Eng. Struct. Dyn. 2019, 48, 1156–1173. [Google Scholar] [CrossRef]
- Sołtysik, B.; Jankowski, R. Non-linear strain rate analysis of earthquake-induced pounding between steel buildings. Int. J. Earth Sci. Eng. 2013, 6, 429–433. [Google Scholar]
- Jameel, M.; Islam, A.B.M.S.; Hussain, R.R.; Hasan, S.D.; Khaleel, M. Non-linear FEM analysis of seismic induced pounding between neighbouring multi-storey structures. Lat. Am. J. Solids Struct. 2013, 10, 921–939. [Google Scholar] [CrossRef]
- Favvata, M.J.; Naoum, M.C.; Karayannis, C.G. Earthquake induced interaction between RC frame and steel frame structures. WIT Trans. Built Environ. 2013, 134, 839–851. [Google Scholar]
- Elwardany, H.; Seleemah, A.; Jankowski, R. Seismic pounding behavior of multi-story buildings in series considering the effect of infill panels. Eng. Struct. 2017, 144, 139–150. [Google Scholar] [CrossRef]
- Bi, K.; Hao, H.; Sun, Z. 3D FEM analysis of earthquake induced pounding responses between asymmetric buildings. Earthq. Struct. 2017, 13, 377–386. [Google Scholar]
- Hughes, P.J.; Sarebanha, A.; Mosqueda, G. Finite element analysis of moat wall pounding in base-isolated buildings. In Proceedings of the 11th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
- Elwardany, H.; Seleemah, A.; Jankowski, R.; El-khoriby, S. Influence of soil-structure interaction on seismic pounding between steel frame buildings considering the effect of infill panels. Bull. Earthq. Eng. 2019, 17, 6165–6202. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Favvata, M.J. Inter-story pounding between multistory reinforced concrete structures. Struct. Eng. Mech. 2005, 20, 505–526. [Google Scholar] [CrossRef]
- Shakya, K.; Wijeyewickrema, A.C. Mid-column pounding of multi-story reinforced concrete buildings considering soil effects. Adv. Struct. Eng. 2019, 12, 71–85. [Google Scholar] [CrossRef]
- PN-EN 338:2016-06 EN Constructional wood - Strength classes. 2016. (In Polish)
- PN-EN 1995-1-1 Eurocode 5: Design of wooden structures. Part 1-1: General principles and rules for buildings. 1995. (In Polish)
- PN-EN 14080:2013-07en Wooden structures - Laminated wood and laminated solid wood - Requirements. 2013. (In Polish)
- Szczepański, M.; Migda, W.; Jankowski, R. Modal analysis of real timber frame houses with different insulation materials. Adv. Sci. Technol. Res. J. 2016, 10, 215–221. [Google Scholar] [CrossRef][Green Version]
- Szczepański, M.; Migda, W.; Jankowski, R. Increasing the seismic resistance of wood-frame buildings by applying PU foam as thermal insulation. Period. Polytech. Civ. Eng. 2019, 63, 480–488. [Google Scholar]
- Dlubal RFEM-FEM Structural Analysis Software. Available online: https://www.dlubal.com/ (accessed on 10 June 2019).
- Central Geological Database. Available online: http://baza.pgi.gov.pl (accessed on 27 December 2016).
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Bertero, V.V.; Collins, R.G. Investigation of the Failures of the OLIVE View Stairtowers during the San Fernando Earthquake and Their Implications on Seismic Design; EERC Report No. 73–26; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1973. [Google Scholar]
- Jankowski, R. Non-linear FEM analysis of earthquake-induced pounding between the main building and the stairway tower of the Olive View Hospital. Eng. Struct. 2009, 31, 1851–1864. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Batchelar, M.; Wallington, C.; Buchanan, A.H. Moment Joints in Timber Frames Using Glued-In Steel Rods: Experimental Investigation of Long-Term Performance; World Conference on Timber Engineering: Riva del Garda, Italy, 2010. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).