Development of a New Simulation Tool Coupling a 2D Finite Volume Overland Flow Model and a Drainage Network Model
Abstract
:1. Introduction
2. Model Representation
2.1. Surface Flow Model
2.2. Infiltration Law: Horton Model
2.3. Discretization of the 2D Model
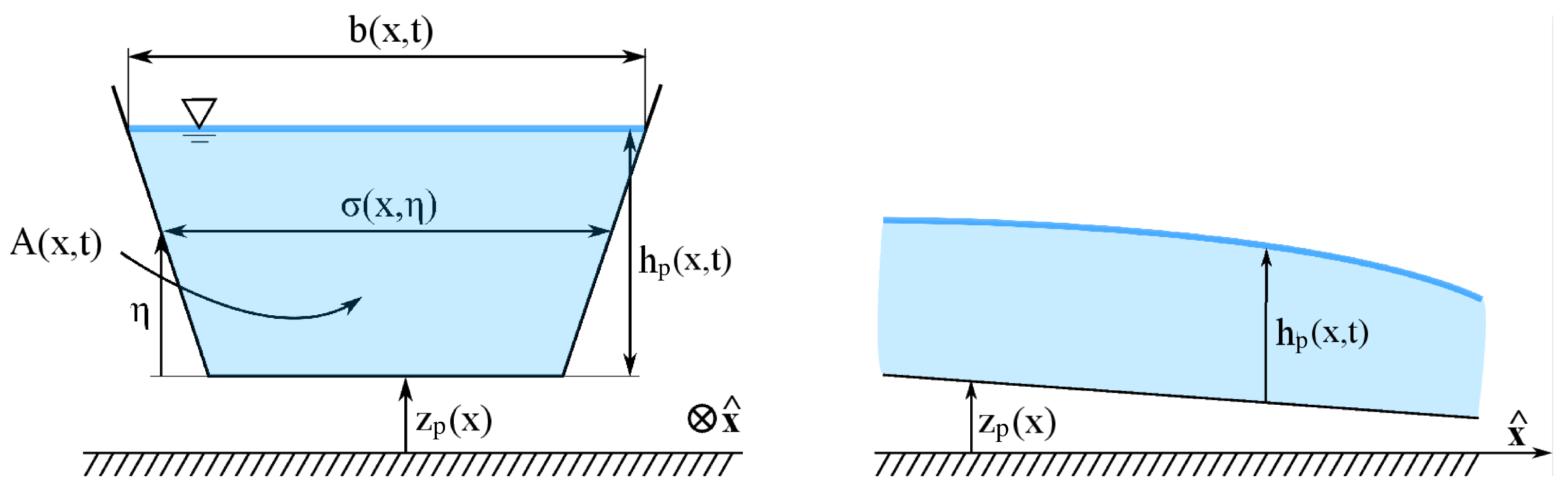
2.4. Drainage System Model
2.5. Preissmann Slot
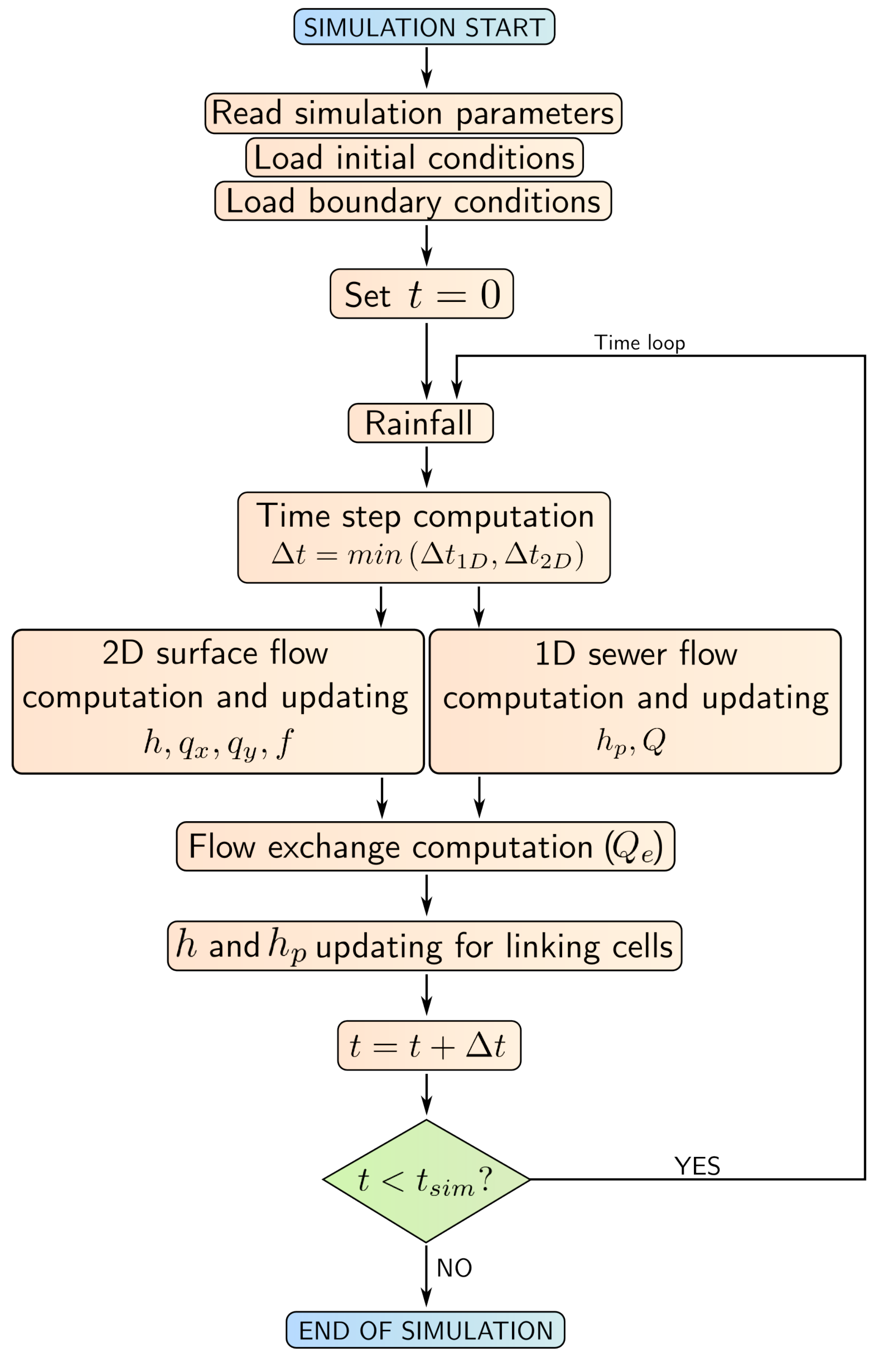
2.6. Exchange between Submodels
2.7. Time Step Synchronization
3. Numerical Cases
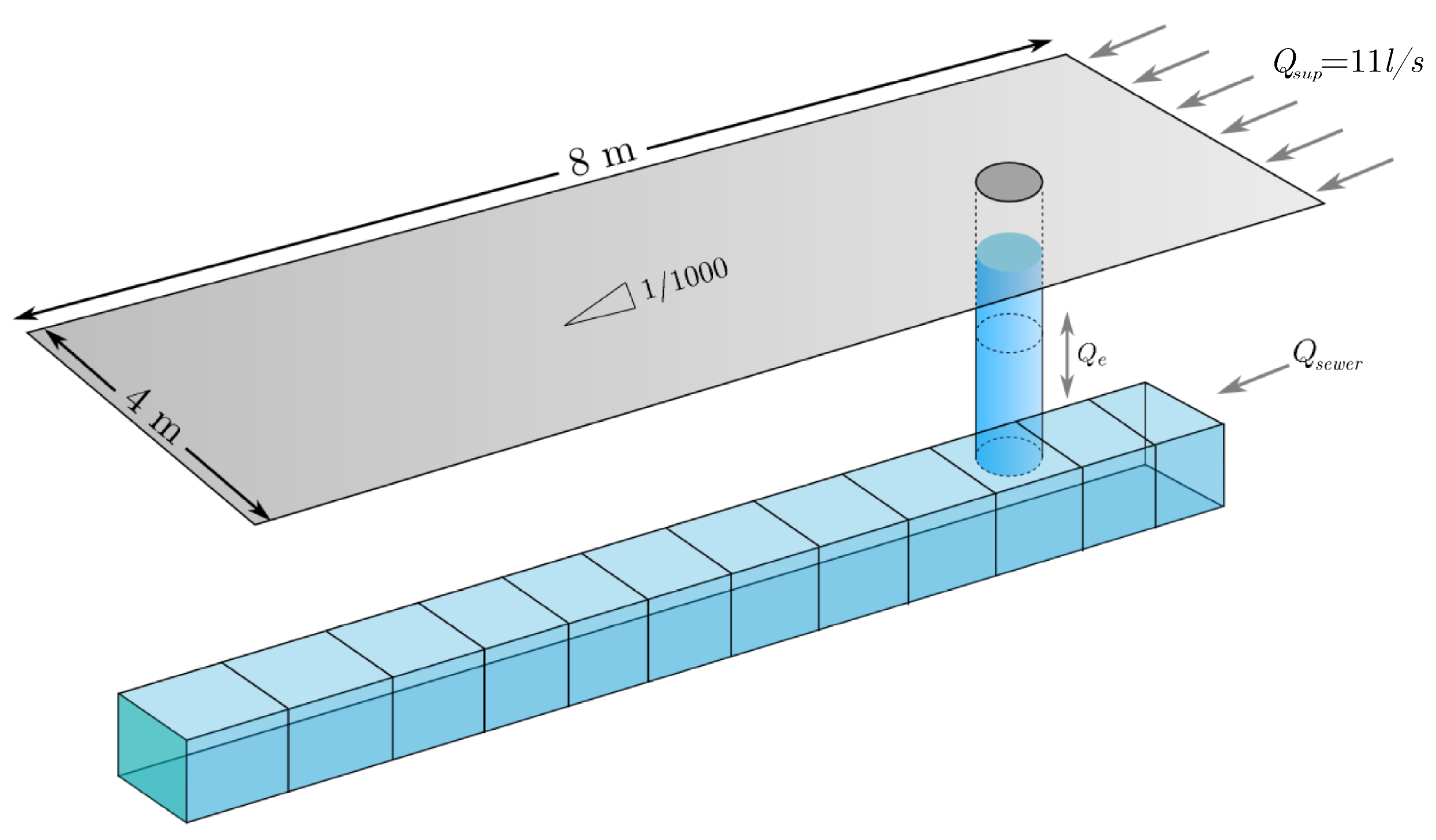
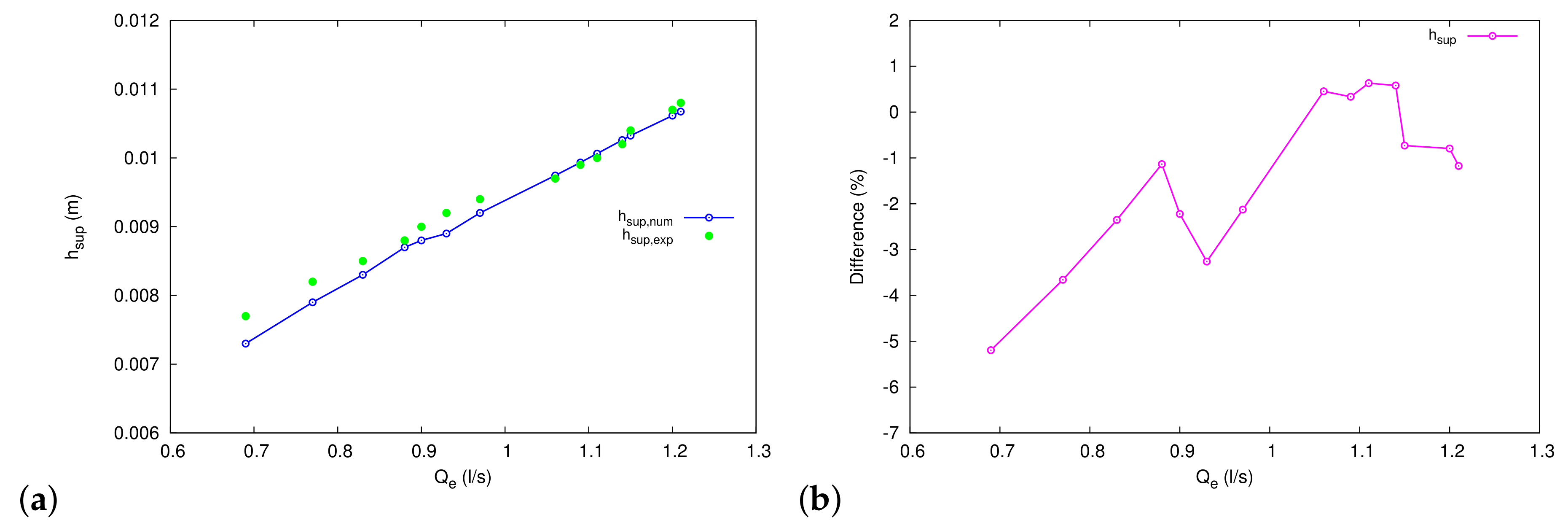
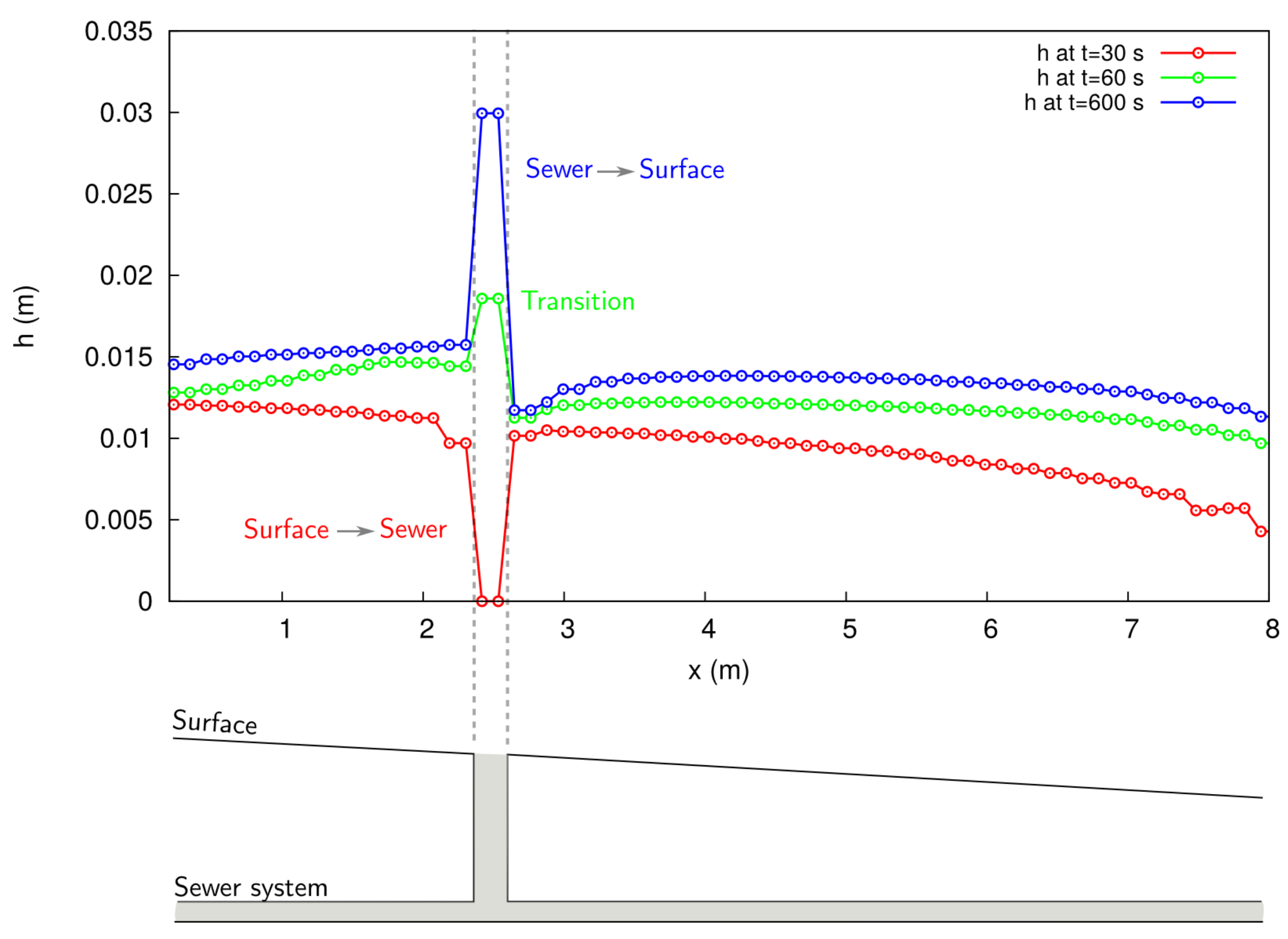
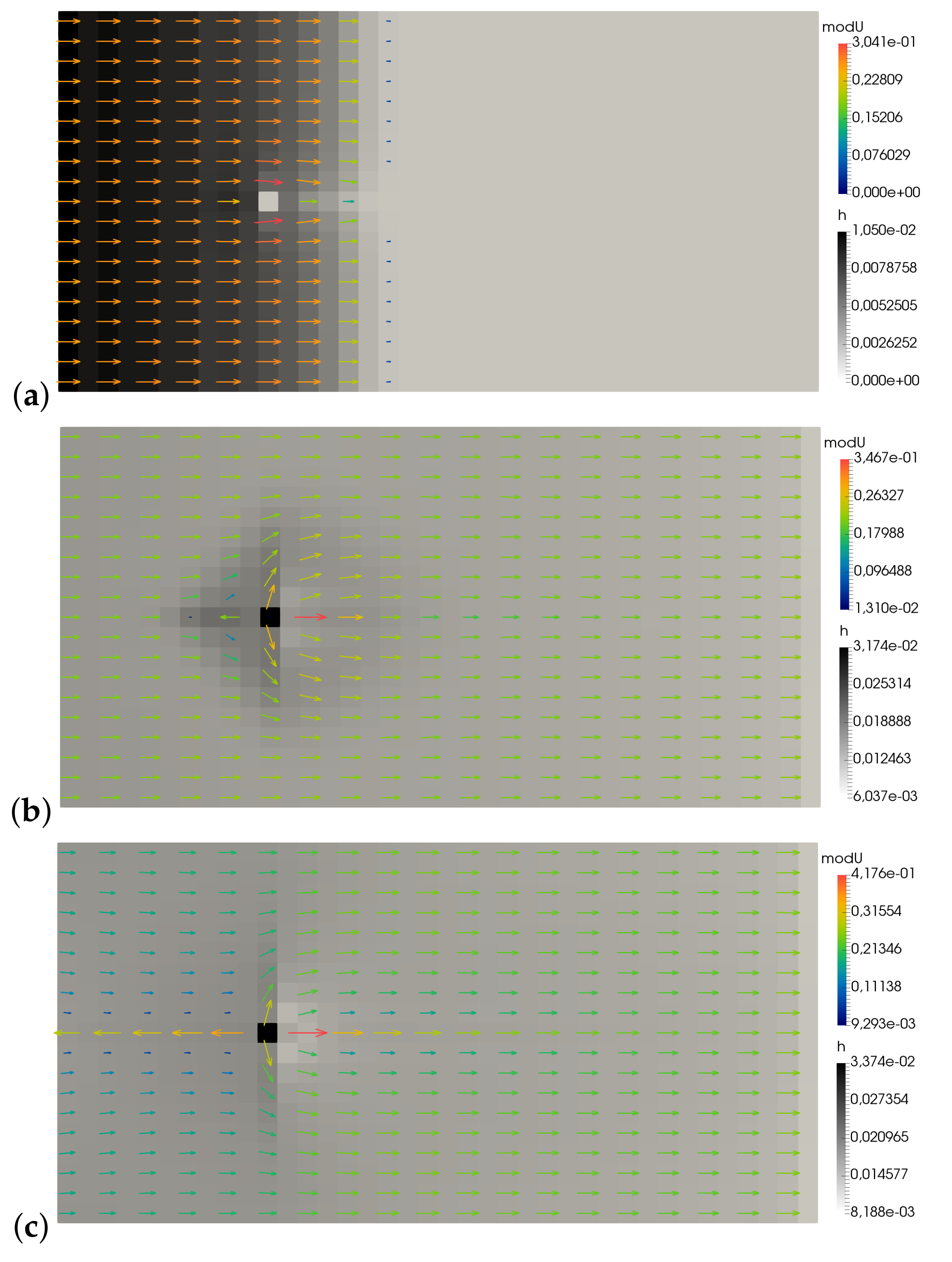
3.1. Single Sewer/Surface Flow Exchange
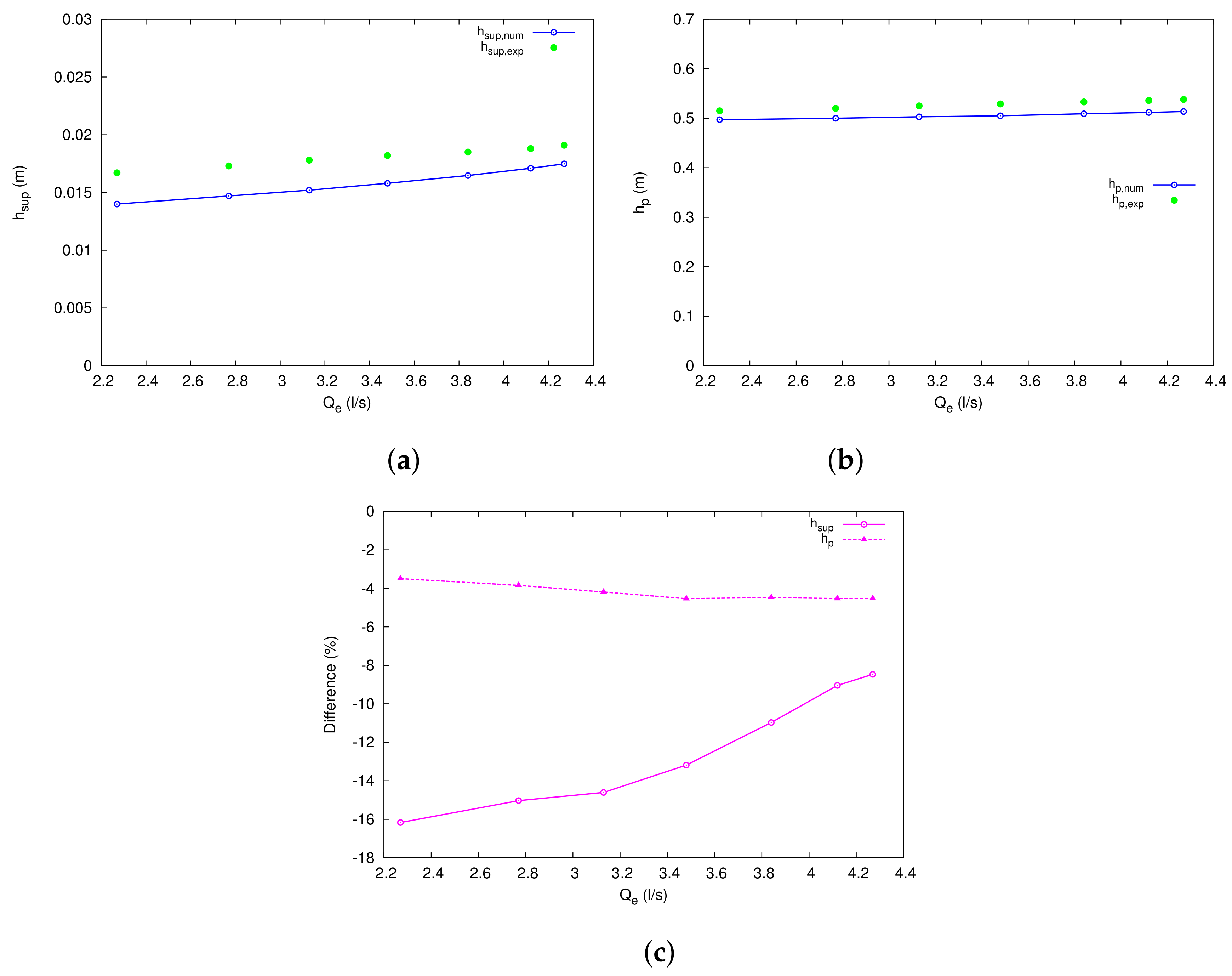
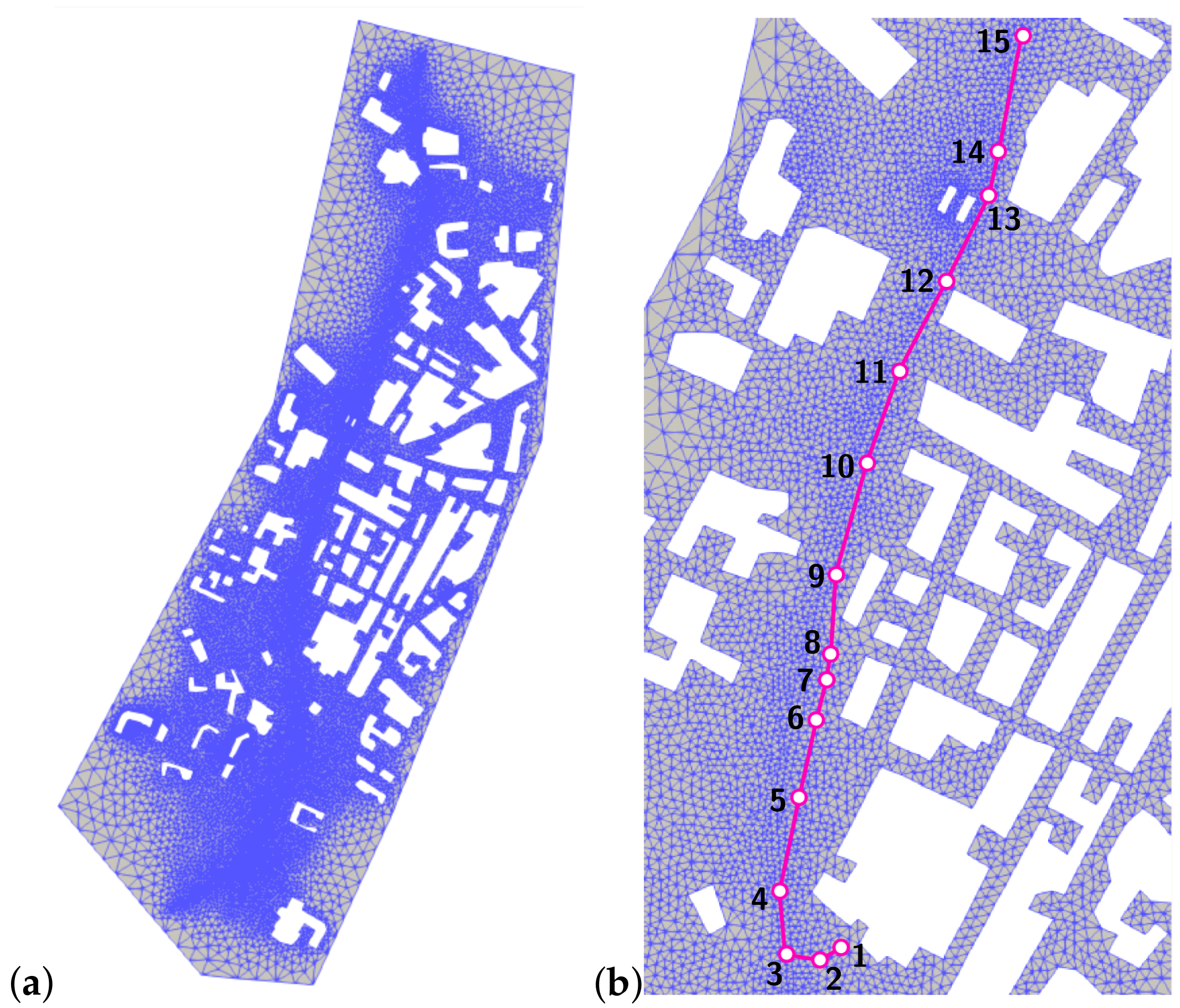
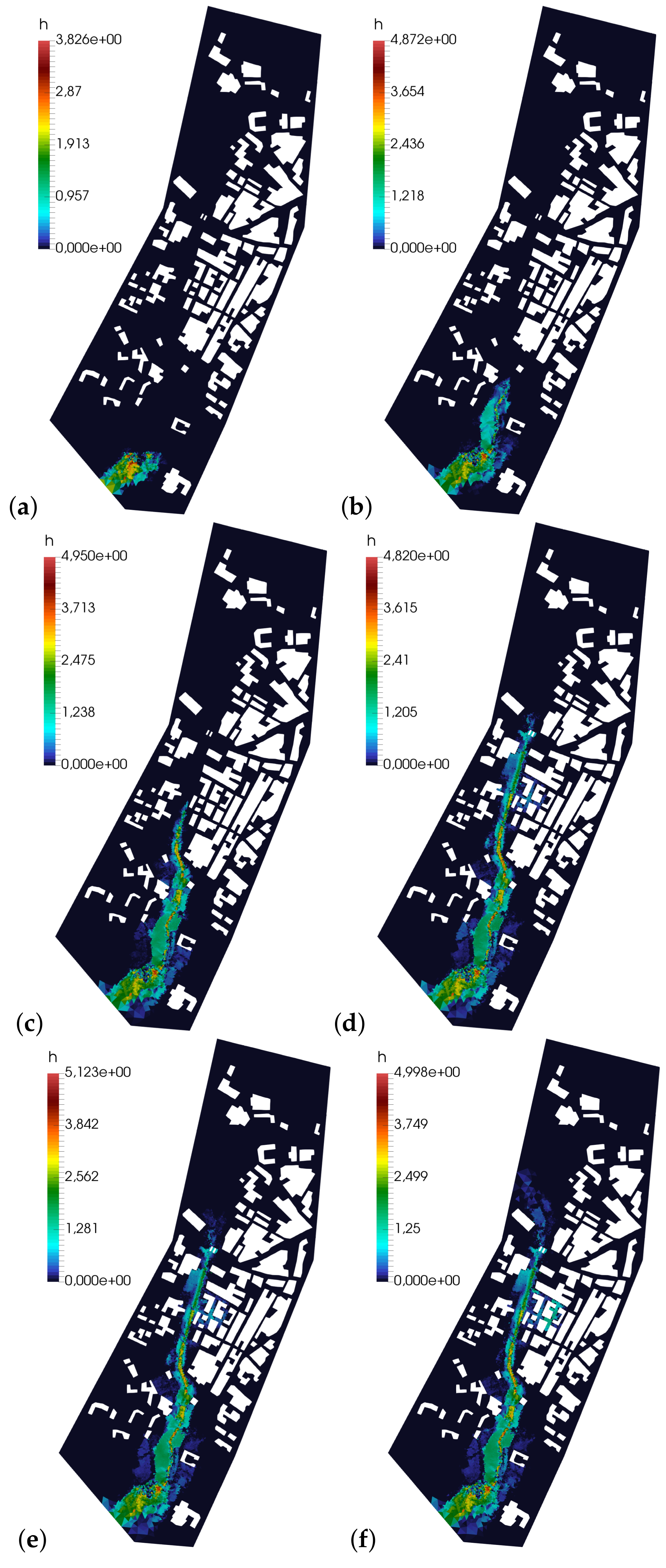
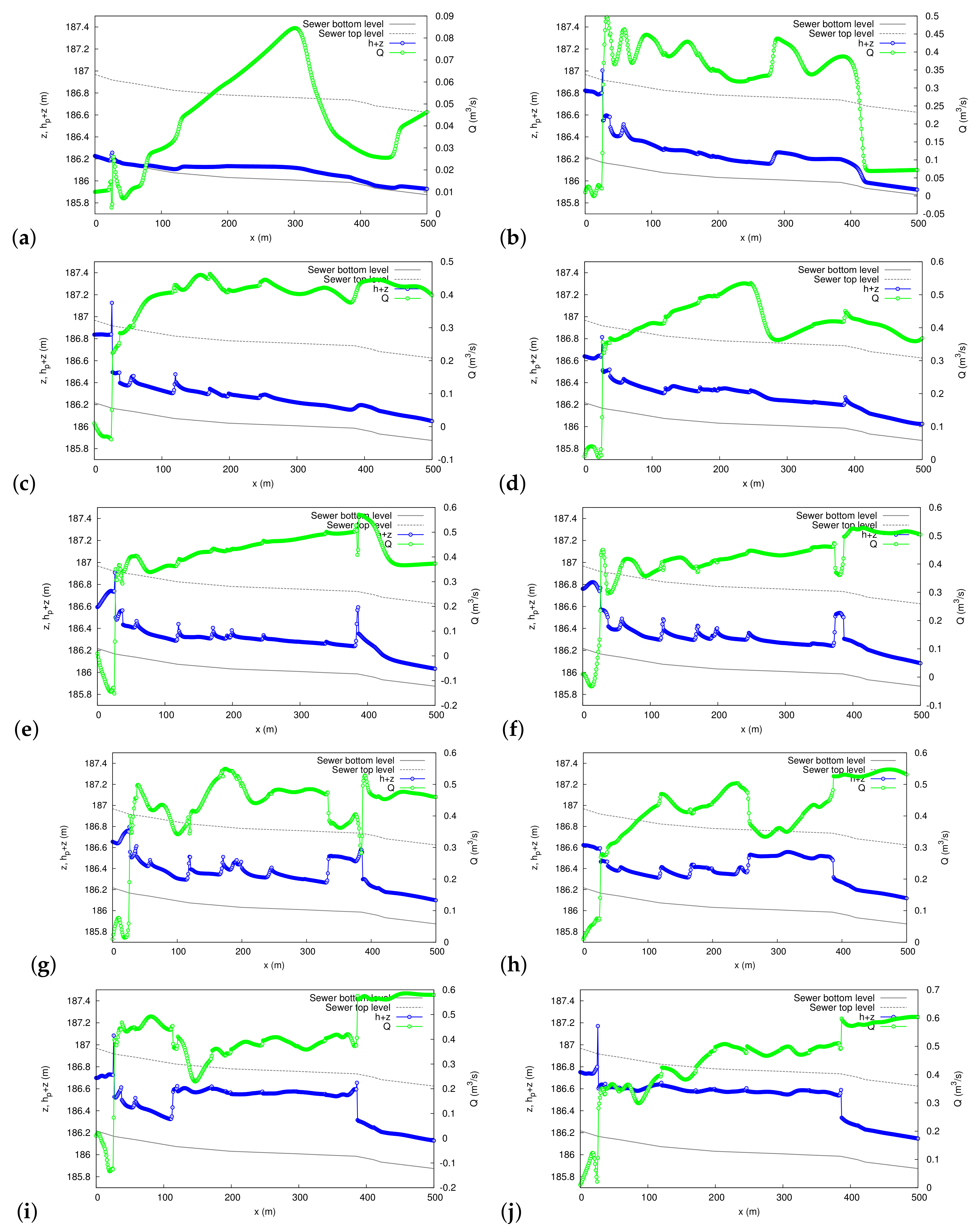
3.2. Application to a Case Study
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vreugdenhil, C. Numerical Methods for Shallow Water Flow; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]
- Burguete, J.; García-Navarro, P. Efficient construction of high-resolution TVD conservative schemes for equation with source terms: Application to shallow water flows. Int. J. Numer. Methods Fluids 2001, 37, 209–248. [Google Scholar] [CrossRef]
- Brufau, P.; Vázquez-Cendón, M.E.; García-Navarro, P. A numerical model for the flooding and drying of irregular domains. Int. J. Numer. Methods Fluids 2002, 39, 247–275. [Google Scholar] [CrossRef]
- Brufau, P.; García-Navarro, P.; Vázquez-Cendón, M.E. Zero mass error using unsteady wetting-drying conditions in shallow flows over dry irregular topography. Int. J. Numer. Methods Fluids 2004, 45, 1047–1082. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Res. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Ponce, V. Diffusion Wave Modeling of Catchment Dynamics. J. Hydraul. Eng. 1986, 112, 716–727. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall-runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; García-Navarro, P. 2D Zero-Inertia Model for Solution of Overland Flow Problems in Flexible Meshes. J. Hydrol. Eng. 2016, 21, 04016038. [Google Scholar] [CrossRef]
- León, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. Application of Godunov-type schemes to transient mixed flows. J. Hydraul. Res. 2009, 47, 147–156. [Google Scholar] [CrossRef]
- García-Navarro, P.; Vázquez-Cendón, M. On numerical treatment of the source terms in the shallow water equations. Comput. Fluids 2000, 29, 951–979. [Google Scholar] [CrossRef]
- Kerger, F.; Archambeau, P.; Erpicum, S.; Dewals, B.J.; Pirotton, M. An exact Riemann solver and a Godunov scheme for simulating highly transient mixed flows. J. Comput. Appl. Math. 2010, 235, 2030–2040. [Google Scholar] [CrossRef]
- Trajkovic, B.; Ivetic, M.; Calomino, F.; D’Ippolito, A. Investigation of transition from free surface to pressurized flow in a circular pipe. Water Sci. Technol. 1999, 39, 105–112. [Google Scholar] [CrossRef]
- Burguete, J.; García-Navarro, P. Implicit schemes with large time step for non-linear equations: Application to river flow hydraulics. Int. J. Numer. Methods Fluids 2004, 46, 607–636. [Google Scholar] [CrossRef]
- García-Navarro, P.; Alcrudo, F.; Priestley, A. An implicit method for water flow modelling in channels and pipes. J. Hydraul. Res. 1994, 32, 721–742. [Google Scholar] [CrossRef]
- Casoulli, V. Semi-implicit finite difference methods for the two-dimensional shallow water equations. J. Comput. Phys. 1990, 86, 56–74. [Google Scholar] [CrossRef]
- Kärnä, T.; de Brye, B.; Gourgue, O.; Lambrechts, J.; Comblen, R.; Legat, V.; Deleersnijder, E. A fully implicit wetting–drying method for DG-FEM shallow water models, with an application to the Scheldt Estuary. Comput. Methods Appl. Mech. Eng. 2011, 200, 509–524. [Google Scholar] [CrossRef]
- Li, S.; Duffy, C.J. Fully-Coupled Modeling of Shallow Water Flow and Pollutant Transport on Unstructured Grids. Procedia Environ. Sci. 2012, 13, 2098–2121. [Google Scholar] [CrossRef]
- Bagheri, J.; Das, S. Modeling of Shallow-Water Equations by Using Implicit Higher-Order Compact Scheme with Application to Dam-Break Problem. J. Appl. Comput. Math. 2013, 2, 1000132. [Google Scholar]
- Tavelli, M.; Dumbser, C. A high order semi-implicit discontinuous Galerkin method for the two dimensional shallow water equations on staggered unstructured meshes. Appl. Math. Comput. 2014, 234, 623–644. [Google Scholar] [CrossRef]
- Kesserwani, G.; Liang, Q. RKDG2 shallow-water solver on non-uniform grids with local time steps: Application to 1D and 2D hydrodynamics. Appl. Math. Model. 2015, 39, 1317–1340. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.; Hsu, M.; Chen, T.; Chang, T. An integrated inundation model for highly developed urban areas. Water Sci. Technol. 2005, 51, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, S.; Prodanovic, D.; Ivetic, M.; Savic, D. SIPSON simulation of interaction between pipe flow and surface overland flow in networks. Water Sci. Technol. 2005, 52, 275–283. [Google Scholar] [CrossRef] [PubMed]
- Fraga, I.; Cea, L.; Puertas, J. Validation of a 1D-2D dual drainage model under unsteady part-full and surcharged sewer conditions. Urban Water J. 2017, 14, 74–84. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J.; Suárez, J.; Jiménez, V.; Jácome, A. Global sensitivity and GLUE-based uncertainty analysis of a 2D-1D dual urban drainage model. J. Hydrol. Eng. 2016, 21, 04016004. [Google Scholar] [CrossRef]
- Hsu, M.; Chen, S.; Chang, T. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Leandro, J.; Chen, A.; Djordjevic, S.; Savic, D. Comparison of 1D/1D and 1D/2D coupled (sewer/surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Leandro, J.; Djordjevic, S.; Chen, A.; Savic, D.; Stanic, M. Calibration of a 1D/1D urban flood model using 1D/2D model results in the absence of field data. Water Sci. Technol. 2011, 64, 1016–1024. [Google Scholar] [CrossRef] [PubMed]
- Seyoum, S.; Vojinovic, Z.; Price, R.; Weesakul, S. Coupled 1D and non inertia 2D flood inundation model for simulation of urban flooding. J. Hydraul. Eng. 2011, 138, 23–34. [Google Scholar] [CrossRef]
- Horton, R. The role of infiltration in the hydrologic cycle. Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Rawls, W.; Yates, P.; Asmussen, L. Calibration of Selected Infiltration Equation for the Georgia Coastal Plain; Report ARS-S-113; Agriculture Research Service: Washington, DC, USA, 1976. [Google Scholar]
- American Society of Civil Engineers (ASCE). Hydrology Handbook, 2nd ed.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 1996. [Google Scholar]
- Fernández-Pato, J.; Morales-Hernández, M.; García-Navarro, P. Implicit finite volume simulation of 2D shallow water flows in flexible meshes. Comput. Methods Appl. Mech. Eng. 2018, 328, 1–25. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P.; Burguete, J.; Brufau, R. The influence of source terms on stability, accuracy and conservation in two-dimensional shallow flow simulation using triangular finite volumes. Int. J. Numer. Methods Fluids 2007, 54, 543–590. [Google Scholar] [CrossRef]
- Rubinato, M.; Martins, R.; Kesserwani, G.; Leandro, J.; Djordjevic, S.; Shucksmith, J. Experimental calibration and validation of sewer/surface flow exchange equations in steady and unsteady flow conditions. J. Hydrol. 2017, 552, 421–432. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; García-Navarro, P. Finite volume simulation of unsteady water pipe flow. Drinking Water Eng. Sci. 2014, 7, 83–92. [Google Scholar] [CrossRef]


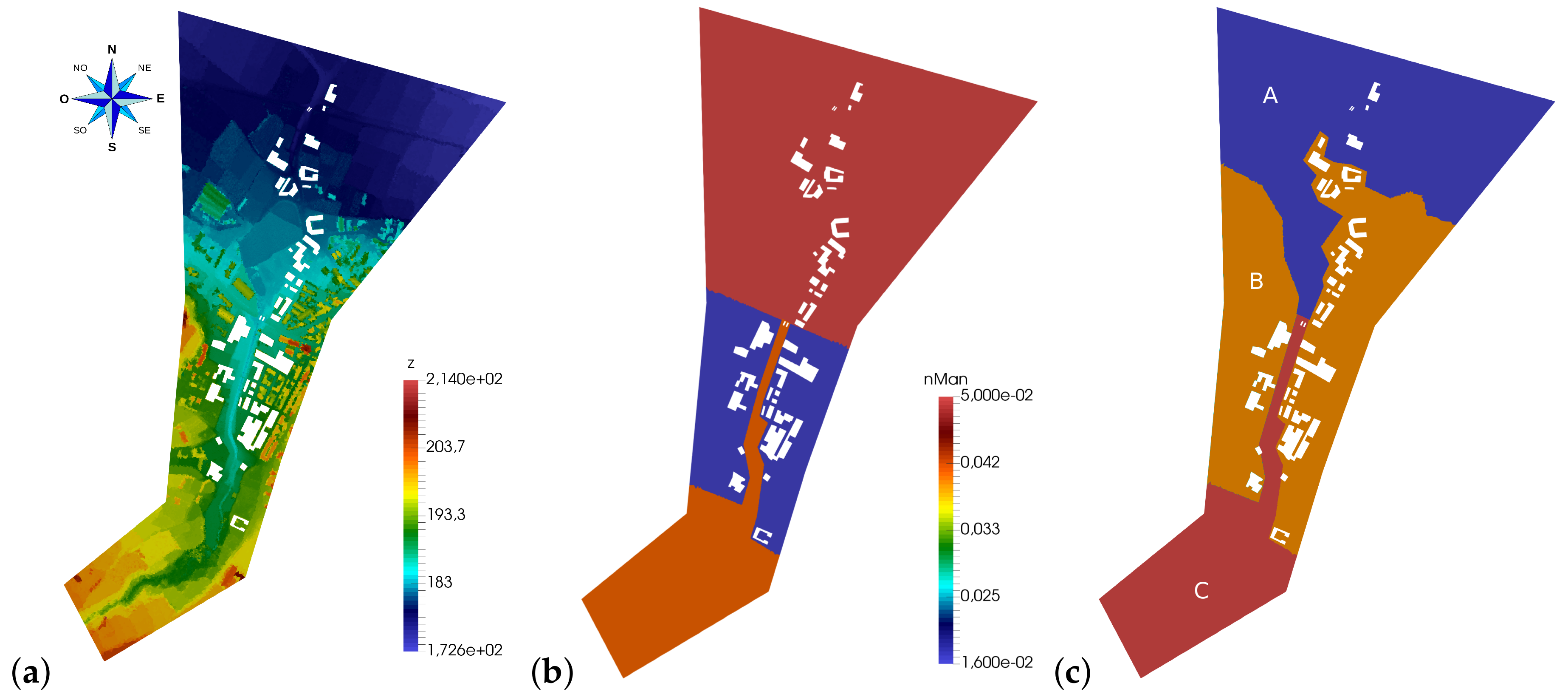


| Zone | k (s) | (m/s) | (m/s) |
|---|---|---|---|
| A | |||
| B | |||
| C |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Pato, J.; García-Navarro, P. Development of a New Simulation Tool Coupling a 2D Finite Volume Overland Flow Model and a Drainage Network Model. Geosciences 2018, 8, 288. https://doi.org/10.3390/geosciences8080288
Fernández-Pato J, García-Navarro P. Development of a New Simulation Tool Coupling a 2D Finite Volume Overland Flow Model and a Drainage Network Model. Geosciences. 2018; 8(8):288. https://doi.org/10.3390/geosciences8080288
Chicago/Turabian StyleFernández-Pato, Javier, and Pilar García-Navarro. 2018. "Development of a New Simulation Tool Coupling a 2D Finite Volume Overland Flow Model and a Drainage Network Model" Geosciences 8, no. 8: 288. https://doi.org/10.3390/geosciences8080288
APA StyleFernández-Pato, J., & García-Navarro, P. (2018). Development of a New Simulation Tool Coupling a 2D Finite Volume Overland Flow Model and a Drainage Network Model. Geosciences, 8(8), 288. https://doi.org/10.3390/geosciences8080288





