River floods represent the most frequent and expensive natural disaster affecting most of the countries around the world [
1]. They take place when the river exceeds its storage capacity and the water excess overflows the banks and fills the adjacent low-lying lands, producing significant social, economic, and environmental impacts [
2], including: loss of human life and negative effects on population, damage to the infrastructure and essential services, damage to crops and animals, spread of diseases, and contamination of the water supply.
Many factors contribute to river floods: heavy rains at river sources, ice jams, the melting of snow pack, and land-use change (such as deforestation and urbanization) are some important factors. Runoff after heavy precipitation is the principal reason for river floods, and as urbanization increases, impervious areas increase as well, leading to higher rates of runoff. Saturated soils, high suspended matter, and landslides also increase the negative impacts of floods.
Predicting river flood extents is a crucial aspect of flood risk management. There are three typical approaches for flood prediction: (i) analyzing the frequency of flooding, through statistical analyses, allows determining the recurrence interval for any year and for a given discharge in the stream (without explicitly characterizing the flood area); (ii) monitoring the progress of storms (e.g., amount of rainfall) can be used to predict short-term flood events; and (iii) the flood hazard maps allow determining the extent of flooded areas based on the estimated discharges for different return periods [
3,
4,
5]. However, the flood hazard itself only assesses the extent and water depth of a flood; it does not assess the consequences on the population, economy, and environment, as
flood risk assessment does. In general, risk refers to the expected losses (in terms of fatalities, or in economic terms as damage to property) of a specific hazard (in this case, flood depth and extent) to a specific element (e.g., a building in the flood hazard area) at risk in a particular future time period or future scenarios [
6,
7]. In this sense, flood risk assessment is the cornerstone of flood mitigation measures, as it helps decision makers and managers take action (by implementing flood prevention or mitigation strategies) to protect the exposed population or assets. Nevertheless, current flood risk management has a higher focus on assessing the damage to assets (economic loses) than the social and environmental damages [
8].
1.1. GIS-Based Multi-Criteria Approach
The combination of multi-criteria decision making (MCDM) with geographical information systems (GIS) proposed in the present research allows integrating the three components of risk assessment (hazard, exposure, and vulnerability), in which the social, economic, and/or environmental vulnerabilities can be considered. The outcome of this methodology is a flood risk map showing the spatial distribution of flood risk along with its intensity level, ranging from very high to very low risk. In MCDM, there are different methods for assessing criterion weights: entropy, ranking, rating, trade-off analysis, and pairwise comparison, among others [
9]. The Analytic Hierarchy Process (AHP) proposed by Saaty [
10] is one of the most common MCDM methods, and it has been widely applied to solve decision-making problems related to water resources [
11]. The purpose of AHP is providing decision makers with the decision, among different alternatives and criteria, that best suits their goal [
11,
12]. This method compares two criteria at a time through a pairwise comparison matrix, in which values of relative importance from one criterion over another criterion are assigned. It provides a measure of a level of consistent judgment supported by a theoretical background. The scale of relative importance ranges between one and nine, where one is equal importance, and nine is extreme importance.
This GIS-based multi-criteria approach has been increasingly used for flood risk assessment, as it presents several advantages. Some more complex alternative methods involve hydraulic and hydrological models for flood hazard assessment, and require information of the monetary value of the assets exposed to evaluate the vulnerability [
13]. In contrast, the proposed approach only requires the spatial layers of the parameters (examples of which are listed below) that contribute to the flood hazard, and land-use and demographic information to evaluate the vulnerability. Therefore, the main advantage of this methodology is the possibility of obtaining a reliable flood risk map with a relatively low monetary and time investment to support stakeholders to evaluate only the areas that need further detailed assessment. Additionally, it is easy to update, uses easy-to-get open source input data, and is flexible in terms of which criteria are included.
1.2. History of Floods in the Greater Toronto Area
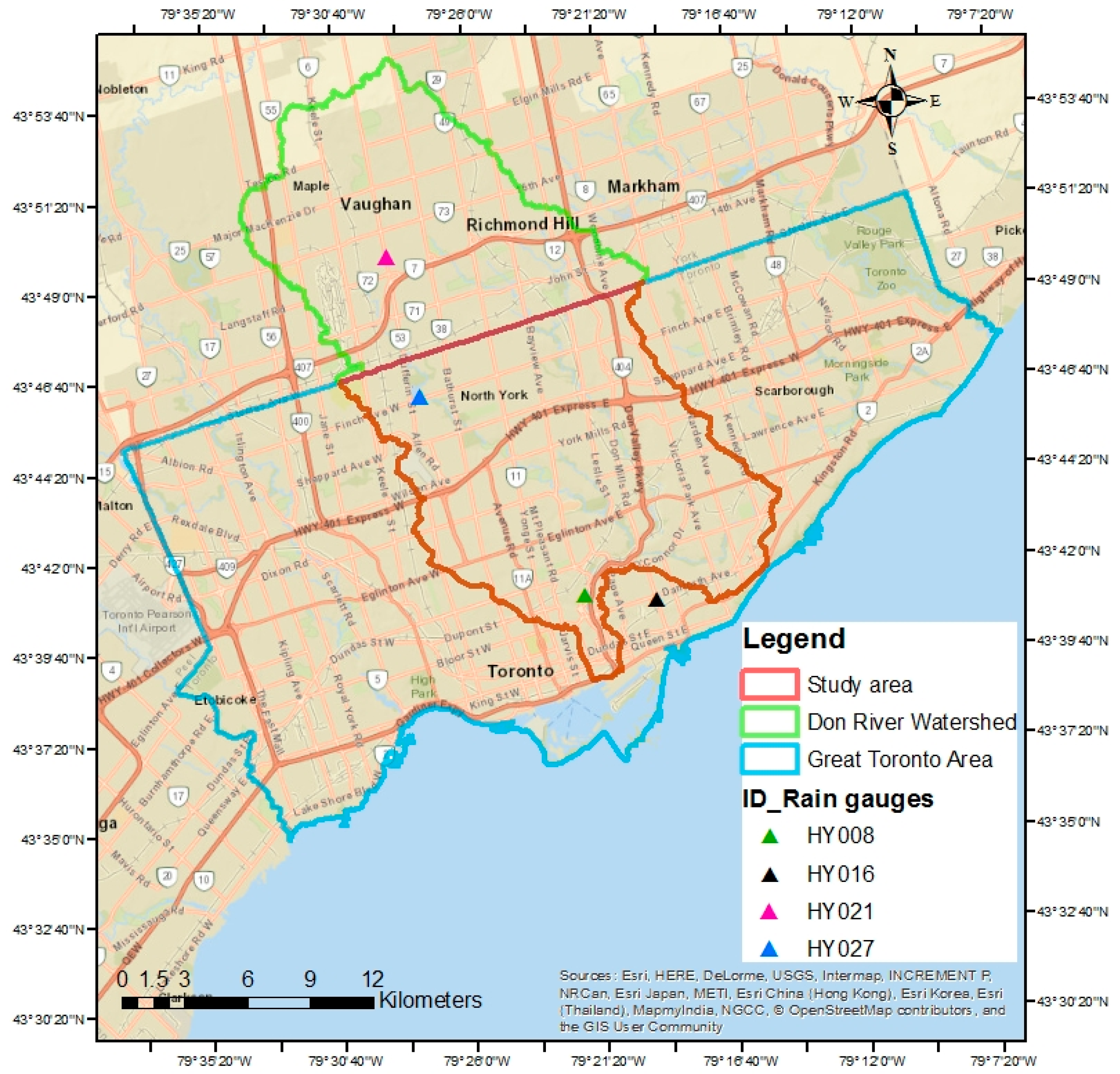
The Great Toronto Area (GTA) is selected as the case study to apply and test the proposed method. It is located in the Don River watershed in Ontario, Canada (see
Figure 1 below). This region has suffered four severe flood events during the last 100 years, each of which has resulted in high economic and social impacts. Hurricane Hazel in 1945 left 81 people dead and also resulted in 1.2 billion dollars (in 2016 dollars) in damages [
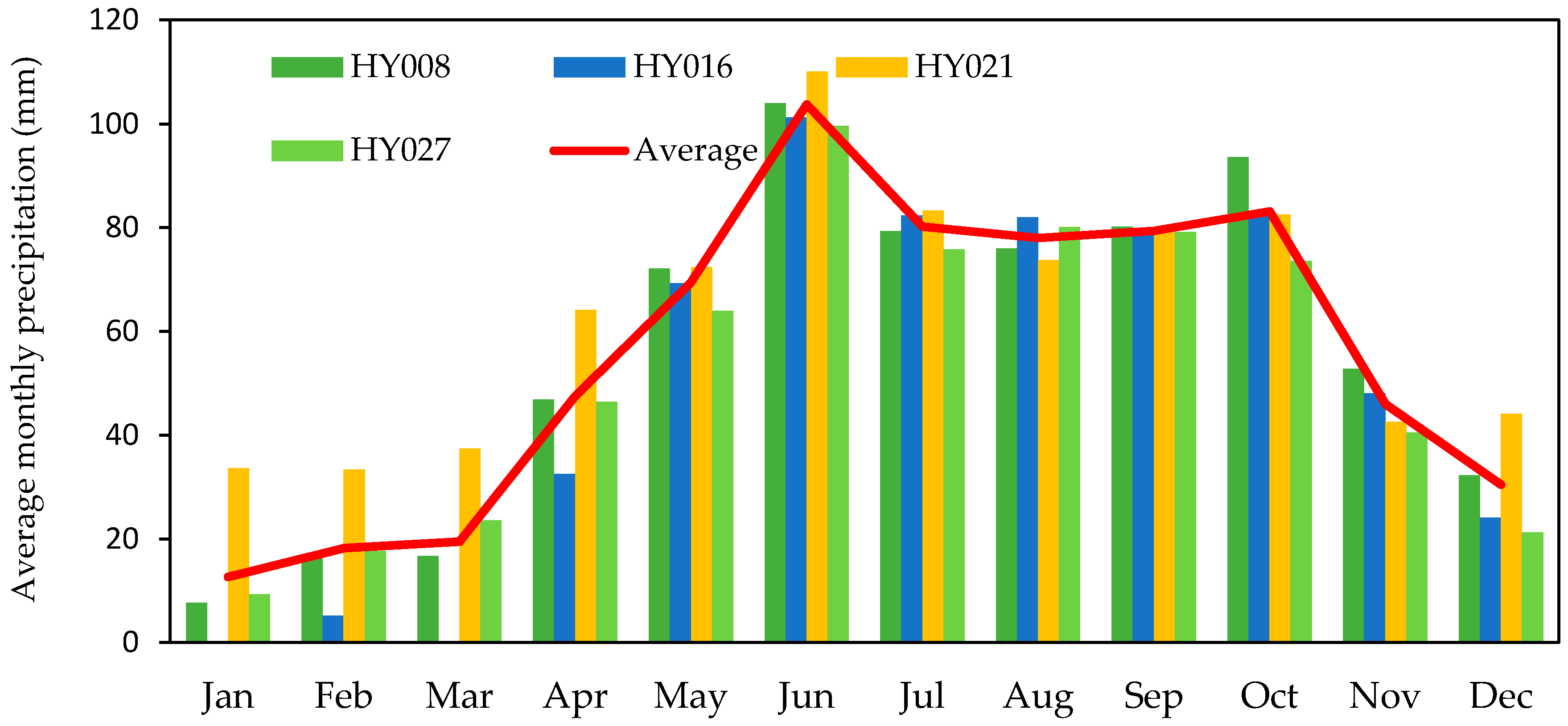
14]. The latest flood event, in 2013, was caused by a heavy storm in which the intensity of precipitation was 90 mm in 2 h, and some gauges reported up to 126 mm in 90 min (compared to an average of 70 mm per month [
15]). There are many factors that make the GTA susceptible to floods. The impervious cover in the study area is estimated in 73% (based on our analyses of the land use in the region). Additionally, large portions of the six tributaries of the lower Don River have been filled or artificially channelized, and significant wetlands have been filled or drained [
16]. Hence, this has resulted in conditions that contribute to an increase in flood susceptibility. Another factor is that the river valley is a non-confining valley; it is about 400 m wide, while the river itself is only 15 m wide [
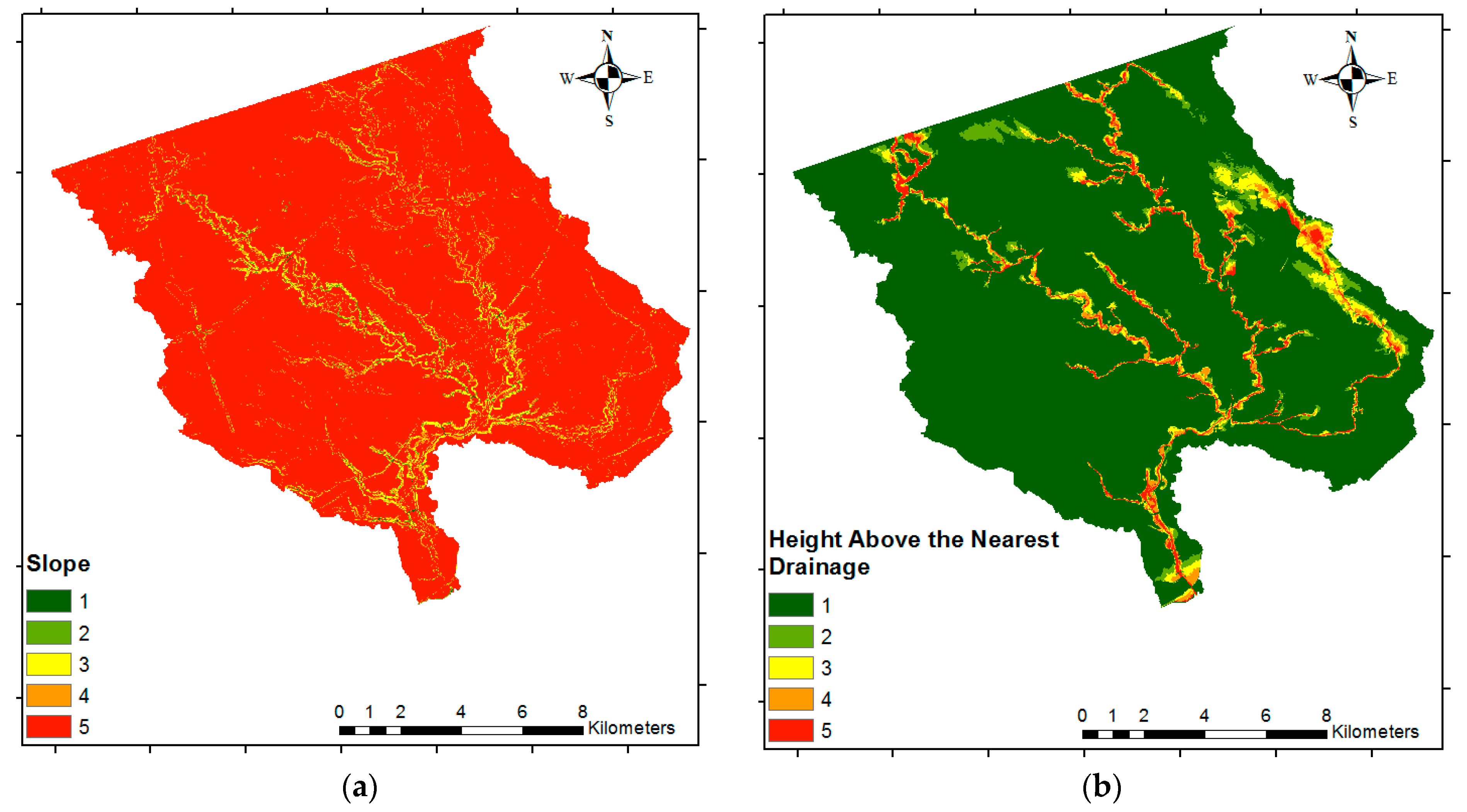
17]. The topography of the GTA also plays an important role, since it is relatively smooth. Flat slopes lead to a decrease in the surface runoff velocity, which results in a longer period of time for the runoff to drain.
Only limited studies of flood risk assessment (which include hazard, social, and economic vulnerability) in the GTA have been developed. A previous study [
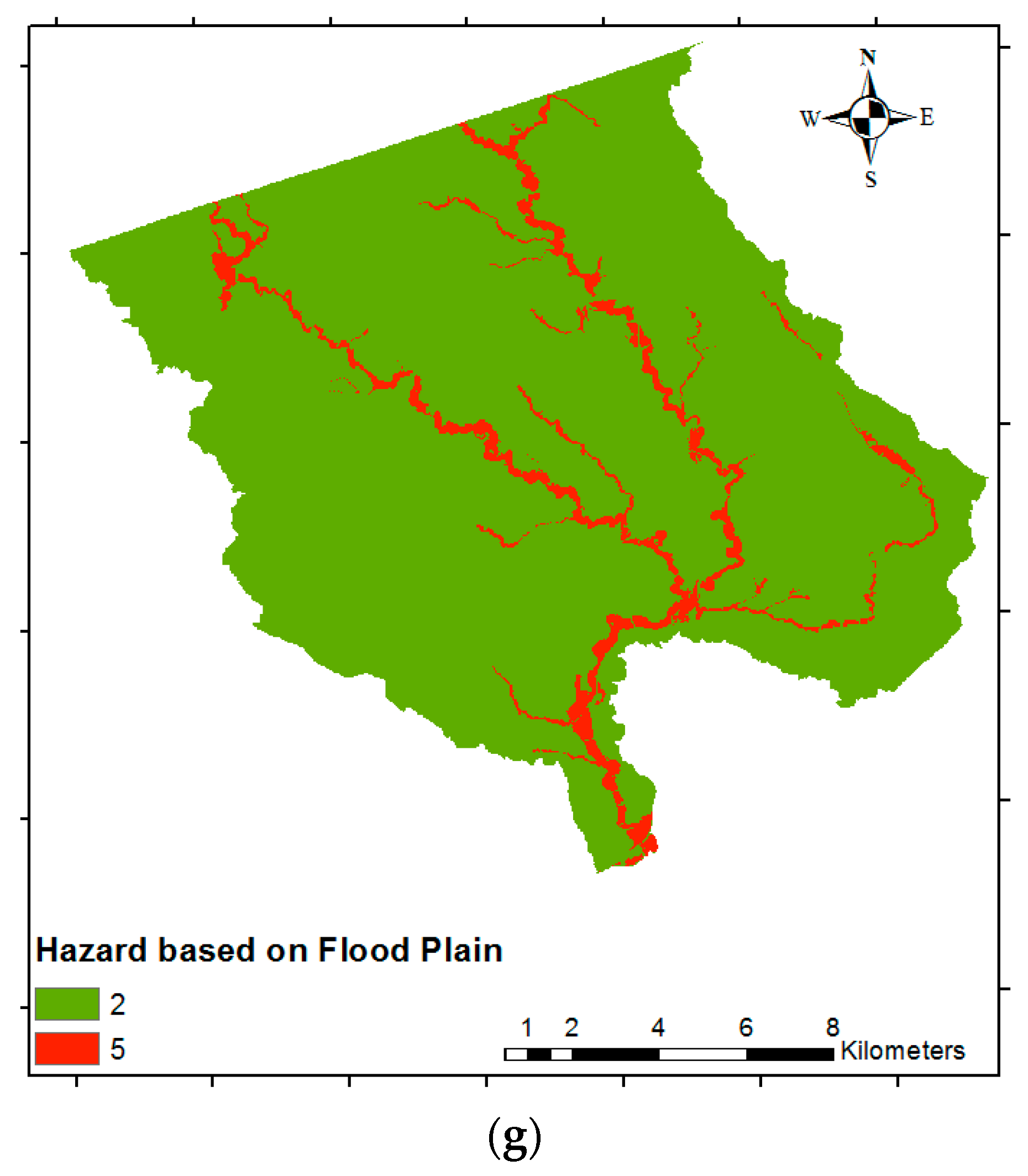
18] (which serves as the basis of the present research) generated flood risk index maps using GIS through the spatial combination of the flood hazard, social, and economic vulnerability layers. The criteria used to generate the flood hazard map were slope, land depression, the floodplain map (provided by the Toronto and Region Conservation Authority, TRCA), and land cover. For the economic vulnerability, a spatial layer that identified large buildings was used. Finally, the social vulnerability was determined by identifying the vulnerable groups from the 2006 census data from Statistics Canada. The limitation of this study was the direct assignment of criteria weights, instead of using a weighting method in the context of MCDM. Assigning criteria weights in this way does not allow obtaining a suitable assessment, as there is no theoretical background that supports a consistent assessment. Another study by Abdalla [
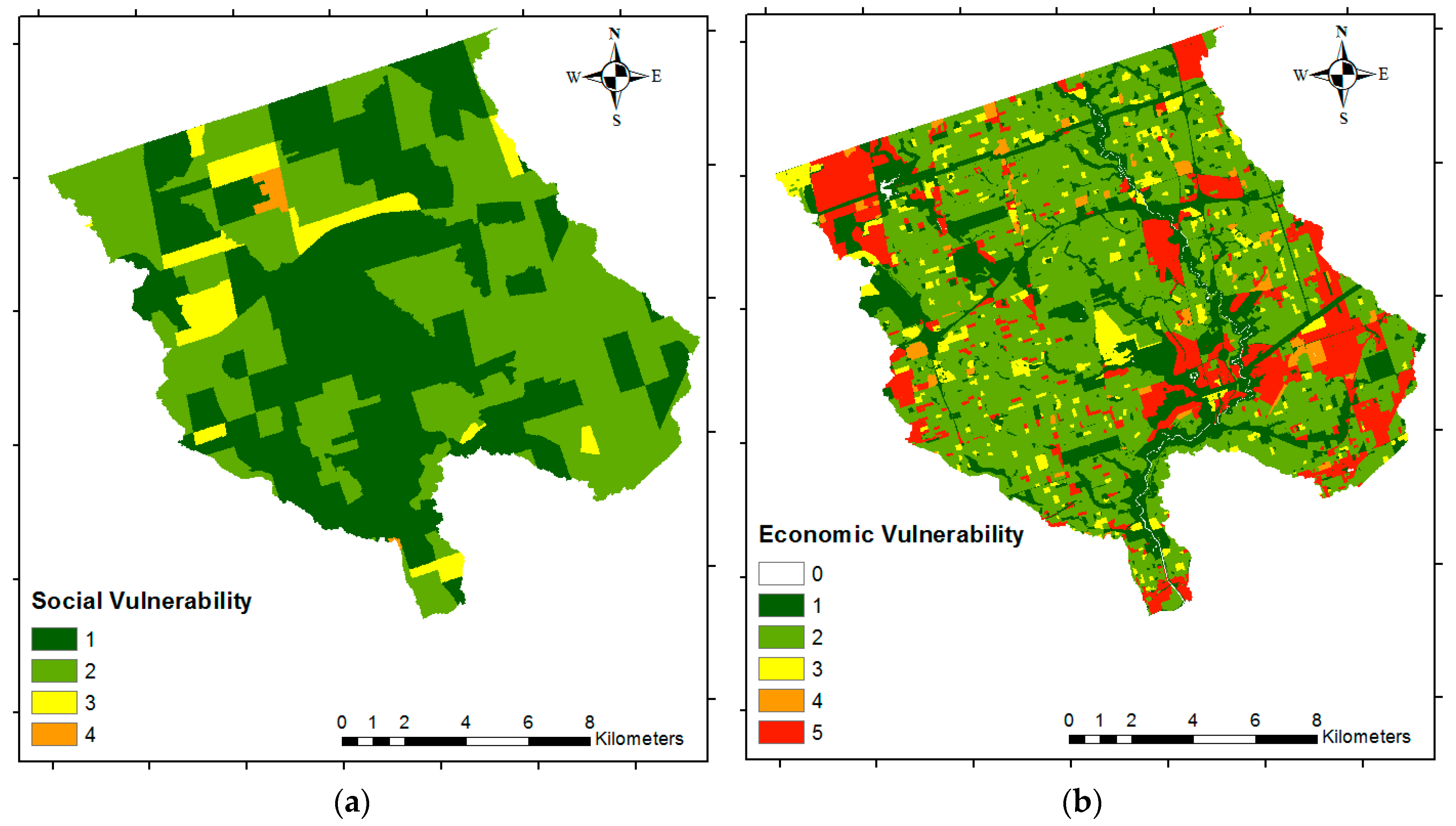
19] used a web-based three-dimensional (3D) GIS approach for flood risk assessment, in which the flood hazard was based on hydraulic models (using the software HEC-RAS) under hypothetical flow rates simulated using the Canadian Hydrographic Service. The footprint of buildings within the flood hazard area was used for analyzing the exposure. Although this approach provides a 3D view of the flood extent, it does not include the economic and social vulnerability. In this sense, this study is a flood hazard assessment instead of a flood risk assessment. Thus, there is a need to develop flood risk maps of the GTA to account for the social and economic vulnerability, with a consistent method to assign weights to the different criteria used.
1.3. Flood Risk Assessment Using GIS and MCDM
Flood risk assessment using the GIS-based multi-criteria methodology is a relatively new approach, and only a few studies have implemented it. A pilot study for the River Mulde in Saxony, Germany [
8], was developed using the multi-attribute utility theory (MAUT) and a disjunctive approach was used to assign weights for four different criteria (economic risk, population, social hot spots, and environmental risk). The flood hazard was obtained through a quasi two-dimensional (2D) hydrodynamic model using HEC-RAS. For the economic risk, the land use and estimates of the value of assets were used along with depth–damage curves (using damage functions). The social risk was based on the population density map. Finally, the social hot spots used the surveyed locations of old people and children, schools, and hospitals [
8]. Similar to AHP, MAUT is a very popular method in MCDM analysis. Nevertheless, MAUT is extremely data-intensive, as it requires a large amount of input data, and the weights are assumed by the decision maker instead of being calculated (as is the case in the proposed AHP process) [
20].
A study from the Iskandar region in Malaysia [
21] used a rating method for assessing criterion weights. The criteria selected for generating the flood susceptibility map included: distance from the main stream and river, elevation, slope, land use, cover type, distance to discharge channel, and population density. One of the limitations of this study is the use of the rating method, as it lacks the theoretical foundation, and thus is difficult to justify the meaning of the weights assigned to the criteria. A study for the Red River Delta, Vietnam [
22] was more sophisticated in terms of the weighting method used and the criteria selected. Similar to in the present paper, the AHP was used as the weighting method. The criteria selected for evaluating the flood hazard, economic, social, and environmental vulnerability are more suitable than the previously listed studies; they are also more difficult to obtain. The flood hazard was based on flood depth, flood duration, and flood velocity. The economic vulnerability used the area of residential buildings, special-use buildings, public infrastructure, and agricultural area. As for the social vulnerability, the population density, risk perception, spiritual values, and income levels were selected. Lastly, the environmental vulnerability was based on pollution (from industries, waste matter, and stagnations of floodwaters), erosion, and open spaces. Hence, when assessing flood risk for large-scale areas or in regions that lack detailed information (as is often the case), these criteria are not possible to use or require more resources, which makes this methodology difficult to implement [
22].
As mentioned above, some of the limitations of previous studies that use the GIS-based multi-criteria flood risk approach include criteria weighting methods that are not appropriate, or in some cases are not used at all. Moreover, the use of more complex criteria (which may be difficult to access or to generate), or conversely the use of very simple criteria can lead to unreliable flood risk maps. In addition, some studies do not consider the social component, which is very important for implementing mitigation measures that are aiming to reduce the number of people affected after a flood event.
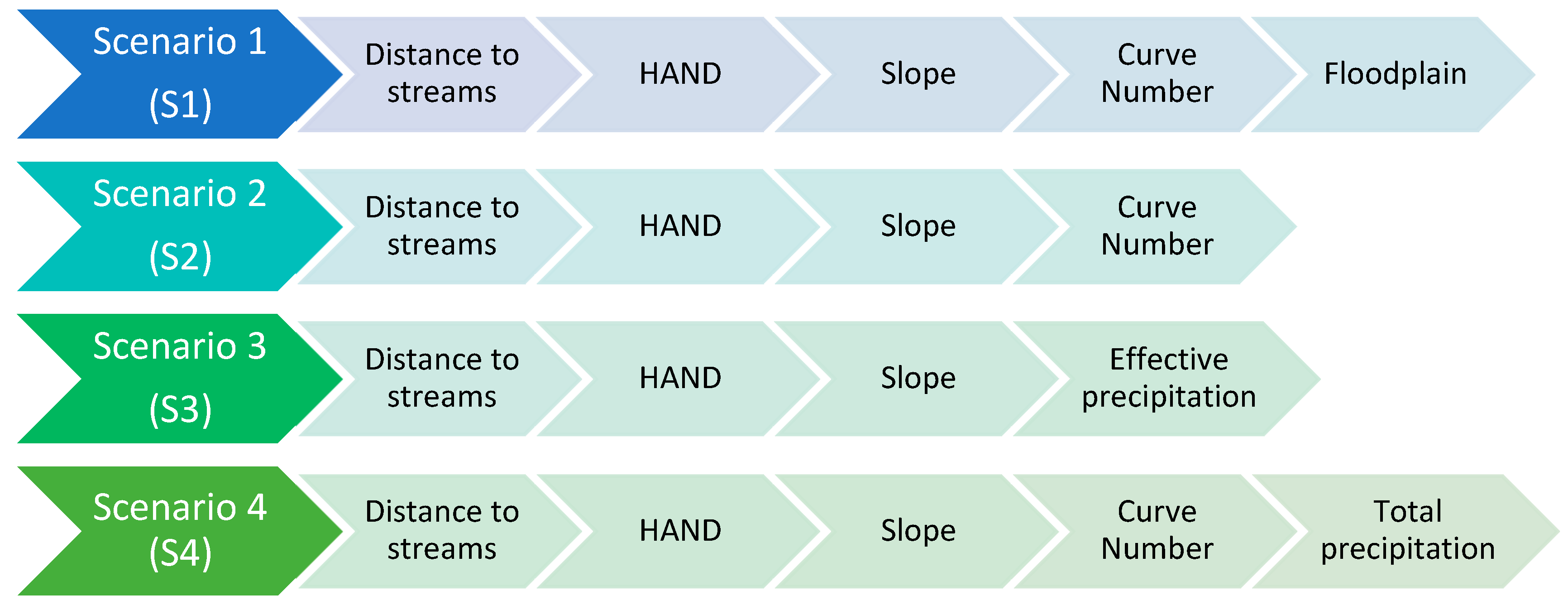
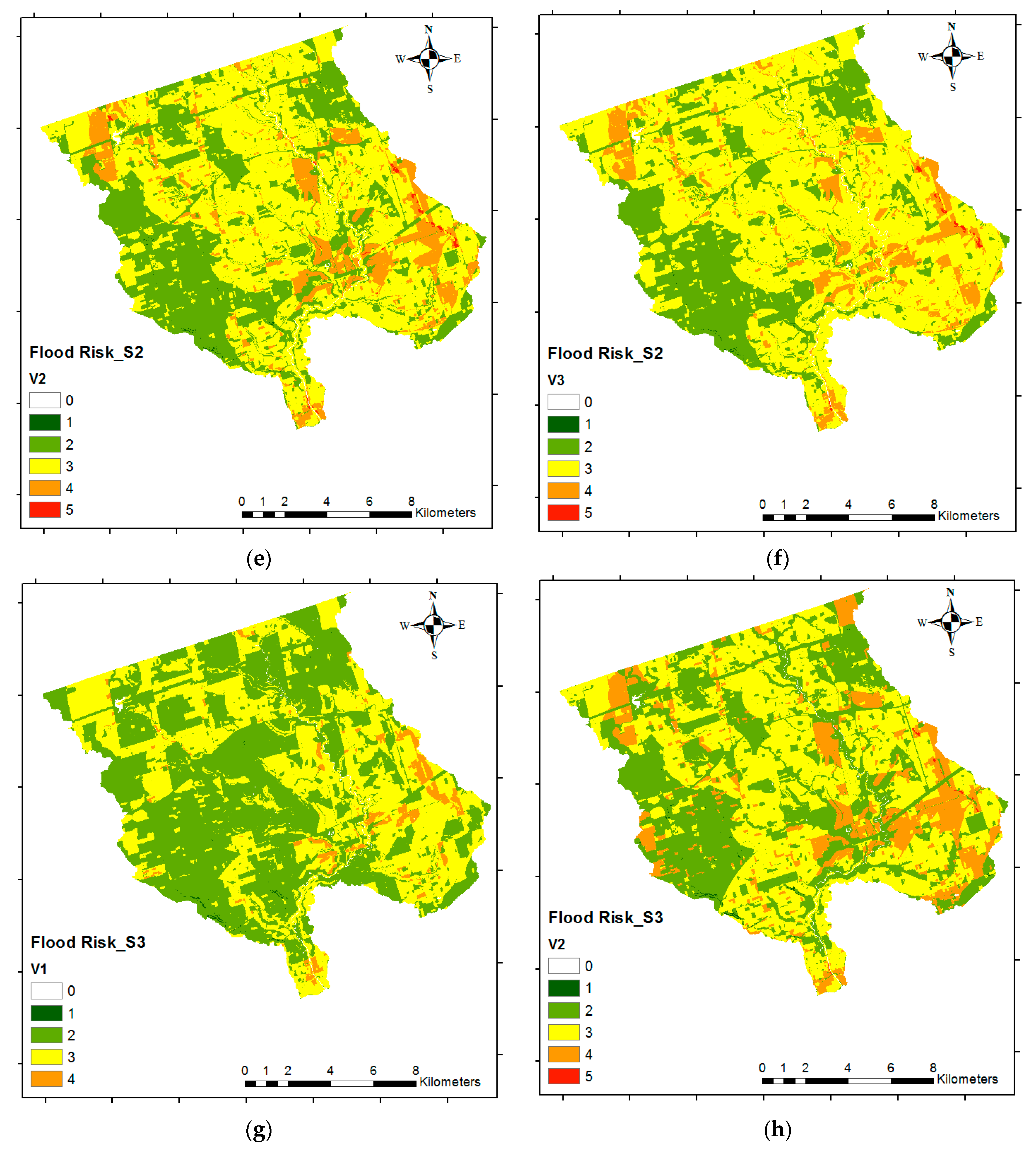
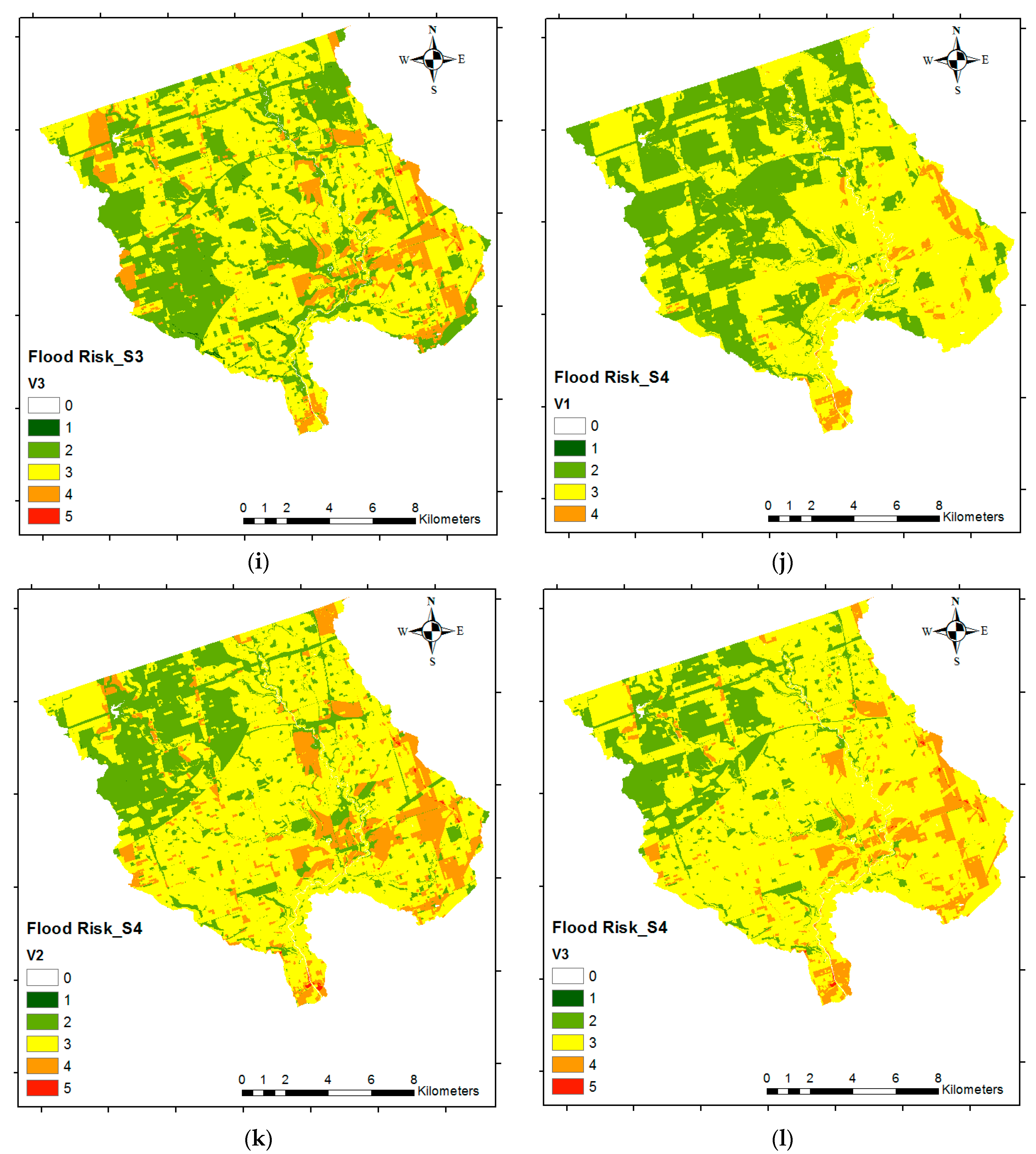
In the present paper, several improvements of the previous study for the GTA [
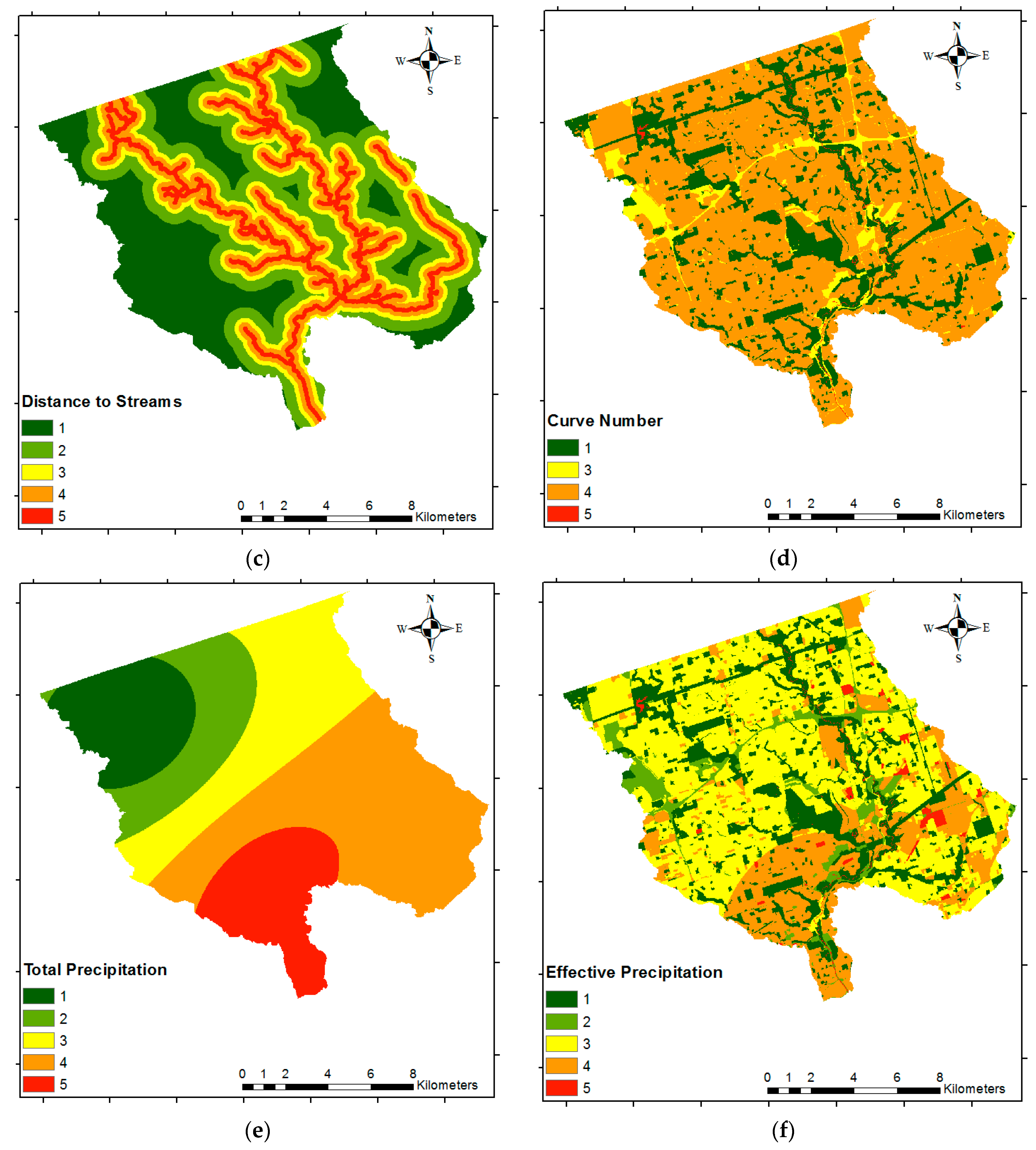
18] are proposed. First, we implement MCDM as part of the methodology for determining the criteria weights. Second, we propose the use of more appropriate flood hazard parameters, including: distance to streams (DS), height above the nearest drainage (HAND), Curve Number (CN) (which is a widely used empirical parameter developed by the United States Department of Agriculture—Soil Conservation Service (SCS), and is commonly used in hydrology for predicting direct runoff [
23]), total precipitation (
TP), and effective precipitation (
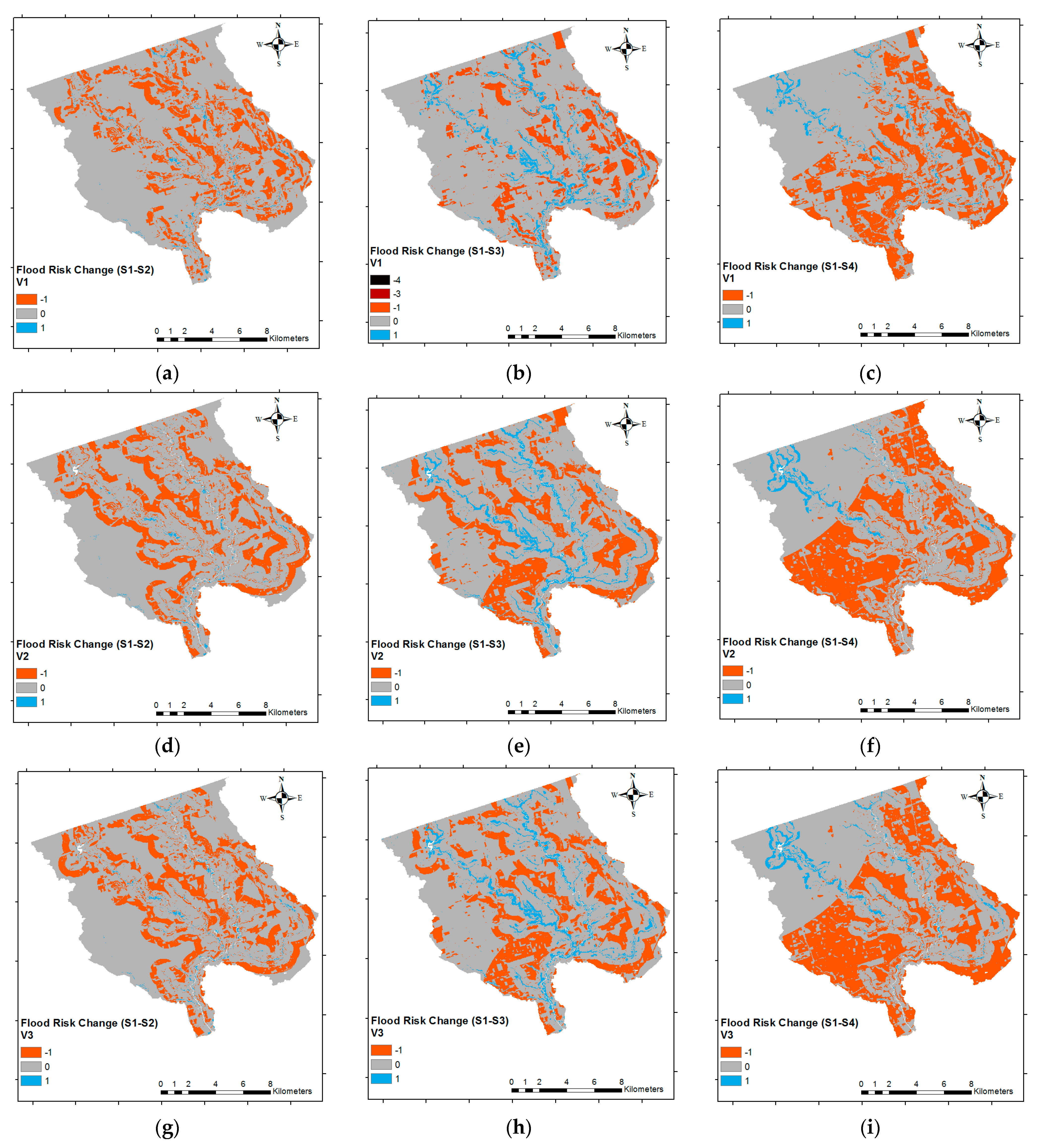
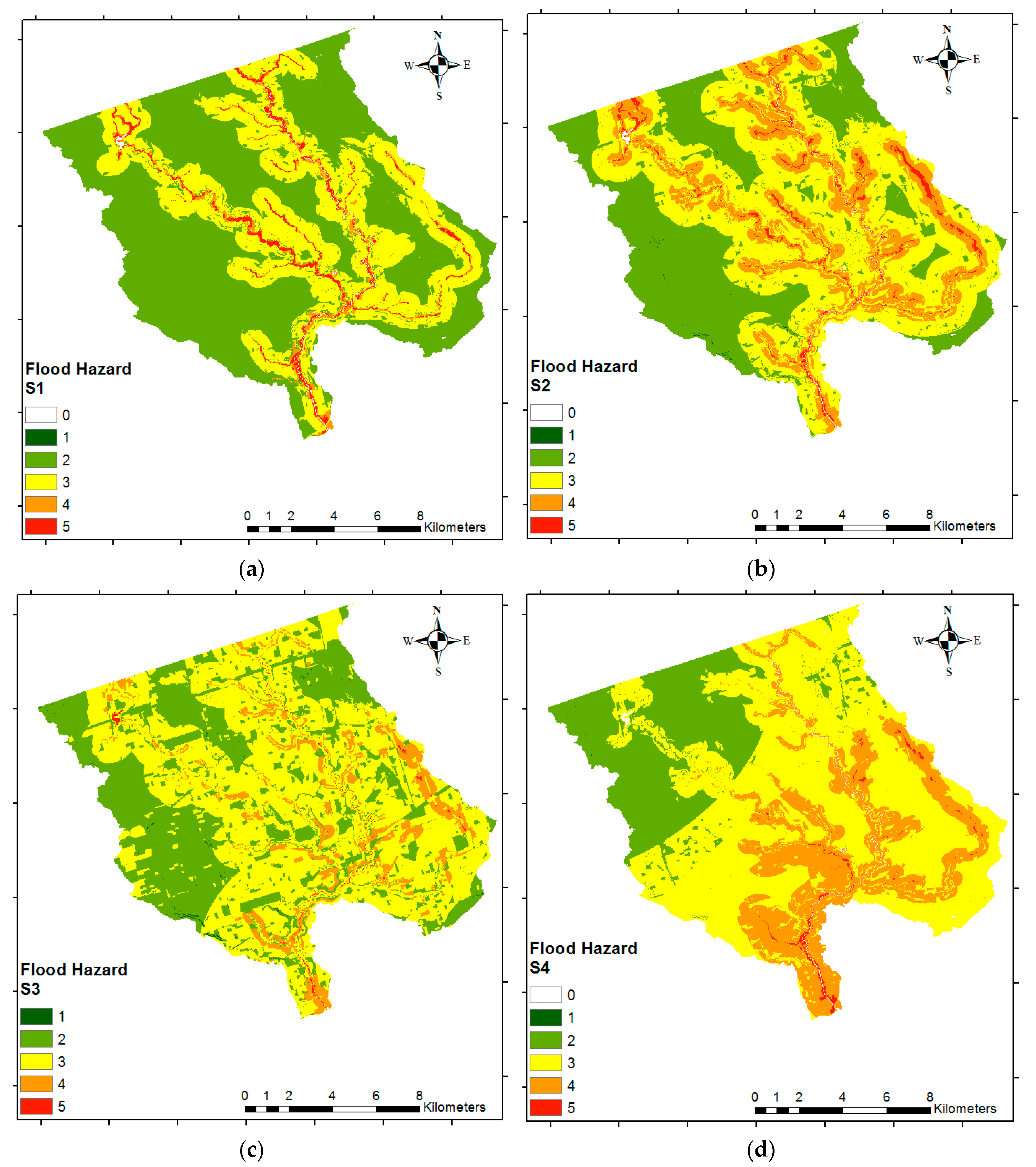
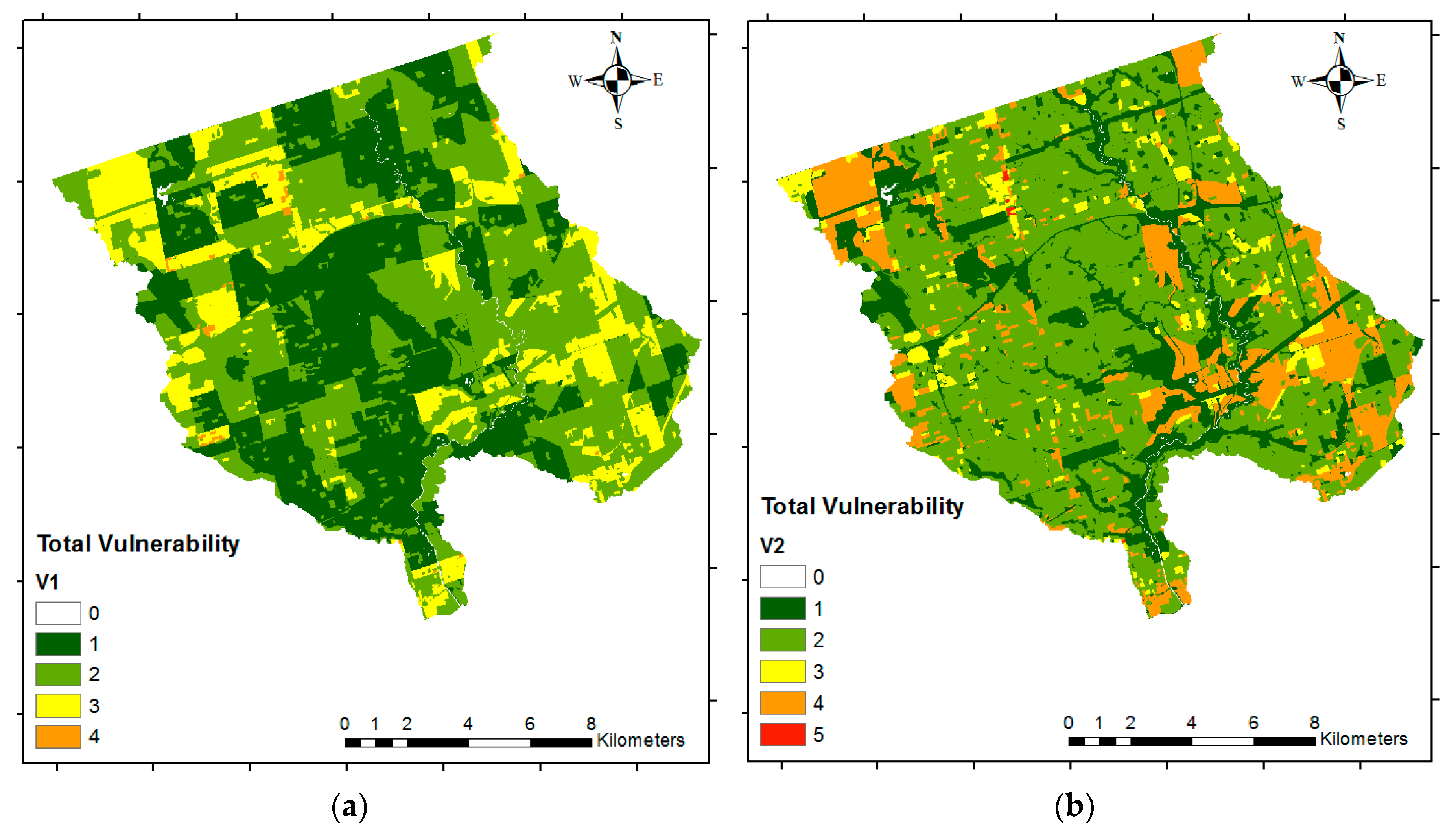
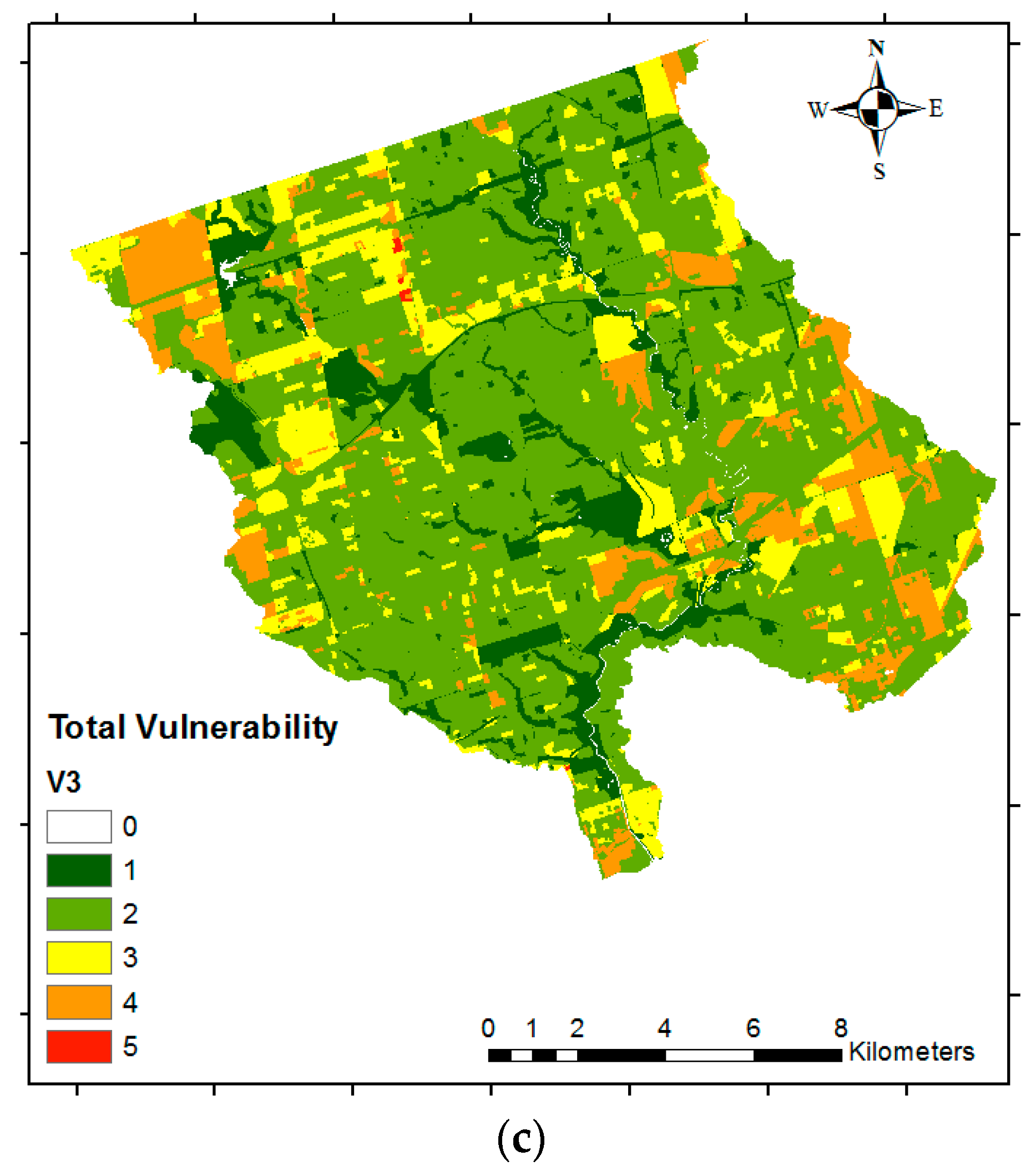
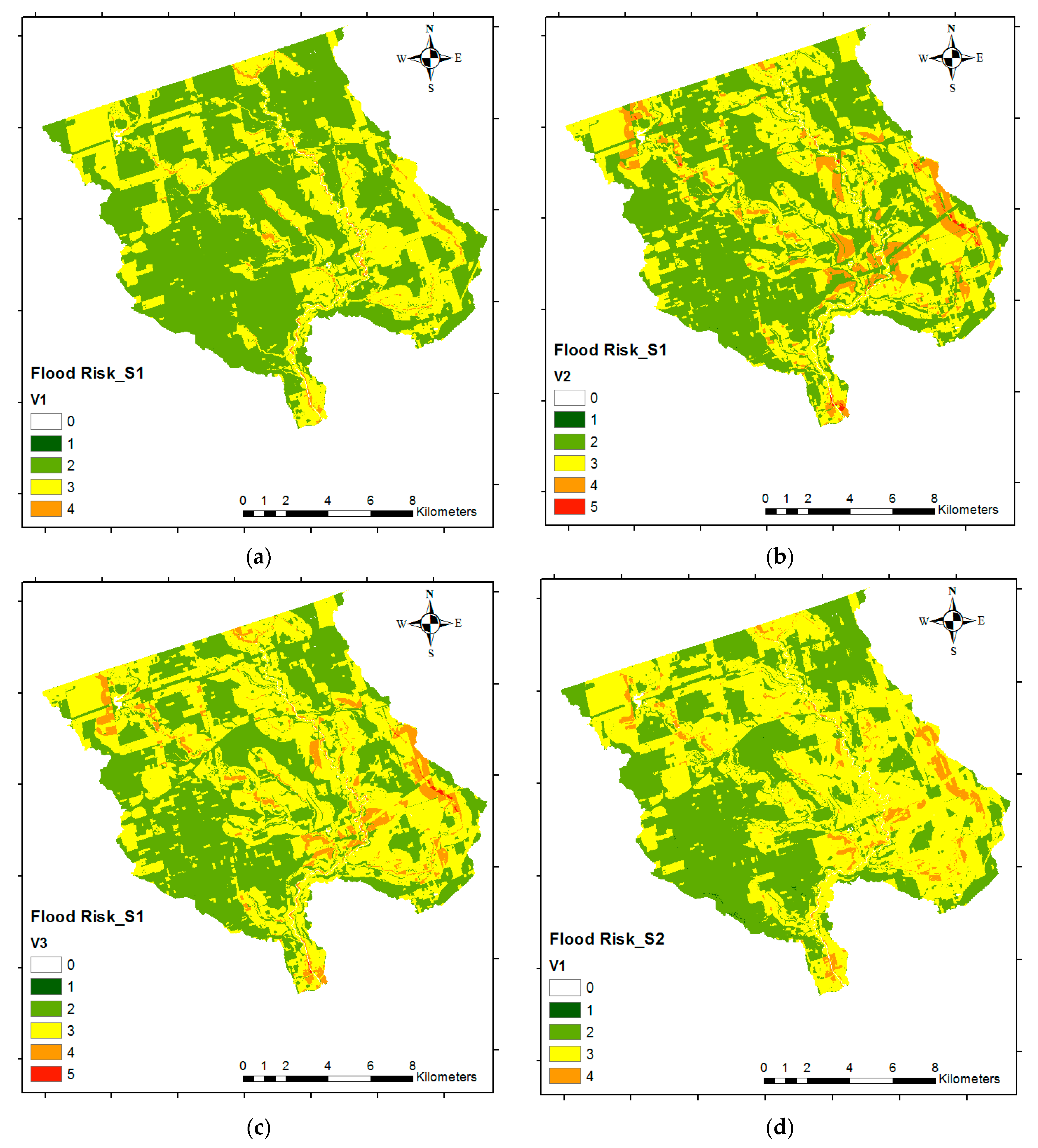
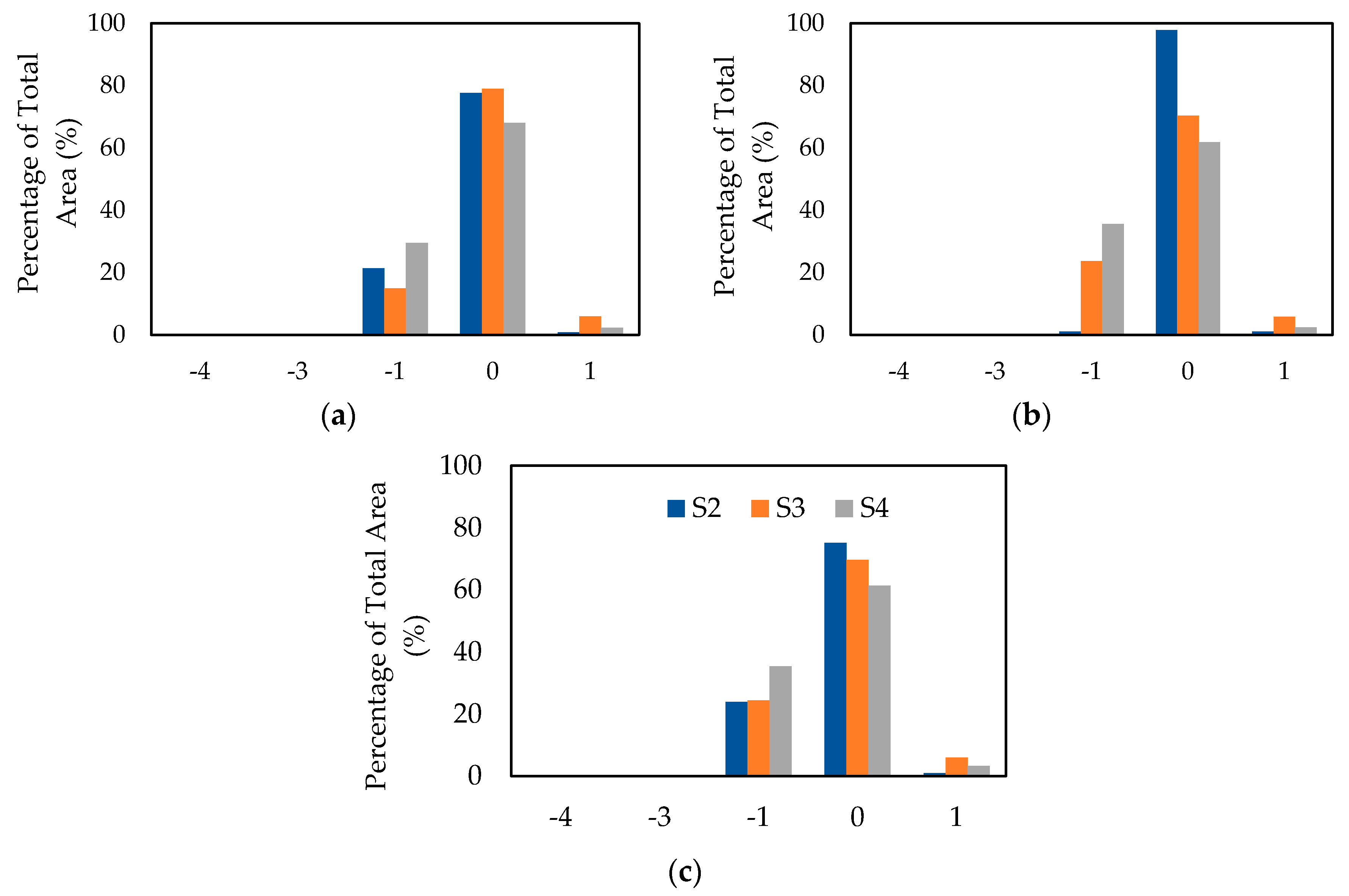
EP). For economic vulnerability, we propose using land-use data instead of large buildings. Lastly, we use the most recent census data (2016) instead of using the previous census (2006) data for determining the social vulnerability. We then use the proposed methods to develop four different flood risk scenarios to demonstrate the utility of the proposed research.
Hence, the aim of the present study is to provide a reliable but simplified method for flood risk mapping based on GIS spatial analysis integrated with AHP, which assesses both the economic and social vulnerability. Furthermore, the current study aims to analyze the criteria that should be considered for each component (using pairwise comparison) in order to generate reliable flood risk maps using inputs that are just suitable and easy to access. The results of this research will provide enhanced flood risk maps for the GTA, compared with the previous studies, which do not include social or economic vulnerability, nor a methodology for calculating criteria weights. Additionally, this research introduces more suitable criteria for flood risk analysis. Note that while the method is demonstrated for a watershed in the GTA, the approach can be easily applied to other watersheds.