An Attempt to Use Non-Linear Regression Modelling Technique in Long-Term Seasonal Rainfall Forecasting for Australian Capital Territory
Abstract
:1. Introduction
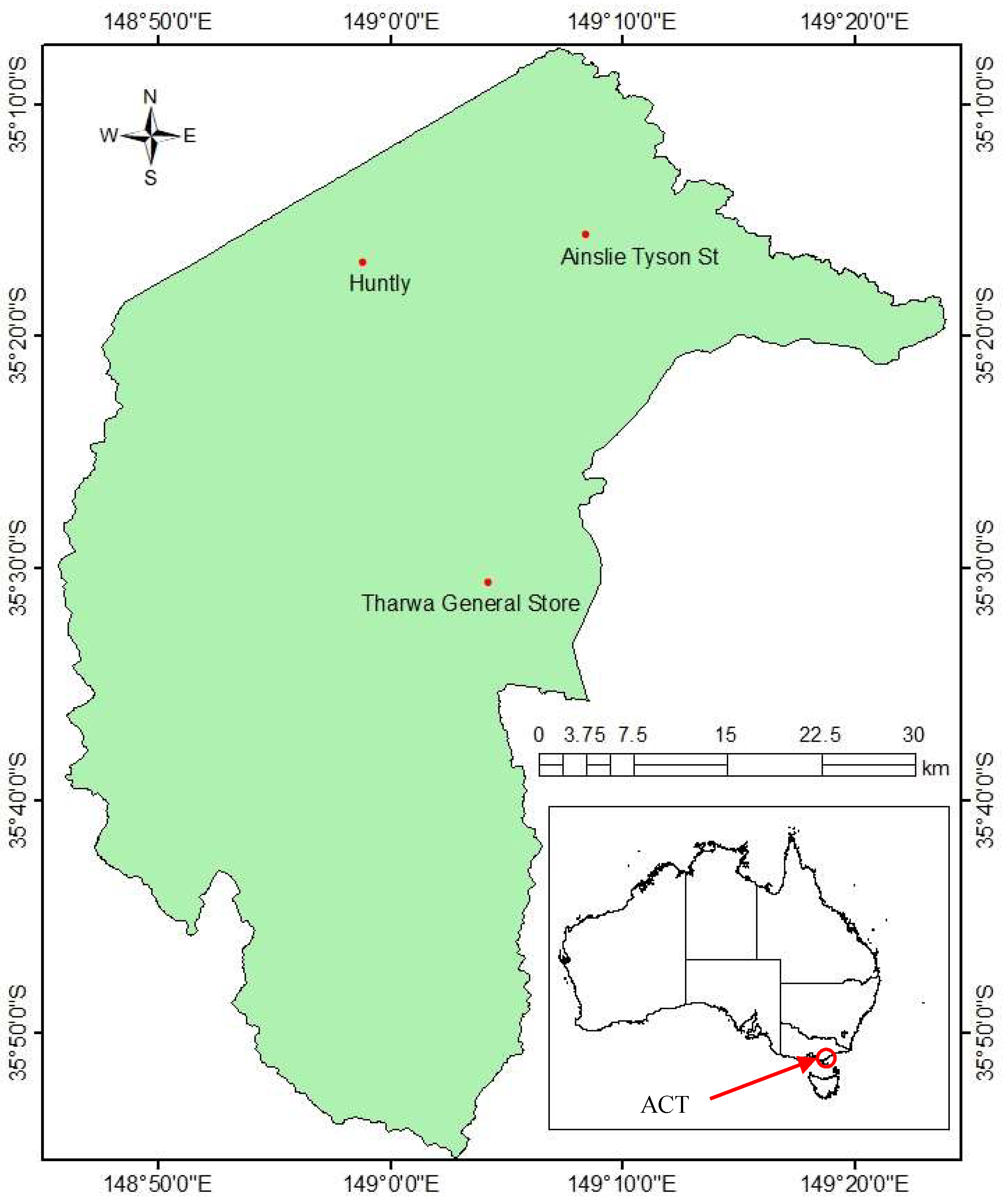
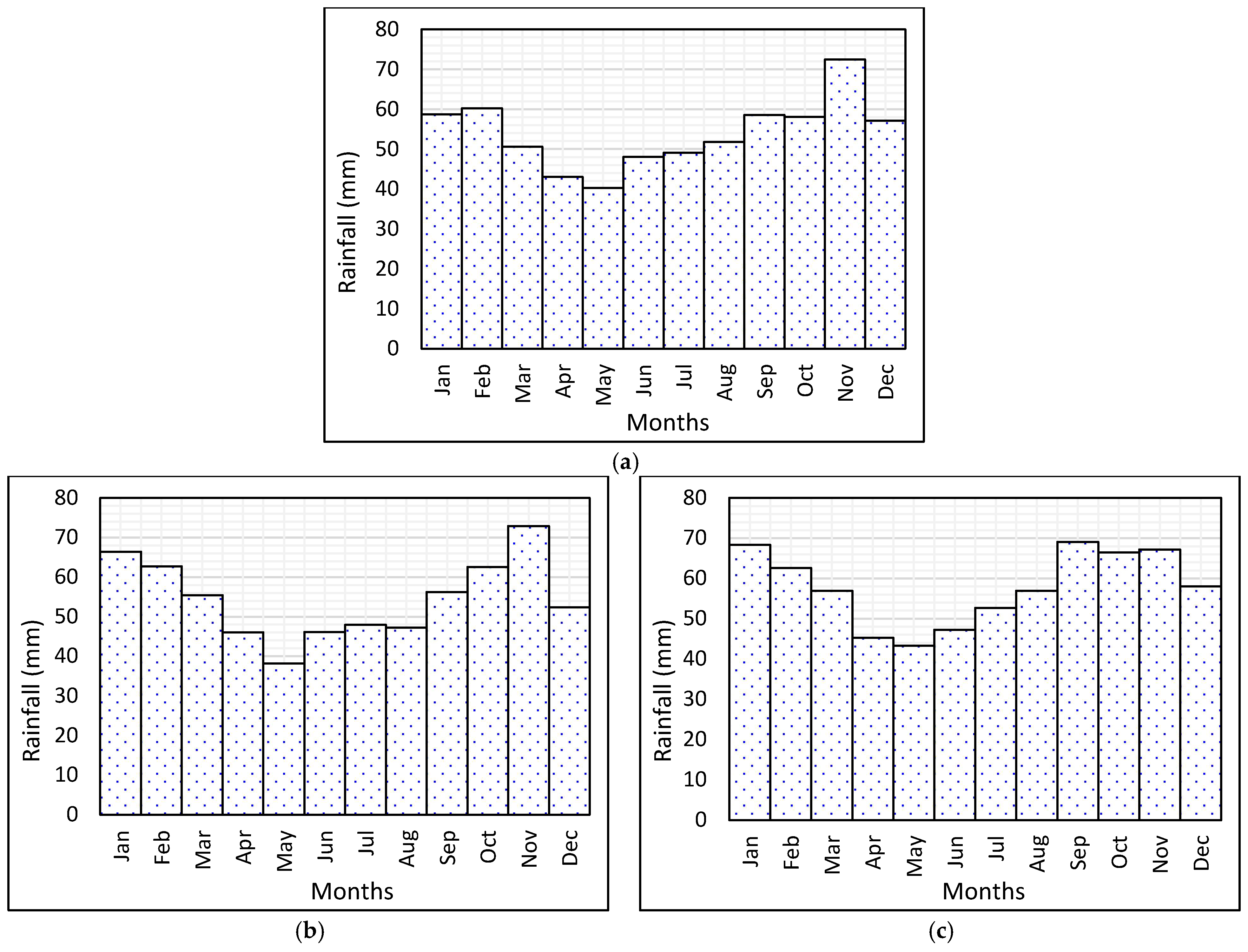
2. Study Area and Data Collection
3. Methods
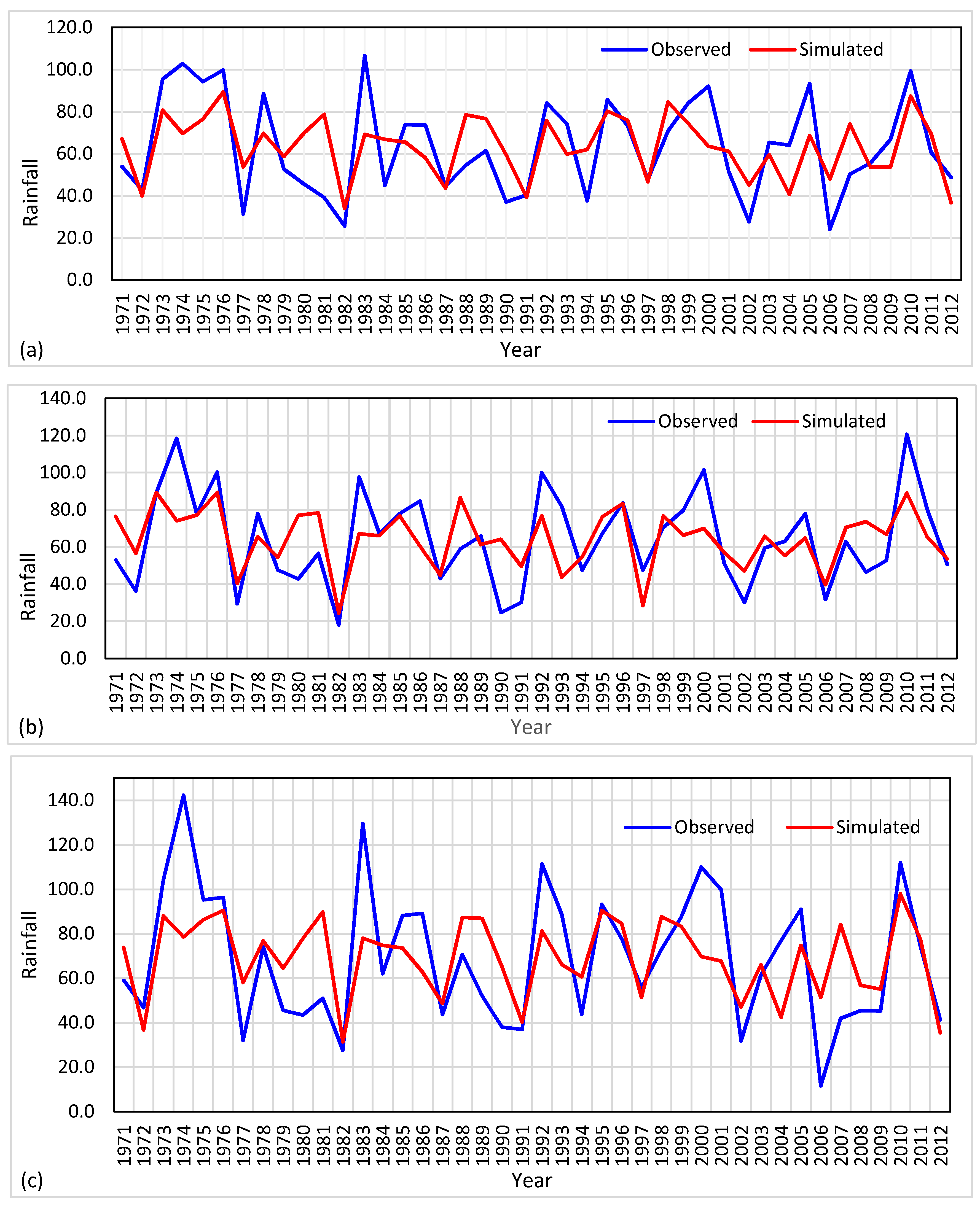
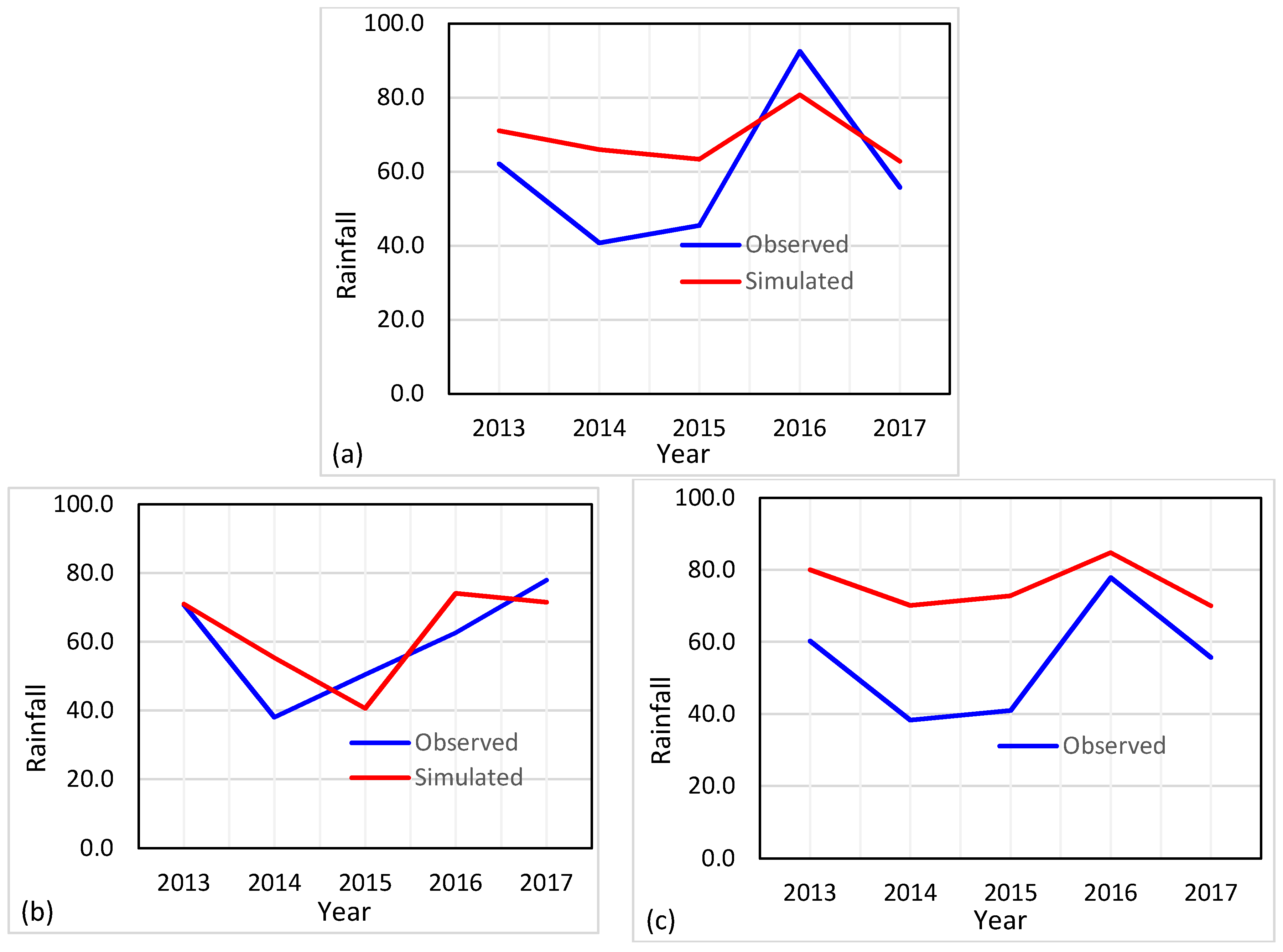
4. Results and Discussion
5. Conclusions and Recommendations
- Cubic function is capable of producing maximum correlation between seasonal rainfall and the climate indices.
- Logarithmic function produces the minimum correlations between seasonal rainfall and the climate indices.
- DMI-SOI based non-linear models are more suitable to predict seasonal rainfall, as they produce higher correlations.
Author Contributions
Funding
Conflicts of Interest
References
- Tennant, W.J.; Hewitson, B.C. Intra-seasonal rainfall characteristics and their importance to the seasonal prediction problems. Int. J. Climatol. 2002, 22, 1033–1048. [Google Scholar] [CrossRef]
- Frias, M.D.; Iturbide, M.; Manzanas, R.; Bedia, J.; Fernandez, J.; Herrera, S.; Cofino, A.S.; Gutierrez, J.M. An R package to visualize and communicate uncertainty in seasonal climate prediction. Environ. Model. Softw. 2018, 99, 101–110. [Google Scholar] [CrossRef]
- Jenicek, M.; Seibert, J.; Zappa, M.; Staudinger, M.; Jonas, T. Importance of maximum snow accumulation for summer low flows in humid catchments. Hydrol. Earth Syst. Sci. 2016, 20, 859–874. [Google Scholar] [CrossRef] [Green Version]
- Crochemore, L.; Ramos, M.H.; Pappenberger, F. Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2016, 20, 3601–3618. [Google Scholar] [CrossRef] [Green Version]
- Winsemius, H.C.; Dutra, E.; Engelbrecht, F.A.; Archer Van Garderen, E.; Wetterhall, F.; Pappenberger, F.; Werner, M.G.F. The potential value of seasonal forecasts in a changing climate in southern Africa. Hydrol. Earth Syst. Sci. 2014, 18, 1525–1538. [Google Scholar] [CrossRef] [Green Version]
- Goddard, L.; Aitchellouche, Y.; Baethgen, W.; Dettinger, M.; Graham, R.; Hayman, P.; Kadi, M.; Martinez, R.; Meinke, H. Providing seasonal-to-interannual climate information for risk management and decision-making. Procedia Environ. Sci. 2010, 1, 81–101. [Google Scholar] [CrossRef]
- Barnston, A.G.; Li, S.; Mason, S.J.; Dewitt, D.G.; Goddard, L.; Gong, X. Verification of the First 11 Years of IRI’s Seasonal Climate Forecasts. J. Appl. Meteorol. Climatol. 2010, 49, 493–520. [Google Scholar] [CrossRef]
- Wang, B. Advance and prospectus of seasonal prediction: Assessment of the APCC/CliPAS 14-model ensemble retrospective seasonal prediction (1980–2004). Clim. Dyn. 2009, 33, 93–117. [Google Scholar] [CrossRef]
- Hossain, I.; Rasel, H.M.; Imteaz, M.A.; Mekanik, F. Long-term seasonal rainfall forecasting: Efficiency of linear modelling technique. Environ. Earth Sci. 2018, 77, 28. [Google Scholar] [CrossRef]
- Mekanik, F.; Imteaz, M.A.; Gato-Trinidad, S.; Elmahdi, A. Multiple linear regression and artificial neural network for long-term rainfall forecasting using large scale climate modes. J. Hydrol. 2013, 503, 11–21. [Google Scholar] [CrossRef]
- Kim, H.M.; Webster, P.J.; Curry, J.A. Seasonal prediction skill of ECMWF System 4 and NCEP CFSv2 retrospective forecast for the Northern Hemisphere winter. Clim. Dyn. 2012, 39, 2957–2973. [Google Scholar] [CrossRef]
- Lim, E.P.; Hendon, H.H.; Anderson, D.L.T.; Charles, A.; Alves, O. Dynamical, statistical-dynamical, and multimodel ensemble forecasts of Australian spring season rainfall. Mon. Weather Rev. 2011, 139, 958–975. [Google Scholar] [CrossRef]
- Manzanas, R.; Frias, M.D.; Cofino, A.S.; Gutierrez, J.M. Validation of 40 year multimodel seasonal precipitation forecasts: The role of ENSO on the global skill. J. Geophys. Res. Atmos. 2014, 119, 1708–1719. [Google Scholar] [CrossRef] [Green Version]
- Rayner, S.; Lach, D.; Ingram, H. Weather forecasts are for wimps: Why water resource managers do not use climate forecasts. Clim. Chang. 2005, 69, 197–227. [Google Scholar] [CrossRef]
- Langford, S.; Hendon, H.H. Assessment of international seasonal rainfall forecasts for Australia and the benefit of multi-model ensembles for improving reliability. In the Centre for Australian Weather and Climate Research Technical Report No. 039; The Centre for Australian Weather and Climate Research: Victoria, Australian, 2011. [Google Scholar]
- Hossain, I.; Rasel, H.M.; Imteaz, M.A.; Moniruzzaman, M. Statistical correlations between rainfall and climate indices in Western Australia. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November–4 December 2015; pp. 1991–1997. [Google Scholar]
- Goddard, L.; Mason, S.J.; Zebiak, S.E.; Ropelewski, C.F.; Basher, R.; Cane, M.A. Current approaches to seasonal to interannual climate predictions. Int. J. Climatol. 2001, 21, 1111–1152. [Google Scholar] [CrossRef] [Green Version]
- Saji, N.H.; Yamagata, T. Interference of teleconnection patterns generated from the tropical Indian and Pacific Oceans. Clim. Res. 2003, 25, 151–169. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. Influence of the Indian Ocean Dipole on the Australian winter rainfall. Geophys. Res. Lett. 2003, 30, 1821. [Google Scholar] [CrossRef]
- Rasel, H.M.; Imteaz, M.A.; Mekanik, F. Evaluating the effects of lagged ENSO and SAM as potential predictors for long-term rainfall forecasting. In Proceedings of the International Conference on Water Resources and Environment (WRE 2015), Beijing, China, 25–28 July 2015; Miklas, S., Ed.; Taylor & Francis Group: London, UK, 2015; pp. 125–129. [Google Scholar]
- Liu, Y.; Fan, K. An application of hybrid downscaling model to forecast summer precipitation at stations in China. Atmos. Res. 2014, 143, 17–30. [Google Scholar] [CrossRef]
- Manzanas, R.; Gutierrez, J.M.; Fernandez, J.; van Meijgaard, E.; Calmanti, S.; Magarino, M.E.; Cofino, A.S.; Herrera, S. Dynamical and statistical downscaling of seasonal temperature forecasts in Europe: Added value for user applications. Clim. Serv. 2018, 9, 44–56. [Google Scholar] [CrossRef]
- Bilgili, M. Prediction of soil temperature using regression and artificial neural network models. Meteorol. Atmos. Phys. 2010, 110, 59–70. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Esha, R.I.; Imteaz, M.A. Seasonal streamflow prediction using large scale climate drivers for NSW region. In Proceedings of the 22nd International Congress on Modelling and Simulation, Hobart, Australia, 3–8 December 2017; pp. 1593–1599. [Google Scholar]
- Pegion, K.; Kirtman, B.P. The impact of air-sea interactions on the simulation of tropical intraseasonal variability. J. Clim. 2008, 21, 6616–6635. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Forecast Verification: A Practitioner's Guide in Atmospheric Science; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
| Index | Linear | Quadratic | Cubic | Exponential | Power | Logarithmic |
|---|---|---|---|---|---|---|
| DMIJun | 0.083 | 0.097 | 0.154 | 0.082 | 0.182 | 0.187 |
| NINO3.4Jun | 0.420 * | 0.428 * | 0.436 * | 0.411 * | 0.153 | 0.157 |
| NINO3.4Jul | 0.462 * | 0.462 * | 0.495 * | 0.456 * | 0.056 | 0.061 |
| NINO3.4Aug | 0.503 * | 0.503 * | 0.524 * | 0.499 * | 0.332 | 0.338 |
| SEIOJun | 0.127 | 0.265 | 0.267 | 0.135 | 0.331 | 0.312 |
| SEIOJul | 0.208 | 0.280 | 0.323 * | 0.218 | 0.305 | 0.309 |
| SEIOAug | 0.236 | 0.242 | 0.243 | 0.232 | 0.099 | 0.098 |
| SOIJun | 0.380 * | 0.385 * | 0.389 * | 0.374 * | −0.055 | 0.071 |
| SOIJul | 0.407 * | 0.407 * | 0.470 * | 0.405 * | 0.451 | 0.242 |
| SOIAug | 0.502 * | 0.517 * | 0.527 * | 0.488 * | 0.002 | 0.002 |
| Index | Linear | Quadratic | Cubic | Exponential | Power | Logarithmic |
|---|---|---|---|---|---|---|
| DMIJun | 0.193 | 0.198 | 0.226 | 0.190 | 0.183 | 0.192 |
| NINO3.4Jun | 0.457 * | 0.480 * | 0.507 * | 0.440 * | 0.232 | 0.240 |
| NINO3.4Jul | 0.518 * | 0.519 * | 0.573 * | 0.508 * | 0.089 | 0.099 |
| NINO3.4Aug | 0.542 * | 0.542 * | 0.589 * | 0.533 * | 0.298 | 0.303 |
| SEIOJun | 0.152 | 0.325 * | 0.329 * | 0.166 | 0.279 | 0.246 |
| SEIOJul | 0.195 | 0.253 | 0.301 * | 0.204 | 0.226 | 0.230 |
| SEIOAug | 0.218 | 0.222 | 0.231 | 0.214 | 0.022 | 0.022 |
| SOIJun | 0.350 * | 0.355 * | 0.355 * | 0.344 * | 0.042 | 0.159 |
| SOIJul | 0.407 * | 0.407 * | 0.472 * | 0.407 * | 0.518 * | 0.376 |
| SOIAug | 0.516 * | 0.532 * | 0.532 * | 0.500 * | 0.071 | 0.070 |
| Index | Linear | Quadratic | Cubic | Exponential | Power | Logarithmic |
|---|---|---|---|---|---|---|
| DMIJun | 0.122 | 0.122 | 0.151 | 0.121 | 0.105 | 0.109 |
| NINO3.4Jun | 0.383 * | 0.387 * | 0.391 * | 0.376 * | 0.288 | 0.283 |
| NINO3.4Jul | 0.450 * | 0.451 * | 0.474 * | 0.448 * | 0.161 | 0.176 |
| NINO3.4Aug | 0.476 * | 0.476 * | 0.510 * | 0.476 * | 0.375 | 0.380 |
| SEIOJun | 0.136 | 0.260 | 0.280 | 0.136 | 0.268 | 0.246 |
| SEIOJul | 0.216 | 0.235 | 0.280 | 0.221 | 0.231 | 0.236 |
| SEIOAug | 0.248 | 0.258 | 0.274 | 0.241 | 0.076 | 0.076 |
| SOIJun | 0.267 | 0.274 | 0.274 | 0.262 | −0.097 | 0.019 |
| SOIJul | 0.322 * | 0.322 * | 0.399 * | 0.321 * | 0.495 * | 0.320 |
| SOIAug | 0.467 * | 0.477 * | 0.478 * | 0.453 * | 0.011 | 0.010 |
| Indices Combination | Correlations | ||
|---|---|---|---|
| Ainslie Tyson St | Tharwa General Store | Huntly | |
| SEIOJun–Nino3.4Jun | 0.533 * | 0.620 * | 0.485 * |
| SEIOJun–Nino3.4Jul | 0.581 * | 0.675 * | 0.549 * |
| SEIOJun–Nino3.4Aug | 0.589 * | 0.661 * | 0.556 * |
| SEIOJul–Nino3.4Jun | 0.544 * | 0.597 * | 0.477 * |
| SEIOJul–Nino3.4Jul | 0.587 * | 0.646 * | 0.537 * |
| SEIOJul–Nino3.4Aug | 0.622 * | 0.629 * | 0.579 * |
| SEIOAug–Nino3.4Jun | 0.463 * | 0.537 * | 0.444 * |
| SEIOAug–Nino3.4Jul | 0.519 * | 0.597 * | 0.516 * |
| SEIOJun–SOIJun | 0.472 * | 0.489 * | 0.400 * |
| SEIOJun–SOIJul | 0.589 * | 0.604 * | 0.494 * |
| SEIOJun–SOIAug | 0.602 * | 0.616 * | 0.530 * |
| SEIOJul–SOIJun | 0.446 * | 0.408 * | 0.338 * |
| SEIOJul–SOIAug | 0.619 * | 0.625 * | 0.547 * |
| SEIOAug–SOIAug | 0.529 * | 0.544 * | 0.493 * |
| DMIJun–SOIJun | 0.545 * | 0.410 * | 0.310 * |
| DMIJun–SOIJul | 0.552 * | 0.710 * | 0.456 * |
| DMIJun–SOIAug | 0.659 * | 0.564 * | 0.507 * |
| Parameters | Ainslie Tyson St | Tharwa General Store | Huntly |
|---|---|---|---|
| R | 0.91 | 0.71 | 0.86 |
| RMSE | 15.62 | 10.68 | 23.08 |
| MAE | 14.2 | 9.0 | 20.9 |
| d | 0.71 | 0.82 | 0.56 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, I.; Esha, R.; Alam Imteaz, M. An Attempt to Use Non-Linear Regression Modelling Technique in Long-Term Seasonal Rainfall Forecasting for Australian Capital Territory. Geosciences 2018, 8, 282. https://doi.org/10.3390/geosciences8080282
Hossain I, Esha R, Alam Imteaz M. An Attempt to Use Non-Linear Regression Modelling Technique in Long-Term Seasonal Rainfall Forecasting for Australian Capital Territory. Geosciences. 2018; 8(8):282. https://doi.org/10.3390/geosciences8080282
Chicago/Turabian StyleHossain, Iqbal, Rijwana Esha, and Monzur Alam Imteaz. 2018. "An Attempt to Use Non-Linear Regression Modelling Technique in Long-Term Seasonal Rainfall Forecasting for Australian Capital Territory" Geosciences 8, no. 8: 282. https://doi.org/10.3390/geosciences8080282






