Abstract
A method is described for the prediction of site-specific surface ground motion due to induced earthquakes occurring in predictable and well-defined source zones. The method is based on empirical Green’s functions (EGFs), determined using micro-earthquakes at sites where seismicity is being induced (e.g., hydraulic fracturing and wastewater injection during shale oil and gas extraction, CO2 sequestration, and conventional and enhanced geothermal injection). Using the EGF approach, a ground-motion field (e.g., an intensity map) can be calculated for a potentially felt induced event originating within the seismic zone. The approach allows site- and path-specific effects to be mapped into the ground-motion field, providing a local ground-motion model that accounts for wave-propagation effects without the requirement of 3D velocity models or extensive computational resources. As a test case, the ground-motion field for the mainshock (ML = 3.4, M = 3.2) resulting from the Basel Enhanced Geothermal System (EGS) was simulated using only seismicity recorded prior to the event. We focussed on peak ground velocity (PGV), as this is a measure of ground motion on which Swiss norms for vibration disturbances are based. The performance of the method was significantly better than a previously developed generic ground-motion prediction equation (GMPE) for induced earthquakes and showed improved performance through intrinsic inclusion of site-specific effects relative to predictions for a local GMPE. Both median motions and the site-to-site ground-motion variability were captured, leading to significantly reduced misfit relative to the generic GMPE. It was shown, however, that extrapolation beyond units of a couple of magnitude leads to significant uncertainty. The method is well suited to a real-time predictive hazard framework, for which shaking estimates are dynamically updated in light of newly recorded seismicity.
1. Introduction
The exploitation of resources in the upper crust has the potential for inducing seismicity due to changes in pore pressure or the stress field [1]. For example, seismicity has long been associated with conventional mining activities [2]. Recent advances have led to an increase in activity that may induce seismic events, particularly where fluid injection is involved [3]. One such example is shale oil and gas extraction through hydraulic fracturing (“fracking”). This technique has been suggested by various national governments as a potential solution for improving national energy security (e.g., [4]) and has been shown to be economically profitable in the United States. Several companies in the United Kingdom are currently planning to drill onshore wells, with many of these in the Bowland Shales of northern England [5]. On the other hand, with focus on green energy and minimising environmental impacts, geothermal energy presents a clean, renewable and therefore environmentally friendly approach to energy production [6]. Deep geothermal techniques have been trialed across Europe, with notable examples in Switzerland (Basel and St. Gallen). However, induced seismicity has proven to be a significant challenge [7,8].
Geothermal energy, geological CO2 storage, and shale hydrocarbon extraction have all led to induced seismicity, including cases that have been documented as being felt [7,9,10] and even damaging [8,11]. The process of shale hydrocarbon extraction (and the associated injection of waste water) and geothermal energy production has therefore come under intense scrutiny and opposition. In the United States, where the industry is well established, a marked increase in felt seismicity (M > 3) occurred [3]. Previously it was argued that this was due to injection to depths of several kilometres [12], but recent work in Canada [13] has shown that processes at shallower depths (i.e., hydraulic fracturing of the reservoir) may also lead to felt seismicity.
As a result of the potential for induced seismicity when injecting a fluid into the subsurface, a challenge for operators is to define how earthquake shaking can be monitored, accurately forecast, and conveyed to regulators and the public [14]. In this sense, there is little difference between the source of induced seismicity, as there is currently no way to reliably predict events on the basis of physical processes. Regulatory guidance in the United Kingdom has been proposed by the Oil and Gas Authority (OGA) to mitigate induced seismicity [15]: threshold magnitudes of ML = 0.0 and ML = 0.5 are imposed. Upon exceeding these thresholds, action must be taken (pressure regulation and suspension, respectively) following the “traffic light” approach [16]. While this is an important step, it does over-simplify a complex problem: the public’s perception and structures’ responses to earthquake ground shaking are not only related to the earthquake magnitude (of which there are many definitions that do not necessarily align). In reality, peak motions, such as peak ground velocity (PGV) at the surface are the critical factor [17,18]. These motions depend not only on the earthquake source magnitude, but on how energetic it is (earthquakes of equal magnitude can be more, or less, energetic as a result of their rupture characteristics), wavefield propagation effects (focussing or defocussing of waves in particular directions), and site amplification effects (different soils can have significantly different effects on the shaking level [19]). Recent work has also shown how ML is typically overestimated at the very short distances typical in these applications [7,20]. In order to gain the public’s trust, operators must therefore openly convey the expected ground shaking that can be expected, rather than simply source magnitudes.
Current state-of-the-art approaches for seismic hazards focus on using ground-motion prediction equations (GMPEs) that provide smooth regional or global average ground-motion fields on the basis of the analysis of data from a myriad of locations [21]. This ergodic approach leads to significantly higher uncertainty than necessary when applied to a small-scale site [21]. The approach presented here is based on a simple application of a well-established method for simulating earthquake ground motion for large tectonic events [22] to a much smaller scale—and with forecasting [23,24] (using monitored micro-seismicity) rather than retrospective application. We avoid much of the uncertainty involved in EGF approaches by assuming that events of interest (3 < M < ~5) can be represented by point sources that have predicable location. The approach is focussed on data collected during micro-seismic monitoring of the site, which, given a sufficiently dense monitoring network, contains all the information required to make accurate and high-spatial-resolution predictions for potential future events.
2. Method
The displacement–time history for an earthquake can be represented as a convolution of the time-dependent moment tensor, , and the gradient of the Green’s function describing the impulse response of the propagation medium between point source m and site n, [25], integrated over the fault area, A. In the frequency domain, the convolution can be represented as a multiplication of the Fourier transform of the far-field representation of the source displacement, , and the Green’s function, . The Green’s function is itself a product of the path (anelastic and geometric attenuation: and ), and site effects: . For small earthquakes, we can typically assume a point source, such that
On the basis of Brune [26] (without loss of generality), the far-field source displacement spectrum is often modelled as being generated from an instantaneously slipping fault as
where is the far-field signal moment (the low-frequency amplitude of the far-field displacement spectrum in Newton metres) and is the source corner frequency. However, various alternative source models have been proposed (e.g., [27,28,29]) that could easily be implemented in this approach.
The Green’s function can be estimated using models of velocity, density, and Q [30], or, if only Fourier amplitude values are required (or if assuming a stochastic phase acceleration time history [31]), through simplified seismological models for path and site effects (e.g., [32]). Both approaches are limited—the former relies on the resolution and accuracy of material properties (velocity, density, and damping), while the latter typically involves simplifications and potential parameter trade-off and uncertainty (e.g., [33]). For induced earthquakes, where sources tend to be located in a confined region (e.g., defined by the pore-pressure gradient from the well-head [34]), we can instead take advantage of the empirical Green’s function (EGF) [22].
The approach taken in this study centres on the fact that given two “point-source” events in the same location, their Green’s functions will be the same. Given this fact, we can modify the recorded Fourier spectrum of a small earthquake [] to account for an increase in earthquake magnitude for a predicted event []:
The adjustment factor can be obtained by taking the ratio of the expected larger earthquake’s source spectrum with that of the smaller earthquake using a simple parametric source (e.g., [26]). A similar EGF approach has been used extensively for the determination of stress drop and path effects in small to moderate earthquakes [35,36,37,38,39]. As long as the larger event can still be considered as a point source, the more complex task of reconstructing the fault geometry using multiple point sources (e.g., [40]) can be avoided. This is normally the case for induced earthquakes, with magnitudes generally considered to be much smaller than for tectonic activity (i.e., typically M < 4). While we may technically break the point-source assumptions at the epicentre, we show that the resulting predictions (of PGV) are not adversely affected in the case of a moderate (M = 3.2) event.
Given two events [the small recorded (EGF) event (denoted by subscript EGF) and the target simulated event (subscript p)] at the same location, recorded at the same site, the ratio of their spectra is given by
if using the Brune [26] source model. This can be further generalized using the stress drop and seismic moment assuming a circular fault [41]:
with
[42], where indicates the Green’s function event () or the simulated event (). Often the stress drop of earthquakes is assumed to be constant (e.g., between approximately 1 and 100 bars) [43], which means that the adjustment factor can be defined simply by the two magnitudes (of the recorded event and target event) and a single value of stress drop. However, we may need to consider the possible scaling of stress drop with depth [44] or magnitude [45].
After adjusting the spectrum of the recorded event, an inverse fast Fourier transform is made to obtain the time series of the larger simulated event. This can be performed with either (i) the recorded event’s (i.e., the EGF’s) phase spectrum (as used here) or (ii) a purely random (stochastic) phase spectrum, as is the case for stochastic simulations [46], or with a combination of the two. From this, engineering parameters such as the PGV and acceleration as well as response spectra are obtained [47].
3. Data
For this preliminary analysis, we used a database of events recorded by the Swiss Seismological Service (SED) in Basel, Switzerland during and after the enhanced stimulation of a deep geothermal system that eventually induced a ML = 3.4 earthquake on December 8, 2006 [48,49,50]. The larger event has been studied in detail and was shown to have M = 3.2 [7]. The events have all been precisely relocated using cross-correlation approaches [51,52]; 54 small events (ML ≤ 2.7, Figure 1) occurring prior to the mainshock and located in the seismic cloud of induced earthquakes were used to provide an estimate of the shaking expected for the M = 3.2 event. Moment magnitudes were estimated using the ML to M conversion of Goertz-Allmann et al. [53]. For the stress drop, a constant value of 5 MPa was used. This was slightly higher than the measured value for the M = 3.2 event (3.5 MPa) but represents a realistic average value in the case that the value is not known a priori [54]. Data were recorded on either Streckeisen STS-2 broadband seismometers or Kinemetrics EpiSensor accelerometers with the instrument response deconvolved using station-specific poles and zeros.
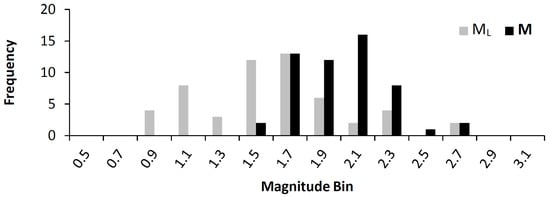
Figure 1.
Histogram of the event magnitudes used to estimate peak ground velocity (PGV) values of the mainshock.
The target for the simulations was to reproduce the ground-motion field of the M = 3.2 event (Figure 2). Here we focussed on PGV, which is useful as it is a measure of ground motion on which Swiss norms for vibration disturbances are based. The GMPE of Douglas et al. [55] is also shown in Figure 2. The GMPE performance is good at distances of interest for induced seismicity, (e.g., R < 30 km), with PGV values falling within the model’s (large) standard deviation. Beyond 50 km (where the GMPE is not calibrated), it systematically underestimates the observations. It is noted that the within-event standard deviation of the GMPE was much larger than that the data exhibited. This was noted by the authors as a result of combining data from various datasets, with lower uncertainty evident if analysing data from specific regions [55].
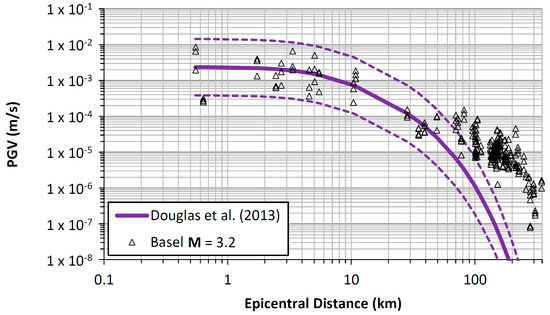
Figure 2.
Peak ground velocity (PGV) (individual horizontal components) from the Basel M = 3.2 event along with the prediction (median and plus/minus one within-event standard deviation) from the ground-motion prediction equation (GMPE) of Douglas et al. [55].
4. Simulation of the M = 3.2 Mainshock
For the 54 EGF events, there were 282 recordings (each with three channels) within 100 km across 15 recording stations (427 records at 49 stations out to 345 km). The EGF predicted PGVs (geometric mean horizontal, plus/minus one standard deviation, σ) are shown in Figure 3 along with the recorded data of the M = 3.2 event, the empirical GMPE of Douglas et al. [55], and the stochastic simulation-based [45] GMPE of Cauzzi et al. [56]. Each predicted PGV is comprised of numerous individual predictions from the 54 EGF events, which facilitated the calculation of the prediction’s standard deviation. Outlier suppression at 5σ was applied to individual predictions (before averaging) to avoid adversely influencing mean predictions. The predicted PGV matched the observed values well, in some cases reflecting site-specific (within-event) offsets relative to the median PGV of the event.
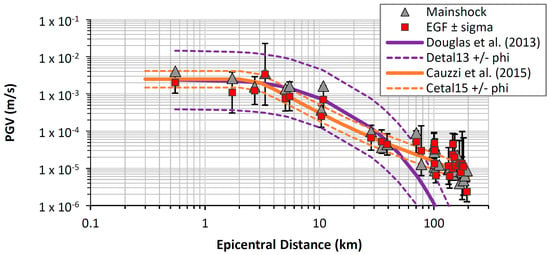
Figure 3.
Comparison of predicted M = 3.2 peak ground velocities (PGVs) from the empirical Green’s function (EGF) events with the observed values (geometric mean) and the ground-motion prediction equations (GMPEs) of Douglas et al. [55] and Cauzzi et al. [56]. Note: PGV values are only plotted where both observation and prediction were available (i.e., where EGF events were available).
For this simulation, EGFs were not individually tested for suitable signal-to-noise ratio beyond cursory visual inspection. We instead relied on the fact that for PGV, the detection and location algorithms used to produce the waveform database and corresponding catalogue implicitly require the presence of a PGV well above the background noise (i.e., in short term/long term average [STA/LTA] algorithms). We note, however, that for increasingly small magnitudes or an increasing recording distance, this will not hold true, in particular, for very long or short spectral ordinates. Careful signal to noise ratio analysis should therefore be performed to define usable band limits of the EGF prior to use in general applications.
In this analysis, we used each EGF event’s phase spectrum to predict the EGF-specific waveform of the mainshock, the PGV from which we later averaged over all EGF events to produce a stable mean and standard deviation. Because we were not concerned with the phase characteristics of the predicted event—in this case we were interested only in the PGV, and in general the response spectrum—we considered this reasonable. Phase variability (and potential impact on PGV) due to variability in source mechanisms of induced events is, however, only mapped into predictions given sufficient EGF events used to generate the mean PGV. In the case that few EGF events are available, it is thus advisable to consider stochastic in addition to empirical phase predictions [46].
It is desirable to predict the likely shaking using the smallest possible events—so that hazards can be updated as closely as possible to real-time. Unfortunately, however, upscaling smaller and smaller events amplifies uncertainties or bias (for example, in the selection of the correct stress drop and M for the small shocks). This is shown by comparing the predictions made using events with only ML ≤ 2 (46 events) and only ML ≤ 1.5 (20 events) (Figure 4). For the case in which ML < 2.0, the predictions were almost unchanged. Using only events with ML < 1.5 led to overestimation of the PGV at most distances—likely as a result of noise contamination of the EGFs. Significant outlier predictions also existed—we therefore suggest that the simulated values are used to represent a statistical distribution of possible motions rather than deterministic predictions.
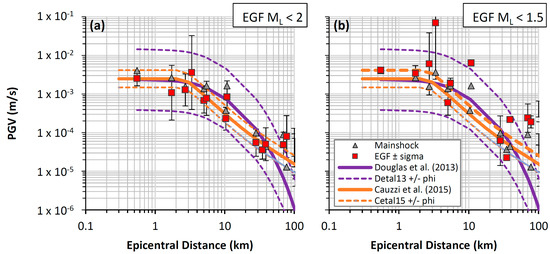
Figure 4.
As for Figure 3 but using only events with ML < 2 (a) and ML < 1.5 (b). Note: In this case, data are plotted only out to 100 km (beyond this distance noise increasingly affected the empirical Green’s function (EGF)).
An advantage of the EGF approach is its implicit inclusion of site-effects. The method therefore has the possibility to map spatial variability in site response, given a dense enough monitoring network. In Basel, several stations were installed within 40 km of the injection site. Using the various predictions (GMPE and EGF) and the available records, we present PGV maps in Figure 5. We note that the predictions of Douglas et al. [55] (top right) predicted a wider extent of shaking out to ~50 km compared to that indicated by the mainshock data. The EGF method (bottom right) and Cauzzi et al. model [56] (top left) predicted similar patterns of PGV, although in the near-field, the EGF method predicted a less regular ground-motion field with a somewhat more focussed region of the highest intensity, which was closer to the distribution of the mainshock data (bottom left). While the model of Cauzzi et al. [56] appeared to have similar predictive power to the EGF approach, we note that this model is a locally derived GMPE—and many regions will not have such a model available. Therefore, the ability for the EGF approach to produce predictions comparable to this model is highly significant. In order to quantitatively compare the methods, Figure 6 shows the predicted PGV (for PGV > 10−5 m/s) compared to the recorded mainshock values alongside the uncertainty of the prediction. We observe that the station-specific predictions were best matched by the Cauzzi et al. [56] model, closely followed by the EGF predictions, which tended to somewhat underestimate the median ground motions. The Douglas et al. model tended to overestimate all but the largest ground motions. Nevertheless, all models consistently predicted the PGV within one standard deviation of the true PGV.
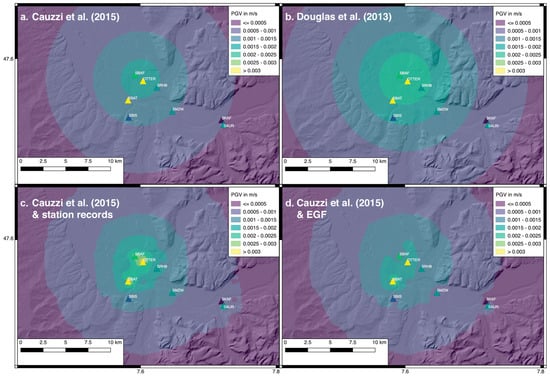
Figure 5.
Peak ground velocity (PGV) maps (background) and M = 3.2 mainshock amplitude (triangles) for the Basel event. The background PGV maps show the predictions of Cauzzi et al. [56] (a); the predictions of Douglas et al. [55] (b); the interpolation of recorded PGV and Cauzzi et al. [56] (c); and the interpolation of empirical Green’s function (EGF) predictions and Cauzzi et al. [56] (d). The triangles in each map are coloured according to the recorded PGV at each station.
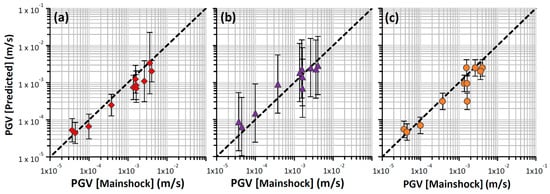
Figure 6.
Comparison of predicted peak ground velocity (PGV) versus mainshock PGV for the empirical Green’s function (EGF) (a) and the models of Douglas et al. [55] (b) and Cauzzi et al. [56] (c).
5. Discussion and Conclusions
As suggested by Pavic et al. [24], the hybrid EGF method is a useful tool, not only for retrospective analyses, but also for predicting earthquake ground motion. We have developed the method specifically for the case of induced seismicity, in which the point-source approximation can be adopted to simplify the method and provide more robust predictions. This has been demonstrated for the Basel M = 3.2 event related to fluid injection during stimulation of the enhanced geothermal system. The EGF method provided predictions comparable to a local GMPE calibrated using thousands of events. In regions where local GMPEs are not available a priori, the method therefore has significant potential. In the case that a local GMPE is available, it may be used alongside EGF predictions to provide robust probabilistic estimates, particularly in the early stages of induced seismicity. While our analysis has focussed on PGV, the method can be generalised to extend to other spectral ordinates of engineering interest (peak ground acceleration and response spectra). It should be noted, however, that the applicability will be limited to a range of oscillator frequencies dependent on the signal-to-noise ratio of the EGF Fourier spectrum and simulation target scenario. For example, it is unlikely that low-frequency (f < 1 Hz) response spectra can be obtained from EGF based on micro-seismic (M < 2) events. The EGF method’s advantage is that it maps path and detailed site effects into the predicted motions in a way that simplified models (e.g., empirical GMPEs) cannot. It is therefore highly location/implementation-specific, but ultimately includes surface motion that is of interest to the public and regulators. The method is, however, limited in predicting motions for events at locations where observations of smaller earthquakes have already been made—which is not an issue for smaller induced events that occur within the seismic cloud, but may not provide realistic results for larger events (non-point source) or for events outside the seismic cloud (i.e., triggered events). Additionally, the uncertainty and possible bias of the prediction increases for increasingly large scaling (i.e., increasingly low input magnitudes).
Further work is required for this method in order to quantitatively assess the range of input magnitudes required; however, in this case, using ML < 2 events did provide a good estimate of the PGV for the main event with ML = 3.4. We also expect that the predictions may be used alongside GMPEs to provide a robust logic-tree approach, with weights reassigned [57] as EGF data are collected. However, further work is required to assess the uncertainty introduced when propagating uncertainties in the stress drop and the M of very small events. In addition, our simple source model, while clearly effective, does not take into account kinematic complexities such as rupture velocity [58] (which often manifest as apparent variabilities in stress drop [59]). The flexibility of the proposed approach would, nevertheless, allow the implementation of any a priori information that may be ascertained as our knowledge increases—either through scientific or methodological advances, or simply through the collection of new data. In this study, we used the phase spectrum of the EGF events for simulation of the mainshock. While this has been shown to be effective, we will investigate the use of a combined stochastic–empirical approach in future work, which may reduce some outlier predictions in the case of limited EGFs. Furthermore, in this analysis we have relied on the fact that events have been detected and (re-)located to ensure their suitability for use as EGFs. However, there is clearly a frequency band limitation that should also be considered, as evidenced in the case of using very small (ML < 1.5) events. In this case, particularly at distances R > 100 km, the signals are not useful as EGFs. A simple solution for this would be the use of a signal-to-noise ratio analysis to define the limits of EGF applicability.
Implementation in a real-time system with dynamically allocated weighting would clearly provide a useful tool in monitoring seismic hazards due to induced seismicity [60]. In such cases, the initial input EGF magnitudes will be low (and should therefore have corresponding high prediction uncertainty for large events); however increasingly large events may be recorded over time—which should result in a reduction in the prediction uncertainty. While probabilistic methods are mainly used to characterise seismic hazards, there is the potential to further reduce uncertainty in the case that a known fault is activated (i.e., deterministic hazard). In such a case, we can isolate seismicity related only to this particular fault (e.g., using cross-correlation) in order to obtain associated EGFs. These fault-specific EGFs can then be used to simulate the ground motion for a larger shock on that particular fault (rather than using the complete volume of seismicity). The resulting ground-motion field would then include the specific effects (e.g., radiation pattern) related to this fault. This would be useful, for example, in the case that a known fault cuts through the injection volume.
Author Contributions
B.E. and S.W. conceived and designed the analysis; B.E. performed the computations; B.E., N.S., and C.C. analyzed the data; B.E. wrote the paper.
Funding
This research was initiated within the framework of the GEOSIM project, funded by the Swiss Federal Office of Energy.
Acknowledgments
This work was funded in part by the GEOSIM project and subsequently through internal funding from the University of Liverpool and the Swiss Seismological Service. We are grateful to two anonymous reviewers for their helpful comments that helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- McGarr, A.; Bekins, B.; Burkardt, N.; Dewey, J.; Earle, P.; Ellsworth, W.; Ge, S.; Hickman, S.; Holland, A.; Majer, E. Coping with earthquakes induced by fluid injection. Science 2015, 347, 830–831. [Google Scholar] [CrossRef] [PubMed]
- Gibowicz, S.J.; Lasocki, S. Seismicity induced by mining: Ten years later. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 44, pp. 39–181. [Google Scholar]
- Ellsworth, W.L. Injection-induced earthquakes. Science 2013, 341, 142. [Google Scholar] [CrossRef] [PubMed]
- DBEIS. Guidance on Fracking: Developing Shale Gas in the UK. Department for Business, Energy & Industrial Strategy. Available online: https://www.gov.uk/government/publications/about-shale-gas-and-hydraulic-fracturing-fracking (accessed on 1 June 2017).
- Andrews, I. The Carboniferous Bowland Shale Gas Study: Geology and Resource Estimation; British Geological Survey for Department of Energy and Climate Change: London, UK, 2013.
- Fridleifsson, I.B. Geothermal energy for the benefit of the people. Renew. Sustain. Energy Rev. 2001, 5, 299–312. [Google Scholar] [CrossRef]
- Edwards, B.; Kraft, T.; Cauzzi, C.; Kästli, P.; Wiemer, S. Seismic monitoring and analysis of deep geothermal projects in St Gallen and Basel, Switzerland. Geophys. J. Int. 2017, 201, 1020–1037. [Google Scholar] [CrossRef]
- Giardini, D. Geothermal quake risks must be faced. Nature 2009, 462, 848–849. [Google Scholar] [CrossRef] [PubMed]
- Clarke, H.; Eisner, L.; Styles, P.; Turner, P. Felt seismicity associated with shale gas hydraulic fracturing: The first documented example in Europe. Geophys. Res. Lett. 2014, 41, 8308–8314. [Google Scholar] [CrossRef]
- Verdon, J.P. Significance for secure CO2 storage of earthquakes induced by fluid injection. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Keranen, K.M.; Savage, H.M.; Abers, G.A.; Cochran, E.S. Potentially induced earthquakes in Oklahoma, USA: Links between wastewater injection and the 2011 Mw 5.7 earthquake sequence. Geology 2013, 41, 699–702. [Google Scholar] [CrossRef]
- Keranen, K.M.; Weingarten, M.; Abers, G.A.; Bekins, B.A.; Ge, S. Sharp increase in central Oklahoma seismicity since 2008 induced by massive wastewater injection. Science 2014, 345, 448–451. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, G.M.; Eaton, D.W.; Ghofrani, H.; Walker, D.; Cheadle, B.; Schultz, R.; Shcherbakov, R.; Tiampo, K.; Gu, J.; Harrington, R.M. Hydraulic fracturing and seismicity in the Western Canada Sedimentary Basin. Seismol. Res. Lett. 2016, 87, 631–647. [Google Scholar] [CrossRef]
- Grigoli, F.; Cesca, S.; Priolo, E.; Rinaldi, A.P.; Clinton, J.F.; Stabile, T.A.; Dost, B.; Fernandez, M.G.; Wiemer, S.; Dahm, T. Current challenges in monitoring, discrimination, and management of induced seismicity related to underground industrial activities: A European perspective. Rev. Geophys. 2017, 55, 310–340. [Google Scholar] [CrossRef]
- OGA. Traffic Light Monitoring Scheme to Mitigate Induced Seismicity. Oil and Gas Authority. Available online: https://www.ogauthority.co.uk/media/3696/traffic-light-system-doc-for-website_may-2017.pdf (accessed on 1 June 2017).
- Bommer, J.J.; Oates, S.; Cepeda, J.M.; Lindholm, C.; Bird, J.; Torres, R.; Marroquin, G.; Rivas, J. Control of hazard due to seismicity induced by a hot fractured rock geothermal project. Eng. Geol. 2006, 83, 287–306. [Google Scholar] [CrossRef]
- Bommer, J.J. Predicting and Monitoring Ground Motions Induced by Hydraulic Fracturing. Report Commissioned by the Oil and Gas Authority. Available online: https://www.ogauthority.co.uk/media/3693/pgv-thresholds-for-control-of-induced-seismic-hazard_v5.pdf (accessed on 1 June 2017).
- Bommer, J.J.; Stafford, P.J.; Edwards, B.; Dost, B.; van Dedem, E.; Rodriguez-Marek, A.; Kruiver, P.; van Elk, J.; Doornhof, D.; Ntinalexis, M. Framework for a ground-motion model for induced seismic hazard and risk analysis in the Groningen gas field, The Netherlands. Earthq. Spectra 2017, 33, 481–498. [Google Scholar] [CrossRef]
- Poggi, V.; Edwards, B.; Fäh, D. Development of hazard-and amplification-consistent elastic design spectra. Soil Dyn. Earthq. Eng. 2018. [Google Scholar] [CrossRef]
- Butcher, A.; Luckett, R.; Verdon, J.P.; Kendall, J.M.; Baptie, B.; Wookey, J. Local magnitude discrepancies for near-event receivers: Implications for the UK traffic-light scheme. Bull. Seismol. Soc. Am. 2017, 107, 532–541. [Google Scholar] [CrossRef]
- Douglas, J.; Edwards, B. Recent and future developments in earthquake ground motion estimation. Earth-Sci. Rev. 2016, 160, 203–219. [Google Scholar] [CrossRef]
- Hartzell, S.H. Earthquake aftershocks as Green’s functions. Geophys. Res. Lett. 1978, 5, 1–4. [Google Scholar] [CrossRef]
- Hutchings, L.; Viegas, G. Application of empirical Green’s functions in earthquake source, wave propagation and strong ground motion studies. In Earthquake Research and Analysis-New Frontiers in Seismology; InTech: London, UK, 2012. [Google Scholar]
- Pavic, R.; Koller, M.G.; Bard, P.-Y.; Lacave-Lachet, C. Ground motion prediction with the empirical Green’s function technique: An assessment of uncertainties and confidence level. J. Seismol. 2000, 4, 59–77. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology: Theory and Methods; W. H. Freeman: San Francisco, CA, USA, 1980. [Google Scholar]
- Brune, J.N. Tectonic stress and spectra of seismic shear waves from earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
- Boatwright, J. A dynamic model for far-field acceleration. Bull. Seismol. Soc. Am. 1982, 72, 1049–1068. [Google Scholar]
- Madariaga, R. High-frequency radiation from crack (stress drop) models of earthquake faulting. Geophys. J. Int. 1977, 51, 625–651. [Google Scholar] [CrossRef]
- Sato, T.; Hirasawa, T. Body wave spectra from propagating shear cracks. J. Phys. Earth 1973, 21, 415–431. [Google Scholar] [CrossRef]
- Bouchon, M. A simple method to calculate Green’s functions for elastic layered media. Bull. Seismol. Soc. Am. 1981, 71, 959–971. [Google Scholar]
- Hanks, T.C.; Mcguire, R.K. The character of high-frequency strong ground motion. Bull. Seismol. Soc. Am. 1981, 71, 2071–2095. [Google Scholar]
- Edwards, B.; Rietbrock, A.; Bommer, J.J.; Baptie, B. The acquisition of source, path, and site effects from microearthquake recordings using q tomography: Application to the United Kingdom. Bull. Seismol. Soc. Am. 2008, 98, 1915–1935. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B.; Wennerberg, L. Fitting the stochastic omega(-2) source model to observed response spectra in western North America—Trade-offs between delta-sigma and kappa. Bull. Seismol. Soc. Am. 1992, 82, 1956–1963. [Google Scholar]
- Bachmann, C.; Wiemer, S.; Goertz-Allmann, B.; Woessner, J. Influence of pore-pressure on the event-size distribution of induced earthquakes. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Baltay, A.; Ide, S.; Prieto, G.; Beroza, G. Variability in earthquake stress drop and apparent stress. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Baltay, A.S.; Hanks, T.C.; Beroza, G.C. Stable stress-drop measurements and their variability: Implications for ground-motion prediction. Bull. Seismol. Soc. Am. 2013, 103, 211–222. [Google Scholar] [CrossRef]
- Calderoni, G.; Rovelli, A.; Singh, S.K. Stress drop and source scaling of the 2009 April l’Aquila earthquakes. Geophys. J. Int. 2012, 192, 260–274. [Google Scholar] [CrossRef]
- Clerc, F.; Harrington, R.M.; Liu, Y.; Gu, Y.J. Stress drop estimates and hypocenter relocations of induced seismicity near Crooked Lake, Alberta. Geophys. Res. Lett. 2016, 43, 6942–6951. [Google Scholar] [CrossRef]
- Goebel, T.; Hauksson, E.; Shearer, P.; Ampuero, J. Stress-drop heterogeneity within tectonically complex regions: A case study of San Gorgonio Pass, southern California. Geophys. J. Int. 2015, 202, 514–528. [Google Scholar] [CrossRef]
- Frankel, A. Simulating strong motions of large earthquakes using recordings of small earthquakes: The Loma Prieta mainshock as a test case. Bull. Seismol. Soc. Am. 1995, 85, 1144–1160. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. Moment magnitude scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Allmann, B.P.; Shearer, P.M. Global variations of stress drop for moderate to large earthquakes. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Goertz-Allmann, B.P.; Edwards, B. Constraints on crustal attenuation and three-dimensional spatial distribution of stress drop in Switzerland. Geophys. J. Int. 2013, 196, 493–509. [Google Scholar] [CrossRef]
- Edwards, B.; Fäh, D. A stochastic ground-motion model for Switzerland. Bull. Seismol. Soc. Am. 2013, 103, 78–98. [Google Scholar] [CrossRef]
- Boore, D.M. Simulation of ground motion using the stochastic method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef]
- Nigam, N.C.; Jennings, P.C. Calculation of response spectra from strong-motion earthquake records. Bull. Seismol. Soc. Am. 1969, 59, 909–922. [Google Scholar]
- Baer, M.; Deichmann, N.; Braunmiller, J.; Clinton, J.; Husen, S.; Fah, D.; Giardini, D.; Kastli, P.; Kradolfer, U.; Wienier, S. Earthquakes in Switzerland and surrounding regions during 2006. Swiss J. Geosci. 2007, 100, 517–528. [Google Scholar] [CrossRef]
- Deichmann, N.; Baer, M.; Clinton, J.; Husen, S.; Fah, D.; Giardini, D.; Kastli, P.; Kradolfer, U.; Wiemer, S. Earthquakes in Switzerland and surrounding regions during 2007. Swiss J. Geosci. 2008, 101, 659–667. [Google Scholar] [CrossRef]
- Deichmann, N.; Giardini, D. Earthquakes induced by the stimulation of an enhanced geothermal system below Basel (Switzerland). Seismol. Res. Lett. 2009, 80, 784–798. [Google Scholar] [CrossRef]
- Deichmann, N.; Kraft, T.; Evans, K.F. Identification of faults activated during the stimulation of the Basel geothermal project from cluster analysis and focal mechanisms of the larger magnitude events. Geothermics 2014, 52, 84–97. [Google Scholar] [CrossRef]
- Kraft, T.; Deichmann, N. High-precision relocation and focal mechanism of the injection-induced seismicity at the Basel EGS. Geothermics 2014, 52, 59–73. [Google Scholar] [CrossRef]
- Goertz-Allmann, B.P.; Edwards, B.; Bethmann, F.; Deichmann, N.; Clinton, J.; Fäh, D.; Giardini, D. A new empirical magnitude scaling relation for Switzerland. Bull. Seismol. Soc. Am. 2011, 101, 3088–3095. [Google Scholar] [CrossRef]
- Edwards, B.; Fäh, D. Measurements of stress parameter and site attenuation from recordings of moderate to large earthquakes in Europe and the Middle East. Geophys. J. Int. 2013, 194, 1190–1202. [Google Scholar] [CrossRef]
- Douglas, J.; Edwards, B.; Convertito, V.; Sharma, N.; Tramelli, A.; Kraaijpoel, D.; Cabrera, B.M.; Maercklin, N.; Troise, C. Predicting ground motion from induced earthquakes in geothermal areas. Bull. Seismol. Soc. Am. 2013, 103, 1875–1897. [Google Scholar] [CrossRef]
- Cauzzi, C.; Edwards, B.; Fäh, D.; Clinton, J.; Wiemer, S.; Kästli, P.; Cua, G.; Giardini, D. New predictive equations and site amplification estimates for the next-generation Swiss shakemaps. Geophys. J. Int. 2015, 200, 421–438. [Google Scholar] [CrossRef]
- Edwards, B.; Douglas, J. Selecting ground-motion models developed for induced seismicity in geothermal areas. Geophys. J. Int. 2013, 195, 1314–1322. [Google Scholar] [CrossRef][Green Version]
- Kane, D.L.; Shearer, P.M.; Goertz-Allmann, B.P.; Vernon, F.L. Rupture directivity of small earthquakes at Parkfield. J. Geophys. Res. Solid Earth 2013, 118, 212–221. [Google Scholar] [CrossRef]
- Deichmann, N. Local magnitude, a moment revisited. Bull. Seismol. Soc. Am. 2006, 96, 1267–1277. [Google Scholar] [CrossRef]
- Mignan, A.; Broccardo, M.; Wiemer, S.; Giardini, D. Induced seismicity closed-form traffic light system for actuarial decision-making during deep fluid injections. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).