From Deterministic to Probabilistic Forecasts: The ‘Shift-Target’ Approach in the Milan Urban Area (Northern Italy)

Abstract

The number of natural catastrophes that affect people worldwide is increasing; among these, the hydro-meteorological events represent the worst scenario due to the thousands of deaths and huge damages to private and state ownership they can cause. To prevent this, besides various structural measures, many non-structural solutions, such as the implementation of flood warning systems, have been proposed in recent years. In this study, we suggest a low computational cost method to produce a probabilistic flood prediction system using a single forecast precipitation scenario perturbed via a spatial shift. In fact, it is well-known that accurate forecasts of heavy precipitation, especially associated with deep moist convection, are challenging due to uncertainties arising from the numerical weather prediction (NWP), and high sensitivity to misrepresentation of the initial atmospheric state. Inaccuracies in precipitation forecasts are partially due to spatial misplacing. To produce hydro-meteorological simulations and forecasts, we use a flood forecasting system which comprises the physically-based rainfall-runoff hydrological model FEST-WB developed by the Politecnico di Milano, and the MOLOCH meteorological model provided by the Institute of Atmospheric Sciences and Climate (CNR-ISAC). The areas of study are the hydrological basins of the rivers Seveso, Olona, and Lambro located in the northern part of Milan city (northern Italy) where this system works every day in real-time. In this paper, we show the performance of reforecasts carried out between the years 2012 and 2015: in particular, we explore the ‘Shift-Target’ (ST) approach in order to obtain 40 ensemble members, which we assume equally likely, derived from the available deterministic precipitation forecast. Performances are shown through statistical indexes based on exceeding the threshold for different gauge stations over the three hydrological basins. Results highlight how the Shift-Target approach complements the deterministic MOLOCH-based flood forecast for warning purposes.

1. Introduction

From a civil protection point of view, hydro-meteorological forecasts can be seen as a powerful tool of non-structural measures to produce early flood warnings and better counteract potential river flood impacts, whose number is increasing worldwide [1]. Nevertheless, in order to be credible by local authorities and, above all, by citizens, a prediction system must be verified [2], and the verification analysis should be conducted with a large sample of consistent forecasts and observations. In this context, Demargne et al. [3] proposed the following key questions to guide forecast verification analysis: How suitable are the forecasts for a given application? Are they sufficiently unbiased for the decisions to be made? Are they sufficiently skillful compared to a reference forecast system to justify the method in use?

The ultimate criterion of a good forecast is the decision adopted from it and, from our point of view, it should communicate the information that an end-user needs. Already proposed by Murphy [4] in 1993, good forecasting is not only a matter of “getting it right”, but also to make the receivers understand it, and, above all, to be able to draw conclusions from it [5]. Adopting this framework, in this analysis, we are not interested in predicting river discharge with an accurate flood peak in magnitude as well as timing, but in predicting the probability of exceeding any threshold before the event, in order to provide early flood warnings to local authorities.

Nowadays, it is well known in the scientific community around the world that ensemble or probabilistic forecasts contain more information than single-valued forecasts [6,7], a key topic of the EFAS (European Flood Awareness System) and HEPEX (https://hepex.irstea.fr/) projects “to demonstrate the added value of hydrological ensemble predictions (HEPS) for emergency management and water resources sectors to make decisions that have important consequences for economy, public health and safety [8]”.

Notwithstanding this, local authorities and citizens continue to disseminate and prefer deterministic hydro-meteorological forecasts, in particular in Italy where this study is set, without including any notion of probability (or chance) of a phenomenon occurring (such as flooding) when the forecast information is communicated. This is possibly an attempt of the authorities to avoid public confusion from multiple, conflicting warnings, while citizens habitually trust a single forecast only, and they are not educated enough to deal with probabilistic prediction.

The use of ensemble prediction systems allows researchers to properly quantify and communicate forecast uncertainties, but from our experience, we are aware that the communication of uncertainties to end-users is difficult and critical [9,10]. For instance, think about a forecast of a 50% probability: users often consider it to indicate that the forecaster is simply “sitting on the fence” [11]. However, if the observed frequency of the event is low, then a 50% probability is a strong signal. Just think of a 50% probability for an airplane to crash before a flight: no passenger would fly on that airplane! Therefore, developments to formalize forecast uncertainty began exploring human expertise and forecasters’ capacity to translate forecast uncertainty into statistical confidence intervals [12].

In addition to initial conditions (e.g., missing data, anthropogenic interferences) and hydrological model uncertainty (e.g., calibration of parameters, conceptualization of the model, etc.), another key issue of forecast output uncertainty [13] is the capacity to correctly identify future precipitation both in space and time, which is especially critical when integrating precipitation on small watersheds for hydrological forecasts with a high impact on QPE (Quantitative Precipitation Estimates). Unfortunately, accurate forecasts of deep moist convection and associated extreme rainfall are arduous to be precisely predicted in terms of amount, timing, and target over small hydrological basins due to uncertainties arising from numerical weather prediction (NWP) models, including physical parameterizations and numerical schemes, and to the rapid growth of errors already affecting the initial atmospheric state. Therefore, a probabilistic forecasting approach that can cope and deal with these uncertainties is required [14,15].

Since only a deterministic precipitation forecast is available to produce hydrological forecasts, in this analysis, we tested a pragmatic approach proposed by Thies et al. [16] to account for the precipitation forecast uncertainty: a low computational cost method was set up to produce probabilistic hydrological forecasts based on spatially shifting a single-valued precipitation forecast scenario using different spatial domain shifts.

In particular, we explore an alternative way of the Thies’ approach: from a deterministic precipitation forecast issued by the MOLOCH meteorological model (described in Section 2.2), we obtain 40 ‘ensemble members’, equivalent to 40 spatial shifts of the predicted rainfall field in eight directions (North, South, West, East, North-West, North-East, South-West, South-East) at each step of 10 km from 0 to 50 km (which approximately is the entire basin dimensions), maintaining the temperature domain so that it is unchanged. This strategy, called the ‘Shift-Target’ (ST) approach, provides 40 discharge forecasts which we assumed to be equally likely in terms of occurrence probability in space and it investigates how the spatial uncertainty may impact the flood forecasts and the potential exceedance of flood warning thresholds.

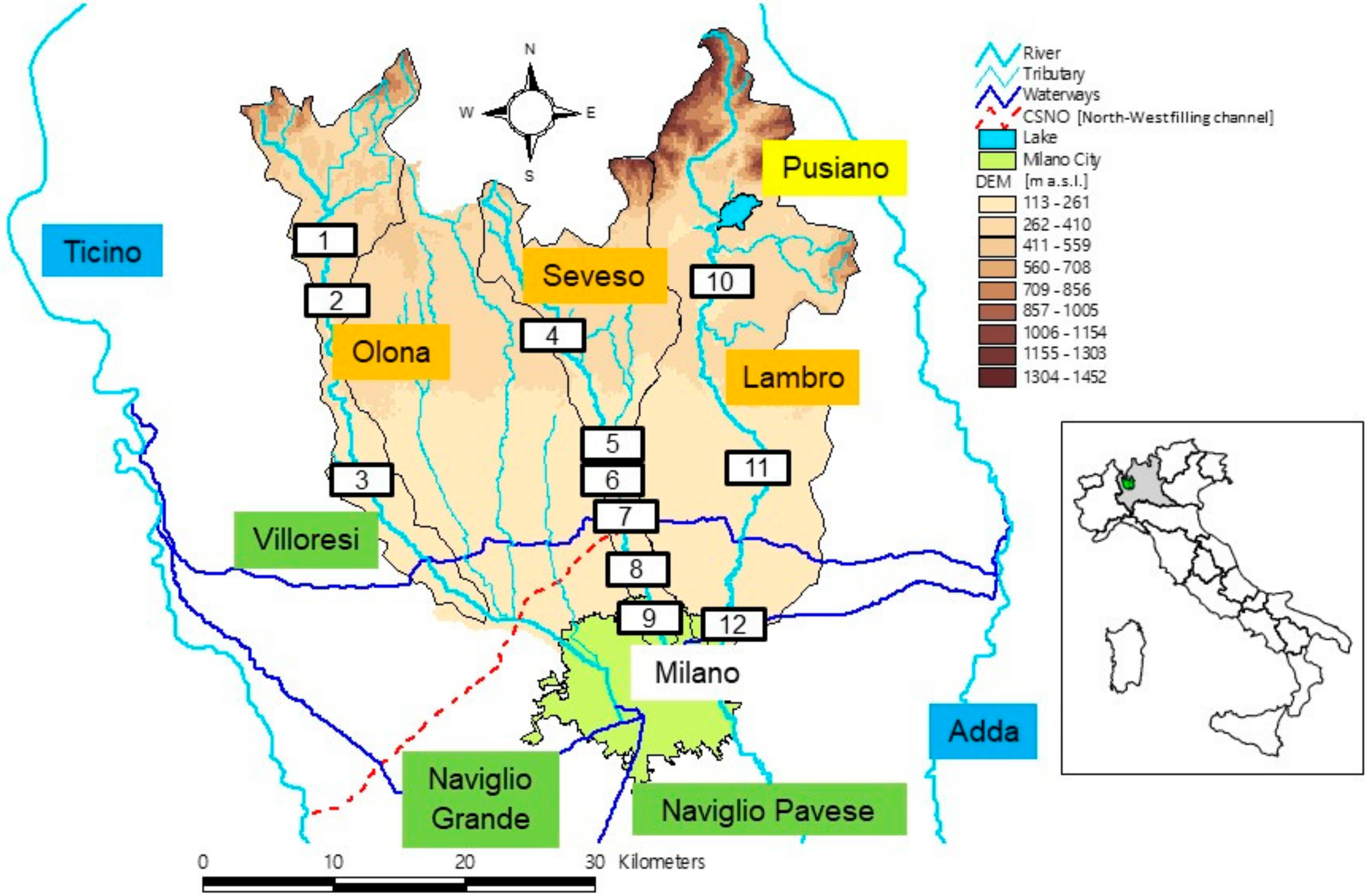
In order to run hydro-meteorological predictions, we use a flood forecasting system which couples the physically based rainfall-runoff hydrological model FEST-WB with the MOLOCH meteorological model as described in Section 2. The area of interest comprises the three hydrological basins of the rivers Seveso, Olona, and Lambro, located in the northern part of Milan, northern Italy: an urban area which has been subjected to a high flood hazard in the past.

This implemented system works every day in real-time and it can be freely consulted at this web site: sol.mmidro.it (MMI, Milano, Italy). This adopted open source policy allows the public to see and exploit the results of our investment in science, and monitoring real-time products can inspire new research that improves techniques; even crowdfunding has been launched between 2017 and 2018.

For a meaningful verification analysis of the system performance, hindcasting (or retrospective forecasting) has been carried out for the period between 2012 and 2015 and the results are based on verification metrics (including contingency scores relative to various exceedance threshold values) for different gauge stations within the three basins.

The paper has a double scope: first, it aims to demonstrate the value of probabilistic hydrological forecasts obtained through the ST procedure in comparison with the single-valued MOLOCH-based hydrological forecast; second, to assess if the proposed shift method can be useful for civil protection services.

The paper is structured as follows: Chapter 2 describes the materials and methods: Section 2.1 shows the area of study which comprises the Milan urban basins; Section 2.2 and Section 2.3 present the MOLOCH meteorological model and the FEST-WB hydrological model, respectively; and Section 2.4 and Section 2.5 describe the coupling strategy and the verification scores, respectively. Chapter 3 shows the performance of the Shift-Target approach based on MOLOCH shift forecasts and Chapter 4 documents this paper’s conclusions.

2. Materials and Methods

2.1. Area of Study

Milan is one of the most densely populated city in Italy with 1,316,000 inhabitants living in 182 km². Several rivers and creeks drain to Milan (Figure 1). The main rivers are the Lambro (area of 500 km²), the Seveso (area of 207 km²), and the Olona (area of 208 km²), plus a number of minor tributaries, for a total drainage surface of about 1300 km².

Several flood events hit Milan in the past so that, starting from the 1970s, a series of structural flood mitigation measures, such as the Ponte Gurone dam over the Olona basin, the North-West filling channel over the Seveso, and the Pusiano dam over the Lambro, have been adopted with the aim of reducing the flood risk in the urban areas in the last decades. However, despite the complex flood protection system, the city was still impacted by floods in recent years: the 18 September 2010 with 80 M€ damages along the Seveso and Lambro rivers, the 8 July 2014 with 55 M€ damages along the Seveso river, the 15 November 2014 with 6 M€ damages along the Seveso and Lambro rivers, and the 15 July 2009 with 30 M€ along the Olona river.

According to Nemec’s [17] recommendation, “to keep the people away from the water, and not the water away from the people”, the implementation of a hydro-meteorological prediction system may provide additional support as a non-structural measure for early warning. In fact, since these basins have a response time of a few hours, warnings with a sufficient lead time will enable civil protection authorities and the public to exercise caution and take preventive measures to mitigate the impacts of flooding [18].

At present, hydro-meteorological forecasts, published online, are implemented over the twelve gauge sections shown in Figure 1. However, for the 2012–2015 reforecasting period, not all the observed data were available; hence the verification analysis (shown in Section 2.5) is carried out for only half of the gauge stations, those with at least 900 days of available data.

2.2. The MOLOCH Meteorological Model

MOLOCH [19] is a non-hydrostatic, fully compressible, convection-resolving model, developed at the CNR-ISAC (National Research Council of Italy, Institute of Atmospheric Sciences and Climate). It integrates the set of atmospheric equations using a latitude–longitude rotated grid and a hybrid terrain-following vertical coordinate, depending on air density, which relaxes to horizontal surfaces at a higher elevation from the ground. Details on numerical schemes and model physics, as well as the results of the application to severe weather events and floods, can be found in [20,21,22]. Time integration is based on a time-split scheme with an implicit treatment of the vertical propagation of sound waves and a forward-backward scheme for the horizontal propagation of gravity and sound waves. Advection is computed using a second order implementation of the Godunov method [23], which is particularly suited to integrate in time the conservation of a scalar quantity [24]. The atmospheric radiation is based on a combined application of the Ritter and Geleyn scheme [25] and the ECMWF scheme [26]. The turbulence scheme is based on an eddy kinetic energy − mixing length (E − l), 1.5-order closure theory [27], where the turbulent kinetic energy equation (including advection) is evaluated. A soil model with seven layers takes into account orography, the geographical distribution of soil types, soil physical parameters, and vegetation coverage, as well as soil physical processes. The microphysical scheme is based on the parameterization proposed by [28] with successive upgrades, and it describes the conversions and interactions of cloud water, cloud ice, and hydrometeors (rain, snow and graupel). MOLOCH is implemented over Italy with a daily operational chain (http://www.isac.cnr.it/dinamica/projects/forecasts) that also comprises the hydrostatic model BOLAM [20], and provides operational forecasts for the following 45 h. The initial and boundary conditions for the BOLAM model are derived from the analyses (00 UTC) and forecasts of the Global Forecast System (GFS, NOAA/NCEP, USA) global model, while MOLOCH is nested (1-way) in BOLAM, initialized with a 3-h BOLAM forecast in order to avoid downscaling based on pure interpolation from the global model. In the period 2012–2017, MOLOCH has undergone continuous development. In particular, its implementation has changed. In fact, its horizontal resolution increased from 2.2 km to 1.25 in October 2016. At present, MOLOCH employs 60 atmospheric levels with output fields available at an hourly frequency.

2.3. The FEST-WB Hydrological Model

For transforming rainfall into runoff, we used the physically-based, spatially distributed FEST-WB (Flash–flood Event–based Spatially distributed rainfall–runoff Transformation, including Water Balance) model, developed by the Politecnico di Milano on top of MOSAICO library [29,30]. The FEST-WB accounts for the main processes of the hydrological cycle: snow melting and accumulation, infiltration, evapotranspiration, surface runoff, flow routing, and subsurface flow. The river basin is discretized with a mesh of regular square cells (200 × 200 m in this study), where water fluxes are calculated at an hourly time step. For further details on the development and application of the FEST-WB, the reader can refer to [31,32,33,34].

2.4. The Coupling Strategy

The proposed forecasting cascade system couples (1-way) the MOLOCH meteorological model with the FEST-WB model using the same strategy adopted in [13,33]. Temperature and precipitation outputs are forced into the hydrological model in order to forecast the main hydrological variables (discharge, evapotranspiration, soil moisture, etc.). In this study, we only focus on forecast runoff in the selected gauge sections mentioned in Section 2 for the entire MOLOCH lead time (45 h), adding 12 h for discharge routing at the end of the hydrological forecasting period to get the entire recession limb of the hydrograph. This choice is due to the chance that the precipitation and the observed peak discharge occur before the end of the forecast horizon but the runoff peaks are forecasted later.

Furthermore, since the first few hours of NWP forecasts are not generally reliable, due to the spin-up time of NWP models, we skipped the first 3 h of forecast, hence 54-h flow hindcasts are produced every day between 10 February 2012 and 31 December 2015, which represent up to ~1400 forecasts in total.

Similar to the method proposed by [35], here we aim to account for the spatial uncertainty of the precipitation forecast provided by the meteorological model for the hydrological basins (especially for smaller ones) by applying the ST method to the single-valued MOLOCH forecast. Forecasting the precipitation cells tens of kilometers away from their correct location could lead to significant errors in the hydrological response of the catchments; especially in these watersheds, which have a prolonged North-South shape.

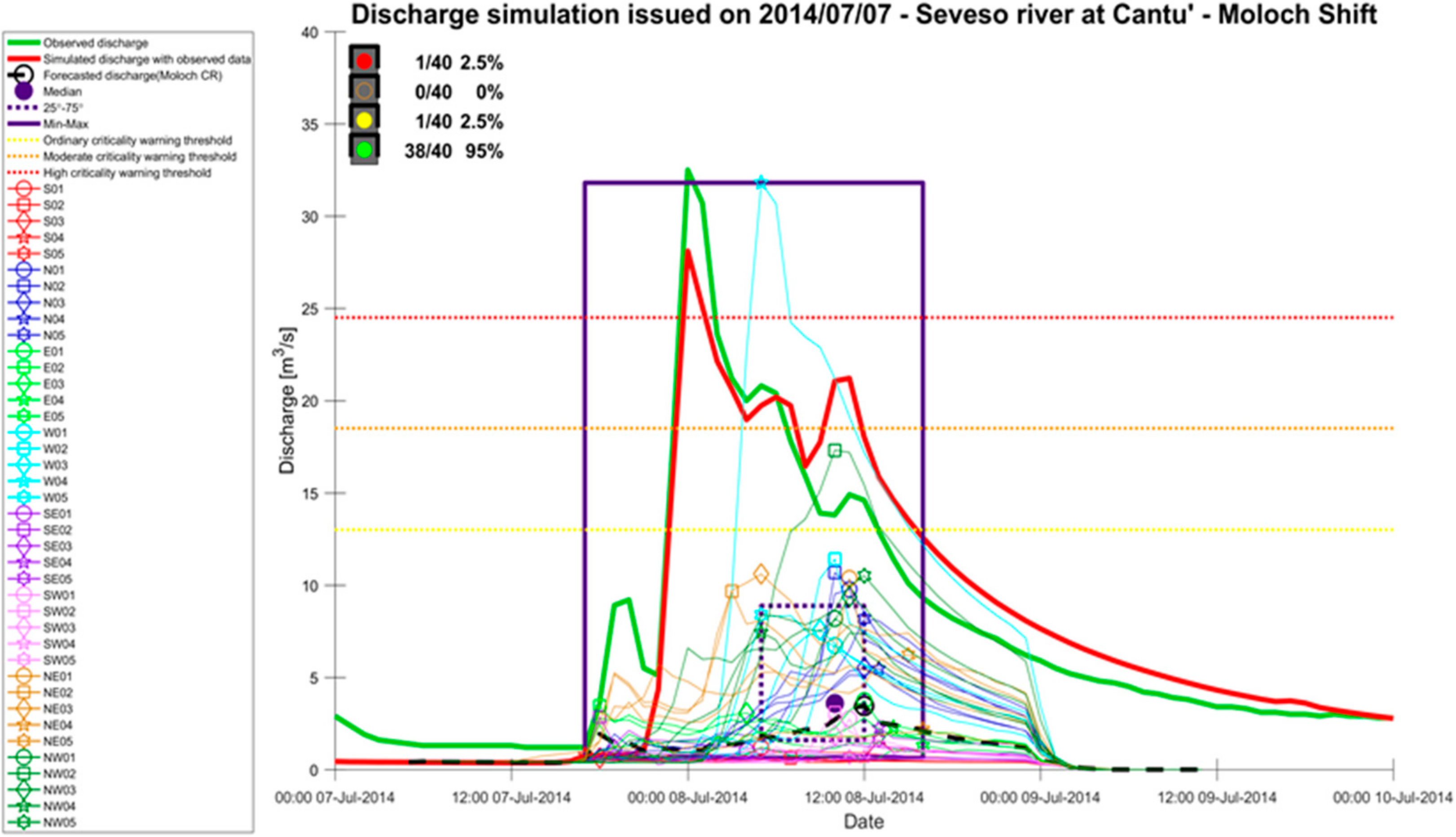
In Figure 2, we show an example of 40 discharge ensemble forecasts produced by the ST method for the Cantù gauging section displayed with the ‘peak-box’ plot proposed by [36].

Figure 2 shows an example for the 8 July 2014 event, which was one of the most severe episodes in the last 20 years in this area. In this case, the 40-km West-shifted forecast (labelled ‘W04’ in Figure 2) exceeded the highest critical warning threshold, whereas the forecast based on the original MOLOCH precipitation did not exceed any of the warning thresholds. This means that if the “unperturbed” Moloch forecast of the precipitation system was affected by a location error of about 40 km westward, then the intense precipitation would have fallen over our watershed, producing a forecast discharge peak of 31.8 m³/s.

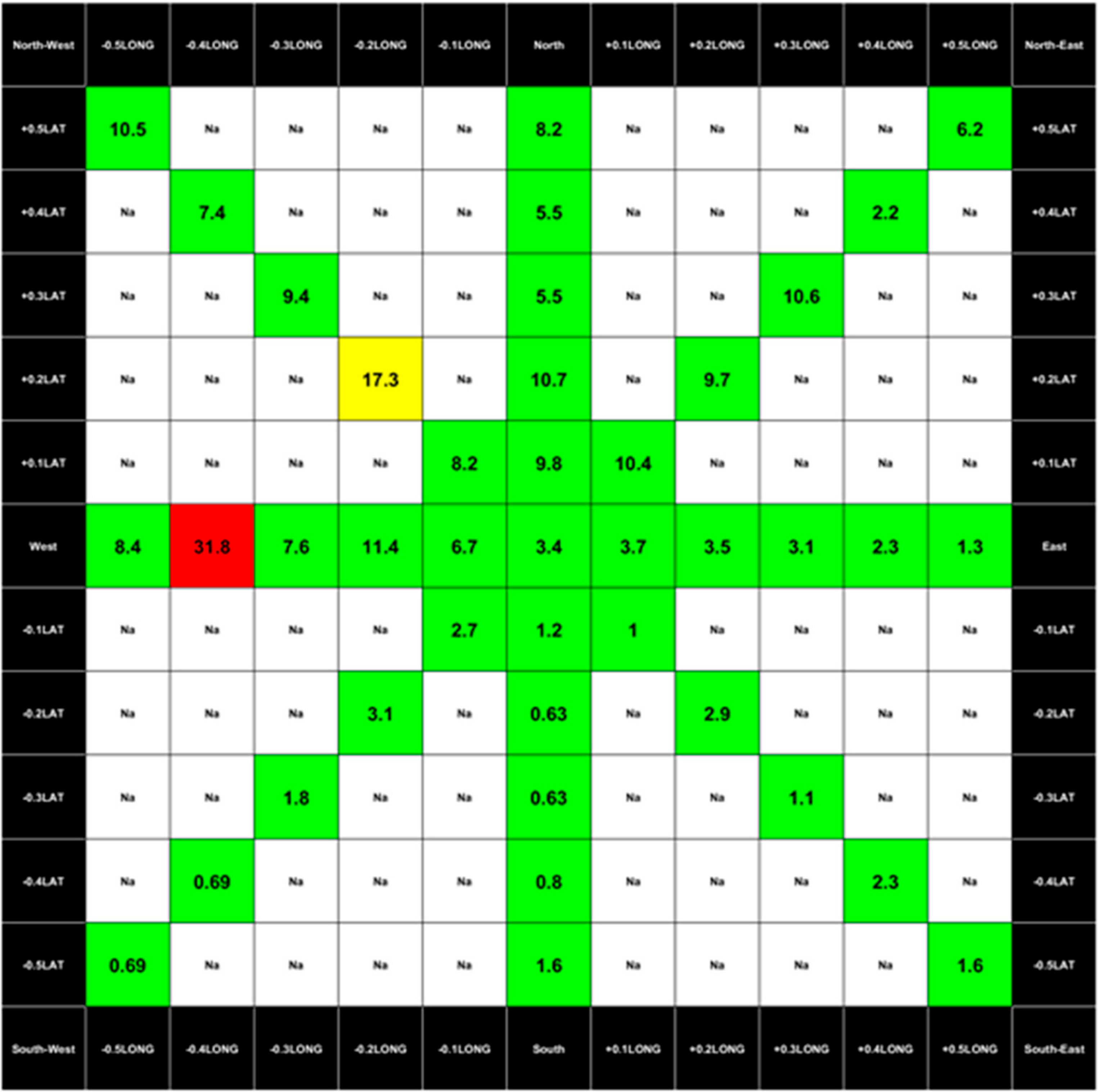
To summarize the warning information given by all flow ensemble forecasts, the ‘Union Jack’ plot (Figure 3) displays the 40 maximum discharges values over the 54-h horizon associated with their spatial shift in all eight directions with a background cell color according to exceeded discharge thresholds.

Representing the 40 forecasted peak discharges on the ‘Union Jack’ with colour-coded impacts meets the requirements of the civil protection services to quickly assess the worst-case scenario based on the potential spatial error of the MOLOCH precipitation forecast.

When operating in real-time, it is possible to follow the evolution of the storm through cell tracking tools, using weather radar images. Forecasters could then evaluate which of the 40 ensemble members may be more realistic based on the storm evolution over the last hours, leading to a better understanding of the ‘most likely’ flooding scenario. Therefore, the Shift-Target approach can provide useful information, letting us know about an a-priori possible flood scenario.

It is worth noting that we are not investigating which is the most probable spatial shift or to calculate a spatial weight of these shifts. Concerning this issue, a specific research activity is actually under development, but this is not the aim of our paper. Here, we simply assume that all the 40 combinations are equally likely. Even an error in the peak time is not taken into consideration, since for local Italian civil protection bodies, the most important information is the exceedance of warning thresholds during the 24-h of the following day, in order to implement flood risk protection measures. Hence, in this framework, we would like to evaluate whether this low computational method, which generates a probabilistic precipitation forecast, performs better than the deterministic MOLOCH, and if its performance can generate an added value for civil protection purposes.

2.5. Verification Scores

Common statistical indexes used in scientific literature (www.cawcr.gov.au/projects/verification) [37] are calculated setting up a 4 × 4 contingency table which compares forecasted and observed events exceeding or not exceeding the three warning thresholds (

Table 1. Performance of flows derived from the single-valued Moloch forecast and from the spatially shifted ensemble forecasts. A refers to Hits, B to Misses, C to False Alarm, and D to Correct Negatives, while the subscripts 1, 2, and 3 are levels of wrong prediction.

		Observed
		No	Yes	Yes	Yes
Forecasted	No	D	B1	B2	B3
	Yes	C1	A	B1	B2
	Yes	C2	C1	A	B1
	Yes	C3	C2	C1	A

); these thresholds are concurrently used by the contingency table and their values are provided for each gauge station by the Regional Civil Protection of Lombardy. Yellow, orange, and red thresholds are related to the discharge with 2-, 5-, and 10-year return periods, respectively.

In this analysis, we calculate the Accuracy, the Bias Score, the Percent False Alarm (PFA), the Percent Missed Alarm (PMA), and the Correct Negatives Ratio (CNR). Since these three latter scores consider the non-occurred events, which are the majority in the dataset, we also calculate the FAR (False Alarm Ratio), the POD (Probability of Detection), and the Probability of Missed Alarm (POMA), especially to assess the performance in those critical situations when a warning threshold has been exceeded, excluding the other corrected non-events. In fact, for low frequency events such as severe weather warnings, there is a high frequency of “not forecast/not occurred” events. This gives high performance values that are misleading with regard to the forecasting of the low frequency event. For a 4 × 4 contingency table, statistical indexes are slightly different from the classical 2 × 2 as in [38,39]. Hence, in

Table 2. Equation formulae used to calculate the common statistical indexes.

	Formula	Best Score	Range
N	∑A + ∑B + ∑C + D	/	/
Accuracy	(∑A + D)/N	100%	0/100%
Bias Score2×2	(A + C)/(A + B)	1	0/+∞
Bias Scoren×n	YesF/YesO	1	0/+∞
PFA	∑C/N	0%	0/100%
PMA	∑B/N	0%	0/100%
FAR2×2	C/(A + C)	0%	0/100%
FARnxn	∑C/YesF	0%	0/100%
POMA2×2	B/(A + B)	0%	0/100%
POMAn×n	∑B/YesO	0%	0/100%
POD2×2	A/(A + B)	100%	0/100%
PODn×n	∑A/YesO	100%	0/100%
CNR2×2	D/(B + D)	100%	0/100%
CNRn×n	D/NoF	100%	0/100%

Percent False Alarm (PFA), Percent Missed Alarm (PMA), False Alarm Ratio (FAR), Probability of Missed Alarm (POMA), Probability of Detection (POD), Correct Negatives Ratio (CNR).

, we report all the equation formulae used to calculate the performance indexes in Section 2.5.

In particular, No_F is the sum of all terms in the first row of Table 1; Yes_F is the sum of the second, third, and fourth row; and Yes_O is the sum of all terms in the second, third, and fourth column.

Furthermore, another issue relates to verifying the magnitude of our mistakes: i.e., how far are false or missed alarms from observations? If a red alert was issued, was my forecast orange, yellow, or green? This kind of error has a different impact for civil protection authorities. Hence, we introduce new statistical indexes (

Table 3. Weighted equation formulae used to calculate the common statistical indexes.

	Formula	Best Score	Range
PFAweighted	∑k(∑Ck × k/s)/N	0%	0/100%
PMAweighted	∑k(∑Bk × k/s)/N	0%	0/100%
FARnxn weighted	∑k(∑Ck × k/s)/(∑C + ∑A + ∑BYesF)	0%	0/100%
POMAnxn weighted	∑k(∑Bk × k/s)/(∑B + ∑A + ∑CYesO)	0%	0/100%

C_YesO refers to those cells containing C in “Yes” observed columns in Table 1, while B_YesF indicates the cells containing B in “Yes” forecasted rows.

) weighted on the distance between observations and false/missed alarms for the three thresholds (yellow, orange, and red). In other words, the closer the wrong prediction is to the Hits, the lesser its error is weighted. The errors are counted as a unit fraction equal to k/s, where k is the step distance from the Hits and s is the number of thresholds (here, it is equal to 3). The worst cases are three steps distance from the Hits, hence dividing it by the number of thresholds, we obtain the unit.

3. Results and Discussion

In this section, we discuss the main results obtained through the comparison between the performances of the single-valued MOLOCH forecasts and the ST ensemble forecasts. First of all, how do these two approaches exactly predict a non-event (green code: no alert)? In

Table 4. Correct Negatives Ratio (CNR) for the MOLOCH deterministic forecast compared with the observed frequency related to the non-event probability higher than 95% for the ST forecasts.

Basin	Section	Moloch (%)	Shift (%)
Seveso	Cantù	96.12	96.89
Olona	Castellanza	97.29	98.27
	Castiglione	99.16	99.46
Lambro	Lambrugo	95.76	96.89
	Milano F.	92.98	93.66
	Peregallo	93.99	94.86

, we report the observed frequency related to the MOLOCH green code prediction, CNR, and the one related to a 95–100% predicted shift probability of the same green code. A good reliability is found: the frequency is always higher than 92% for both the MOLOCH and ST forecasts at every gauge station: this is proof that the two procedures are able to correctly predict non-events with a slight improvement in the ST.

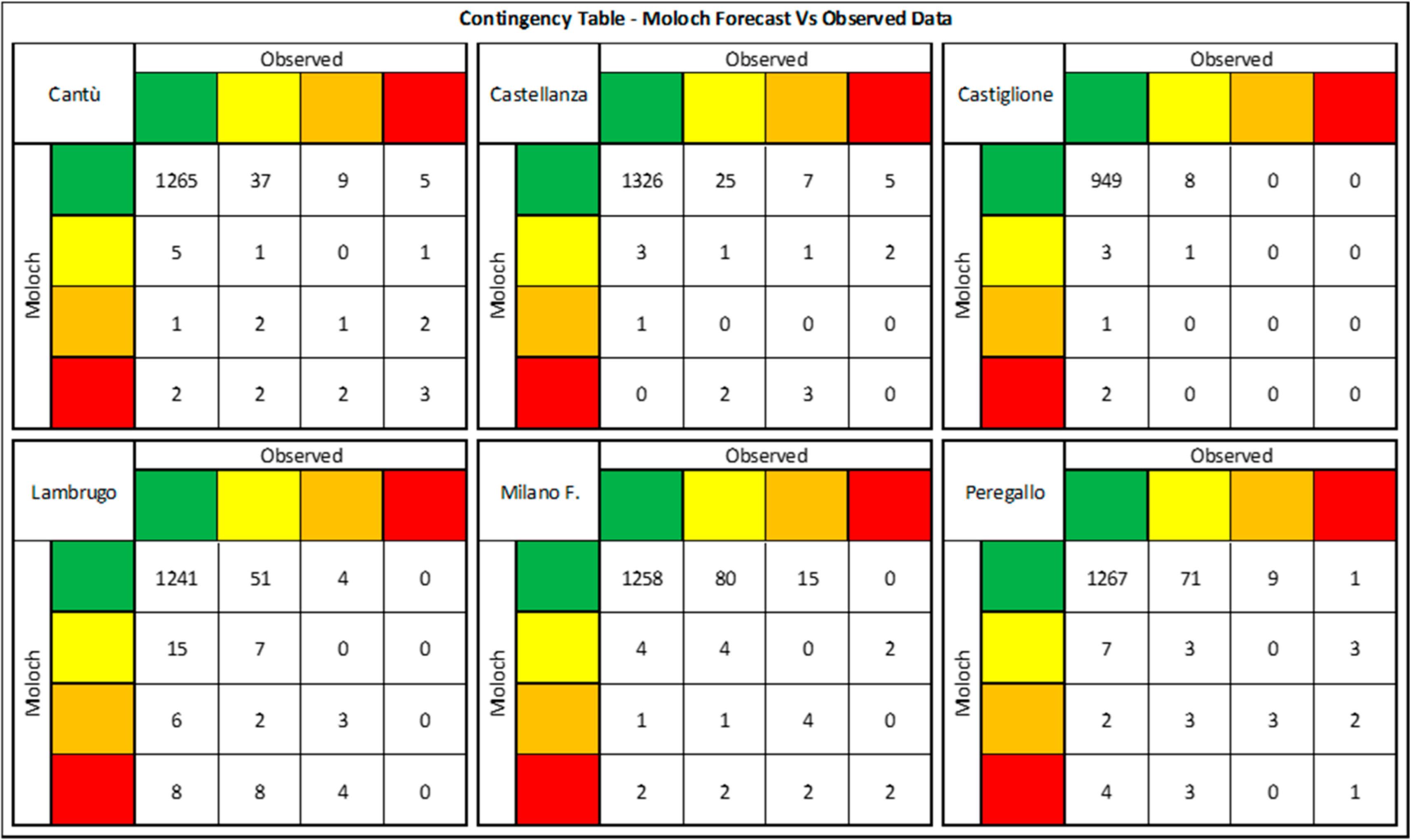
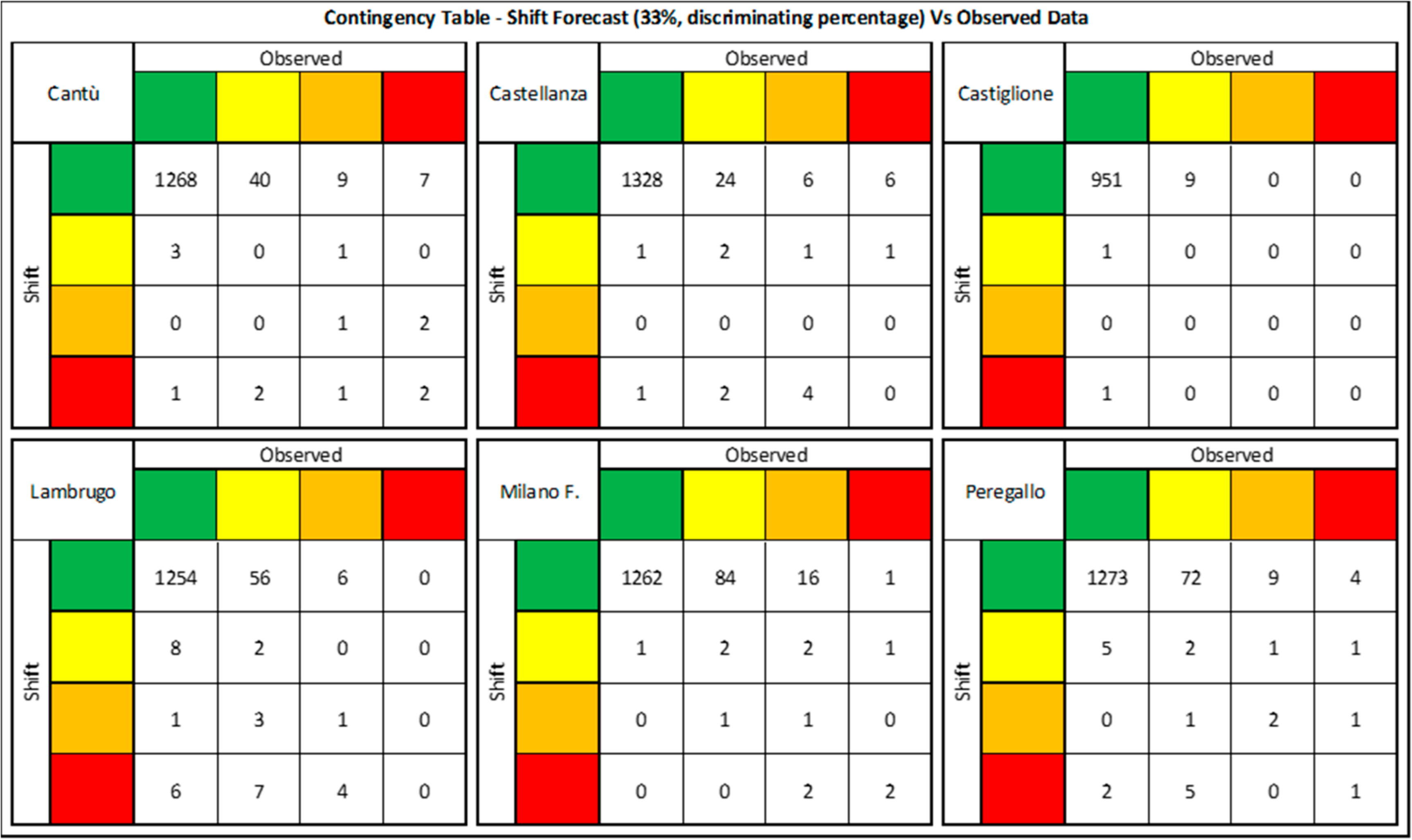
To evaluate the performance of the ST in comparison with the deterministic MOLOCH, we calculate contingency tables for MOLOCH vs. observations, and ST vs. observations (Figure 4 and Figure 5, respectively) in every gauge section. To build these contingency tables for the ST, a categorical forecast has to be assigned from the probabilities of the four alert codes. Our strategy is to choose, as representative of ensembles, the worst critical warning level from red to green, issued with a probability level equal or higher than a given percentage. However, in order to assess a suitable significant percentage to be applied to our instances, we experimented many alternatives. We started with the 33% threshold exceedance probability (at least 14 ensembles out of 40) derived from the Map D-Phase project outcomes [40,41], then we tried with 20% (8 out of 40) and 10% (4 out of 40). Results obtained for the 33% and 20%, for the sake of brevity not shown here, reveal that the unperturbed MOLOCH forecast is slightly preferable: most of the verification scores are similar but better, compared to those of the ST. This can be interpreted as a high skill reached by the deterministic model: i.e., it is not necessary to shift the precipitation domain since its accuracy is itself satisfactory. Maybe, this is not true with other deterministic weather models and this could be an issue for further investigations.

Nevertheless, given the nature of this “non-conventional” ensemble approach, we focus on the contingency scores based on the 10% probability level, since it is not so significant to have a high percentage of exceeding thresholds as to identify that four members out of 40 (equal to 10%) can at least cause dangerous flood scenarios. In Figure 4 and Figure 5, all the contingency tables for the MOLOCH and ST model, respectively, are reported; one for every gauge station analyzed.

Starting from all these data, we have calculated many verification scores reported in

Table 5. Statistical indexes calculated from the MOLOCH “unperturbed” contingency tables.

MOLOCH	Cantù	Castellanza	Castiglione	Lambrugo	Milano F.	Peregallo
Accuracy	94.92%	96.44%	98.55%	92.74%	92.08%	92.39%
Bias Score	0.34	0.28	0.78	0.67	0.21	0.31
PFA	1.05%	0.65%	0.62%	3.19%	0.87%	1.38%
PMA	4.04%	2.91%	0.83%	4.08%	7.04%	6.24%
FAR	63.64%	69.23%	85.71%	81.13%	50.00%	61.29%
POMA	83.08%	86.96%	88.89%	69.62%	86.61%	86.87%
POD	7.69%	2.17%	11.11%	12.66%	8.93%	7.07%

for MOLOCH and

Table 6. Statistical indexes calculated from the Shift-Target contingency tables.

Shift-Target	Cantù	Castellanza	Castiglione	Lambrugo	Milano F.	Peregallo
Accuracy	94.47%	96.00%	96.89%	90.59%	91.50%	91.88%
Bias Score	0.58	0.67	2.78	1.19	0.34	0.56
PFA	2.17%	1.82%	2.39%	6.00%	1.96%	2.83%
PMA	3.36%	2.18%	0.73%	3.41%	6.54%	5.29%
FAR	76.32%	80.65%	92.00%	86.17%	71.05%	70.91%
POMA	69.23%	65.22%	77.78%	58.23%	80.36%	73.74%
POD	12.31%	8.70%	22.22%	12.66%	6.25%	12.12%

for ST. First of all, the Bias Score shows a tendency of the MOLOCH model to underforecast, while the ST underforecasts or overforecasts, depending on the investigated section; in general, this latter marks better values.

In Figure 4 and Figure 5, the high number of Correct Negatives (D in Table 1) that lead to a high Accuracy score in every section for both approaches is evident. In addition, the Percent False Alarm and Percent Missed Alarm scores, which have a percentage lower than 8%, are very favorable since these scores consider both the events and non-events. Unfortunately, the small number of False Alarm and Missed Alarm values is not relevant compared to the one of Correct Negatives, and therefore, these scores are not consistent when we refer to only those cases that have exceeded the thresholds.

Hence, to compare the two approaches in-depth, we take into account FAR, POMA, and POD, since they do not consider the Correct Negatives and they fully highlight the performance differences. The ST has a POD higher in four out of the six gauge sections, equal at Lambrugo, and lower at Milano via Feltre: therefore, this shows the MOLOCH’s main tendency to underforecast, as already shown by the Bias Score.

With regard to the FAR, MOLOCH prevails on ST in all sections. The opposite comment can be made for POMA, which is lower for the ST than for MOLOCH. Therefore, the MOLOCH is more suitable to reduce False Alarm (FA), while the ST minimizes Missed Alarm (MA) better, which is more important for civil protection purposes, because flood damages for a missed alarm have a higher economic cost in comparison with counteractions to activate a false alarm; hence this can be considered a plus for the ST approach.

By definition, in a 4 × 4 contingency table, the obtained skill scores are less satisfactory than a traditional 2 × 2, since the same events, which should be considered as Hits in the 2 × 2, can also be Hits, but even Missed or False Alarms in a 4 × 4 instead, due to the discretization of warning levels. Hence, in

Table 7. Weighted statistical indexes calculated from the MOLOCH “unperturbed” contingency tables.

MOLOCH	Cantù (%)	Castellanza (%)	Castiglione (%)	Lambrugo (%)	Milano F. (%)	Peregallo (%)
PFAW	0.52	0.29	0.38	1.80	0.46	0.77
PMAW	1.84	1.43	0.28	1.46	2.76	2.42
FARW	31.82	30.77	52.38	45.91	26.39	34.41
POMAW	37.95	42.75	29.63	24.89	33.93	33.67

and

Table 8. Weighted statistical indexes calculated from the Shift contingency tables.

Shift-Target	Cantù (%)	Castellanza (%)	Castiglione (%)	Lambrugo (%)	Milano F. (%)	Peregallo (%)
PFAW	1.37	1.14	1.63	3.41	1.14	1.72
PMAW	1.47	1.07	0.24	1.16	2.49	2.05
FARW	48.25	50.54	62.67	48.94	41.23	43.03
POMAW	30.26	31.88	25.93	19.83	30.65	28.62

, we calculate the same indexes shown in Table 5 and Table 6 regarding False Alarms and Missed Alarms, but weighted in order to distinguish the level in the error prediction.

Here, these new indexes improve the percentage by about 30–50% for the two methods. In particular, the FAR decreases an average of 32% for MOLOCH and 30% for ST, while the POMA is 50% for MOLOCH and 43% for ST. This means that when a warning is wrongly issued, the code error is generally not so far from the observed one. Nevertheless, we are not interested in the absolute scores, but in the comparison between the two approaches.

4. Conclusions

Hydro-meteorological systems are nowadays set up with multi-models or multi-analysis approaches gathering deterministic and ensemble forecasts, with the latter being widespread in the scientific community, in order to provide probabilistic information. However, even when using different weather models, a large uncertainty still remains, especially for small river catchments, concerning the location of forecast precipitation. Hence, the proposed study shows the implementation of a different approach using the deterministic high-resolution MOLOCH meteorological model coupled with the FEST-WB hydrological model to obtain probabilistic forecasts. It consists of shifting the precipitation field at in eight directions from 10 to 50 km a step of 10 km, so that the results are 40 discharge forecasts over each analyzed gauge section. The performance of the Shift-Target approach is compared with the “unperturbed” MOLOCH forecast over a period of four years from 10 February 2012 till 31 December 2015. The results show how the ST does not worse the quality of the forecast in comparison with the one by MOLOCH, and in some cases, it is even better.

The potentiality of the ST can be seen as an a-priori rainfall generator that can be used in real-time, above all, during convective events when precise thunderstorm cell forecasting is difficult over small river basins, but probable flood scenarios, obtained by spatial shift forecasts, can already be forecasted. Notwithstanding this, the ST approach is conditioned by the unperturbed MOLOCH forecast in terms of QPF (Quantitative Precipitation Forecasts): if the MOLOCH totally misses the precipitation intensity, e.g., underestimating over the entire area, no shift will improve the forecast. Nevertheless, this approach, obtained with a low computation method, has demonstrated that it is able to provide useful information with respect to the deterministic MOLOCH run, in case of a misplacement of precipitation field.

Future developments will concentrate on enlarging our dataset to investigate more flood episodes and to verify with a more robust stochastic approach, which is the probability distribution of spatial, timing, and intensity of precipitation error.