Basin Resonance and Seismic Hazard in Jakarta, Indonesia
Abstract
1. Introduction
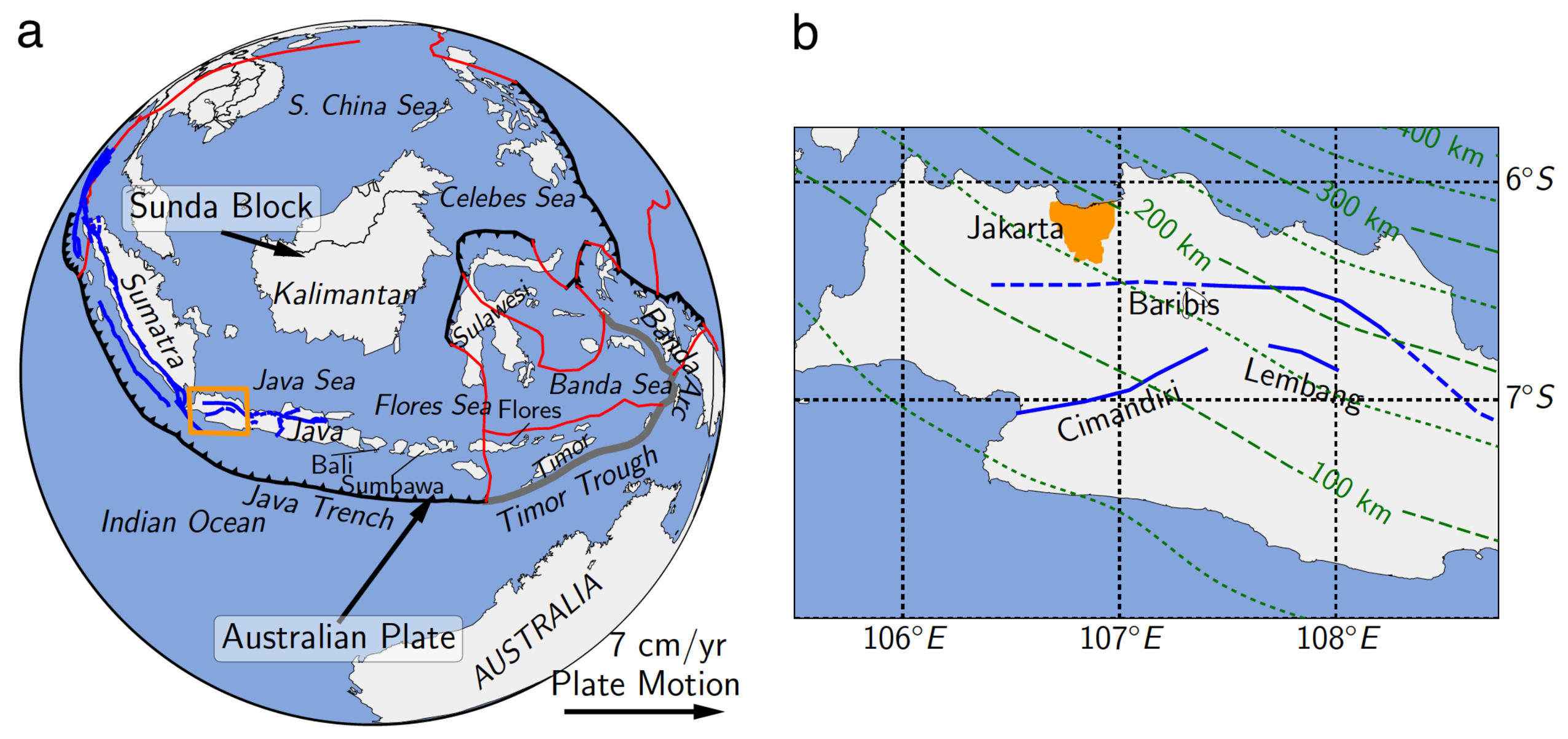
2. Tectonic Setting of Jakarta and Surroundings
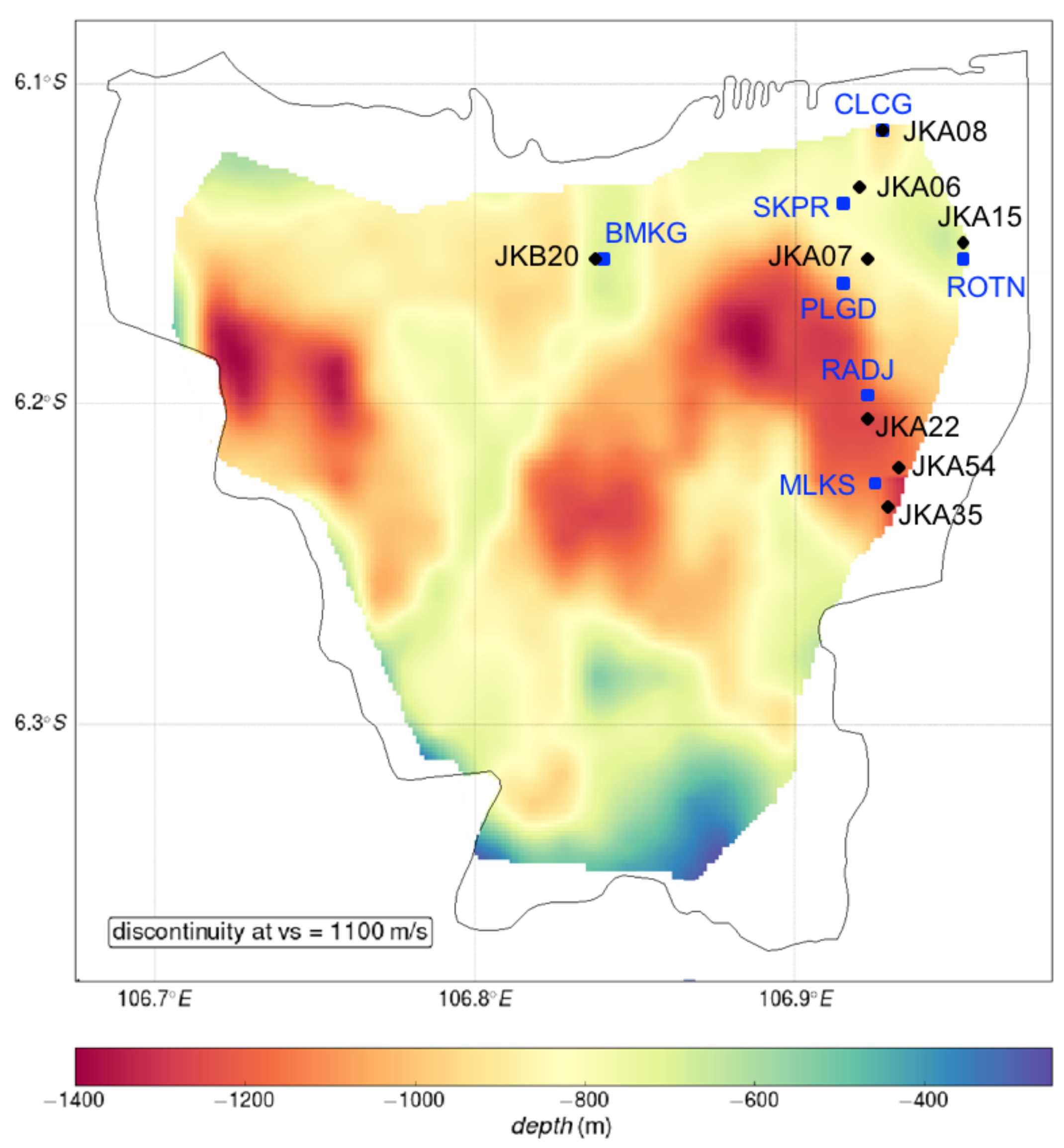
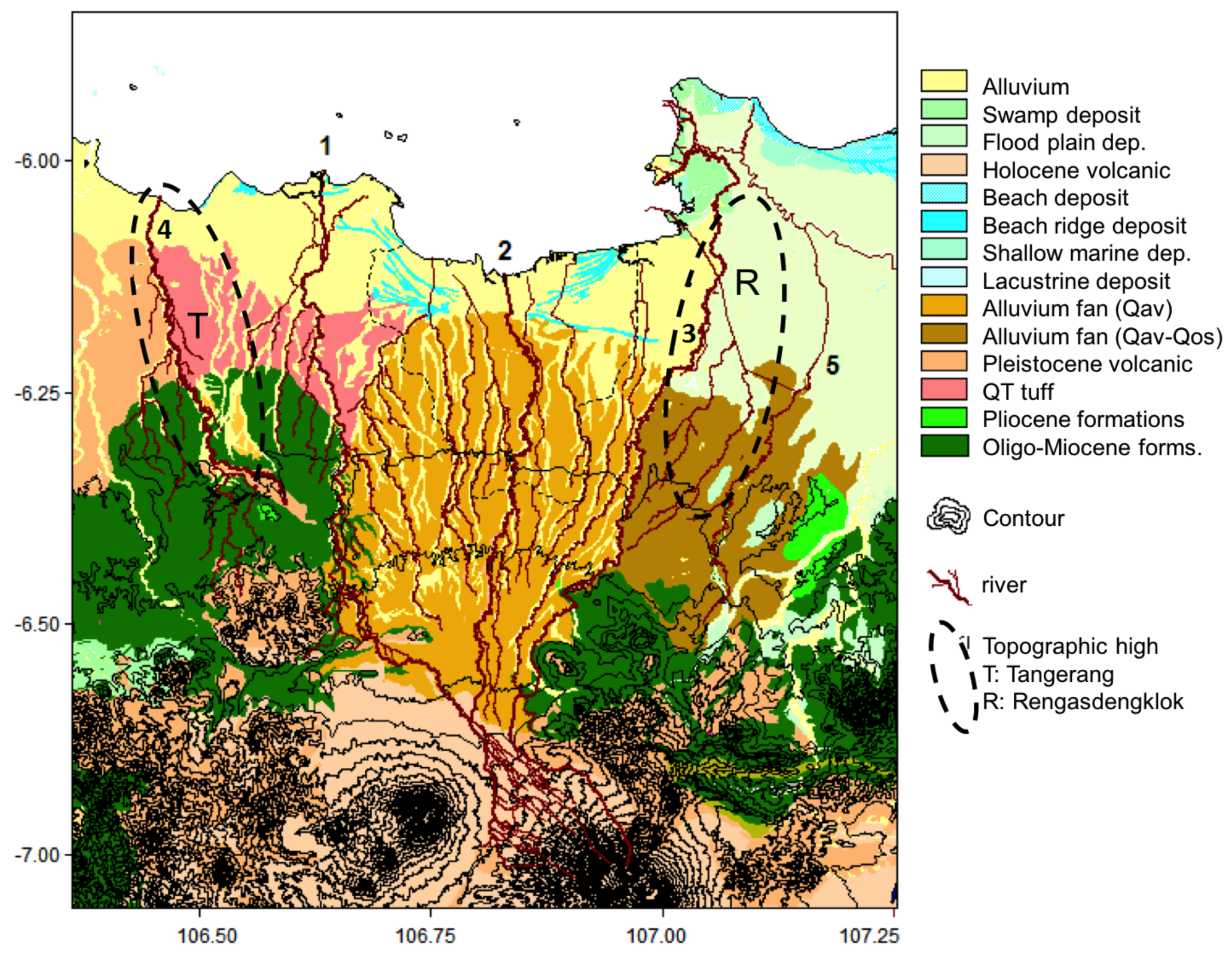
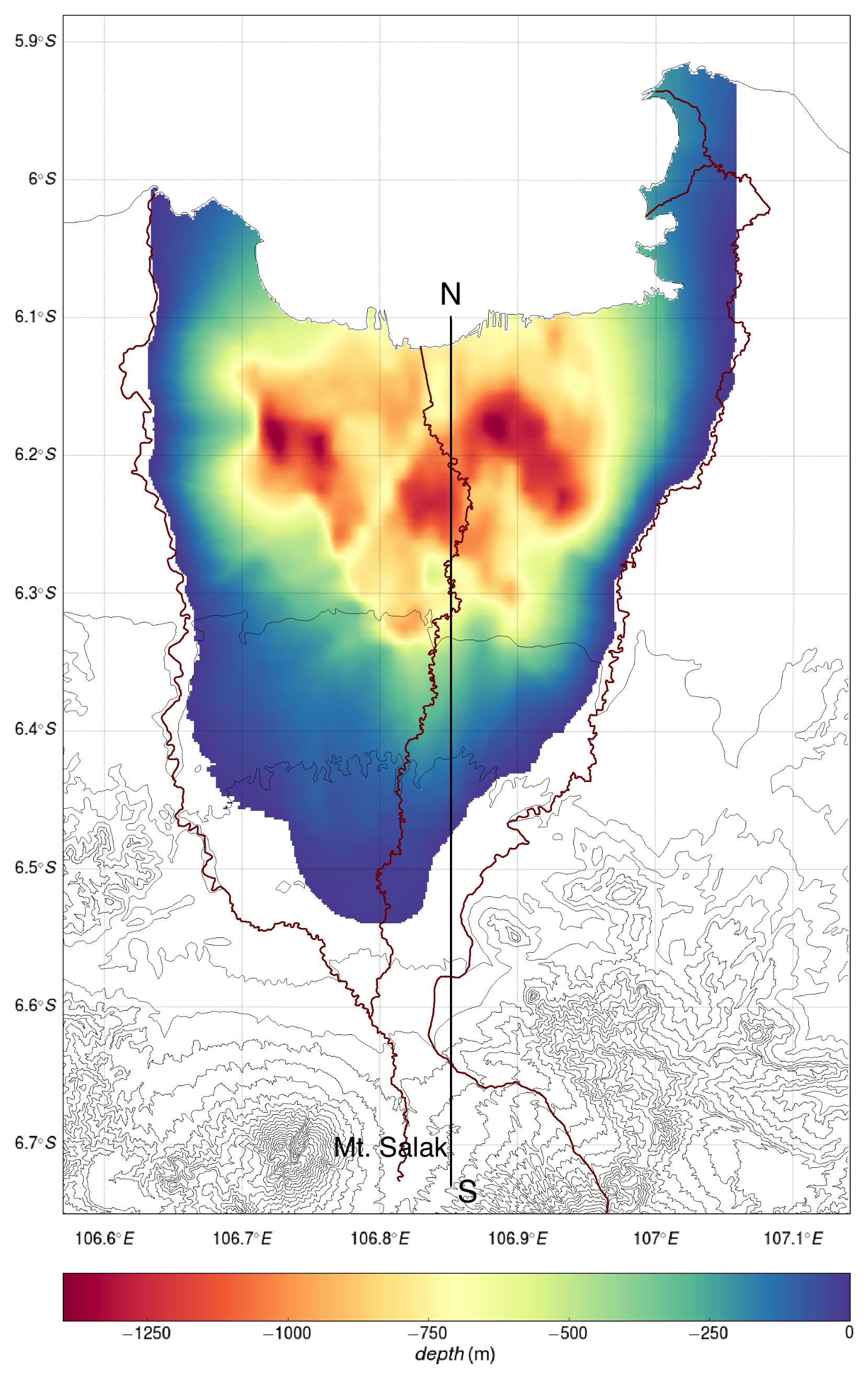
3. The Jakarta Basin
4. Material and Methods
4.1. Ground Motion Prediction Equations (GMPEs)
4.2. Numerical Simulation of Seismic Waves
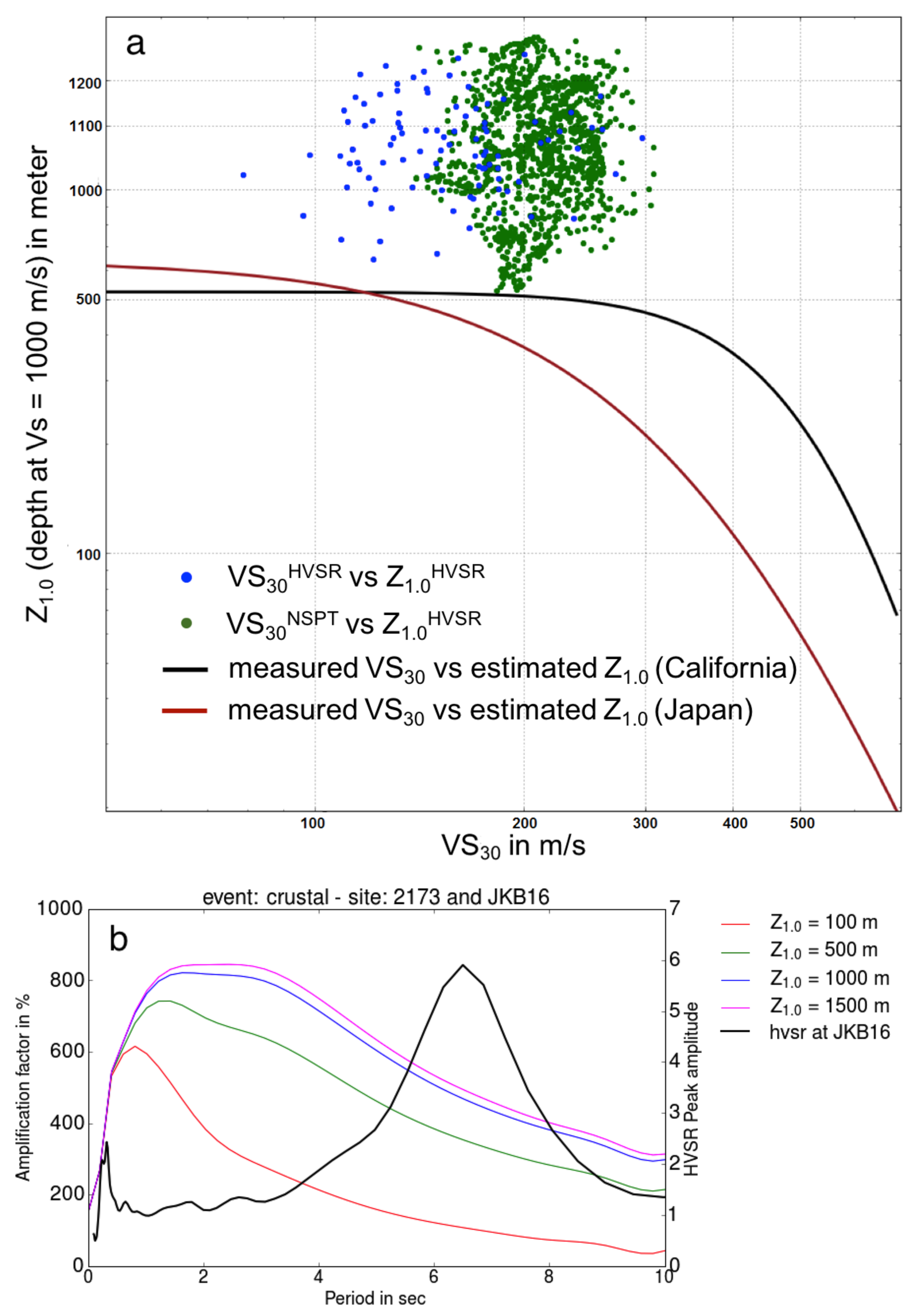
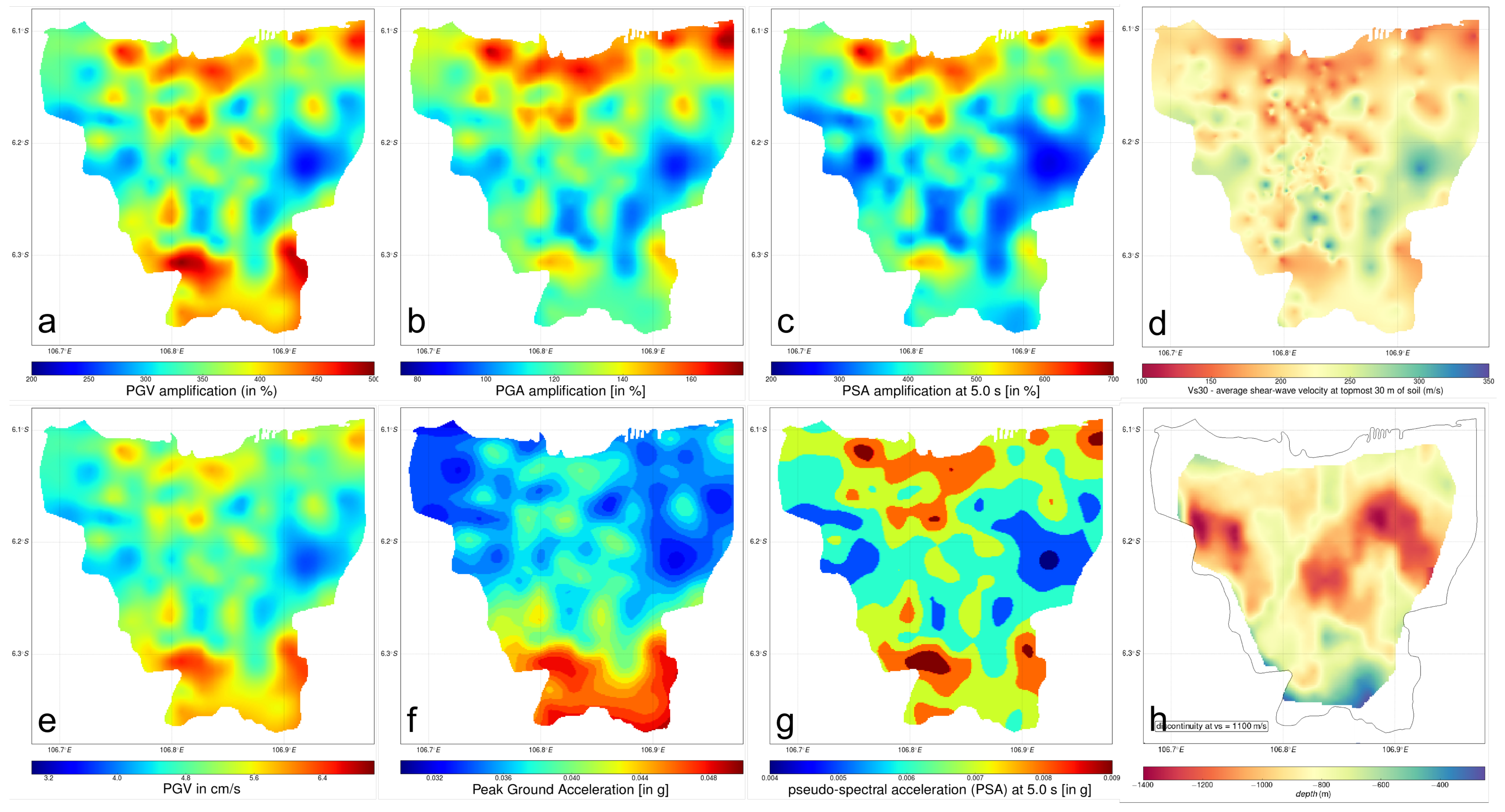
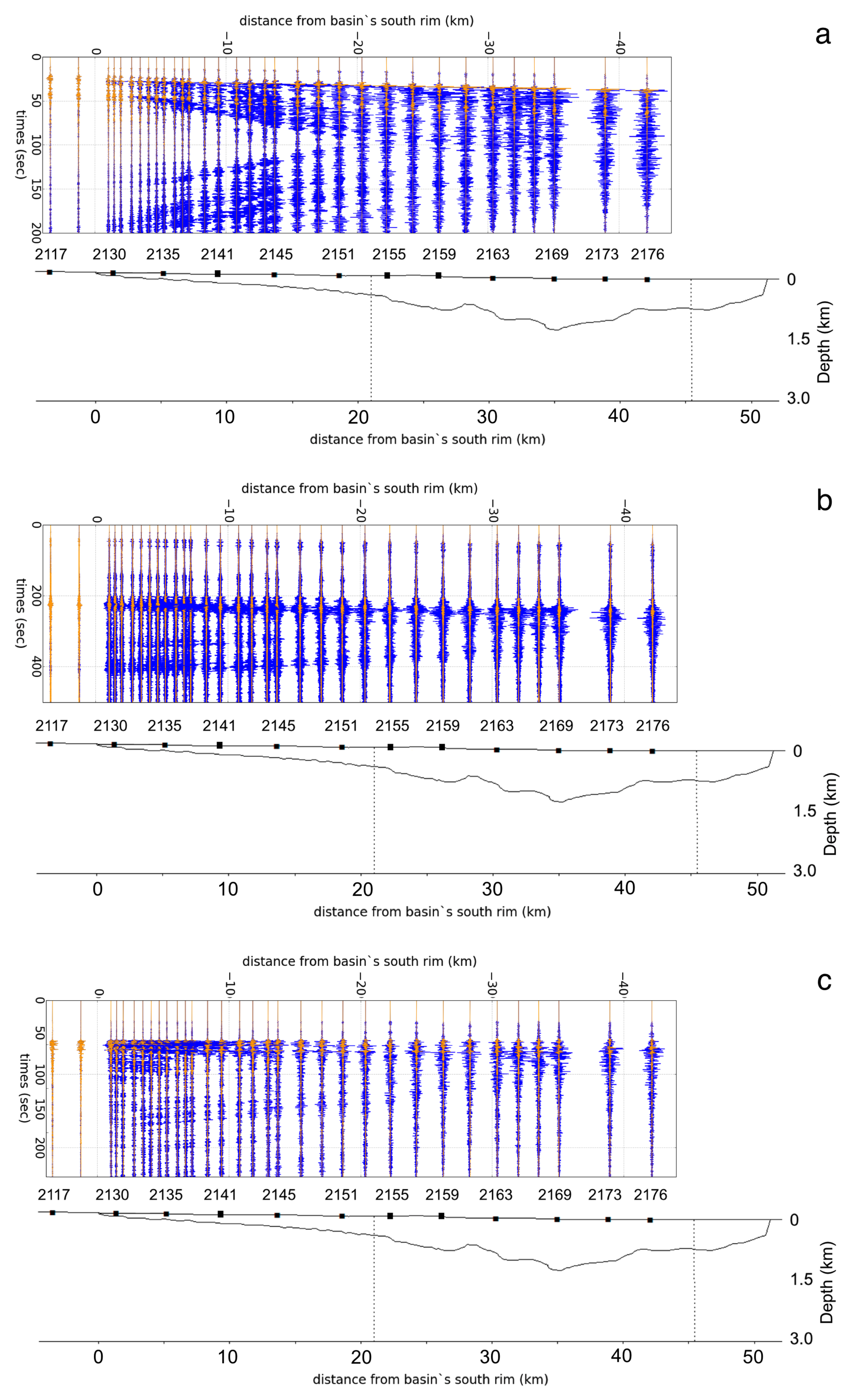
5. Results
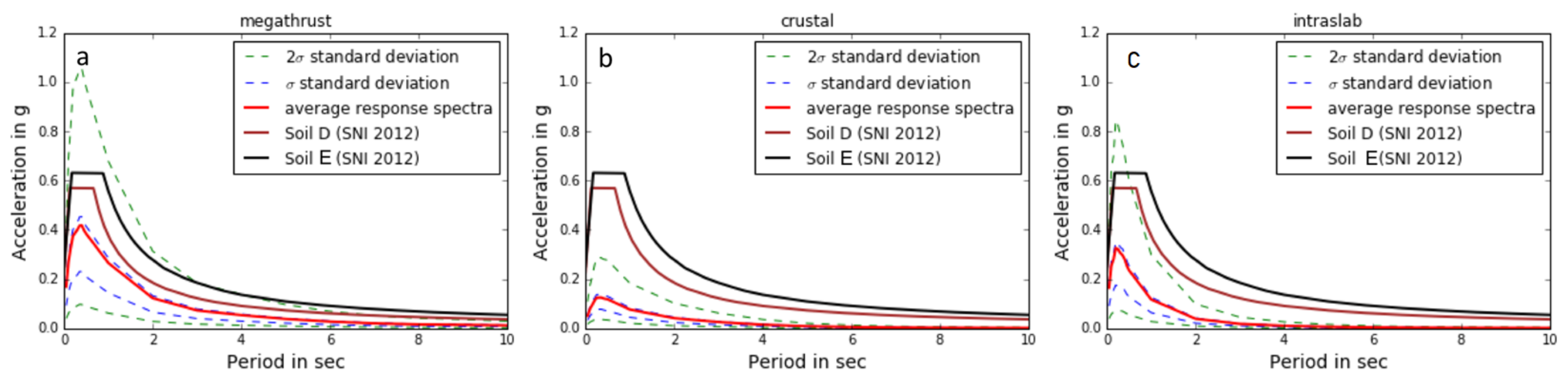
5.1. GMPE Modeling Results
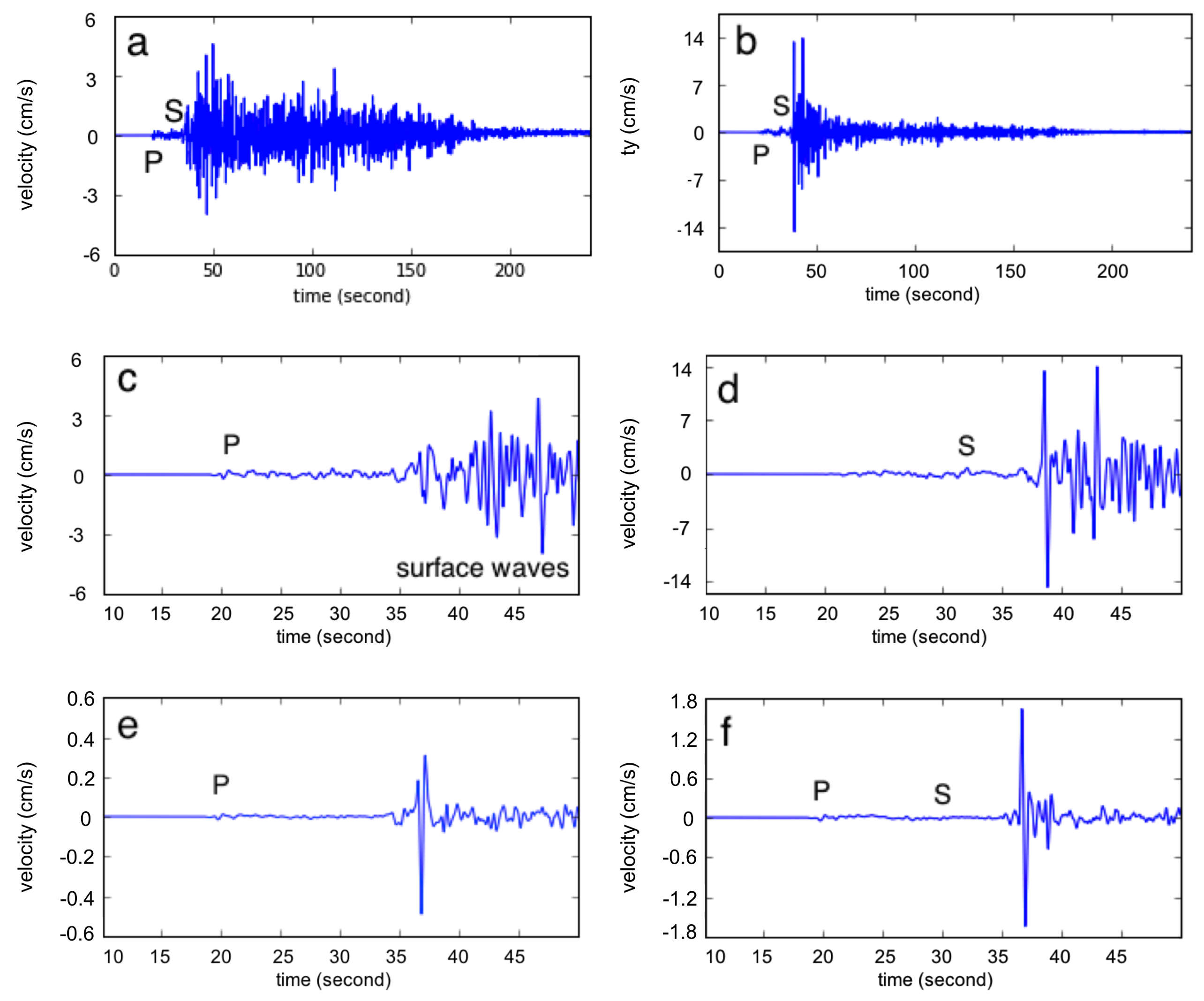
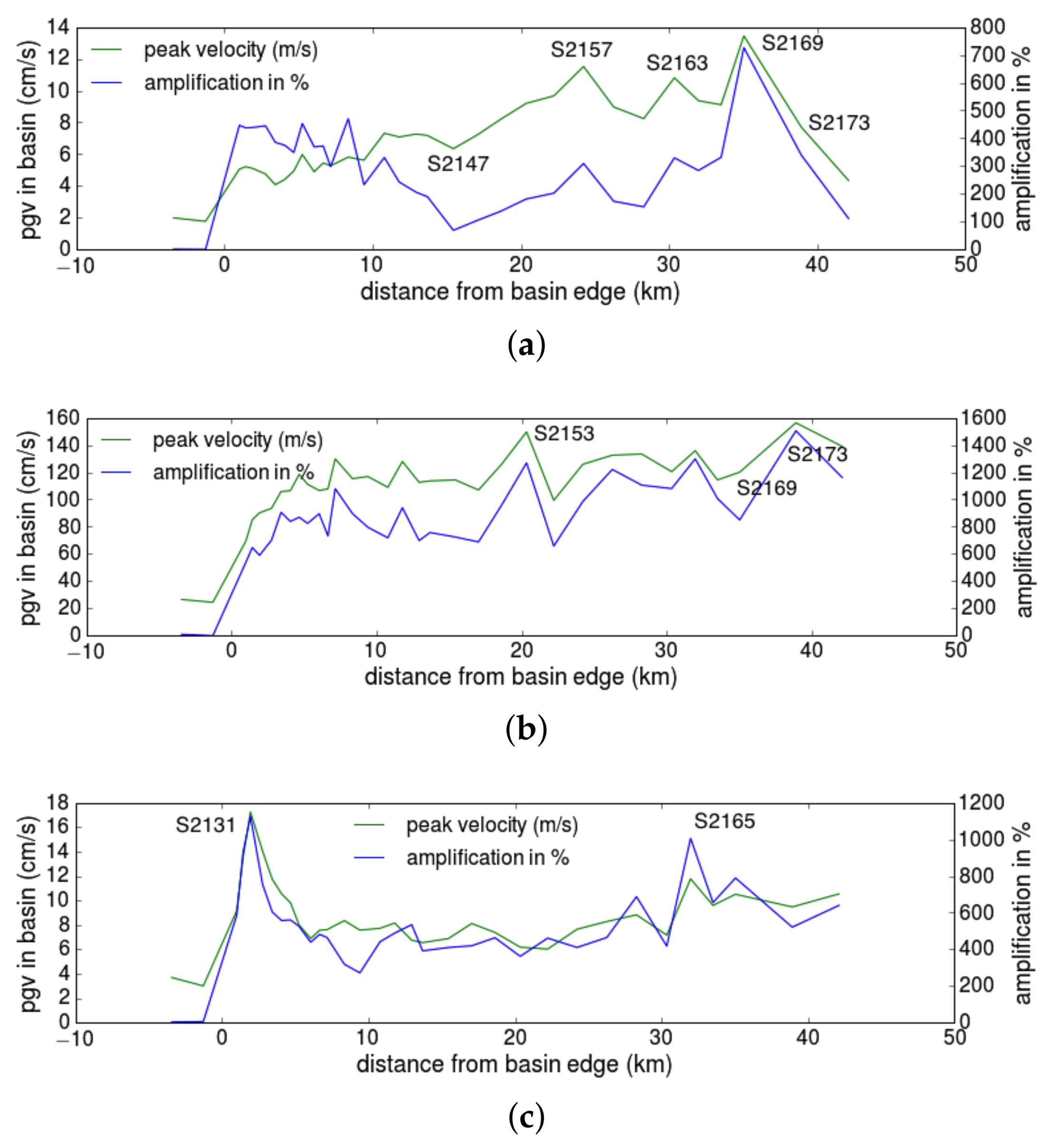
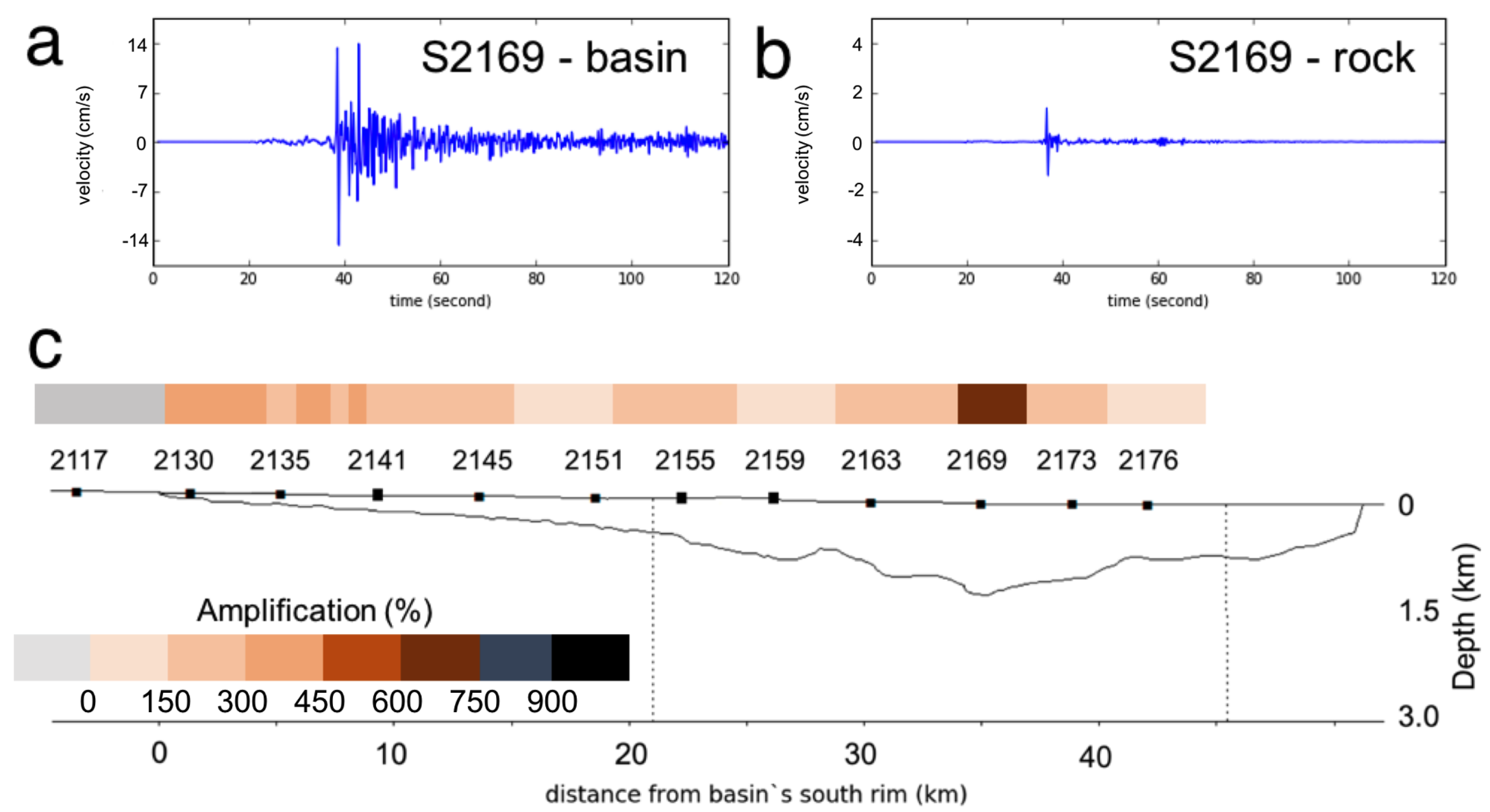
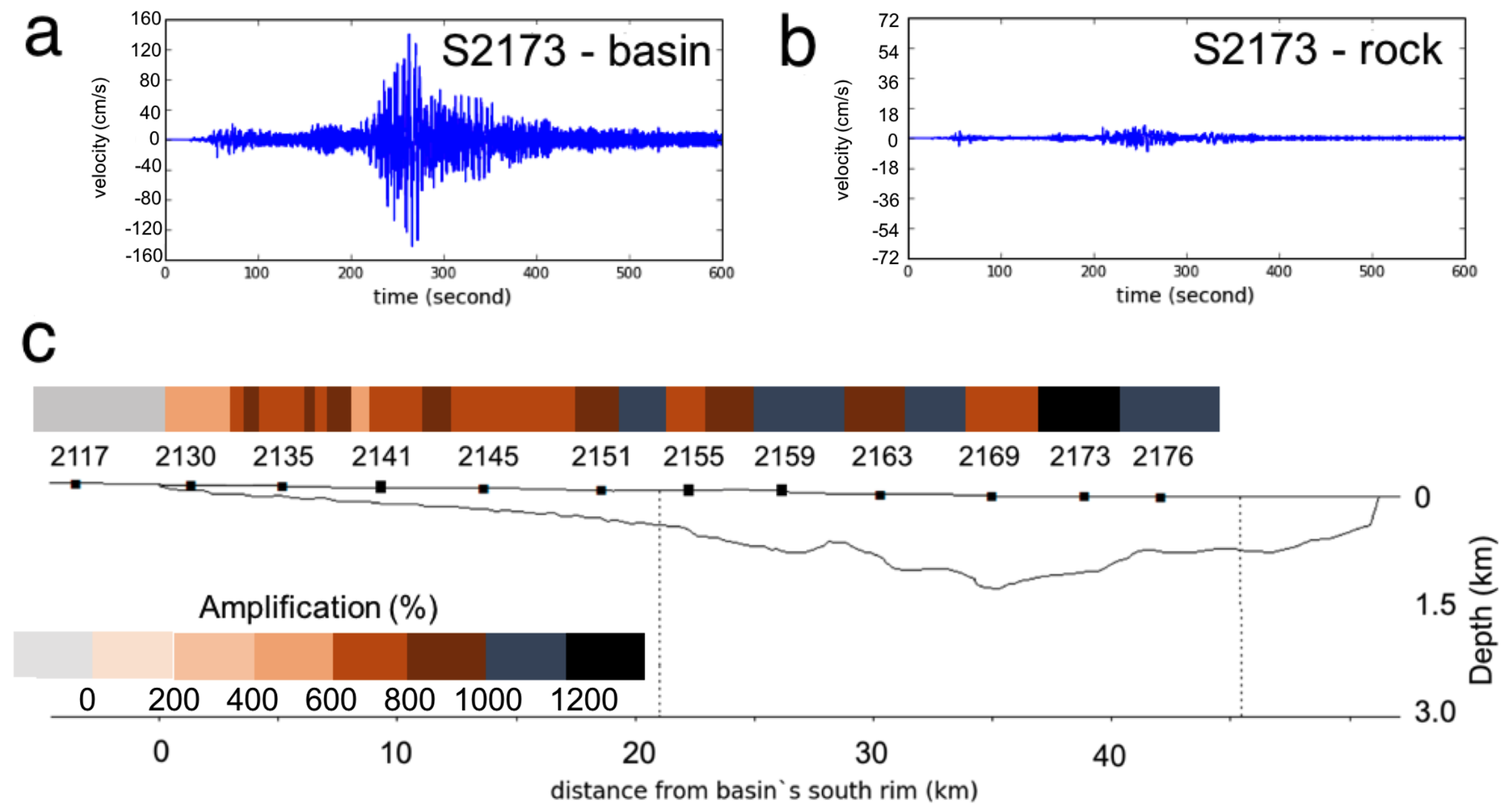
5.2. Numerical Simulation Results
6. Discussion
6.1. GMPE-Seismic Hazard
6.2. Numerical Simulations–Peak Ground Velocity (PGV)
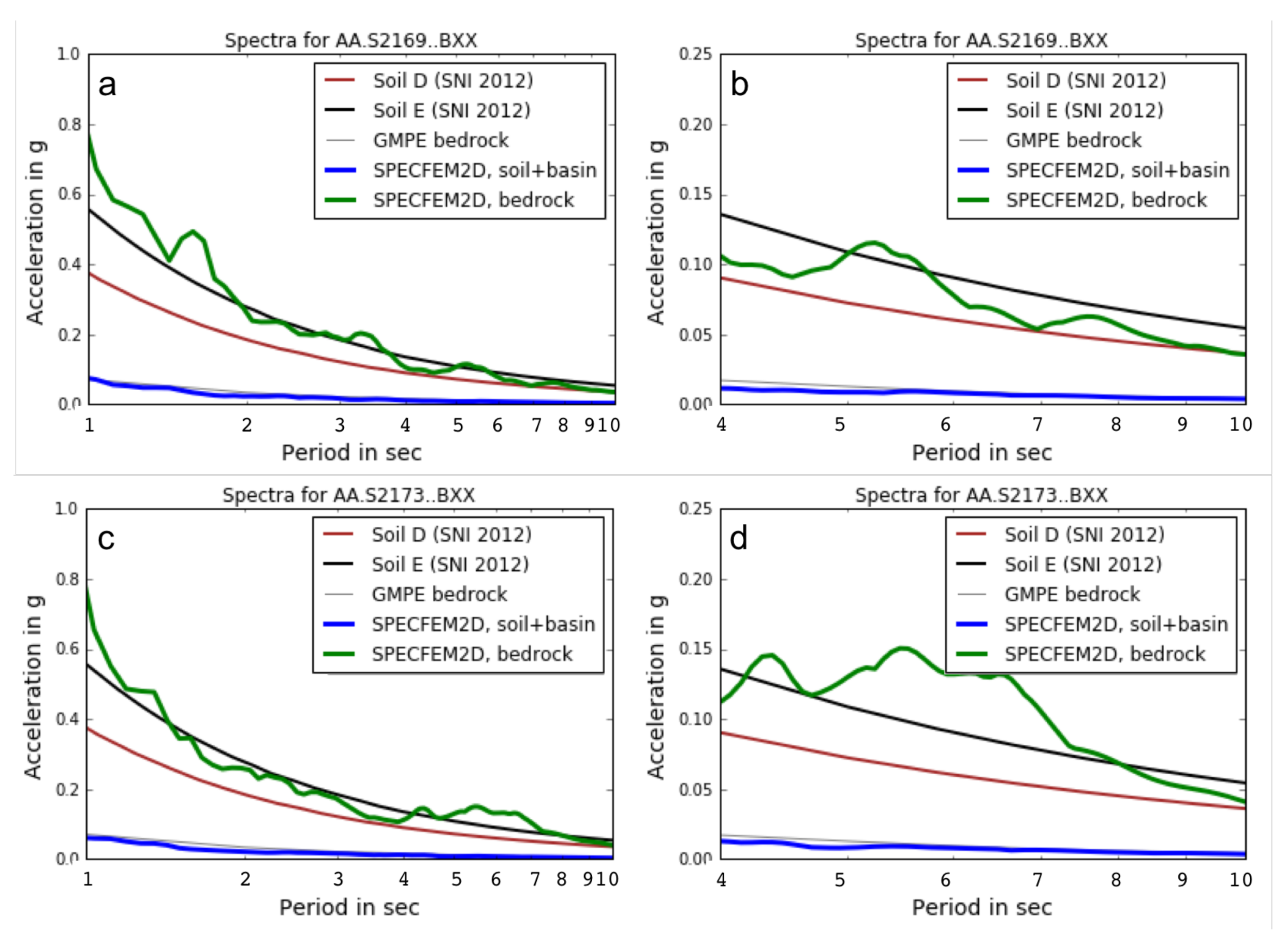
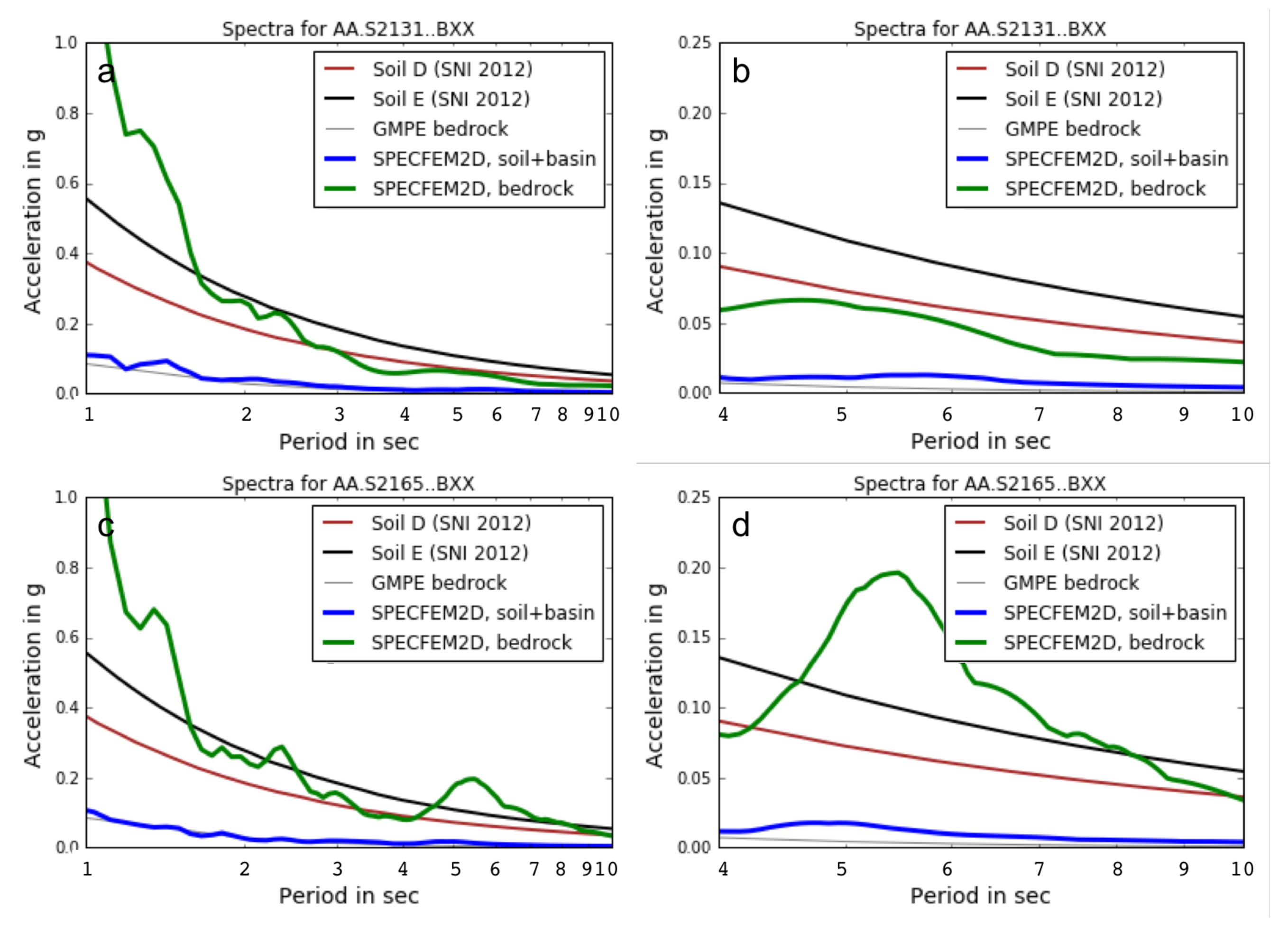
6.3. Numerical Simulation-Response Spectral Acceleration
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AEA2015, AEA2015S | Abrahamson et al. 2005, Abrahamson et al. 2015 Intra-slab |
| CY2014, CY2008 | Chiou & Young 2014, Chiou & Young 2008 |
| CB2014 | Campbell & Bozorgnia 2014 |
| GEM | Global Earthquake Model |
| HVSR | Horizontal-to-vertical spectral ratio |
| NGA GMPE | Next Generation Attenuation Ground Motion Prediction Equation |
| PGV | Peak Ground Acceleration |
| PSA | Pseudo-spectral acceleration |
References
- Cruz-Atienza, V.M.; Tago, J.; Sanabria-Gómez, J.D.; Chaljub, E.; Etienne, V.; Virieux, J.; Quintanar, L. Long Duration of Ground Motion in the Paradigmatic Valley of Mexico. Nature 2016, 6, 38807. [Google Scholar] [CrossRef]
- Rial, J.A.; Saltzman, N.G.; Hui, L. Earthquake-induced resonance in Sedimentary Basin. Am. Sci. 1992, 80, 566–578. [Google Scholar]
- Galetzka, J.; Melgar, D.; Genrich, J.F.; Geng, J.; Owen, S.; Lindsey, E.O.; Xu, X.; Bock, Y.; Avouac, J.-P.; Adhikari, L.B.; et al. Slip pulse and resonance of the Kathmandu basin during the 2015 Gorkha earthquake, Nepal. Science 2015, 349, 1091–1095. [Google Scholar] [CrossRef] [PubMed]
- Brinkhoff, T. City Population. 2017. Available online: http://citypopulation.de/world/Agglomerations.html (accessed on 12 December 2017).
- Nata, T.P.; Witsen, B. A Relation of the Bad Condition of the Mountains about the Tungarouse and Batavian Rivers, Having Their Source from Thence, Occasioned by the Earthquake between the 4th and 5th of January, 1699. Drawn up from the Account Given by the Tommagon Porbo Nata, (Who Hath Been There) and Sent to the Burgermaster Witsen, Who Communicated It to the R. Society, of Which He is a Member. Philos. Trans. 1699, 22, 595–598. [Google Scholar]
- Albini, P.; Musson, R.M.W.; Gomez Capera, A.A.; Locati, M.; Rovida, A.; Stucchi, M.; Viganó, D. Global Historical Earthquake Archive and Catalogue (1000–1903); GEM Foundation: Pavia, Italy, 2013. [Google Scholar]
- Musson, R.M.W. A Provisional Catalogue of Historical Earthquakes in Indonesia; British Geological Survey: Nottinghamshire, UK, 2012. [Google Scholar]
- Chiou, B.; Youngs, R. Update of the Chiou and Youngs NGA Model for the Average Horizontal Component of Peak Ground Motion and Response Spectra. Earthq. Spectr. 2014, 30, 1117–1153. [Google Scholar] [CrossRef]
- Campbell, K.W.; Bozorgnia, Y. NGA-West2 Ground Motion Model for the Average Horizontal Components of PGA, PGV, and 5% Damped Linear Acceleration Response Spectra. Earthq. Spectr. 2014, 30, 1087–1115. [Google Scholar] [CrossRef]
- Graves, R.W.; Pitarka, A.; Sommerville, P. Ground-motion amplification in the Santa Monica area: Effects of shallow basin-edge structure. Bull. Seismol. Soc. Am. 1998, 88, 1224–1242. [Google Scholar]
- Bard, P.Y.; Bouchon, M. The two-dimensional resonance of sediment-filled valleys. Bull. Seismol. Soc. Am. 1985, 75, 519–541. [Google Scholar]
- Furumura, T.; Chen, L. Parallel simulation of strong ground motions during recent and historical damaging earthquakes in Tokyo, Japan. Parallel Comput. 2005, 31, 149–165. [Google Scholar] [CrossRef]
- Cipta, A.; Cummins, P.; Dettmer, J.; Saygin, E.; Irsyam, M.; Rudyanto, A.; Murjaya, J. Seismic Velocity Structure of the Jakarta Basin, Indonesia, using Trans-dimensional Bayesian Inversion of Horizontal-to-Vertical Spectral Ratios. Geophys. J. Int. 2018, in press. [Google Scholar]
- Abrahamson, N.A.; Gregor, N.; Addo, K. BC Hydro Ground Motion Prediction Equations for Subduction Earthquakes. Earthq. Spectra 2016, 32, 23–44. [Google Scholar] [CrossRef]
- Marafi, M.A.; Eberhard, M.O.; Berman, J.W. Effects of the Yufutsu Basin on Structural Response during Subduction Earthquakes. In Proceedings of the 16th WCEE 2017, Santiago, Chile, 9–13 January 2017. No. 2629. [Google Scholar]
- Komatitsch, D.; Vilotte, J.P. The spectral element method: An efficient tool to simulate the seismic response of 2D and 3D geological structure. Bull. Seismol. Soc. Am. 1998, 88, 368–392. [Google Scholar]
- Abidin, H.Z.; Andreas, H.; Gumilar, I.; Fukuda, Y.; Pohan, Y.E.; Deguchi, T. Land subsidence of Jakarta (Indonesia) and its relation with urban development. Nat. Hazards 2011, 18, 232–242. [Google Scholar] [CrossRef]
- Ng, A.H.-M.; Ge, L.; Li, X.; Abidin, H.Z.; Andreas, H.; Zhang, K. Mapping land subsidence in Jakarta, Indonesia using persistent scatterer interferometry (PSI) technique with ALOS PALSAR. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 232–242. [Google Scholar] [CrossRef]
- Nguyen, N.; Griffin, J.; Cipta, A.; Cummins, P. Indonesia’s Historical Earthquakes Modelled Examples for Improving the National Hazard Map; Geoscience Australia: Canberra, Australia, 2015. [Google Scholar]
- Simons, W.J.F.; Socquet, A.; Vigny, C.; Ambrosius, B.A.C.; Abu, S.H.; Promthong, C.; Subarya, C.; Sarsito, D.A.; Matheussen, S.; Morgan, P.; et al. A decade of GPS in Southeast Asia: Resolving Sundaland motion and boundaries. J. Geophys. Res. 1997, 112. [Google Scholar] [CrossRef]
- Hall, R. Hydrocarbon basins in SE Asia: Understanding why they are there. Petrol. Geosci. 2009, 15, 131–146. [Google Scholar] [CrossRef]
- Pusat Studi Gempa Nasional (National Center for Earthquake Studies). Peta Sumber dan Bahaya Gempa Indoensia Tahun 2017; Pusat Litbang Perumahan dan Pemukiman PU: Bandung, Indonesia, 2017. [Google Scholar]
- Dardji, N.; Villemin, T.; Ramnoux, J.P. Paleostresses and strike-slip movement: The Cimandiri Fault Zone, West Java, Indonesia. J. Southeast Asian Stud. 1994, 9, 3–11. [Google Scholar] [CrossRef]
- Abidin, H.Z.; Andreas, H.; Kato, T.; Ito, T.; Meilano, I.; Kimata, F.; Natawidjaja, D.; Harjono, H. Crustal deformation studies in Java (Indonesia) using GPS. J. Earthq. Tsunami 2009, 3, 77–88. [Google Scholar] [CrossRef]
- Supartoyo, I.A.; Sadisun, E.; Suparka, A. Cimandiri Fault Activity at Sukabumi Area, West Java, Indonesia (Based on Morphometry Analysis). In Proceedings of the ISEGA I, Bandung, Indonesia, 13 October 2013. [Google Scholar]
- Marliyani, G.I.; Arrowsmith, R. Tectonic Geomorphology of the Hanging Wall Blocks of the Cimandiri Fault Zone, West Java, Indonesia. In Proceedings of the American Geophysical Union Fall Meeting, T41C-4650, San Francisco, CA, USA, 15 December 2014. [Google Scholar]
- Handayani, L.; Maryati, M.; Kamtono, M.; Mukti, M.M.R.; Sudrajat, Y. Audio-Magnetotelluric Modeling of Cimandiri Fault Zone at Cibeber, Cianjur. Indones. J. Geosci. 2017, 4, 39–47. [Google Scholar] [CrossRef][Green Version]
- Meilano, I.; Abidin, H.Z.; Andreas, H.; Gumilar, I.; Sarsito, D.; Rino, R.H.; Harjono, H.; Kato, T.; Kimata, F.; Fukuda, Y. Slip Rate Estimation of the Lembang Fault West Java from Geodetic Observation. J. Dis. Res. 2012, 7, 12–18. [Google Scholar] [CrossRef]
- Simandjuntak, T.O.; Barber, A.J. Contrasting Tectonic Styles in the Neogene Orogenic Belts of Indonesia; Geological Society: London, UK, 1996; Volume 106, pp. 185–201. [Google Scholar]
- Koulali, A.; McClusky, S.; Susilo, S.; Leonard, Y.; Cummins, P.; Tregoning, P.; Meilano, I.; Efendi, J.; Wijanartob, A.B. The kinematics of crustal deformation in Java from GPS observations: Implications for fault slip partitioning. Earth Planet. Sci. Lett. 2017, 458, 69–79. [Google Scholar] [CrossRef]
- Allmendinger, R.W. Modern Structural Practice: A Structural Geology Laboratory Manual for the 21st Century v.1.7.0 ©2015–2017. 2017. Available online: http://www.geo.cornell.edu/geology/faculty/RWA/structure-lab-manual/ (accessed on 12 December 2017).
- Kingston, J. Undiscovered Petroleum Resources of Indonesia; U.S. Geological Survey: Reston, VA, USA, 1988.
- Putra, S.D.; Suryantini, H.; Srigutomo, W. Thermal modeling and heat flow density interpretation of the onshore Northwest Java Basin, Indonesia. Geotherm. Energy 2016, 4. [Google Scholar] [CrossRef]
- Campbell, K.W.; Bozorgnia, Y. NGA-West2 Campbell-Bozorgnia Ground Motion Model for the Horizontal Components of PGA, PGV, and 5%-Damped Elastic Pseudo-Acceleration Response Spectra for Periods Ranging from 0.01 to 10 s; PEER, Report No. 2013/06; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2013. [Google Scholar]
- Pagani, M.; Monelli, D.; Weatheril, G.; Danciu, L.; Crowley, H.; Silva, V.; Henshaw, P.; Butler, L.; Nastasi, M.; Panzeri, L.; et al. OpenQuake Engine: An Open Hazard (and Risk) Software for the Global Earthquake Model. Seismol. Res. Lett. 2011, 85, 692–702. [Google Scholar] [CrossRef]
- Ridwan, M. Development of an Engineering Bedrock Map Beneath Jakarta Based on Microtremor Array Measurements; Study of Ground Subsurface in Jakarta by Using Microtremor Array Method: Identifi- cation of Engineering Bedrock Depth and Site Class; Institut Teknologi Bandung: Bandung, Indonesia, 2016. [Google Scholar]
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Q. Rep. RTRI 1989, 30, 25–33. [Google Scholar]
- Gosar, A. Site effects and soil-structure resonance study in the Kobarid basin (NW Slovenia) using microtremors. Nat. Hazards Earth Syst. Sci. 2010, 10, 761–772. [Google Scholar] [CrossRef]
- Saygin, E.; Cummins, P.R.; Cipta, A.; Hawkins, R.; Pandhu, R.; Murjaya, J.; Masturyono; Irsyam, M.; Widiyantoro, S.; Kennett, B.L.N. Imaging architecture of the Jakarta Basin, Indonesia with transdimensional inversion of seismic noise. Geophys. J. Int. 2016, 204, 918–931. [Google Scholar] [CrossRef]
- Molnar, S.; Cassidy, J.F.; Olsen, K.B.; Dosso, S.E.; He, J. Earthquake ground motion and 3D Georgia basin amplification in SW British Columbia: Deep Juan de Fuca plate scenario earthquakes. Bull. Seismol. Soc. Am. 2014, 104, 301–320. [Google Scholar] [CrossRef]
- Molnar, S.; Cassidy, J.F.; Olsen, K.B.; Dosso, S.E.; He, J. Earthquake ground motion and 3D Georgia basin amplification in SW British Columbia: Shallow blind-thrust scenario earthquakes. Bull. Seismol. Soc. Am. 2014, 104, 321–335. [Google Scholar] [CrossRef]
- Hauksson, A.; Teng, T.L.; Henyey, T.L. Results from a 1500 m Deep, Three-level Downhole Seismometer Array: Site Response, Low Q values and fmax. Bull. Seismol. Soc. Am. 1987, 7, 1883–1904. [Google Scholar]
- Pilz, M.; Parolai, S.; Stupazzini, M.; Paoluci, R.; Zschau, J. Modelling basin effects on earthquake ground motion in the Santiago de Chile basin by a spectral element code. Geophys. J. Int. 2011, 187, 929–945. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, Z.; Xu, J. Interference between seismic body wave and secondary surface wave resulting in the peak collapse ratios of buildings. J. Appl. Geophys. 2010, 72, 1–9. [Google Scholar] [CrossRef]
- Shoji, Y.; Tanii, K.; Kamiyama, M. The Duration and Amplitude Characteristics of Earthquake Ground Motions with Emphasis on Local Site Efects. In Proceedings of the Conference the 13th WCEE, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 436. [Google Scholar]
- Irsyam, M.; Sengara, W.; Aldiamar, F.; Widiyantoro, S.; Triyoso, W.; Hilman, D.; Kertapati, E.; Meilano, I.; Suhardjono, S.; Asrurifak, M.; et al. Development of Seismic Hazard Maps of Indonesia for Revision of Seismic Hazard Map in SNI 03-1726-2002; Research Report; Bandung Institute of Technology: Bandung, Indonesia, 2010. [Google Scholar]
- Sato, K.; Asano, K.; Iwata, T. Long-period ground motion characteristics of the Osaka Sedimentary Basin during the 2011 Great Tohoku Earthquake. In Proceedings of the Fifteenth World Conference on Earthquake Engineering, Lisabon, Portugal, 24–28 September 2012. [Google Scholar]
- Tsai, V.C.; Bowden, D.C.; Kanamori, H. Explaining extreme ground motion in Osaka basin during the 2011 Tohoku earthquake. Geophys. Res. Lett. 2017, 44, 7239–7244. [Google Scholar] [CrossRef]
- Singh, S.K.; Ordaz, M. On the origin of long coda observed in the lake-bed strong-motion records of Mexico City. Bull. Seismol. Soc. Am. 1993, 83, 1298–1306. [Google Scholar]
- Pusat Litbang Perumahan dan Pemukiman PU. 2011. Available online: http://puskim.pu.go.id/Aplikasi/desain_spektra_indonesia_2011/ (accessed on 20 November 2017).
- Sukamta, N.; Alexander, D. State of Practice of Performance-Based Seismic Design in Indoensia. I. J. High-Rise Build. 2012, 1, 211–220. [Google Scholar]


| Layer | Rho | Max Depth | ||||
|---|---|---|---|---|---|---|
| (kg m−3) | (ms−1) | (m−1) | (m) | |||
| Basin | 1200 | 1600 | 582 | 44 | 25 | 1385 |
| Layer 2 | 2200 | 4100 | 2300 | 283 | 150 | 3000 |
| Layer 3 | 2900 | 5100 | 2800 | 450 | 450 | 13,467 |
| Layer 4 | 3200 | 6500 | 3200 | 500 | 500 | 15,000 |
| Layer 5 | 3800 | 8000 | 4000 | 600 | 700 | 120,000 |
| Station | PGV-C | Ampli-C | PGV-M | Ampli-M | PGV-S | Ampli-S |
|---|---|---|---|---|---|---|
| Station | (cm/s) | (%) | (cm/s) | (%) | (cm/s) | (%) |
| S2117 | 1.98 | 1 | 26.44 | 8 | 3.68 | 2 |
| S2124 | 1.77 | 0 | 24.39 | −2 | 3 | 5 |
| S2129 | 5.05 | 447 | 69.49 | 539 | 9.15 | 586 |
| S2130 | 5.21 | 437 | 85.07 | 646 | 13.52 | 930 |
| S2131 | 5.08 | 439 | 90.2 | 589 | 17.24 | 1125 |
| S2132 | 4.75 | 445 | 93.46 | 701 | 14.03 | 754 |
| S2133 | 4.07 | 385 | 105.82 | 906 | 11.74 | 604 |
| S2134 | 4.4 | 375 | 106.43 | 838 | 10.54 | 557 |
| S2135 | 4.94 | 349 | 118.45 | 869 | 9.8 | 560 |
| S2136 | 5.98 | 453 | 111.16 | 824 | 8 | 525 |
| S2137 | 4.89 | 369 | 106.6 | 895 | 6.88 | 439 |
| S2138 | 5.44 | 372 | 107.74 | 731 | 7.56 | 481 |
| S2139 | 5.27 | 297 | 129.84 | 1079 | 7.6 | 465 |
| S2140 | 5.81 | 470 | 115.27 | 896 | 8.34 | 318 |
| S2141 | 5.62 | 233 | 116.89 | 795 | 7.56 | 271 |
| S2142 | 7.32 | 331 | 108.93 | 718 | 7.72 | 441 |
| S2143 | 7.08 | 242 | 127.94 | 939 | 8.15 | 488 |
| S2144 | 7.27 | 205 | 112.59 | 697 | 6.74 | 534 |
| S2145 | 7.17 | 190 | 113.63 | 757 | 6.54 | 391 |
| S2147 | 6.34 | 69 | 114.33 | 723 | 6.87 | 409 |
| S2149 | 7.2 | 104 | 106.95 | 688 | 8.11 | 419 |
| S2151 | 8.19 | 137 | 125.93 | 959 | 7.37 | 463 |
| S2153 | 9.19 | 181 | 149.67 | 1269 | 6.17 | 361 |
| S2155 | 9.67 | 202 | 99.34 | 657 | 6.01 | 461 |
| S2157 | 11.52 | 309 | 125.83 | 985 | 7.64 | 410 |
| S2159 | 8.97 | 173 | 132.54 | 1221 | 8.27 | 464 |
| S2161 | 8.23 | 153 | 133.4 | 1105 | 8.82 | 687 |
| S2163 | 10.81 | 330 | 120.44 | 1080 | 7.16 | 417 |
| S2165 | 9.36 | 284 | 135.84 | 1298 | 11.77 | 1005 |
| S2167 | 9.11 | 331 | 114.37 | 1007 | 9.59 | 655 |
| S2169 | 13.45 | 726 | 120.02 | 849 | 10.5 | 789 |
| S2173 | 7.7 | 339 | 156.37 | 1505 | 9.47 | 521 |
| S2176 | 4.34 | 111 | 139.01 | 1162 | 10.53 | 640 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cipta, A.; Cummins, P.; Irsyam, M.; Hidayati, S. Basin Resonance and Seismic Hazard in Jakarta, Indonesia. Geosciences 2018, 8, 128. https://doi.org/10.3390/geosciences8040128
Cipta A, Cummins P, Irsyam M, Hidayati S. Basin Resonance and Seismic Hazard in Jakarta, Indonesia. Geosciences. 2018; 8(4):128. https://doi.org/10.3390/geosciences8040128
Chicago/Turabian StyleCipta, Athanasius, Phil Cummins, Masyhur Irsyam, and Sri Hidayati. 2018. "Basin Resonance and Seismic Hazard in Jakarta, Indonesia" Geosciences 8, no. 4: 128. https://doi.org/10.3390/geosciences8040128
APA StyleCipta, A., Cummins, P., Irsyam, M., & Hidayati, S. (2018). Basin Resonance and Seismic Hazard in Jakarta, Indonesia. Geosciences, 8(4), 128. https://doi.org/10.3390/geosciences8040128






