A Calorimetric and Thermodynamic Investigation of the Synthetic Analogue of Mandarinoite, Fe2(SeO3)3·5H2O
Abstract
:1. Introduction
2. Experimental Methods
2.1. Sample Preparation
2.2. Calorimetric Methods
3. Results
3.1. Sample Characterization
3.2. Enthalpy of Formation
3.3. Heat-Capacity Behavior
4. Discussion
4.1. The Gibbs Energy of Formation
4.2. Stability of Mandarinoite in the Oxidation Zone
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Charykova, M.V.; Krivovichev, V.G. Mineral systems and the thermodynamics of selenites and selenates in the oxidation zone of sulfide ores—A review. Mineral. Petrol. 2017, 111, 121–134. [Google Scholar] [CrossRef]
- Krivovichev, V.G.; Charykova, M.V.; Vishnevsky, A.V. The Thermodynamics of Selenium Minerals in Near-Surface Environments. Minerals 2017, 7, 188. [Google Scholar] [CrossRef]
- Charykova, M.V.; Krivovichev, V.G.; Lelet, M.I.; Yakovenko, O.S.; Suleimanov, E.V.; Depmeier, W.; Semenova, V.V.; Zorina, M.L. A calorimetric and thermodynamic investigation of the synthetic analogues of cobaltomenite, CoSeO3∙2H2O, and ahlfeldite, NiSeO3∙2H2O. Am. Mineral. 2014, 99, 742–748. [Google Scholar] [CrossRef]
- Charykova, M.V.; Lelet, M.I.; Krivovichev, V.G.; Ivanova, N.M.; Suleimanov, E.V. A calorimetric and thermodynamic investigation of the synthetic analogue of chalcomenite, CuSeO3·2H2O. Eur. J. Mineral. 2017, 29, 269–277. [Google Scholar] [CrossRef]
- Lelet, M.I.; Charykova, M.V.; Krivovichev, V.G.; Efimenko, N.M.; Platonova, N.V.; Suleimanov, E.V. A Calorimetric and Thermodynamic Investigation of Zinc and Cadmium Hydrous Selenites. J. Chem. Thermodyn. 2017, 115, 63–73. [Google Scholar] [CrossRef]
- Dunn, P.J.; Pecker, D.R.; Sturman, B.D. Mandarinoite—New ferric-iron selenite from Bolivia. Can. Mineral. 1978, 16, 605–609. [Google Scholar]
- Hawthorne, F.C. The crystal structure of mandarinoite, Fe3+2Se3O9·6H2O. Can. Mineral. 1984, 22, 475–480. [Google Scholar]
- Holzheid, A.; Charykova, M.V.; Krivovichev, V.G.; Ledwig, B.; Fokina, E.L.; Poroshina, K.L.; Platonova, N.V.; Gurzhiy, V.V. Thermal behavior of ferric selenite hydrates (Fe2(SeO3)3·3H2O, Fe2(SeO3)3·5H2O) and the water content in the natural ferric selenite mandarinoite. Chem. Erde 2018, 78, 228–240. [Google Scholar] [CrossRef]
- Séby, F.; Potin-Cautier, M.; Giffaut, E.; Borge, G.; Donard, O.F.X. A critical review of thermodynamic data for selenium species at 25 °C. Chem. Geol. 2001, 171, 173–194. [Google Scholar] [CrossRef]
- Olin, A.; Nolang, B.; Osadchii, E.G.; Ohman, L.-O.; Rosen, E. Chemical Thermodynamics of Selenium; Elsevier: Amsterdam, The Nertherlands, 2005; 851p. [Google Scholar]
- Charykova, M.V.; Krivovichev, V.G.; Depmeier, W. Thermodynamics of arsenates, selenites and sulphates in oxidising zone of sulphides ore deposits. Part I: Thermodynamic properties at standard conditions. Geol. Ore Depos. 2010, 52, 759–770. [Google Scholar] [CrossRef]
- Chukhlantsev, V.G.; Tomashevsky, G.P. The Solubility of Selenites of Certain Metals. Zh. Anal. Khim. 1957, 12, 296–301. (In Russian) [Google Scholar]
- Rai, D.; Felmy, A.R.; Moore, D.A. The solubility product of crystalline ferric selenite hexahydrate and the complexation constant of FeSeO3+. J. Sol. Chem. 1995, 24, 735–752. [Google Scholar] [CrossRef]
- Krivovichev, V.G.; Charykova, M.V.; Yakovenko, O.S.; Depmeier, W. Thermodynamics of Arsenates, Selenites, and Sulfates in the Oxidation Zone of Sulfide Ores. IV. Eh–pH Diagrams of the Me–Se–H2O Systems (Me = Co, Ni, Fe, Cu, Zn, Pb) at 25 °C. Geol. Ore Depos. 2011, 53, 514–527. [Google Scholar] [CrossRef]
- Giester, G.; Pertlik, F.; Brandstätter, F. A revision of the formula Fe2(SeO3)3 6H2O to Fe2(SeO3) 3H2O. Mater. Res. Bull. 1996, 31, 1189–1193. [Google Scholar] [CrossRef]
- Rai, D.; Mattigod, S.; Moore, D. Characterization of Fe2(SeO3)3·6H2O, a new synthetic ferric selenite. Mater. Res. Bull. 1988, 23, 1621. [Google Scholar] [CrossRef]
- Furukawa, G.T.; McCoskey, R.E.; King, G.J. Calorimetric Properties of Benzoic Acid from 0 to 410. J. Res. Natl. Bur. Stand. 1951, 47, 256–261. [Google Scholar] [CrossRef]
- Ditmars, D.A.; Ishihara, S.; Chang, S.S.; Bernstein, G. Enthalpy and Heat-Capacity Standard Reference Material: Synthetic Sapphire (α-Al2O3) from 10 to 2250 K. J. Res. Natl. Bur. Stand. 1982, 87, 159–163. [Google Scholar] [CrossRef]
- Varushchenko, R.M.; Druzhinina, A.I.; Sorkin, E.L. Low-temperature heat capacity of 1-bromoperfluorooctane. J. Chem. Thermodyn. 1997, 29, 623–637. [Google Scholar] [CrossRef]
- Lelet, M.I.; Sharkov, V.V.; Nurgaliev, I.F.; Suleymanov, Y.V. A new hardware solution in reaction calorimetry. Vestn. Nizhny Novgorod State Univ. 2011, 3, 97–101. [Google Scholar]
- Glushko, V.P. (Ed.) Thermal Constants of Compounds; Academy of Science, SSSR: Moscow, Russia, 1965–1982; Volume 1–10. (In Russian) [Google Scholar]
- Melnikov, P.; Nascimento, V.A.; Arkhangelsky, I.V.; Zanoni Consolo, L.Z.; de Oliveira, L.C.S. Thermal decomposition mechanism of iron(III) nitrate and characterization of intermediate products by computerized modeling. J. Therm. Anal. Cal. 2014, 115, 145–151. [Google Scholar] [CrossRef]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I.; Bailey, S.M.; Churney, K.L.; Nuttall, R.L. The NBS tables of chemical thermodynamic properties: Selected values for inorganic and C1 and C2 organic substances in (SI) units. J. Phys. Chem. Ref. Data 1982, 11 (Suppl. 2), 1–392. [Google Scholar]
- Dachs, E.; Geiger, C.A. Heat capacities and vibrational entropies of mixing of pyrope-grossular (Mg3Al2Si3O12-Ca3Al2Si3O12) garnet solid solutions: A low temperature calorimetric and thermodynamic investigation. Am. Mineral. 2006, 91, 894–906. [Google Scholar] [CrossRef]
- Grundmann, G.; Förster, H.-J. Origin of the El Dragón Selenium Mineralization, Quijarro Province, Potosí, Bolivia. Minerals 2017, 7, 68. [Google Scholar] [CrossRef]
- Campostrini, I.; Gramaccioli, C.M. Selenium-rich secondary minerals from the Baccu Locci mine (Sardinia, Italy). Neues Jahrb. Mineral. Abh. 2001, 177, 37–59. [Google Scholar] [CrossRef]
- Charykova, M.V.; Krivovichev, V.G.; Ivanova, N.M.; Semenova, V.V. Thermodynamics of Arsenates, Selenites, and Sulfates in the Oxidation Zone of Sulfide Ores. XI. Solubility of Synthetic Chalcomenite Analog and Zinc Selenite at 25 °C. Geol. Ore Depos. 2015, 57, 691–698. [Google Scholar] [CrossRef]
- Charykova, M.V.; Vishnevsky, A.V.; Krivovichev, V.G.; Fokina, E.L.; Ivanova, N.M.; Platonova, N.V.; Semenova, V.V. Thermodynamics of Arsenates, Selenites and Sulfates in the Oxidation Zone of Sulfide Ores. XII. Mineral Equilibria in the Cd–Se–H2O System at 25 °C. Geol Ore Depos. 2016, 58, 636–645. [Google Scholar] [CrossRef]

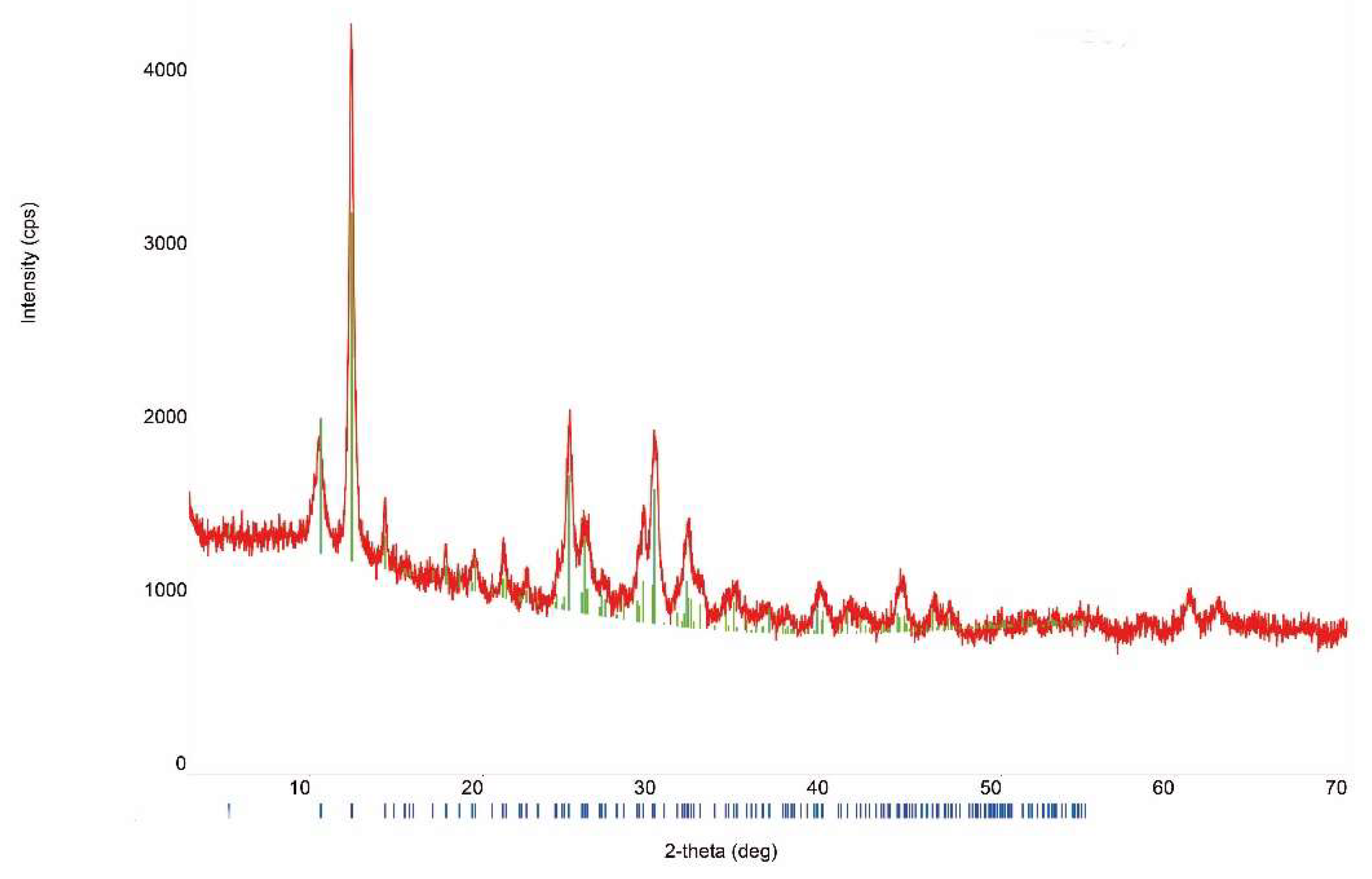
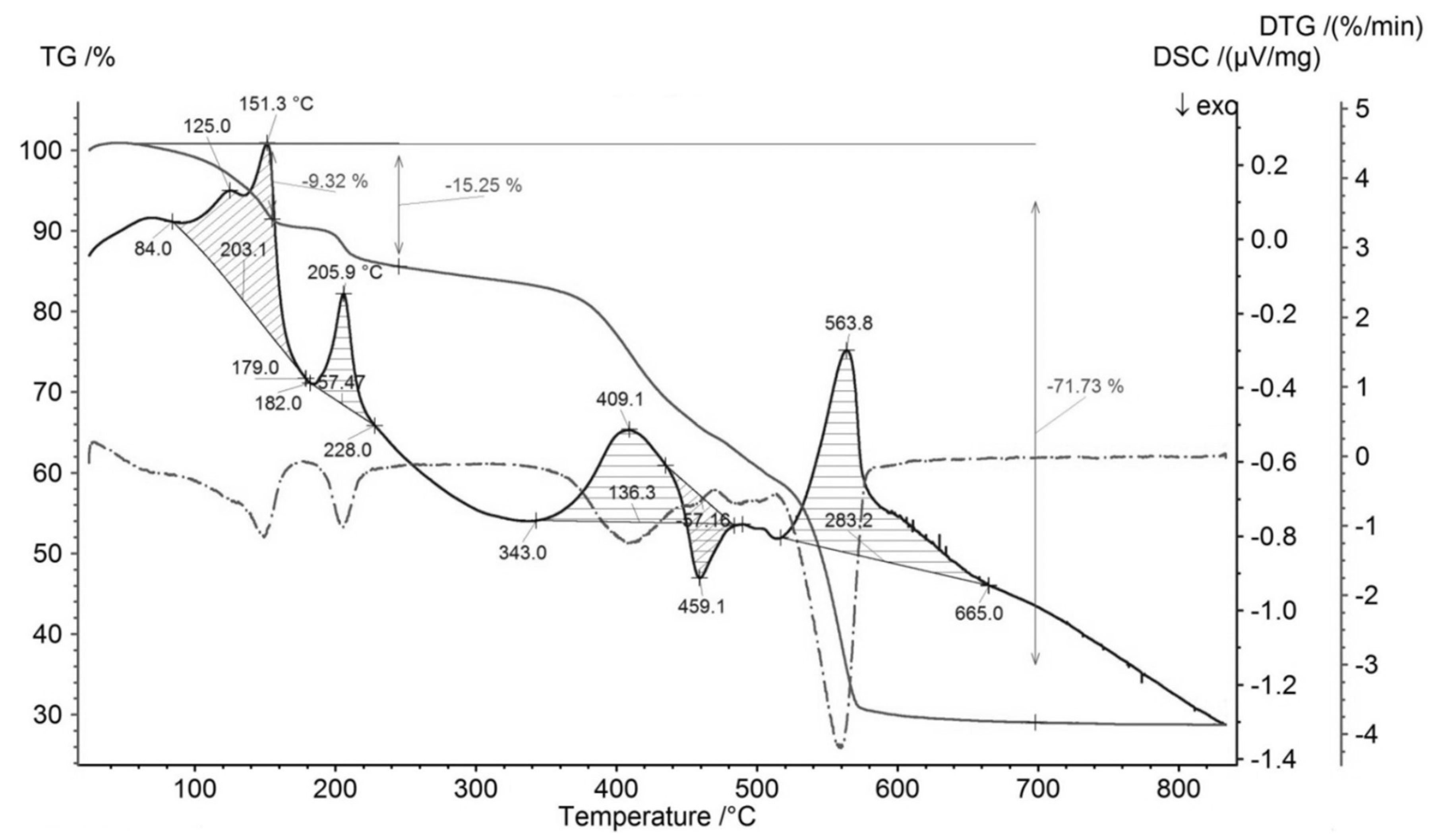

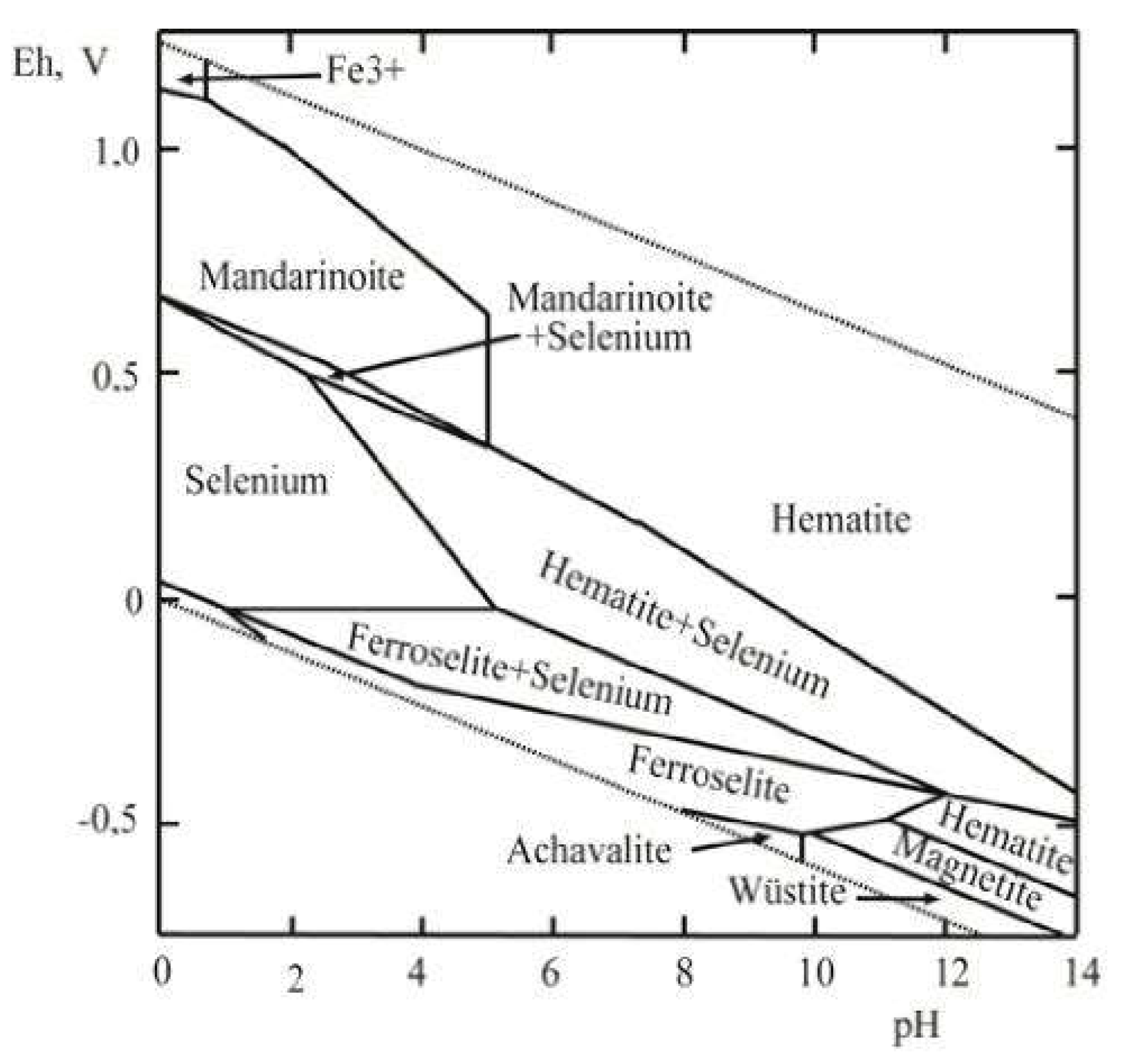

| Compound | Source | Initial Mass Fraction Purity | Purification Method | Final Mass Fraction Purity | Analysis Method |
|---|---|---|---|---|---|
| Selenium(IV) oxide | Alfa Aesar | 0.994 | None a | ||
| Iron(III) chloride·6H2O | Alfa Aesar | ≥0.97 | None a | ||
| Sodium selenate | Vecos | 0.998 | None a | ||
| Sodium nitrate | Vecos | 0.998 | None a | ||
| Iron(III) nitrate nonahydrate | Vecos | 0.998 | None a | ||
| Hydrofluoric acid (45%) | Halopolymer | 0.9999 | Nonea | ||
| Synthetic | 0.97 | XRD b, XRF bc |
| Cell Parameters | Mandarinoite Fe2(SeO3)3·4H2O | Mandarinoite Fe2(SeO3)3·6H2O | Synthetic Analogue of Mandarinoite #9 | Synthetic Analogue of Mandarinoite #16 |
|---|---|---|---|---|
| а, Å | 16.78(3) | 16.810(4) | 16.824(6) | 16.771(13) |
| b, Å | 7.86(1) | 7.880(2) | 7.849(3) | 7.825(5) |
| c, Å | 9.96(6) | 10.019(2) | 10.010(4) | 10.008(6) |
| β, 0 | 98.3(6) | 98.26(2) | 98.20(2) | 98.21(4) |
| V, Å3 | 1313(4) | 1308(2) | 1300(1) | |
| Source | [6] | [7] | [8] | This work |
| No. | Reaction | /kJ·mol−1 |
|---|---|---|
| (1) | + (HF solution) → (solution A1) | 33.52 33.56 32.54 33.00 32.28 Mean 32.98 ± 0.71 |
| (2) | + (solution A1) → (solution A2) | −131.25 −127.35 −123.09 −130.68 −134.25 Mean −129.32 ± 4.90 |
| (3) | + (HF solution) → (solution B1) | 5.16 5.43 5.66 5.24 Mean 5.37 ± 0.35 |
| (4) | + (solution B1) → (solution B2) | 110.10 108.60 108.60 109.50 106.56 Mean 108.67 ± 1.67 |
| (5) | + (solution B2) → (solution B3) | −9.23 −8.45 −10.14 −10.27 −8.71 −9.75 −10.01 −9.10 −9.49 −8.84 −8.84 Mean −9.35 ± 0.42 |
| Substance | /J·K−1·mol−1 |
|---|---|
| Fe, cr | 30.04 |
| Se, cr | 42.442 |
| O2, gas | 205.138 |
| H2, gas | 130.684 |
| T/K | ||||
|---|---|---|---|---|
| [0] | [0] | [0] | [0] | [0] |
| 5 | 0.319 | 0.0005 | 0.162 | 0.055 |
| 10 | 5.381 | 0.010 | 1.226 | 0.263 |
| 15 | 15.07 | 0.061 | 5.259 | 1.200 |
| 20 | 26.09 | 0.163 | 11.05 | 2.904 |
| 25 | 38.44 | 0.323 | 18.14 | 5.227 |
| 30 | 55.55 | 0.557 | 26.64 | 8.064 |
| 35 | 63.83 | 0.872 | 36.31 | 11.41 |
| 40 | 64.91 | 1.189 | 44.78 | 15.06 |
| 45 | 73.68 | 1.533 | 52.88 | 18.81 |
| 50 | 84.70 | 1.929 | 61.21 | 22.63 |
| 70 | 131.4 | 4.093 | 97.17 | 38.70 |
| 90 | 178.7 | 7.199 | 136.0 | 55.96 |
| 110 | 220.0 | 11.20 | 175.9 | 74.14 |
| 130 | 256.6 | 15.97 | 215.7 | 92.86 |
| 150 | 290.5 | 21.44 | 254.8 | 111.9 |
| 170 | 322.5 | 27.57 | 293.1 | 130.9 |
| 190 | 352.7 | 34.33 | 330.7 | 150.0 |
| 210 | 381.2 | 41.67 | 367.4 | 169.0 |
| 230 | 408.3 | 49.57 | 403.3 | 187.8 |
| 250 | 434.2 | 57.99 | 438.4 | 206.4 |
| 270 | 459.6 | 66.93 | 472.8 | 224.9 |
| 273.15 | 463.6 | 68.39 | 478.1 | 227.8 |
| 290 | 485.1 | 76.38 | 506.5 | 243.1 |
| 298.15 | 495.7 | 80.37 | 520.1 | 250.5 |
| 310 | 511.6 | 86.34 | 539.7 | 261.2 |
| 320 | 525.5 | 91.53 | 556.2 | 270.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lelet, M.I.; Charykova, M.V.; Holzheid, A.; Ledwig, B.; Krivovichev, V.G.; Suleimanov, E.V. A Calorimetric and Thermodynamic Investigation of the Synthetic Analogue of Mandarinoite, Fe2(SeO3)3·5H2O. Geosciences 2018, 8, 391. https://doi.org/10.3390/geosciences8110391
Lelet MI, Charykova MV, Holzheid A, Ledwig B, Krivovichev VG, Suleimanov EV. A Calorimetric and Thermodynamic Investigation of the Synthetic Analogue of Mandarinoite, Fe2(SeO3)3·5H2O. Geosciences. 2018; 8(11):391. https://doi.org/10.3390/geosciences8110391
Chicago/Turabian StyleLelet, Maxim I., Marina V. Charykova, Astrid Holzheid, Brendan Ledwig, Vladimir G. Krivovichev, and Evgeny V. Suleimanov. 2018. "A Calorimetric and Thermodynamic Investigation of the Synthetic Analogue of Mandarinoite, Fe2(SeO3)3·5H2O" Geosciences 8, no. 11: 391. https://doi.org/10.3390/geosciences8110391
APA StyleLelet, M. I., Charykova, M. V., Holzheid, A., Ledwig, B., Krivovichev, V. G., & Suleimanov, E. V. (2018). A Calorimetric and Thermodynamic Investigation of the Synthetic Analogue of Mandarinoite, Fe2(SeO3)3·5H2O. Geosciences, 8(11), 391. https://doi.org/10.3390/geosciences8110391





