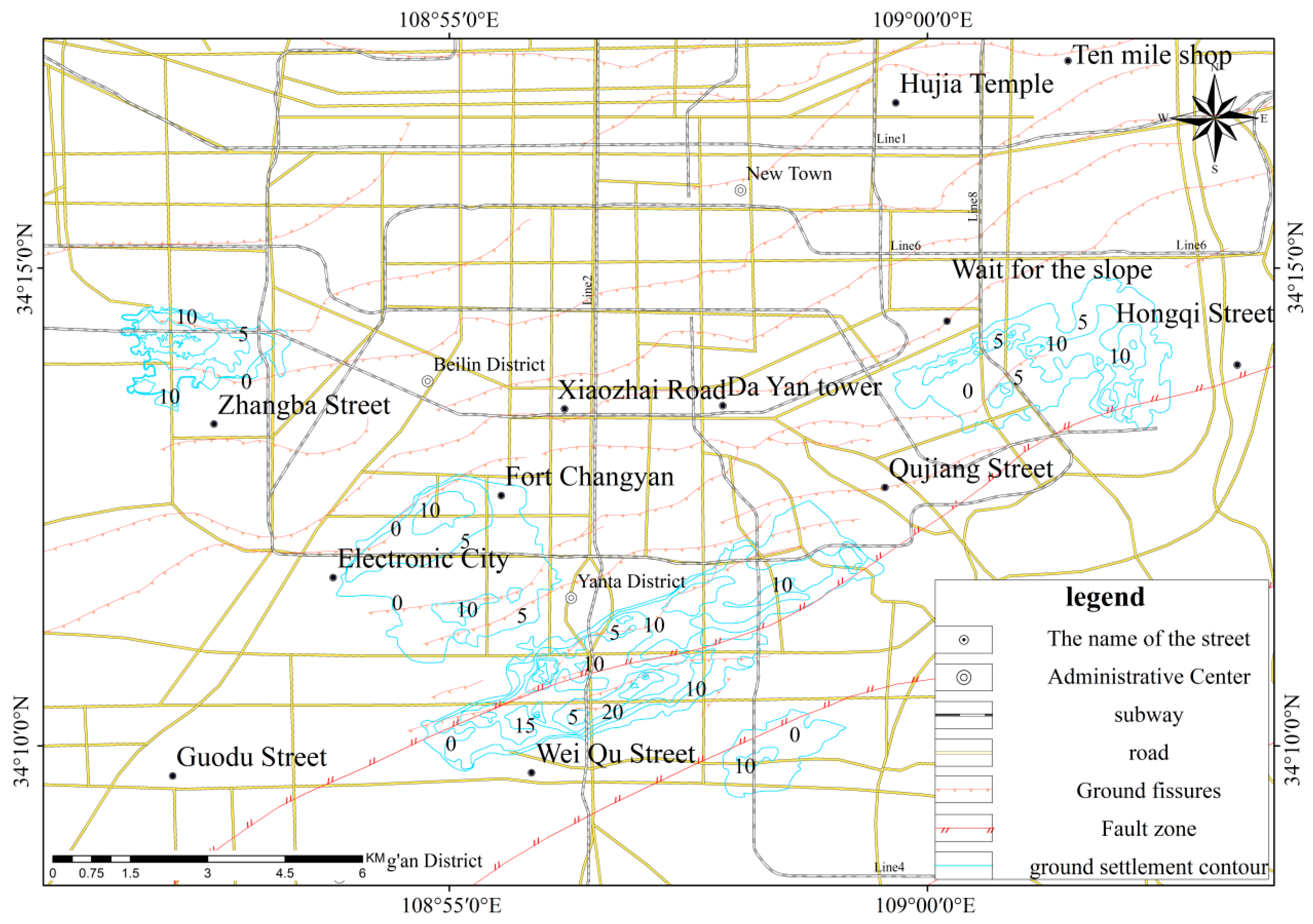
Figure 1.
The transportation location map of the study area.
Figure 1.
The transportation location map of the study area.
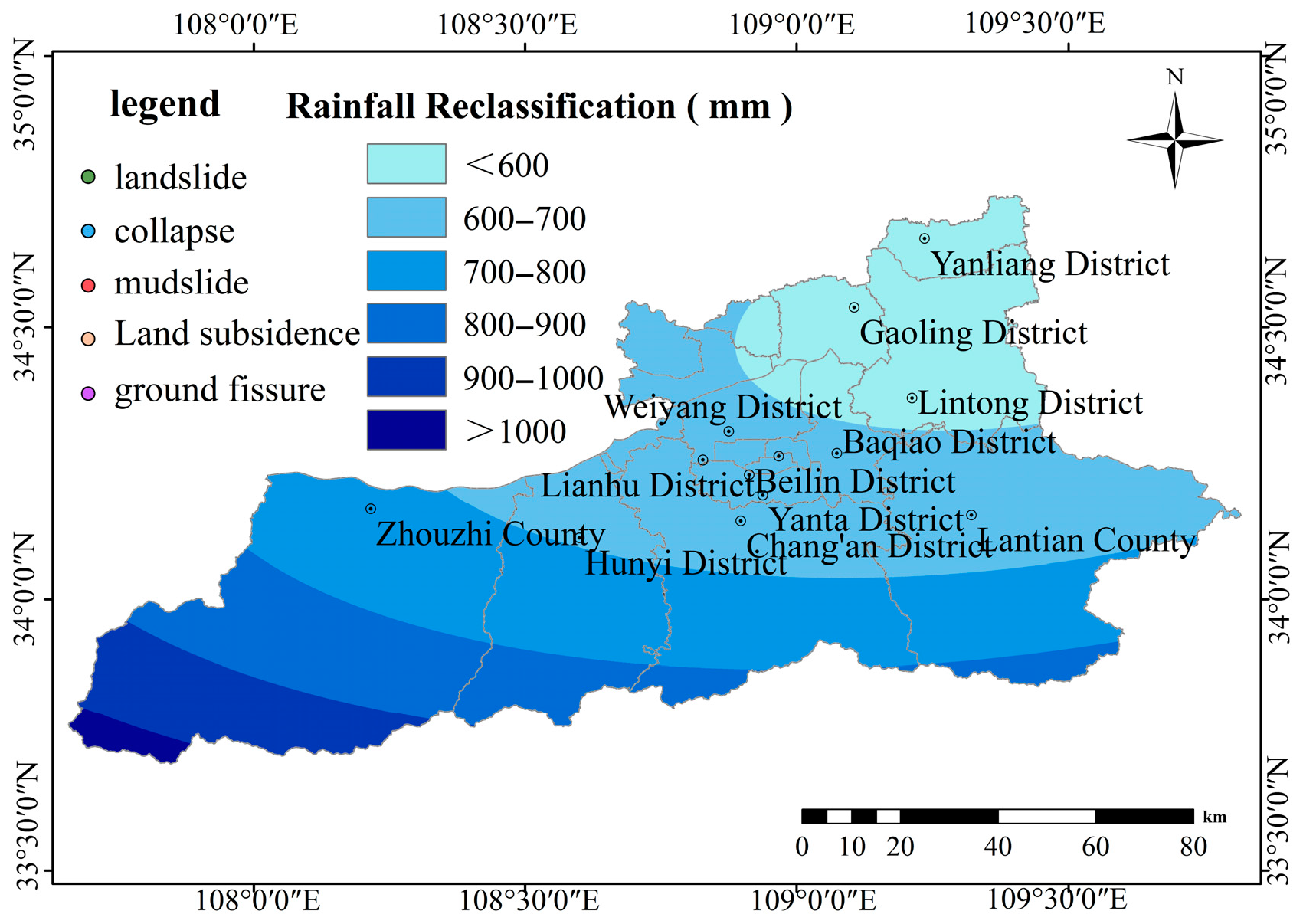
Figure 2.
The 2024 rainfall contour map of the study area.
Figure 2.
The 2024 rainfall contour map of the study area.
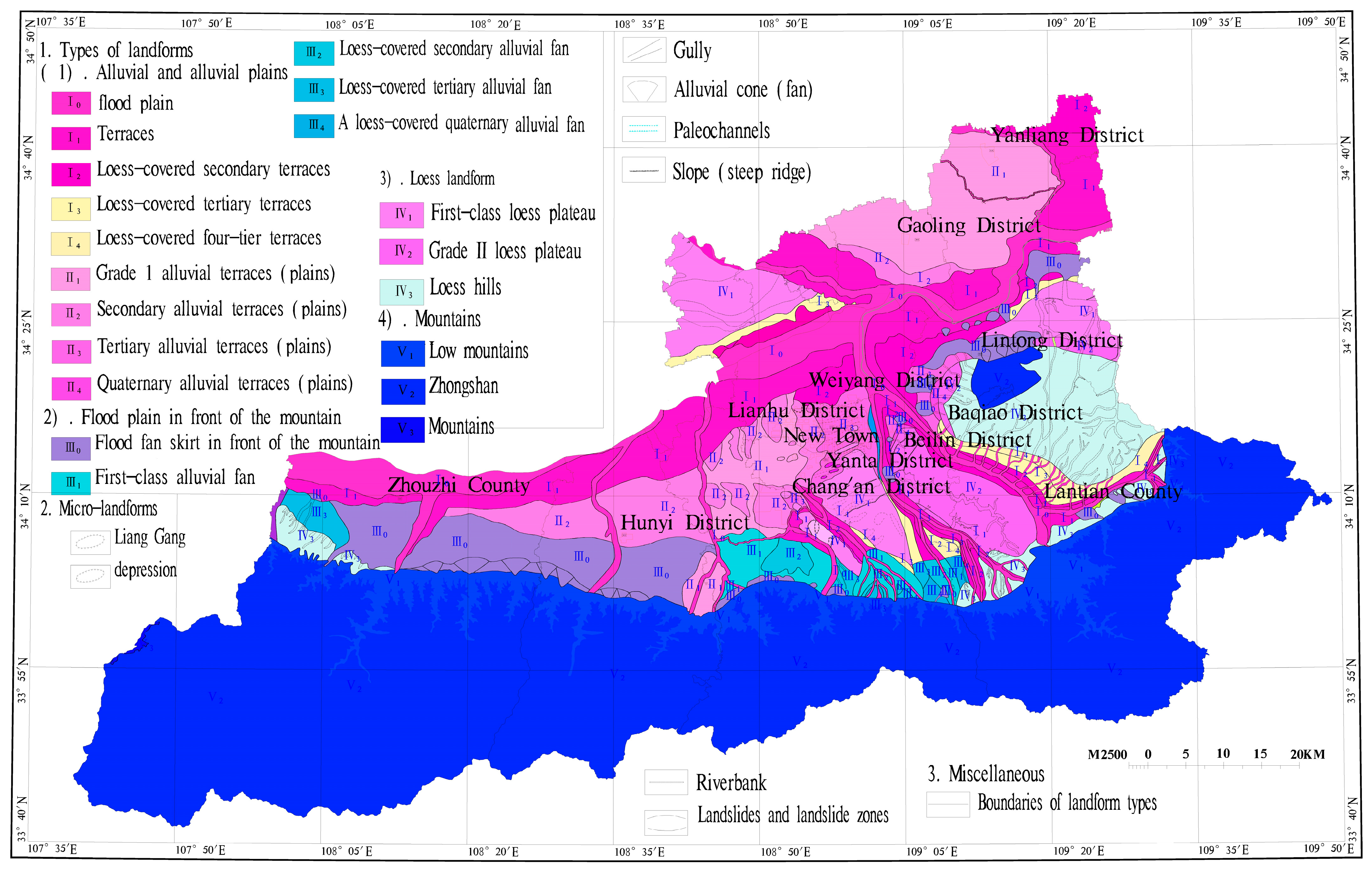
Figure 3.
A topographic and geomorphological map of the study area.
Figure 3.
A topographic and geomorphological map of the study area.
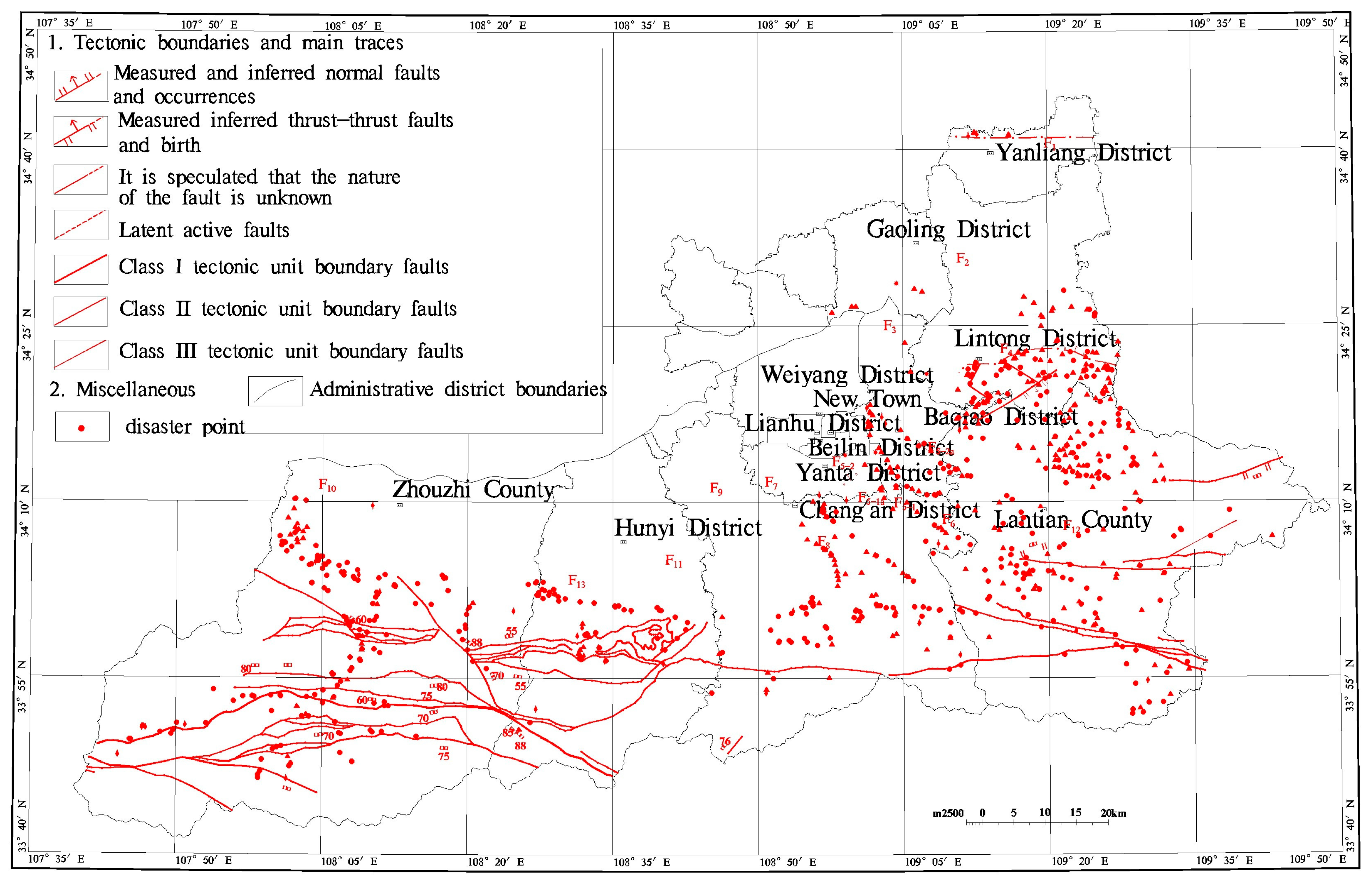
Figure 4.
A geological structure map of the study area.
Figure 4.
A geological structure map of the study area.
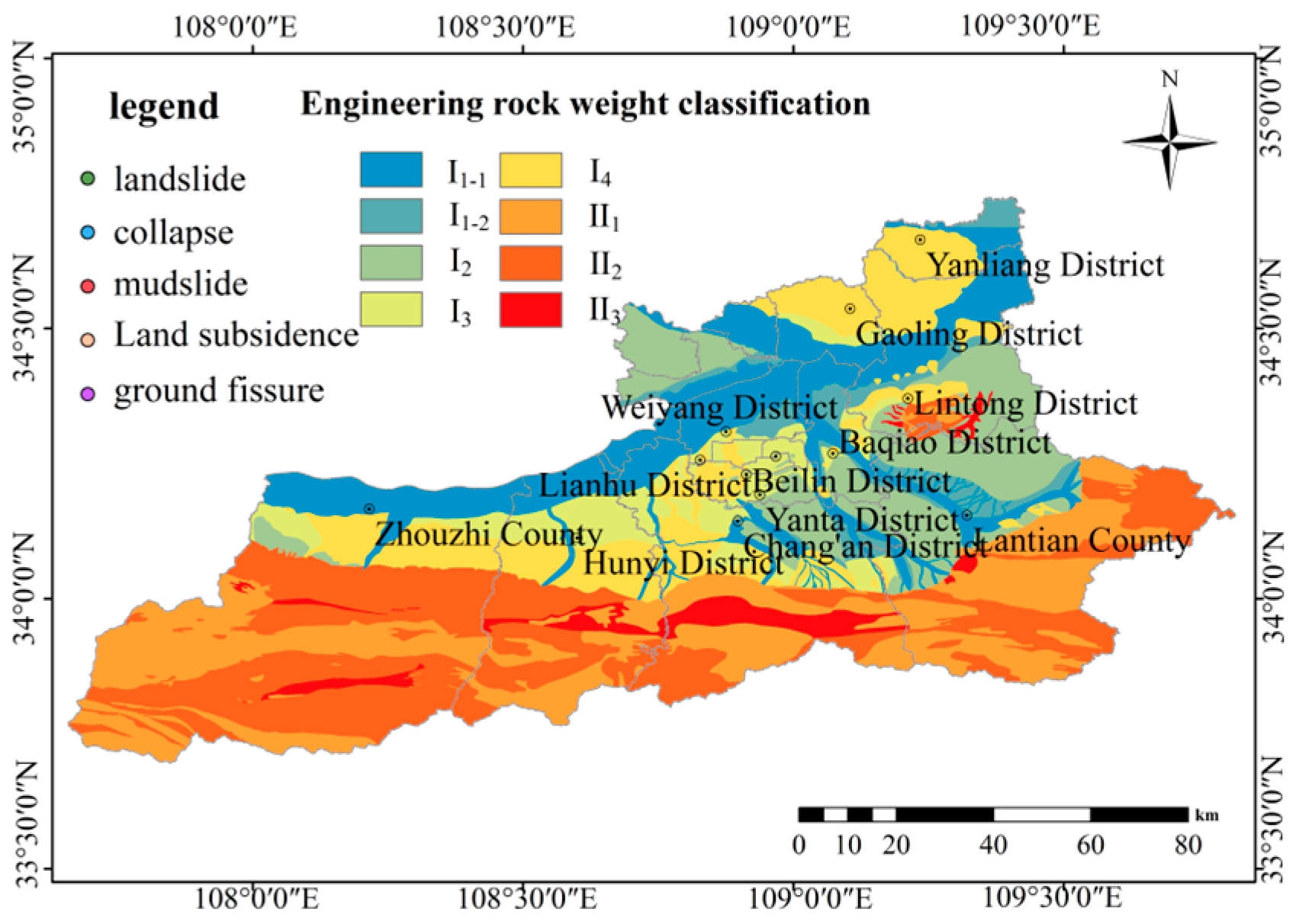
Figure 5.
An engineering geological map of the study area.
Figure 5.
An engineering geological map of the study area.
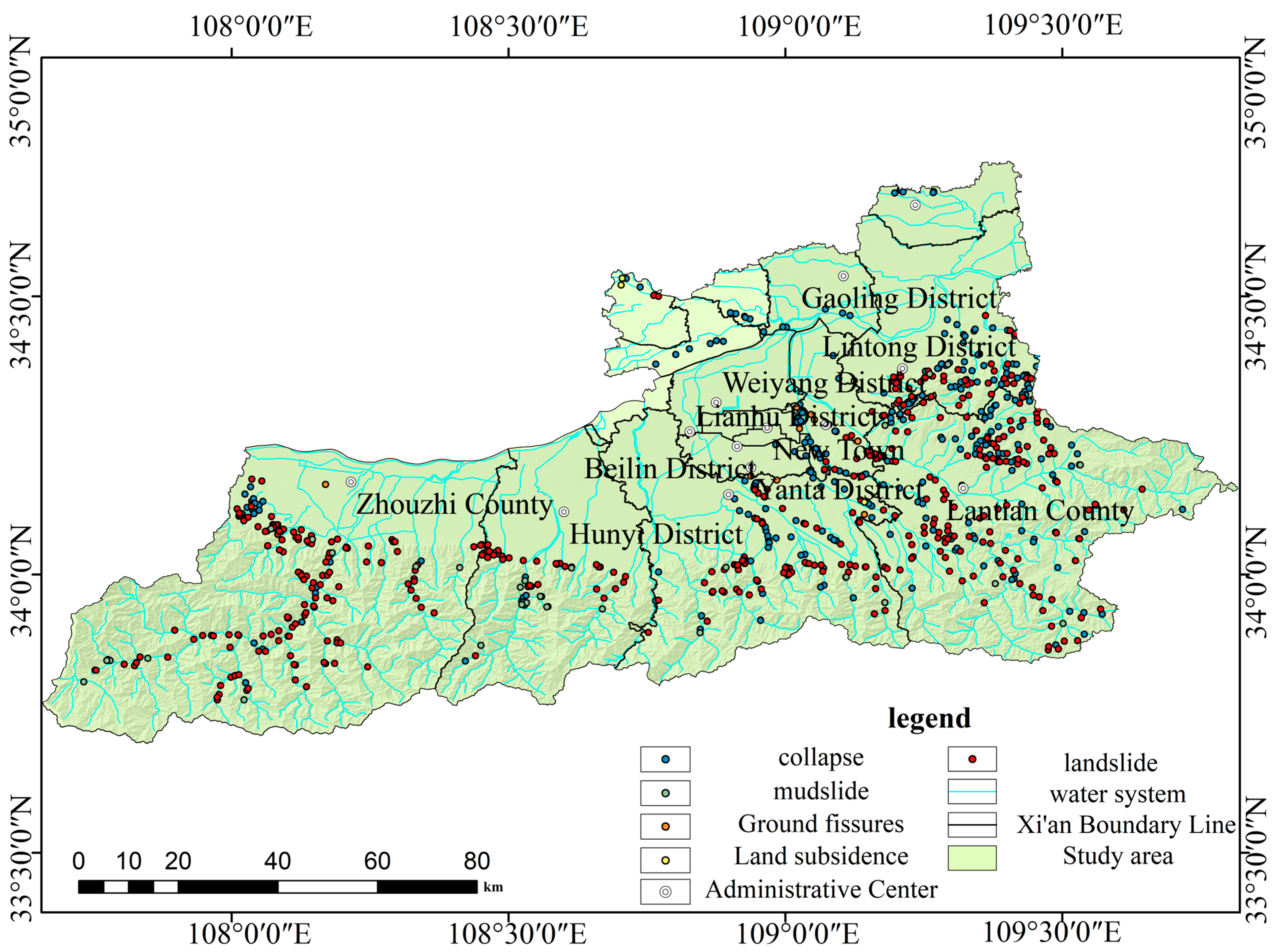
Figure 6.
The distribution map of geological hazard hidden danger points in the study area.
Figure 6.
The distribution map of geological hazard hidden danger points in the study area.
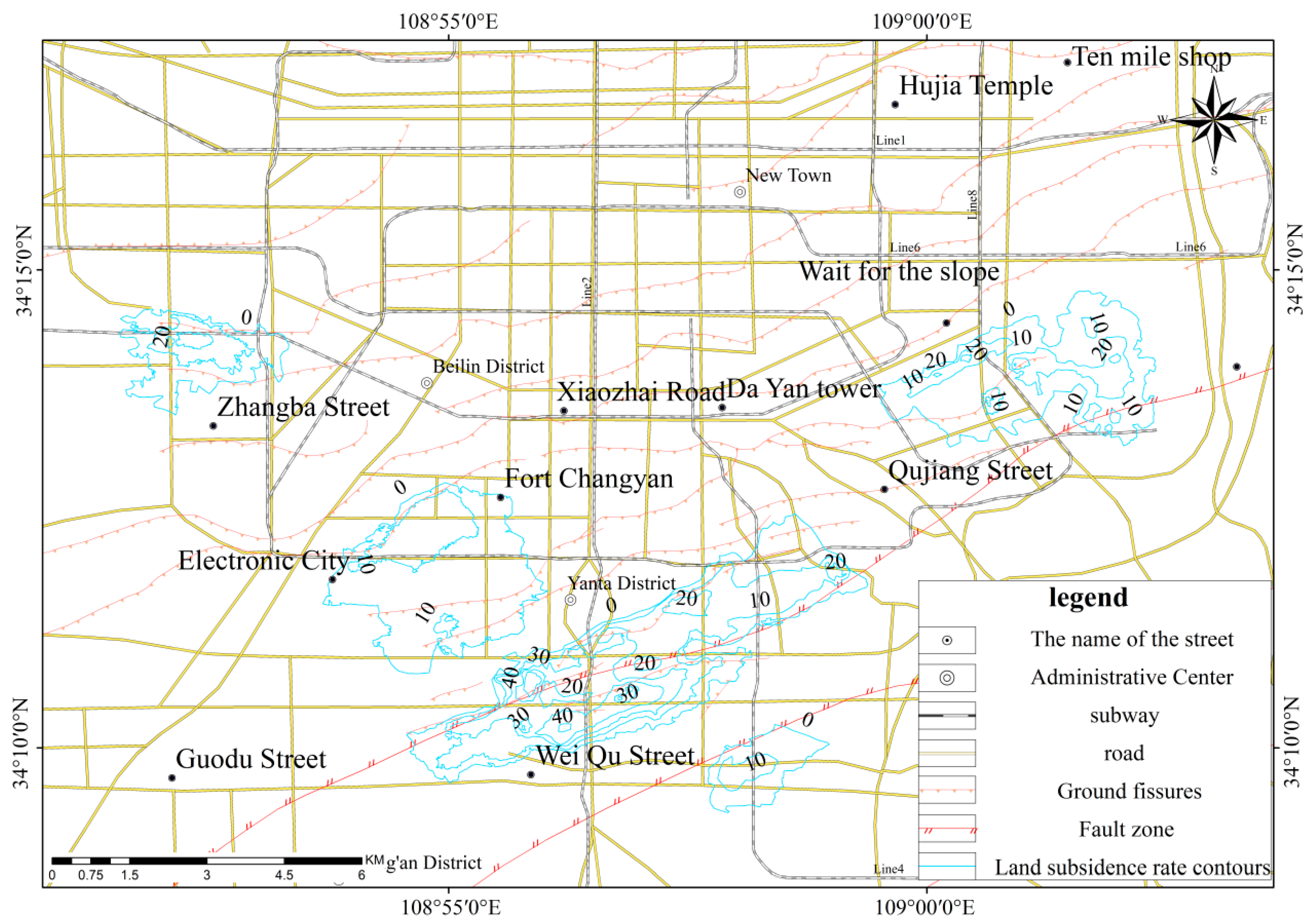
Figure 7.
The ground subsidence rate contour map of the study area.
Figure 7.
The ground subsidence rate contour map of the study area.
Figure 8.
The cumulative ground subsidence contour map of the study area.
Figure 8.
The cumulative ground subsidence contour map of the study area.
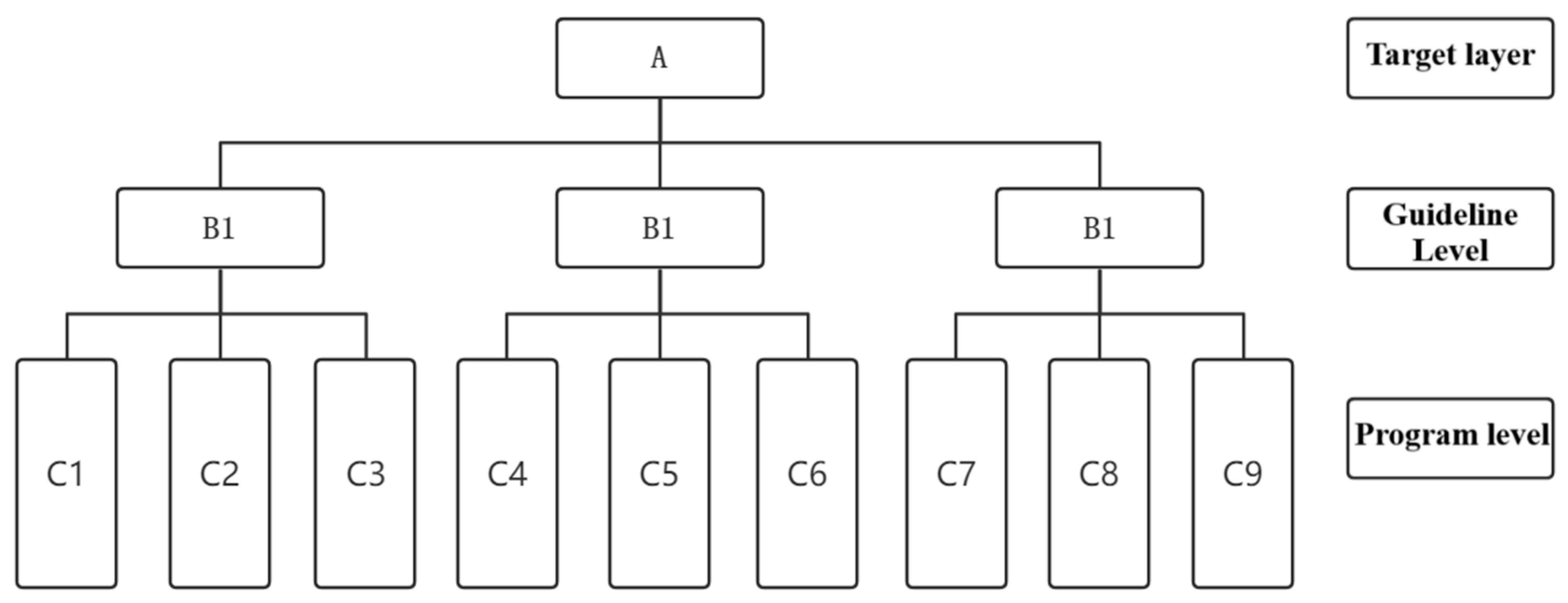
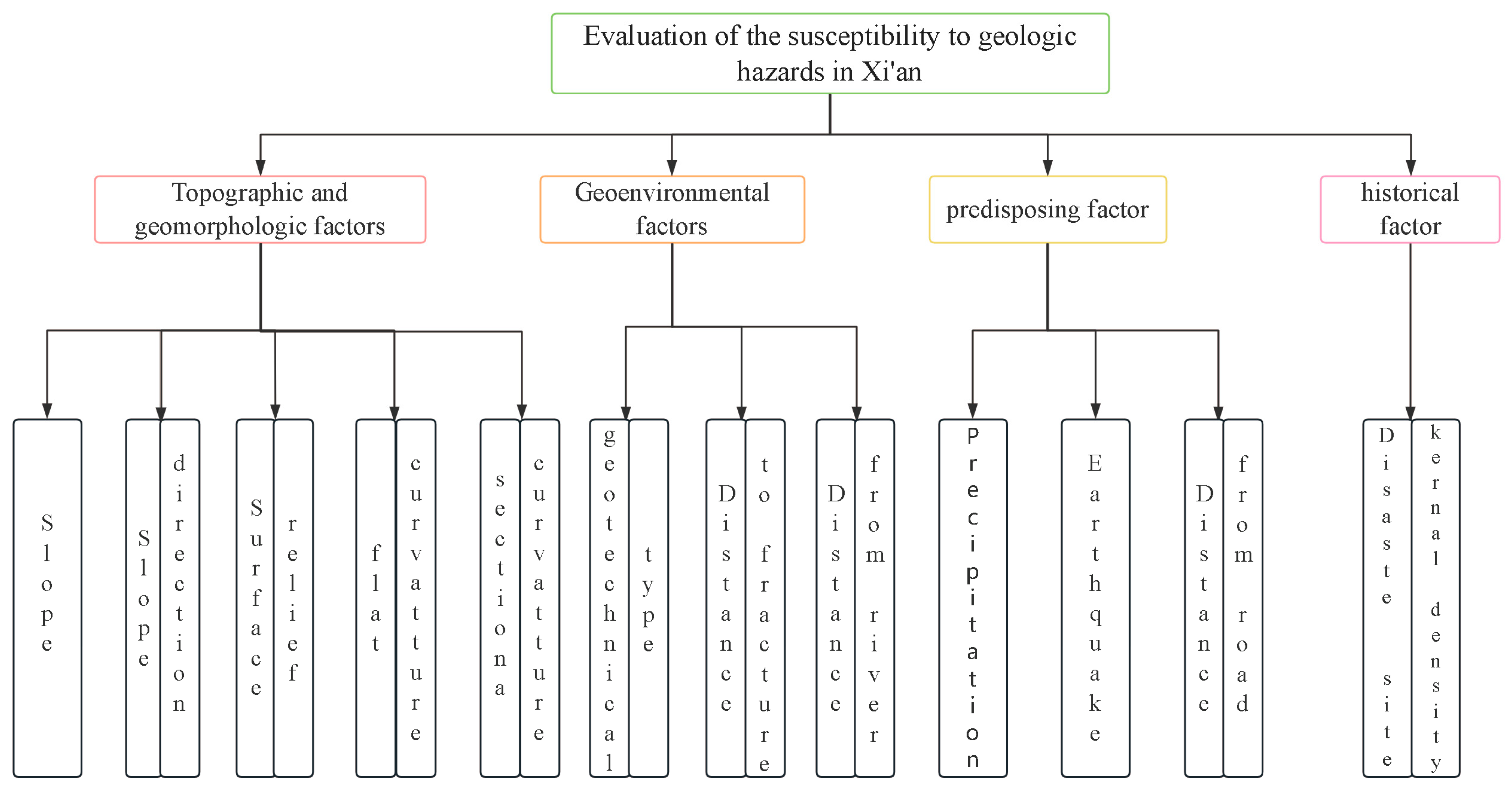
Figure 9.
A schematic diagram of the analytic hierarchy process model.
Figure 9.
A schematic diagram of the analytic hierarchy process model.
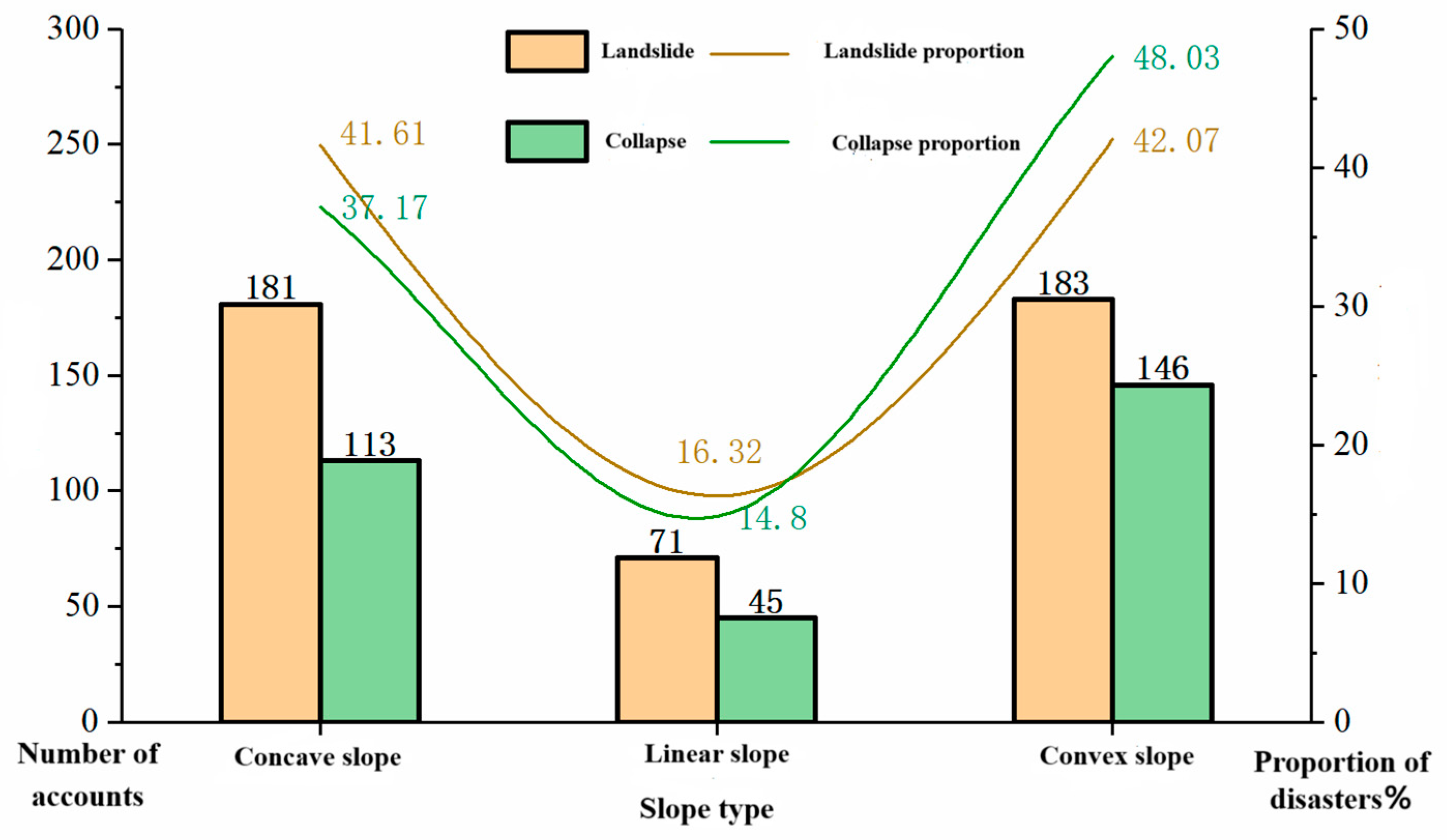
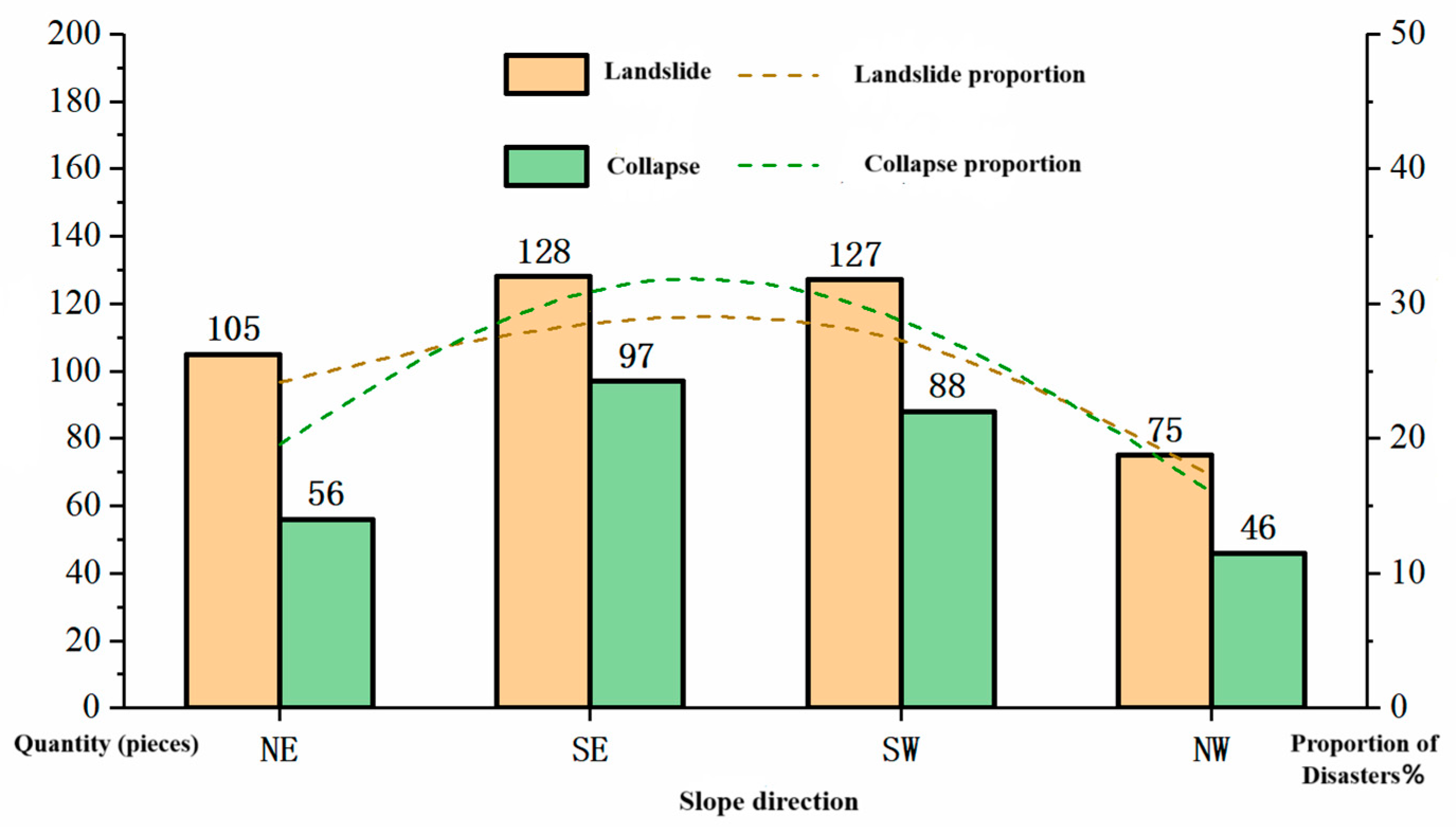
Figure 10.
A diagram of the relationship between the number of landslides and collapse hazards and slope profile types.
Figure 10.
A diagram of the relationship between the number of landslides and collapse hazards and slope profile types.
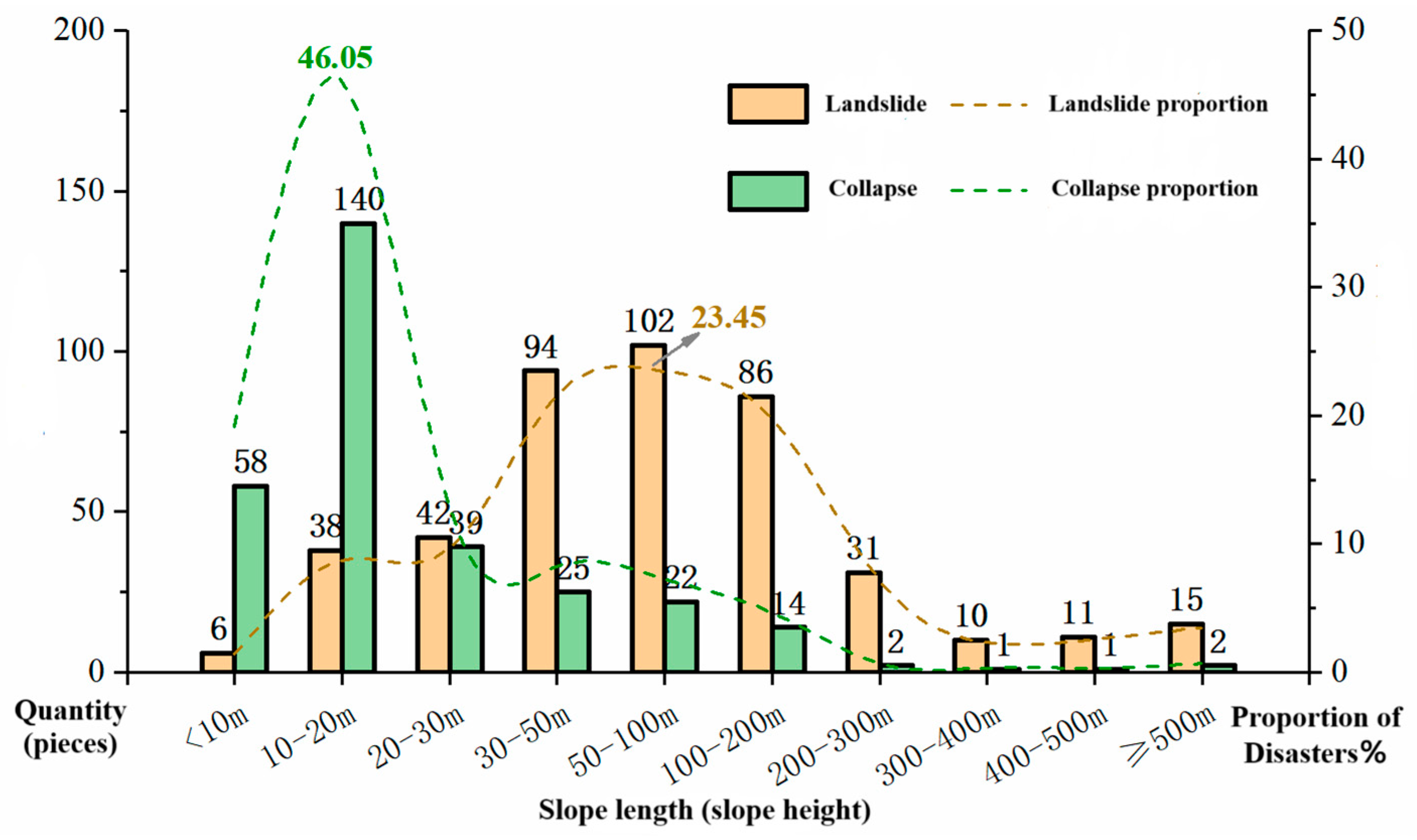
Figure 11.
A diagram of the relationship between the number of landslides and collapse hazards and slope length.
Figure 11.
A diagram of the relationship between the number of landslides and collapse hazards and slope length.
Figure 12.
A diagram of the relationship between the number of landslides and collapse hazards and slope aspect.
Figure 12.
A diagram of the relationship between the number of landslides and collapse hazards and slope aspect.
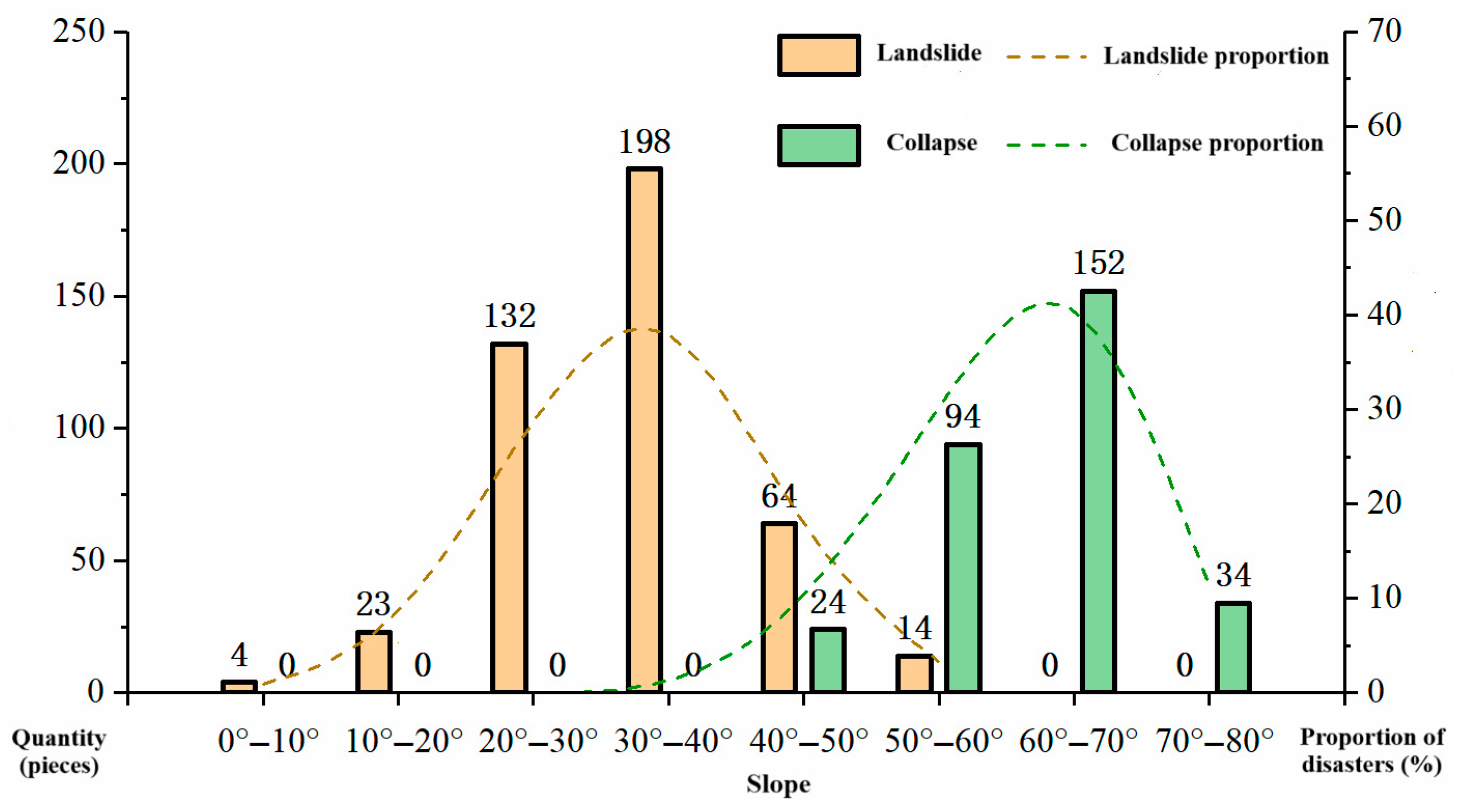
Figure 13.
A diagram of the relationship between the number of landslides and collapse hazards and slope gradient.
Figure 13.
A diagram of the relationship between the number of landslides and collapse hazards and slope gradient.
Figure 14.
A schematic diagram of the relationship between the geological structure and distribution of geological hazards.
Figure 14.
A schematic diagram of the relationship between the geological structure and distribution of geological hazards.
Figure 15.
Slope gradient classification map.
Figure 15.
Slope gradient classification map.
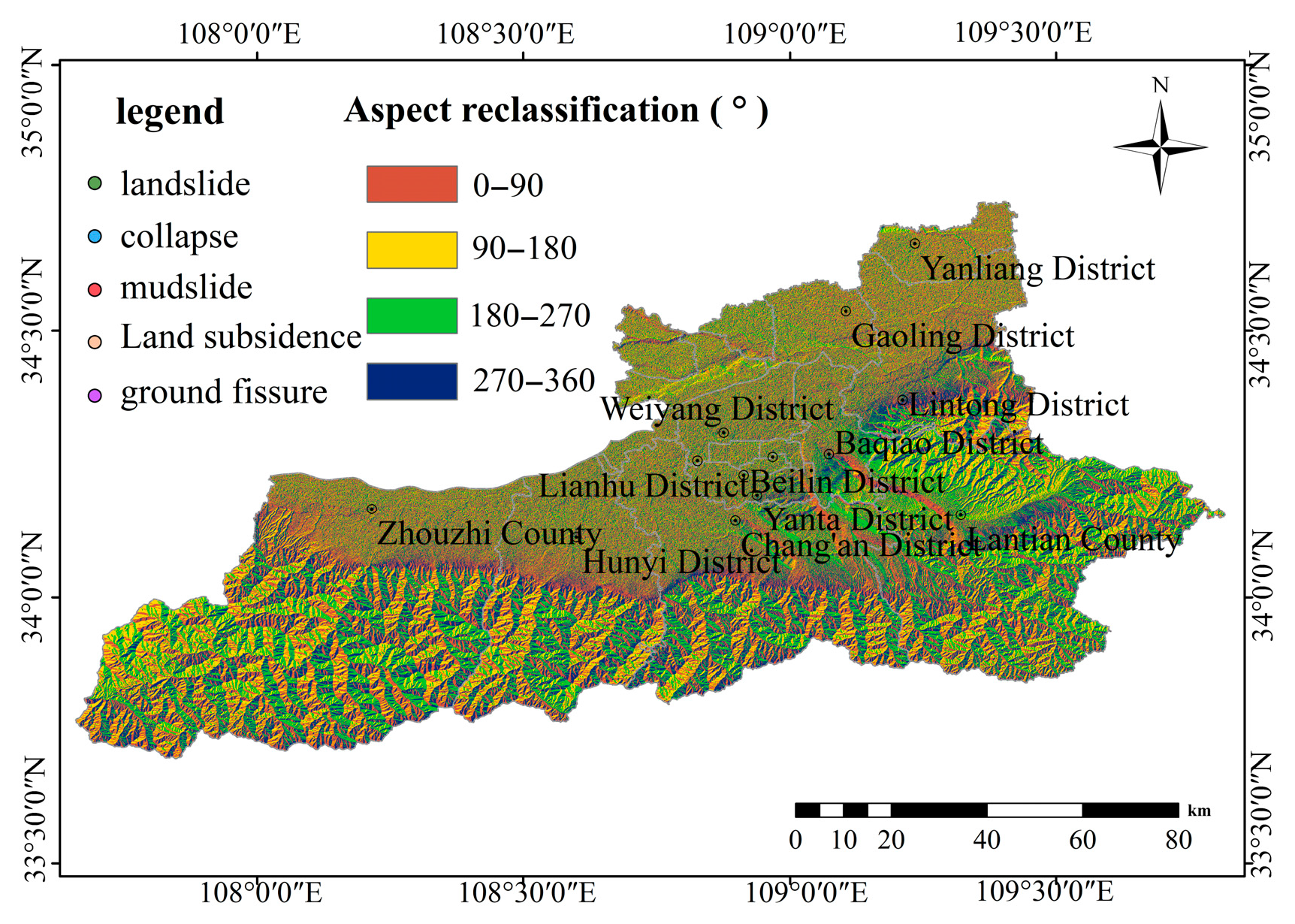
Figure 16.
Slope aspect classification map.
Figure 16.
Slope aspect classification map.
Figure 17.
Plan curvature classification map.
Figure 17.
Plan curvature classification map.
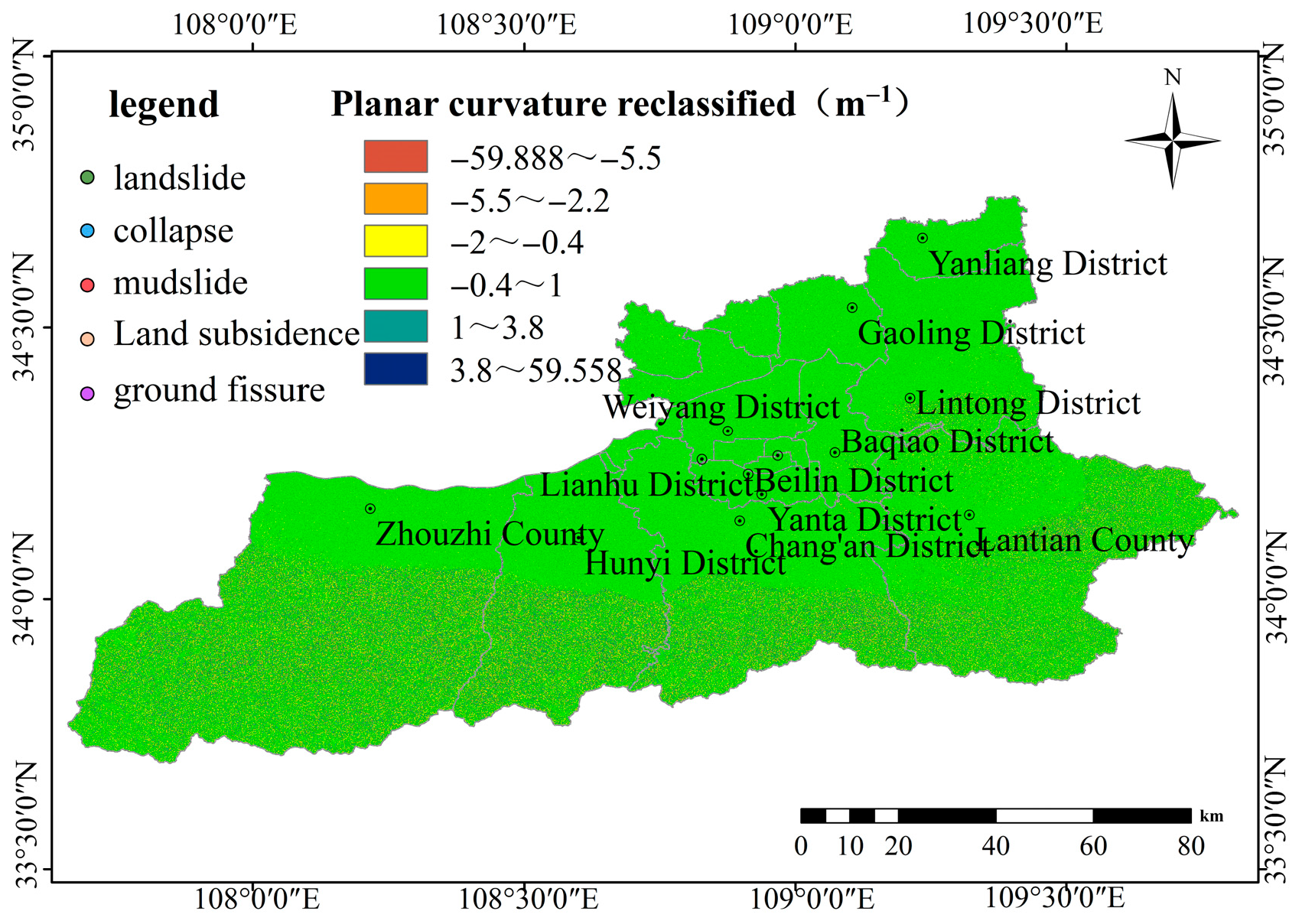
Figure 18.
Planar curvature classification map.
Figure 18.
Planar curvature classification map.
Figure 19.
Rock and soil mass type classification map.
Figure 19.
Rock and soil mass type classification map.
Figure 20.
Profile curvature classification map.
Figure 20.
Profile curvature classification map.
Figure 21.
Distance to fault classification map.
Figure 21.
Distance to fault classification map.
Figure 22.
Distance to drainage system classification map.
Figure 22.
Distance to drainage system classification map.
Figure 23.
Rainfall classification map.
Figure 23.
Rainfall classification map.
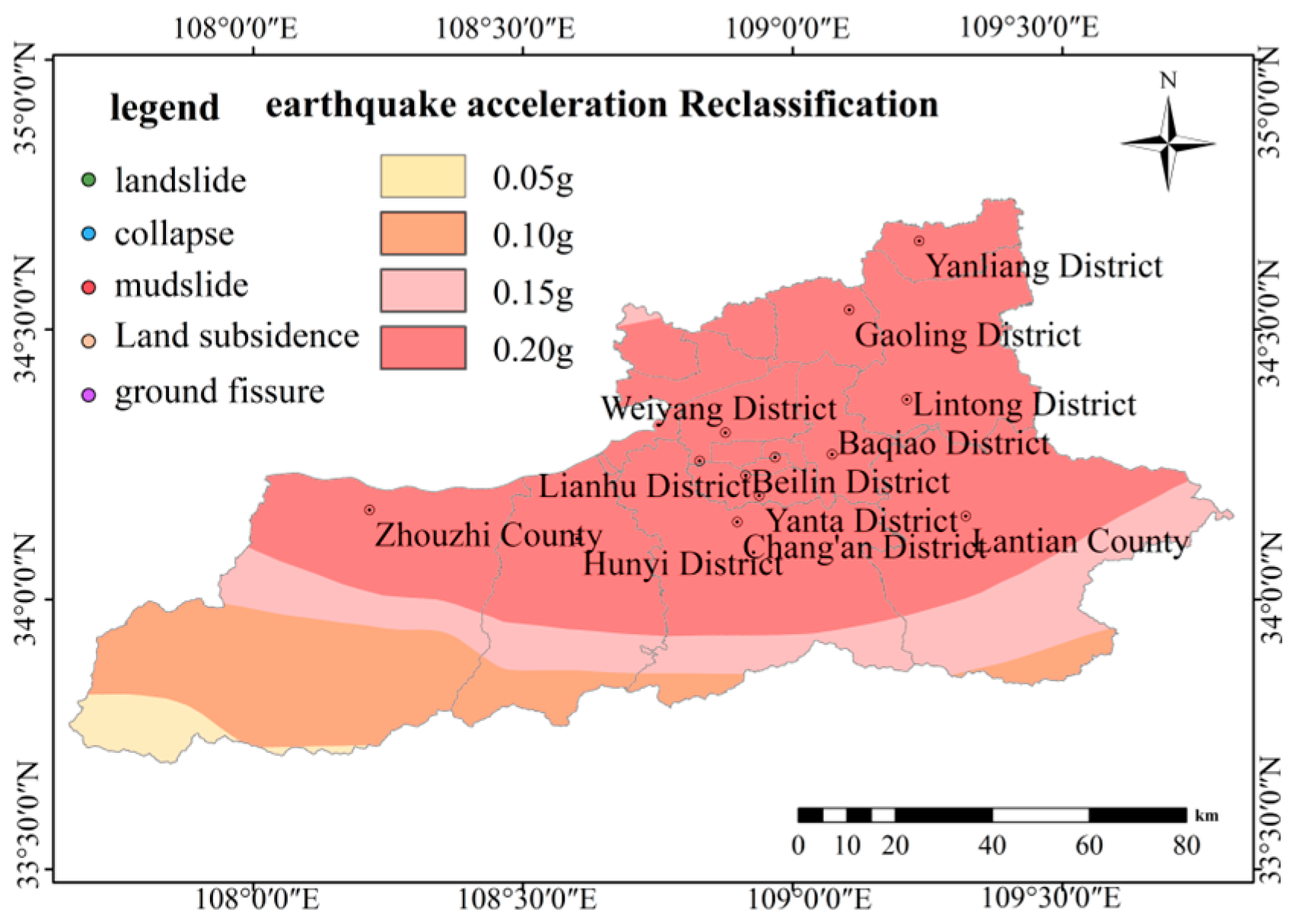
Figure 24.
Seismic acceleration classification map.
Figure 24.
Seismic acceleration classification map.
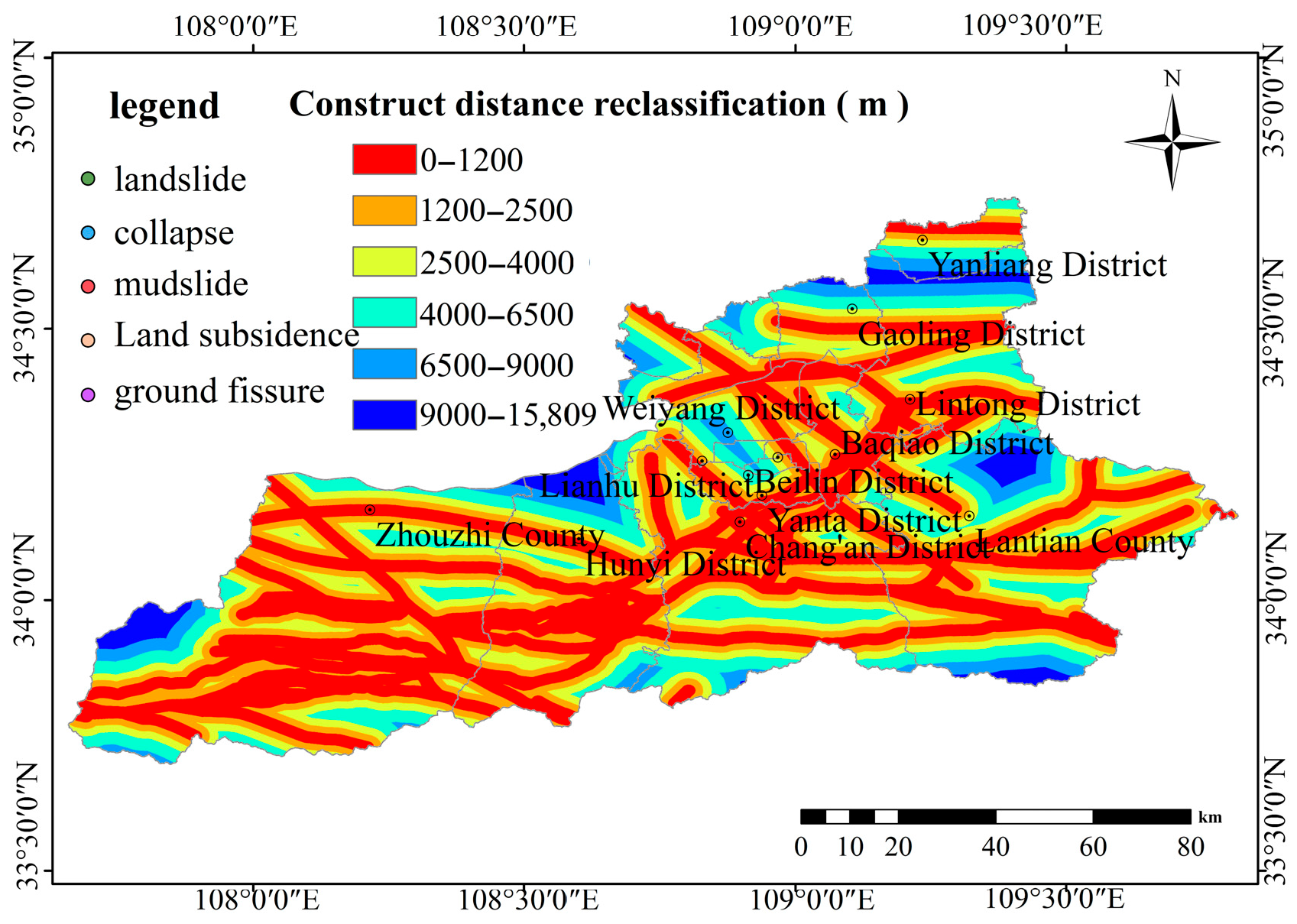
Figure 25.
Distance to road classification map.
Figure 25.
Distance to road classification map.
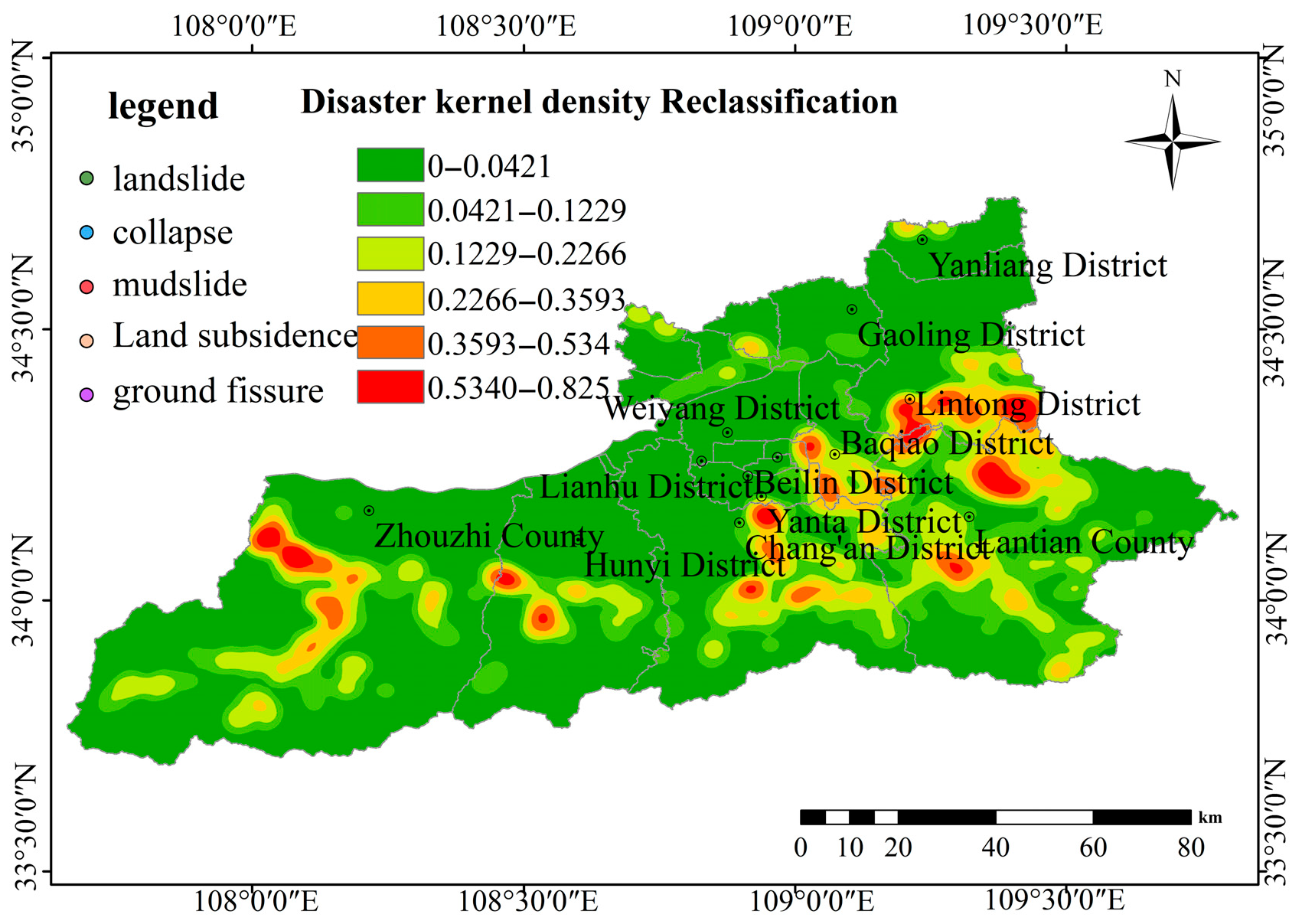
Figure 26.
Hazard point kernel density classification map.
Figure 26.
Hazard point kernel density classification map.
Figure 27.
A diagram of the analytic hierarchy process system.
Figure 27.
A diagram of the analytic hierarchy process system.
Figure 28.
The evaluation results map generated using the unweighted information value method.
Figure 28.
The evaluation results map generated using the unweighted information value method.
Figure 29.
The evaluation results map generated using the subjective weighted information value method.
Figure 29.
The evaluation results map generated using the subjective weighted information value method.
Figure 30.
The evaluation results map generated using the objective weighted information value method.
Figure 30.
The evaluation results map generated using the objective weighted information value method.
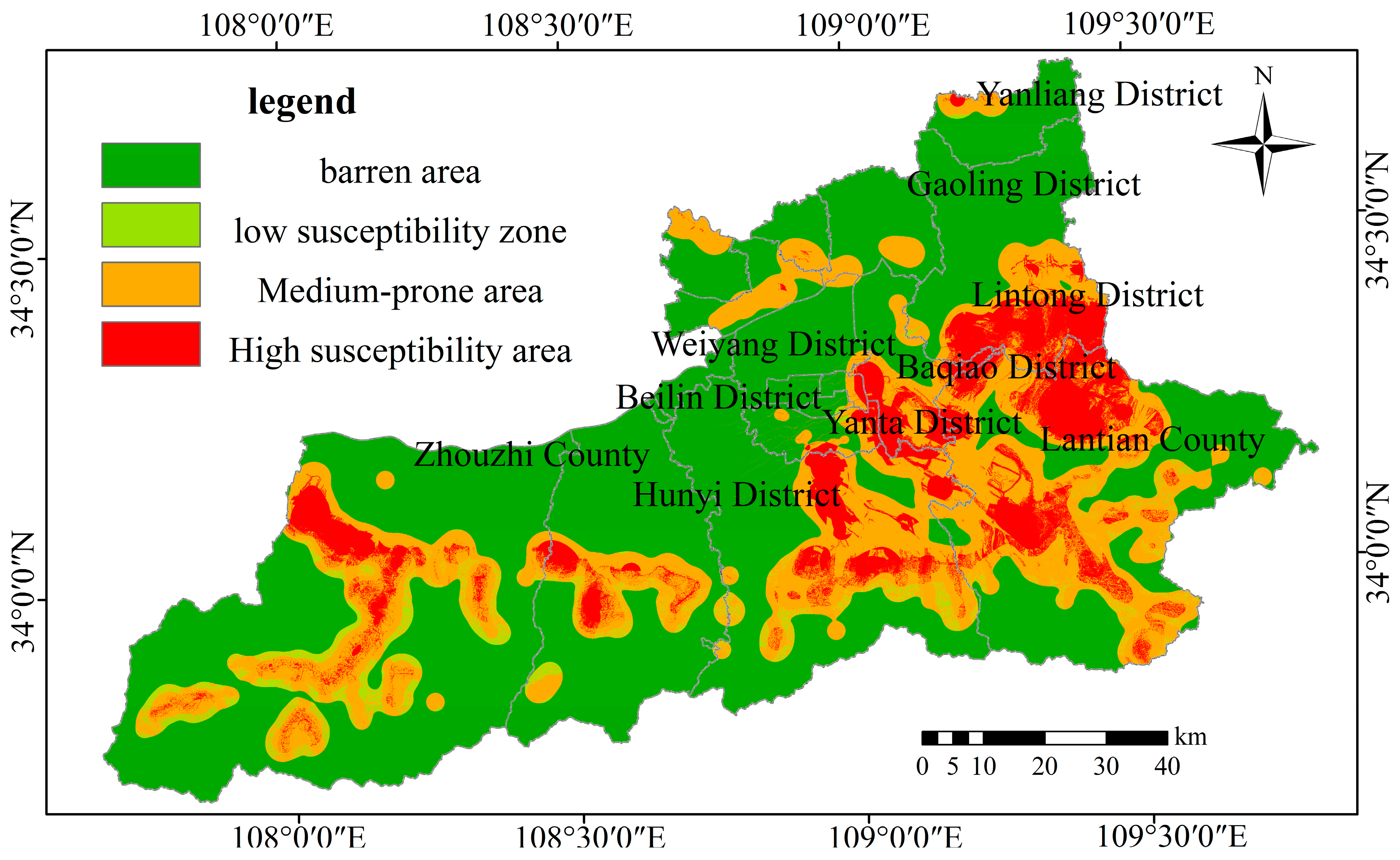
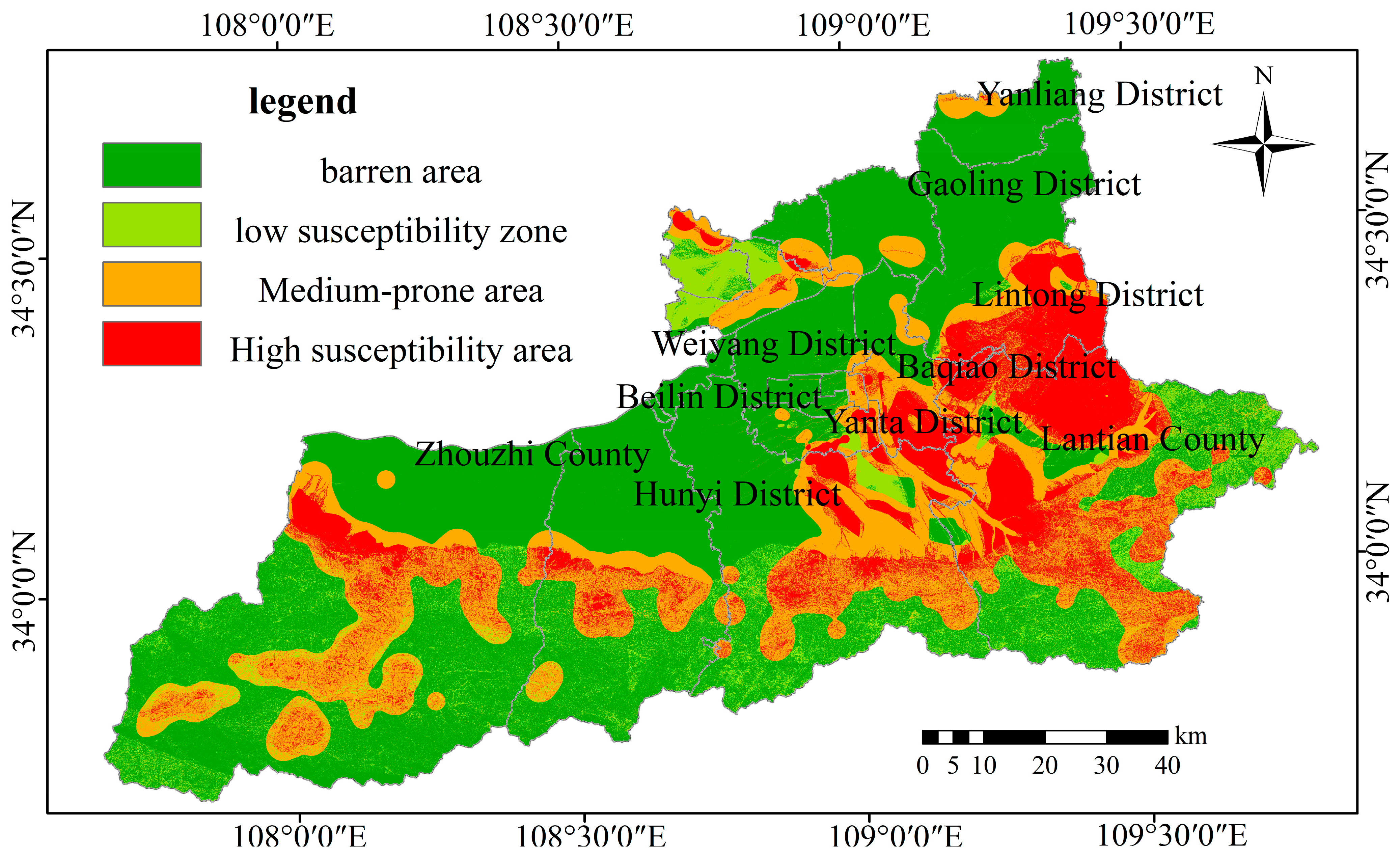
Figure 31.
The evaluation results map generated using the comprehensive weighted information value method.
Figure 31.
The evaluation results map generated using the comprehensive weighted information value method.
Figure 32.
Photos of high-risk areas.
Figure 32.
Photos of high-risk areas.
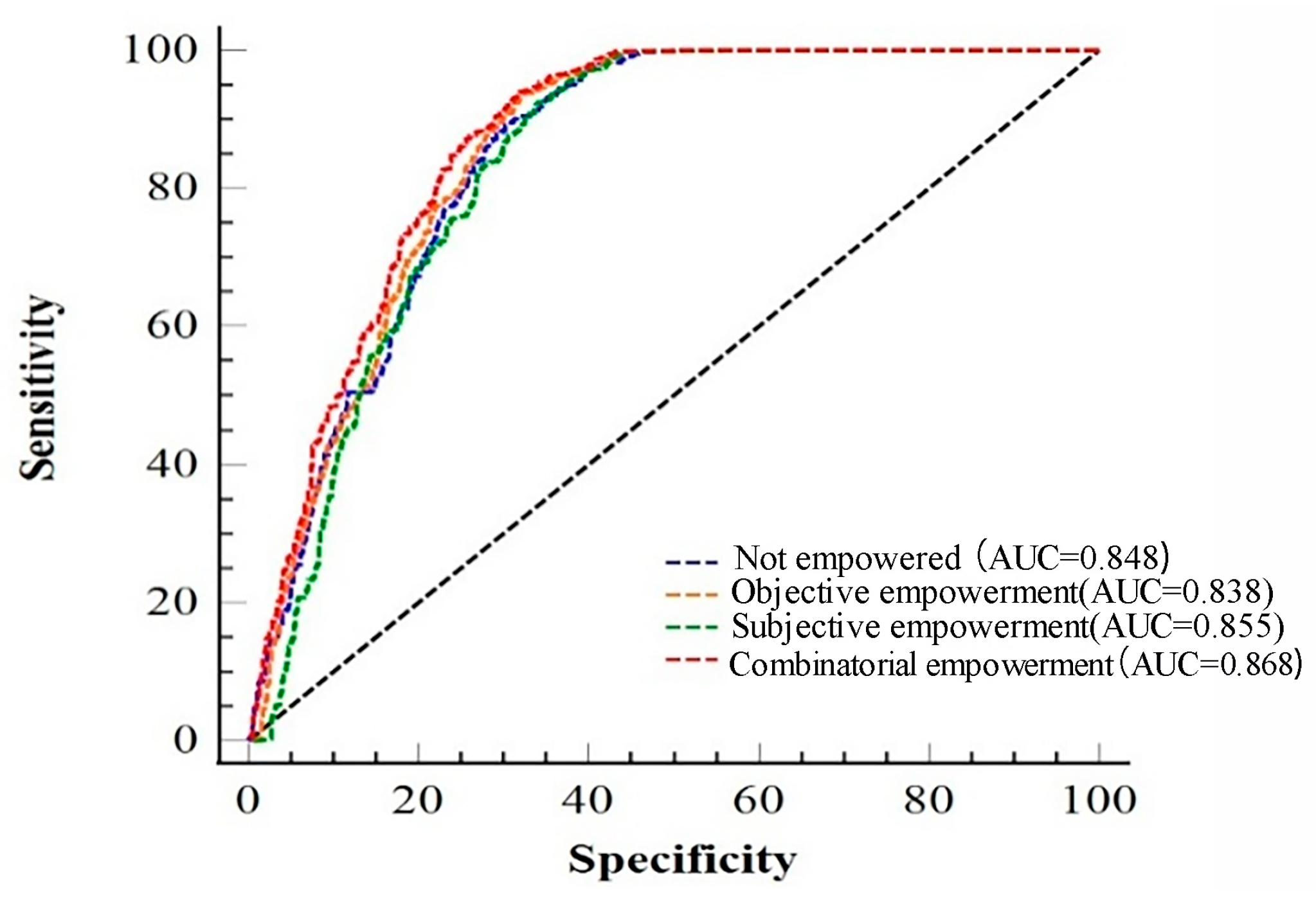
Figure 33.
A comparison of ROC curves for different weighting models.
Figure 33.
A comparison of ROC curves for different weighting models.
Table 1.
The stratigraphic and lithological characteristics of the study area.
Table 1.
The stratigraphic and lithological characteristics of the study area.
| Boundary | System | Formation Complex | Description |
|---|
| Neoarchean | | Taihua Group | Exposed in Lishan of Lintong and west of Bayuan Town in Lantian County, uplifted to the surface by fault block action. The lithological structure is mainly composed of gneiss. |
| Paleoproterozoic | | Tietonggou Formation | Exposed in Bayuan Town and Lanqiao Town of Lantian County and Lishan area of Lintong District. The lithology is mainly metamorphic clastic rocks. |
| Guozhuang Rock Formation | Mainly distributed in the Qinling Mountains, with original rocks mainly composed of terrigenous clastic rocks. |
| Yanlinggou Rock Formation | Mainly distributed in Qinggangbian of Huyi District and west of Chenhe Town in Zhouzhi County, with lithology mainly composed of carbonate rocks. |
| Shangdianfang Rock Formation | Mainly distributed around Shangdianfang in Taibai County, sporadically distributed with small area, classified as metamorphism of greenschist and amphibolite facies. |
| Paleoproterozoic | | Dizhuanggou Rock Formation | Mainly distributed at the southwestern boundary of Houzhenzi Town in Zhouzhi County, appearing as elongated strips with small area. |
Shaba and Heilongtan Formation
Group Combined Layer | Only exposed 9.0–13.9 km south of Houzhenzi Town in Zhouzhi County, comprising small area. |
| Neoproterozoic | | Xiong’er Formation | Distributed in Bayuan Town of Lantian County, mainly volcanic rocks interbedded with terrigenous clastic rocks. |
| Guangdongping Rock Formation | Exposed between Mazhao Town and Chenhe Town in Zhouzhi County, distributed in east–west bands. The lithology is mainly metamorphic volcanic rocks. |
| Sichakou Rock Formation | Exposed in Pangguang Town of Huyi District, distributed in east–west bands, representing a suite of volcanic–sedimentary to terrigenous sedimentary clastic rocks. |
| Songshugou Rock Formation | Distributed as remnant blocks south of Huangcaopo in Heihe, Zhouzhi, and north of Wangjihe Town. The rock characteristics are mainly metamorphic basic volcanic rocks interbedded with minor clastic rocks. |
| Lower Paleozoic | | Danfeng Rock Formation | Extends from Houzhenzi Town to Wangjihe Town in Zhouzhi County in elongated strips, representing a tectonic mélange located in the main plate suture zone. |
| Luohansi Rock Formation | Extends from Houzhenzi Town in Zhouzhi County to Huyi District, with main lithology including sandstone, carbonate rocks, and volcaniclastic rocks. |
| Erlangping Rock Formation | Distributed in all four southern counties in elongated strips. The lithology is mainly volcanic rocks. |
| Taowan Rock Formation | Exposed near Lanqiao Town in elongated strips, with lithology mainly comprising metamorphic rocks, containing clastic rocks, clay rocks, and carbonate rocks. |
| Upper Paleozoic | Devonian | Fenbiigou Formation | Mainly exposed in Shouyang Mountain of Zhouzhi County. The lithology is mainly metamorphic clastic rocks. |
| Chigou Formation | Exposed in Situn Town of Zhouzhi County, elongated strips trending NWW. The lithology is mainly sandstone with minor slate and phyllite. |
| Qingshiya Formation | Exposed in Situn Town and Wangjihe Town of Zhouzhi County. The lithology is mainly clay rocks interbedded with carbonate rocks and clastic rocks. |
| Tongyusi Formation | Exposed south of Situn Town in Zhouzhi County, with lithology mainly clastic rocks interbedded with clay rocks and minor carbonate rocks. |
| Dafenggou Formation | Distributed around Situn Town in Zhouzhi County, with lithology mainly comprising sandstone in littoral facies. |
| Gudaoling Formation | Mainly distributed around Situn Town in Zhouzhi County, with lithology mainly comprising carbonate rocks interbedded with clay rocks and fine clastic rocks. |
| Carboniferous | Eryuhe Formation | Exposed around Xiaowangjian in Zhouzhi. The lithology is mainly carbonaceous slate interbedded with gravel-bearing quartz sandstone and siltstone. |
| Permian | Shihezi Formation | Distributed in Chenhe Town of Zhouzhi County, extending in east–west bands. The lower lithology is mainly mudstone and sandstone; the upper part consists of fine sandstone and sandy and argillaceous mudstone. |
| Mesozoic | Triassic | Wulichuan Formation | Distributed near Liuyehe in Zhouzhi and Pengjiawan in Lantian County. The lower lithology is mainly quartz conglomerate; the upper part consists of sandy slate and quartz sandstone. |
| Cretaceous | Donghe Formation | Distributed around Situn Town in Zhouzhi County. The lithology is mainly clastic rocks. |
| Cenozoic | Paleogene | Honghe Formation | Exposed in the middle and upper reaches of various gullies in Lishan, with lithology mainly comprising mudstone interbedded with sandstone and siltstone. |
| Bailuyuan Formation | Exposed near Bailuyuan, with lithology mainly comprising sandstone interbedded with mudstone and sandstone. |
| Cenozoic | Paleogene | Ganhe Formation | Mainly sandstone and sandy conglomerate, interbedded with argillaceous rocks. |
| Neogene | Lengshuigou Formation | Distributed around Lantian. The lithology is mainly sandy mudstone interbedded with sandstone, with conglomerate at the bottom. |
| Koujiagcun Formation | Mainly exposed in Maodong Village, Baqiao District, Xi’an. The lithology is mainly mudstone and sandy mudstone. |
| Bahe Formation | Mainly distributed in Lantian County and Lintong District. The lithology is mainly mudstone and sandy mudstone. |
| Lantian Formation | Mainly distributed around Lantian. The lithology is mainly clay rocks and sandy clay rocks. |
| Quaternary | Glaciofluvial Deposits | Mainly distributed near Gongwangling in Lantian County and valley exits at the front of the Qinling Mountains. The lithology is mainly sandy gravel. |
| Eolian Deposits | Mainly distributed in Bailuyuan, with lithology of loess containing calcareous nodules and multiple paleosol layers. |
| Eolian Deposits | Mainly distributed in the northern loess hilly area and tableland area of Lantian County. The lithology is mainly sandy gravel layers and paleosols, containing calcareous nodules and interbedded with multiple paleosol layers. |
| Proluvial Deposits | Only exposed at the proluvial fan south of Yangzhuang Subdistrict in Chang’an District, with small distribution area. Mainly sandy gravel, boulders, and silty clay layers. |
| Eolian Deposits | Large distribution area, commonly called “Malan Loess”. |
| Moraine | Located around Taibai Mountain, formed by accumulation of materials transported in different ways after glacier melting. Composed of clastic materials with extremely poor sorting, poor roundness, and no directional arrangement. |
| Landslide Gravity Deposits | Distributed in Dizhai Subdistrict of Baqiao District, with material composition mainly comprising loess and paleosols containing calcareous nodules. |
| Alluvial–Proluvial Deposits | Mainly distributed in Yanliang District and Gaoling District. The material composition is mainly fine- to medium-coarse sand and silty clay layers. |
| Proluvial Deposits | Mainly distributed at the front of Qinling Mountains and Lishan, with material composition mainly comprising sandy gravel, boulders, and silty clay layers. |
| Alluvial Deposits | Widely distributed, located at the same position as the first geomorphological terrace, with material composition mainly comprising sand, sandy gravel, and silty clay layers. |
| Proluvial Deposits | Mainly distributed at the front of Qinling Mountains and Lishan, with material composition mainly comprising sandy gravel, boulders, and silty clay layers. |
| Alluvial Deposits | Widely distributed, located at the same position as geomorphological floodplains, with material composition mainly comprising sand, sandy gravel, and silty clay layers. |
Table 2.
A statistical table of sudden-onset geological hazard types.
Table 2.
A statistical table of sudden-onset geological hazard types.
| No. | Sudden-Onset Geological Hazards | Classification Criteria | Quantity (Locations) | Percentage |
|---|
| 1 | Landslides | Material Composition | Loess landslides | 206 | 47.36% |
| Accumulation layer landslides | 210 | 48.28% |
| Rock landslides | 19 | 4.36% |
| Scale | Small | 334 | 76.78% |
| Medium | 63 | 14.48% |
| Large | 31 | 7.13% |
| Extra-large | 6 | 1.38% |
| Giant | 1 | 0.23% |
| Profile Morphology | Convex | 181 | 41.61% |
| Concave | 183 | 42.07% |
| Linear | 71 | 16.32% |
| 2 | Collapses | Material Composition | Loess collapses | 242 | 79.61% |
| Accumulation layer collapses | 14 | 4.60% |
| Rock collapses | 48 | 15.79% |
| Scale | Small | 228 | 75.00% |
| Medium | 64 | 21.05% |
| Large | 10 | 3.29% |
| Extra-large | 1 | 0.66% |
| 3 | Ground Collapse | Scale Type | Small | 7 | 87.50% |
| Medium | 0 | 0.00% |
| Large | 1 | 12.50% |
| 4 | Mudslide | Basin Morphology | Hillslope-type debris flows | 11 | 36.67% |
| Valley-type debris flows | 19 | 63.33% |
| Deposit Volume | Small | 21 | 70.00% |
| Medium | 8 | 26.67% |
| Large | 0 | 0.00% |
| Extra-large | 1 | 3.33% |
Table 3.
Scale values and their meanings.
Table 3.
Scale values and their meanings.
| Scale (Cij) | Meaning |
|---|
| 1 | Factors i and j are equally important |
| 3 | Factor i is slightly more important than factor j |
| 5 | Factor i is obviously more important than factor j |
| 7 | Factor i is significantly more important than factor j |
| 9 | Factor i is extremely more important than factor j |
| 2, 4, 6, 8 | Importance levels are in intermediate states |
| Reciprocals of the above scale values | Represent the degree of importance of factor j compared to factor i |
Table 4.
Judgment Matrix C.
Table 4.
Judgment Matrix C.
| C | C1 | C2 | C3 | …… | Cn |
|---|
| C1 | c11 | c12 | c13 | …… | c1n |
| C2 | c21 | c22 | c23 | …… | c2n |
| C3 | c31 | c32 | c33 | …… | c3n |
| …… | …… | …… | …… | …… | …… |
| Cn | cn1 | cn2 | cn3 | …… | cnn |
Table 5.
The average randomized consistency indicator RI value.
Table 5.
The average randomized consistency indicator RI value.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
Table 6.
The regional distribution of geological hazard hidden danger points.
Table 6.
The regional distribution of geological hazard hidden danger points.
| Region | Number of Geological Hazard Hidden Danger Points | Percentage of Total Disaster Points | Disaster Point Quantity Ranking |
|---|
| Landslides | Collapses | Mudslide | Ground Collapse | Ground Fissures | Total |
|---|
| Lantian County | 122 | 86 | 3 | 0 | 0 | 211 | 26.81% | 1 |
| Zhouzhi County | 144 | 22 | 10 | 0 | 1 | 177 | 22.49% | 2 |
| Chang’an District | 67 | 58 | 6 | 1 | 3 | 135 | 17.15% | 3 |
| Lintong District | 45 | 58 | 2 | 1 | 0 | 106 | 13.47% | 4 |
| Baqiao District | 16 | 40 | 0 | 1 | 4 | 61 | 7.75% | 5 |
| Huyi County | 37 | 8 | 9 | 0 | 0 | 54 | 6.86% | 6 |
| Xixian New Area | 4 | 13 | 0 | 2 | 0 | 19 | 2.41% | 7 |
| Yanliang District | 0 | 6 | 0 | 0 | 2 | 8 | 1.02% | 8 |
| Gaoling District | 0 | 5 | 0 | 1 | 0 | 6 | 0.76% | 9 |
| Chanba Ecological District | 0 | 4 | 0 | 1 | 0 | 5 | 0.64% | 10 |
| Yanta District | 0 | 3 | 0 | 1 | 0 | 4 | 0.51% | 11 |
| International Port District | 0 | 1 | 0 | 0 | 0 | 1 | 0.13% | 12 |
| Total | 435 | 304 | 30 | 8 | 10 | 787 | — | — |
Table 7.
A table of the relationship between geological hazard quantities and geomorphological types.
Table 7.
A table of the relationship between geological hazard quantities and geomorphological types.
| Hazard Type | Number of Hazard Points | Total |
|---|
| Alluvial and Alluvial–Pluvial Plains | Piedmont Pluvial Plain Areas | Loess Landform Areas | Mountainous Regions |
|---|
| Landslides | 31 | 5 | 136 | 263 | 435 |
| Collapses | 61 | 17 | 150 | 76 | 304 |
| Debris Flows | - | 1 | 2 | 27 | 30 |
| Ground Collapse | 6 | - | 2 | - | 8 |
| Ground Fissures | 8 | - | 2 | - | 10 |
| Total | 106 | 23 | 292 | 366 | 787 |
Table 8.
A statistical table of the relationships between geomorphological types and geological hazards.
Table 8.
A statistical table of the relationships between geomorphological types and geological hazards.
| Geomorphological Type | Area (km2) | Geological Hazard Points |
|---|
| Number | Percentage |
|---|
| Alluvial and Alluvial–Pluvial Plain Areas | 3188.08 | 106 | 13.47% |
| Piedmont Pluvial Plain Areas | 873.96 | 23 | 2.92% |
| Loess Landform Areas | 1279.10 | 292 | 37.10% |
| Mountainous Regions | 5248.20 | 366 | 46.51% |
Table 9.
A statistical table of distribution quantities of geological hazard hidden danger points in different stratigraphic ages.
Table 9.
A statistical table of distribution quantities of geological hazard hidden danger points in different stratigraphic ages.
| Stratigraphic Age | Landslides | Collapses | Mudslides | Ground Collapse | Ground Fissures | Total | Percentage |
|---|
| Quaternary | 156 | 173 | 5 | 8 | 10 | 352 | 44.73% |
| Neogene | 32 | 23 | 0 | 0 | 0 | 55 | 6.99% |
| Paleogene | 32 | 46 | 1 | 0 | 0 | 79 | 10.04% |
| Upper Paleozoic | 41 | 14 | 4 | 0 | 0 | 59 | 7.50% |
| Middle Paleozoic | 18 | 1 | 1 | 0 | 0 | 20 | 2.54% |
| Lower Paleozoic | 68 | 19 | 9 | 0 | 0 | 96 | 12.19% |
| Proterozoic | 73 | 14 | 10 | 0 | 0 | 97 | 12.33% |
| Neoarchean | 15 | 14 | 0 | 0 | 0 | 29 | 3.68% |
| Total | 435 | 304 | 30 | 8 | 10 | 787 | — |
Table 10.
A statistical table of geological hazard quantities in different rock and soil mass zones.
Table 10.
A statistical table of geological hazard quantities in different rock and soil mass zones.
| Rock and Soil Mass Zone Code | Area (km2) | Geological Hazard Types |
|---|
| Collapses | Landslides | Debris Flows | Ground Collapse | Ground Fissures |
|---|
| Silty clay + sandy gravel dual-layer structure zone (I1-1) | 1721.61 | 40 | 12 | - | 1 | 2 |
| Loess (interbedded with paleosol) + sand, sandy gravel dual-layer structure zone (I1-2) | 410.78 | 25 | 19 | - | 1 | 2 |
| Loess (interbedded with paleosol) single-layer structure zone (I2) | 1291.64 | 148 | 139 | 3 | 3 | 2 |
| Loess, loess-like soil, and sandy gravel multi-layer structure zone (I3) | 717.93 | 11 | 5 | - | 3 | 2 |
| Sandy gravel, sandy clay multi-layer structure zone (I4) | 1416.82 | 7 | 9 | 2 | - | 2 |
| Massive hard intrusive rock engineering geological zone (II1) | 2236.67 | 30 | 80 | 8 | - | - |
| Massive hard to moderately hard intermediate to high-grade metamorphic rock engineering geological zone (II2) | 2451.27 | 35 | 143 | 16 | - | - |
| Layered moderately hard to weak sedimentary rock engineering geological zone (II3) | 342.17 | 8 | 28 | 1 | - | - |
| Total | 10,588.9 | 304 | 435 | 30 | 10 | 8 |
Table 11.
A classification and statistical table of factors influencing geological hazards.
Table 11.
A classification and statistical table of factors influencing geological hazards.
| Influencing Factor | Classification | Area (km2) | Hazard Points | Influencing Factor | Classification | Area (km2) | Hazard Points |
|---|
| Slope Gradient (°) | 0~10 | 5231.6 | 4 | Rock and Soil Mass Types | I1-1 | 1721.59 | 55 |
| 10~20 | 1157.62 | 23 | I1-2 | 410.78 | 47 |
| 20~30 | 1610.37 | 132 | I2 | 1291.66 | 295 |
| 30~40 | 1616.81 | 198 | I3 | 717.94 | 21 |
| 40~50 | 794.215 | 88 | I4 | 1416.83 | 20 |
| 50~60 | 171.923 | 108 | II1 | 2236.68 | 118 |
| 60~70 | 23.43 | 152 | II2 | 2469.88 | 194 |
| 70~80 | 1.558 | 34 | II3 | 342.17 | 37 |
| 80~90 | 0.006 | 0 | Distance to Faults (m) | 0~1200 | 3638.99 | 388 |
| Slope Aspect (°) | 0~90 | 3390.9 | 177 | 1200~2500 | 2533.83 | 170 |
| 90~180 | 2322.28 | 238 | 2500~4000 | 1913.14 | 87 |
| 180~270 | 2399.08 | 237 | 4000~6500 | 1586.72 | 77 |
| 270~360 | 2495.27 | 135 | 6500~9000 | 616.76 | 41 |
| Surface Relief | 0~7 | 5484.441 | 332 | 9000~15,809.26 | 318.08 | 24 |
| 7~16 | 1916.21 | 324 | Hazard Point Kernel Density (points/km2) | 0~0.042 | 6501.6 | 1 |
| 16~24 | 1744.91 | 92 | 0.042~0.123 | 1823.72 | 90 |
| 24~34 | 1079.1 | 27 | 0.123~0.227 | 1237.4 | 196 |
| 34~50 | 335.071 | 10 | 0.227~0.359 | 602.78 | 189 |
| 50~245 | 47.798 | 2 | 0.359~0.534 | 312.78 | 179 |
| Rainfall (mm) | <600 | 3638.99 | 130 | 0.534~0.825 | 129.25 | 132 |
| 600~700 | 2533.83 | 302 | Plan Curvature | −59.888~−5.5 | 71.3602 | 2 |
| 700~800 | 1913.14 | 260 | −5.5~−2.2 | 430.265 | 31 |
| 800~900 | 1586.72 | 70 | −2.2~−0.4 | 2513.08 | 221 |
| 900~1000 | 616.76 | 25 | −0.4~1 | 6170.73 | 426 |
| >1000 | 318.08 | 0 | 1~3.8 | 1232.8 | 95 |
| | | | 3.5~59.558 | 189.296 | 12 |
| Distance to Drainage Systems | 0~300 | 2261.27 | 240 | Profile Curvature | −80.939~−5.3 | 145.699 | 6 |
| 300~500 | 1355.63 | 110 | −5.3~−1.9 | 576.348 | 49 |
| 500~1000 | 2853.92 | 201 | −1.9~−0.1 | 3547.06 | 235 |
| 1000~3000 | 3662.43 | 220 | −0.1~1.5 | 5379.03 | 398 |
| 3000~5000 | 416.032 | 15 | 1.5~5.0 | 791.59 | 91 |
| 5000~7574.21 | 58.2366 | 1 | 5.0~65.145 | 167.804 | 8 |
| Earthquake | <0.05 | 264.796 | 1 | Distance to Roads | 0~50 | 304.462 | 56 |
| 0.05~0.10 | 1826.71 | 87 | 50~150 | 581.768 | 104 |
| 0.10~0.20 | 1637.64 | 80 | 150~250 | 511.704 | 83 |
| >0.20 | 6878.37 | 619 | 250~500 | 1101 | 156 |
| | | | 500~1000 | 1641.95 | 169 |
| | | | >1000 | 6466.64 | 219 |
Table 12.
Weight coefficient values obtained using the analytic hierarchy process.
Table 12.
Weight coefficient values obtained using the analytic hierarchy process.
| Indicator | A | B | C | D | E | F | G | H | I | J | K | L |
|---|
| Weight | 0.102 | 0.018 | 0.102 | 0.018 | 0.018 | 0.040 | 0.070 | 0.029 | 0.131 | 0.055 | 0.170 | 0.247 |
Table 13.
Weight coefficient values obtained using the entropy weight method.
Table 13.
Weight coefficient values obtained using the entropy weight method.
| Indicator | A | B | C | D | E | F | G | H | I | J | K | L |
|---|
| Weight | 0.137 | 0.124 | 0.163 | 0.017 | 0.018 | 0.145 | 0.026 | 0.009 | 0.193 | 0.027 | 0.006 | 0.135 |
Table 14.
Combined weighting weight coefficient values.
Table 14.
Combined weighting weight coefficient values.
| Indicator | A | B | C | D | E | F | G | H | I | J | K | L |
|---|
| Weight | 0.116 | 0.061 | 0.127 | 0.018 | 0.018 | 0.082 | 0.052 | 0.021 | 0.156 | 0.044 | 0.104 | 0.201 |
Table 15.
The information values of selected assessment indicators.
Table 15.
The information values of selected assessment indicators.
| Factor Type | Assessment Factor | Value Range | Hazard Point Proportion | Area Proportion | Hazard Point Density Ratio | Information Value I |
|---|
| Topography and Geomorphology | Slope Gradient (°) | 0~10 | 0.54% | 49.32% | 0.64 | −4.51 |
| | | 10~20 | 3.11% | 10.91% | 3.35 | −1.25 |
| | | 20~30 | 17.86% | 15.18% | 1.33 | 0.16 |
| | Slope Aspect (°) | 0~90 | 22.49% | 31.97% | 0.70 | −0.35 |
| | | 90~180 | 30.24% | 21.89% | 1.38 | 0.32 |
| Geological Environment | Rock and Soil Mass Types | I1-1 | 6.99% | 16.23% | 0.43 | −0.84 |
| | | I2 | 37.48% | 12.18% | 3.08 | 1.12 |
| Triggering Factors | Rainfall (mm) | <600 | 16.52% | 16.00% | 1.03 | 0.03 |
| | | 600~700 | 38.37% | 32.77% | 1.17 | 0.16 |
Table 16.
Total variance explained.
Table 16.
Total variance explained.
| Component | Initial Eigenvalues | Rotation Sums of Squared Loadings |
|---|
| Total | Variance | Cumulative | Total | Variance | Cumulative |
|---|
| 1 | 3.233 | 26.938 | 26.938 | 2.308 | 19.234 | 19.234 |
| 2 | 1.523 | 12.693 | 39.631 | 2.252 | 18.769 | 38.003 |
| 3 | 1.354 | 11.285 | 50.916 | 1.492 | 12.432 | 50.435 |
| 4 | 1.069 | 10.908 | 61.824 | 1.094 | 9.117 | 59.551 |
| 5 | 1.046 | 8.716 | 70.540 | 1.079 | 8.988 | 68.540 |
| 6 | 0.949 | 7.911 | 76.450 | | | |
| 7 | 0.791 | 6.595 | 83.046 | | | |
| 8 | 0.690 | 5.754 | 88.800 | | | |
| 9 | 0.511 | 4.262 | 93.062 | | | |
| 10 | 0.463 | 3.857 | 96.919 | | | |
| 11 | 0.264 | 2.204 | 99.123 | | | |
| 12 | 0.105 | 0.877 | 100.000 | | | |
Table 17.
Component matrix.
Table 17.
Component matrix.
| | Component |
|---|
| 1 | 2 | 3 | 4 | 5 |
|---|
| Slope | 0.31 | 0.71 | −0.34 | 0.13 | −0.57 |
| Aspect | −0.08 | −0.82 | −0.11 | 0.03 | −0.16 |
| Relief amplitude | 0.56 | 0.77 | −0.05 | 0.14 | −0.057 |
| Plan curvature | −0.40 | 0.43 | −0.857 | 0.01 | −0.051 |
| Profile curvature | −0.33 | 0.23 | −0.859 | −0.41 | −0.080 |
| Engineering geological rock and soil type | −0.48 | 0.13 | 0.61 | 0.58 | 0.04 |
| Distance to fault structures | 0.24 | 0.19 | 0.30 | −0.89 | 0.27 |
| Distance to river systems | −0.0116 | −0.203 | 0.43 | 0.13 | 0.20 |
| Precipitation | 0.0398 | 0.298 | 0.798 | 0.30 | 0.91 |
| Peak ground acceleration | −0.36 | −0.193 | 0.61 | 0.080 | 0.34 |
| Distance to roads | 0.47 | 0.06 | −0.43 | 0.76 | 0.27 |
| Disaster point kernel density | 0.93 | 0.47 | 0.62 | 0.30 | 0.46 |
Table 18.
Statistical table of hazard point density in different zones of various models.
Table 18.
Statistical table of hazard point density in different zones of various models.
| Susceptibility Zone | Unweighted Information Value | | Subjective Weighted Information Value | | Objective Weighted Information Value | | Comprehensive Weighted Information Value | |
|---|
| | Number of Hazard Points | Proportion (%) | Number of Hazard Points | Proportion (%) | Number of Hazard Points | Proportion (%) | Number of Hazard Points | Proportion (%) |
| Non-susceptible Area | 0 | 0 | 1 | 0.12 | 0 | 0 | 1 | 0.13 |
| Low-Susceptibility Area | 2 | 0.25 | 4 | 0.51 | 18 | 2.29 | 4 | 0.51 |
| Moderate-Susceptibility Area | 256 | 32.53 | 232 | 29.48 | 267 | 33.92 | 203 | 25.79 |
| High-Susceptibility Area | 529 | 67.22 | 550 | 69.89 | 502 | 63.79 | 579 | 73.57 |
| Total | 787 | 100 | 787 | 100 | 787 | 100 | 787 | 100 |