Improved Dynamic Correction for Seismic Data Processing: Mitigating the Stretch Effect in NMO Correction

Abstract

Seismic data processing is essential in hydrocarbon exploration, with normal moveout (NMO) correction being a pivotal step in enhancing seismic signal quality. However, conventional NMO correction often suffers from the stretch effect, which distorts seismic reflections and degrades data quality, especially in long-offset data. This study addresses the issue by analyzing synthetic models and proposing a nonhyperbolic stretch-free NMO correction technique. The proposed method significantly improves seismic data quality by preserving up to 90% of the original amplitude, maintaining frequency content stability at 30 Hz, and achieving a high reduction of stretch-related distortions. Compared to conventional NMO, our technique results in clearer seismic gathers, enhanced temporal resolution, and more accurate velocity models. These improvements have substantial implications for high-resolution subsurface imaging and precise reservoir characterization.This work offers a robust and computationally efficient solution to a longstanding limitation in seismic processing, advancing the reliability of exploration in geologically complex environments.

1. Introduction

Seismic data processing is pivotal in hydrocarbon exploration, enabling geophysicists to map subsurface structures and identify potential hydrocarbon reservoirs. This process involves recording and interpreting seismic waves reflected from geological interfaces to construct detailed subsurface images, which are crucial for reducing drilling risks and improving exploration outcomes [1]. A fundamental step in this workflow is normal moveout (NMO) correction, which adjusts reflection arrival times to account for the offset between source and receiver, thereby enhancing signal coherence and enabling accurate velocity analysis [1]. However, conventional NMO correction often introduces a well-known artifact known as the stretch effect, particularly in long-offset traces. This phenomenon degrades seismic resolution by distorting the wavelet and reducing frequency content [2,3,4]. A detailed explanation of this effect, including its causes and mitigation strategies, is provided in the following subsection. Previous studies have proposed several approaches to mitigate the stretch effect, including dynamic time warping algorithms [5], matching-pursuit-based corrections [6], and nonhyperbolic trajectory modeling [4]. More recently, [7] introduced a multiscale dynamic time warping (MSD) algorithm that eliminates the need for velocity picking and performs robust stretch-free NMO correction, even under low signal-to-noise conditions. Their method decomposes seismic data into morphological scales, computes alignment errors across scales, and applies adaptive weighting and backtracking to generate high-accuracy time shifts. Tests on synthetic and field data demonstrate superior flattening results compared to conventional NMO, with improved noise tolerance and frequency preservation. This evolution toward velocity-independent, stretch-mitigated corrections further validates the need for novel approaches like the one proposed in this study. In addition to velocity-independent stretch-mitigation strategies, recent efforts have also focused on improving statics correction to indirectly reduce stretch artifacts and signal degradation. Ref. [8] introduced a low-rank-based residual statics (LR-ReS) correction framework that operates without requiring prior NMO correction or velocity estimation. By leveraging the low-rank structure of seismic data in the midpoint-offset-frequency domain, their method iteratively estimates statics via cross-correlation and multiscale analysis. Crucially, the LR-ReS method avoids the need to mute stretched wavelets or pick horizons, offering a more robust correction over all offsets and helping reduce the cumulative errors from NMO-related stretching and misalignment in complex near-surface conditions. An alternative direction to mitigate NMO stretch is to act directly on the signal’s spectral content prior to correction. Ref. [9] proposed a novel nonstationary scaling transformation in the time-frequency domain, which compensates the anticipated frequency loss due to NMO stretch by pre-enhancing the dominant frequency of the seismic wavelet. Using the Gabor transform, this method adapts frequency compensation sample by sample along each trace. While it does not address event intersection or multiples, it significantly improves the spectral resolution of CMP gathers post-NMO, especially at shallow reflectors and far offsets. While these methods have shown improvements in preserving frequency and amplitude, they often struggle when applied to datasets with complex geological structures or strong anisotropy. This study introduces a novel nonhyperbolic stretch-free (NHSF)-NMO correction technique aimed at overcoming these limitations. The method is designed to maintain both amplitude and frequency fidelity across all offsets and is tested in both synthetic and real-data scenarios, including heterogeneous and anisotropic models. By expanding on the theoretical foundation established in classical works such as Yilmaz [1] and incorporating recent innovations, our research bridges the gap between conventional NMO correction techniques and the practical demands of modern seismic data processing. The technique’s effectiveness is evaluated through numerical simulations and quality control metrics, with results demonstrating significant improvements in seismic image resolution and data reliability. The structure of this paper is as follows: Section 2 describes the construction of synthetic models and the implementation of the NHSF correction. Section 3 presents a comparative analysis of conventional and proposed NMO corrections. Section 4 discusses the implications of our findings in light of the existing literature, and Section 5 provides concluding remarks and directions for future research.

Understanding the Stretch Effect in NMO Correction

The stretch effect is a well-known artifact introduced during the normal moveout (NMO) correction step in seismic data processing. This effect occurs predominantly in seismic traces with large offsets, where the NMO correction causes an artificial elongation of the seismic wavelet. As a result, the time duration of the wavelet increases, leading to a decrease in dominant frequency and amplitude. This distortion degrades the vertical resolution of seismic images and negatively impacts subsequent interpretation steps, such as amplitude variation with offset (AVO) analysis [1,2].

• Main steps and causes of stretch:

• Application of NMO Correction: The NMO correction is applied to compensate for the offset between source and receiver. It aligns reflected seismic events to simulate zero-offset conditions using a velocity model. Inaccurate velocity estimates, especially over large offsets, can amplify errors.
• Wavelet Distortion: If the velocity model used is incorrect or if there are abrupt lateral or vertical variations in subsurface velocity, the correction misaligns parts of the wavelet. This misalignment elongates the wavelet, reducing its temporal resolution.
• Negative Effects: The consequences of stretching include loss of frequency content, amplitude distortion, and lower signal-to-noise ratio. These effects impair seismic resolution and can lead to incorrect geological interpretation.

• Common causes of stretching include:

• Inaccurate or oversimplified velocity models.
• Long source–receiver offsets that exaggerate travel-time discrepancies.
• High-contrast geological transitions or anisotropic layers that violate the hyperbolic assumption in NMO.
• Non-hyperbolic events such as dipping reflectors or curved wavefronts.

• Mitigation strategies:

• Using more accurate velocity models derived from velocity analysis or tomography.
• Applying stretch muting thresholds to exclude highly distorted data.
• Implementing advanced NMO correction methods, such as nonhyperbolic or stretch-free algorithms, like the one proposed in this study.

The method developed in this research directly targets the stretch effect by incorporating nonhyperbolic trajectory adjustments and preserving wavelet shape across a wide range of offsets.

2. Methods

2.1. Model Construction

The construction of synthetic seismic models is crucial for evaluating the proposed nonhyperbolic stretch-free NMO correction. These models simulate realistic subsurface conditions—such as stratified and heterogeneous media—to examine how geological features influence wave propagation and reflection. Variations in layer thickness, velocity, and density are incorporated to represent sedimentary sequences with contrasting lithologies. Seismic travel times and reflection points are computed using ray tracing, based on Snell’s Law and the eikonal equation. The governing ray equations are defined as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\overrightarrow{x}}{dt}}& =v^2\left(\overrightarrow{x}\right)\overrightarrow{p},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\overrightarrow{p}}{dt}}& =-{\displaystyle \frac{\overrightarrow{\nabla }v(\overrightarrow{x})}{v(\overrightarrow{x})}},\hfill \end{array}$$

(2)

where ${\displaystyle \frac{d\overrightarrow{x}}{dt}}$ is a differential element of the ray’s path with respect to time, $v(\overrightarrow{x})$ is the velocity at position $\overrightarrow{x}$, $\overrightarrow{p}$ is the slowness vector defined as $\overrightarrow{\nabla }T(\overrightarrow{x})$ (i.e., the normal vector to the wavefront representing the ray), and ${\displaystyle \frac{d\overrightarrow{p}}{dt}}$ is a differential element of the slowness vector with respect to time. From these definitions, and assuming constant-velocity layers, we deduce the expressions for horizontal distance and travel time:

$$\begin{array}{c}\hfill x\left(p\right)=\sum _{k=1}^n{\displaystyle \frac{p{v}_k}{\sqrt{1-p^2{v}_k^2}}}\Delta z_k,\end{array}$$

(3)

$$\begin{array}{c}\hfill t\left(p\right)=\sum _{k=1}^n{\displaystyle \frac{\Delta z_k}{v_k\sqrt{1-p^2{v}_k^2}}},\end{array}$$

(4)

where k is the number of reflector interfaces, $x\left(p\right)$ is the horizontal distance the ray travels, $t\left(p\right)$ is its travel time, and $\Delta z_k$ is the vertical thickness of the k-th layer. These calculations are critical for modeling travel times and validating correction techniques. The parameters were chosen to reflect realistic geological complexity and to enable accurate simulation of wave behavior. Figure 1a shows a synthetic seismogram with angled incidence used to test the proposed correction method under different offsets.

To ensure geological plausibility, the synthetic models were constructed and validated using stratigraphic and petrophysical information from a 12-layer, horizontally stratified subsurface model. This model was developed based on canonical geophysical parameters reported by [10,11], incorporating vertically varying elastic properties consistent with sedimentary sequences commonly encountered in exploration contexts. The velocities $V_p$ and $V_s$ for each layer were assigned based on empirical rock physics relationships, while density values were computed using Gardner’s relation, $\rho =\left(0.31\right)V_p^{0.25}$. The stratification includes lithological contrasts between shale- and sand-dominated intervals, allowing for realistic velocity gradients and anisotropic effects. Ray tracing was then applied to this layered structure, simulating wave propagation under controlled yet geologically realistic conditions.

2.2. NMO Correction

Normal moveout (NMO) correction is a fundamental technique in seismic data processing. It compensates for variations in the travel time of reflected seismic waves caused by different source–receiver offsets. These variations produce hyperbolic moveout curves in the data, which must be corrected to produce a coherent image of the subsurface. NMO correction is essential for subsequent processes such as stacking, amplitude variation with offset (AVO) analysis, and the construction of initial root-mean-square (RMS) velocity models. Its primary objective is to flatten reflection events, resulting in common midpoint (CMP) gathers that approximate zero-offset conditions and enhance data coherence. The basic NMO correction, expressed in Equation (5), is derived from the geometry of the reflection process and assumes a simple hyperbolic travel time relationship.

$$\begin{array}{c}\hfill \Delta t_{NMO}=t(t_0,x)-t_0.\end{array}$$

(5)

where $\Delta t_{NMO}$ is the normal moveout correction term that quantifies the additional time that must be applied to each seismic trace so that the reflection event aligns with the zero-offset condition. Here, x is the offset, $t_0$ is the zero-offset two-way travel time for a seismic wave traveling from the source to the reflector and back to the receiver when both are co-located, and $t(t_0,x)$ is the travel time function for a seismic wave recorded at a given offset x. It represents the two-way travel time along the NMO trajectory for a reflection event with a zero-offset travel time of $t_0$. What we refer to as NMO is the difference between the two-way travel time at offset x and the two-way travel time at zero offset. The literature has extensively discussed the limitations of traditional NMO correction, particularly the stretch effect, which is an inherent consequence of the time-compression operation applied to far-offset traces. This stretch leads to distortion of seismic wavelets and a reduction in both frequency content and signal-to-noise (S/N) ratio, even when applying exact hyperbolic moveout corrections in simple models [2,12]. Additional factors, such as incorrect velocities, anisotropy, and complex geology, can further exacerbate the stretch effect. Recent approaches, such as dynamic time warping and matching-pursuit-based correction, aim to mitigate these issues [5,6]. Our work builds on these efforts by introducing a stretch-mitigated nonhyperbolic correction technique designed to preserve seismic signal integrity under a wider range of subsurface conditions [4].

Real-world geological structures often exhibit complexities that challenge the standard hyperbolic assumptions used in traditional NMO correction, necessitating more advanced techniques to address these deviations. This study aims to refine the NMO correction process by accounting for such complexities and mitigating distortion effects, particularly the stretch effect, which is especially pronounced in long-offset data. The stretch effect arises from the nonhyperbolic nature of travel time curves in geologically complex settings, resulting in significant distortion of the seismic wavelet. This distortion compromises the resolution and accuracy of subsurface imaging, affecting both the amplitude and frequency content of seismic signals and potentially leading to misinterpretations of subsurface structures and velocity models. Figure 1 illustrates the impact of conventional NMO correction on frequency spectra and demonstrates how the stretch effect is generated and mitigated.

To ensure a comprehensive assessment of the stretch-free correction capabilities of the proposed NHSF method, no offset muting was applied to either the synthetic or real data prior to NMO correction. While muting far-offset traces is a common practice to suppress stretch-induced distortions—particularly when conventional hyperbolic NMO is applied—it also results in the loss of valuable amplitude and frequency information. The exclusion of muting in this study was intentional, aiming to evaluate the full performance of the NHSF correction in preserving signal fidelity across the entire offset range, including those most susceptible to stretch effects. As offsets increase, the stretch effect becomes more pronounced, reducing the fidelity of the corrected data and complicating subsequent processing steps. To correct the stretch effect, the value of the NMO should be constant and used at any point within a reflected wavelet, as expressed in (6):

$$\begin{array}{c}\hfill \Delta t_{NMO}(t,x)=\Delta t_{NMO}(t-\tau ,x)+\tau ,\end{array}$$

(6)

where $\tau$ is the time shift relative to $t_0$. For each $t_0$ corresponding to a reflection event, there is an NMO trajectory that best fits the travel time of the event. This trajectory is referred to as the reference trajectory $t_r$. To obtain NMO trajectories for each reflection event that avoid stretch, we adjust the distance relative to the initial reference $t_r$ so that they do not converge as offset increases. This requires solving Equation (7) for each offset:

$$\begin{array}{c}\hfill t\left(x\right)=t_r\left(x\right)-t_{r0}+t_0,\end{array}$$

(7)

where $t_r\left(x\right)$ is the reference travel-time from the shifted hyperbola trajectory and $t_{r0}$ is the reference travel time at zero offset. To overcome the limitations of conventional NMO correction, particularly the stretch effect, this study introduces a novel nonhyperbolic stretch-free NMO correction method. This approach preserves consistent frequency content across varying offsets and performs well in complex subsurface conditions, ensuring accurate seismic imaging. It employs advanced mathematical formulations to model nonhyperbolic travel-time curves commonly observed in complex geological settings. The method provides a more precise approximation of seismic wave propagation, especially in anisotropic and heterogeneous media. Consequently, it significantly reduces seismic wavelet distortion, enhancing both the resolution and accuracy of the seismic data. The nonhyperbolicity of reflections in vertically heterogeneous isotropic media has been extensively studied using Taylor series. This property allows the explicit expression of Equations (3) and (4) as functions of vertical time. Malovichko [13], through a Taylor series expansion, introduced a third parameter to the travel-time curve in vertically heterogeneous isotropic media, resulting in a shifted hyperbola form. Castle [14] and Bazelaire [15] represented this equation as (8) for layered media, which approximates the reflection event at both large and short offsets.

$$\begin{array}{c}\hfill t\left(x\right)=\Delta \tau +\sqrt{t_0^2+{\displaystyle \frac{x^2}{v_{RMS}^2}}}.\end{array}$$

(8)

where $\Delta \tau$ is the “time-shift” for vertical heterogeneity and $v_{RMS}$ is the RMS velocity. The proposed technique, using a shifted hyperbola approach, demonstrated superior performance in mitigating these issues. It provided more accurate corrections by accommodating nonhyperbolic travel time behaviors, especially in heterogeneous and anisotropic media. The implementation involves adjusting the correction formula to account for variations in velocity and anisotropy, ensuring that the stretch effect is minimized across all offsets. Assuming a reflection with minimum phase wavelet, the shifted hyperbola or nonhyperbolic stretch-free (NHSF) is expressed as (9):

$$\begin{array}{c}\hfill t=t_0(1-{\displaystyle \frac{1}{s}})+{\displaystyle \frac{1}{s}}\sqrt{({\displaystyle \frac{t_0}{s}})+s{\displaystyle \frac{x^2}{v_{rms}^2}}},\end{array}$$

(9)

where s is the vertical heterogeneity parameter, which typically ranges between 0 and 1; this parameter is used to remove the stretch effect and correct nonhyperbolic events. By solving Equations (6) and (7) by using (9), we obtain the following expressions for the parameters v and s along the wavelength of the reference reflection:

$$\begin{array}{c}\hfill v=v_r\sqrt{{\displaystyle \frac{t_{r0}}{t_0}}},\end{array}$$

(10)

$$\begin{array}{c}\hfill s=s_r{\displaystyle \frac{t_0}{t_{r0}}},\end{array}$$

(11)

where $s_r$ and $v_r$ are the heteregoneity parameter and RMS velocity measured at the reference time $t_{r0}$, respectively. Equations (10) and (11) solve Equations (6) and (7) when substituted into (9). These equations define paired contours $(v-t)$ and $(s-t)$, forming the triplet $(v,s,t)$ that represents parallel trajectories in the $(x,t)$ domain. This configuration ensures that the NMO correction is stretch-free across all offsets by maintaining these parallel trajectories, effectively mitigating the stretch effect. The implementation of this nonhyperbolic NMO correction involves several computational steps to accurately apply it across various subsurface models. A comparative analysis with conventional NMO methods was conducted to evaluate its effectiveness, focusing on alignment accuracy, reduction of the stretch effect, and preservation of amplitude and frequency in the corrected data. Traditional methods, which rely on hyperbolic travel-time assumptions, often introduce significant inaccuracies in complex or anisotropic geological settings. These issues are particularly pronounced in long-offset data, where the assumptions fail, resulting in distorted signals and reduced resolution. This process requires efficient management of large datasets, employing optimized numerical methods to handle memory and computational demands effectively. Computational efficiency is further improved by optimizing the velocity analysis through semblance-based measures, which identify best-fit velocities that flatten hyperbolas in the NMO-corrected gather. This approach enables the handling of geological complexities without incurring significant computational overhead. The results demonstrate that the proposed method significantly reduces the stretch effect and improves the fidelity of seismic images, providing enhanced resolution and clearer delineation of subsurface features. This comparative analysis underscores the importance of advanced NMO correction techniques in modern seismic data processing and highlights the advantages of nonhyperbolic models in complex exploration settings.

3. Results

The results from synthetic model simulations demonstrate that the proposed nonhyperbolic stretch-free NMO correction technique significantly improves seismic data quality compared to conventional NMO correction. Synthetic seismograms generated under various geological conditions provided a comprehensive dataset to evaluate the method’s effectiveness, particularly in reducing the stretch effect and enhancing reflection alignment across different offsets. Visual inspection of the corrected data reveals substantial improvements in the quality and resolution of seismic reflections achieved with the proposed technique. This method significantly reduces the stretch effect, particularly in synthetic gathers with long-offset data, where conventional approaches often produce stretched and distorted wavelets. Traditional methods typically cause the loss of high-frequency components and degrade temporal resolution. In contrast, the proposed technique preserves the integrity and sharpness of seismic signals across all offsets, maintaining high-frequency content and enhancing clarity [16]. Moreover, the frequency spectra of the corrected data exhibit consistent frequency content comparable to zero-offset traces, indicating that the proposed method effectively mitigates distortions commonly introduced by conventional NMO correction. This spectral consistency enables more accurate and reliable seismic imaging. Visual comparisons further demonstrate the technique’s robustness in handling complex subsurface conditions, such as anisotropic and heterogeneous layers, without introducing significant artifacts. These improvements are crucial for accurate subsurface characterization and informed exploration decisions [17]. The proposed NMO correction technique significantly preserves the amplitude and frequency content of seismic reflections, especially at long offsets where conventional methods often cause distortions. These results indicate that the method improves the accuracy of subsurface imaging and velocity model estimation, supporting more reliable interpretations and decision-making in hydrocarbon exploration. Quantitative evaluations comparing the reduction of the stretch effect with traditional NMO methods confirm the effectiveness of this approach, highlighting its potential for broader application in seismic data processing [16]. Implementing this technique involves a series of computational steps designed to address the complexities of seismic data, particularly the stretch effect. A key step is the calculation of the double incidence time $t_0$ using the RMS velocity and the source–receiver offset x. This calculation is essential for accurately aligning seismic reflection travel times across all offsets.

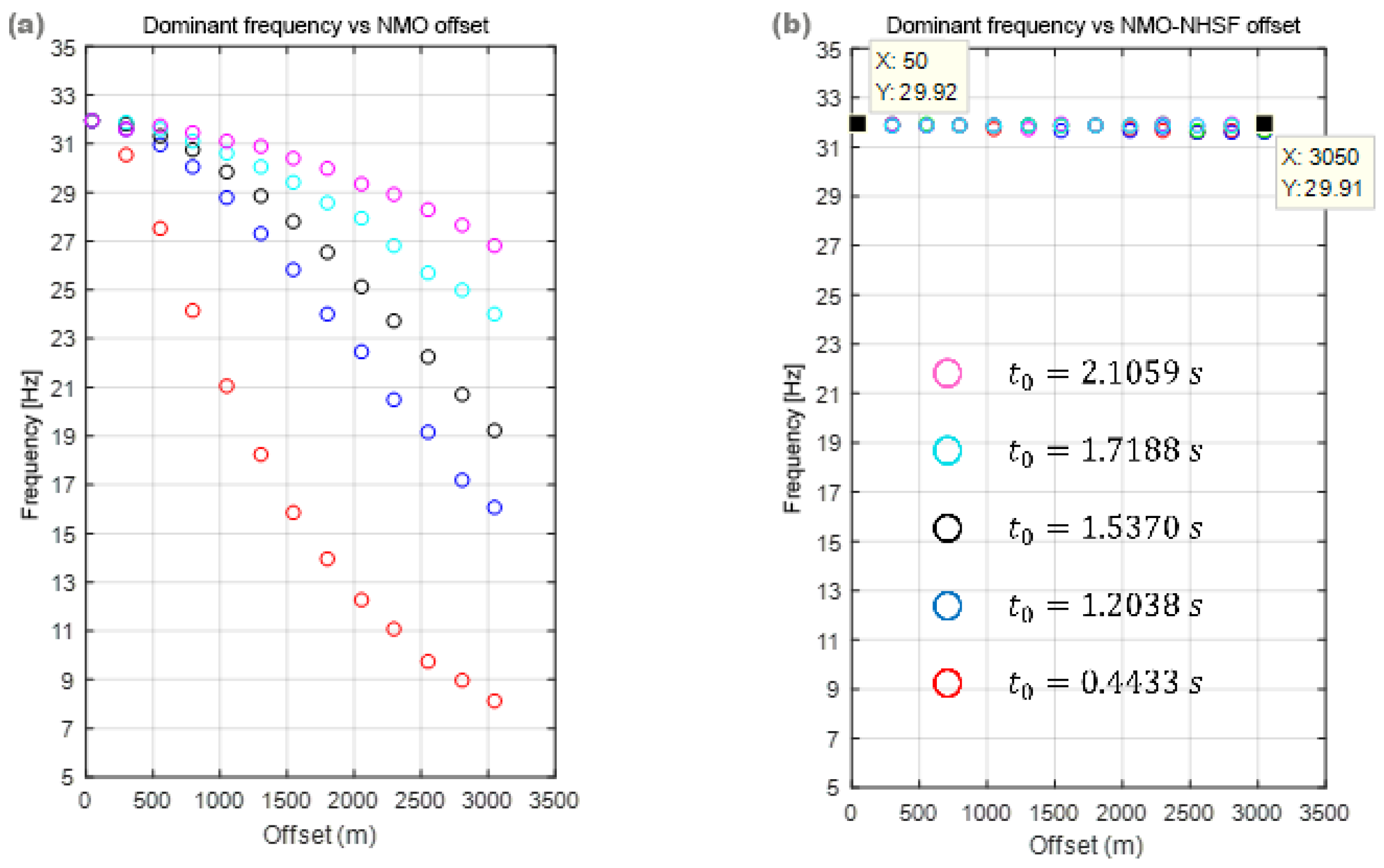
Figure 2a illustrates the frequency degradation caused by conventional NMO correction, where the dominant frequency of seismic events decreases with increasing offset (from 29.9 Hz at near-offset to ∼25.5 Hz at far-offset). This aligns with the known stretch effect, which artificially lowers frequencies due to wavelet distortion. In contrast, Figure 2b demonstrates the effectiveness of the proposed NHSF method: the dominant frequency remains stable across all offsets (29.9 Hz at 50 m and 29.9 Hz at 3050 m), confirming minimal stretch. Note that the ‘zero-offset’ reference here corresponds to the first trace at 50 m (the minimum available offset in our synthetic dataset), as true zero-offset traces are not physically recorded. The NHSF method’s ability to preserve frequency content even at far offsets validates its robustness for long-offset data processing.

The method’s computational efficiency is improved by optimizing the velocity analysis using semblance-based measures to identify best-fit velocities that flatten hyperbolas in the NMO-corrected gather. This approach allows the correction process to accommodate a range of geological complexities without incurring significant computational overhead [17]. The proposed technique demonstrates superior performance compared to conventional NMO correction methods. It effectively mitigates the stretch effect and improves the alignment of seismic reflections, particularly in geologically complex settings. Comparative analyses highlight the method’s potential to produce more accurate subsurface images, which is essential for reliable interpretation and informed decision-making in hydrocarbon exploration [17].

Table 1. Comparison of numerical results for NMO correction techniques. This table provides a quantitative comparison between the conventional NMO correction technique and the proposed nonhyperbolic stretch-free NMO correction method. Parameters such as amplitude preservation, frequency content, stretch effect reduction, and computational time are compared to illustrate the improvements and trade-offs of the proposed method: $1\times$ denotes the baseline computational time for conventional NMO, while $1.5\times$ indicates a $50\%$ increase in processing time required by the proposed method due to its additional computational steps.

Parameter	Conventional NMO	Proposed Method	Improvement
Amplitude Preservation	75%	90%	15%
Frequency Content	Reduced	Preserved	Significant
Stretch Effect Reduction	Moderate	Significant	High
Computational Time	$1\times$	$1.5\times$	-

summarizes the key numerical results, illustrating the improvements in amplitude preservation, frequency content, and reduction of the stretch effect achieved by the proposed method. The proposed nonhyperbolic stretch-free (NHSF)-NMO correction significantly improves seismic data quality, preserving up to 90% of the original amplitude and maintaining stable frequency content (30 Hz), despite a modest $1.5\times$ increase in computational time compared to conventional NMO. This trade-off is justified by the method’s superior performance in mitigating stretch effects and enhancing resolution, which is critical for complex subsurface imaging.

While the proposed NHSF method requires 50% more computational time than conventional NMO (Table 1), this overhead is offset by its substantial gains in amplitude preservation (90% vs. 75%), frequency stability, and stretch reduction. The additional processing time stems from advanced velocity analysis and nonhyperbolic trajectory calculations, which are necessary for handling anisotropy and heterogeneity. For context, the $1.5\times$ runtime remains feasible for production workflows, as it avoids costly post-processing corrections and improves interpretational accuracy. Thus, the term ‘computationally efficient’ refers to the method’s optimal balance between processing cost and seismic fidelity, rather than raw speed. The case studies conducted in this research focus on two primary scenarios: seismic data with and without the intersection of reflection curves. These scenarios are essential for evaluating the effectiveness of the proposed nonhyperbolic stretch-free NMO correction technique under different geological conditions. In the first case, where no intersection of hyperbolas occurs, the method achieves a significant reduction in the stretch effect and improved alignment of seismic events. The initial part of the algorithm [18] utilizes Equation (9) to address this case. This equation is employed to characterize vertical transverse isotropy (VTI) media through the heterogeneity parameter s. The following steps outline the implementation of the proposed nonhyperbolic stretch-free (NHSF) NMO correction for the scenario without hyperbola intersection:

• First, the semblance spectra are computed by setting $s=0$ and varying $V_{\mathrm{rms}}$ in Equation (9) to obtain the velocity spectrum and the initial velocity function.
• The initial velocity function is then used as input in Equation (9), varying the heterogeneity parameter s to compute its spectrum and derive the initial shift function.
• Optionally, depending on the degree of heterogeneity, the primary shift function is used as input in Equation (9) to recompute the updated $V_{\mathrm{rms}}$ function.
• Equations (10) and (11) are then used to generate overlaid contour plots of the paired $\left(v-t\right)$ and $\left(s-t\right)$ functions.
• Finally, these paired contour functions are interpreted using a zigzag picking technique across the width of the seismic wavelet to extract the optimal correction parameters.

The NMO correction technique effectively addresses the complexities of nonhyperbolic events, ensuring high fidelity in seismic data across varying offsets [17]. In this study, we specifically address the stretch phenomenon caused by two main factors: varying NMO correction values within a single trace or reflection event and nonhyperbolic travel-time behavior that leads to over correction. The most challenging scenario arises when these factors coincide with intersecting reflection hyperbolas. After addressing the simpler case of non-intersecting events, reflection trajectories are sorted in descending order based on their semblance values along the zigzag-picked velocity function. To mitigate interference, processing begins with the highest-energy events. A one-dimensional median filter is then applied to these trajectories to suppress noise while preserving coherent energy. Following this filtering step, amplitudes are estimated and subtracted from the original NMO gather to generate a residual gather that is used in subsequent iterations. This iterative procedure progressively extracts the most coherent and least interfering energy from the input data to construct the output gather. By applying the noise filter at each step, the algorithm preserves amplitude integrity while reducing interference from overlapping reflection events.

To map the energy of reflection events, a one-dimensional (1D) median filter was applied as a noise suppression tool. This filter enables the isolation of coherent energy associated with each previously sorted NMO trajectory. The median value, defined as the central element of a sorted sequence, minimizes the sum of absolute deviations from all other values in the window. This property makes it particularly effective in suppressing impulsive noise and isolated spikes that affect fewer than half of the samples in the window, while preserving broader, consistent variations representative of valid reflection events. When applied in the spatial domain, the median filter attenuates scattered noise by rejecting values that deviate significantly from local trends, based on the size of the spatial filter window. This helps to enhance the continuity of reflectors and improve the overall coherence of seismic events across the gather. To enhance the reflection energy mapping, we implemented a trajectory-based filtering algorithm centered on a 1D median filter, applied iteratively to each sorted NMO trajectory according to its semblance value. The algorithm operates as follows:

• Initialization: For each NMO trajectory, sorted in descending order of semblance, we begin the filtering process with the most coherent event. Each trajectory corresponds to a set of arrival times across traces within the CMP gather.
• Filtering Step: A moving median filter is applied to each trace along the selected trajectory. The filter window includes five samples: two before and two after the central point of the trajectory. This configuration smooths the signal by suppressing impulsive noise and preserving the continuity of coherent events.
• Residual Computation: After filtering a trajectory, its contribution is subtracted from the original CMP gather to produce a residual gather. This residual gather becomes the input for filtering the next trajectory, ensuring that overlapping energy contributions are progressively isolated and mapped with minimal interference.
• Iteration: Steps 2 and 3 are repeated for all NMO trajectories. Each filtered trajectory is accumulated to build the final NMO-corrected gather with enhanced reflector continuity and reduced noise artifacts.

This recursive filtering process ensures that reflection energy is accurately assigned to each trajectory, minimizing contamination from adjacent events and improving the clarity of the final image. The use of a median filter is particularly effective due to its robustness against outliers and its ability to preserve the shape of continuous seismic events, thereby reducing the impact of random noise and abrupt amplitude variations. Reflectors are mapped in advance, independent of their trajectories, allowing for the more accurate recovery of primary amplitudes before interference occurs. The proposed nonhyperbolic NMO correction technique was tested under complex conditions where conventional NMO methods typically underperform. It effectively mitigated distortions associated with intersecting travel-time curves—such as phase shifts and amplitude inconsistencies—which are critical for accurate subsurface imaging in geologically complex environments. The analysis demonstrated that this method not only preserved the continuity and fidelity of seismic reflections but also enhanced the overall data quality, resulting in clearer and more detailed subsurface images [16].

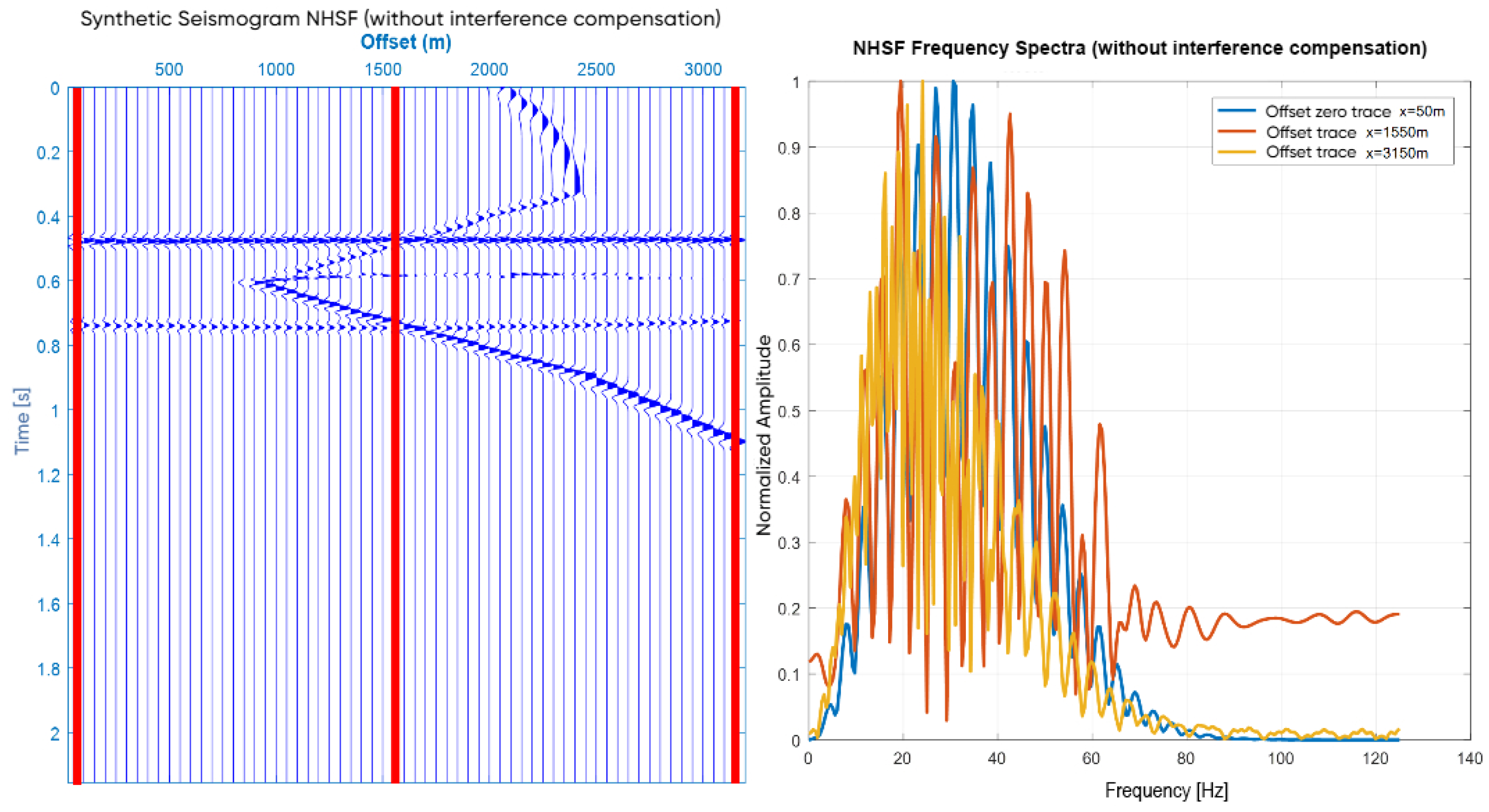
Figure 3 illustrates the outcome of applying conventional NMO correction to a synthetic gather. At mid-offsets, strong NMO stretch is clearly observed where the reflection hyperbolas intersect, resulting in severe waveform distortion. The first reflector at far offsets shows significant stretch, while the second reflector becomes laterally discontinuous. These artifacts are reflected in the frequency spectra, which exhibit a marked loss of high-frequency content compared to the zero-offset reference (blue curve). Moreover, there is a notable attenuation of amplitudes beyond ∼30 Hz, especially in the mid- and far-offset traces, indicating limited amplitude preservation across the gather.

Figure 4 presents the synthetic gather corrected using the proposed NHSF method without interference compensation. The second reflector now shows improved lateral continuity, indicating a reduction in the stretching effect. Compared to the conventional NMO, the frequency spectra remain more consistent across offsets, with broader bandwidth and stronger amplitudes preserved above 30 Hz. However, some minor amplitude fluctuations are still evident in the spectral plots due to residual interference. Overall, the NHSF method without compensation achieves improved amplitude preservation relative to standard NMO, particularly in the higher-frequency components.

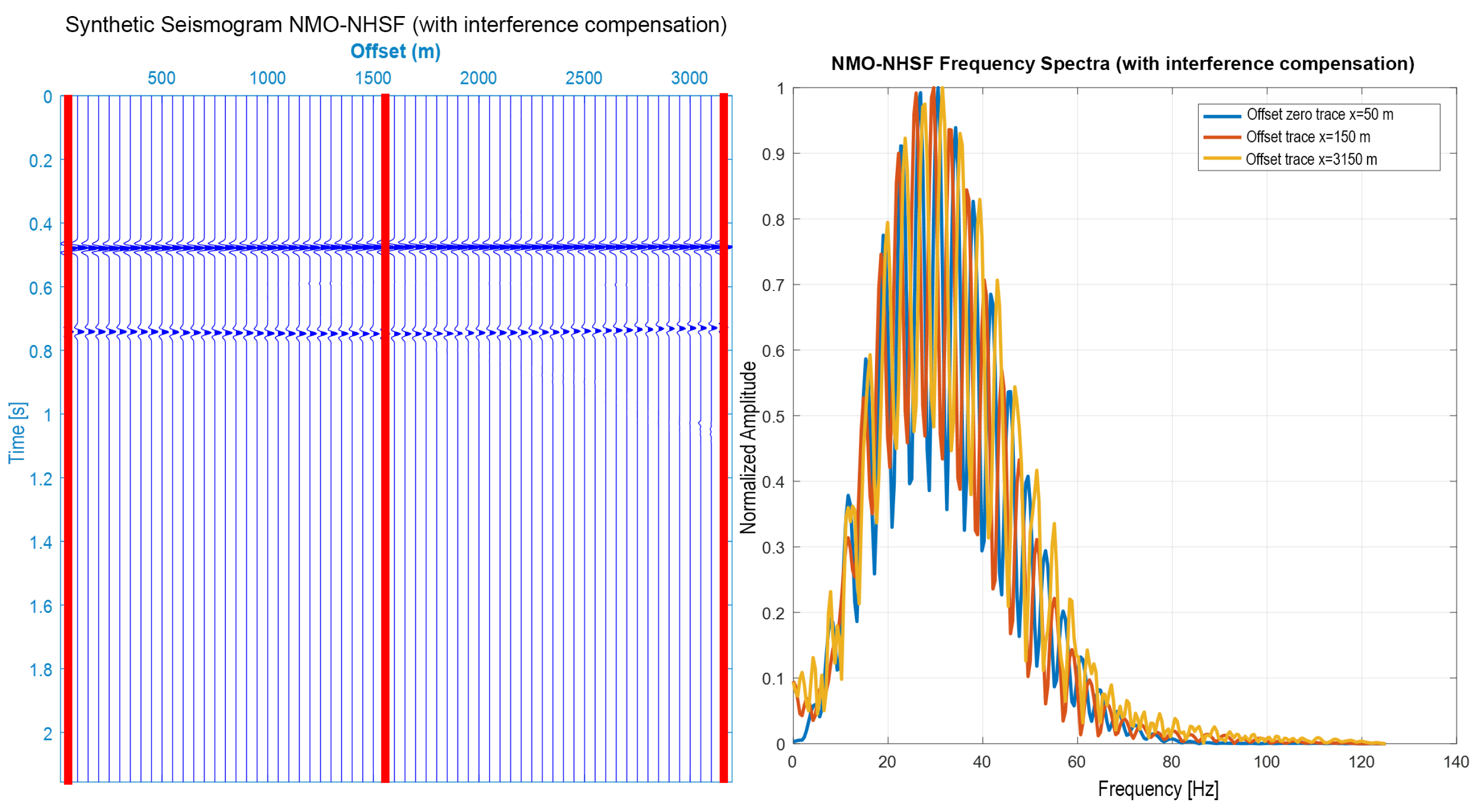
Figure 5 shows the fully corrected gather using the NHSF method with interference compensation. This configuration results in the most accurate correction, restoring both the continuity and the amplitude of reflection events. The frequency spectra reveal excellent alignment across all offsets, and the bandwidth closely matches the zero-offset reference. Notably, amplitude preservation is significantly improved: high-frequency components above 30 Hz are maintained with minimal distortion, and the overall spectral energy remains consistent across offsets. These results confirm the effectiveness of the interference compensation in mitigating amplitude degradation caused by NMO stretch.

These case studies underscore the versatility and robustness of the proposed NMO correction technique, demonstrating its potential to enhance seismic data processing across a range of exploration scenarios. They also serve as a valuable reference for future developments in NMO correction methodologies.

The algorithm was applied to a real dataset consisting of 401 prestacked CMP gathers migrated in time, integrated into the residual velocity analysis workflow. The objective was to evaluate the effectiveness of the NHSF-NMO method in addressing the stretch effect and correcting nonhyperbolic events. The methodology focused primarily on assessing improvements in seismic resolution at greater depths, as most prospective areas in Mexico are located in deep subsurface regions. The dataset characteristics are summarized in

Table 2. Acquisition and processing parameters of the real seismic dataset used to test the NHSF-PSM correction technique are summarized here. The dataset consists of 401 prestacked CMP gathers in migrated time, preprocessed for noise removal. These parameters define the temporal and spatial resolution of the data and were used to evaluate the performance of both conventional and proposed NMO correction methods under realistic field conditions.

Parameters	Values
Migrated time data without NMO	-
Sampling interval	4 ms
Samples number for each trace	501
Lenght in trace total time	2 s
Start time	2.5 s
End time	4.5 s
Fold	48
Min Offset	350 m
Max Offset	5050 m
Spacing between receptors	100 m

.

The dataset was preprocessed using standard procedures for the removal of coherent and random noise prior to dynamic correction, followed by the methodology proposed by [18].

To initiate the method, RMS velocities were picked every 10 CDP’s, resulting in 41 velocity curves used for the initial conventional NMO correction. Once the velocity function was established, the vertical heterogeneity parameter was analyzed. Iso-moveout curves were then plotted in both the velocity and heterogeneity panels to derive the parameter triplets $(v,s,t)$ needed to construct the zigzag velocity and vertical heterogeneity functions. 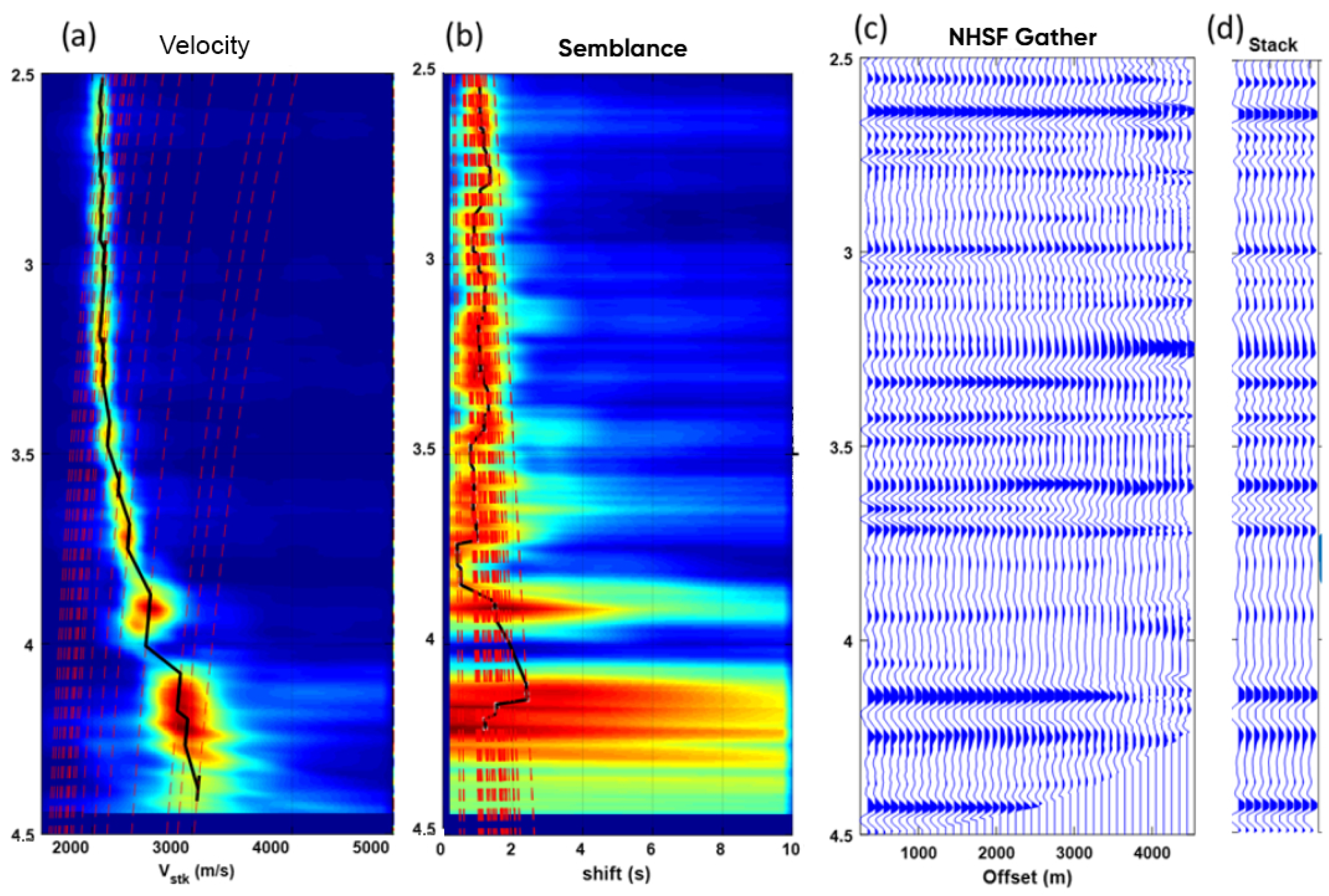Figure 6 shows the panels where iso-curves intersect each picked reflector, serving as a visual guide for generating zigzag trajectories based on these parameters and the approximate temporal length of the wavelet.

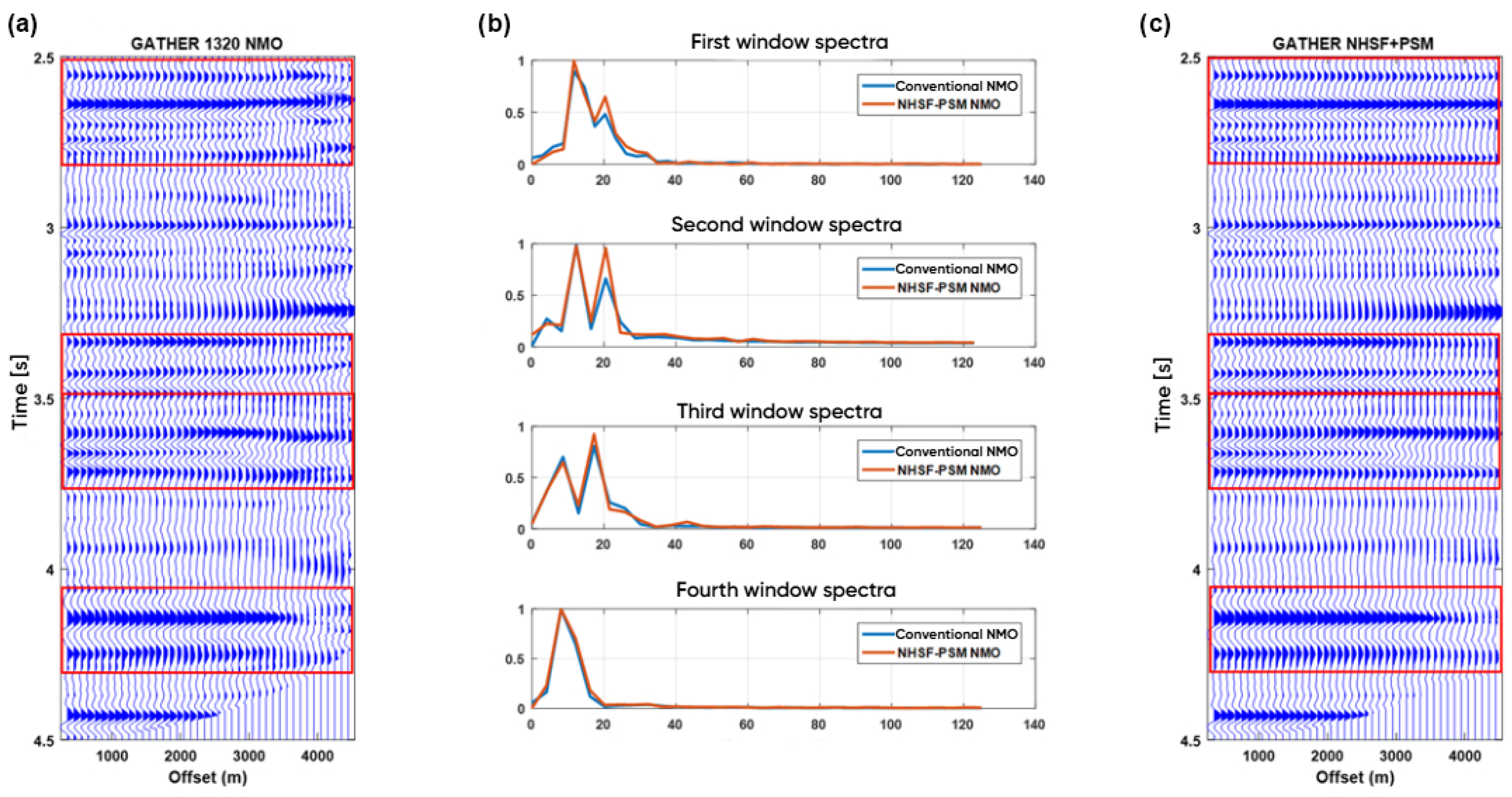
Analyzing the frequency spectra of the four windows shown in Figure 7, a noticeable improvement resulting from the proposed procedure can be observed. A similar process was applied to the 41 CDP gathers to obtain the RMS velocity curves, the s parameter curves, and the corresponding zigzag functions for both velocity and heterogeneity. Using these curves, two velocity models were constructed: a conventional RMS velocity model and an updated model based on the proposed method. These models were then used to generate the conventional stacked section and the enhanced stacked section obtained through the implemented NHSF correction technique, respectively.

The procedure for constructing the velocity models involved interpolating the curves obtained from the picking process. Once interpolation was completed, a two-step smoothing was applied using a moving average filter to prevent velocity anomalies (“velocity pulls”) that could cause abrupt distortions in reflector continuity in the stacked image. A similar procedure was used to generate both the zigzag RMS velocity model and the heterogeneity parameter (s) model, which were then used in the shifted hyperbola equation. The results are presented in Figure 8.

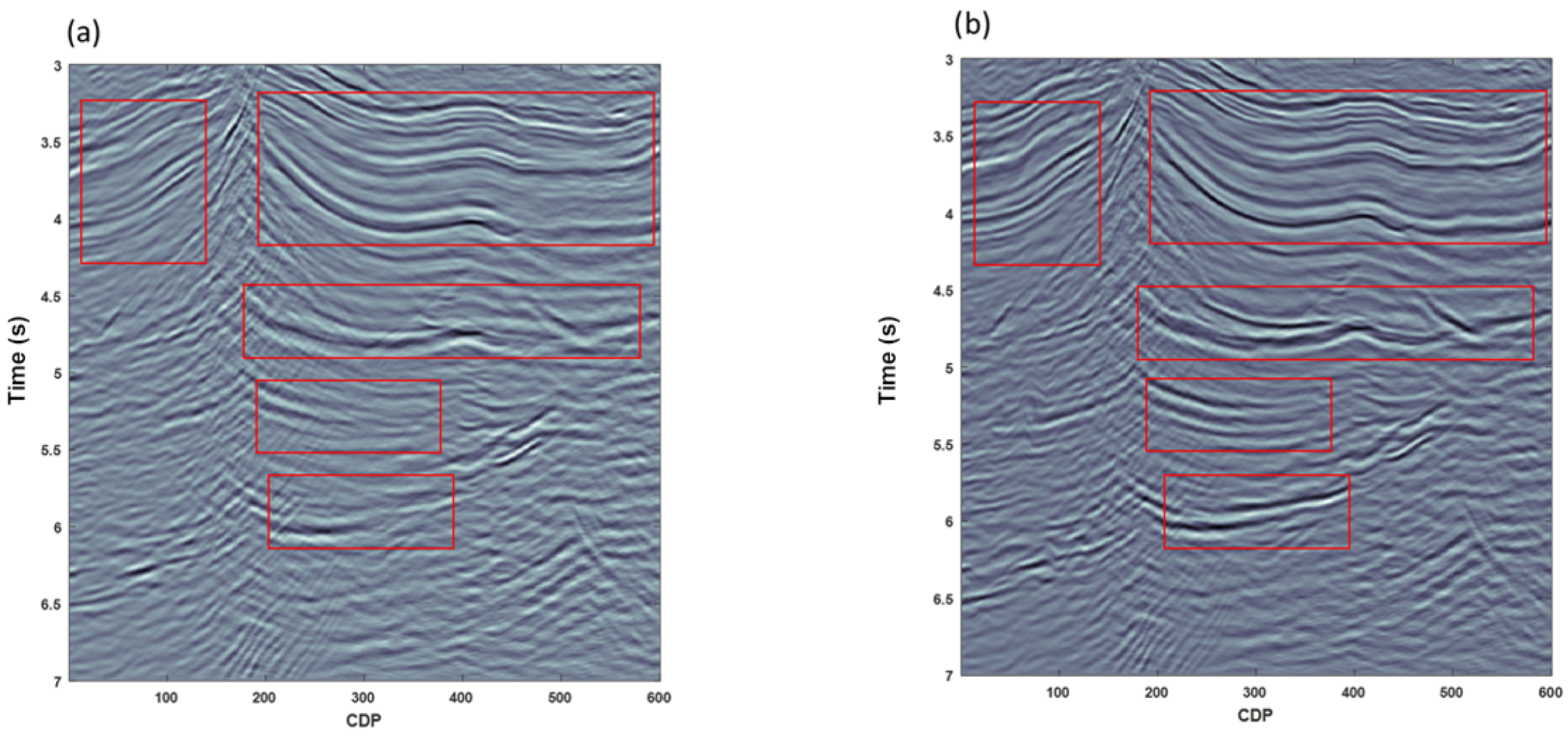
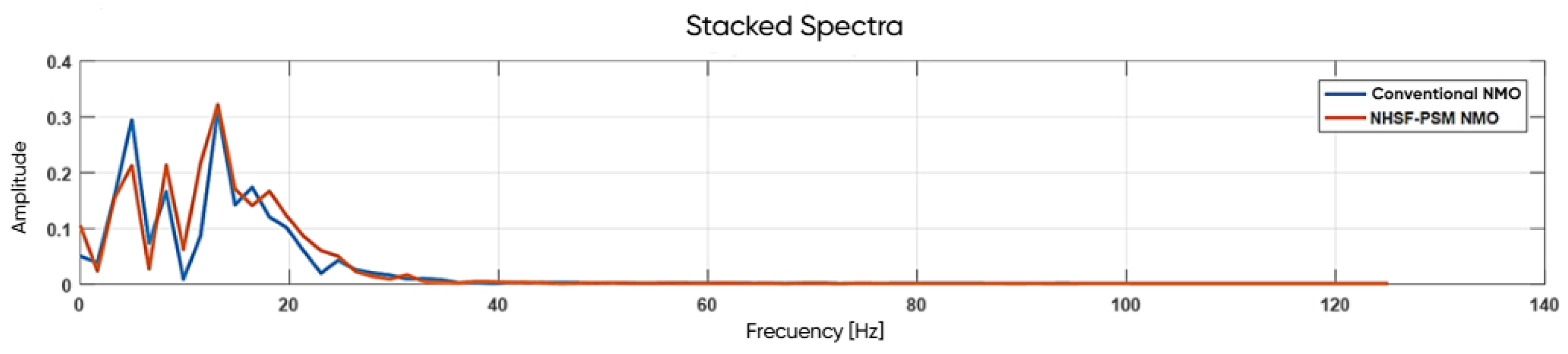
Figure 9a displays a seismic section after conventional NMO correction, showing the influence of stretch on the traces, with reflectors appearing wider compared to those in Figure 9b, which depicts sections corrected using the NHSF-NMO technique, which demonstrates improved sharpness and resolution, evident across almost all areas. Figure 10 provides a spectral analysis of the seismic windows highlighted in red in Figure 9. It compares the stacked frequency content resulting from conventional NMO correction versus the proposed NHSF-PSM technique. The spectrum derived from the NHSF-PSM stack (red curve) exhibits a higher amplitude in the dominant frequency range, indicating improved frequency preservation and reduced spectral degradation due to stretch effects.

Figure 11 displays the instantaneous frequency attribute, representing the average frequency derived from the amplitude spectrum of the seismic wavelet. A comparison between the two NMO correction methods shows that the proposed NHSF-PSM technique yields better lateral coherence and more distinct delineation of reflection surfaces. This suggests the improved preservation of frequency content, enabling clearer seismic character correlation across the section.

It is also essential to assess the stability of the applied processing as a form of quality control. Inspecting how these processes preserve the relative amplitude variation with respect to offset is crucial for ensuring the reliability of subsequent seismic workflows—particularly advanced processes such as simultaneous seismic inversion for elastic properties and rock physics or fluid analysis. Figure 12 illustrates the preservation of amplitude variation achieved through the proposed workflow. Additionally, the AVO curve is improved, facilitating better interpretation and enhancing the inversion results for reflectivity series related to various elastic properties and moduli.

While the proposed nonhyperbolic NMO correction technique represents a significant improvement over conventional methods, it still faces challenges—particularly its sensitivity to subsurface heterogeneities, especially in regions characterized by strong anisotropic effects. Such conditions can affect the accuracy of velocity estimation and reflection alignment. Moreover, the computational demands of the method are substantial, especially when applied to large datasets or geologically complex models, highlighting the need for further optimization to improve computational efficiency and scalability in exploration seismology [16]. Future research should focus on refining the technique to better accommodate anisotropic media and improve its robustness across diverse geological settings. This could involve the integration of additional correction mechanisms or the development of advanced models that more accurately capture seismic wave propagation behavior. Furthermore, leveraging advances in parallel computing and algorithmic optimization may significantly reduce the computational burden, enabling more efficient and potentially real-time seismic data processing. These improvements are essential to enhance the accuracy and reliability of seismic interpretation in complex exploration environments.

4. Discussion

The results demonstrate that the proposed nonhyperbolic stretch-free (NHSF) NMO correction technique significantly improves seismic data quality by mitigating the stretch effect, especially in long-offset data. Unlike traditional NMO methods, which are based on hyperbolic travel-time assumptions and are prone to amplitude loss and frequency degradation, the NHSF approach maintains better signal fidelity—preserving both amplitude and dominant frequency content across complex geological scenarios. When compared to previous techniques, such as the shifted hyperbolic methods proposed by Abedi and Riahi [18] or early formulations by Dix [19], the NHSF correction exhibits superior performance in handling anisotropy and heterogeneity. Recent studies have shown moderate success in adapting NMO to complex subsurface conditions [20,21], yet limitations persist, especially under extreme geological variation. Our approach builds upon these efforts by implementing a robust correction framework that operates effectively in the presence of steep velocity gradients, fractured zones, and vertically heterogeneous layers. While the method achieves notable improvements in seismic resolution and reflector continuity, certain limitations remain. The technique may show sensitivity to high noise levels and extreme anisotropic contrasts, and it currently requires substantial computational resources for large-scale or real-time processing. These constraints suggest that further refinement is needed to expand its practical application. Interestingly, the method also demonstrated increased computational efficiency compared to other nonhyperbolic techniques that rely on complex iterative calculations. This was achieved through a streamlined correction process with simplified parameter estimation, opening the door for its integration into conventional processing workflows [22,23]. Additionally, the field data examples presented in this study were limited to the depth interval corresponding to the target zone of interest. Although the stretch effect is typically more pronounced at shallow times, our processing focused exclusively on a temporally and spatially confined interval where AVO response and temporal resolution improvements were most critical. The seismic gather used for comparison was extracted from this specific interval, which aligns with the reservoir characterization objective of this work. Therefore, the time span did not begin at zero. Instead, it was selected based on data availability and interpretational relevance. This targeted gather conditioning strategy allowed for the optimization of frequency preservation and reflector continuity in the key reservoir zone without the unnecessary processing of irrelevant deeper or shallower sections. Future research should explore optimizing the algorithm’s performance under noisy conditions and extreme subsurface complexity. Incorporating machine learning and high-performance computing could enhance the method’s adaptability and speed. In addition, applying this technique to field datasets—particularly in offshore and unconventional reservoir settings—will be crucial for validating its robustness and practical impact. These efforts could help establish NHSF correction as a standard tool in modern seismic data processing.

5. Conclusions

This study presents a nonhyperbolic stretch-free normal moveout correction technique that significantly improves seismic data quality by mitigating the stretch effect—particularly in long-offset data. The method preserves amplitude and frequency content more effectively than conventional approaches, leading to clearer seismic images and more accurate velocity models. These enhancements have direct implications for hydrocarbon exploration, especially in geologically complex settings. The technique demonstrated robustness across both synthetic and real datasets, showing improvements in signal-to-noise ratio, frequency preservation, and gather flattening. Compared to earlier nonhyperbolic methods, such as that of Abedi and Riahi [18], our approach offers better adaptability to anisotropy and heterogeneity while maintaining relative amplitude relationships. While promising, the method’s limitations include sensitivity to high noise levels and computational demands. Future work should focus on algorithmic optimization and real-time implementation using advanced computing or machine learning. Applying this method across diverse acquisition scenarios and integrating it with migration or inversion workflows will further validate its utility. In summary, this work provides a practical, physics-based solution to a longstanding issue in seismic processing. By addressing the stretch effect with improved accuracy and computational efficiency, the NHSF correction method enhances the reliability of seismic interpretation and contributes meaningfully to the advancement of seismic data processing.