Abstract
In intermittent gas lift (IGL), not all the liquid initially in the tubing is usually produced at the surface in one cycle. This is due to a concept known as fallback, which occurs when some amount of the initial liquid column drops back to join the next slug. We conducted a review of earlier works on IGL and the behavior of the fallback factor. The dependence on the fallback factor on the operational conditions such as slug velocity, valve opening pressure, valve closing pressure, casing–tubing pressure ratio, diameter of tubing, and amount of gas injected during IGL are discussed in this paper. The effect on the shape and stability of the nose of the Taylor bubble on the lifting efficiency of the bubble is also explained. In trying to reduce the fallback factor per cycle, there have been recommendations to combine gas lift with plunger lift. We also present the results of this combination and the effects on the fallback factor in gas-assisted plunger lift (GAPL). More light is shed on the behavior of the velocity of the liquid slug and how it affects the fallback factor during IGL. The behavior of the fallback factor with an increase or decrease in plunger velocity during GAPL is also presented in this paper. This review is categorized into experimental and numerical studies on fallback factor to evaluate their impact on production efficiency in IGL and GAPL. Additionally, different formulas for fallback proposed by different literature are compiled.
1. Introduction
As production continues, the bottomhole pressure declines with time until a point is reached where the bottomhole pressure is not enough to lift the oil to the surface. At this point, an artificial lift method needs to be employed for production to continue. There are different types of artificial lift methods, such as gas lift, plunger lift, sucker rod pumping, and electronic submersible pumping, just to mention a few. In this paper, we will focus on two particular types of gas lift methods known as intermittent gas lift (IGL) and gas-assisted plunger lift (GAPL).
As an extension of natural flow, continuous gas lift is achieved by continuously injecting high-pressure gas at the lowest feasible depth to aerate the rising hydrocarbon stream, lowering the flowing bottom hole pressure and maximizing reservoir inflow [1]. At the early stages when artificial lifts are required for production and gas lifts are selected as the suitable method for a well, continuous gas lifts are commonly employed.
1.1. Intermittent Gas Lift (IGL)
Intermittent gas lift is a cyclic production technique that involves periodically injecting gas into the annular space between the production casing and the production tubing at the wellhead to create a high-pressure volume of gas. At the appropriate time, this gas is suddenly released into the tubing through the gas lift valve at the bottom of the production tubing [2]. This gas, which is released, forms a Taylor bubble beneath the liquid slug, which aids the liquid in reaching the surface by reducing the effective density of the oil. This kind of gas lift may be taken into consideration when a reservoir becomes depleted in order to sustain profitable primary oil recovery [3]. However, the instability of the process and the abundance of independent variables contribute to the difficulty of intermittent gas lift [4]. The cyclic nature of IGL makes it more suitable for relatively low-producing wells, typically less than 100 barrels of liquid per day (BLPD) [5].
The cyclic injection process in IGL introduces dynamic flow behaviors. Most notably, the phenomenon of fallback, where a portion of the lifted liquid fails to reach the surface, impacts the overall lifting efficiency. The concept of fallback factor is discussed in the section below.
1.2. Fallback Factor
As a result of the buoyant force, gas moves at a velocity higher than that of the liquid slug in upward multiphase flow. The gas penetrates a portion of the liquid slug, and some of the liquid falls back in the form of droplets or in a film along the tubing wall [6]. This phenomenon is known as fallback. Fallback and fallback factor are defined below.
fallback (fraction);
fallback factor (fraction normalized by depth);
initial amount of liquid slug (volume, length, or mass);
final amount of liquid slug (volume, length, or mass);
depth of valve.
The difference between fallback and fallback factor is that fallback is a fraction or percentage, while fallback factor is a fraction or percentage expressed as a function of depth. The ability to predict and control liquid fallback determines the efficiency of intermittent gas lift operation [6]. Despite a great deal of prior research, there is still no accurate method to estimate with any degree of accuracy the liquid fallback or the liquid slug velocity in the presence of several variables [4].
Given the challenges posed by fallback factor in IGL, techniques such as gas-assisted plunger lift (GAPL) have been implemented to improve recovery by minimizing fallback losses. The GAPL technique has been discussed in the section below.
1.3. Gas-Assisted Plunger Lift (GAPL)
As discussed earlier, in IGL, a low-density fluid (gas) is used to propel a high-density fluid (liquid) from downhole to the surface, and some amount of the liquid will fall back to join the next slug. Plunger lift (PL) is sometimes used in conjunction with gas lift to further minimize liquid fallback. Because the plunger and the slug of liquid above it are pushed to the surface by pressure beneath the plunger, the plunger minimizes the fallback of liquids [7]. Plunger lift in conjunction with gas lift is divided into two types: plunger-assisted gas lift (PAGL) and gas-assisted plunger lift (GAPL). Both PAGL and GAPL use a plunger and injection gas to maximize the potential of the well. While GAPL uses conventional plungers with intermittent gas injections, PAGL uses both continuous gas injection and a continuous flow plunger [8]. In order for the conventional plunger to reach the bottomhole spring assembly, this application needs a certain amount of shut-in time. To avoid unnecessary operating expenses, GAPL optimizes gas utilization by removing injections from the well during shut-in time, thereby reducing the possibility of over-injection and injection gas loss to the reservoir [9]. In this paper, the relationship between GAPL and fallback factor will be discussed.
2. Intermittent Gas Lift (IGL) and Fallback Factor
2.1. Experimental Studies on IGL and Fallback Factor
Winkler [10] was able to calculate liquid fallback from a pressure survey on a 5200 ft well with 2-inch tubing on IGL. The plot from the pressure survey is shown in Figure 1.
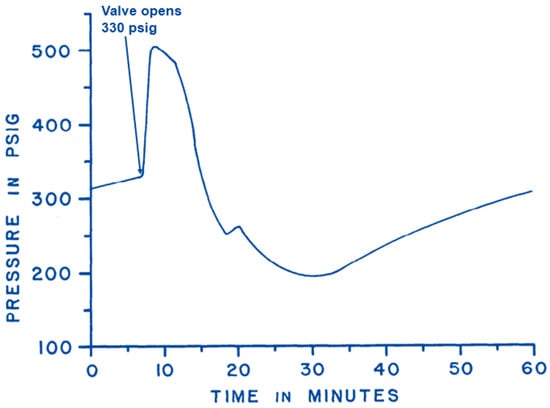
Figure 1.
Estimating the liquid fallback from the pressure survey using the downhole tubing pressure at the valve location [10].
The gas lift valve was at a depth of 4996 ft, and the pressure bomb for the survey was located at 5000 ft depth. From Figure 1, the pressure in the tubing above the valve right before the valve opens is 330 psig. Deducting the tubing backpressure from this and using the measured static fluid gradient of 0.31 psi/ft, the initial amount of the slug is about 3.5 barrels. The well was producing 1.5 barrels of liquid per cycle instead of producing 3.5 barrels. Hence, the percentage of liquid fallback was estimated as 63%. Expressing this as a fallback factor will be 12.6% per 1000 ft. This means 12.6% of the liquid is lost every 1000 ft.
Brown et al. [11] conducted fallback factor experiments on an 8000 ft well to analyze the effects of the port sizes of gas lift valves and chokes on the percent of liquid recovered and the fallback factor. The percent recovery increased with the pilot valve port size for the range of sizes used, even for the same gas injection requirements. Brown et al. [11] also concluded that efforts should be made to eliminate any flow restrictions in the flowlines, as that contributes to the increase in the amount of liquid fallback. White et al. [12] proposed an analytical model for the fallback factor based on the depth of the valve, slug velocity, and bubble penetrating velocity. However, White et al. [12] struggled to accurately model the bubble-penetrating velocity. Figure 2 shows a schematic diagram of IGL proposed by White et al. [12] where D is the depth, is the initial length of liquid, is the length of liquid produced, and is the amount of liquid fallback. It was proposed by a series of mathematical operations that the fallback can be modeled as follows:
where and are the slug velocity and the bubble penetrating velocity, respectively. From the model proposed by [12], the fallback factor depends on the velocity ratio since the depth will not change. As the velocity ratio increases ( increases or decreases), the fallback factor decreases. The fallback factor becomes minimum when the bubble-penetrating velocity is zero. They conducted experiments where the port area-to-tubing ratio, initial amount of slug, casing–tubing pressure, pipe ID, and casing volume were varied. They observed that the fallback factor also decreases with an increase in the casing–tubing pressure ratio. It was assumed that the penetrating velocity of a gas bubble through a liquid in a particular tubing is a constant for all practical purposes, and since there was generally no change in the penetrating velocity for scenarios of experiments conducted, this validated their assumption. Also, the velocity of the slug reaches a constant value quickly after the start of injection [12].
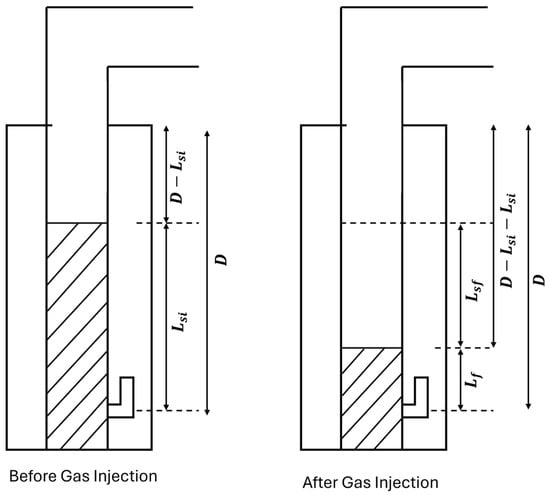
Figure 2.
Schematic diagram of an intermittent gas lift well before and after gas injection for modeling the liquid fallback [12].
Brill et al. [6] continued the work on IGL by providing an analytical description of the behavior of liquid slugs in vertical conduits using a 1500 ft test well with 1¼-inch and 1½-inch nominal tubing diameters [6]. At the end of experiments conducted, Brill et al. [6] developed a conceptual model for intermittent gas lift and an empirical fallback correlation for different slug lengths. The limitation of this empirical correlation for fallback is that it varies for different slug lengths, and another correlation is required when considering a slug of different length. Brill et al. [6] observed that the liquid slug initially undergoes high acceleration, then attains a constant velocity as it travels up the tubing. The velocity increases again when it is produced at the surface. This validates the assumption made by [12]. It was also observed that higher percentage recoveries were measured for when gas injection continues until the liquid slug reaches the surface as the liquid slug is unloaded to the surface flowline. Brill et al. [6] also came up with a dimensionless parameter known as the fallback number.
fallback number;
time-average penetrating velocity of gas;
time-average slug velocity.
Brill et al. [6] plotted the fallback number against the Froude number to measure the fallback , as shown in Figure 3. It can be observed that the fallback decreases as the Froude number increases. This is because for a given tubing size, as the slug velocity increases, the amount of gas that penetrates the liquid slug per unit time decreases. Hence, the fallback factor decreases [6].
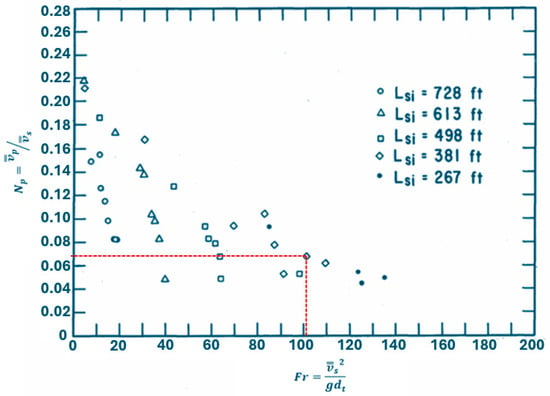
Figure 3.
Fallback as a function of slug velocity for a 1¼-inch tubing showing fallback decreases with increasing slug velocity (modified to find the fallback at a slug velocity of 1000 ft/min) [6].
According to Hernandez et al. [13], a good approximation of the average slug velocity is 1000 ft/min. Using an average slug velocity of 1000 ft/min for an initial slug length of 381 ft, then according to Figure 3, the fallback is about 0.07.
Doerr [14] investigated the loss of liquid in a 0.95-inch tubing intermittent gas-lift system. He created a theoretical method that links bubble and liquid velocities to film thickness in order to account for liquid loss. In further research, [15] observed that a significant amount of the produced liquid at the surface was a result of the entrained liquid in the gas afterflow behind the slug. That is a factor [12] did not consider, so a new approach was proposed by [15].
According to Neely et al. [15], a certain amount of entrained liquid can be contained and maintained in equilibrium by an ascending gas column. This liquid can be suspended but cannot be raised higher. This would be similar to a continuous, vertical, two-phase gas–liquid flow with zero net liquid velocity and a finite gas velocity. If this condition occurs in intermittent gas lift after the liquid slug and the gas afterflow have reached the surface, the suspended liquid will fall back as unrecovered liquid [15].
Schmidt et al. [16] proposed a hydrodynamic model for intermittent gas lift and conducted experiments in a 60 ft high and 3-inch diameter test facility to verify the simulation. It was observed that a significant portion of the liquid produced at the surface was due to the afterflow [16]. Similar to [15], Schmidt et al. [16] acknowledged that this produced liquid due to the afterflow could exceed 50% of the produced liquid. The fallback factor decreased as the injection pressure increased.
Again, Schmidt et al. [16] observed that the liquid slug accelerates rapidly, and then the velocity increases by a small amount until it reaches the surface. This was a discrepancy, as [6,12,15] observed that velocity remains constant after the rapid acceleration of the slug. This discrepancy could be due to the nature of friction. [16] conducted experiments with a 3-inch tubing length of 60 ft, while [6] conducted experiments with 1¼-inch and 1½-inch tubing of length 1500 ft. This means that the slug traveling up the tubing in [6] will experience more friction compared to the slug in [16]. This could be the reason why slight velocity increments are observed in [16] and not in [6]. The others who conducted their experiments in test wells did not observe this small velocity increment because of the smaller diameter and longer length of the test facility. Hence, the slug encounters more friction. This makes it unable to accelerate continuously.
In a study involving experiments with liquid slugs of 200 to 1400 ft, Hernandez et al. [4] found out that the two most relevant variables in optimizing the fallback factor in intermittent gas lift are the injection pressure and the total volume of gas injected per cycle. Increasing injection pressure increases slug velocity, which generally decreases fallback factor. Based on the results from a 3½ in tubing diameter, Hernandez et al. [4] showed that for a low seat-to-bellow ratio of the valve, slugs of length 200 ft were not able to be produced at the surface when the injection pressure was 900 psi. This is due to the small volume of gas injected per unit time when the valve opens.
If the gas rate is too high, the gas breaks through the liquid slug, which increases the liquid fallback. When the gas rate is too low, the gas bubbles through the liquid slug, which also increases the fallback. Hernandez et al. [4] concluded that if an optimum gas injection pressure and the amount of gas per cycle are chosen, the fallback can be lowered to nearly 0% of the initial length of liquid for the range of values of the slug length studied. Therefore, an accurate method for determining an optimal gas injection rate and gas injection pressure is required. Hernandez et al. [4] observed that increasing the volume of gas injected and decreasing the wellhead pressure increases the fallback factor.
Hernandez et al. [17] conducted research and proved the relevance of downhole pressure and temperature surveys on intermittent gas lift. In their paper, they suggested the need to use downhole surveys to calculate the liquid gradient in intermittent gas lift rather than calculating from the API oil gravity. They recorded about a 30% increase in production when this method was applied to 10 wells in the Lake Maracaibo gas lift field. Hernandez et al. [17] defined fallback factor as follows:
where:
- is the fallback factor; is the initial length of the liquid slug; is the length of the produced liquid per cycle; is the depth of the gas lift valve.
Hernandez et al. [13] conducted a field experiment to determine some important variables in the process at conditions similar to those employed in intermittent gas lift wells in Lake Maracaibo. In their experiment, a total of 16 sensors were fixed along the tubing to measure pressure and temperature within the tubing as well as in the annulus. They realized that the range of the initial length of the liquid column employed had little effect on the results [13]. This contradicts the results from [6], which showed varying fallback behavior for different initial slug lengths. Hernandez et al. [13] also realized that the higher the gas injection pressure, the better the lifting efficiency of the gas. They calculated the volume of gas required per cycle using energy balance. They realized that the values deviated from the experimental values, so a dynamic model was needed to accurately predict the intermittent gas lift phenomenon.
Hernandez et al. [13] also measured percentage fallback for two different initial liquid column lengths as a function of the volume of gas injected per cycle. The results were similar to that observed by [4]. Hernandez et al. [13] also conducted experiments on different liquids to observe the effect of liquid viscosity on fallback factor. They observed that the volume of gas required to achieve minimum fallback in 15 oAPI oil was twice the amount required to achieve minimum fallback in water and 23 oAPI. This confirms that the fallback factor increases with the viscosity of the liquid.
Carlson and Bordalo [2] did laboratory experiments on intermittent gas lift and fallback factor where the operational conditions were varied, and the corresponding fallbacks were measured. The operational parameters that varied were valve opening pressure, valve closing pressure, the slug length, and the volume of gas injected per cycle. In their paper, they defined fallback as follows:
fallback (fraction);
the mass of the initial liquid slug;
the mass of liquid slug produced at the surface.
Carlson and Bordalo [2] compared the relationship between fallback and diameter for two different valve opening pressures. Decreasing the valve closing pressure is similar to increasing the injection volume of the gas and reduces fallback. Increasing valve opening pressure increases the slug velocity and reduces fallback. They observed that the fallback factor increases with an increase in diameter. Carlson and Bordalo [2] concluded that this is because at larger diameters, the gas–liquid interface below the slug becomes unstable. This allows gas to easily penetrate the liquid slug, leading to larger fallback factor. The fallback factor also increases with decreasing valve opening pressure because of lower slug velocities. It was observed that the fallback factor increases with an increase in valve closing pressure. This is because a lesser amount of gas is injected into the tubing when the valve stays open for a short period of time [2].
Carlson and Bordalo [2] also studied the effect of the volume of gas injected as a function of recovery. Recovery is defined as the ratio of the produced amount of liquid to the initial amount of liquid. Higher recovery means lower fallback. They compared the recovery of two different slug loads and diameters (0.4 bar for a 2-inch diameter and 0.7 bar for a 1.5-inch diameter) at different valve opening pressures. It was observed that in both cases, increasing injection volume increases the percentage recovery, but the recovery for the 0.4 bar load and 2-inch diameter is relatively low. This is due to the combined effect of the decrease in slug length and an increase in diameter. For the same volume of injected gas, a decrease in slug length will allow more gas to penetrate the slug. This leads to an increase in fallback. The increase in diameter results in a decrease in the stability of the gas–liquid interface beneath the slug, which also leads to an increase in fallback [2].
Also, it was pointed out by [11] that the existence of surface chokes and many 90-degree bends on the surface will increase the fallback factor. Yadav et al. [18] recommended that a sweeping pipe bend be used at the Christmas tree to reduce fallback factor. The idea was implemented on three wells, and there was an average increase in liquid production of approximately 20% for the 5 wells that this was implanted in [18].
Table 1 summarizes most of the experimental studies that have been conducted on IGL and fallback factor. The experimental setup and the findings from the corresponding studies are also presented in Table 1.

Table 1.
Summary of experimental studies on IGL and fallback factor.
Table 2 presents a summary of all the different formulas for fallback proposed by different scholars. Formulas proposed by [2,4,10] follow the generalized fallback formula we proposed in Equation (1).

Table 2.
Summary of formulas for fallback proposed by different scholars.
2.2. Numerical Studies on IGL and Fallback Factor
Liao [19] proposed a mechanistic approach to simulating the intermittent gas lift operation. He wrote differential equations on the various stages of the IGL operation and solved the system of differential equations iteratively using the Euler iteration method. From his calculations, he also observed that the liquid slug accelerates rapidly, and then the velocity increases slowly until it reaches the surface, where it accelerates again. He attributed the slow increase in velocity to the combined effect of the reduction in tubing pressure at the top of the gas bubble and the decrease in length of the liquid slug as it travels. Liao [19] tried to determine the patterns for the slip velocity coefficient because increasing the slip velocity coefficient increases the fallback factor.
Pestana et al. [20] conducted a numerical simulation for intermittent gas lift. The simulator could predict the production, fallback, and the amount of gas consumed for a given well. However, they did not perform enough tests from real well data to prove the accuracy of the simulator, but it proved to be accurate with a few well data. Pestana et al. [20] made mention that during the decompression stage (the flow of gas in the tubing after the slug has surfaced) of the IGL cycle, the gas velocity has a strong effect on the fallback factor because the amount of liquid produced due to afterflow will depend on the gas velocity during the decompression stage.
Some studies suggest that the ability of a gas to efficiently lift a given amount of liquid to the surface depends on the geometry of the nose of the Taylor bubble produced [21]. White and Beardmore [22] did some research on the lifting efficiency of Taylor bubbles and related it to three non-dimensional quantities, which are the Eotvos number , the Froude number , and the viscosity number .
density of liquid;
density of gas;
diameter of tubing;
liquid surface tension;
slug velocity;
acceleration due to gravity.
Zheng et al. [23] conducted research on the same dimensionless numbers using computational fluid dynamics (CFD) and related the results to the shape of the Taylor bubble as shown in Figure 4, Figure 5 and Figure 6. The streamlines represent the liquid phase, and the blue bubble represents the Taylor bubble. From Figure 4, it can be observed that the edge of the nose of the Taylor bubble is shaped in the form of an ellipsoid, and the nose becomes less pointed with increasing . The curvature of the tail of the Taylor bubble is convex in (a) and in (b), but it takes a concave shape with a further increase in . The shape of the tail of the Taylor bubble shown in (c) results when the flow is viscosity dominated. From Figure 5, it is observed that the nose of the Taylor bubble becomes sharper with a decrease in , and the tail shape of the Taylor bubble changes from the concave shape to a blunter surface as decreases. The sharpness of the Taylor bubble nose increases with surface tension. A Taylor bubble with a sharper nose has an increased liquid film thickness at the front, reducing the falling film velocity. The velocity of the falling film reduces because the liquid film developing region extends to the nose of the Taylor bubble. Once the liquid film velocity is reduced, the gas can push most of the liquid film to the surface. This will result in a lower fallback. From Figure 6, the shape of the nose of the Taylor bubble remains almost the same throughout, indicating how weakly the value of the Froude number affects the nose of the Taylor bubble. For the range of Froude numbers simulated, the divergence of the streamlines reduces close to the nose of the Taylor bubble with increasing Froude number. This shows less penetration of the Taylor bubble in the liquid phase with increasing Froude number. According to Brill et al. [6], the fallback increases with increasing Froude number for high Froude numbers. However, since there was no variation in the shape of the nose of the Taylor bubble for the range of Froude numbers simulated by [23], we cannot draw any conclusion on how the Froude number affects the nose of the Taylor bubble. Hence, more research using computational fluid dynamics needs to be conducted on the behavior of the nose of the Taylor bubble for higher Froude numbers (values between 20 and 150).
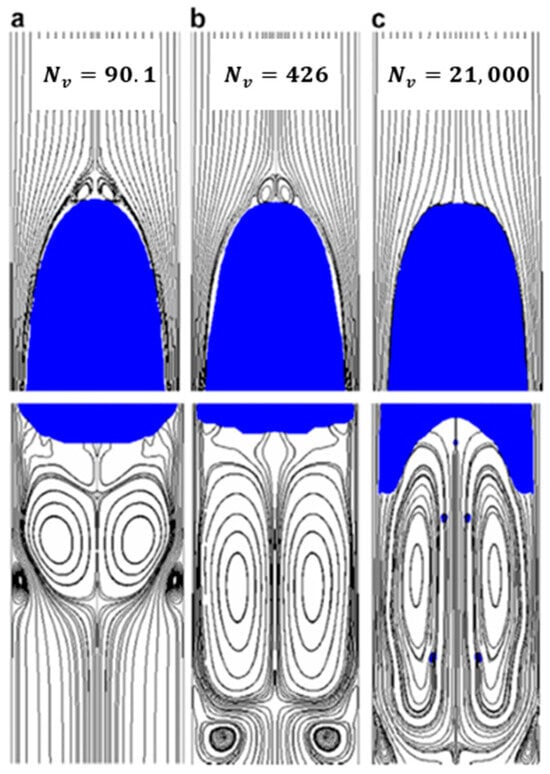
Figure 4.
Effects of different values of on the Taylor bubble shape with = 158 in a stagnant liquid: (a) ; (b) ; and (c) , showing that the nose of the Taylor bubble becomes less pointed with increasing [23].
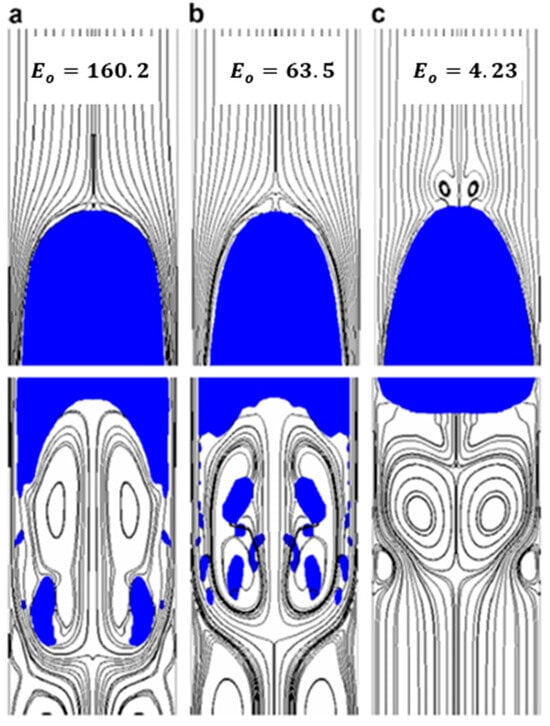
Figure 5.
Effects of different values of on the Taylor bubble shape with in a stagnant liquid: (a) ; (b) ; and (c) , showing that the nose of the Taylor bubble becomes sharper with decreasing [23].
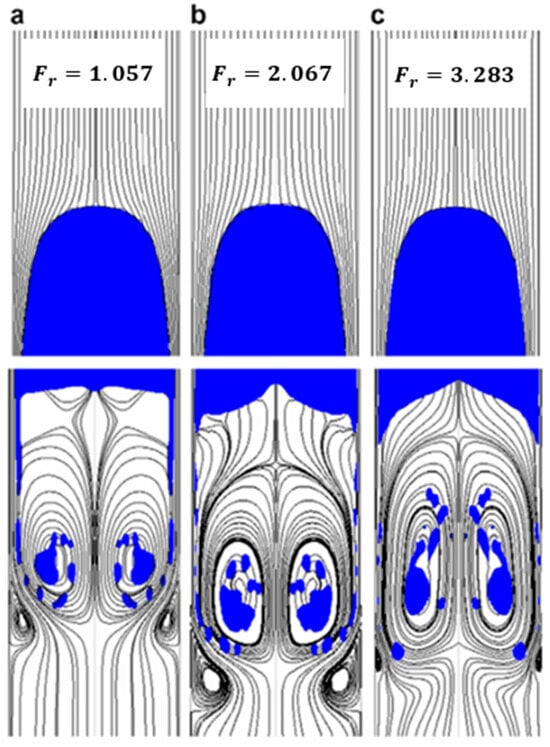
Figure 6.
Effects of different values of on the Taylor bubble shape with and : (a) ; (b) ; and (c) , showing that the nose of the Taylor bubble barely changes with changing [23].
Table 3 summarizes some of the numerical studies that have been conducted on IGL and fallback factor. The method and the findings from the corresponding studies are also presented in Table 3.

Table 3.
Summary of numerical studies on IGL and fallback factor.
3. Gas Assisted Plunger Lift (GAPL) and Fallback Factor
3.1. Experimental Studies on GAPL and Fallback Factor
There have been several studies on plunger lift as an artificial lift method. Foss and Gaul [24] conducted research with 100 wells from the Ventura field. They developed a force balance on the plunger conditions that give the lowest casing-head pressure needed to propel a plunger and a liquid or slug to the surface. Foss and Gaul [24] made some assumptions in their analysis by neglecting fallback, liquid column weight, plunger friction, and difference in pressure due to fluid entry below the plunger. Foss and Gaul [24] also assumed a constant plunger rise velocity of 1000 ft/min and a fall velocity of 2000 ft/min through gas and 172 ft/min through liquid to predict cycle time of the plunger and production amounts for a continuous cycle. Hacksma [25] used the model proposed by [24] together with an inflow performance relationship to estimate the minimum GLR (gas–liquid ratio) needed for plunger lift operation and the optimum GLR that gives the maximum production. He concluded that a plunger-lifted well with gas available to propel the plunger and the liquid slug as soon as it falls to the bottom represents the optimum plunger cycle. Lea [26] presented a more detailed dynamic model of plunger lift operations, which involves the estimation of the velocity of the plunger and the liquid slug as the plunger travels up the tubing. However, the possibility of gas slipping past the plunger as the plunger and the liquid slug travel up was not considered. He considered the liquid slug and the plunger as one control volume. The fallback of liquid was also neglected in the model. Lea [26] compared the model with that of [24] and showed that the model proposed by [24] overpredicts the gas requirement for a given cycle by 16%, which proved that plunger rise velocities are not constant.
White [27] conducted a reduced-scale experiment where fallback in gas lift was studied with and without a plunger. He conducted over 150 test runs, and plunger variations were also made. The results obtained are shown in Figure 7 below. It is observed that the use of the plunger increased the recovery vastly at low casing–tubing pressure ratios. Also, there were observed variations in the behavior of the plungers. Again, he observed that drilling a hole in the center increased the ability of the solid or capillary plunger to effectively propel the liquid. This is because the small hole allows high-velocity gas to pass through, which creates a piston-like nature of gas interface just above the plunger to propel the liquid. White [27] considered a particular intermittent gas lift installation illustrated by Figure 8 with a well depth, varied initial liquid length, and different casing-to-tubing ratios. The result of this study is shown in Figure 9. Despite the changes in the initial slug length-to-depth ratios and casing pressure-to-tubing pressure ratios, the amount of liquid recovered remained almost the same (90%) for when a plunger is not being used, as shown by the blue straight line. White [27] also showed adding a plunger lift to a gas lift reduces the injection gas requirement.
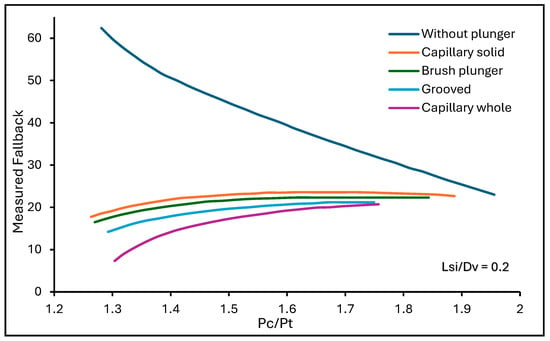
Figure 7.
Comparison of fallback with ratio of casing and tubing pressure for with and without a plunger showing the behavior of fallback with and without the plunger for initial slug length-to-valve ratio of 0.2 [27].
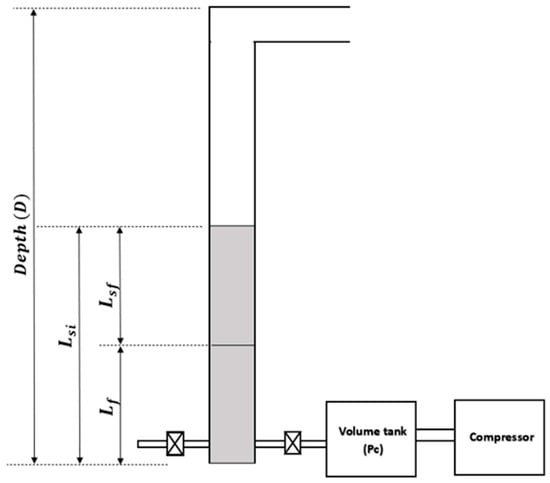
Figure 8.
A model of the artificial lift system for the study of fallback factor in GAPL [27].
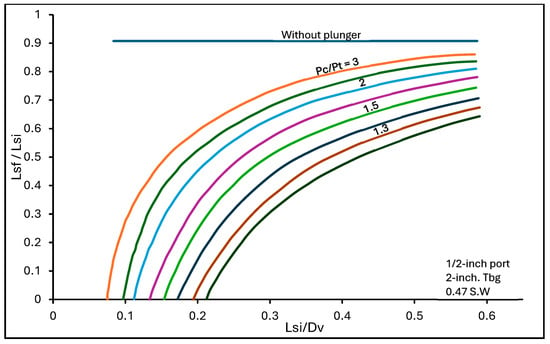
Figure 9.
Comparison of recovery with ratio of initial length of slug and depth of valve highlighting how the recovery does not vary with initial slug-to-valve depth ratio when without a plunger [27].
Mower et al. [28] conducted a laboratory study that involved modification of the model proposed by [24] by including liquid fallback and gas slippage for about twelve different plungers. A 735 ft laboratory test well was equipped with four mandrels spaced at about 179 ft intervals from a depth of 715 ft to 179 ft, each with a pressure transducer. They observed that the amount of liquid fallback depends on the plunger velocity. The least square fit of fallback against the velocity of the plunger obtained is shown in Figure 10. From Figure 10, it can be observed that the liquid fallback generally increases with an increase in average plunger velocity. The plunger that had the best behavior with increasing plunger velocity is the one that has the least slope in Figure 10. From Figure 10, it is plunger No. 8, and the plunger type for plunger No. 8 is an expanding blade plunger.
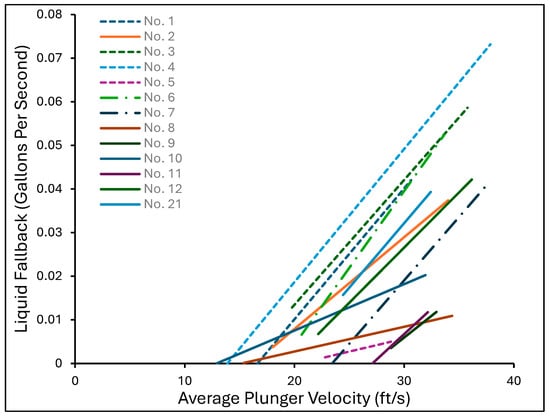
Figure 10.
Comparison of fallback with average plunger velocity and the behavior of fallback with average plunger velocity for different types of plungers [28].
Marcano and Chacin [29] came up with another dynamic model for the plunger cycle and then incorporated their model into a computer program. They accounted for fallback in their model using empirical data from Mower et al. [28]. Hernandez et al. [30] studied the behavior of liquid fallback as a function of injection pressure, volume of gas injected, and initial liquid column above the plunger. Liquid fallback was plotted against the average velocity of the plunger, and they saw that fallback was increasing with an increase in plunger velocity. This validates the observation made by [28].
Mantecon [5] conducted a study to optimize gas lift performance in Barrow Island. Before the optimization, there were chokes present in about 15 of 86 wells on conventional gas lift (CGL). There were also many elbows and bends existing at the surface, and these increase the liquid fallback. Mantecon [5] pointed out that for a well with low bottomhole pressure, having a high surface back pressure reduces production and increases the gas injection requirement. Other means, such as deepening the gas injection point, increasing the surface orifice, and running a larger port size of the bottomhole valve, can be used to stabilize the well when heading is detected rather than using surface chokes. Also, five wells were selected for the IGL and plunger lift study. The wells were initially on continuous gas lift and were converted to IGL after two months. Two of the wells were switched to PL after another two months. He observed a 19% increase in the oil production rate in one of the wells and a decrease in the gas injection of about 20 MCFD. No increase in production was observed in the second well, but the gas injection decreased by 80 MCFD.
Baruzzi and Alhanati [31] conducted a reduced experiment to analyze plunger lift performance. They noticed that the velocity of the liquid slug reduces greatly when it reaches the surface, and some liquid falls back through the plunger–tubing clearance. They attributed these changes to the surface restrictions and plunger inertia that makes the plunger penetrate the slug. This agrees with recommendations that pressure losses at the surface should be reduced through the elimination of surface restrictions and sharp bends [11]. Akhiiartdinov et al. [32] conducted research using a 2-inch tubing and 35-foot-long polycarbonate pipe to validate some of the assumptions made during the development of previous models. The pipe was instrumented with high-speed instruments such as pressure sensors, proximity sensors, optical sensors, and cameras. Akhiiartdinov et al. [32] estimated the plunger velocity with 6 high-speed proximity sensors spaced 1.5 ft apart. The experiment was carried out by varying the casing pressure, and a logging piston was used as the plunger tracked the pressure at the bottom and at the front of the plunger. Akhiiartdinov et al. [32] observed that the velocity of the plunger increases with the casing pressure.
Akhiiartdinov et al. [32] also calculated the slug velocities for different casing pressures using Equation (9) from the momentum balance from the model proposed by [19] using pressure measurements from the facility. They compared them with the slug velocities measured experimentally. The results calculated slug velocities and measured slug velocities were in good agreement, and this validates the assumption made by [19] when developing the model that the liquid slug contains no gas.
mass of the liquid slug;
velocity at the slug front;
pressure at the front of the plunger;
pressure at the slug front;
time;
area of tubing;
Moody friction factor for the slug;
height of slug;
diameter of tubing;
acceleration due to gravity.
Tan et al. [33] conducted both experimental and numerical studies on the lifting efficiency of plungers, considering the sealing performance of the plungers with the tubing wall. It was observed that the smaller the clearance between the plunger and the tubing wall, the better the lifting efficiency (the lower the liquid fallback). This observation agrees with the observation made by [31,33], who also observed that the lower the gas injection rate, the higher the fallback factor because the plunger would not have enough energy to propel the liquid column to the surface. This agrees with the observation made by [4].
Table 4 summarizes some of the experimental studies that have been conducted on GAPL and fallback factor. The experimental setup used and the findings from the corresponding studies are also presented in Table 4.

Table 4.
Summary of experimental studies on GAPL and fallback factor.
3.2. Numerical Studies on GAPL and Fallback Factor
Kannan [8] analyzed data from wells on GAPL in the Delaware Basin and developed a model for it using a transient multiphase simulator. A late-life case was simulated with 80% water cut and 1000 psi reservoir pressure to evaluate the feasibility of GAPL as a late-life artificial lift method. They ran similar simulations for the gas lift only and PL so that a comparison can be made. According to the simulation results, the well on GAPL will consistently produce oil, while the well on plunger lift alone will be fully laden and unable to do so. Less than 20 BLPD of liquid will be produced by the well using gas lift alone, compared to 42 BLPD using GAPL.
4. Discussion
4.1. Comparison Between Experimental and Numerical Studies
Experimental studies on fallback factor in IGL have been the foundation of identifying key operational variables such as slug velocity, injection pressure, tubing pressure, and viscosity. Earlier field-based experimental studies relied on pressure surveys and physical observations to estimate the fallback factor [10,15,16]. These studies highlighted the complex nature of IGL, such as gas penetration velocity and liquid afterflow. Experimental results also highlighted other factors that can influence the fallback. These factors include surface restrictions, tubing geometry, and the stability of the gas–liquid interface [6,11]. However, some of the complex fluid behavior, like Taylor bubble dynamics, could not be precisely studied using experiments alone.
In contrast, numerical studies on IGL have aimed to simulate these intricate behaviors by modeling dynamic slug behavior. Numerical studies like [19,23] allowed for deeper theoretical understanding of behaviors such as slip velocity and dimensionless numbers that relate to the shape of the Taylor bubble. These studies offered predictive capabilities of the system and helped explain how changes in physical properties influence fallback factor.
Similarly, for GAPL systems, experimental studies provided valuable field-related observations. Studies like those from [27,28,33] quantified how fallback factor is affected by gas injection rate, plunger velocity, and plunger–tubing clearance. On the numerical side, [32,33] used force and momentum balance, sometimes validated with experimental data, to simulate the plunger dynamics and predict fallback factor. Unlike IGL models, GAPL models tend to be less complex because they involve relatively more controlled, piston-like flow and fewer multiphase interactions. This makes them relatively easier to validate.
To sum up, experimental studies offer indispensable empirical evidence and field relevance under varied operational conditions. Numerical studies, although powerful for scenario testing, rely heavily on assumptions and require robust validation from experimental data.
4.2. Feasibility Analysis on Methods to Reduce Fallback Factor
While various methods for reducing fallback factor have been proposed, the feasibility and cost-effectiveness of their field applications may vary based on the conditions in the actual field. Analytical and field studies conducted by [34] demonstrated that increasing the gas injection pressure improves the lifting performance of the plunger, but the curve plateaus. Therefore, an optimum injection pressure can be found from this curve to avoid over-injection of gas.
Also, field studies have shown that transition from conventional gas lift or PAGL to GAPL reduces the fallback factor and gas injection requirement. A study conducted by [9] showed that transitioning from PAGL to GAPL increases production slightly and reduces the gas injection requirement by two-thirds.
Additionally, recent work presented by [18] by replacing the 90-degree bend at the wellhead with sweeping pipes reduced the surface backpressure. This resulted in an increase in the average production of about 20% per well for the 5 wells that this was implanted in.
5. Conclusions
This review was conducted on IGL, GAPL, and their relationship with the fallback factor. From this review, it is important to point out that more experimental and computational studies need to be conducted to understand the behavior of long Taylor bubbles and long liquid slugs in multiphase fluid flow similar to those encountered in intermittent gas lift. We have analyzed studies on the behavior of Taylor bubbles from multiphase flow literature. However, the length of the Taylor bubbles is smaller compared to the ones encountered in IGL and GAPL. For this reason, research on the behavior of long Taylor bubbles, typically over 1000 pipe diameters, needs to be conducted both experimentally and by using CFD. Also, studies on Taylor bubbles need to be conducted to establish the critical length to categorize a Taylor bubble as long or short.
Additionally, more numerical studies on gas-assisted plunger lift need to be conducted, as we lack literature in this area of research. The behavior of the plunger and the fallback factor also need to be studied for different viscosities. The conclusions from this review are primarily for vertical and near-vertical wells. The following are some of the conclusions that were gathered from literature about the behavior of the fallback factor in intermittent gas lift and gas-assisted plunger lift:
- Surface restrictions such as chokes increase the fallback factor, and efforts should be made to eliminate surface restrictions and reduce the number of sharp bends at the surface [11].
- Higher percentages of recoveries are observed when the gas injection continues until the liquid slug reaches the surface [6].
- Fallback factor decreases with increasing slug velocity [6].
- Fallback factor decreases with increasing casing–tubing pressure ratio [12].
- Increasing the volume of gas injected per cycle reduces the fallback factor in IGL [4,13].
- Fallback factor increases with increase in viscosity [13].
- Fallback factor increases with increasing the diameter of the tubing for the same gas injection rate and volume [2].
- Employing GAPL minimizes the fallback factor by a significant amount compared to IGL. This is because the solid interface (plunger) reduces the gas penetration in the liquid slug at lower velocities [27].
- GAPL also reduces the injection gas requirement [27].
- Liquid fallback increases with increasing plunger velocity in GAPL [28,30].
- Not only does GAPL minimize the fallback factor, but it also makes it possible to lift from deeper wells, which increases the life of artificial lift by delaying switching to rod pumping [8].
Author Contributions
Conceptualization, E.M.; methodology: EM.; software, E.M.; validation, E.M. and S.L.; formal analysis, E.M.; investigation, E.M.; resources, E.M.; data curation, E.M.; writing—original draft preparation, E.M.; writing—review and editing, S.L.; visualization, E.M.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Texas Tech Gas Lift Consortium. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript, and in the decision to publish the results.
Data Availability Statement
No additional data were used in this review.
Acknowledgments
The authors would like to acknowledge the following companies, which are sponsors of the Texas Tech Gas Lift Consortium: Occidental Petroleum (OXY), Endeavor Energy, Conoco Philips, Exxon Mobil, Apache, Fasken Oil and Ranch, Precise, Estis, B&L Pipeco, Fesco Ltd., ChampionX, FlexSteel, ProLiftCo, Cameron, Weatherford, Amplified Industries, Patriot Premium Threading Services, Kimray, Mako Lift, and Standard Energy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chacin, J.E. Selection of Optimum Intermittent Lift Scheme for Gas Lift Wells. In Proceedings of the University of Tulsa Centennial Petroleum Engineering Symposium, Tulsa, OK, USA, 29–31 August 1994; pp. 301–313. [Google Scholar]
- Carlson, O.; Bordalo, S.N. Experimental Study of the Dynamics and Stability of Intermittent Gas-Lift in a Laboratory Scale Model. In Proceedings of the Society of Petroleum Engineers—SPE Latin America and Caribbean Mature Fields Symposium, Salvador, Bahia, Brazil, 15–16 March 2017; pp. 6–8. [Google Scholar]
- Pittman, R.W. Gas Lift Design and Performance. In Proceedings of the International Petroleum Exhibition and Technical Symposium of the Society of Petroleum Engineers, Dallas, TX, USA, 18–26 March 1982; p. 1. [Google Scholar]
- Hernandez, A.; Luisana, M.; Gonzalo, G.; Miguel, M.; Sergio, C.; Oswaldo, R.; Intevep, S.A. Field Scale Research on Artificial Lift. In Proceedings of the Fifth Latin American and Caribbean Petroleum Engineering Conference and Exhibition, Rio de Janeiro, Brazil, 30 August–3 September 1997; pp. 2–7. [Google Scholar]
- Mantecon, J. Gas-Lift Optimisation on Barrow Island, Western Australia. In Proceedings of the SPE Asia Pacific Oil & Gas Conference & Exhibition, Singapore, 8–10 February 1993; pp. 237–242. [Google Scholar]
- Brill, J.P.; Doerr, T.C.; Aime, J.M.; Brown, K.E. An Analytical Description of Liquid Slug Flow in Small-Diameter Vertical Conduit. J. Pet. Technol. 1967, 19, 419–431. [Google Scholar] [CrossRef]
- Maggard, J.B.; Wattenbarger, R.; Scott, S.L. Texas A&M University Modeling Plunger Lift for Water Removal from Tight Gas Wells. In Proceedings of the SPE/CERI Gas Technology Symposium, Calgary, AB, Canada, 3–5 April 2000; pp. 2–6. [Google Scholar]
- Kannan, S.K.; Boyer, M.; Petroleum, A.; Yuan, G.; Lu, H.; Fai-Yengo, G. Modeling and Optimization of Gas-Assisted Plunger Lift GAPL by a Transient Simulator: A Case Study of a Permian Shale Well. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 15–17 October 2019; pp. 2–13. [Google Scholar]
- Burns, M. Plunger-Assisted Gas Lift and Gas-Assisted Plunger Lift. In Proceedings of the SPE Artificial Lift Conference and Exhibition—Americas, The Woodlands, TX, USA, 28–30 August 2018; pp. 2–5. [Google Scholar]
- Winkler, H.W. The Application of Pressure and Temperature Surveys to Gas Lift Installations. In Proceedings of the Southwestern Petroleum Short Course, Lubbock, TX, USA, 23–24 April 1959; p. 49. [Google Scholar]
- Brown, K.; Jessen, F. Members AIME Evaluation of Valve Port Size, Surface Chokes and Fluid Fall-Back in Intermittent Gas-Lift Installations. J. Pet. Technol. 1962, 14, 315–322. [Google Scholar] [CrossRef]
- White, G.W.; O’connell, B.T.; Davis, R.C.; Berry, R.F.; Leon, A.; Stacha, A. An Analytical Concept of the Static and Dynamic Parameters Of Intermittent Gas Lift. J. Pet. Technol. 1963, 15, 301–307. [Google Scholar] [CrossRef]
- Hernandez, A.; Gasbarri, S.; Machado, M.; Marcano, L.; Manzanilla, R.; Guevara, J. Field-Scale Research on Intermittent Gas Lift. In Proceedings of the SPE Mid-Continent Operations Symposium, Oklahoma City, OK, USA, 28–31 March 1999; pp. 1–5. [Google Scholar]
- Doerr, T.C. Experimental Study of Liquid Loss in Intermittent Gas-Lift Systems; The University of Texas at Austin: Austin, TX, USA, 1972. [Google Scholar]
- Neely, A.B.; Montgomery, J.W.; Vogel, J. A Field Test and Analytical Study of Intermittent Gas Lift. Soc. Pet. Eng. J. 1974, 14, 502–511. [Google Scholar] [CrossRef]
- Schmidt, Z.; Of Tulsa, U.; Doty, D.R.; Lukong, P.B.; Of Tulsa, S.U.; Fernandez, O.F.; James, S.A.; Brill, P. Hydrodynamic Model for Intermittent Gas Lifting of Viscous Oil. J. Pet. Technol. 1984, 36, 475–484. [Google Scholar] [CrossRef]
- Hernandez, A.; Garcia, G.; Concho, A.M.; Garcia, R.; Navarro, U. Downhole Pressure and Temperature Survey Analysis for Wells on Intermittent Gas Lift. In Proceedings of the SPE International Petroleum Conference and Exhibition, Villahermosa, Mexico, 3–5 March 1998; pp. 205–212. [Google Scholar]
- Yadav, M.P.; Malhotra, S.K.; Kumar, A.; Devshali, S. Production Enhancement in Intermittent Gas Lift Wells Using Sweeping Pipe Bend-Successful Case Histories from Various Onshore Fields in India. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 15–18 November 2021; pp. 4–7. [Google Scholar]
- Liao, T. Mechanistic Modeling of Intermittent Gas Lift. Ph.D Dissertation, The University of Tulsa, Tulsa, OK, USA, 1991. [Google Scholar]
- Pestana, T.; Bordalo, S.; Filho, A.B.; Brasileiro, P. Numerical Simulation in the Time Domain of the Intermittent Gas-Lift and Its Variants for Petroleum Wells. In Proceedings of the SPE Artificial Lift Conference-Americas, Cartagena, Colombia, 21–22 May 2013; pp. 2–6. [Google Scholar]
- Croce, D.; Zerpa, L. Mechanistic Model for the Design and Operation of an Intermittent Gas Lift System for Liquid Loaded Horizontal Gas Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 21–23 September 2021; p. 3. [Google Scholar]
- White, E.T.; Beardmore, R.H. The Velocity of Rise of Single Cylindrical Air Bubbles through Liquids Contained in Vertical Tubes. Chem. Eng. Sci. 1961, 17, 351–361. [Google Scholar] [CrossRef]
- Zheng, D.; He, X.; Che, D. CFD Simulations of Hydrodynamic Characteristics in a Gas-Liquid Vertical Upward Slug Flow. Int. J. Heat Mass Transf. 2007, 50, 4151–4165. [Google Scholar] [CrossRef]
- Foss, D.L.; Gaul, R.B. Plunger-Lift Performance Criteria with Operating Experience-Ventura Avenue Field. In Proceedings of the Pacific Coast District, API Division of Production, Los Angeles, CA, USA, 2 May 1965; pp. 124–140. [Google Scholar]
- Hacksma, J. Users Guide to Predict Plunger Lift Performance. In Proceedings of the Southwestern Petroleum Short Course, Lubbock, TX, USA, 20–21 April 1972; pp. 109–118. [Google Scholar]
- Lea, J.F. Dynamic Analysis of Plunger Lift Operations. J. Pet. Technol. 1982, 34, 2617–2629. [Google Scholar] [CrossRef]
- White, G.W. Combine Gas Lift, Plungers to Increase Production Rate. World Oil 1982, 195, 69–74. [Google Scholar]
- Mower, L.N.; Lea, J.F.; Beauregard, E.; Ferguson, P.L. Defining the Characteristics and Performance of Gas-Lift Plungers. In Proceedings of the Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Las Vegas, NV, USA, 22–26 September 1985; pp. 1–12. [Google Scholar]
- Marcano, L.; Chacin, J. Mechanistic Design of Conventional Plunger-Lift Installation. In Proceedings of the Second Latin American Petroleum Engineering Conference, Caracas, Venezuela, 8 March 1992; pp. 15–24. [Google Scholar]
- Hernandez, A.; Maracano, L.; Caicedo, S.; Cabunaru, R.; Members, S.A. Liquid Fall-Back Measurements in Intermittent Gas Lift with Plunger. In Proceedings of the Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Houston, TX, USA, 3–6 October 1993; pp. 3–6. [Google Scholar]
- Baruzzi, J.O.A.; Alhanati, F.J.S. Optimum Plunger Lift Operation. In Proceedings of the Production Operations Symposium, Oklahoma City, OK, USA, 2–4 April 1995; pp. 117–131. [Google Scholar]
- Akhiiartdinov, A.; Pereyra, E.; Sarica, C. Experimental and Theoretical Analysis of a Pressure-Driven Logging Piston During the Liquid Displacement Process. Exp. Therm. Fluid Sci. 2020, 115, 110090. [Google Scholar] [CrossRef]
- Tan, X.; Deng, Y.; Luo, A.; Li, X.; Tian, W.; Li, X.; Liu, Y.; Zhou, C. Experimental and Numerical Simulation Research on Sealing Performance and Drainage Efficiency of Different Types of Plungers. Geoenergy Sci. Eng. 2023, 224, 211517. [Google Scholar] [CrossRef]
- Bello, O.; Falcone, G.; Xu, J.; Scott, S. Performance Evaluation of a Plunger Assisted Intermittent Gas Lift System. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 27–29 March 2011; pp. 1–20. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).