Moon-Induced Differential Rotation in Earth’s Interior: A Comprehensive Conceptual Model

Abstract

This study presents a novel conceptual model to explain the differential rotation within Earth’s layers, a phenomenon observed through seismic wave studies but not fully understood. While geodynamo theory and electromagnetic coupling models have been proposed to explain this phenomenon, our model offers an alternative perspective focusing on the Moon’s tidal forces. Our model proposes that the Moon’s tidal forces play a crucial role in this process, acting as a braking mechanism on Earth’s rotation. We hypothesize that these tidal forces initially decelerate the Earth’s crust and mantle, with this effect sequentially transmitted to deeper layers. A key aspect of our model is the role of the liquid outer core in mediating this process. We suggest that the liquid state of the outer core delays the transmission of tidal friction, resulting in differential rotation between layers in contact with it. This delay mechanism provides a potential explanation for the observed rotational differences between the mantle and core. Our model demonstrates that about 66,000 years after the Moon’s formation, the tidal force slowed the crust–mantle rotation by approximately 5.5 degrees per year more than the core. Furthermore, we estimate that the frictional heat generated at the boundaries of differential rotation is about 0.3478 TW. At this rate, the outer core temperature would increase by approximately 13.4 K per billion years. This thermal effect may have significant implications for the long-term evolution of Earth’s core, potentially slowing its cooling rate and maintaining its liquid state. Our model thus provides a new perspective on the interplay between lunar tidal forces, Earth’s internal structure, and its thermal evolution, offering insights into the complex dynamics of our planet’s interior.

1. Introduction

For centuries, it had been accepted without doubt that the Earth’s interior layers rotate at the same angular velocity. This understanding was challenged when evidence of differential rotation emerged, leading to significant changes in our view of Earth’s internal dynamics. It is primarily due to the immense pressure and resulting viscosity within the Earth’s core [1,2]. Such a thermodynamic environment of the Earth’s interior led to the concept that the high viscosity in the layer would not naturally allow any differential rotational movement. As new research and technological advancements emerged in the 1980s, evidence revealed the possibility of varying rotational speeds within Earth’s layers, indicating a more complex internal dynamical process than previously thought.

The concept of Earth’s inner core’s differential rotation was initially put forward by Gubbins (1981) [3], who suggested that magnetic torques, generated by fluid movement in the outer core, could cause the inner core to spin westward faster by approximately 0.2 degrees per year. This idea was significantly advanced by geodynamo simulations, which demonstrated that the inner core could rotate faster by about 2–3 degrees longitude per year relative to the solid mantle and surface [4,5]. Motivated by these findings, Song and Richards (1996) [6], Su et al. (1996) [7], and Creager (1997) [8] sought observational evidence in seismic data, estimating the differential rotation to be between 0.2 and 3 degrees per year. Zhang et al. (2005) [9] found that the Earth’s inner core rotates faster than the mantle and crust, at an estimated rate of 0.3 to 0.5 degrees per year. Despite these results, the existence of this inner core’s super-rotation remains controversial due to an uncertainty in the data analyses, as questioned by Souriau et al. (1997) [10] and Souriau (1998) [11]. More recent studies have utilized P-wave backscattering from nuclear explosions to provide more precise measurements of inner core movements, revealing the complex, oscillatory nature of these movements and further contributing to our understanding of this phenomenon [12,13,14,15].

The phenomenon of Earth’s inner core’s differential rotation has been extensively explored through various mechanisms and studies of Earth’s rotation and internal structure (e.g., [16]). Two interconnected theories, the geodynamo theory and electromagnetic coupling models, provide key insights into this phenomenon. The geodynamo theory posits that Earth’s intrinsic magnetic field is generated by convective flows within its fluid outer core [4,5,17,18]. Building on this concept, electromagnetic coupling models suggest that interactions between the generated magnetic field and the solid inner core could drive the inner core’s differential rotation [4,5]. These approaches primarily focus on internal geodynamic processes, providing insights into the complex interactions between the core and mantle that could influence inner core rotation. Further understanding is still needed regarding the initial causes of geomagnetism at Earth’s formation and the continual drivers of convection within the outer core.

In contrast to these internal perspectives, another approach to understanding Earth’s rotational behavior considers the potential influence of external forces. This perspective examines the effects of the Moon’s gravitational pull on Earth’s rotational behavior. Research on lunar tidal forces has focused on tidal torque and its impact on Earth’s rotation rate [19,20,21], as well as tidal friction and Earth’s rotational deceleration [22,23,24]. Despite these advancements, a comprehensive explanation of how lunar tidal forces directly influence differential rotation within Earth’s layers, particularly the inner core, remains elusive. While Mohazzabi and Skalbeck (2015) [22] touched upon this topic, their focus was primarily on core oscillations rather than inner core super-rotation mechanisms. Therefore, there is a need for research that directly links lunar tidal forces to inner core differential rotation, potentially resolving long-standing questions about the nature and drivers of inner core super-rotation.

Our research addresses this gap by proposing a conceptual framework to understand how the Moon’s tidal forces, present since its formation, are continuously transmitted through Earth’s layers to the current era. Through theoretical considerations, we explore the dynamic relationship between Earth’s rotation and the Moon’s tidal impact. We propose a new conceptual approach where the interaction between the Moon’s differential tidal force and Earth’s seawater acts as a natural braking mechanism, analogous to brake pads decelerating a spinning wheel, where this deceleration effect is sequentially transmitted through Earth’s interior. This new theoretical perspective allows us to examine the potential mechanisms of differential rotation within Earth’s layers.

The remainder of this paper is structured as follows: We first present the theoretical framework of our model, followed by our methodology for quantifying tidal friction within the Earth. We then present the results of our conceptual model, showing how tidal forces can lead to differential rotation. Finally, we discuss the implications of our findings for understanding Earth’s geodynamo and long-term rotational behavior.

2. Tidal Friction and Earth’s Rotational Deceleration

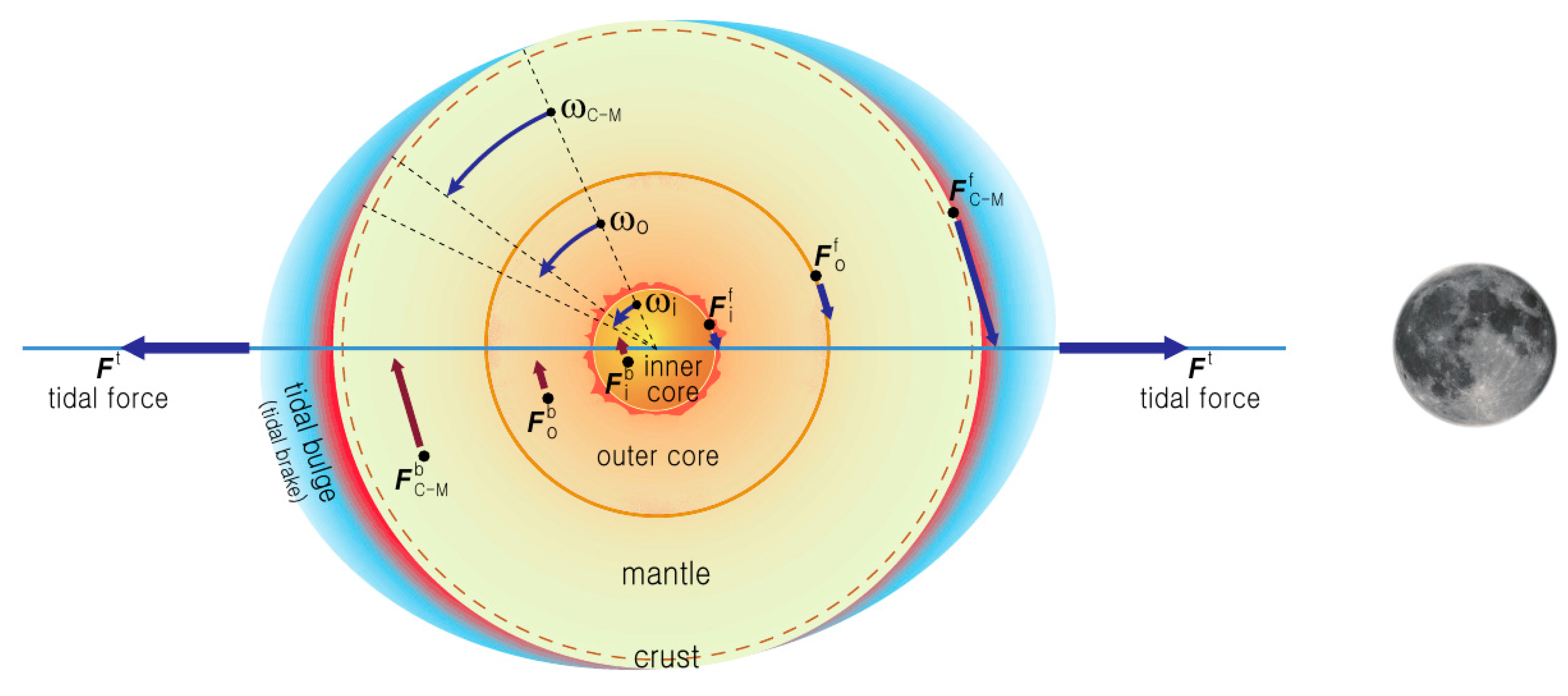
The oceans, unlike the solid parts of the Earth, exhibit distinct reactions to tidal forces [20,25]. The fluid nature of seawater makes it particularly susceptible to the tidal forces exerted by the Moon and the Sun within the Earth’s rotational framework. This susceptibility results in the effective capture and subsequent dragging of seawater, leading to the formation of a stationary tidal bulge. It is noteworthy that these tidal effects occur independently of the magnitude ratio to Earth’s gravity, as they are differential forces arising from gravitational differences. As the solid earth passes under this bulge, it experiences tidal waves (Figure 1). This interaction is akin to the mechanism of disc brakes, where brake pads squeeze against a rotor to slow down a rotating object, as depicted in Figure 2. The friction between seawater and the Earth’s crust due to tidal forces leads to gradual deceleration of the Earth’s rotation. Earth’s rotation is gradually slowing due to tidal friction, resulting in the Moon’s recession. This complex interaction has been the subject of numerous studies. Recent research has quantified the lunar recession rate. Deines and Williams (2016) [23] calculated a rate of about 3.005 cm/yr based on paleontological data. During the late Neoproterozoic (~620 Myr ago), the rate was estimated at 2.17 ± 0.31 cm/yr. Current lunar laser ranging measurements show a rate of 3.82 ± 0.07 cm/yr [26,27,28], nearly double the rate estimated for that era.

The change in Earth’s rotation rate, influenced by tidal friction, has been corroborated through a range of scientific studies and observations. This includes data from paleontological fossils, geological evidence, astronomical observations, gravity observations at tidal stations, and tracking observations of satellites [20,23,26,29,30]. These studies collectively indicate the angular acceleration of the Earth’s rotation falls within the range of −4.33 × 10⁻²² and −6.0 × 10⁻²² rad/s² (i.e., deceleration).

In modeling the long-term changes in Earth’s rotation, we consider the period shortly after the Moon’s formation, approximately 4.5 billion years ago (between 4.51 and 4.45 Gyr ago) [31,32]. We define $t_0$ as the specific moment when the Moon’s tidal forces began to act and had just established distinct angular velocities among Earth’s internal layers. We set this time as our reference point $t=0$. At $t_0$, we propose that each layer of the Earth (crust–mantle, outer core, and inner core) had a distinct initial angular velocity ${\mathsf{\omega }}_0$. We assume a uniform rotation just before the Moon’s formation, based on the likelihood that the Earth’s high-viscosity interior would have quickly synchronized any initial rotational differences among layers. We hypothesize that this difference in angular velocities may be due to the varying physical and chemical properties of Earth’s layers, potentially resulting in differential responses to the initial tidal forces. These distinct velocities serve as the initial conditions for our model. From this initial state, we assume that the angular velocity of each layer has been decreasing at a constant rate. The mean tidal force acting on Earth is found to be proportional to an exponential function in the first-order approximation, $\overline{F}\left(t\right)\propto F_{0 }{e}^{-\mathsf{\lambda }t}$, through Taylor expansion of the inverse cube of the Earth–Moon distance. Since this exponentially decreasing tidal force serves as the external force in the differential equation governing Earth’s rotation, the special solution for the angular velocity must follow the same exponential form. Therefore, the angular velocity (ω) at a given time $t$ for each layer can be expressed using its initial angular velocity (ω₀) and the reduction rate (λ) as follows:

$$\mathit{\omega }\left(t\right)={\mathsf{\omega }}_{0 }{e}^{-\mathsf{\lambda }t}.$$

(1)

In this model, λ remains constant across all layers, representing a uniform rate of angular velocity reduction throughout the Earth. This assumption simplifies our analysis while still allowing for differential rotation between layers due to their distinct initial angular velocities (${\mathsf{\omega }}_0$). This constant reduction rate assumption follows classical approaches in Earth rotation studies (e.g., [33]), providing a reasonable first-order approximation for modeling long-term rotational evolution over geological timescales. Differentiating (1) with respect to $t$, we obtain the rate of change in angular velocity:

$${\displaystyle \frac{d}{dt}}\mathit{\omega }\left(t\right)=-\mathsf{\lambda }{\mathsf{\omega }}_{0 }{e}^{-\mathsf{\lambda }\mathrm{t}}.$$

(2)

To determine the reduction rate (λ) and the initial angular velocity (${\mathsf{\omega }}_0$), we used the deceleration of Earth’s rotation as calculated by Deines and William (2016) [23]. Based on their analysis of paleontological data, they determined that the range of $d\omega /dt$ is $-\left(5.969\pm 1.762\right)\times {10}^{-7}$ rad/yr². The value reported by Deines and Williams (2016) [23] falls in the middle of the range of estimates provided by the aforementioned studies and can be regarded as a representative measure of Earth’s rotational deceleration. In our study, we will use the median value of this range, $-5.996\times {10}^{-22}$ rad/s², and assume it as the current acceleration rate. This estimate is very close to the value of $-5.98\times {10}^{-22}$ rad/s² obtained by Christodoulidis et al. (1988) [20] using precision laser and Doppler range data from artificial satellites. We acknowledge that this assumption, based on past geological time scales, introduces uncertainty and may not accurately reflect the present-day rate. However, it provides a basis for our calculations in the absence of more current data. The present angular velocity of Earth, $\omega \left(t_p\right)$, is $7.2921158\times {10}^{-5}$ rad/s at $t_p$ = 4.5 × 10⁹ yr. This value will be considered to correspond to the angular velocity of the oceans, crust, and mantle. Using these values along with the assumed acceleration rate of $-5.996\times {10}^{-22}$ rad/s² at $t_p$ = 3.88 × 10⁹ yr (Deines and William, 2016) [23], we calculated the initial angular velocity, ${\omega }_{0 }$, as 2.0123677 × 10⁻⁴ rad/s for those layers and the reduction rate, $\mathsf{\lambda }$, as 2.2560109 × 10⁻¹⁰/yr (

Table 1. Characteristics and dynamics of Earth’s major layers (seawater, crust–mantle, outer core, and inner core), including their mass, moment of inertia, distance from Earth’s center to the top boundary, initial angular velocities, current values of angular velocity, angular deceleration, and energy release rate. Layer masses and radii are based on established Earth science data [34,35]. The value of 2.2560109 × 10⁻¹⁰/yr⁻¹ is used as the reduction rate, λ, for the calculations. Braking force and energy release rate are given for each layer’s top boundary.

Earth’s Internal Layers	Seawater	Crust–Mantle	Outer Core	Inner Core
Mass (kg)	1.400 × 1021	4.043 × 1024	1.835 × 1024	9.675 × 1022
Moment of Inertia (kg·m2)	3.793 × 1034	7.124 × 1037	9.150 × 1036	5.860 × 1034
Distance to Top Boundary from Earth Center (m)	6.371 × 106	6.366 × 106	3.485 × 106	1.220 × 106
ω0 (rad/s)	2.0125721 × 10−4	2.0125721 × 10−4	2.0125873 × 10−4	2.0126026 × 10−4
ω (rad/s)	7.2921158 × 10−5	7.2921158 × 10−5	7.2921709 × 10−5	7.2922262 × 10−5
$\left|{\displaystyle \frac{d\mathsf{\omega }}{dt}}\right|$ (rad/s2)	5.2131437 × 10−22	5.2131437 × 10−22	5.2131832 × 10−22	5.2132228 × 10−22
Braking Force (N)	3.103666 × 106	5.8338737 × 109	1.3687412 × 109	2.5040565 × 107
Energy Release Rate at Boundary (W)		2.7081778 × 1012	3.4784113 × 1011	2.2277377 × 109

). These values are applied to the outermost layer of Earth, which we treat as a single-mantle layer for this study, except in special cases. This approach can be extended to Earth’s inner layers as well. The calculated λ value suggests an e-folding time for Earth’s rotational deceleration of approximately 3.86 billion years across all layers. It is important to note that different methodologies for calculating deceleration can lead to variations in the reduction rate and initial angular velocities. Our results should be considered as estimates based on the available paleontological data and the assumptions made in our model.

The tidal bulge raised by the Moon’s tidal force (${\mathit{F}}^t$) interacts with the Earth’s surface, particularly the ocean floor, generating friction. This frictional force (${\mathit{F}}^f$) acts in a direction opposing Earth’s rotation, effectively slowing its rotational speed (Figure 1). The mechanism is analogous to brake pads rubbing against a disc rotor (Figure 2). Frictional drag at the ocean bottom causes a delay in the tidal bulge’s arrival relative to the Moon’s passage through the observer’s meridian [36]. This tidal lag is crucial in understanding the deceleration process. The decelerating effect can be quantified using the torque equation:

$$\mathit{N}=\mathit{r}\times {\mathit{F}}^f,$$

(3)

where $\mathit{r}$ represents the distance from the axis of rotation. This torque acts to slow down the Earth’s rotation by applying a force opposite to the direction of rotation at a distance r from the rotation axis. The torque ($\mathit{N}$) can also be expressed as the product of the Earth’s moment of inertia ($I_E$) and the angular acceleration (${\displaystyle \frac{d\omega }{dt}}$), as shown in the following equation:

$$\mathit{N}=I_E{\displaystyle \frac{d\omega }{dt}}.$$

(4)

Given the angular acceleration rate and the calculable moment of inertia of the Earth ($I_E$), the tidal friction (${\mathit{F}}^f$) exerted on the entire Earth can be estimated using Equations (3) and (4). This approach allows us to indirectly estimate the tidal friction, which is difficult to measure directly, from observational data of Earth’s rotational deceleration. It implies the average effect on the Earth’s entire system, although the actual tidal friction may vary with location and time.

3. Braking Forces in Earth’s Rotational Deceleration

The Earth is composed of distinct layers—crust, mantle, outer core, and inner core—each with unique compositions and physical states. Unlike in a rigid body model where tidal forces acting on the outermost surface would instantaneously decelerate the entire planet uniformly, the reality would be more complex. The presence of these distinct layers suggests that tidal forces are unlikely to act as immediate braking forces on all layers simultaneously. Therefore, we propose a model of discrete tidal force transfer within Earth’s layers. This model suggests that the tidal force is transferred discretely from the surface through various layers, including the transitions between solid and liquid states, ultimately reaching the liquid outer core and solid inner core. Our analysis focuses on the interfaces between these discrete layers, particularly at the boundaries involving fluid layers, examining the transmission of deceleration forces originating from surface tidal forces.

Imagine the Earth around the time of the Moon’s formation, with the entire body rotating uniformly. Here, the oceanic tidal bulge acts analogously to brake pads applying pressure on the mantle, thereby slowing down these layers. As a result, tidal friction initially serves as a braking mechanism for the mantle. The deceleration experienced by the mantle, in turn, creates friction at its boundary with the core below, which rotates faster than the now-slowed mantle. This interaction means the reduced velocity of the upper layer exerts a braking force on the faster-moving lower layer. In this framework, we refine the definition of the braking force to more accurately represent the physical dynamics of Earth’s rotational deceleration. The braking force is strictly defined as the net force required to equalize the normalized rate of change in angular velocity (${\displaystyle \frac{1}{\omega }}{\displaystyle \frac{d\omega }{dt}}$) that remains constant across all layers. This concept is illustrated in Figure 1, showing how the braking force acts to maintain this equilibrium of relative deceleration rates across Earth’s layers. This refined definition provides a more accurate representation of the long-term evolution of Earth’s rotational dynamics, accounting for the different initial rotational speeds of various layers while maintaining a consistent framework for their deceleration. According to this framework, the tidal force induced by the Moon does not accumulate nor is it lost but instead is entirely consumed as braking forces within the Earth. Therefore, tidal friction is subsequently transferred from the mantle to the subsequent adjacent layer, determined by the magnitude of the braking force. This braking force can be conceptualized as the sequential redistribution of tidal friction, directed from the Earth’s surface toward its center.

For two adjacent layers in equilibrium, the tidal friction transferred to the lower layer is determined by subtracting the braking force that decelerates the upper layer from the tidal friction acting on the upper layer. This relationship applies to the following pairs of adjacent layers: seawater and crust–mantle, crust–mantle and outer core, and outer core and inner core. Hence, these relationships can be expressed as

$${\mathit{F}}_{\mathrm{s}}^{\mathrm{f}}-{\mathit{F}}_{\mathrm{s}}^{\mathrm{b}}={\mathit{F}}_{\mathrm{C}-\mathrm{M}}^{\mathrm{f}},$$

(5)

$${\mathit{F}}_{\mathrm{C}-\mathrm{M}}^{\mathrm{f}}-{\mathit{F}}_{\mathrm{C}-\mathrm{M}}^{\mathrm{b}}={\mathit{F}}_{\mathrm{o}}^{\mathrm{f}},$$

(6)

$${\mathit{F}}_{\mathrm{o}}^{\mathrm{f}}-{\mathit{F}}_{\mathrm{o}}^{\mathrm{b}}={\mathit{F}}_{\mathrm{i}}^{\mathrm{f}},$$

(7)

$${\mathit{F}}_{\mathrm{i}}^{\mathrm{f}}={\mathit{F}}_{\mathrm{i}}^{\mathrm{b}},$$

(8)

where the subscripts such as s, C-M, o, and i denote seawater, crust–mantle, outer core, and inner core, respectively. Summing these equations yields

$${\mathit{F}}_{\mathrm{s}}^{\mathrm{f}}={\mathit{F}}_{\mathrm{s}}^{\mathrm{b}}+{\mathit{F}}_{\mathrm{C}-\mathrm{M}}^{\mathrm{b}}+{\mathit{F}}_{\mathrm{o}}^{\mathrm{b}}+{\mathit{F}}_{\mathrm{i}}^{\mathrm{b}}.$$

(9)

This final equation signifies that the total braking force equals the tidal friction exerted on seawater, indicating that the tidal force is entirely consumed to decelerate the rotation of all Earth’s layers. Notably, this analysis addresses the equilibrium of forces achieved by the tidal force’s interaction with interlayer forces since the Moon’s formation.

The angular velocity of the Earth’s crust–mantle layer (C–M), as determined in (1), is considered to be ${\omega }_{\mathrm{C}-\mathrm{M}}\left(t_0\right)=2.0125721\times {10}^{-4}$ rad/s at $t_0$ and ${\omega }_{\mathrm{C}-\mathrm{M}}\left(t_p\right)=7.2921158\times {10}^{-5}$ rad/s at present ($t_p$). Current observations indicate that the inner core rotates approximately 2 degrees per year faster than the crust–mantle [6,7,8]. Consequently, the angular velocity of the inner core at the present time can be estimated using

$${\omega }_{\mathrm{i}}\left(t_p\right)={\omega }_{\mathrm{C}-\mathrm{M}}\left(t_p\right)+2 \mathrm{deg}/\mathrm{yr}.$$

(10)

The value of ${\omega }_{\mathrm{i}}\left(t_p\right)$ is determined to be $7.2922262\times {10}^{-5}$ rad/s. To determine the inner core’s rotation rate, we apply the concept of equal normalized rate of change in angular velocity across layers, as defined by the logarithmic derivative of angular velocity:

$$-\lambda ={\displaystyle \frac{{dln\omega }_{\mathrm{i}}}{dt}}={\displaystyle \frac{{dln\omega }_{\mathrm{C}-M}}{dt}} .$$

(11)

By integrating Equation (11), from $t_0$ to $t_p$, we can obtain the value for ${\omega }_{\mathrm{i}}\left(t_0\right)$ as 2.0126026 × 10⁻⁴ rad/s. This calculation indicates that shortly after Earth’s formation, the inner core rotated approximately ~5.5 deg/yr faster than the crust–mantle, showing a larger initial difference in rotation rates between these layers. Figure 3 illustrates the rotational speed of the crust–mantle and inner core at two distinct time points (t₀ and t₁), plotted as a function of the radius (r). The outer core’s rotation is inferred by interpolating the rotational curves of the crust–mantle and the inner core, considering an intermediate pattern resulting from angular momentum transport in the fluid outer core. Near the inner core, high angular momentum is transported outward (increasing r direction), while near the mantle, low angular momentum is transported inward (decreasing r direction). Between these two regions exists an inflection point where the transport of high angular momentum from the inner core balances with the transport of low angular momentum from the mantle. This creates an angular velocity distribution in the outer core that is concave downward (∂²ω/∂r² < 0) near the inner core and concave upward (∂²ω/∂r² > 0) near the mantle, with a neutral point of angular momentum transport in between. However, the actual rotation profile of the outer core may be more complex due to the presence of turbulent flows and convection patterns. Based on the observed 2 deg/yr super-rotation of the inner core, we estimate the outer core rotation as 1 deg/yr faster than the mantle, giving ω₀ = 2.0125873 × 10⁻⁴ rad/s (Table 1). The figure illustrates that as time progresses, each layer’s rotational speed diminishes, resulting in a downward shift of the speed curve along the speed axis. Given the gradually decreasing tidal friction that has acted over geological time since the Moon’s formation and substantial viscosity of the outer core, all Earth’s layers are inferred to maintain a quasi-equilibrium state, decelerating at equal relative rates, while the inner core’s rotational speed decreases more rapidly than that of the crust–mantle.

The braking force ($F^b$) acting on a given layer (bounded by radii r₁ and r₂) is calculated using the layer’s moment of inertia ($I$) and its rate of angular velocity change. The current angular deceleration for each layer is obtained using Equation (2), based on the estimates of λ and current angular speed (Table 1). The braking force for a particular layer is expressed in scalar form as

$$F^b={\displaystyle \frac{I}{r_2}}{\displaystyle \frac{d\omega }{dt}} ,$$

(12)

where $I={\displaystyle \frac{2\left(r_2^5-r_1^5\right)}{5\left(r_2^3-r_1^3\right)}}M$, $M$ is the mass of the layer, and $r_2$ is the distance from the Earth’s center to the point of force application. Table 1 presents each layer’s specific characteristics, including mass, radius, moment of inertia, and the current values of individual braking forces. These calculations are based on the present-day angular velocities and decelerations. The sum of all braking forces equals the tidal force acting on the entire Earth, with a significant portion, approximately 82%, of this tidal force being utilized to decelerate the crust–mantle, while the remaining force acts on the seawater, outer core, and inner core, regulating their rotation.

4. Core–Mantle Slippage

This section considers the more practical issues related to the outer core’s liquid state and the core–mantle boundary (CMB). We examine a model with a discontinuous boundary between two distinct layers: the upper layer, which has already experienced the effects of tidal friction and consequently slowed down, and the lower layer, where tidal friction has not yet been imparted, leaving it unaffected by the slowdown. When the force transmitted from the upper layer is applied to the lower layer, two primary scenarios arise, depending on whether these two distinct layers will rotate in unison or not. This essentially represents a situation where the layers might either slip relative to each other or not, contingent on the relative strength between the transmitted force and the bonding force holding the layers together.

In the first scenario, the force transmitted from the upper layer is weaker than the bonding force binding the two layers. This means the force is insufficient to break the bonding or to cause any slipping between the layers. As a result, the lower layer responds almost instantaneously to the fully propagated force from the upper layer. Thus, this force acts as a braking force, causing the lower layer to decelerate until it matches the rotational speed of the upper layer, resulting in synchronized rotation of both layers. While shear forces may cause some deformation at the layer interface, this study aims to limit its scope to how the transmitted force functions to decelerate the lower layer.

In the second scenario, when the transmitted force exceeds the bonding force between the layers, it causes a breakdown in their coupling. This phenomenon might happen particularly at the solid–liquid layer interfaces, such as the boundary between the Earth’s solid mantle and liquid cores. At these interfaces, when the solid layer begins to move over the fluid layer, the maximum static friction force is substantially lower than that occurring between solid bodies. Thus, even a relatively small force can initiate sliding between layers. As slippage accelerates at these interfaces, the friction generated from viscous stress increases rapidly, approximately proportional to 1.5 to 2 squares of the relative speed at the boundary, as documented by Pucci et al. (2019) [36]. The relative speed might continue to increase until the resistance equals the force transmitted from above, thus setting an upper limit to the slip speed. However, under the tremendous pressure at the CMB, we surmise that slippage could occasionally become highly turbulent, potentially agitating the liquid outer core. This turbulent process might lead to the fragmentation of mantle material, resulting in significant avalanches.

We now consider the crust–mantle boundary, applying the scenarios discussed earlier, to examine the interactions at this critical interface of Earth’s internal layers. To understand whether the crust can move independently from the mantle, we must consider the governing forces. Specifically, to initiate relative motion between the Earth’s crust and mantle, a force must exceed the maximum static friction between these layers. This frictional force is given by

$$F_{max}=\mu mg,$$

(13)

where $\mu$ is the coefficient of friction, m is the crust’s mass, and g is the acceleration due to gravity. According to Polyansky et al. (2016) [37], the friction coefficient between the crust and mantle is estimated to be approximately 0.9. The crust’s mass, roughly 10²² kg, constitutes less than 1% of the Earth’s total mass. Using these values, we calculate the maximum friction force, $F_{max}$, to be approximately 8.82 × 10²² N. The tidal force of about 6.5 × 10¹⁰ N is significantly smaller than the frictional force at the crust–mantle interface, indicating that the tidal force cannot overcome the coupling between these layers. This situation corresponds to the first scenario discussed earlier, where the crust and mantle rotate together with the same deceleration. Consequently, we can treat the crust and mantle as a single layer in this study. Nevertheless, we can speculate that if these braking forces persistently act over extended periods at the boundaries between layers of different compositions, particularly at the mantle–crust interface, these forces could gradually induce stress at the layer interfaces. This stress might potentially weaken the cohesive strength between such layers over time. In this context, it is conceivable that the asthenosphere could be a potential candidate for such behavior.

At the boundary where Earth’s silicate mantle and metallic inner core both meet the liquid outer core, we encounter a situation analogous to the second scenario discussed above. Our focus here is specifically on the mantle–outer core interaction. Unlike the first scenario, we speculate that in the early period following the Moon’s formation, tidal forces might not have been transferred instantaneously from the mantle to the liquid outer core. This resulted in differential slippage at the core–mantle boundary. During this phase, tidal forces predominantly affected the mantle, rather than immediately transferring inward to the outer core. The outer core maintained its angular momentum and rotational velocity to some extent without experiencing significant deceleration, while the mantle’s rotation slowed. This mechanism led to a substantial velocity differential between the mantle and outer core rotation rates (Figure 3).

To better understand tidal force transmission within the liquid outer core, we conceptualize it as composed of thin layers. As tidal forces penetrate deeper, they initially decelerate the upper layers. This deceleration then cascades to lower layers in a step-by-step process. In this conceptual framework, such a cumulative effect begins to impact the entire outer core, resulting in varying rotational speeds compared to other Earth layers, as illustrated in Figure 3. This pattern of differential speeds occurs due to the delayed transmission of tidal forces through the outer core.

Meanwhile, a critical question arises regarding the persistent rotational speed differences at the Earth’s mantle–outer core interface: Could the disparity in rotational velocities continue to expand, potentially allowing the outer core to rotate much faster independently of the mantle’s rotation? This situation is analogous to a ship moving swiftly though the ocean; the faster it sails, the greater the water’s resistance becomes due to a sharp increase in fluid viscosity-induced friction at higher relative speeds (e.g., [36]). However, in a system constrained by finite tidal forces, the rotational speed gap between the mantle and outer core is unlikely to widen indefinitely. As the mantle, initially sliding over the outer core, encounters increasing viscous force, an equilibrium might eventually be reached between the braking force and viscous force. From a momentum conservation perspective, the increased friction in the upper part of the outer core should lead to its deceleration. Although there is some counteracting momentum from the lower part, the continuous deceleration force from the upper part results in a gradual slowing of the entire outer core. Consequently, a pattern of rapidly decreasing rotational speed becomes evident in the upper part of the outer core, as illustrated in Figure 3.

In our conceptual model, initially, we speculate that the entire Earth rotated at the same angular speed during the early stages of its formation. Shortly after the Moon’s emergence, tidal forces caused the mantle and crust to slow down by approximately ~5.5 deg/yr more than the inner core. An intriguing aspect to consider is the duration required to achieve this angular speed difference ($\Delta \omega$) of 5.5 deg/yr. By applying the initial angular speeds and deceleration rates of each year, the elapsed time, $\tau$, can be calculated as follows:

$$\tau ={\displaystyle \frac{2\Delta \omega }{\left\{\frac{d{\omega }_{\mathrm{i}}\left(t_0\right)}{dt}+\frac{d{\omega }_{\mathrm{C}-\mathrm{M}}\left(t_0\right)}{dt}\right\}}}={\displaystyle \frac{ 5.5}{\left\{\frac{d{\omega }_{\mathrm{i}}\left(t_0\right)}{dt}+\frac{d{\omega }_{\mathrm{C}-\mathrm{M}}\left(t_0\right)}{dt}\right\}}}$$

(14)

Using (1) and (2), we obtain an approximate value of ~66,000 years for $\tau$.

If a constant tidal force continues to influence the outer core over an extended period, it could be hypothesized that this force, transmitted between the mantle and the inner core through a Couette flow in the fluid outer core, might eventually lead to the alignment of the rotational speeds of both the inner and outer cores with that of the mantle. This process would achieve synchronization by effectively dampening the super-rotation. However, it is crucial to acknowledge that the tidal force is gradually diminishing over time as the Moon progressively distances itself from the Earth. With the diminishing external force, the outer core is unlikely to ever fully align its rotational speed with the mantle’s. As long as this diminishing external force, the tidal force, continues to act on the Earth, the outer core is unlikely to ever synchronize its rotational speed with that of the mantle. Consequently, differential rotation between the outer core and the mantle is strongly anticipated. A similar speed discrepancy might also emerge at the interface between the liquid outer core and the solid inner core. The waning tidal force is expected to gradually reduce differential rotations; the deceleration rate in rotational speed depends on the timescale over which the Moon’s tidal force diminishes.

As long as the Moon continues to exert a tidal force serving as a braking mechanism on the Earth, particularly influencing the liquid outer core, the Earth’s cores will continue to rotate differentially relative to the mantle and crust. Therefore, our conceptual model offers a plausible insight into explaining the origin of differential rotation within the Earth. We speculate that the tidal forces from the Moon play a more fundamental role in this process. In this context, continuous differential rotation generates friction inside the outer core, potentially disturbing the outer core and inducing electromagnetic fields that may contribute to the formation of Earth’s magnetic field. While electromagnetic forces contribute to this phenomenon [5,7], our model proposes that these forces may not be the initial drivers of the Earth’s inner core’s differential rotation. However, these different perspectives on differential rotation need not be mutually exclusive. The differential rotation resulting from the braking forces could generate turbulent flows and vortices in the outer core, potentially contributing to the geodynamo and magnetic field variations. Hence, we envision that such turbulence might play a role in the geomagnetic reversal phenomena observed in the paleomagnetic record.

5. Rotational Energy Release Through Tidal Braking

As tidal friction reduces the Earth’s angular velocity, the diminished rotational energy is expected to manifest as frictional heating, particularly at the boundaries between layers. The time rate of the change in rotational energy released in each layer, ${\displaystyle \frac{dE}{dt}}$, can be calculated using the formula for the deceleration of rotation:

$${\displaystyle \frac{dE}{dt}}=I\omega {\displaystyle \frac{d\omega }{dt}}.$$

(15)

Although the deceleration varies slightly among different layers, the impact of this variation on the energy rate is negligible because the inertial moment of each layer dominates in (15). Therefore, for simplicity, the mantle’s deceleration is used to calculate the energy release rate in each layer. The present energy release rate in each layer is listed in Table 1. A significant amount of energy, ~2.708 TW, is mainly released around the interface between seawater and the crust–mantle. In the outer core, ~0.3478 TW of energy is released. These values are comparable to those reported by Ray et al. (1996) [38]. Notably, a substantial amount of energy is likely released around the CMB due to considerable friction from differential rotation near this boundary. Lay et al. (2008) [39] and Nakagawa (2020) [40] suggest that the current heat flow across the CMB (core–mantle boundary) ranges between 8 and 16 TW. The frictional heat in the outer core, converted from the Earth’s rotational energy (~0.3478 TW), contributes approximately 2.2~4.3% of the estimated heat flow across the CMB from those studies. While this frictional heat contributes a relatively small portion to the CMB heat flow, it should be considered in comprehensive models of the Earth’s heat budget. For the inner core, an energy release of ~2.228 GW occurs around the interface between the outer and the inner cores. Based on our conceptual model, which suggests that Earth’s rotational deceleration was higher in the past, we can infer that frictional heat generation would have been significantly greater than the current estimates.

The total energy release rate within the Earth, as detailed in Table 1, primarily corresponds to the energy dissipated due to the Earth’s differential rotation. Most of this dissipation occurs at the boundary between seawater and the crust–mantle, attributed to the large moment of inertia of the crust–mantle. This energy is negligible when compared to the solar energy received by the sea. About 11.37% of the total energy is generated within the outer core and its adjacent boundaries, with a significant portion likely originating at the mantle boundary. If all this energy were used for heating the outer core, the temperature increase rate of the core, ${\displaystyle \frac{dT}{dt}}$, can be calculated as follows:

$$\epsilon =c m {\displaystyle \frac{dT}{dt}}$$

(16)

where c and m represent the specific heat and mass of the outer core, respectively, and T denotes its temperature. Using the specific heat of iron (446 J/kg/K) and the mass of the outer core (1.835 × 10²⁴ Kg), the temperature increase rate is approximately ~4.25 × 10⁻¹⁶ K/s. Based on the heat flux of 12 ± 0.5 TW across the core–mantle boundary [41], the current cooling rate of the outer core is estimated to be approximately 109.8 ± 4.6 K per billion years. In contrast, our calculations suggest that frictional heat generation at the core–mantle boundary due to differential rotation associated with the current deceleration of the mantle could heat the outer core by about 13.4 K over one billion years.

While this frictional heating effect is relatively small compared to the cooling rate, it contributes to maintaining the liquid state of the outer core to some degree. The interaction between the Moon’s gravitational influence and the liquid outer core dynamics might be one of the factors extending the period during which the outer core remains in a liquid state, thereby sustaining the Earth’s geomagnetic field. Furthermore, we speculate that the frictional force at the boundary between the mantle and the outer core might not only generate heat but also induce stirring within the outer core. This potential stirring action could cause significant disturbances and possibly contribute to the generation and maintenance of the Earth’s magnetic field.

6. Conclusions

This study presents a theoretical model offering new insights into the mechanism of differential rotation within the Earth. Our approach suggests potential connections between tidal forces and Earth’s internal dynamics. Our model of lunar tidal forces as a driver for differential rotation should be considered alongside the geodynamo theory and electromagnetic coupling models. Rather than replacing these established explanations, this tidal-force-based conceptual framework offers a complementary perspective that may work in conjunction with electromagnetic mechanisms to fully explain the complex dynamics of the Earth’s internal rotation. Central to this process is the role of the Earth’s liquid outer core. Its unique state, being liquid under immense pressure, is key to the delayed transmission of tidal forces, resulting in differential rotation within the Earth.

Our model proposes that the Moon’s tidal forces, acting as a braking mechanism, initially slow the Earth’s crust and mantle; this deceleration subsequently affects the liquid outer core, where the tidal forces are not transmitted instantaneously. Our model suggests that approximately ~66,000 years after the Moon’s formation, the tidal forces could have slowed the crust–mantle system by about 5.5 degrees per year relative to the cores. As the Moon gradually recedes from Earth over geological time, the gradual weakening of these tidal forces has caused the differential rotation to decrease progressively following our proposed exponential decay model, reaching the approximately 2 degrees per year observed in the present day.

The energy release from this process, especially prominent at the core–mantle boundary and within the outer core, may significantly impact Earth’s internal thermal dynamics. The frictional force at the boundary between the mantle and the outer core might not only generate heat but also induce stirring within the outer core, potentially contributing to the generation and maintenance of Earth’s magnetic field. The model indicates that this tidal-induced differential rotation provides an additional heat source alongside other internal heat sources, playing a supplementary role in maintaining the liquid state of the outer core through these thermal and mechanical effects.

While this conceptual framework is limited in scope and requires further validation through numerical simulations and observational evidence, its strength lies in its ability to provide an integrated explanation for multiple Earth processes through a single, coherent mechanism. We anticipate that this study will serve as a theoretical foundation for future investigations, paving the way for numerical simulations, detailed modeling, and observational studies to further validate and refine our understanding of Earth’s core dynamics.