Investigating Rayleigh Wave Dispersion Across the Carpathian Orogen in Romania
Abstract
1. Introduction
2. Data and Methods
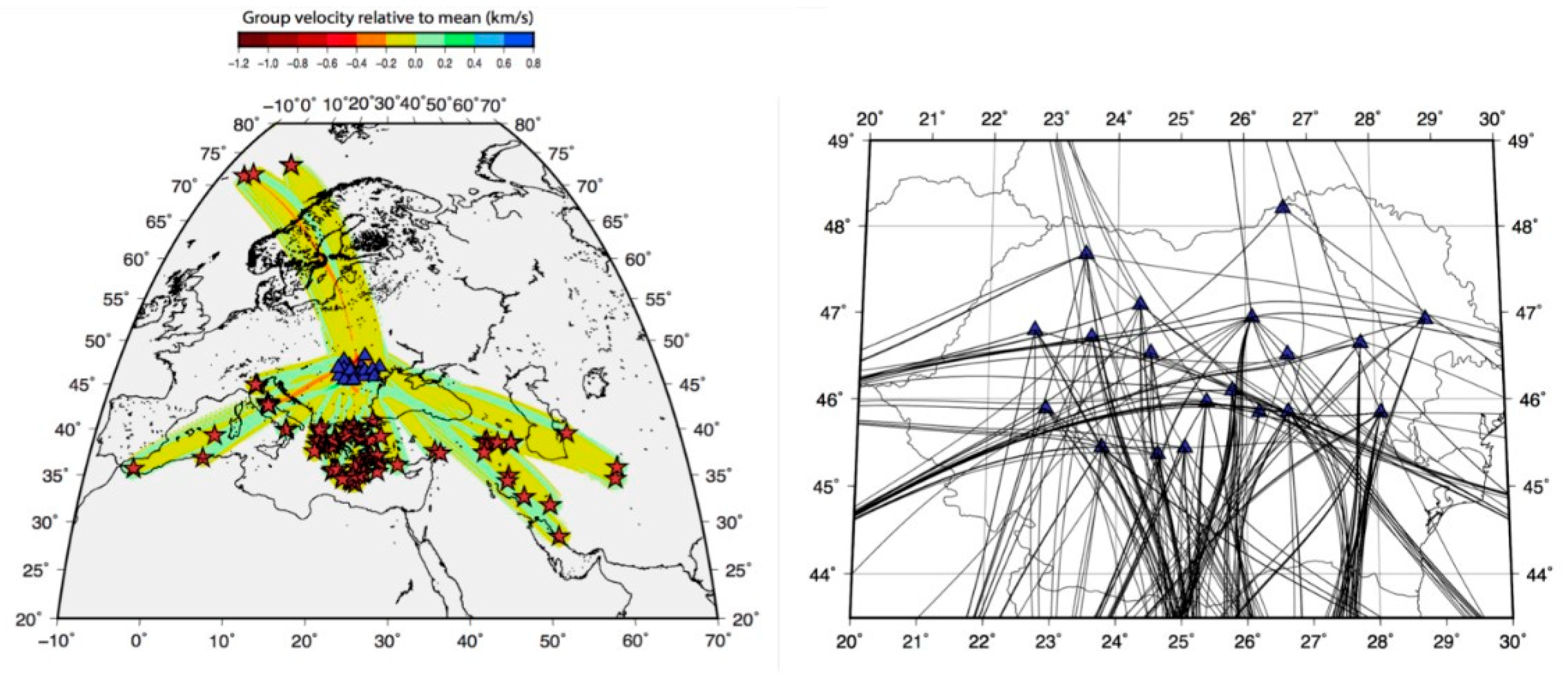
2.1. Earthquake Data and Seismic Stations
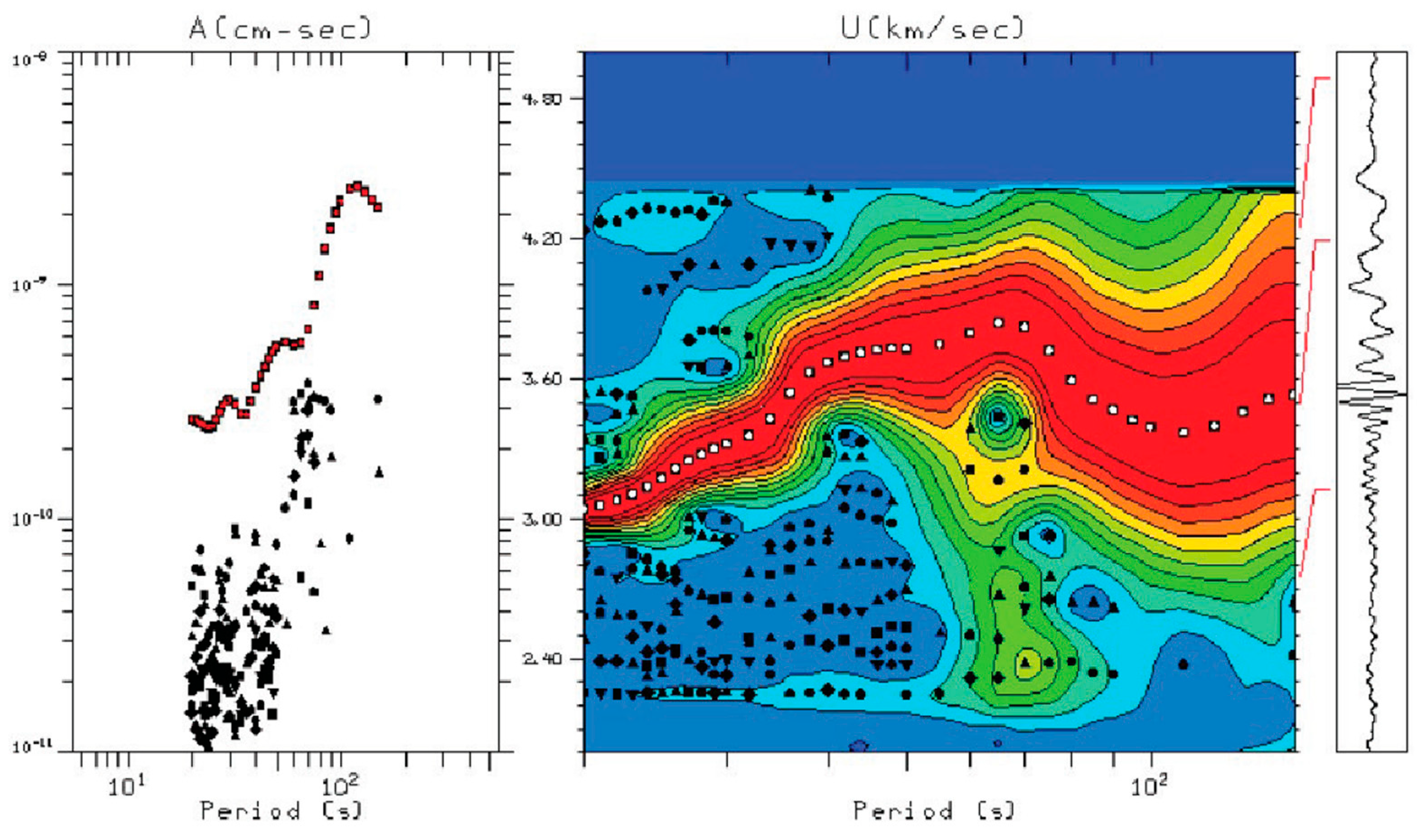
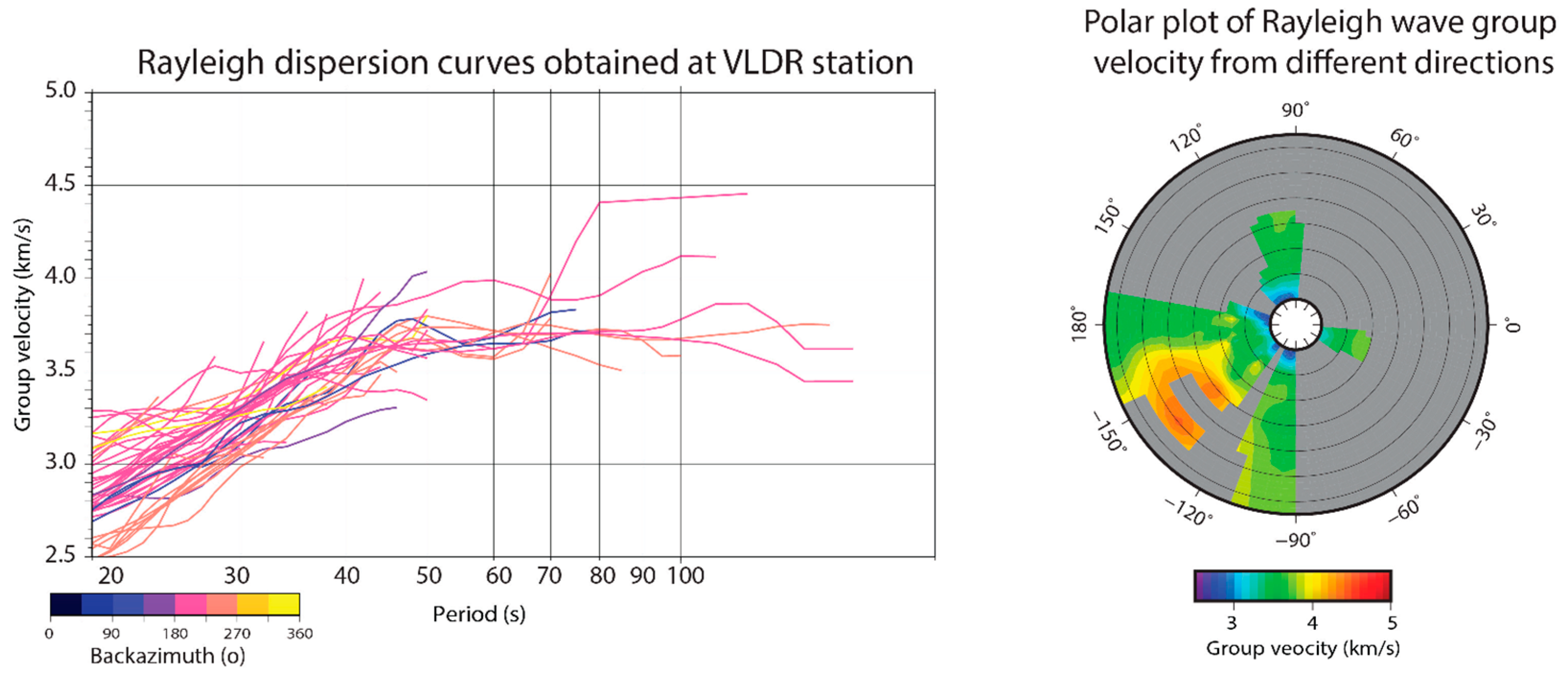
2.2. Rayleigh Wave Dispersion
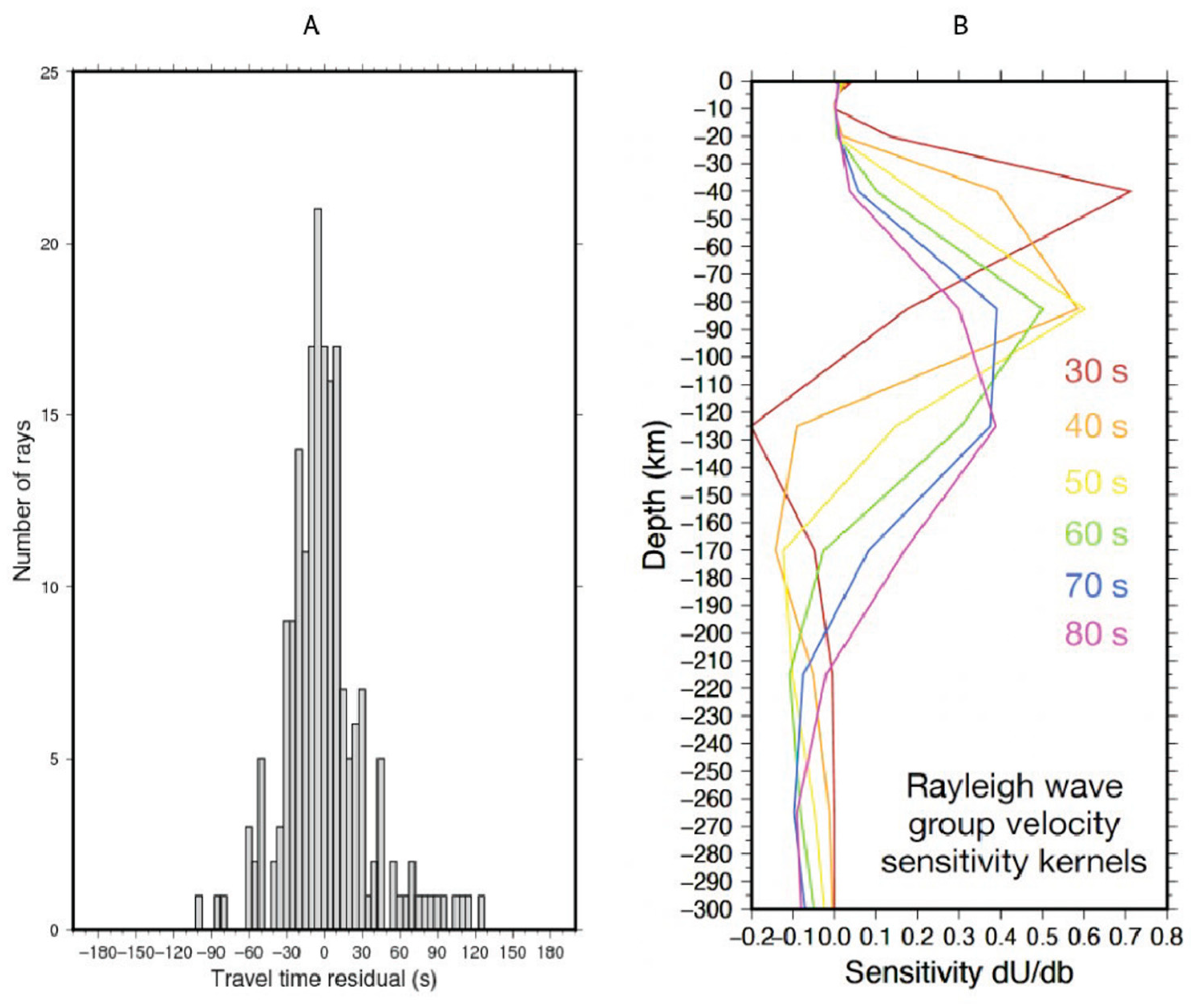
2.3. Seismic Tomography: The Fast Marching Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RSN | Romanian National Seismic Network |
| ALCAPA | Alpine–Carpathian Pannonian |
| SKS | Core-refracted shear wave anisotropy |
| CPS | Computer Codes for Seismology |
| MFT | Multiple filter technique |
| FMST | Fast marching surface tomography |
| EEC | East European Craton |
References
- Csontos, L.; Vörös, A. Mesozoic plate tectonic reconstruction of the Carpathian region. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2004, 210, 1–56. [Google Scholar] [CrossRef]
- Matenco, L.; Bertotti, G. Tertiary tectonic evolution of the external East Carpathians (Romania). Tectonophysics 2000, 316, 255–286. [Google Scholar] [CrossRef]
- Schmid, S.M.; Bernoulli, D.; Fügenschuh, B.; Matenco, L.; Schefer, S.; Schuster, R.; Tischler, M.; Ustaszewski, K. The Alpine-Carpathian-Dinaridic orogenic system: Correlation and evolution of tectonic units. Swiss J. Geosci. 2008, 101, 139–183. [Google Scholar] [CrossRef]
- Mason, P.R.; Seghedi, I.; Szákacs, A.; Downes, H. Magmatic constraints on geodynamic models of subduction in the East Carpathians, Romania. Tectonophysics 1998, 297, 157–176. [Google Scholar] [CrossRef]
- Szakács, A.; Pécskay, Z.; Gál, Á. Patterns and trends of time–space evolution of Neogene volcanism in the Carpathian–Pannonian region: A review. Acta Geod. Et Geophys. 2018, 53, 347–367. [Google Scholar] [CrossRef]
- Seghedi, I.; Maţenco, L.; Downes, H.; Mason, P.R.; Szakács, A.; Pécskay, Z. Tectonic significance of changes in post-subduction Pliocene–Quaternary magmatism in the south east part of the Carpathian–Pannonian Region. Tectonophysics 2011, 502, 146–157. [Google Scholar] [CrossRef]
- Schivardi, R.; Morelli, A. Surface wave tomography in the european and mediterranean region. Geophys. J. Int. 2009, 177, 1050–1066. [Google Scholar] [CrossRef]
- Shan, B.; Xiong, X.; Zhao, K.; Xie, Z.; Zheng, Y.; Zhou, L. Crustal and uppermantle structure of south China from Rayleigh wave tomography. Geophys. J. Int. 2017, 208, 1643–1654. [Google Scholar] [CrossRef]
- Chen, Y.; Badal, J.; Hu, J. Love and rayleigh wave tomography of the qinghaitibet plateau and surrounding areas. Pure Appl. Geophys. 2010, 167, 1171–1203. [Google Scholar] [CrossRef]
- Ajourlou, P.; Darbyshire, F.; Audet, P.; Milne, G.A. Structure of the crust and upper mantle in Greenland and northeastern Canada: Insights from anisotropic Rayleigh-wave tomography. Geophys. J. Int. 2024, 239, 329–350. [Google Scholar] [CrossRef]
- Timkó, M.; El-Sharkawy, A.; Wiesenberg, L.; Fodor, L.; Wéber, Z.; Lebedev, S.; Eckel, F.; Meier, T. Crustal and upper mantle 3-D Vs structure of the Pannonian region from joint earthquake and ambient noise Rayleigh wave tomography. Geophys. J. Int. 2024, 239, 1313–1334. [Google Scholar] [CrossRef]
- El-Sharkawy, A.; Meier, T.; Lebedev, S.; Behrmann, J.H.; Hamada, M.; Cristiano, L.; Weidle, C.; Köhn, D. The slab puzzle of the Alpine-Mediterranean region: Insights from a new, high-resolution, shear wave velocity model of the upper mantle. Geochem. Geophys. Geosystems 2020, 21, e2020GC008993. [Google Scholar] [CrossRef]
- Estève, C.; Gosselin, J.; Audet, P.; Schaeffer, A.; Schutt, D.; Aster, R. Surface wave tomography of the northern Canadian Cordillera using earthquake Rayleigh wave group velocities. J. Geophys. Res. Solid Earth 2021, 126, e2021JB02196. [Google Scholar] [CrossRef]
- Martin, M.; Wenzel, F.; Group, C.W. High-resolution teleseismic body wave tomography beneath se-romania-ii. imaging of a slab detachment scenario. Geophys. J. Int. 2006, 164, 579–595. [Google Scholar] [CrossRef]
- Piromallo, C.; Morelli, A. P wave tomography of the mantle under the Alpine-Mediterranean area. J. Geophys. Res. Solid Earth 2003, 108, no. B2. [Google Scholar] [CrossRef]
- Zaharia, B.; Enescu, B.; Radulian, M.; Popa, M.; Koulakov, I.; Parolai, S. Determination of the lithospheric structure from carpathians arc bend using local data. Rom. Rep. Phys. 2009, 61, 748–764. [Google Scholar]
- Baron, J.; Morelli, A. Full-waveform seismic tomography of the vrancea, romania, subduction region. Phys. Earth Planet. Inter. 2017, 273, 36–49. [Google Scholar] [CrossRef]
- Petrescu, L.; Mihai, A.; Borleanu, F. Slab tear and rotation imaged with core-refracted shear wave anisotropy. J. Geodyn. 2023, 157, 101985. [Google Scholar] [CrossRef]
- Braeck, S.; Podladchikov, Y.Y.; Medvedev, S. Spontaneous dissipation of elastic energy by selflocalizing thermal runaway. Phys. Rev. 2009, 80, 046105. [Google Scholar] [CrossRef]
- John, T.; Medvedev, S.; Rüpke, L.H.; Andersen, T.B.; Podladchikov, Y.Y.; Austrheim, H. Generation of intermediate-depth earthquakes by self-localizing thermal runaway. Nat. Geosci. 2009, 2, 137–140. [Google Scholar] [CrossRef]
- Petrescu, L.; Borleanu, F.; Radulian, M.; Ismail-Zadeh, A.; Maţenco, L. Tectonic regimes and stress patterns in the Vrancea Seismic Zone: Insights into intermediate-depth earthquake nests in locked collisional settings. Tectonophysics 2021, 799, 228688. [Google Scholar] [CrossRef]
- Mihai, A.; Moldovan, I.A.; Toader, V.E.; Radulian, M.; Placinta, A.O. Correlations between geomagnetic anomalies recorded at Muntele Rosu seismic Observatory (Romania) and seismicity of Vrancea zone. Rom. Rep. Phys. 2019, 71, 714. [Google Scholar]
- Ren, Y.; Grecu, B.; Stuart, G.; Houseman, G.; Hegedüs, E.; South Carpathian Project Working Group. Crustal structure of the Carpathian–Pannonian region from ambient noise tomography. Geophys. J. Int. 2013, 195, 1351–1369. [Google Scholar] [CrossRef]
- Herrmann, R.B. Computer programs in seismology: An evolving tool for instruction and research. Seismol. Res. Lett. 2013, 84, 1081–1088. [Google Scholar] [CrossRef]
- Rawlinson, N.; Sambridge, M. The fast marching method: An effective tool for tomographic imaging and tracking multiple phases in complex layered media. Explor. Geophys. 2005, 36, 341–350. [Google Scholar] [CrossRef]
- Rawlinson, N.; Sambridge, M. Seismic traveltime tomography of the crust and lithosphere. Adv. Geophys. 2003, 46, 81–199. [Google Scholar]
- Cara, M.; Leveque, J. Oriented olivine crystals in the upper mantle: A test from the inversion of multimode surface-wave data. Phys. Earth Planet. Inter. 1987, 47, 246–252. [Google Scholar] [CrossRef]
- Mainprice, D. 2.16 seismic anisotropy of the deep earth from a mineral and rock physics perspective. Treatise Geophys. 2010, 2, 437. [Google Scholar]
- Ji, S.; Li, L. Feldspar microboudinage paleopiezometer and its applications to estimating differential stress magnitudes in the continental middle crust (examples from west Yunnan, China). Tectonophysics 2021, 805, 228778. [Google Scholar] [CrossRef]
- Olaiz, A.J.; Muñoz-Martín, A.; de Vicente, G.; Vegas, R.; Cloetingh, S.A.P.L. European continuous active tectonic strain–stress map. Tectonophysics 2009, 474, 33–40. [Google Scholar] [CrossRef]
- Ritzwoller, M.H.; Levshin, A.L. Eurasian surface wave tomography: Group velocities. J. Geophys. Res. Solid Earth 1998, 103, 4839–4878. [Google Scholar] [CrossRef]
- Toyokuni, G.; Zhao, D. Whole-mantle tomography beneath eastern Mediterranean and adjacent regions. Geophys. J. Int. 2025, 241, 1155–1172. [Google Scholar] [CrossRef]
- Rawlinson, N.; Pozgay, S.; Fishwick, S. Seismic tomography: A window into deep Earth. Phys. Earth Planet. Inter. 2010, 178, 101–135. [Google Scholar] [CrossRef]
- Petrescu, L.; Stuart, G.; Tataru, D.; Grecu, B. Crustal structure of the Carpathian orogen in romania from receiver functions and ambient noise tomography: How craton collision, subduction and detachment affect the crust. Geophys. J. Int. 2019, 218, 163–178. [Google Scholar] [CrossRef]
- Popa, M.; Radulian, M.; Grecu, B.; Popescu, E.; Placinta, A. Attenuation in southeastern carpathians area: Result of upper mantle inhomogeneity. Tectonophysics 2005, 410, 235–249. [Google Scholar] [CrossRef]
- Tondi, R.; Achauer, U.; Landes, M.; Davi, R.; Besutiu, L. Unveiling seismic and density structure beneath the Vrancea seismogenic zone, Romania. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Ducea, M.N.; Barla, A.; Stoica, A.M.; Panaiotu, C.; Petrescu, L. Temporal-geochemical evolution of the Persani volcanic field, eastern Transylvanian Basin (Romania): Implications for slab rollback beneath the SE Carpathians. Tectonics 2020, 39, e2019TC005802. [Google Scholar] [CrossRef]
- Bracco Gartner, A.J.; Seghedi, I.; Nikogosian, I.K.; Mason, P.R. Asthenosphere-induced melting of diverse source regions for East Carpathian post-collisional volcanism. Contrib. Mineral. Petrol. 2020, 175, 54. [Google Scholar] [CrossRef]
- Bokelmann, G.; Rodler, F.A. Nature of the Vrancea seismic zone (Eastern Carpathians)–New constraints from dispersion of first-arriving P-waves. Earth Planet. Sci. Lett. 2014, 390, 59–68. [Google Scholar] [CrossRef]
- Kay, R.W.; Kay, S.M. Delamination and delamination magmatism. Tectonophysics 1993, 219, 177–189. [Google Scholar] [CrossRef]
- Yang, Y.; Forsyth, D.W. Rayleigh wave phase velocities, small-scale convection, and azimuthal anisotropy beneath southern California. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Gorczyk, W.; Guillot, S.; Gerya, T.V.; Hattori, K. Asthenospheric upwelling, oceanic slab retreat, and exhumation of UHP mantle rocks: Insights from Greater Antilles. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihai, A.; Petrescu, L.; Moldovan, I.-A.; Radulian, M. Investigating Rayleigh Wave Dispersion Across the Carpathian Orogen in Romania. Geosciences 2025, 15, 228. https://doi.org/10.3390/geosciences15060228
Mihai A, Petrescu L, Moldovan I-A, Radulian M. Investigating Rayleigh Wave Dispersion Across the Carpathian Orogen in Romania. Geosciences. 2025; 15(6):228. https://doi.org/10.3390/geosciences15060228
Chicago/Turabian StyleMihai, Andrei, Laura Petrescu, Iren-Adelina Moldovan, and Mircea Radulian. 2025. "Investigating Rayleigh Wave Dispersion Across the Carpathian Orogen in Romania" Geosciences 15, no. 6: 228. https://doi.org/10.3390/geosciences15060228
APA StyleMihai, A., Petrescu, L., Moldovan, I.-A., & Radulian, M. (2025). Investigating Rayleigh Wave Dispersion Across the Carpathian Orogen in Romania. Geosciences, 15(6), 228. https://doi.org/10.3390/geosciences15060228





