Abstract
In subsurface geological mapping, it is more than advisable to compare different solutions obtained with neural and other algorithms. Here, for such comparison, we used the previously published and well-prepared dataset of subsurface data collected from the Bjelovar Subdepression, a 2900 km2 large regional macrounit in the Croatian part of the Pannonian Basin System. Data on depth were obtained for the youngest (the shallowest) Lonja Formation (Pliocene, Quaternary) and mapped using neural network (NN), inverse distance weighting (IDW), and ordinary kriging (OK) algorithms. The obtained maps were compared based on square error (using k-fold cross-validation) and the visual interpretation of isopaches. Two other algorithms were also tested, namely, random forest (RF) and extreme gradient boosting (XGB) algorithms, but they were rejected as inappropriate for this purpose solely based on the visuals of the obtained maps, which did not follow any interpretable geological structures. The results showed that NN is a highly adjustable method for interpolation, with adjustment for numerous hyperparameters. IDW showed its strength as one of the classical interpolators, and its results are always located close to the top if several methods are compared. OK is the relative winner, showing the flexibility of variogram analysis regarding the number of data points and possible clustering. The presented variogram model, even with a relatively high sill and occasional nugget effect, can be well fitted into OK, giving better results than other methods when applied to the presented area and datasets. This was not surprising because kriging is a well-established method used exclusively for interpolation. In contrast, NN and machine learning algorithms are used in many fields, and these algorithms, particularly the fitting of hyperparameters in NN, simply cannot be the best solution for all.
1. Introduction
Subsurface mapping is one of the most crucial geological structural interpretation techniques, especially for mapping deep regional markers and solving regional geological settings of the analyzed area. Although there is no exact interpolator, some algorithms offer significant advantages compared with others. Traditionally, kriging techniques (including geostatistical simulations) offer the most reliable maps, although their effectiveness largely depends on the dataset size and the statistical and spatial distribution of data. For smaller datasets (fewer than 20 values), purely linear statistical interpolation methods (e.g., inverse distance and nearest neighbourhood) are often the winning choice. However, in the past two decades, some interpolation algorithms have been incorporated into neural network (NN) algorithms, allowing the mapping of variables like other interpolation algorithms. Due to the complexity of neural architecture, there are many more parameters (activation functions, number of layers, etc.) that could be set than in “classical” interpolation algorithms (search radius, distance weighting, etc.), which make the results difficult to verify.
In geology, interpolation is often used to estimate spatial variables like porosity, depth, or lithology from discrete data points. Among various techniques and methods, ordinary kriging (OK), inverse distance weighting (IDW), and NN are commonly applied for the generation of spatial predictions [1,2,3,4]. These methods vary in complexity, assumptions, and applicability, as illustrated by research in the Bjelovar Subdepression and the Croatian part of the Pannonian Basin System (CPBS) [5,6,7].
Such approaches are also used in different geological, even geoscientific, applications. For example, the authors of [8] used convolution neural networks for surficial geology mapping (glacial and glaciofluvial variables) in the South Rae geological region, Northwest Territories, Canada. They reported an accuracy between 59 (independent test area) and 76% (locally trained). Merging the classes of these variables increased average accuracy for the independent test area to 68%, representing an increase of 4% compared with the random forest (RF) machine learning algorithm.
Another interesting (surficial) geological mapping of mineral resources is given in [9], where lithological units in a mineral-rich area in the southeast of Iran are analyzed. The authors applied convolutional neural networks for improvements in previously used machine learning and remote sensing methods. The combination of neural networks and advanced spaceborne thermal emission and reflection radiometer data led to the highest accuracy.
Looking more in the past, NN was previously applied for the exploration of hydrocarbon reservoirs in Northern Croatia, i.e., the CPBS. Relatively simple models were published in [10] for three oil and gas fields. The analyzed variables included hydrocarbon saturation (also represented by a categorical variable), average reservoir porosity (calculated from logs), and seismic attributes. The results suggested that neural algorithms offer better insight into clastic Neogene reservoirs in Northern Croatia.
Mapping is a process always linked to uncertainties that have roots in many causes. The number of data points is the most famous factor, but there are also other variables like measurement errors, the clustering of measured data, the physical complexity of mapped variables, the adaptivity of interpolation algorithms, the fitting of interpolation parameters, and many others that also play a role. Here, the analysis was performed on a relatively large dataset (several tens of measured points) clustered on specific hydrocarbon field areas and using two mathematically advanced interpolation methods, i.e., the OK and NN algorithms. This dataset was collected from the Bjelovar Subdepression, Northern Croatia, and includes the data points belonging to depths of the bottom of the youngest lithostratigraphic formation in that area. This is the Lonja Formation of the Pliocene and Quaternary ages. The formation is filled with different clastics that are weakly lithified in deeper and loosely consolidated in shallower parts. The advanced nature of the method means that there are numerous parameters to set up before interpolation, and any improvisation could lead to ambiguous or clearly wrong results. However, a simpler method was also included in the analysis, namely, IDW, representing one of the most adaptable interpolation methods for a large set of different datasets regarding the size and origin of data. These three methods were compared with cross-validation and the visual geological interpretation of maps.
Another two methods, RF and XGB, were also preliminarily tested for mapping. However, the results were completely geologically non-interpretable; i.e., subsurface structures could not be meaningfully interpreted, so they were eliminated from further consideration and cross-validation comparison with the three previously mentioned methods.
OK is part of the broader set of algorithms uniquely named as geostatistics. It is applied in numerous geosciences, mostly (but not exclusively) in the 2D and 3D space. The crucial advantage of geostatistics is spatial modelling, most often performed by variogram analysis. This is also the strongest set of algorithms based on kriging for dealing with anisotropy. Geostatistics was also developed independently from spatial statistics thanks to the early works of Krige [11] and Mathéron [12,13,14] and was later improved with examples and theories published in numerous books from the 1970s to the 1990s, like Journel and Hujibregts [15], Ripley [2], Isaaks and Srivastava [16], Cressie [17], Deutsch and Journel [18], and others. Geostatistical algorithms were developed in gold mining from the very beginning, but the largest development followed hydrocarbon reservoir characterization. Eventually, their mapping advantages were spread across almost all geosciences, where kriging, cokriging (both deterministic), and stochastics are widely developed and localized for specific datasets using one of the available techniques.
Almost simultaneously, another model for prediction was developed in the domain of artificial intelligence [3,19], introducing the concepts of perceptron, connections, and neurons as basic elements, which can have several inputs and only one output and be activated or remain inactive, based on the activation function result. All data enter through the input layer, are then processed in the hidden ones, and the results are given in the output layer. The first large upgrade of the NN architecture was the introduction of the back (error) propagation algorithm, which overcame the linearity of perceptron architecture and used many hidden layers. Such a type of network calculated the difference between true and wanted response, i.e., the error that can be backed into the network and fitting results in subsequent iterations, changing, e.g., the activation function or weights added to some neurons. However, the backprop sending information to previous layers can significantly decrease the learning rate and even paralyze the process. The next improvement is named the Resilient Propagation Algorithm [20], which uses training through epochs, where weighting coefficients are adjusted after all the patterns or connections for input data are set. The resilient algorithm is four to five times faster than the standard backprop algorithm.
Unlike traditional interpolation methods such as OK or IDW, which rely on explicit spatial relationships and assumptions about spatial correlation, NNs learn complex patterns and non-linear relationships directly from the data. Since they require larger datasets and careful tuning of hyperparameters, NNs offer robust performance. However, the hyperparameter tuning process can sometimes outweigh the positives. The lack of a larger dataset can make them overcomplicated to use.
Besides the mentioned methods, some unconventional machine learning algorithms for interpolation, such as RF and XGB, were also tested. RF and XGB are machine learning algorithms that, while powerful for general regression tasks, are unconventional for interpolation because they lack inherent spatial awareness. RF builds an ensemble of decision trees by averaging predictions, while XGB sequentially builds trees to correct errors using gradient boosting; both focus on minimizing errors rather than explicitly modelling spatial relationships. Traditional interpolation methods like kriging or IDW directly incorporate spatial coordinates and distances, leveraging spatial correlation and variograms to make predictions. In contrast, RF and XGB treat coordinates as generic input features and require additional feature engineering, such as distance metrics, to account for spatial geometry. These methods are global rather than local, relying on patterns from the entire dataset rather than just nearby points. Additionally, they function as “black box” models, lacking the interpretability of geostatistical methods. Despite this, RF and XGB are sometimes preferred for their ability to handle complex, non-linear relationships, incorporate additional variables, and avoid the need for variogram modelling, making them flexible and easy to use with larger datasets or multi-variable problems [21,22,23,24].
2. Geological Setting
The Bjelovar Subdepression is a southwestern, rhomboidal branch of the Drava Depression (enlarged subdepression borders are shown in the lower-left corner graphic of Figure 1). It covers about 2900 km2 to the southwest and bordering the Sava Depression, which is the SW margin of the Pannonian Basin System (the margin borders are shown in Figure 1). The subdepression is an isolated part of the depression where, consequently, the thickness of the Neogene–Quaternary sediments is rarely more than 3000 m (compared with 7000+ metres in the central Drava Depression). Surface and subsurface mapping results in the Bjelovar Subdepression and surrounding areas are presented in [25,26,27,28,29,30] and other papers. Subsurface structures often be followed on basic (surface) geological maps (scale 1:100,000) of the sheets in Bjelovar [31] and Daruvar [32,33].
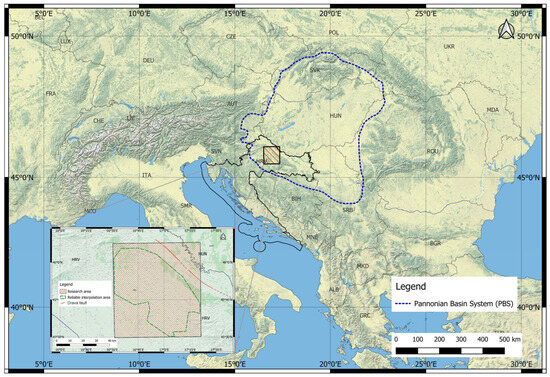
Figure 1.
Location of the research area.
The Bjelovar Subdepression has mostly been explored during hydrocarbon and geothermal drilling and production. The most promising targets were discovered within structural traps and reservoirs of the Badenian (16.4–13.0 Ma) sediments, often forming single hydrodynamic units with the uppermost parts of Palaeozoic and/or Mesozoic basement rocks. Well data are mostly collected from the fields in the central subdepressional area as well as at the NE margin, i.e., the Bilogora Mt. The area is covered by several regional wells that offer scarce data in the inter-field areas and numerous 2D seismic sections that fill the gaps among regional wells and fields. Generally, data are very irregularly distributed and clustered, which makes it hard to produced reliable regional subsurface maps [34].
Maps given by Malvić [34] as basic regional solutions were represented by polygons with 19 tops, where a larger set (including well and seismic data) was interpolated manually and a smaller one (only from averaged thickness points collected in the fields or from regional wells) was interpolated by OK [5]. They are also used as borders of mapping areas in this work as well as base solutions for comparison with the maps given here.
The Bjelovar Subdepression is considered a regional geotectonic unit of the second order in the CPBS. Geological evolution mostly be correlated with the evolution of the Pannonian Basin System (PBS) (Figure 1) [26,35,36]. As it largely started with the creation of the Central Paratethys, its stratigraphy can be followed at its own, regional, chronostratigraphic scale, events, and units, e.g., described in [35,36,37,38,39]. Here, we used the official regional chronostratigraphic units valid for the Central Paratethys and correlated with Tethys ones [40], as disputably (but widely accepted as) Pontian due to previously published data, where the given ages and time intervals are used (e.g., [41], according to [42]).
However, the marginal unit development of some depositional features was attenuated, especially regarding the source facies and thickness of possible reservoir rocks. The subdepression was opened along the main transcurrent fault system together with other longitudinal and perpendicular fault systems. The effects of the central Drava Fault (located in the lower-left graphic of Figure 1, approximately between state subdepression borders) [26,35] play a crucial role in the activation of all subdepressional fault zones. The strong tectonic uplift formed the Miocene basement starting in the Early Palaeogene. However, there was a major event in the Early Badenian (16.4–15.0 Ma), when a marine transgression covered the entirety of Northern Croatia [43]. Sedimentation was mostly in alluvial fans [26,34,43], and the sea level was progressively rising [44]. The sedimentation rate was lower than the rate of transtension, resulting in the continuous deepening of the area. The sources of sediments were located mostly locally, from the eroded and weathered pre-Miocene basement or carbonate reefs. In the Middle and Late Badenian (15.0–13.0 Ma), transtensional tectonics weakened and derived siliciclastic, and carbonates changed from coarse-grained into fine-grained.
This was followed by the first transpression (Sarmatian–Early Pannonian, i.e., 13.0–9.3 Ma). The sea environment gradually vanished and changed into a lake, where salinity was reduced into brackish water. The second transtensional period started in the Late Pannonian (9.3–7.1 Ma) and lasted to the end of the Early Pontian (7.1–6.3 Ma). A major feature is the sedimentation of very thick alternations of sandstones and marlstones in a lacustric environment. Major clastic sources were located in the Eastern Alps, and derived materials were redeposited several times on regional tectonic ramps, eventually reaching the Bjelovar Subdepression (but part of it was resedimented more on the east). Tectonic changes entered a second transpressional phase which lasted from the Late Pontian (6.3–5.6 Ma) until today. This finally reduced the water environments to numerous but small freshwater lakes, swamps, and rivers. The margins of the subdepression are formed in present day locations with the complete uplifting of the Bilogora Mountain (Figure 2, SW margin) and the additional rising of the Papuk and Psunj Mountains (Figure 2, SE margin) [45]. The locations of the main structures and faults in the Bjelovar Subdepression are shown in Figure 2 [5], and the faults’ names and displacements are given in Table 1 [5].
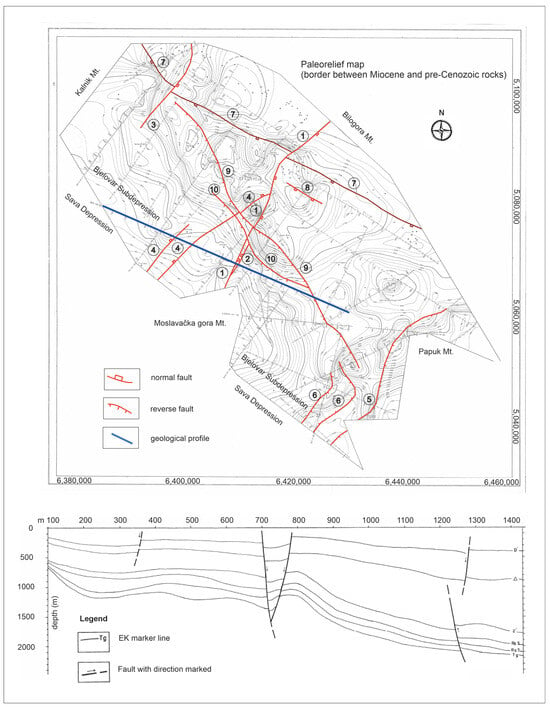
Figure 2.
Locations of main structures and faults in the Bjelovar Subdepression’s Neogene and Quaternary sediments [5,46]. Fault numbers correspond with Table 1.

Table 1.
Faults and vertical displacements (in metres) in the Bjelovar Subdepression [5]. Faults are shown in Figure 2.
3. Data and Methods
The dataset consists of the e-log marker depths of the lithostratigraphic formations interpreted in the Bjelovar Subdepression. The depths (and consequently thicknesses) of the formation’s tops and bottoms were interpreted on the well logs (mostly of spontaneous potential, gamma ray, and different resistivity logs). That was possible because in all formations, the tops and bottoms are defined as regional e-log markers (lithological marls) easily recognized on well logs. Only in the case of the oldest Neogene formation is the bottom just a border between clastics and the weathered basement (carbonate, magmatic, and metamorphic), but it is also recognizable as an e-log border on resistivity logs. After they had been recognized in well data, all e-log markers were extrapolated across the subdepression along seismic sections [5,34]. The thickness of the shallowest Lonja Formation was used to test the interpolation algorithms in this paper (Supplementary S1). It is defined by the D’ e-log marker as the bottom and the surface as the top. The dataset used for this purpose consisted of 191 points representing formation depths at different locations. The locations were defined by coordinates in the Croatian Terrestrial Reference System 1996, Universal transverse Mercator projection for zone 34N for the area of Croatia, which is a two-dimensional reference system for use in the Croatian territory [47]. Different methods of interpolation were all applied to the dataset using the Python 3.12 programming language and accompanying packages that will be mentioned later in the text. E-log markers and depths were uploaded as a pandas dataframe [48].
In order to compare different algorithms for the interpolation of the spatial data, the kriging method was used as a base model whose performance would have to be matched by other methods. The reason behind this is that kriging is widely used in subsurface geological mapping [7,49]. Kriging is a stochastic interpolation method that utilizes the spatial correlation between sampled points, modelled through variograms, to provide both predictions and uncertainty estimates [50]. It is particularly suited for cases with well-distributed data points, as demonstrated by Špelić et al. [6] in sampling and re-mapping the Bjelovar Subdepression using OK.
OK gave good results on the research area in previous investigations and is, in general, good for cases where local variations exist, but the mean is not globally defined [5,6]. For the abovementioned reasons, OK was also used in this analysis as one of the interpolation algorithms.
A variogram analysis was performed with the pykrige [51] and scikit learn [52] packages, which internally support six different variogram models. After testing, the spherical model was chosen and calculated for several scenarios, as shown in Figure 3. The analysis reveals a clear anisotropy [53,54,55]. The east–west direction (0°) shows the highest variability, with a steep increase and a high sill, indicating that spatial dependence decreases quickly over shorter distances. Additionally, the north–south direction (90°) exhibits a near-linear model without reaching a clear sill, suggesting that variability continues to increase with distance and that there is no clear spatial link among the data. However, two other models showed easier interpretable results. The perpendicular direction (45° NE-SW), which also follows the secondary axis of the subdepression, shows a model with low range but also a sill, and are both quite easily interpreted. Eventually, the main subdepressional axis, i.e., the longitudinal one (135° NW-SE), showed the best fit, with a clearly defined range (larger than in the perpendicular axis) and sill.
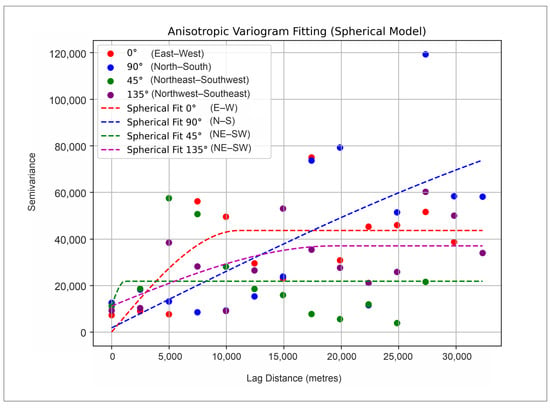
Figure 3.
Variogram analysis with four scenarios showing anisotropy in spatial variability.
It is important to note that variogram fitting could be performed differently, and some other theoretical models, or ranges in such models, could be selected. However, this is not the first time that kriged mapping has been performed in this subdepression, and previously, in all cases, the structural axes were used as starting variogram axes (main and subordinate). This is why here the NE-SW and NW-SE axes were chosen for mapping variogram models because they just follow the main axes of the subdepression’s shape. Moreover, each point of the experimental variogram was calculated from more data pairs than on the N-S or E-W axes. However, due to the clustering of data, located mostly on sections and very low-numbered well points, for the N-S, E-W, and NE-SW axes, there was no model where goodness-of-fit would be “appropriate”. Only on the NW-SE axis were the outliers not so often like those on the other three analyzed axes.
Along with OK, a simpler interpretation model was applied. IDW is a straightforward method where the unknown value of a variable is estimated based on known values within a defined search radius. This search area can be either a circle or an ellipse, including some or all data points, depending on geological or other criteria. It is mostly used by including all relevant points within the area. Each data point’s influence is weighted inversely to its distance from the unknown value, ensuring that closer points have more influence on the estimate [56].
The NN interpolation assumes the prediction of values in a grid based on the optimization of hyperparameters in its architecture. In a simplified mathematical representation, NN can be represented layer by layer as Equations (1) and (2):
where
—layer index;
—weighted sum of inputs at layer l;
—weight matrix for layer l;
—bias vector for layer l;
—activation for layer l applied as a function;
—output (activation) from layer l.
For the output layer, there is no activation function if it is for regression.
Even though most of the machine learning algorithms require normal distribution and/or a similar range of parameters being used for learning, this is not the case with NNs. This is due to their nature of pattern recognition. However, scaling is highly encouraged for input variables here too [57,58] (Equation (3)).
where
—the mean of x and y in the training data;
—the standard deviation of x and y.
The given default NN model architecture (Table 2) can be mathematically per layers (Equation (4)), loss function (Equation (5)), and a weight update known as an optimizer (Equation (6)). There are generally two approaches to NN hyperparameter optimization. The hyperparameter tuner employed in this NN was Keras Tuner [59] with a random search approach to find the best combination of hyperparameters in order to minimize the validation Root Mean Square Error (RMSE).

Table 2.
Default NN model where hyperparameters have been set up according to dataset size.
The process of constructing and fitting the NN began by defining a customizable model through the flexible framework (Supplementary S2), where key hyperparameters, such as the number of hidden layers (1 to 5), the number of neurons per layer (16 to 128 in increments of 16), the activation functions (relu, tanh, or sigmoid), and the optimizers (adam, sgd, or rmsprop), were defined as tuneable options. Additionally, the loss function (Mean Square Error (MSE) or Mean Absolute Error (MAE)) was also optimized. The tuner (exploring tuneable options) iteratively explored up to 20 different hyperparameter combinations, averaging performance across two executions per trial, using 80% of the data for training and 20% for validation. After evaluating each combination for 100 epochs with a batch size of 8, the tuner selected the best-performing hyperparameters based on MSE. The resulting optimal model was then trained for 100 epochs on the training data, achieving further refinement before being evaluated on a separate test set. The discovered hyperparameters, such as the number of layers, units per layer, activation functions, optimizer, and loss function, were displayed alongside the final test loss for transparency and reproducibility (Supplementaries S1 and S2). The other approach is manual tuning based on expert opinion and experience. This means that, in the base NN model, one hyperparameter is modified at a time. This firstly establishes the way that the hyperparameters affect interpolation, and, secondly, the best option, based on expert opinion, was compared to the other methods of interpolation.
where
—weighted sum of inputs at layer l;
—weight matrix for layer l;
—input feature vector;
—bias vector for layer l;
—output (activation) from layer l;
—loss function (MSE);
—number of samples in the batch;
—true value for sample i;
—predicted value for sample I;
—weight update (Adam);
—learning rate;
—bias-corrected estimate of variance (in optimizer);
—small constant to prevent division by zero;
—bias-corrected estimate of mean (in optimizer).
In addition, two non-casual estimation methods were tested. These are the RF and XGB interpolation methods, which leverage machine learning to estimate values at unsampled locations based on training data patterns. RF operates on a bagging principle, constructing multiple decision trees from random subsets of the data and averaging their outputs. This approach makes RF robust against noise and overfitting while also allowing for feature importance analysis. However, RF tends to produce boxy, step-like interpolation patterns that do not always capture smooth geological variations, making it less suitable for continuous spatial phenomena [60]. RF can mathematically be described (Equation (7)) by MSE for each node where the data branches if they are used as a regression [61]:
where
—number of data points;
—true value for sample i;
—predicted value for sample i.
On the other hand, XGB follows a boosting mechanism, where trees are built sequentially, with each tree correcting the errors of the previous one [62,63]. This results in improved accuracy and the ability to model non-linear relationships effectively. XGB also includes built-in regularization to mitigate overfitting, but like RF, it often generates interpolation surfaces that appear unnatural due to the decision-tree-based learning approach. Despite achieving low error metrics, both methods struggle to reproduce geologically realistic patterns, as they lack an explicit consideration of spatial continuity and autocorrelation [61]. While smoothing techniques, such as Gaussian filters, can help mitigate these issues, they may also introduce artificial distortions, further separating the model’s output from true geological structures [61].
Even though RF and XGB are highly used and referenced methods in regression problems [21,22,64], mostly predictions, there is still limited research on spatial interpolation as the results that have been seen so far are still behind the traditional geostatistical approaches.
4. Results
4.1. Interpolation Methods
The extent of all interpolation was defined as a rectangular boundary containing all the data locations inside it. The boundaries of the subdepression are given as blue lines. The grid was defined as the equally distributed cells spaced 100 m in both the x and y directions. That accounted for 4,550,000 grid points in a grid sized 700 × 650 cells.
4.1.1. OK Maps
The variogram analysis confirms that thickness values are spatially correlated within the range, after which spatial dependence diminishes. The points (Figure 3) represent the experimental semivariogram, and their scatter could be affected by a smaller dataset in directional analysis and/or clustering. The range was weighted for the direction of 45°. The kriging map (Figure 4) reveals the largest thickness in the central part of the subdepression, which unevenly decreases towards the margins. Just on the margins, the obtained map showed the largest differences from a previous map taken from [5], which was the most comprehensive map of the subdepression up to now. This was expected due to a lack of data on the edges, but in general, the main structures are visible on similar locations. Both maps are overlaid with the main subdepression fault zones (Figure 2), although such zones are not used in any interpolation performed here because the software cannot deal properly with fault throws of any kind.
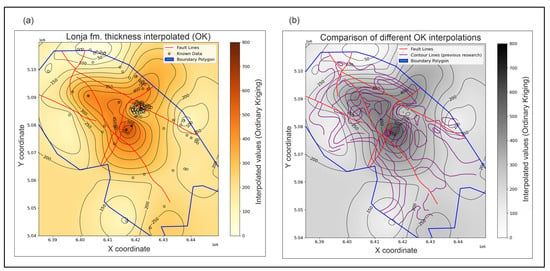
Figure 4.
The OK maps of the e-log marker D’ depths (the shallowest Lonja Formation thickness). (a) Map interpolated in this research with pykrige [5,52]. (b) Map from previous research (Figure 1) [5,52].
4.1.2. IDW Map
The results of the IDW interpolation were two maps (Figure 5) generated with two different power values: two in Figure 5a and three in Figure 5b. The power parameter determines how the influence of a data point diminishes with distance, affecting how local or global features will be emphasized. On the map where the power is set to 2, the interpolated surface appears smoother, with a smaller impact of the bull’s eye effect due to the larger influence of distant points. The lower p value sometimes tends to over-smooth local variations, but here, this is not the case (see Figure 4 for comparison). In contrast, Figure 5b (p = 3) exhibits sharper gradients and more localized effects. In geological contexts, such as thickness interpolation here, this can be important as the thickness is changed gradually, except in the vicinity of a fault zone with a high throw. Some authors recommend to use p = 2 as the most appropriate value for the mapping of the CPBS [65].
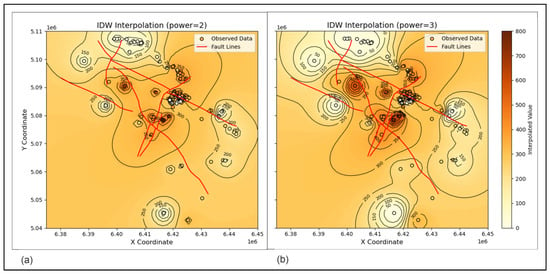
Figure 5.
The IDW maps of the e-log marker D’ depths (the shallowest Lonja Formation thickness) for the cases of (a) power = 2 and (b) power = 3.
4.1.3. NN Maps
Using NN for the interpolation of thicknesses offers a different data-driven approach to understanding spatial variability. Such a network is defined with parameters and hyperparameters. Learning spatial patterns directly from the data offers the possibility to incorporate features like spatial coordinates. All the hyperparameters that were described previously (Table 2) were defined with the tensorflow package [66,67], and the main application advantages (Table 3) and (hyper)parameters (Table 4) are described in this discussion. The maps obtained with NN are shown in Figure 6.

Table 3.
Comparison of the maps obtained with different algorithms, both conventional (OK and IDW) and unconventional (NN), based on several CV metrics.

Table 4.
Comparative overview of the interpolation methods being used in the case of the youngest Lonja Formation in the Bjelovar Subdepression.
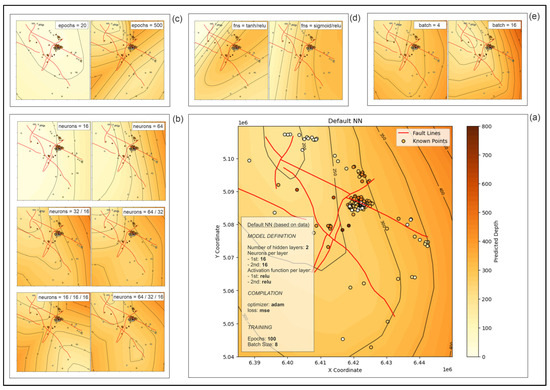
Figure 6.
The NN maps of the e-log marker D’ depths (the shallowest Lonja Formation thickness) based on selected architecture (a) and changes that could be made based on the number of hidden layers and neurons in them (b), epochs (c), activation functions (d), and the size of the batch (e), as shown in Table 5.
The optimization of NN was performed (Figure 7) using different hyperparameters that were defined as the best by Keras Tuner [60] (Supplementaries S1 and S2). The NN with an optimized architecture of the layers is described by the following Equations (8):
where
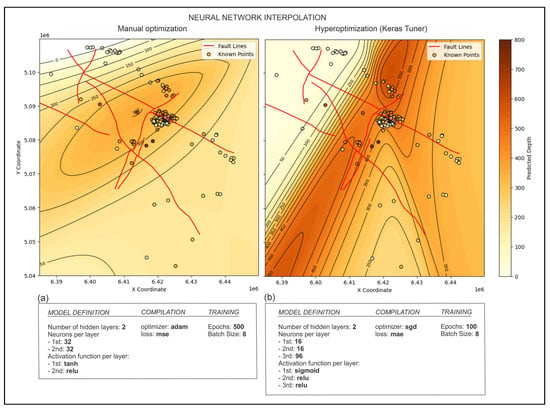
Figure 7.
The optimization of NN hyperparameters (a) manually and (b) with random search as part of the Keras Tuner package [59].
—pre-activation output of shape (n, 32), (n, 32), and (n, 1);
—number of samples in the dataset
—weight matrix of shape (2, 32), (32, 32), (32, 1);
—bias vector of shape (32, ), (32, ), (1, );
—final predicted depth values.
4.1.4. RF and XGB
Although not used as dedicated interpolation algorithms (due to coming from the domain of machine learning), RF and XGB are tested here as approaches for such a purpose thanks to the availability of their algorithms and relatively quick estimations. However, the obtained interpolations left a lot to deal with in terms of geological interpretation, as the map of the thicknesses shows structures that are not geologically sound.
Both RF and XGB created interpolation surfaces based on decision trees, which inherently partition the feature space into discrete, box-like regions. This resulted in sharp, abrupt transitions between predicted values, which did not reflect the natural gradual transitions among structural contours (Figure 8a and Figure 9a). The sharp breaks did not even follow the major fault zones, which makes these representations completely inapplicable to the geological mapping of the Bjelovar Subdepression. However, some improvements were achieved with the use of the Gaussian filter for smoothing (Figure 8b,c and Figure 9b,c) because the filter effectively reduces local noise and artificial discontinuities, ensuring that the interpolated surface respects the inherent spatial correlation of subsurface layers. Thus, the results are still of use for geological mapping.
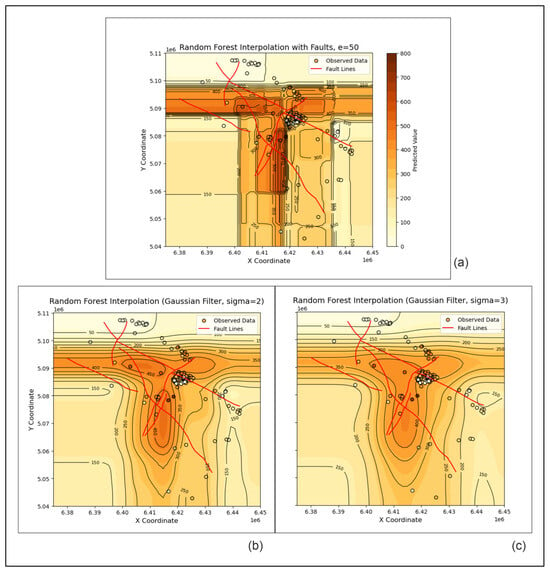
Figure 8.
The random forest maps of the e-log marker D’ depths (the shallowest Lonja Formation thickness) with (a) blocky results and (b,c) Gaussian smoothing.
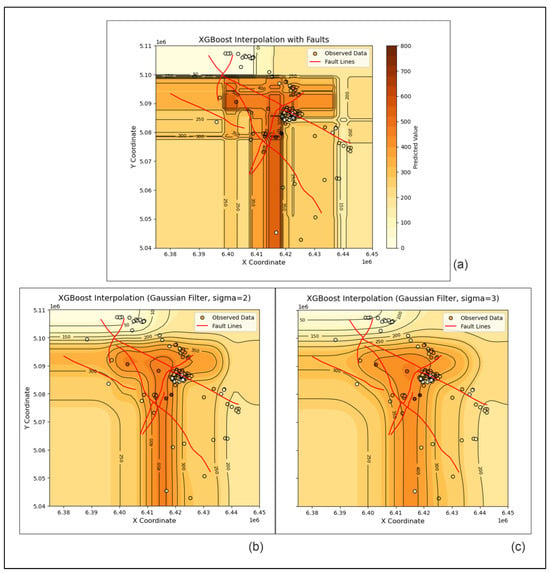
Figure 9.
The extreme gradient boosting maps of the e-log marker D’ depths (the shallowest Lonja Formation thickness) with (a) blocky results and (b,c) Gaussian smoothing.
5. Discussion
Based on the comparison of OK, IDW, NN, RF, and XGB, distinct differences in their predictive performances were observed. Among these methods, the last two were disqualified from further consideration due to their noninterpretable visual results. Furthermore, OK produced the smallest error metrics (Equations (7), (9) and (10)), closely followed by IDW (Table 3). The values were computed using the abovementioned equations for MAE, MSE, and RMSE on the whole dataset (all 191 points). All metrics were calculated in the same manner for all methods for them to be comparable. The cross-validation of the results was used in a way that the dataset was split into 80–20 portions (training/test data) five times (k-fold = 5), so that different parts of the dataset were being used for testing the algorithms at different times. The metrics were calculated five times for each split and method individually after the model was already trained. The metrics shown in Table 3 are the averages of the five splits to ensure that the algorithm has captured the whole data trend and not just the trend for the specific split. Despite extensive hyperparameter tuning, NN did not outperform OK.
where
—final predicted depth values;
—observed depth values;
—number of observed depths.
OK also offered the most geologically realistic interpolation due to its ability to model spatial dependence and anisotropy through several variogram scenarios. However, further expertise could partially refit the shown variogram models and probably slightly change the structural contour shapes and CV values. IDW was simpler and computationally faster. It performed well in regions with denser data points but lacked OK’s ability to model spatial anisotropy. This often led to over-smoothing in dense regions and under-smoothing in sparse areas. This latter effect is shown on the IDW maps presented here, where the bull’s eye effect is clearly visible on both solutions (p = 2 and 3). Eventually, NN demonstrated flexibility in capturing non-linear relationships, but its performance was probably hindered by clustered data and a lack of larger spatial correlation across the entire subdepression.
One key observation from this study concerns hyperparameter optimization in NN. It can improve numerical accuracy (cross-validation) but may not lead to geologically plausible results. Hyperparameter tuning, as performed with tools like Keras Tuner [60], optimizes short-term statistical but not geological ones. For example, models optimized for RMSE may produce over-smoothing or abrupt transitions that fail to capture real geological features. Incorporating domain-specific features, preferably more than one, such as fault lines or lithological boundaries, could enhance the geological relevance of neural models. The main observed features of the OK, IDW, and NN models are listed in Table 4. The very specific optimization hyperparameters for the applied NN are given in Table 5.

Table 5.
Descriptions and usage examples for the adjustable hyperparameters in the NN model defined with the tensorflow package [66,67].
All equations representing the NN architecture and underlying functions are presented in Table 5 and can be found in more detail in secondary sources, e.g., [66,68,69,70,71]. Here, they were used for the definition of the default (base) NN model, where the hyperparameters were defined according to dataset size. Such a base model consisted of two hidden layers with 16 neurons in each layer, and, during its upgrade, the hyperparameters were defined as shown in Table 4 using TensorFlow package [66,67] (Supplementaries S1 and S2).
This section could finish with some thoughts on uncertainties in estimations and the choice of the right algorithm. Although OK was superior in this analysis, its advantages were not found to be extremely high, and its results did not overwhelm those of IDW and NN. In fact, the OK algorithm, especially the used variogram, is associated with inherent uncertainties. There is an opportunity to use a secondary variable in OK mapping and apply the cokriging algorithm; in particular, the use of seismic data as a secondary variable in geostatistical mapping is a well-known approach. However, not only can seismic data be used as secondary input, but there are also plenty of sources which can take such a role, like local elevation terrain [72], which is a variable available in almost all geological mappings. However, due to the large time span of the subdepression’s evolution (more than 16.4 Ma), the present-day relief (i.e., the elevations) cannot be directly followed in the subsurface, even if the youngest unit (of a Quaternary period and Pliocene epoch) is mapped, due to inversion tectonics. Moreover, the available seismic data and sections are not approximately regularly distributed across the area, so their inclusion in cokriging algorithms could force the clustering and lead to a worse estimation than that of OK. In fact, a comparison of cokriging and OK would be a useful separate analysis for this area, if such interest arose in the future. In such case, a careful study of datasets and meaningful correlations between primary and secondary variables and geostatistical algorithms [72] should precede new geostatistical mappings, which could preferably be performed in some well-known and documented open-source geostatistical package [73].
Involving new algorithms, like cokriging, requires a secondary variable, which could be the presented seismic data, especially because they are converted into depths, the variable also derived from well data. Here, the seismic values are used as a primary variable, maintaining a single dataset. The reason behind this was the fact that well data were used for solving (with the tracking of amplitude) structure extensions, including faults, in the subdepression. The tracking was based on several time–depth velocity rules, so errors were inevitable, especially in the contact areas of different velocities. However, there is another possibility to keep seismic “depths” as a separate class of secondary variable data, calculate the correlation with the primary variable (depths in wells), and apply cokriging for mapping. In such case, the mentioned geostatistical algorithm would finish the “tracking of depths” between wells, along sections, on its own, using variograms for both variables and solving structural relations in the inter-well area.
Observing cokriging still does not include stochastics as a feature of the kriging method, even when it is applied and interpreted as a deterministic one. The problem of sampling new data from the existing ones is still present, especially when the dataset is smaller and, consequently, uncertainties about range, distribution, and locations are larger. There is a well-known approach in subsurface geological volume variable estimation called the Monte Carlo. Interestingly, Schiavo [74] proved that (only) 10% of the Monte Carlo-analyzed volume, modelled for the flow model (hydrological conductivity), was enough to reach full numerical stability.
However, in the results presented here, the great advantage is that the kriged map represents, in fact, the kriged (continuous) field, where additional sampling (like Monte Carlo) is not necessary if we consider the obtained map to be reasonably accurate, as in this case. But such kriged fields include uncertainties, at least in the variogram model as well as in the kriging variance, which can be later developed through stochastics into simulations. It is especially interesting that some authors, e.g., [75], developed a methodology for replacing the experimental variogram with its uncertainty margins. Consequently, variogram parameters can be interpreted probabilistically and with several realizations.
6. Conclusions
Each method investigated here demonstrated unique strengths and limitations that influence their suitability for subsurface geological interpolation. There are a few main points that we would now like to highlight:
- It is well known that OK is dependent on the quality of variogram analysis, i.e., the number of data points and possible clustering. Here, we show that a variogram model, even one with a relatively high sill and occasional nugget effect, can be well fitted into a mapping model and surpass other methods applied to the presented area and datasets.
- A variogram model, with all included uncertainties, easily found spatial anisotropies, which had an origin in the structural shape (and, consequently, the tectonic zone’s directions, throws, and strike of depositional features) of the subdepression. Here, two variogram models representing anisotropy were chosen, one on the main subdepressional axis (135° NW-SE) and the other on the subordinate (45° NE-SW). As expected, the main axis variogram showed the best fit with the experimental points and the definition of range (about 15,000 m) and nugget (approx. 10,000).
- NN showed that it is a highly adjustable method for interpolation, where numerous hyperparameters can be adjusted. However, its high adjustability only makes the process more complex while geological representativeness still cannot be guaranteed or even achieved as in OK. In fact, in NN, hyperparameter optimization does help the statistical accuracy of a trained model, but it can be irrelevant to the geology of the area. That could be a pitfall in automated NN fitting. This is why our manually tuned models outperformed automatized tuners, such as Keras Tuner, because the best fitted model (the one with the smallest errors) in general follows geological and spatial facts and data.
- IDW showed its strength as one of the classical interpolators with which the results are always located close to the top if several methods are compared. In contrast, the RF and XGB algorithms were found to be completely inapplicable to subsurface geological mapping, at least for the presented dataset and the area of the Bjelovar Subdepression.
- Even methods like OK, IDW, and NN will also perform poorly in the absence of enough numerous datasets, sometimes characterized with clustering. However, in the case of the analyzed dataset, any of those methods can be recommended for future mapping in the Bjelovar Subdepression and the entire CPBS (with similar datasets). The manually optimized NN could always be the second (supplementary) approach to OK (here, OK vs. NN RMSE was 100.53 vs. 122.15), used for checking the structural results and comparing cross-validation values, expecting similar or sometimes maybe slightly better values. If NN is considered to be time-consuming or unreliable for the fitting of certain parameters, the supporting method can be IDW, which is a simple and easily understandable algorithm in which the error is comparable with that of the advanced NN (here, NN vs. IDW RMSE was 123.66 vs. 122.15).
- Neural algorithms in mapping are still rarely used, but here, we gave an example of such an application based on real subsurface geological data collected in clastics. Secondly, but equally importantly, here it was shown that even in such an abundant dataset, although partially clustered, the kriging method is still an option that could surpass a neural algorithm with several modifications of its parameters.
- Moreover, OK is better than the machine learning RF and XGB algorithms, which are completely unsuitable for this purpose. This was not surprising because kriging is a well-established method exclusively used for interpolation. In contrast, NN and machine learning algorithms are used in so many fields that their algorithms, including the fitting of hyperparameters in NN, simply cannot be the best solution for all types of applications.
- These novelties, mentioned in the previous two points, can be considered as especially important for other researchers with experience in geological mapping.
- It is worth mentioning that the kriging algorithm intrinsically includes uncertainties (like kriging variance but also uncertainties linked to deterministic estimation in each grid cell). As the kriged map was the best option presented in this work, it is meaningful to assume that future improvement of this work should move in the direction of mapping using stochastic Gaussian simulation, which can be investigated as a better option than the fitting of NNs, whether automatically or using expert opinions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences15060206/s1, Table S1: Sample of the input data; Table S2: Exact hyperparameters that were manually optimized for the purposes of this research; Table S3: Best tuned hyperparameters based on the set-up ranges.
Author Contributions
Conceptualization, A.B. and T.M.; methodology, A.B.; validation, T.M.; investigation, A.B., T.M., J.O. and J.K.; writing—original draft preparation, A.B., T.M., J.O. and J.K.; writing—review and editing, A.B., T.M., J.O. and J.K.; visualization, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset is available on request from the authors.
Acknowledgments
The authors thank the anonymous reviewers and editors for their generous and constructive comments that have improved this paper. This research was partially carried out within the projects “Mathematical researching in geology IX and X” (led by T. Malvić) and “Geophysical investigations of shallow, deep and very deep geological models in the wider Dinaric area 2” (led by J. Kapuralić).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OK | Ordinary kriging |
| IDW | Inverse distance weighting |
| NN | Neural network |
| RF | Random forest |
| XGB | Extreme gradient boosting |
| CV | Cross-validation |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
References
- Chen, P. A Rapid Supervised Learning Neural Network for Function Interpolation and Approximation. IEEE Trans. Neural Netw. 1996, 7, 1220–1230. [Google Scholar] [CrossRef]
- Ripley, B.D. Spatial Statistics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Rosenblatt, F. The Perceptron: A Perceiving and Recognizing Automaton; Report; Project PARA; Cornell Aeronautical Laboratory: Ithaca, NY, USA, 1957; 58p. [Google Scholar]
- Achite, M.; Tsangaratos, P.; Pellicone, G.; Mohammadi, B.; Caloiero, T. Application of Multiple Spatial Interpolation Approaches to Annual Rainfall Data in the Wadi Cheliff Basin (North Algeria). Ain Shams Eng. J. 2024, 15, 102578. [Google Scholar] [CrossRef]
- Malvić, T. Geological Maps of Neogene Sediments in the Bjelovar Subdepression (Northern Croatia). J. Maps 2011, 7, 304–317. [Google Scholar]
- Špelić, M.; Malvić, T.; Saraf, V.; Zalović, M. Remapping of Depth of E-Log Markers between Neogene Basement and Lower/Upper Pannonian Border in the Bjelovar Subdepression. J. Maps 2016, 12, 45–52. [Google Scholar] [CrossRef]
- Kiš, I.M. Comparison of Ordinary and Universal Kriging Interpolation Techniques on a Depth Variable (a Case of Linear Spatial Trend), Case Study of the Šandrovac Field. Rud.-Geol.-Naft. Zb. 2016, 31, 41–58. [Google Scholar] [CrossRef]
- Latifovic, R.; Pouliot, D.; Campbell, J. Assessment of Convolution Neural Networks for Surficial Geology Mapping in the South Rae Geological Region, Northwest Territories, Canada. Remote Sens. 2018, 10, 307. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Heidari, E.; Pour, A.B.; Pradhan, B.; Müller, D.; Chandra, R. A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data. Remote Sens. 2022, 14, 819. [Google Scholar] [CrossRef]
- Malvić, T.; Velić, J.; Horváth, J.; Cvetković, M. Neural Networks in Petroleum Geology as Interpretation Tools. Cent. Eur. Geol. 2010, 53, 97–115. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. Chem. Metall. Min. Soc. S. Afr. 1952, 52, 119–139. [Google Scholar] [CrossRef]
- Georges, M.; Fernand, B. Traité de Géostatistique Appliquée; Bureau de recherches géologiques et minières; Tome, I., Ed.; Technip: Paris, France, 1962. [Google Scholar]
- Georges, M. Principles of Geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar]
- Matheron, G. Les Variables Régionalisées et Leur Estimation. Une Application de La Théorie Des Fonctions Aléatoires Aux Sciences de La Nature; Masson: Échandens, Switzerland, 1965. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Isaaks, E.; Srivastava, R. An Introduction to Applied Geostatistics; Oxford University Press Inc.: Oxford, UK, 1989. [Google Scholar]
- Cressie, N. The Origins of Kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide (Applied Geostatistics Series), 2nd ed.; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm. In Proceedings of the IEEE International Conference on Neural Networks, Nagoya, Japan, 25–29 October 1993; pp. 586–591. [Google Scholar]
- Srivardhan, V. Adaptive Boosting of Random Forest Algorithm for Automatic Petrophysical Interpretation of Well Logs. Acta Geod. Geophys. 2022, 57, 495–508. [Google Scholar] [CrossRef]
- Feng, R.; Grana, D.; Balling, N. Imputation of Missing Well Log Data by Random Forest and Its Uncertainty Analysis. Comput. Geosci. 2021, 152, 104763. [Google Scholar] [CrossRef]
- Behnamian, A.; Millard, K.; Banks, S.N.; White, L.; Richardson, M.; Pasher, J. A Systematic Approach for Variable Selection with Random Forests: Achieving Stable Variable Importance Values. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1988–1992. [Google Scholar] [CrossRef]
- Micić Ponjiger, T.; Šešum, S.; Naugolnov, M.V.; Pilipenko, O. Lithology Classification by Depositional Environment and Well Log Data Using XGBoost Algorithm. In Proceedings of the Data Science in Oil and Gas 2021, DSOG 2021, Online, 4–6 August 2021; EAGE Publishing BV: Utrecht, The Netherlands, 2021. [Google Scholar]
- Kranjec, V.; Prelogović, E.; Hernitz, Z.; Blašković, I. O litofacijelnim odnosima mlađih neogenskih i kvartarnih sedimenata u širem području Bilogore (sjeverna Hrvatska). Geološki Vjesn. 1971, 24, 47–55. [Google Scholar]
- Malvić, T. Strukturni i Tektonski Odnosi te Značajke Ugljikovodika Širega Područja Naftnoga Polja Galovac-Pavljani; Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb: Zagreb, Croatia, 1998. [Google Scholar]
- Malvić, T. Ležišne vode naftnoga polja Galovac-Pavljani. Hrvat. Vode 1999, 7, 139–148. [Google Scholar]
- Pletikapić, V. Naftoplinonosnost Dravske potoline. Nafta 1964, 9, 250–254. [Google Scholar]
- Pletikapić, V.; Gjetvaj, I.; Jurković, M.; Urbiha, H.; Hrnčić, L. Geologija i naftoplinonosnost Dravske potoline. Geološki Vjesn. 1964, 17, 49–78. [Google Scholar]
- Prelogović, E.; Hernitz, Z.; Blašković, I. Primjena morfometrijskih metoda u rješavanju strukturno-tektonskih odnosa na području Bilogore (sjev. Hrvatska). Geološki Vjesn. 1969, 22, 525–531. [Google Scholar]
- Magdalenić, Z.; Novosel, S. Tumač za List Bjelovar—Sedimentnopetrografske Karakteristike Nevezanih Stijena Neogena i Kvartara; Savezni geoloski zavod, Beograd. 1986. Available online: https://www.hgi-cgs.hr/wp-content/uploads/2020/07/Bjelovar.pdf (accessed on 11 May 2025).
- Jamičić, D. Osnovna Geološka Karta M 1:100.000—List Daruvar; Geološki Zavod Zagreb: Zagreb, Croatia, 1988. [Google Scholar]
- Jamičić, D.; Vragović, M.; Matičec, D. Osnovna Geološka Karta SFRJ 1:100 000, Tumač za List Daruvar; Geološki Zavod Srbije: Beograd, Serbia, 1988. [Google Scholar]
- Malvić, T. Naftnogeološki Odnosi i Vjerojatnost Pronalaska Novih Zaliha Ugljikovodika u Bjelovarskoj Uleknini [Oil-Geological Relations and Probability of Discovering New Hydrocarbon Reserves in the Bjelovar Sag]; Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb: Zagreb, Croatia, 2003. [Google Scholar]
- Royden, L. Late Cenozoic Tectonics of the Pannonian Basin System. In The Pannonian Basin: A Study in Basin Evolution. AAPG Memoir 45; Royden, L.H., Horvath, F., Eds.; AAPG: Tulsa, OK, USA, 1988. [Google Scholar]
- Rögl, F. Palaeogeographic Considerations for Mediterranean and Paratethys Seaways (Oligocene to Miocene). Ann. Des Naturhistorischen Mus. 1998, 99, 279–310. [Google Scholar]
- Rögl, F. Stratigraphic Correlation of the Paratethys Oligocene and Miocene. Mitteilungen Ges. Geol. Bergbaustud. Osterr. 1996, 41, 65–73. [Google Scholar]
- Rögl, F.; Steininger, F. Neogene, Parathetys, Mediterranean and Indo-Pacific Seaways. In Fossil and Climate; Brenchey, P., Ed.; Wiley and Sons: Hoboken, NJ, USA, 1984; pp. 171–200. [Google Scholar]
- Steininger, F.; Rögl, F.; Müller, C. Chronostratigraphie Und Neostratotypen: Miozän Der Zentralen Paratethys, Band VI; Schweizerbart Science Publishers: Stuttgart, Germany, 1978. [Google Scholar]
- Piller, W.E.; Harzhauser, M.; Mandic, O. Miocene Central Paratethys Stratigraphy—Current Status and Future Directions. Stratigraphy 2007, 4, 151–168. [Google Scholar] [CrossRef]
- Malvić, T.; Velić, J. Neogene Tectonics in Croatian Part of the Pannonian Basin and Reflectance in Hydrocarbon Accumulations; InTech: London, UK, 2011. [Google Scholar]
- Haq, B.U.; van Eysinga, F.W.B. Geological Time Table, 5th ed.; Elsevier Science Ltd.: London, UK, 1998. [Google Scholar]
- Pavelić, D. Tectonostratigraphic Model for the North Croatian and North Bosnian Sector of the Miocene Pannonian Basin System. Basin Res. 2001, 13, 359–376. [Google Scholar] [CrossRef]
- Pavelić, D.; Miknic, M.; Šrlat, M.S. Early To Middle Miocene Facies Succession in Lacustrine and Marine Environments on the Southwestern Margin of the Pannonian Basin System (Croatia). Geol. Carpathica 1998, 49, 433–443. [Google Scholar]
- Prelogović, E. Neotektonska karta SR Hrvatske. Geološki Vjesn. 1975, 28, 97–108. [Google Scholar]
- Malvić, T. Regional Geological Settings and Hydrocarbon Potential of Bjelovar Sag (Subdepression), R. Croatia. Naft. 2004, 55, 273–288. [Google Scholar]
- National Spatial Data Infrastructure (NIPP). Coordinate Reference System. Available online: https://www.nipp.hr/default.aspx?id=3207 (accessed on 10 February 2025).
- The Pandas Development Team. pandas-dev/pandas: Pandas. 2020. Available online: https://zenodo.org/records/13819579 (accessed on 11 May 2025). [CrossRef]
- He, Y.; Chen, D.; Li, B.G.; Huang, Y.F.; Hu, K.L.; Li, Y.; Willett, I.R. Sequential Indicator Simulation and Indicator Kriging Estimation of 3-Dimensional Soil Textures. Soil Res. 2009, 47, 622. [Google Scholar] [CrossRef]
- Malvić, T. Primjena Geostatistike u Analizi Geoloških Podataka; INA—Industrija Nafte: Zagreb, Croatia, 2008. [Google Scholar]
- Murphy, B.; Yurchak, R.; Müller, S. GeoStat-Framework/PyKrige; V1.7.2; UFZ Leipzig: Leipzig, Germany, 2024. [Google Scholar]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Zhao, F.H.; Zhu, A.X.; Qin, C.Z. Spatial Distribution Pattern Analysis Using Variograms over Geographic and Feature Space. Geo-Spat. Inf. Sci. 2024, 1–15. [Google Scholar] [CrossRef]
- Nansen, C. Use of Variogram Parameters in Analysis of Hyperspectral Imaging Data Acquired from Dual-Stressed Crop Leaves. Remote Sens. 2012, 4, 180–193. [Google Scholar] [CrossRef]
- MacCormack, K.; Arnaud, E.; Parker, B.L. Using a Multiple Variogram Approach to Improve the Accuracy of Subsurface Geological Models. Can. J. Earth Sci. 2018, 55, 786–801. [Google Scholar] [CrossRef]
- Malvić, T.; Ivšinović, J.; Velić, J.; Sremac, J.; Barudžija, U. Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia. Stats 2020, 3, 68–83. [Google Scholar] [CrossRef]
- McDonald, A. Data Quality Considerations for Petrophysical Machine-Learning Models. Petrophysics 2021, 62, 585–613. [Google Scholar]
- Bahri, Y.; Dyer, E.; Kaplan, J.; Lee, J.; Sharma, U. Explaining Neural Scaling Laws. Proc. Natl. Acad. Sci. USA 2024, 121, e2311878121. [Google Scholar] [CrossRef]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. Keras Tuner. 2019. Available online: https://github.com/keras-team/keras-tuner (accessed on 12 February 2025).
- Madison Schott Random Forest Algorithm for Machine Learning. Available online: https://medium.com/capital-one-tech/random-forest-algorithm-for-machine-learning-c4b2c8cc9feb (accessed on 11 February 2025).
- Li, Z.; Lu, T.; Yu, K.; Wang, J. Interpolation of GNSS Position Time Series Using GBDT, XGBoost, and RF Machine Learning Algorithms and Models Error Analysis. Remote Sens. 2023, 15, 4374. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boost. System; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Sun, L. Application and Improvement of Xgboost Algorithm Based on Multiple Parameter Optimization Strategy. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 1822–1825. [Google Scholar]
- Krkač, M.; Bernat Gazibara, S.; Arbanas, Ž.; Sečanj, M.; Mihalić Arbanas, S. A Comparative Study of Random Forests and Multiple Linear Regression in the Prediction of Landslide Velocity. Landslides 2020, 17, 2515–2531. [Google Scholar] [CrossRef]
- Barudžija, U.; Ivšinović, J.; Malvić, T. Selection of the Value of the Power Distance Exponent for Mapping with the Inverse Distance Weighting Method—Application in Subsurface Porosity Mapping, Northern Croatia Neogene. Geosciences 2024, 14, 155. [Google Scholar] [CrossRef]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep Learning With TensorFlow: A Review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Ravichandiran, S. Hands-On Deep Learning Algorithms with Python; Packt Publishing: Birmingham, UK, 2019; ISBN 978-1-78934-415-8. [Google Scholar]
- Lichtner-Bajjaoui, A.; Vives, J. A Mathematical Introduction to Neural Networks. Master’s Thesis, Universitat de Barcelona, Barcelona, Spain, 2021. [Google Scholar]
- Obuchowski, A. Understanding Neural Networks 2: The Math of Neural Networks in 3 Equations. Available online: https://becominghuman.ai/understanding-neural-networks-2-the-math-of-neural-networks-in-3-equations-6085fd3f09df (accessed on 31 January 2025).
- Saravanan, D.K. A Gentle Introduction To Math Behind Neural Networks. Available online: https://towardsdatascience.com/introduction-to-math-behind-neural-networks-e8b60dbbdeba (accessed on 31 January 2025).
- Schiavo, M. Spatial modeling of the water table and its historical variations in Northeastern Italy via a geostatistical approach. Groundw. Sustain. Dev. 2024, 25, 101186. [Google Scholar] [CrossRef]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: Cambridge, UK, 2009; 288p, ISBN 9780521514149. [Google Scholar]
- Schiavo, M. Numerical impact of variable volumes of Monte Carlo simulations of heterogeneous conductivity fields in groundwater models. J. Hydrol. 2024, 634, 131072. [Google Scholar] [CrossRef]
- Mälicke, M.; Guadagnini, A.; Zehe, E. SciKit-GStat Uncertainty: A software extension to cope with uncertain geostatistical estimates. Spat. Stat. 2023, 54, 100737. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).