3D Simultaneous Inversion and Modeling of Full Tensor Gravity and Gravity Data for Salt Imaging

Abstract

In this study, we performed three-dimensional gravity modeling and inversion of the Vinton Dome, a well-known onshore salt structure located in southwestern Louisiana, USA, by simultaneously integrating Full Tensor Gravity (FTG) and conventional gravity data using a simulated-annealing approach. The process begins with the application of Tensor Euler Deconvolution (ETD), which provides a physically consistent initial model for inversion. This method extends the traditional Euler deconvolution by incorporating both the three diagonal components of the gravity-gradient tensor and the three components of the gravity field, thereby enhancing the frequency content and stability of the solutions. By combining FTG gradients and gravity data, the proposed workflow improves the precision of subsurface modeling, particularly in delineating salt-body boundaries and estimating their depth. The integration of ETD-derived initialization with joint inversion results in a more accurate reconstruction of density contrasts, offering a powerful approach for characterizing complex geologic structures such as the Vinton Dome.

1. Introduction

Imaging salt structures remains a major challenge in geophysical exploration, as conventional seismic methods often yield low-quality images in the presence of salt bodies. Salt domes—intrusive structures that pierce thick sedimentary sequences as they rise toward the surface (Belenitskaya [1])—are particularly important in hydrocarbon exploration because they can form traps both beneath and along their flanks (Ratcliff et al. [2]). The strong impedance contrasts between salt and surrounding sediments generate complex diffractions and illumination artifacts that hinder seismic imaging.

In contrast, the pronounced density contrasts between salt and country rocks produce distinctive gravity anomalies, making gravity and Full Tensor Gravity (FTG) surveys valuable tools for subsalt characterization [3,4,5]. Conventional gravity surveys—such as Bouguer or Free-Air gravity—capture large-scale regional variations, whereas FTG gradiometry measures spatial derivatives of the gravitational field, emphasizing shorter wavelengths and improving depth control. Although gradiometric data are typically employed for depth estimation, when combined with gravity data, they also enhance the delineation of horizontal boundaries due to their directional sensitivity. This complementary behavior provides the motivation for the joint inversion approach presented in this study.

In addition to gravimetric data acquisition, gradiometric surveys are valuable because their inherently higher frequency content provides detailed information about shallow subsurface structures and is less affected by deeper or regional sources [6,7,8]. Gradiometric and gravimetric data therefore offer complementary perspectives on the same geological features. While gradiometric surveys are particularly effective at delineating horizontal boundaries and capturing high-frequency anomalies, gravimetric data generally offer better depth constraints and are dominated by lower-wavenumber components.

Several studies have applied gravity and gradiometric data to characterize salt structures and other high-contrast geological bodies. Although these approaches have improved subsurface imaging, most treat FTG and scalar gravity data separately, limiting their ability to recover complex density contrasts. The complementary nature of these datasets—where gravity provides large-scale sensitivity and FTG resolves sharper gradients—motivates their simultaneous use.

The main scope of this study is to develop and validate a three-dimensional joint inversion framework that integrates FTG gradient and gravity observations to enhance the structural delineation of salt bodies. The proposed methodology combines a tensor–Euler-derived initial model, a wavenumber-enrichment scheme to balance spectral information, and a simulated annealing algorithm to optimize density distributions. Therefore, this work not only introduces techniques to better exploit gradiometric tensor measurements but also demonstrates their applicability through a real-data case study at the Vinton Dome, Louisiana.

To achieve a more accurate and stable initial model for inversion, this study incorporates several complementary techniques designed to enhance source localization and depth estimation. One such technique is the Euler Deconvolution method, which estimates the position and depth of anomalous bodies based on field gradients. Zhang et al. [9] extended this approach into a tensor-based formulation known as Euler Tensor Deconvolution (ETD), which, when applied to both gravity and FTG datasets, improves the spatial definition of subsurface sources. We also integrate the methodology developed by Zapotitla-Roman [10], Ortiz-Aleman et al. [11] to refine depth estimates using gravimetric data. Furthermore, to strengthen the robustness of the initial model, we enrich the signal’s spectral content by combining the distinct frequency responses of gravity and gradiometry data. This fusion produces a third, spectrally balanced signal that enhances the resolution of density variations and improves subsequent inversion performance.

These techniques collectively support the construction of an initial three-dimensional density model that represents the most probable geometry and depth of the main anomalous bodies. This preliminary model is generated by combining the source positions estimated through Euler Tensor Deconvolution with the spectral information obtained from gravity and FTG data fusion. The resulting density distribution serves as the starting point for the inversion process, providing a physically consistent framework that constrains the search space and guides the optimization toward realistic subsurface configurations.

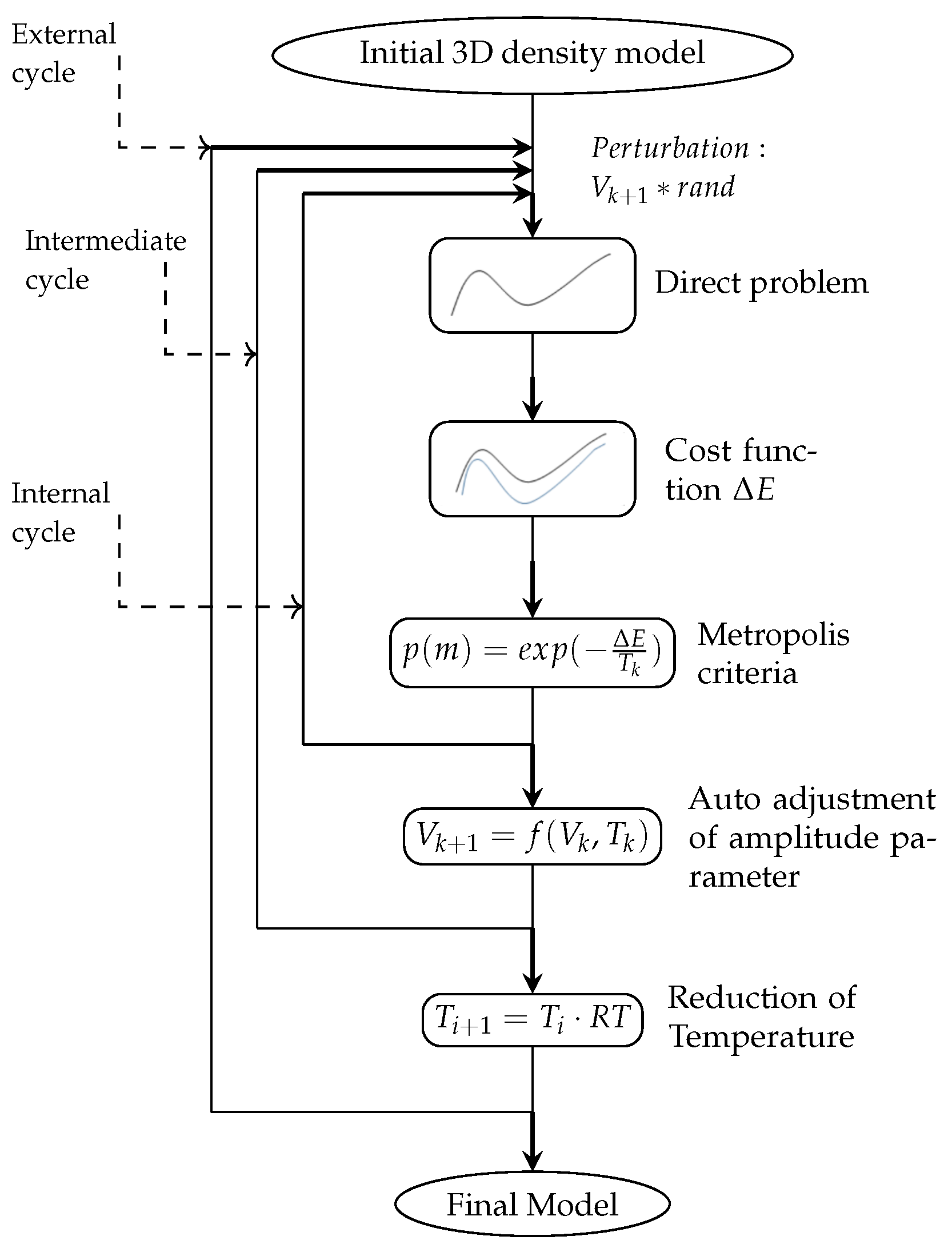
Simulated Annealing (SA) is employed as the global optimization algorithm to refine this initial model and minimize the misfit between observed and calculated gravity and FTG data. SA is particularly effective for this application because it can escape local minima and explore complex multidimensional parameter spaces, ensuring convergence toward a near-optimal density distribution. In our implementation, SA iteratively perturbs density values within the predefined model domain, accepting or rejecting updates based on the Boltzmann probability criterion. This process continues until the overall misfit and total energy function stabilize, producing a final model that best fits both datasets simultaneously [12]. SA’s main drawback lies in its high computational demand; for this reason, it is sometimes replaced by faster linear inversion methods, which, however, may become trapped in local minima [13,14]. This heuristic method has been widely applied in various scientific domains, particularly in the inversion of geophysical data such as magnetic, electric, and gravity surveys [11,15,16,17,18]. Because of its computational intensity, SA is often applied to problems involving relatively few parameters. Moreover, as the dimensionality of the solution space increases, it is common to optimize parameters sequentially—further increasing the method’s computational cost [19].

One of the main objectives of this work is to leverage both the gradiometric tensor and the gravimetric vector datasets through the introduction of a cost function that simultaneously utilizes all available data, thereby generating a more realistic model that satisfies all nine real datasets rather than only one. Although this approach requires a substantial amount of information for each additional component, this challenge is addressed through the use of parallel programming to ensure feasible computing times. The generation of sensitivity matrices for the inversion, as well as the iterative computation of the forward problem, were optimized using OpenMP 5.0 directives.

The structure of this paper is as follows: Section 2 presents the theoretical framework, beginning with the fundamentals of potential-field theory and the formulation of the gravity and gradiometry equations (Section 2.1), followed by the description of the Simulated Annealing (SA) algorithm and its application to the inverse problem (Section 2.2). Section 3 contains the results. Section 3.1 outlines the geological and geophysical context of the Vinton Dome. Section 3.2 describes the gravimetric and gradiometric datasets and preprocessing procedures, including the residual of the vertical gravity component (Section 3.2.1), the reconstruction of the horizontal components (Section 3.2.2), and the wavenumber enrichment process (Section 3.2.3). Section 3.3 details the generation of the initial model using Euler Tensor Deconvolution. Section 3.4 presents the inverse problem based on synthetic and real FTG data. Section 3.5 presents the first inversion model, and Section 3.6 presents the second and final inversion model and its geological interpretation. Finally, Section 4 provides the discussion and concluding remarks, followed by practical recommendations and a summary of methodological limitations.

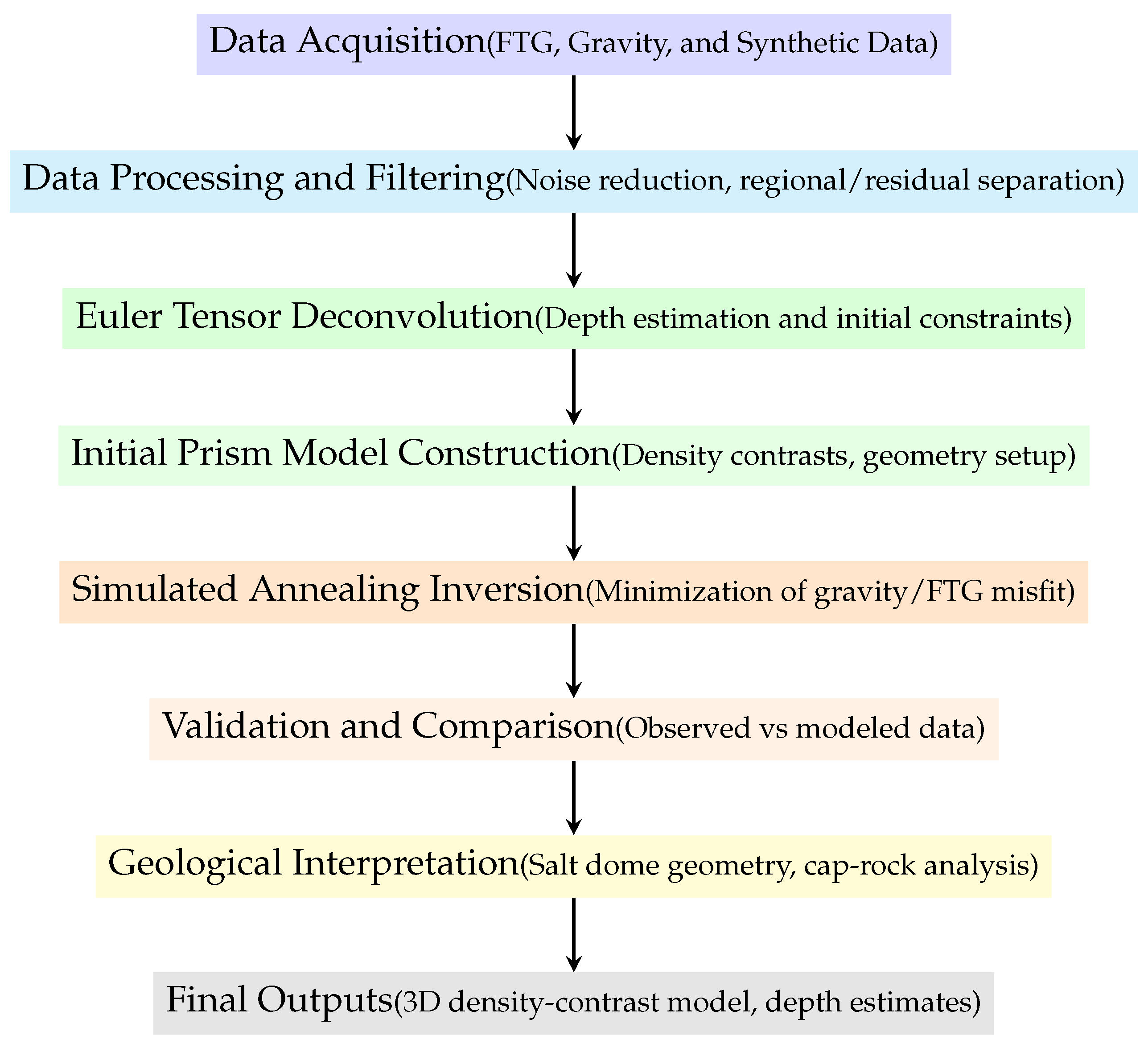
To summarize the methodological sequence developed in this study, Figure 1 presents a schematic workflow of the entire gravity–FTG modeling and inversion process. The procedure begins with the acquisition and preprocessing of the measured FTG and gravity datasets, including noise reduction, Free-Air and terrain corrections, and regional–residual separation. Subsequently, Euler Tensor Deconvolution (ETD) is applied to obtain preliminary source positions and depth estimates, which serve as constraints for constructing the initial prism-based density model. This model is then refined through a simulated annealing inversion that jointly minimizes the misfit between the observed and modeled gravity and FTG fields. The final steps involve validating the inversion results and interpreting the 3D density-contrast model in terms of the geological structure of the Vinton Dome.

2. Theoretical Framework

2.1. Gravitational Field Theory

The mathematical expressions summarized in this section follow the principles of classical potential-field theory (Blakely [20]; Telford et al. [21]) and are presented to provide the necessary background for the joint gravity and FTG inversion. The formulation of the gravity potential, gradient tensor components, and their spectral relations are standard results and do not represent a new development in this work. These relationships are included for completeness and serve as the foundation for the inversion strategy, which constitutes the main methodological contribution of this study.

2.1.1. Gravitational Field Vector

Classical gravitational interaction is completely stated by the universal gravity law of Newton, which is expressed in terms of the gravitational field vector $\overrightarrow{\mathcal{G}}$, which for extended gravitational sources takes the form

$$\overrightarrow{\mathcal{G}}=-G{\int }_{\mathrm{source}}\rho \left({\overrightarrow{r}}^{\prime }\right){\displaystyle \frac{\widehat{\Delta r}}{{(\Delta \overrightarrow{r})}^2}}d{V}^{\prime },$$

(1)

where $G=6.67428\times {10}^{-11}{\mathrm{m}}^3/{\mathrm{s}}^2\mathrm{kg}$ is the universal gravity constant, $\overrightarrow{\Delta r}=\overrightarrow{r}-{\overrightarrow{r}}^{\prime }$ is the vector from the position of the source (${\overrightarrow{r}}^{\prime }$) to the observation point $\overrightarrow{r}$, $\rho =\rho \left({\overrightarrow{r}}^{\prime }\right)$ is the matter density function of the source, and the minus sign represents the attractive character of gravitational force.

As the gravitational field is conservative (i.e., $\overrightarrow{\nabla }\times \overrightarrow{\mathcal{G}}=0$), it follows that it can be derived by differentiating a scalar function (potential), $\overrightarrow{\mathcal{G}}=-\overrightarrow{\nabla }\mathcal{U}$, where $\mathcal{U}$ is such a (gravitational) scalar potential. Let us take the short-hand notation ${\partial }_i=\partial /\partial {\xi }_i$ where ${\xi }_1\equiv x$, ${\xi }_2\equiv y$ and ${\xi }_3\equiv z$ constitute the typical Cartesian coordinates. In such a coordinate system, the i-th component of the gravity vector is ${\mathcal{G}}_i=-{\partial }_i\mathcal{U}$ where $i=1,2,3$. From Equation (1), it follows that the gravitational scalar potential for an extended source is

$$\mathcal{U}\left(\overrightarrow{r}\right)=-G{\int }_{\mathrm{body}}{\displaystyle \frac{\rho \left({\overrightarrow{r}}^{\prime }\right)}{\left|\Delta \overrightarrow{r}\right|}}d{V}^{\prime },$$

(2)

from which it follows that the i-th component of the gravity field vector is

$${\mathcal{G}}_i\left(\overrightarrow{r}\right)=-{\partial }_i\mathcal{U}=G{\int }_{\mathrm{source}}\rho \left({\overrightarrow{r}}^{\prime }\right){\displaystyle \frac{{\xi }_i-{\xi }_i^{\prime }}{{\left|\Delta \overrightarrow{r}\right|}^3}}d{V}^{\prime }$$

(3)

The geophysical units of the gravitational field are mGal (1 Gal = 1 cm/s²).

2.1.2. Gravitational Field Gradient Tensor (Gradiometry)

Gradiometry is the technique that measures and predicts the derivatives of the gravity vector instead of the field itself, as it is done by gravimetry. Therefore, gradiometric data are expressed in the unit called Eötvös (E), where 1E = 0.1 μGal/m.

The gradient of the gravity field leads to a second-rank (covariant) symmetric tensor whose i, j-th component is given by the partial derivative of the j-th component of the gravity vector with respect to the ${\xi }_i$ coordinate, i.e.,

$${\mathfrak{G}}_{ij}={\partial }_i{\mathcal{G}}_j=-{\partial }_i{\partial }_j\mathcal{U}$$

In virtue of Equation (3), the components of the gravitational field gradient tensor (also known as the gradiometric tensor) are

$${\mathfrak{G}}_{ij}\left(\overrightarrow{r}\right)=G{\int }_{\mathrm{source}}\rho ({\overrightarrow{r}}^{\prime }){\displaystyle \frac{{\left|\Delta \overrightarrow{r}\right|}^2{\delta }_{ij}-3\left({\xi }_i^{\prime }-{\xi }_i^{\prime }\right)\left({\xi }_j^{\prime }-{\xi }_j^{\prime }\right)}{{\left|\Delta \overrightarrow{r}\right|}^3}}d{V}^{\prime }$$

(4)

In order to be able to process numerically gravity and gradiometry datasets, it is imperative to discretise the above equations.

2.2. Numerical Approximation

In virtue of the superposition principle, it can always be assumed that the source producing a gravitational anomaly may always be decomposed into a series of differential (rectangular) prisms of volume $d{V}^{\prime }=d{x}^{\prime }d{y}^{\prime }d{z}^{\prime }$, each one with a constant density ${\rho }_0$. If we set a reference Cartesian frame such that the sides of the rectangular prisms are always parallel to the coordinate axes, then each of such differential prisms ought to have initial and final limits ${{\xi }^{\prime }}_i^{\left(1\right)}\le d{{\xi }^{\prime }}_i\le {{\xi }^{\prime }}_i^{\left(2\right)}$.

2.2.1. Gravimetric Model

From Equation (3), it follows that each prism contribution to the observed value $\mathcal{G}$ in the observation point $\overrightarrow{r}={\sum }_{i=1}^3{\xi }_i{\widehat{e}}_i$ can be numerically approximated by [22]

$$\begin{array}{c}\hfill {\mathcal{G}}_n=G{\rho }_0\sum _{i,j,k=1}^2{\mu }_{ijk}\{{\eta }_{nk}arctan\left({\displaystyle \frac{{\eta }_{li}{\eta }_{mj}}{{\eta }_{nk}{r}_{ijk}}}\right)\\ \hfill -ln\left[{(r_{ijk}+{\eta }_{mj})}^{{\eta }_{li}}{(r_{ijk}+{\eta }_{li})}^{{\eta }_{mj}}\right]\}\end{array}$$

(5)

where $l,m,n=1,2,3$, $l\ne m\ne n$, ${\eta }_{lm}={\xi }_l-{{\xi }^{\prime }}_l^{\left(m\right)}$, $r_{ijk}^2={\eta }_{1i}^2+{\eta }_{2j}^2+{\eta }_{3k}^2$ and ${\mu }_{ijk}={(-1)}^i{(-1)}^j{(-1)}^k$ [3,23].

2.2.2. Gradiometric Model

Following the rectangular differential prisms model from the previous subsection, the elements of the gradiometric tensor can be numerically computed by

$$\begin{array}{c}\hfill {\mathfrak{G}}_{lm}=\\ \hfill G{\rho }_0\sum _{i,j,k=1}^2{\mu }_{ijk}\{arctan\left({\displaystyle \frac{|{ϵ}_{ljk}|{\eta }_{j\left(j\right)}{\eta }_{k\left(k\right)}}{{\eta }_{l\left(m\right)}{r}_{ijk}}}\right){\delta }_{lm}\\ \hfill +\left(1-{\delta }_{lm}\right)ln\left[|{ϵ}_{lmk}|{\eta }_{k\left(k\right)}+r_{ijk}\right]\}\end{array}$$

(6)

where ${\delta }_{ij}$ is the Kronecker Delta (the elements of the identity tensor), ${ϵ}_{ijk}$ is the Levi–Civita symbol, and ${\eta }_{l\left(m\right)}={\eta }_{lm}$ with $m={\delta }_{1m}i+{\delta }_{2m}j+{\delta }_{3m}k$.

2.3. Euler Tensor Deconvolution (ETD) for Constructing the Initial Model

The ETD method is a core component of our workflow, serving to estimate the position, depth, and structural index of subsurface sources from gravity and full tensor gravity (FTG) data. ETD extends the classical Euler Deconvolution by incorporating the complete gravity gradient tensor, which provides directional information that enhances source localization. In the context of this study, ETD is used to generate a physically meaningful initial model of the underground formations. This model defines the geometry and approximate density contrasts of anomalous bodies, offering a privileged starting point for the subsequent inversion. By providing a well-constrained initial solution, ETD not only improves the stability and convergence of the simulated annealing process but also reduces computation time and helps guide the optimization toward geologically realistic configurations.

Euler Deconvolution, first proposed by Thompson [24] as a method to estimate the depth of potential sources (gravitational and magnetic), uses the Euler homogeneity relation for scalar fields, which states that $\phi$ is a homogeneous function of degree n if

$${\alpha }^n\varphi \left(x_1,\dots ,x_n\right)=\varphi \left(\alpha x_1,\dots ,\alpha x_n\right)$$

(7)

where $\varphi$ is a scalar function of n variables and $\alpha$ is a constant. Differentiating Equation (7) with respect to $\alpha$ yields

$$\mathit{\eta }·\nabla \varphi =-n\varphi$$

(8)

where $\mathit{\eta }={\sum }_{i=1}^n{\eta }_i{\widehat{e}}_i$ and ${\eta }_i={\xi }_i-{\xi }_i^{\prime }$. Reid et al. [25] points out that, in order to better isolate the gravitational anomalies from the gravity field generated by near sources, it is convenient to separate the observed field in a field generated by the main source, f, and a perturbation (constant in the observation window) called background field, B. Thus, Equation (8) takes the form

$$\mathit{\eta }·\nabla f=-nf+nB$$

(9)

which has four unknowns (the position of the source and the background field), so at least four observation points are required to solve the system. For m observation points, the system takes the form

$$\sum _{i=1}^3\left({\partial }_i{f}_j\right){\xi }_i^{\prime }+nB=\sum _{i=1}^3{\xi }_i{\partial }_i{f}_j+n{f}_i$$

(10)

$\forall j=1,\dots ,m$.

This procedure was extended to the gradiometric tensor by Zhang et al. [9]. This approach, known as the Euler Tensor Deconvolution, extends Equation (10) to three equations:

$$\sum _{j=1}^3\left({\xi }_j^{\prime }{\mathfrak{G}}_{ij}\right)+n{B}_i=\sum _{j=1}^3{\xi }_j{\mathfrak{G}}_{ij}+n{\mathcal{G}}_i$$

(11)

$\forall j=1,\dots ,3$. Equations (10) consist of six equations per observation point, and 6 unknowns (source coordinates and three components of the background field).

2.4. Inverse Theory

In inverse theory, the forward problem refers to the computation of measured quantities with respect to the parameters of the system, while the inverse problem consists of the estimation of the parameters through observed values [26]. Measurements $m_i$ and parameters $p_j$ are always related through functions of the form $m_i=f\left(p_j\right)\forall i=1,\dots ,N;j=1,\dots ,M$, where N is the number of observations and M is the number of parameters. If the relation is linear, or the problem can be linearised, the problem can be set in matrix form as [27]

$$\mathbf{m}=\mathfrak{K}\mathbf{p}$$

(12)

where $\mathbf{m}$ is the observed (measured) data vector, $\mathfrak{K}$ is known as the sensitivities kernel and $\mathbf{p}$ is the parameters vector.

Nevertheless, for real cases, it often happens that there are two data vectors, one coming from the observed data, ${\mathbf{m}}^{\left(\mathbf{O}\right)}$, and other coming from theoretically computed data, ${\mathbf{m}}^{\left(\mathbf{C}\right)}$. Data inversion consists of finding a parameter vector that provides a ${\mathbf{m}}^{\left(\mathbf{C}\right)}$ as similar to ${\mathbf{m}}^{\left(\mathbf{O}\right)}$ as possible. There are several ways to quantify the similitude between both measured data vectors. From the family of $L_m$ norms, in geophysics it is customary to use the $L_2$ norm because it provides a similar weight to all data, as well as stability [26,27],

$$e={\left[\sum \left({\mathbf{m}}^{\left(\mathbf{O}\right)}-{\mathbf{m}}^{\left(\mathbf{C}\right)}\right)\right]}^{{\displaystyle \frac{1}{2}}}$$

(13)

The error Equation (13), also called the objective or cost function, allows the problem to be regarded as the mathematical problem of finding the minimum value of e in the space of parameters. Although there are numerous techniques to optimize (minimize or maximize) functions [28,29,30], the selection of one heavily relies on the existence or not of local extreme (minima or maxima), as well as the existence of non-stability or non-differentiable regions of the cost function. As potential methods like gravitational and magnetic ones present non-uniqueness, several local extremes exist, thus requiring an optimization scheme able to find the global extreme of the referred function. A very robust method for such a purpose is SA.

Simulated Annealing

SA, first proposed by Kirkpatrick et al. [31], is a heuristic technique able to find global extremes. A high energy (cost) initial state is considered, which decreases with iterations until a lower energy (thermodynamic equilibrium) state is reached, yielding the global extreme of the function Kirkpatrick [32]. SA has been proven to work better with the normalised version of the $L_2$ norm [12,33],

$$e={\displaystyle \frac{{\sum }_{k=1}^N{\left[{\mathbf{m}}_{\mathbf{k}}^{\left(\mathbf{O}\right)}-{\mathbf{m}}_{\mathbf{k}}^{\left(\mathbf{C}\right)}\right]}^2}{{\sum }_{k=1}^N{\left[{\mathbf{m}}_{\mathbf{k}}^{\left(\mathbf{O}\right)}\right]}^2}}.$$

(14)

The algorithm departs from the initial state by affecting the parameters with an aleatory perturbation. For each perturbation, the value of the cost function of the whole system is computed; if such a value is lower than in the previous step, the perturbed model is accepted as a new model, and the next iteration follows. In order for the algorithm not to get stuck in a local extreme, if the evaluated cost function value is greater than in the previous state, the probability to accept this perturbed model is given by

$$P\left(\mathbf{p}\right)=exp\left(-\Delta E/T\right),$$

(15)

which asymptotically tends to Boltzmann’s probability density function [34]. In Equation (15), $\Delta E$ is known as the energy increment, and is the difference in the cost function values of both the initial and the perturbed models, and T is the system’s temperature, which is governed by a potential cooling function Nagihara and Hall [35]:

$$T_k=T_i{\left(RT\right)}^k,$$

(16)

where k stands for the iteration, i is the initial temperature, and $0<RT<1$. In order to optimise the cooling process, we implement a step to adjust the amplitude of the perturbations at each step. To do so, the scaling factor of the perturbation is computed as

$$V_{k+1}\left(r\right)=\left\{\begin{array}{cc}{V}_k\left(1+c\frac{r+0.6}{0.4}\right),\hfill & r>0.6\hfill \\ {\displaystyle \frac{V_k}{1+c\frac{0.4-r}{0.4}}},\hfill & r<0.4\hfill \end{array}\right.$$

(17)

where r is the quotient between the number of accepted and the number of rejected models [36,37].

In Figure 2, we show the flowchart of the SA algorithm herein implemented, which consists of three nested cycles:

• External cycle: controls the decrease in temperature.
• Intermediate cycle: controls the amplitude of perturbations.
• Inner cycle: Assesses the perturbed models for their acceptance or rejection.

2.5. Forward Problem Optimization

One of the main drawbacks of SA is the high number of times the forward problem ought to be solved. To accelerate this process, the strategy proposed by Ortiz-Alemán et al. [33], Ortiz-Alemán and Martin [38] only requires solving the complete forward problem (Equation (12)) once before initiating the iterations. On the other hand, it is possible to accelerate the SA process by perturbing all the parameters $p_j$ simultaneously, instead of changing them one by one consecutively, as is commonly done.

Assuming that the j-th parameter perturbation is given by $\Delta p_j$, and in virtue of Equation (12), the perturbed model (data vector) is given by

$${\mathbf{m}}_{\mathrm{per}}={\mathbf{m}}_{\mathrm{ini}}+{\mathfrak{K}}_{ij}{p}_j$$

(18)

3. Results

In this study, two categories of gravity data were used: measured and synthetic. The measured dataset corresponds to the FTG survey acquired by Bell Geospace over the Vinton Dome in southwestern Louisiana, USA. This dataset includes the gravity field ($g_z$) and the six independent components of the gravity gradient tensor ($G_{xx},G_{yy},G_{zz},G_{xy},G_{xz},G_{yz}$), recorded in milligals (mGal) and Eotvös, respectively. The synthetic data were generated through forward modeling using the prism-based configuration described in Section 4 to assess the inversion performance.

The gravity field used in this study represents the observed gravity anomaly, which includes both Free-Air and terrain corrections and is therefore equivalent to a Bouguer-type anomaly. The gradiometric quantities correspond to the measured FTG gradients obtained from the same airborne survey. All quantities are consistently expressed in mGal for gravity components and in Eotvös for tensor gradients throughout the manuscript.

3.1. Vinton Dome Geological Setup

The Vinton Dome is a classic piercement-type salt structure located in southwestern Louisiana, USA, within the Gulf Coast Basin. It consists of Louann Salt that intruded through overlying sedimentary sequences of Tertiary and Quaternary age. The dome forms an asymmetric structure with a steep northern flank and a gently dipping southern limb Nelson and Fairchild [39]. The salt core is overlain by a cap-rock complex composed primarily of anhydrite, limestone, and minor shale, formed through dissolution and reprecipitation processes at the salt–sediment interface Nelson and Fairchild [39].

The main density contrasts responsible for the gravity anomaly are summarized as follows: the salt core has an average density of 2200–2250 kg/m³, the cap rock reaches 2600–2700 kg/m³, and the surrounding sediments range from 2400–2500 kg/m³. These contrasts, approximately 400–500 kg/m³, are consistent with the amplitude and wavelength of the observed gravity and FTG anomalies. The positive gravity response over the cap-rock zone and the negative anomaly above the salt mass confirm the vertical density inversion typical of Gulf Coast salt domes.

This structure provides an ideal case for testing gravity and Full Tensor Gravity (FTG) inversion methods due to its well-defined geometry and documented subsurface characteristics. Measurements of the gradiometric field (FTG) were acquired from 3 to 6 July 2008, by Bell Geospace Inc. [40].

The values of the vertical component of the gravitational field in the study area were derived by integrating the tensor components and improving the accuracy of the result with ground-based gravity measurements [40].

3.2. Gravimetric Data

Before being able to apply the Euler Tensor Deconvolution (ETD), it is necessary to obtain the horizontal components of the gravitational field, as well as to remove the residual effect of the vertical component.

3.2.1. Residual of the Vertical Component

The residual is obtained by modeling the regional effect with a plane derived through the least squares method. The resulting geometric expression is shown in Equation (19).

$$z=-0.215108x+0.045668y-22.821229$$

(19)

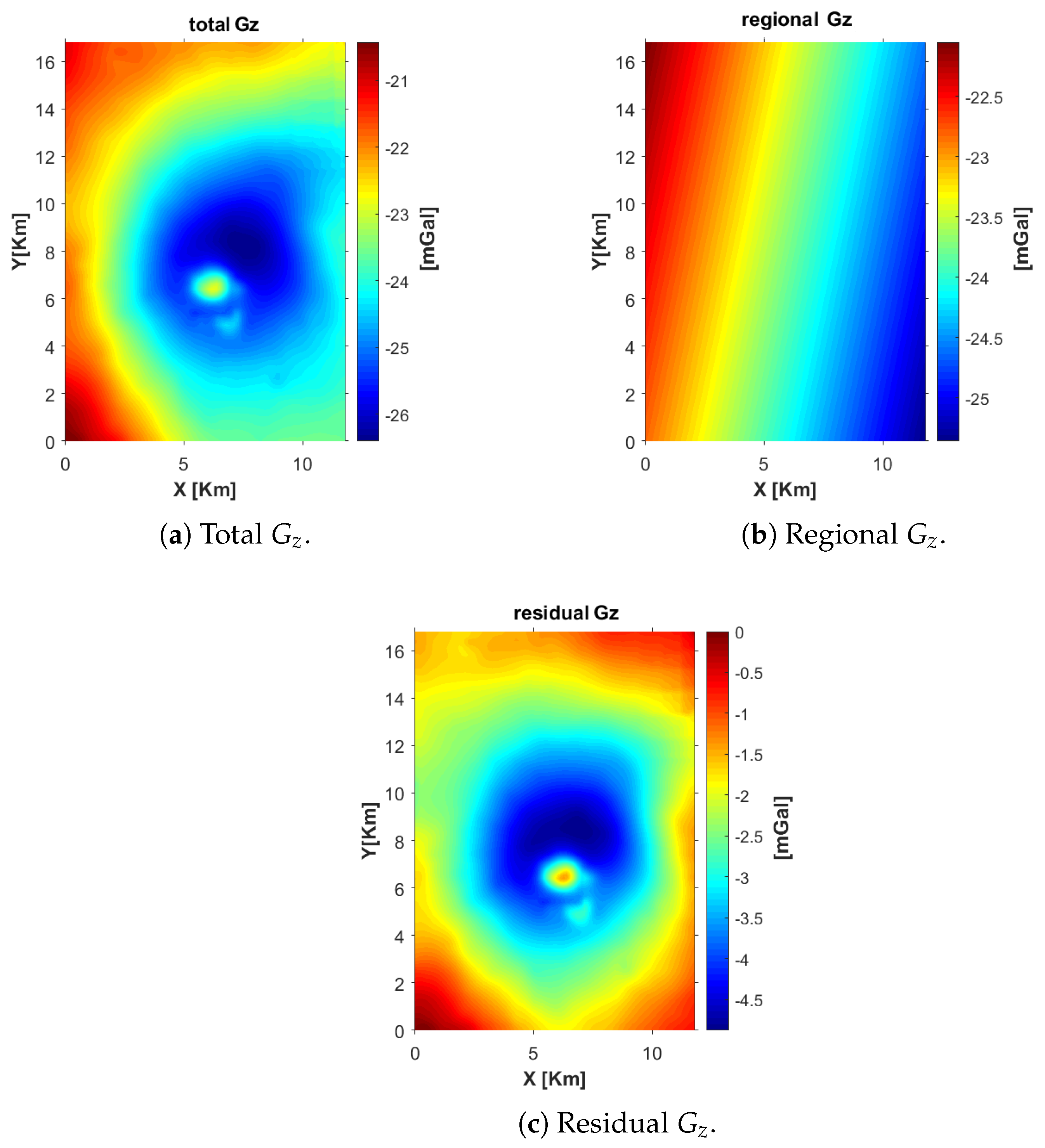
The residual of the vertical component was computed by subtracting the regional field, which represents the long-wavelength background gravity signal associated with deep crustal structures and broad density trends. This regional component was estimated by applying a second-order polynomial surface fitting to the observed gravity data, ensuring that only wavelengths larger than the expected dimensions of the Vinton Dome were captured. The subtraction isolates the short-wavelength anomalies related to the salt structure itself. The contrast between these three datasets—observed, regional, and residual—can be observed in Figure 3, where the residual field clearly delineates the boundaries of the salt dome.

3.2.2. Horizontal Components

The horizontal gravity components ($g_x$ and $g_y$) are not directly measured but are computed from the Full Tensor Gravity (FTG) gradients and the vertical component ($g_z$) using spectral differentiation and integration methods. These reconstructed fields are employed solely for modeling purposes, as they provide complementary directional information that enhances inversion resolution but are not standard observables in exploration practice.

Following Mickus and Hinojosa [41], and under the assumptions of harmonic potential fields, uniform sampling, and constant observation height, the components of the gravity-gradient tensor can be estimated from gravity data by spectral differentiation, where Fourier-domain operators convert spatial derivatives into multipliers. However, this procedure is numerically ill-posed: each derivative multiplies the spectrum by $\left|k\right|$, so computing second derivatives (the tensor components) amplifies noise approximately by ${\left|k\right|}^2$. In addition, the process typically requires upward or downward continuation, which further destabilizes the high-wavenumber content and introduces edge effects. In the Fourier domain, differentiation corresponds to multiplication by $i{k}_x$ or $i{k}_y$; thus, second derivatives scale with $k_x^2$, $k_x{k}_y$, and $k_y^2$, explaining the strong noise magnification when attempting to synthesize $G_{ij}$ from gravity data.

For this reason, we do not rely on gradients synthesized from gravity alone. Instead, we use directly measured FTG data and perform a joint inversion of the measured FTG and gravity fields. In our workflow, gravity provides long-wavelength sensitivity to regional structure, while measured FTG preserves short-wavelength information and directional constraints. Their combination reduces non-uniqueness, improves boundary definition, and stabilizes the inversion compared with using gravity (or gravity-derived gradients) alone.

Table 1. Equations to compute horizontal gravitational components from the gradiometric tensor and from $G_z$.

From	To Compute ${\mathit{g}}_{\mathit{x}}$	To Compute ${\mathit{g}}_{\mathit{y}}$
Consecutive derivatives	$g_x={\mathcal{F}}^{-1}\left(\frac{1}{ip}{G}_{xx}\right)$	$g_y={\mathcal{F}}^{-1}\left(\frac{1}{iq}{G}_{yy}\right)$
Cross derivatives	$g_x={\mathcal{F}}^{-1}\left(\frac{1}{iq}{G}_{xy}\right)$	$g_y={\mathcal{F}}^{-1}\left(\frac{1}{ip}{G}_{yx}\right)$
z derivatives	$g_x={\mathcal{F}}^{-1}\left(\frac{1}{k}{G}_{xz}\right)$	$g_y={\mathcal{F}}^{-1}\left(\frac{1}{k}{G}_{yz}\right)$
$G_z$	$g_x={\mathcal{F}}^{-1}\left(\frac{ip}{k}{G}_z\right)$	$g_y={\mathcal{F}}^{-1}\left(\frac{iq}{k}{G}_z\right)$

shows the equations used to obtain the horizontal gravitational components.

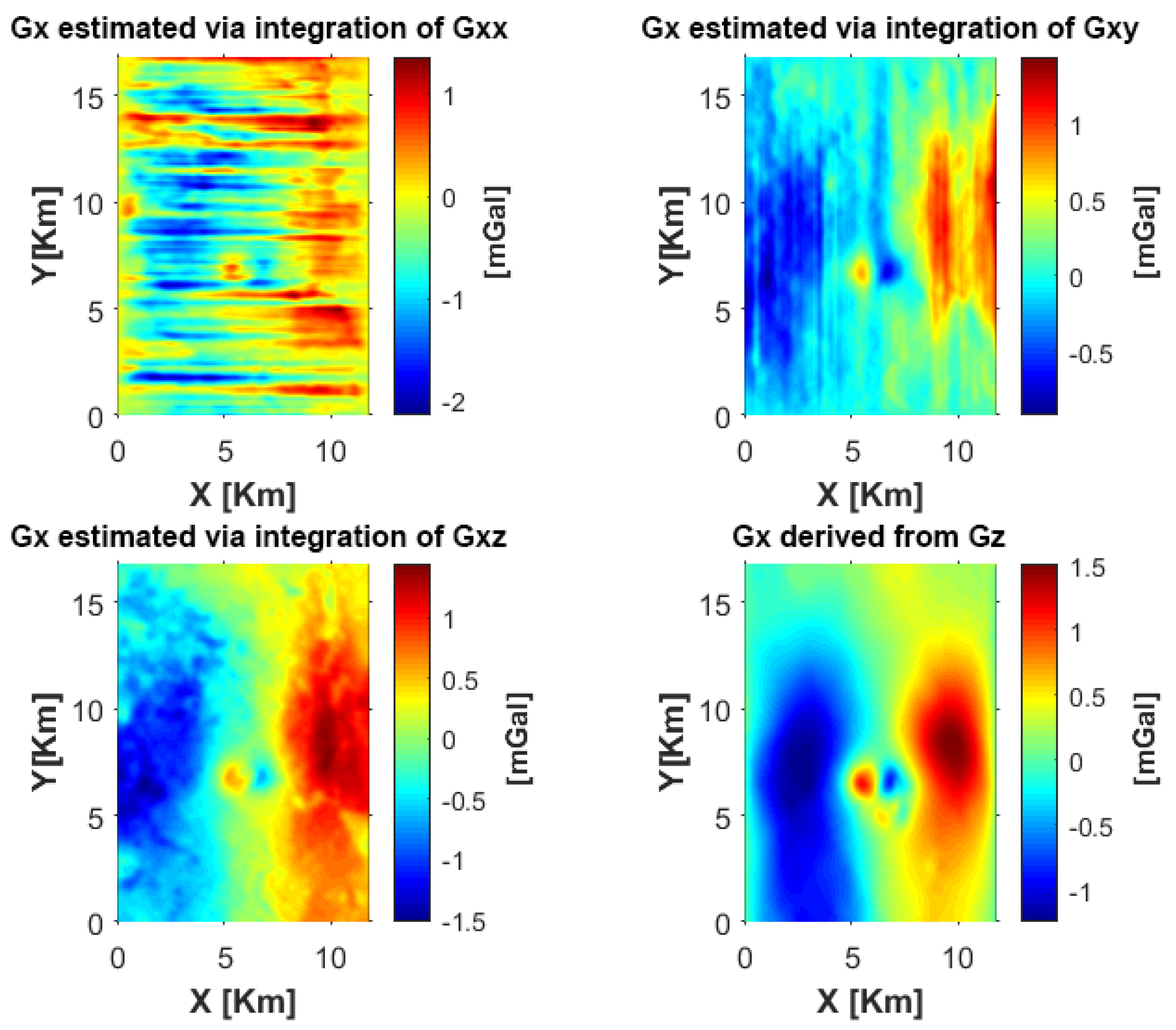
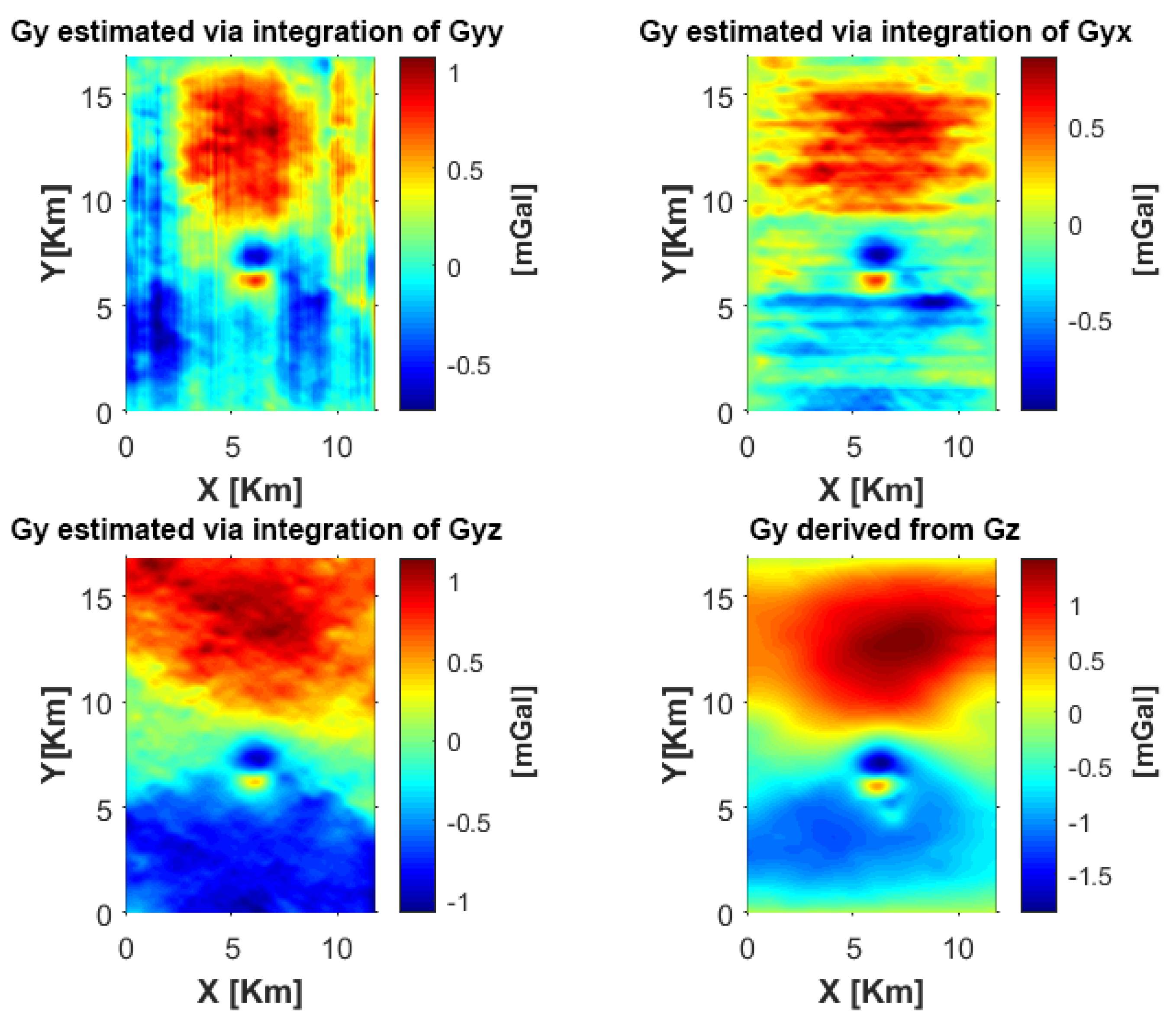
The results of the application of the two methods to compute the mentioned horizontal components are shown in Figure 4 and Figure 5. In them, it is clear that the estimations from the gravitational field have a greater content of low wavenumbers than those estimated through the gradiometric tensor. In the same way, the maps obtained from the integration in the wavenumber domain have a greater content of high wavenumbers.

3.2.3. Wavenumber Enrichment

The results obtained from the integration of the cross derivatives and the consecutive derivatives were unsatisfactory. Therefore, only the components derived from $G_z$ and from $G_{xz}$ and $G_{yz}$ were retained. Because each component contained information dominated by either high or low wavenumbers, we applied the methodology proposed by Bell Geospace [40] to combine them. To achieve this, we computed the amplitude spectra of both data sets and determined a cutoff wavenumber that served as a threshold for merging the results. Wavenumbers lower than this threshold were extracted from the fields derived from $G_z$, whereas the higher wavenumbers were incorporated from the derivatives of the tensor’s vertical components.

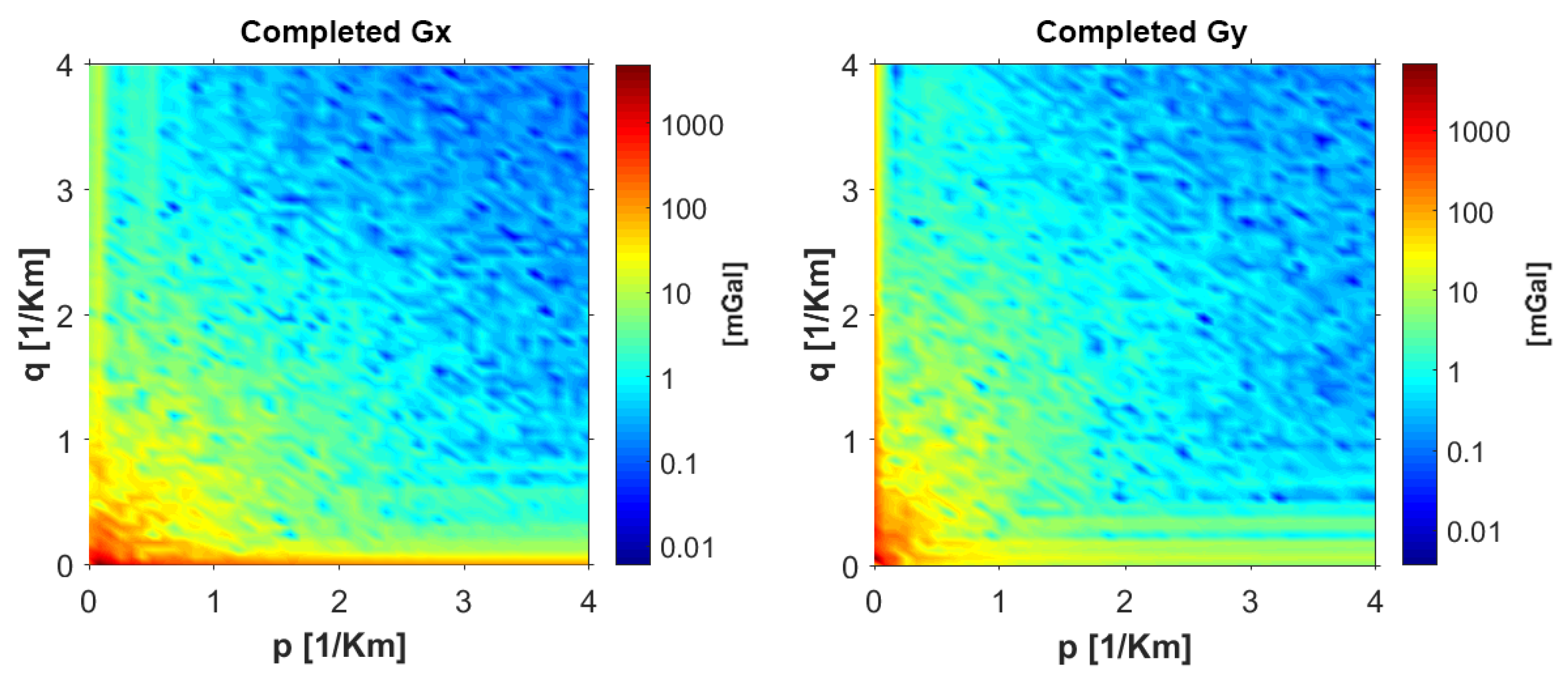
The amplitude spectra of the combined components are shown in Figure 6. To generate the new horizontal components, the cutoff wavenumbers for the x and y directions were determined as 1.4050 × 10⁻⁴ [1/km] and 1.7856 × 10⁻⁴ [1/km], respectively. The corresponding amplitude spectra of the fused components are presented in Figure 7. The term “completed signal” refers to the spectrally fused field obtained by adding the high-frequency components of the FTG data to the low-frequency portion of the gravity signal, thereby restoring the full wavenumber content of the horizontal gradients.

The resulting horizontal components exhibit a broader spectral range and higher wavenumber content than their predecessors. The corresponding maps are illustrated in Figure 6, Figure 7 and Figure 8.

3.3. Initial Model (Euler Tensor Deconvolution)

To construct the initial model for the simulated annealing inversion, we first applied the Euler Tensor Deconvolution (ETD) algorithm, derived from the method proposed by Thompson [24], to the Vinton Dome gravity and Full Tensor Gravity (FTG) data. Specifically, the horizontal gravity components ($g_x$ and $g_y$) were used together with the diagonal elements of the gravity gradient tensor ($G_{xx}$, $G_{yy}$, and $G_{zz}$) to estimate the position and depth of the main anomalous sources. Several window sizes were tested, producing minor variations in the calculated depths while maintaining consistent structural indices of $N=2$ for gravity and $N=3$ for FTG data, following Stavrev and Reid [42]. The ETD-derived source solutions were interpolated along profiles to generate a three-dimensional density-contrast model, which served as the initial configuration for the inversion.

The initial model consists of an ensemble of rectangular prisms arranged in four stacked blocks whose lateral dimensions increase with depth, forming a pyramidal structure that approximates the geometry of the Vinton Dome. This configuration compensates for the natural decay of potential-field amplitudes with depth and significantly reduces the number of prisms, thereby decreasing computational time. Densities were assigned as density contrasts rather than absolute values, using the depth–density relationship of Nelson and Fairchild [39] to quantify the contrast between salt, cap rock, and surrounding sediments.

$$\begin{array}{cc}\hfill x_0{T}_{xx}+y_0{T}_{xy}+z_0{T}_{xz}+N{B}_x& =\hfill \\ \hfill x{T}_{xx}+y{T}_{xy}+z{T}_{xz}+N{T}_x\end{array}$$

(20)

$$\begin{array}{cc}\hfill x_0{T}_{yx}+y_0{T}_{yy}+z_0{T}_{yz}+N{B}_y& =\hfill \\ \hfill x{T}_{yx}+y{T}_{yy}+z{T}_{yz}+N{T}_y\end{array}$$

(21)

$$\begin{array}{cc}\hfill x_0{T}_{zx}+y_0{T}_{zy}+z_0{T}_{zz}+N{B}_z& =\hfill \\ \hfill x{T}_{zx}+y{T}_{zy}+z{T}_{zz}+N{T}_z\end{array}$$

(22)

$$\begin{array}{c}\hfill x_0{F}_x+y_0{F}_y+z_0{F}_z+N{B}_{xx}=\\ \hfill x{F}_x+y{F}_y+z{F}_z+NF\end{array}$$

(23)

$$\begin{array}{c}\hfill x_0{G}_x+y_0{G}_y+z_0{G}_z+N{B}_{yy}=\\ \hfill x{G}_x+y{G}_y+z{G}_z+NG\end{array}$$

(24)

$$\begin{array}{c}\hfill x_0{H}_x+y_0{H}_y+z_0{H}_z+N{B}_{zz}=\\ \hfill x{H}_x+y{H}_y+z{H}_z+NH\end{array}$$

(25)

And considering that $F={\displaystyle \frac{\partial g_x}{\partial x}}$, $G={\displaystyle \frac{\partial g_y}{\partial y}}$ and $H={\displaystyle \frac{\partial g_z}{\partial z}}$, the following matrix equation follows

$$\begin{gathered} \left(\begin{array}{cccccc}{F}_x^1& F_y^1& F_z^1& N& 0& 0\\ G_x^1& G_y^1& G_z^1& 0& N& 0\\ H_x^1& H_y^1& H_z^1& 0& 0& N\\ F_x^2& F_y^2& F_z& N& 0& 0\\ G_x^2& G_y^2& G_z^2& 0& N& 0\\ H_x^2& H_y^2& H_z^2& 0& 0& N\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ F_x^m& F_y^m& F_z^m& N& 0& 0\\ H_x^m& H_y^m& H_z^m& 0& N& 0\\ H_x^m& H_y^m& H_z^m& 0& 0& N\end{array}\right)\left(\begin{array}{c}{x}_0\\ y_0\\ z_0\\ B_{xx}\\ B_{yy}\\ B_{zz}\end{array}\right)= \\ \left(\begin{array}{c}x{F}_x^1+y{F}_y^1+z{F}_z^1+NF\\ x{G}_x^1+y{G}_y^1+z{G}_z^1+NG\\ x{H}_x^1+y{H}_y^1+z{H}_z^1+NH\\ x{F}_x^2+y{F}_y^2+z{F}_z^2+NF\\ x{G}_x^2+y{G}_y^2+z{G}_z^2+NG\\ x{H}_x^2+y{H}_y^2+z{H}_z^2+NH\\ ⋮\\ x{F}_x^m+y{F}_y^m+z{F}_z^m+NF\\ x{G}_x^m+y{G}_y^m+z{G}_z^m+NG\\ x{H}_x^m+y{H}_y^m+z{H}_z^m+NH\end{array}\right) \end{gathered}$$

(26)

Following a similar procedure for the gravitational vector, the following system is obtained

$$\begin{gathered} \left(\begin{array}{cccccc}{g}_{xx}^1& g_{xy}^1& g_{xz}^1& N_g& 0& 0\\ g_{yx}^1& g_{yy}^1& g_{yz}^1& 0& N_g& 0\\ g_{zx}^1& g_{zy}^1& g_{zz}^1& 0& 0& N_g\\ g_{xx}^2& g_{xy}^2& g_{xz}^2& N_g& 0& 0\\ g_{yx}^2& g_{yy}^2& g_{yz}^2& 0& N_g& 0\\ g_{zx}^2& g_{zy}^2& g_{zz}^2& 0& 0& N_g\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ g_{xx}^m& g_{xy}^m& g_{xz}^m& N_g& 0& 0\\ g_{yx}^m& g_{yy}^m& g_{yz}^m& 0& N_g& 0\\ g_{zx}^m& g_{zy}^m& g_{zz}^m& 0& 0& N_g\end{array}\right)\left(\begin{array}{c}{x}_{g0}\\ y_{g0}\\ z_{g0}\\ B_{gx}\\ B_{gy}\\ B_{gz}\end{array}\right)= \\ \left(\begin{array}{c}x{g}_{xx}^1+y{g}_{xy}^1+z{g}_{xz}^1+N{g}_x^1\\ x{g}_{yx}^1+y{g}_{yy}^1+z{g}_{yz}^1+N{g}_y^1\\ x{g}_{zx}^1+y{g}_{zy}^1+z{g}_{zz}^1+N{g}_z^1\\ x{g}_{xx}^2+y{g}_{xy}^2+z{g}_{xz}^2+N{g}_x^2\\ x{g}_{yx}^2+y{g}_{yy}^2+z{g}_{yz}^2+N{g}_y^2\\ x{g}_{zx}^2+y{g}_{zy}^2+z{g}_{zz}^2+N{g}_z^2\\ ⋮\\ x{g}_{xx}^m+y{g}_{xy}^m+z{g}_{xz}^m+N{g}_x^m\\ x{g}_{yx}^m+y{g}_{yy}^m+z{g}_{yz}^m+N{g}_y^m\\ x{g}_{zx}^m+y{g}_{zy}^m+z{g}_{zz}^m+N{g}_z^m\end{array}\right) \end{gathered}$$

(27)

In both cases, the system is solved for the source positions and for the values of the environment field B. It ought to be remarked that in each system, a structural index N that is linked to the geometry of the source must be used.

In this work we use the procedure by Zapotitla-Roman [10], by first applying the ETD, and we keep the horizontal components of the solutions so to later substitute them in Equations (28)–(30).

$$\begin{array}{c}\hfill z_{g0}{g}_{xz}=x{g}_{xx}+y{g}_{xy}+z{g}_{xz}+N_g{g}_x\\ \hfill -\left(x_{g0}{g}_{xx}+y_{g0}{g}_{xy}+N_g{B}_{gx}\right)\end{array}$$

(28)

$$\begin{array}{c}\hfill z_{g0}{g}_{yz}=x{g}_{yx}+y{g}_{yy}+z{g}_{yz}+N_g{g}_y\\ \hfill -\left(x_{g0}{g}_{yx}+y_{g0}{g}_{yy}+N_g{B}_{gy}\right)\end{array}$$

(29)

$$\begin{array}{c}\hfill z_{g0}{g}_{zz}=x{g}_{zx}+y{g}_{zy}+z{g}_{zz}+N_g{g}_z\\ \hfill -\left(x_{g0}{g}_{zx}+y_{g0}{g}_{zy}+N_g{B}_{gz}\right)\end{array}$$

(30)

These equations have been obtained by applying the ETD to the gravitational field, thus obtaining a better estimation of depth.

By applying the previous algorithms, we obtained the following solutions depicted in Figure 9.

From these solutions, we proposed the discretization of a volume, as shown in

Table 2. Features of the prism assembly used to model the Vinton Dome.

		Range [km]	Dimension [km]	Prisms Number	Density Range [kg/cm3]
Block 1	X	4.2–9.0	4.8	48	100 to 400
	Y	4.0–9.5	4.5	55
	Z	0.1–0.5	0.4	4
Block 2	X	3.2–9.6	6.4	32	0 to 100
	Y	3.8–11.0	7.2	36
	Z	0.5–1.5	1.0	5
Block 3	X	2.9–9.8	6.9	23	−100 to 100
	Y	3.7–11.8	9.1	27
	Z	1.5–3.0	1.5	5
Block 4	X	2.0–10.0	8.0	8	−400 to −100
	Y	3.5–12.5	9.0	9
	Z	3.0–6.0	3.0	3

.

From the solutions found through ETD, the model is interpolated (Figure 10). The color scale represents density contrasts (kg/m³) relative to the encasing sediments. The higher-density cap-rock and lower-density salt materials are clearly differentiated but should not be interpreted as absolute densities.

3.4. Inverse Problem

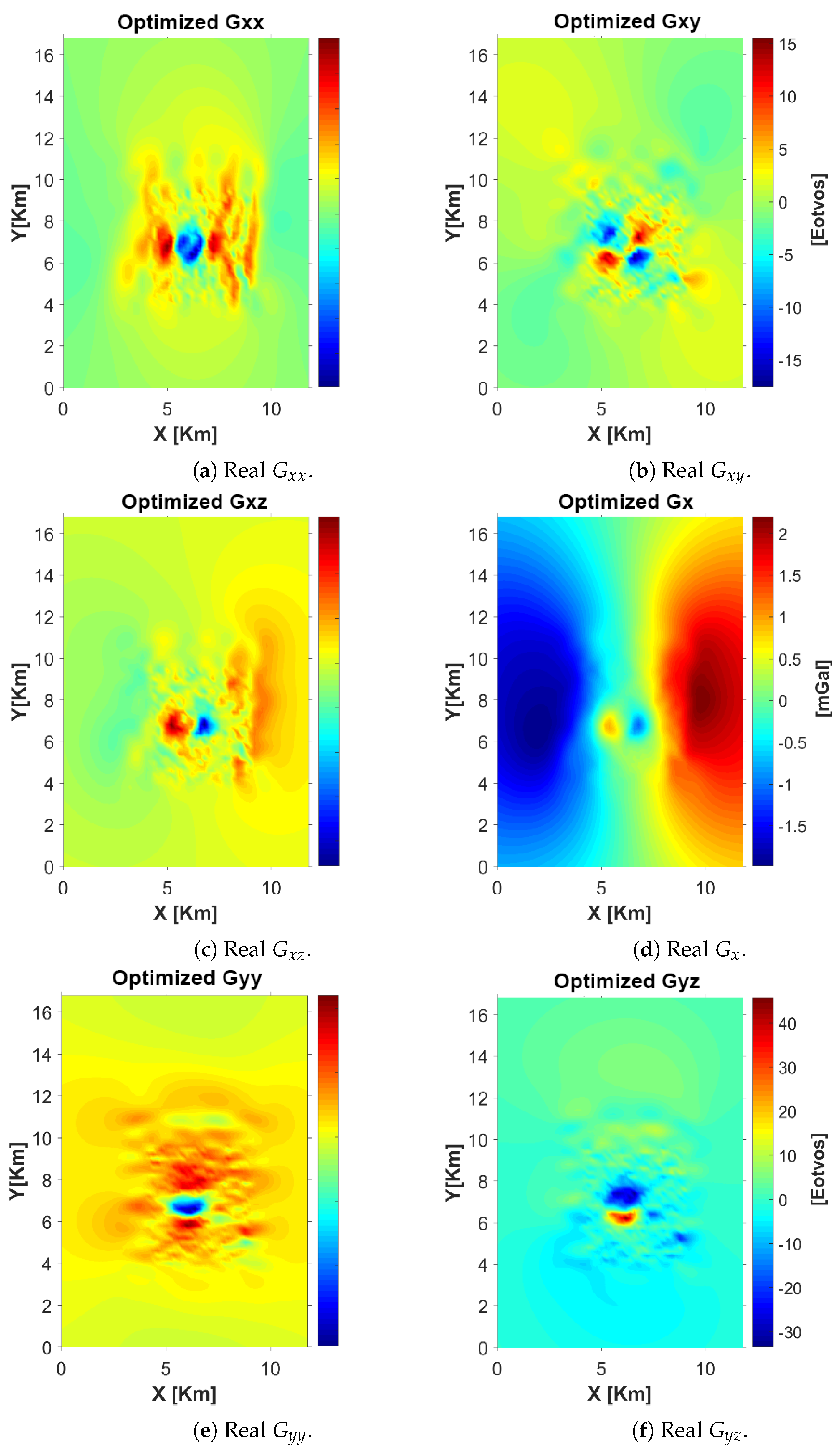
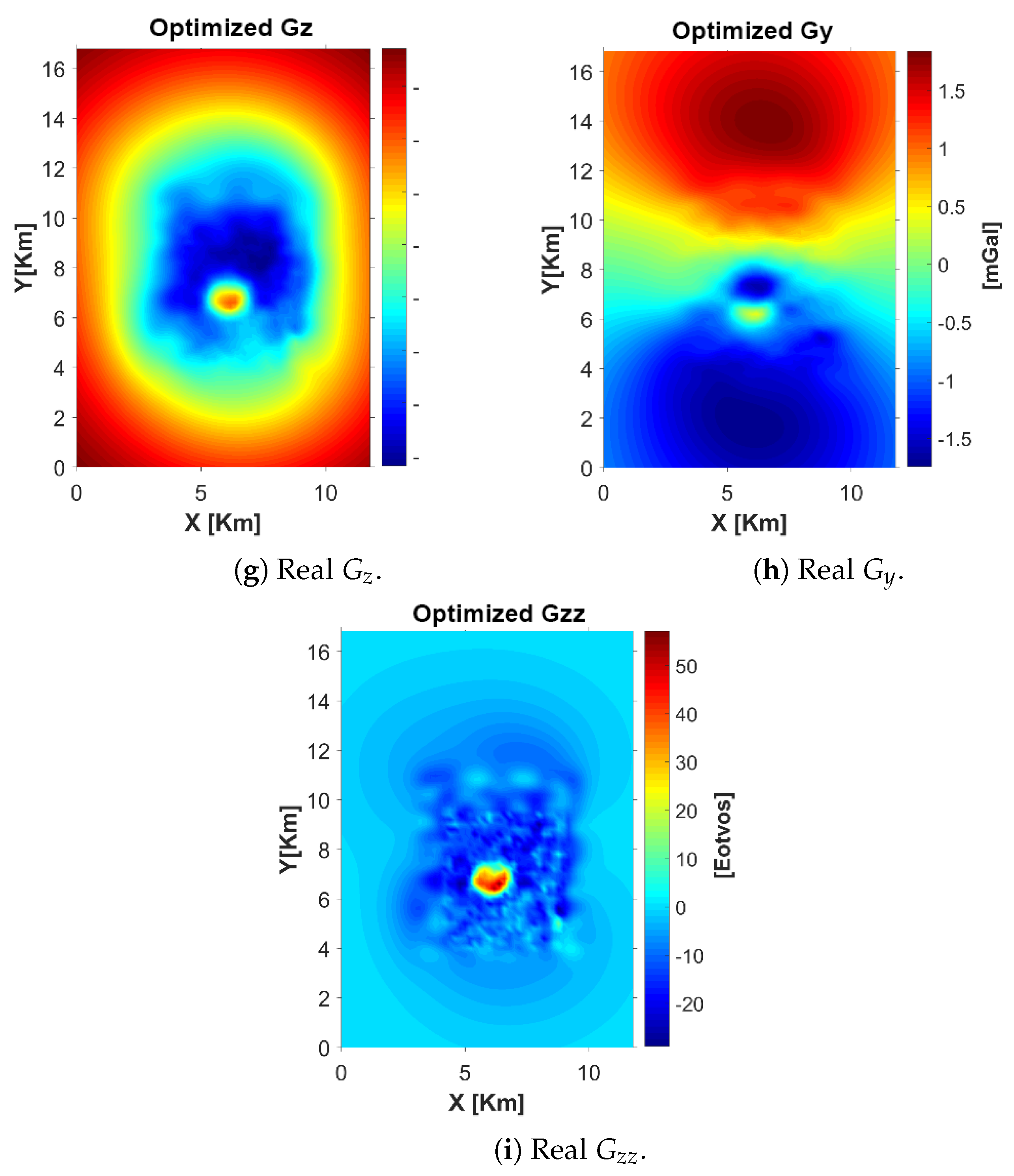
The initial synthetic data (Figure 11) were generated from a forward model based on the prism ensemble shown in the previous subsection, using the theoretical gravity and FTG responses computed with the analytical formulas of Nagihara and Hall [35] for rectangular prisms. These synthetic datasets were used to validate the inversion algorithm and ensure convergence before applying it to the real data.

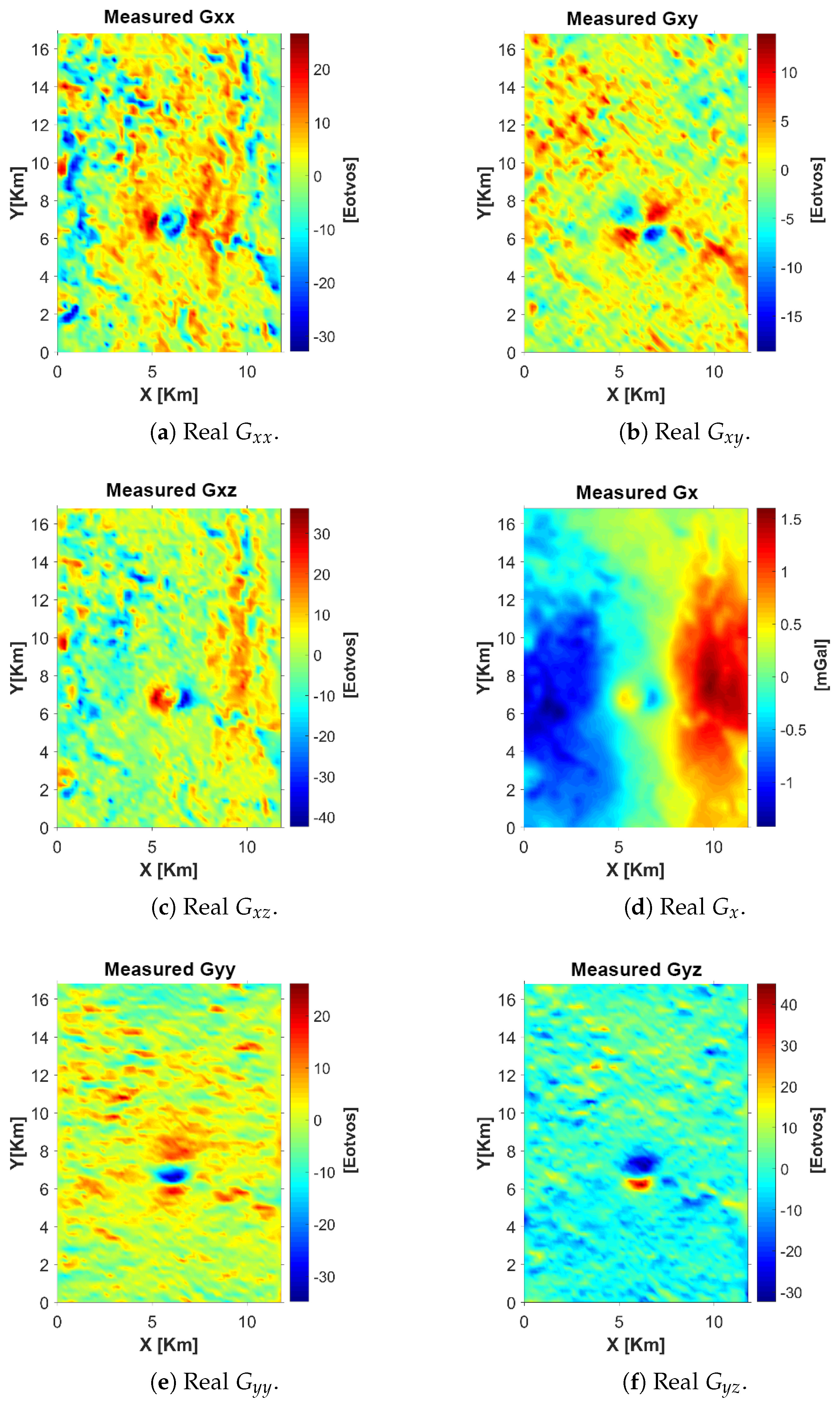
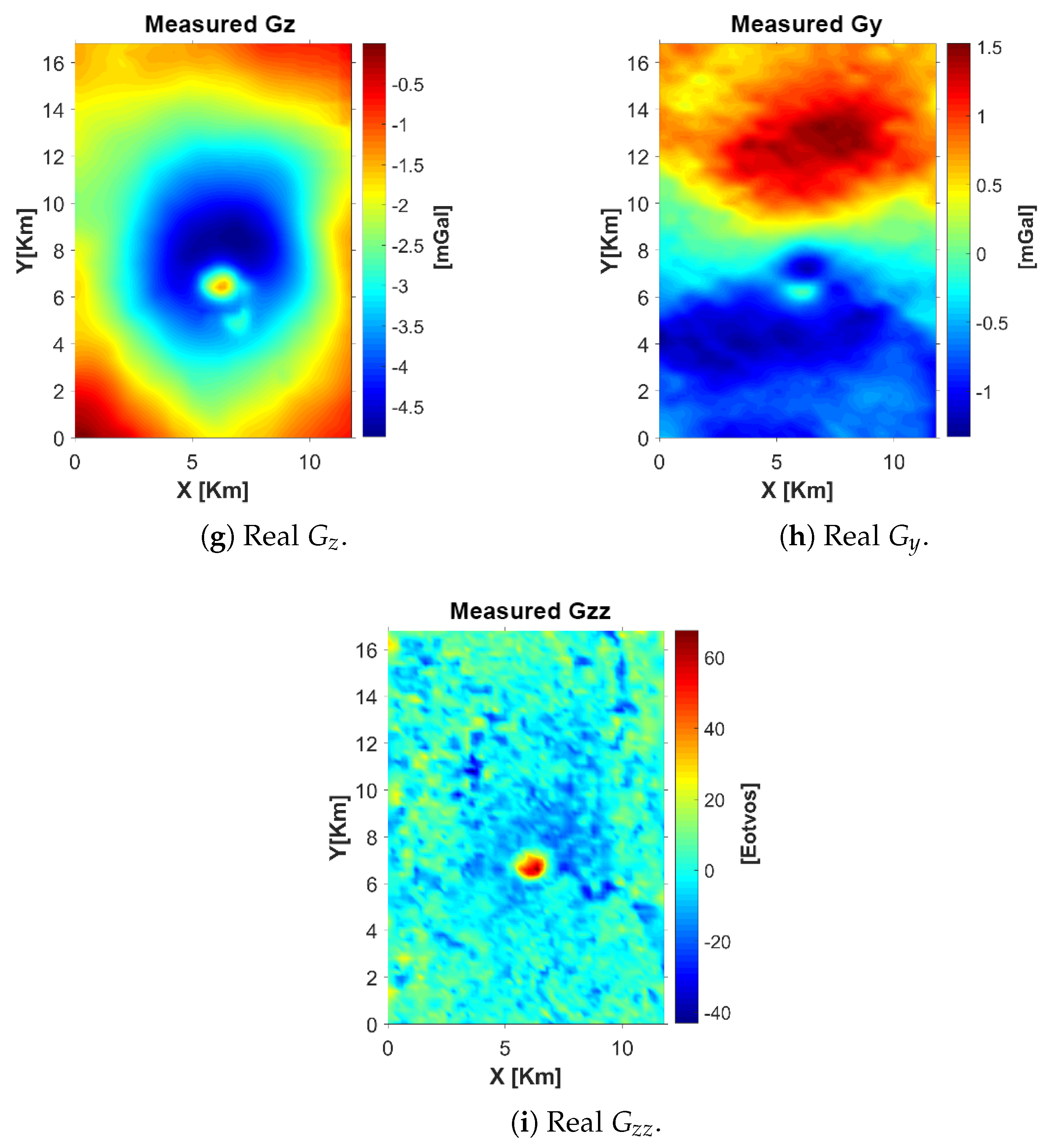
The real dataset (Figure 12) used in this study corresponds to the FTG survey acquired by Bell Geospace (2008) over the Vinton Dome area in Louisiana, USA. Measurements were obtained using an airborne Full Tensor Gradiometer, a high-resolution instrument equipped with three orthogonal pairs of accelerometers mounted on rotating disks. The survey consisted of 53 flight lines and 17 tie lines, with average line lengths of 16.7 km and 11.7 km, respectively. Flight-line spacing was 125 m near the survey center and 250 m toward the edges, while tie lines were spaced 1 km apart.

The vertical gravity component ($g_z$) was derived by integrating the tensor components and refined using ground-based gravity readings. To maximize spectral consistency, the tensor signals were filtered with a high-pass filter and the gravimetric data with a low-pass filter, combining their complementary high- and low-frequency contents. This fusion produced a broader spectral signal suitable for joint inversion.

The available datasets were previously corrected by the provider for Full Tensor Noise Reduction, free-air effects, and topography.

The complementary ground-based gravity measurements were obtained from a local network of 43 observation points distributed across the central portion of the Vinton Dome area, with an average spacing of approximately 500 m between stations. The positional accuracy of each station was better than ±0.5 m, and gravity readings were accurate within ±0.05 mGal. These data were used to constrain the long-wavelength component of the $g_z$ field and to validate the airborne FTG-derived vertical gravity. Although airborne Full Tensor Gravity (FTG) data inherently contain noise due to aircraft motion, Bell Geospace (2008) applied proprietary corrections, including full-tensor noise reduction, terrain adjustment, and free-air correction, which significantly improved the vertical gravity accuracy. The resulting $G_z$ precision is estimated to be within 3–5 Eötvös, consistent with the specifications reported by Bell Geospace [40] for high-resolution FTG surveys. Regarding density contrasts, realistic values were adopted based on core and log-derived measurements compiled by Nelson and Fairchild [39] and regional Gulf Coast data. The salt core exhibits densities between 2200–2250 kg/m³, the cap rock 2600–2700 kg/m³, and the surrounding clastic sediments 2400–2500 kg/m³. The contrast range of approximately 400–450 kg/m³ used in the inversion reflects these measured properties and aligns with published geophysical models of the Vinton Dome and similar Gulf Coast salt structures.

Topographic corrections were applied using in-flight altimetry data and an average density of 1.8 g/cm³, while free-air corrections were referenced to the elevation of the flight lines. The Full Tensor Noise Reduction process ensured that only consistent variations present across all tensor components were retained, effectively suppressing noise and preserving genuine geological signals.

Cost Function

We considered two options for the cost function. Both proposals compute it as a linear combination of the missfit according to the $L_2$ norm of each component, as shown in the equation:

$$\begin{array}{c}\hfill E_T=c_1{e}_{gz}+c_2\left(e_{gx}+e_{gy}\right)+c_a{e}_{gzz}+\\ \hfill c_b\left(e_{gxz}+e_{gyz}\right)+c_c\left(e_{gxx}+e_{gyy}\right)+c_d{e}_{gxy}\end{array}$$

(31)

Using the simulated annealing algorithm, we discovered the coefficients’ values that maximize or minimize the value of $E_T$ within a set of synthetic data. To achieve this, we employed a complex synthetic model simulating real data, as depicted in Figure 13.

The values of the coefficients maximising and minimising the cost function are shown in

Table 3. Values of the coefficients that maximise and minimise the cost function. These values were found through simulated annealing.

	Min	Max
$c_1$	0.793817	0.008442
$c_2$	0.0123330	0.0159304
$c_a$	0.038510	0.026529
$c_b$	0.038500	0.1427988
$c_c$	0.0299680	0.0074158
$c_d$	0.006968	0.062359
$E_{\mathrm{initial}}$	0.760330	0.939756

.

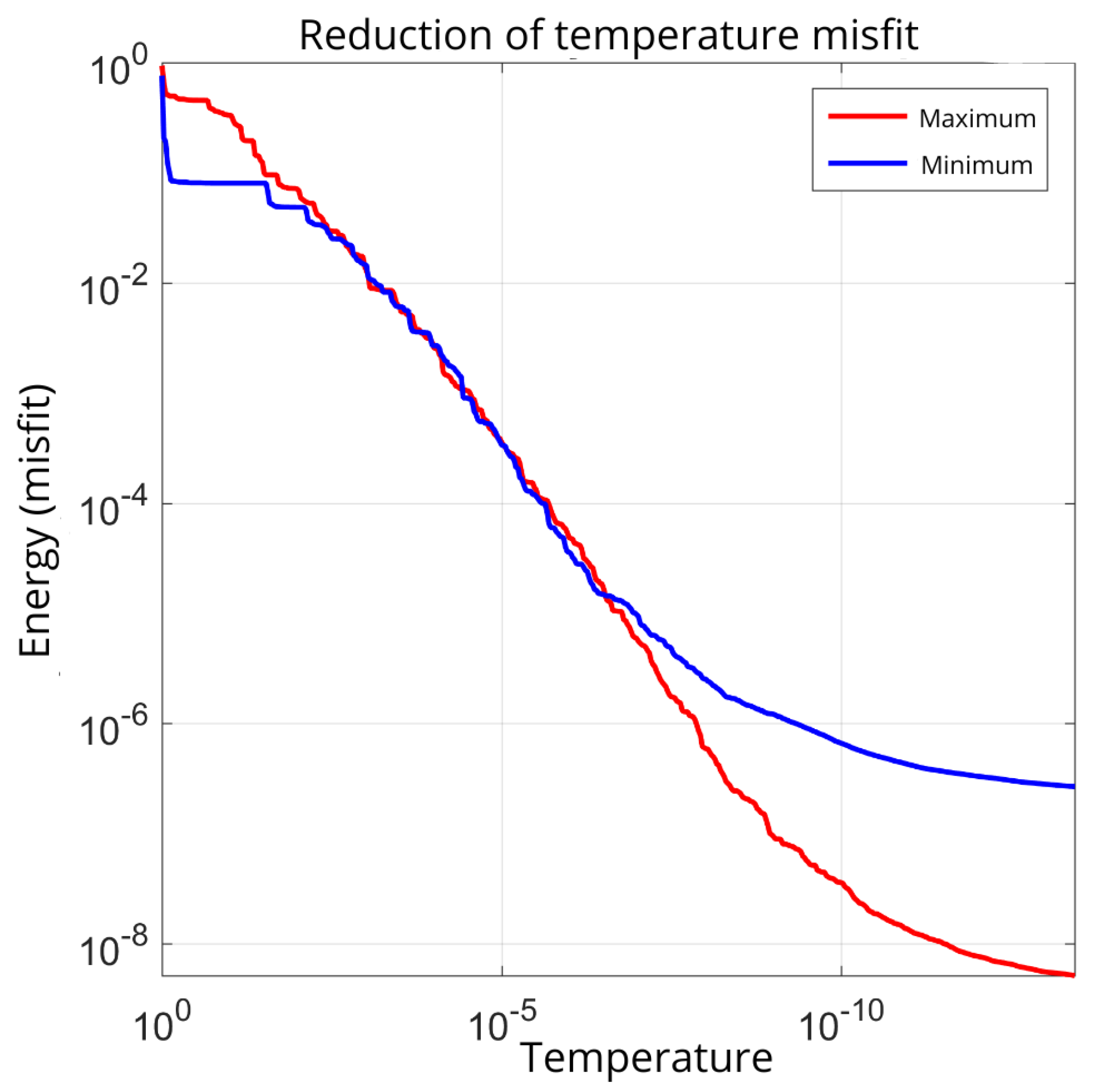
The behaviour of the cost function with both the minimising and maximising parameters is shown in Figure 14. Clearly, the behaviour of the cost function with the maximising parameters is better at low temperatures, so these parameters are chosen for the inversion scheme.

3.5. First Inversion

The first inversion results are shown in

Table 4. Coefficients obtained from the first inversion of data from the Vinton Dome.

Coefficient	Value
$c_1$	0.05954
$c_2$	0.26634
$c_a$	0.12292
$c_b$	0.13982
$c_c$	0.00057
$c_d$	0.00404
$E_{\mathrm{initial}}$	8.7036

.

In Figure 15, the curve illustrating the reduction in energy of the system with respect to the temperature of the Vinton Dome for the initial inversion is displayed.

On the other hand, in Figure 16, we display the final configuration of the assembled model with prisms resulting from the first inversion of data.

Finally, in

Table 5. Configuration of the first inversion for the Vinton Dome.

Parameters	Values
Number of parameters	19,641
Number of observation points	5100
Initial temperature	1
Final temperature	1.0293 × ${10}^{-10}$
Temperature decrements	3000
Value of parameter $Nt$	2
Value of parameter $Ns$	4
$RT$ Factor	0.95
Accepted models	233,584,285
Rejected models	237,799,715
Initial energy	8.7035
Final energy	0.3078

, we present the configuration of the first inversion conducted for the Vinton Dome.

Optimal Temperature

From the first inversion, we identified the temperature interval in which the total energy decreased most significantly. Based on this observation, we performed the inversion again while maintaining this temperature for additional iterations (annealing). Before the second inversion, a mean filter was applied, and the resulting model is shown in Figure 17.

3.6. Second Inversion

The new coefficients for the cost function can be observed in

Table 6. Coefficients used for the second inversion of the Vinton Dome.

Coefficient	Value
$c_1$	0.08116
$c_2$	0.09104
$c_a$	0.11403
$c_b$	0.12336
$c_c$	0.12545
$c_d$	0.12506
$E_{\mathrm{initial}}$	0.594001

.

The results of the second inversion for the Vinton Dome data, utilizing the filtered data from the first inversion as the initial model, are presented in

Table 7. Configuration of the second inversion for the Vinton Dome, in which we used the filtered model as the initial model.

Parameters	Values
Number of parameters	19,641
Number of observation points	5100
Initial temperature	1
Final temperature	1.0293 × 10−4
Temperature decrements	100
Value of parameter $Nt$	2
Value of parameter $Ns$	4
$RT$ Factor	0.95
Accepted models	14,261,234
Rejected models	1,451,566
Initial energy	0.594001
Final energy	0.551141

.

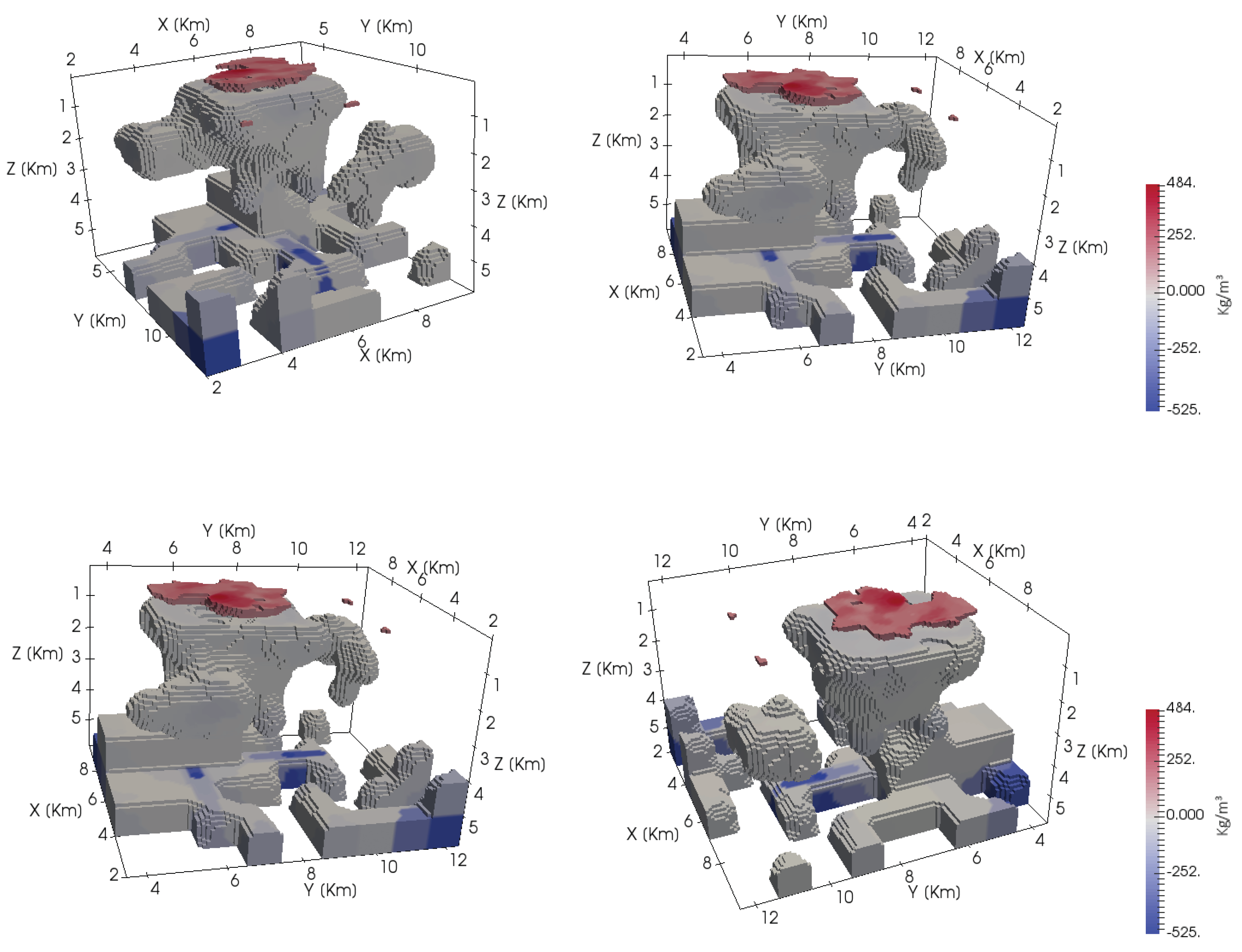
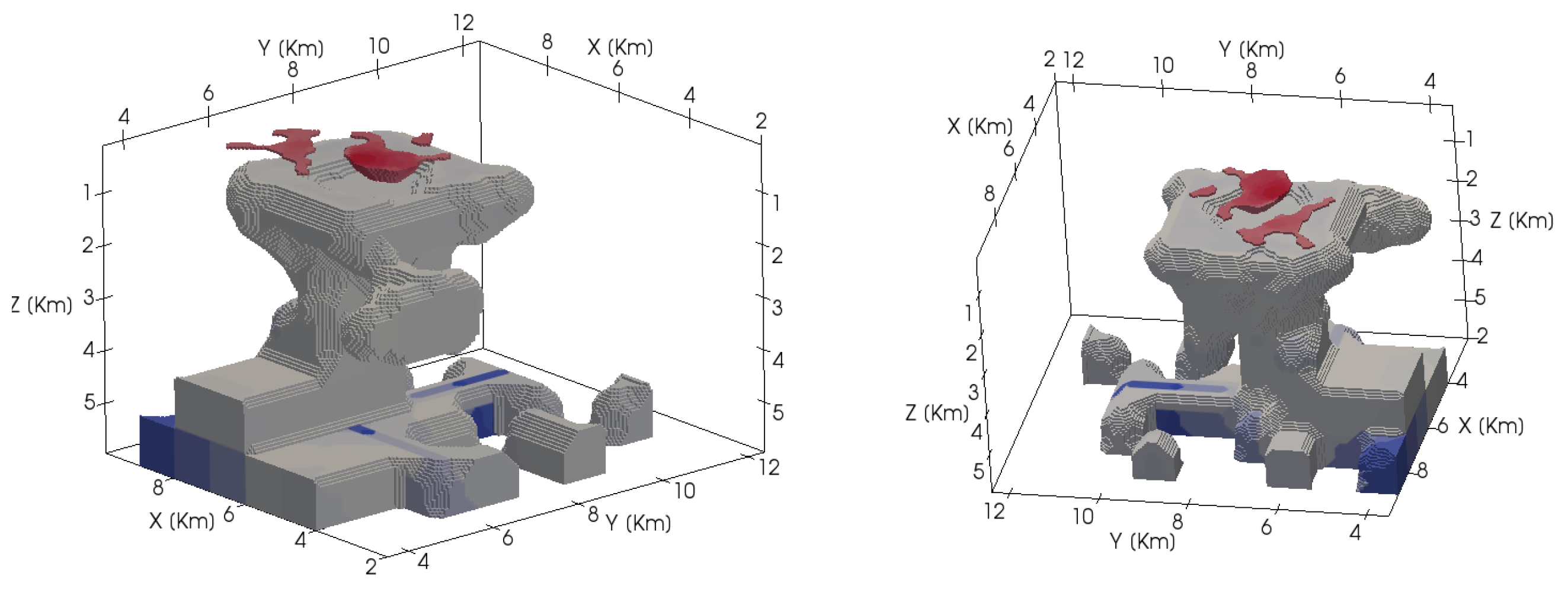
The final inversion model (Figure 18) successfully delineates the principal salt body and its overlying cap rock. The high-density layer highlighted in red above the dome corresponds to the cap rock—an anhydrite- and limestone-rich assemblage that overlies the Vinton salt mass. Its density contrast relative to the surrounding sediments (≈+0.45 kg/m³) is consistent with previous geophysical and drilling observations [39].

Although the prism-based inversion yields a blocky geometry that does not exactly reproduce the smooth outline of a natural salt dome, the recovered structure effectively captures the main features of the Vinton Dome—the upward-bulging salt mass and the overlying cap rock. The apparent irregularities arise from the discrete prism representation used in the simulated annealing algorithm, which was selected to reduce computational cost while preserving the overall density distribution. The resulting morphology and depth range are consistent with published geological and geophysical interpretations of the Vinton Dome [39].

It is important to note that, although the recovered structure exhibits a diapiric geometry with steep flanks and an upward-narrowing core, this morphology is consistent with the internal architecture of the Vinton Dome described by Nelson and Fairchild [39]. The term “salt dome” is traditionally applied to these Gulf Coast piercement structures, which typically evolve into diapiric forms as the salt ascends through overlying strata. Therefore, the geometry shown in Figure 18 accurately reflects the diapiric character of the Vinton Dome while remaining consistent with its regional classification as a salt dome.

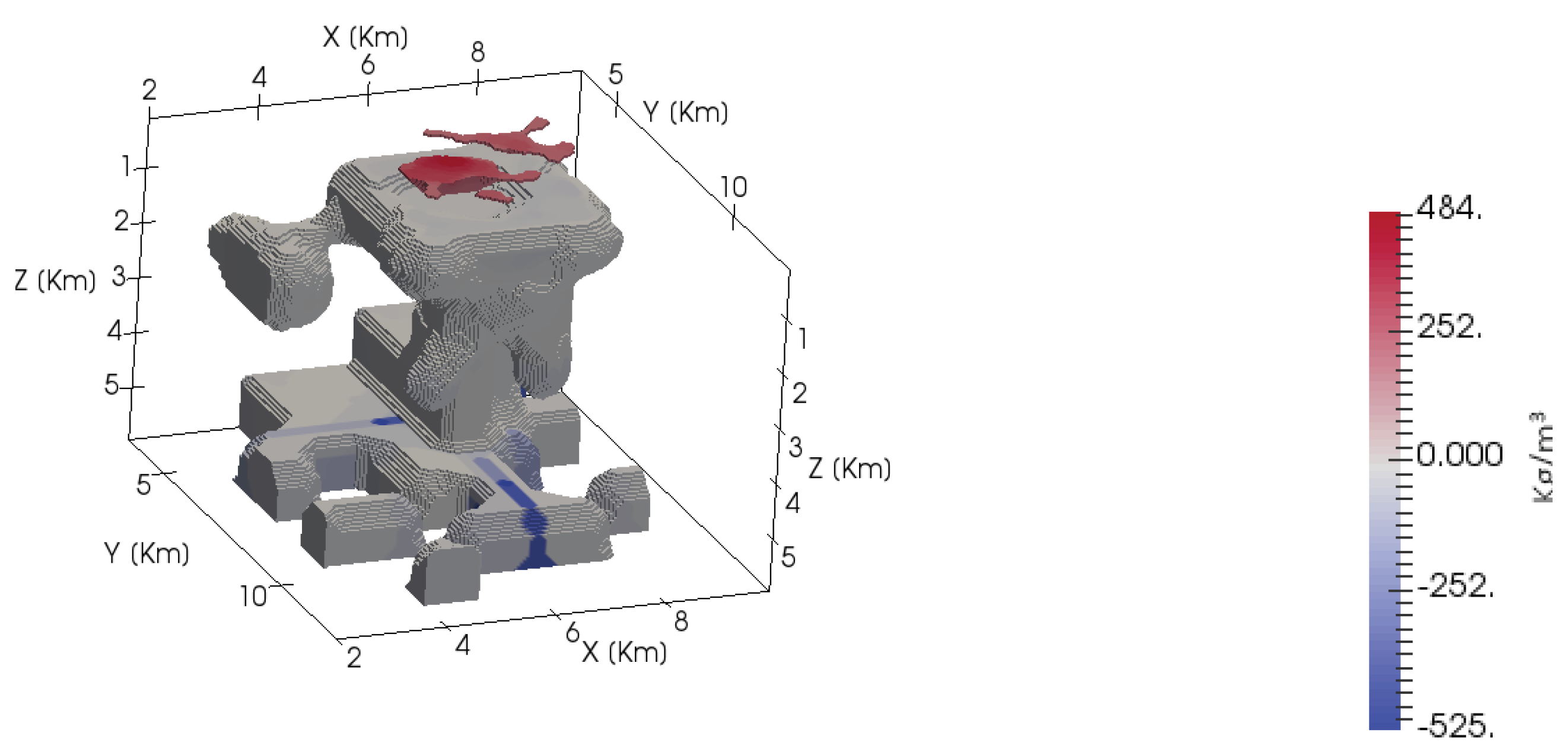
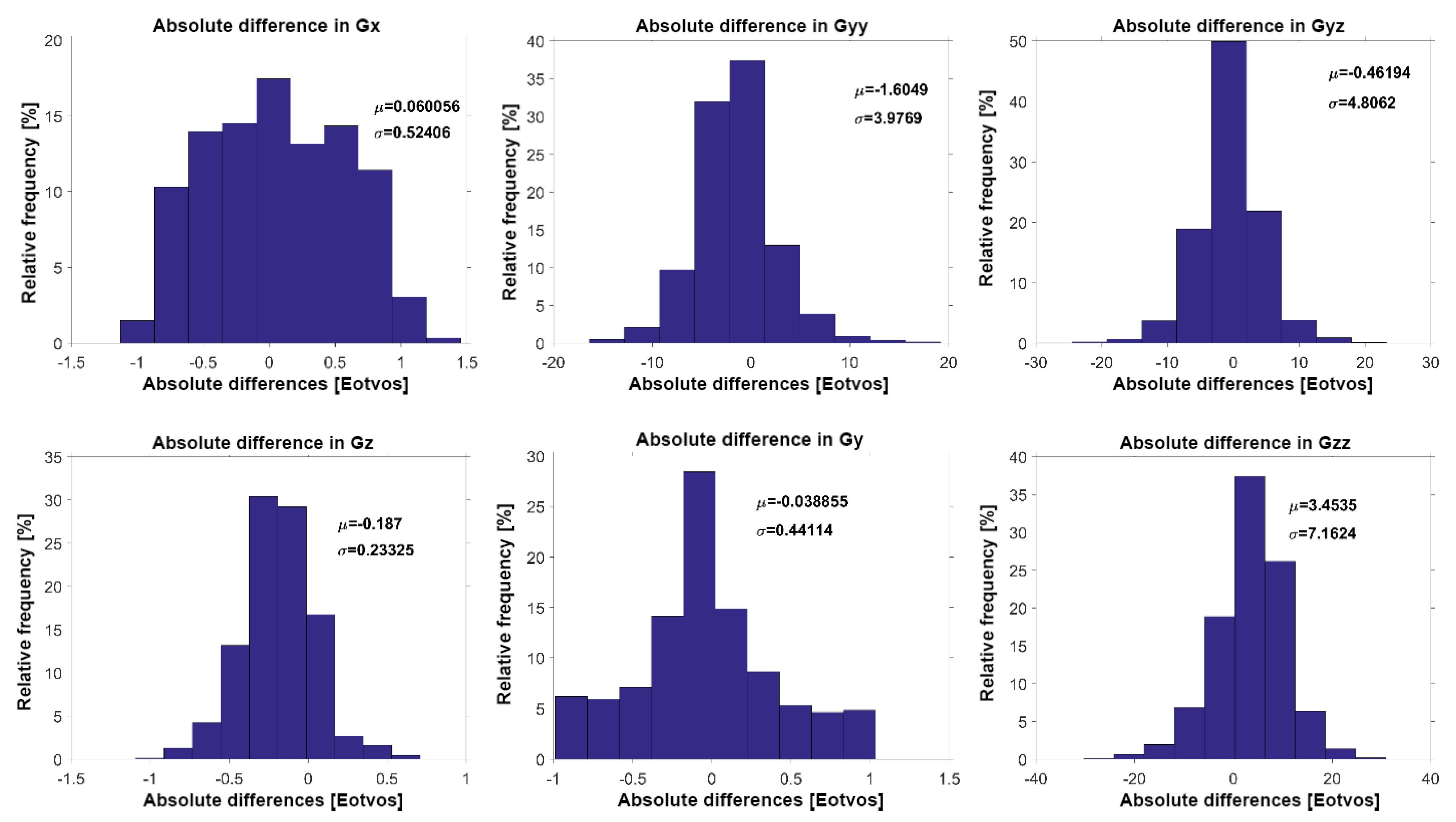
To assess the final model for the Vinton Dome, its gravity and gradiometric responses can be observed in Figure 19. On the other hand, the differences between the optimal response (Figure 19) and the original data (see Figure 12) can be observed in Figure 20.

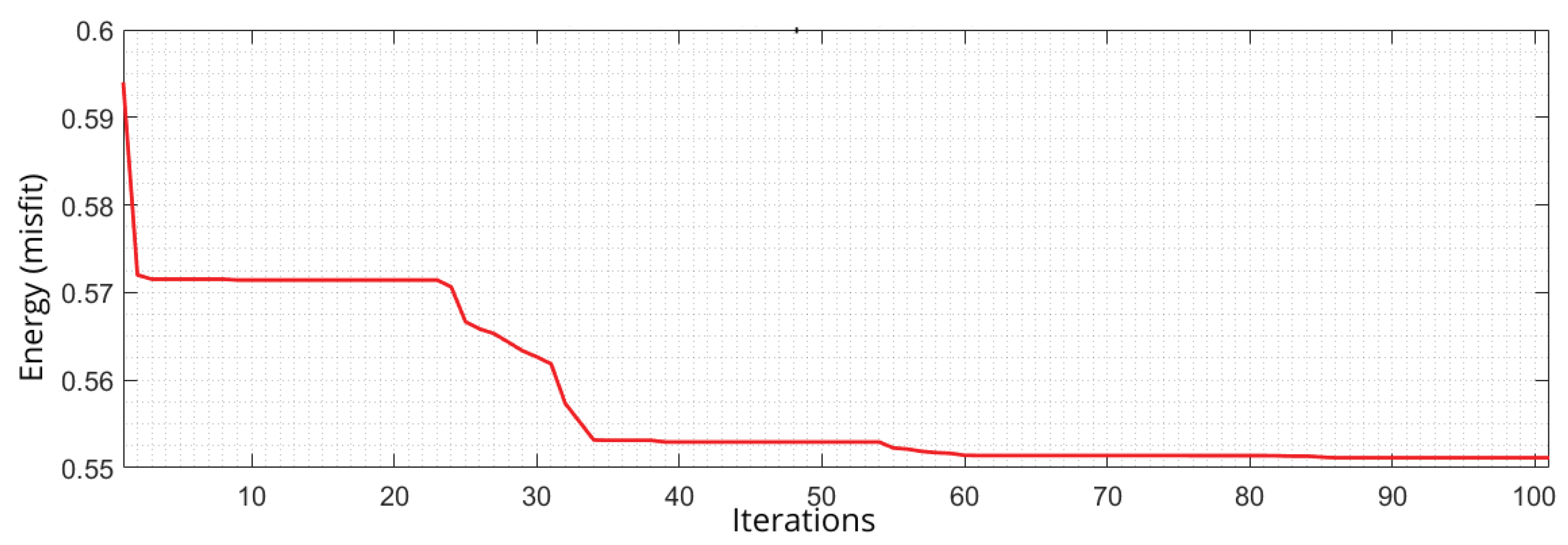
Finally, in Figure 21, we plot the energy decrease as a function of iterations, rather than temperature, since we keep the annealing temperature constant.

4. Discussion and Final Remarks

The final inversion model indicates that the salt body extends from a depth of approximately 0.5–0.8 km at its crest to around 3.2–3.5 km at its base. These depth estimates are consistent with previously published geological and seismic interpretations of the Vinton Dome, which report salt-root depths between 3 and 3.6 km [39,41]. The model also reproduces the shallow high-density cap rock (0–0.3 km thick) observed in drilling data. The close agreement between the inverted and reported depths validates the joint gravity–FTG approach and confirms the stability of the simulated-annealing optimization process.

The use of Euler Tensor Deconvolution (ETD) was instrumental in constructing a robust initial model. The gradiometric data effectively delineated the lateral extent of the source, whereas the gravimetric data refined the depth estimates due to their distinct decay with distance between the source and observation points. The resulting ETD solutions tended to cluster, forming a discernible “shell” around the main body of the source.

Enhancing the high-wavenumber content in the horizontal components of the gravimetric field led to improved estimates, enabling consistent fusion of datasets from different instruments. This procedure demonstrated potential for broader application; however, it remains essential to match component amplitudes prior to fusion to prevent spectral bias.

The proposed cost function allowed the simultaneous use of nine components (six gradiometric and three gravimetric), thereby exploiting all available information and producing a model that satisfactorily fits the measured datasets. Although heuristic methods are computationally demanding, the use of parallel computing and convergence-acceleration techniques mitigated this limitation, resulting in practical run times even with increasing data volume.

Together, the adopted techniques enabled efficient inversion and produced geologically consistent results. Applying a mean filter helped remove isolated, non-physical features, while maintaining an optimal temperature range further reduced the objective function, promoted convergence, and outperformed typical local inversion algorithms that are prone to entrapment in nearby minima.

Employing the full set of gravity-gradient tensor components in the inversion, rather than relying solely on the vertical component, provided clear advantages. Complementing gradiometry with gravimetry enriched the low-frequency content, improving depth estimates for deeper sources. Nevertheless, careful management of computational cost remains crucial, as it scales directly with the number of parameters.

4.1. Recommendations and Limitations

4.1.1. Detailed Understanding of Local Geology

Before applying the algorithm, it is essential to develop a thorough understanding of the Vinton Dome’s geology and tectonic framework, including the geometry and distribution of salt bodies and their relationships with surrounding formations and the cap rock.

4.1.2. Consideration of Cap Rock Effects

The cap rock can influence the morphology of salt structures and modify their geophysical response. When applying ETD, its presence and physical properties should be explicitly considered to minimize interpretational bias.

4.1.3. Calibration of the Initial Model

The initial model should be calibrated using all available geophysical and, where possible, well data. This ensures that the starting configuration reflects key geological characteristics—including the cap rock—and enhances the stability of subsequent ETD and inversion stages.

4.1.4. Validation with Independent Data

Whenever possible, validate results with independent datasets such as additional wells or complementary geophysical surveys. Cross-validation improves reliability and helps identify potential biases, particularly those associated with cap rock effects.

4.1.5. Geological Complexity

The Vinton Dome area exhibits complex, multi-layered geology that can limit model resolution and accuracy. Such complexity should be explicitly acknowledged during interpretation.

4.1.6. Data Resolution

The accuracy of the inversion results depends strongly on data quality and resolution. High-quality, high-resolution measurements are crucial for obtaining reliable outcomes.

4.1.7. Interpretation Bias

Interpretations may be influenced by prior assumptions or analyst bias. When feasible, compare results obtained under different model constraints or using alternative datasets and regularization parameters.

4.1.8. Algorithmic Limitations

Although effective, ETD and simulated annealing have inherent limitations:

• Computational complexity: Both methods can be computationally intensive, particularly for large datasets or highly parameterized models.
• Sensitivity to initial parameters: Their performance depends on starting conditions and parameter tuning (e.g., structural index in ETD; temperature schedule in SA).
• Model assumptions: Deviations from theoretical assumptions or inaccuracies in input data may introduce bias.
• Scope of application: Extremely heterogeneous media or highly noisy datasets may not be adequately represented.
• Interpretation challenges: Correct use and interpretation require expertise in geophysics, geology, and numerical modeling.