A Bayesian Geostatistical Approach to Analyzing Groundwater Depth in Mining Areas

Abstract

This study addresses the spatial variability of groundwater levels within a mining basin in Greece. The objective is to develop an accurate spatial model of groundwater levels in the area to support an integrated groundwater management plan. Hydraulic heads were measured in 72 observation wells, which are irregularly distributed, primarily in mining zones. Multiple geostatistical approaches are evaluated to identify an optimal model based on cross-validation metrics. We introduce a novel trend model that includes the surface elevation gradient, as well as the proximity of wells to the riverbed, utilizing a modified Box–Cox transformation to normalize residuals. The results indicate that Regression Kriging with a non-differentiable Matérn variogram outperforms Ordinary Kriging in cross-validation accuracy. The study provides maps of the piezometric head and kriging variance within a Bayesian framework, being among the first to quantify and incorporate river-distance effects within regression kriging for groundwater.

1. Introduction

Groundwater is a vital resource for environmental sustainability, agriculture, and industrial applications, particularly in regions where surface water resources are scarce. Monitoring groundwater levels provides crucial insights into aquifer health, informing sustainable water management practices. In aquifer systems, groundwater levels are typically monitored through hydraulic head measurements taken from borehole locations. However, monitoring wells are often limited in number and unevenly distributed due to financial constraints or logistical challenges [1]. This lack of uniform monitoring can lead to sparse datasets that inadequately represent the spatial variability of groundwater levels across a study area, particularly in complex geological environments, such as mining basins.

Geostatistical methods provide powerful tools for analyzing spatial data and have been widely applied in groundwater studies to model aquifer surfaces with greater accuracy. These methods, including Kriging techniques, use statistical relationships among sample points to interpolate values at unsampled locations. Kriging methods are beneficial for groundwater studies because they can produce spatial models of aquifer surfaces, even when direct measurements are sparse or unevenly distributed [2]. By incorporating auxiliary spatial variables, such as surface elevation or rainfall data, geostatistical models can enhance estimation accuracy by accounting for local geographic and environmental factors [1]. The inclusion of auxiliary information as drift terms in spatial models has proven effective in capturing complex spatial patterns that simpler interpolation methods might overlook [3].

Ordinary Kriging (OK) is a widely used Kriging variant that assumes a constant mean across the study area and calculates estimates based solely on spatial correlations of sampled data points [4]. OK has been used in several groundwater studies to map piezometric head fields and analyze groundwater distribution patterns. However, OK has limitations, especially in non-stationary environments where groundwater levels may exhibit spatial trends or gradients. For example, the influence of elevation or proximity to surface water bodies can create trends that OK fails to capture. In such cases, more sophisticated approaches, such as Regression Kriging (RK) or Kriging with External Drift (KED), may be utilized, as they incorporate trend information to accommodate these spatial variations [5]. Deep Learning Methods (DL) have been successfully used in groundwater-level predictions [6].

Regression Kriging and Kriging with External Drift improve upon OK by integrating secondary information through external drift terms. RK, in particular, combines a regression model with Kriging to interpolate the residuals, providing a flexible framework that allows for the inclusion of multiple auxiliary variables to improve spatial estimates [7,8]. The KED and RK methods have been successfully applied to model water table elevations in various studies. For example, Rivest et al. [9] demonstrated that using a finite-element model to approximate hydraulic head as an external drift in KED yielded more accurate results compared to the OK method. These methods are advantageous because they enable the use of readily available secondary information, such as digital elevation data, to capture the natural gradients of groundwater levels more effectively than OK [10]. Wang et al. utilized a large amount of groundwater-level spatiotemporal records along with precipitation and temperature as auxiliary variables to enhance predictions [6].

However, these methods are not without challenges. For instance, KED’s reliance on secondary variable covariance structure can complicate model construction, particularly when secondary data are irregularly distributed [2,11]. Deep Learning methods rely on large datasets and often require multiple auxiliary variables in space–time, which are rarely available without extensive data collection campaigns [6]. RK, on the other hand, separates trend estimation from residual interpolation, which allows the use of more advanced regression techniques and facilitates the independent interpretation of the trend and residual components. This separation is advantageous in regions with limited data, as RK enables the integration of multiple data sources to enhance estimation precision [12,13].

This study focuses on the spatial variability of groundwater levels in a mining basin in Greece. In recent years, this region has experienced considerable declines in groundwater levels due to overexploitation. Accurate mapping of groundwater levels in such areas is crucial for developing effective groundwater management plans that address the vulnerability of resources [14]. Here, we evaluate various geostatistical approaches for modeling the groundwater surface and its associated uncertainty. We introduce a novel auxiliary variable that incorporates the distance of wells from a temporary riverbed within the basin, which correlates strongly with groundwater levels. In addition, we propose a modified Box–Cox transformation to normalize data, improving model performance by addressing skewness and stabilizing variance [15,16].

The proposed approach utilizes Regression Kriging with a non-differentiable Matérn variogram model, which provides flexibility in modeling spatial dependencies, particularly at short distances. The Matérn variogram’s smoothness parameter allows it to capture the groundwater level’s local continuity and differentiability more accurately, addressing challenges found in other geostatistical models [17,18]. This study’s methodology incorporates Bayesian uncertainty analysis, enabling a robust quantification of prediction intervals and model reliability. Bayesian methods enable the incorporation of prior information into the geostatistical framework, providing a comprehensive approach to handling model and parameter uncertainties, which is crucial when working with sparse data [19,20].

This study presents an integrated geostatistical approach for groundwater-level estimation in a mining basin, utilizing RK with novel trend modeling and a Bayesian framework. The proposed methodology enhances model accuracy by accounting for spatial variability and uncertainty, providing a valuable tool for groundwater resource management in complex hydrogeological settings. Several spatial models are investigated to map water table elevations and their associated uncertainties. We propose a new trend model that involves, in addition to surface elevation, the distance of the wells from the riverbed. We also propose and use a modified Box–Cox transformation to normalize the residuals.

The findings of this study align closely with those of previous research that has applied geostatistical methods to groundwater modeling. Similar to Varouchakis and Hristopulos [5], who utilized auxiliary variables such as elevation to enhance spatial estimation in sparsely monitored basins, this study enhances Regression Kriging (RK) with novel drift terms, including river proximity, to achieve improved predictive performance. Additionally, the high correlation (r = 0.74) between river distance and groundwater levels mirrors results by Desbarats et al. [7], who demonstrated improved accuracy using DEMs as covariates. Bayesian kriging employed here further echoes the work of Pilz and Spöck [19], emphasizing the quantification of uncertainty in spatial predictions. Overall, this study extends prior findings by integrating both topographic and hydrologic factors into a unified Bayesian RK framework, outperforming Ordinary Kriging approaches seen in studies like Nikroo et al. [10].

The remainder of this article is organized as follows. In Section 2, we present statistics for the data (hydraulic head) and hydrogeological information for the basin. Section 3 details the geostatistical methodology employed in this work. Section 4 presents a new auxiliary variable that is used in the augmented trend model of the hydraulic head. In Section 5, we derive Bayesian uncertainty and present the interpolation results for the observation wells using RK. This section also reports the results of the cross-validation analysis.

Additionally, we highlight spatial patterns that are important for the groundwater resources in the study basin. In Section 6, a discussion of the results is conducted. Finally, Section 7 delivers the conclusions.

2. Materials and Methods

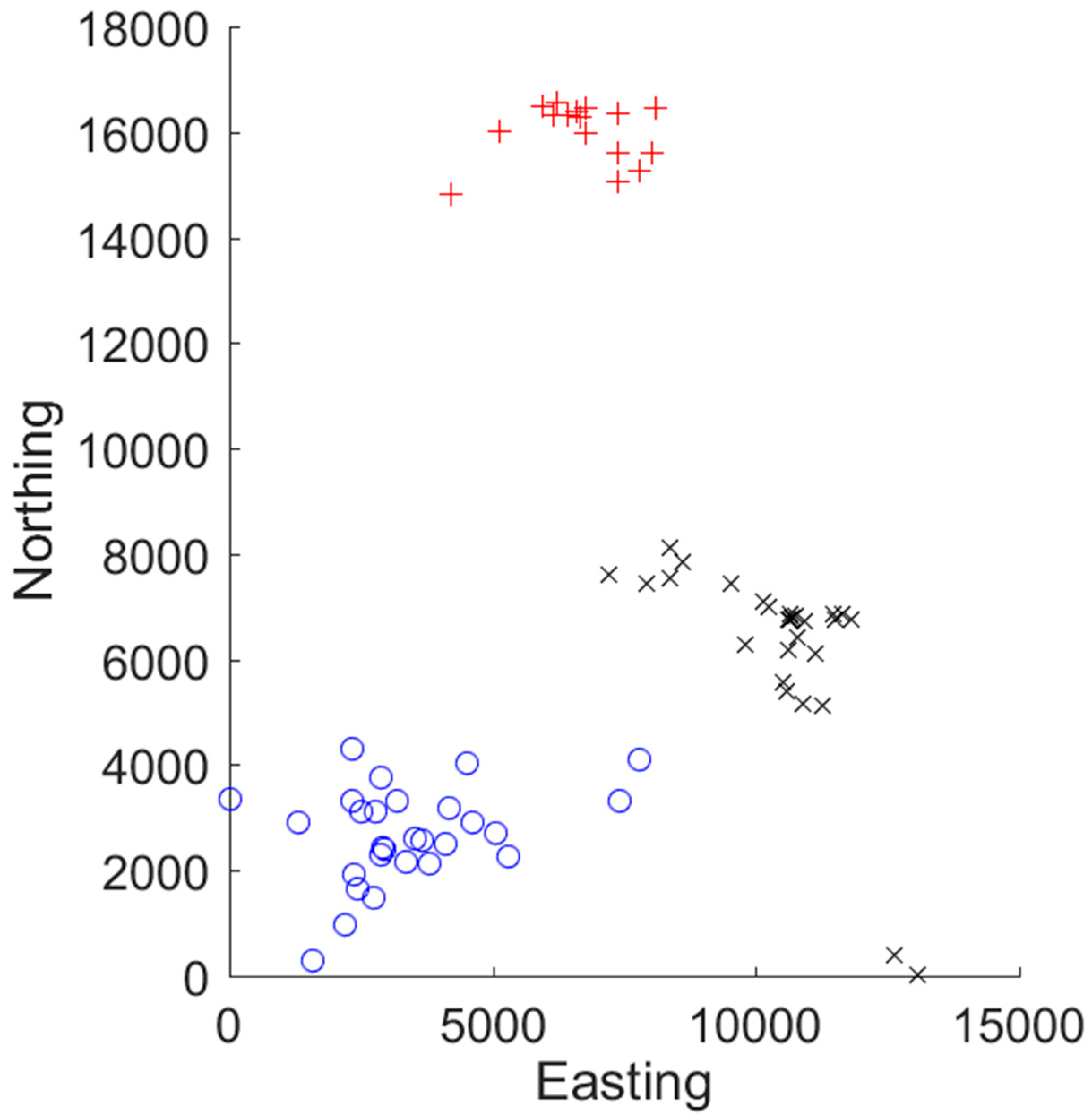
Three mines are located in the area of interest (due to confidentiality reasons, we cannot disclose the exact location). Hydrogeologically, the study area can be characterized as semipermeable with discontinuities hosted in the vertical profile of three hydrostratigraphic units [21]. The data used in this research consist of 10-year biannual average water-level measurements (below surface, mbsl) from 72 drill holes. The descriptive statistics before the transformation are as follows: min value: 4 m, max: 208 m, mean: 41.82 m, median: 28 m, standard deviation: 45.57 m. The boreholes are located around the mines (Figure 1).

This study models groundwater levels as a spatial random field (SRF) to analyze the spatial variability in hydraulic head across the mining basin. Let $\left\{Z\right(\mathit{s}): \mathit{s} \in D\}$ represent the SRF for groundwater levels over a spatial domain D. For measured points within the domain, denote the sampled SRF as $\left\{z\left({\mathit{s}}_i\right)\right\}$, where $S = \left\{{\mathit{s}}_1, {\mathit{s}}_2, \dots , {\mathit{s}}_{\mathit{n}}\right\}$ represents the set of sampling locations. The objective is to predict the hydraulic head at unsampled locations $P = \left\{p_1, p_2, \dots , p_m\right\}$ using geostatistical interpolation methods. The spatial models investigated include Ordinary Kriging (OK) and Regression Kriging (RK), both of which utilize normalizing transformations.

Ordinary Kriging (OK)

OK is a widely used geostatistical interpolation method that assumes a constant mean across the study area. The interpolated value at an unsampled location is calculated as a weighted sum of values at sampled points [2]. OK performs well in stationary fields but can be limited in non-stationary environments, where trend effects or gradients affect the spatial distribution of groundwater levels [1]. In such cases, methods that account for trends or secondary variables, such as Regression Kriging, offer enhanced accuracy.

Regression Kriging (RK)

Regression Kriging (RK) combines a regression model to estimate global trends in the data with OK applied to the residuals, allowing for greater flexibility and the incorporation of auxiliary information. In RK, the SRF is expressed as a combination of the trend component and residuals. The trend component can integrate secondary spatial variables, such as elevation or proximity to rivers, to improve spatial estimates [7,8]. RK has demonstrated benefits in groundwater studies by enhancing interpolation accuracy and making the model more interpretable in terms of its trend and residual components, particularly in cases where primary data are limited [12,13].

Normalizing Transformations

For OK and RK, data normality is desirable for optimal performance. A common approach to achieve normality is by applying a transformation to the data. This study employs a modified Box–Cox transformation, which is effective in handling non-Gaussian data, particularly when negative values or skewness are present [15,16]. The transformation stabilizes variance and adjusts for skewness, resulting in a distribution closer to Gaussian. The modified Box–Cox transformation used is given by the formula:

$$y≔g_{\mathit{\kappa }}\left(z\right)={\displaystyle \frac{{\left(z-z_{min}+{b_1}^2\right)}^{b_2}-1}{b_2}}, {\mathit{\kappa }}^T=\left(\begin{array}{c}{b}_1\\ b_2\end{array}\right)$$

(1)

$$\left(\widehat{b_1},\widehat{b_2}\right)=\arg \underset{\left(b_1,b_2\right)}{\min }\left\{{\left[{\displaystyle \frac{\widehat{m_y}\left(b_1,b_2\right)-\widehat{y_{0.5}}\left(b_1,b_2\right)}{\widehat{{\sigma }_{Y\left(b_1,b_2\right)}}}}\right]}^2+{\left[\widehat{k_Y}\left(b_1,b_2\right)-3\right]}^2\right\},$$

(2)

where $b_1,b_2$ are the power exponent and the offset parameter, respectively. The latter allows z to take negative values, making it applicable to fluctuations. The parameters $\left(\widehat{b_1},\widehat{b_2}\right)$ are estimated via numerical solution of the equations ${\widehat{s}}_Y=0, {\widehat{k}}_Y=3$ where ${\widehat{s}}_Y$ and ${\widehat{k}}_Y$are, respectively, the sample skewness and kurtosis coefficient. The minimization is performed using the Nelder–Mead simplex optimization method [5].

Trans-Gaussian Kriging

Trans-Gaussian Kriging (TGK) takes into account the modified Box–Cox transformation presented in Equations (1) and (2). Assume that $Z\left(\mathit{s}\right)= \phi \left(Y\right(\mathit{s}\left)\right)$, where $Y\left(\mathit{s}\right)$ follows a multivariate Gaussian distribution, and the function $\phi \left(\cdot \right)$ is a known bijective function that is twice differentiable. Function $Y\left(\mathit{s}\right)$ is defined as an intrinsically stationary SRF with mean $m_Y$ and semivariogram ${\gamma }_Y\left(\mathit{h}\right).$ For unknown $m_Y$, Ordinary Kriging ${\widehat{Y}}_{OK}\left({\mathit{s}}_0\right)=p_{OK}(Y;{\mathit{s}}_0)$ is used to predict $Y\left({\mathit{s}}_0\right)$. An estimate of $Z\left({\mathit{s}}_0\right)$ is then given by $\widehat{Z}\left({\mathit{s}}_0\right)= \phi \left({\widehat{Y}}_{OK}\left({\mathit{s}}_0\right)\right)$. However, the output ${\widehat{Z}}_{OK}\left({\mathit{s}}_0\right)$ is a biased predictor, if $\phi \left(\cdot \right)$ is a nonlinear transformation. The trans-Gaussian predictor suggests a bias correcting approximation,

$$p_{TGK}\left(Z;{\mathit{s}}_0\right)=\phi \left(p_{OK}(Y;{\mathit{s}}_0)\right)+{\displaystyle \frac{{\phi }^{″}\left({\widehat{m}}_Y\right)}{2}}\left[{\sigma }_{OK}^2(Y;{\mathit{s}}_0)-2{\mu }_Y\right],$$

(3)

where ${\widehat{m}}_Y$ is the OK estimate of $m_Y$, ${\mu }_Y$ is the Lagrange multiplier of the OK system, ${\phi }^{″}(·)$ is the second-order derivative of the transformation, and ${\sigma }_{OK}^2(Y;{\mathit{s}}_0)$ is the OK variance.

In general, TGK offers a flexible approach for modeling non-Gaussian groundwater data by transforming the original variable into a Gaussian-distributed one through a suitable, monotonic function. In this study, TGK addressed the skewness in hydraulic head data, enhancing interpolation accuracy compared to Ordinary Kriging. The approach preserved spatial structure while enabling unbiased back-transformation of estimates. Its advantage lies in handling extreme values and stabilizing variance, which are common in heterogeneous mining basins. Compared to Box–Cox transformations, TGK offers a more generalized framework that is adaptable to various distributional shapes.

Variogram Calculation and Modeling

The variogram is a core tool in geostatistics, quantifying spatial dependencies by expressing the average squared difference between paired observations as a function of their separation distance. The empirical variogram is modeled to derive parameters for interpolation. In this study, we apply the Matérn variogram model, which incorporates a smoothness parameter that enables fine-tuning of the model’s continuity and differentiability, crucial for capturing the subtle fluctuations in groundwater levels [16,17]. This model offers flexibility in spatial interpolation, which is particularly beneficial for complex hydrogeological studies. The Matérn variogram model is defined as

$$\widehat{\gamma }(\mathit{h})={\sigma }^2\left\{1-{\displaystyle \frac{2^{1-\nu }}{\Gamma \left(\nu \right)}}{\left({\displaystyle \frac{\left|\mathit{h}\right|}{\xi }}\right)}^{\nu }{K}_{\nu }\left({\displaystyle \frac{\left|\mathit{h}\right|}{\xi }}\right)\right\},$$

(4)

where $\xi >0$ is the correlation length (or range) parameter, σ² > 0 is the variance, $\Gamma (·)$, is the Gamma function, $K_{\nu }(·)$ is the modified Bessel function of the second kind, order ν, where ν is the smoothness parameter, and |h| is the Euclidean distance. For ν = 0.5, the Matérn model corresponds to the exponential, whereas when $v\to \infty$ the Gaussian model is recovered.

Spatial Model Validation

Cross-validation (LOOCV) involves partitioning the dataset into training and testing subsets to evaluate model performance. For each subgroup, a set of observed data points was excluded, and the model was recalibrated based on the remaining data. The model then predicted values at the excluded locations, allowing for a comparison between the predicted and observed groundwater levels. This leave-one-out approach helps assess the model’s predictive accuracy and robustness.

Table 1. List of cross-validation metrics used to compare the true and estimated values of the hydraulic head field.

Mean absolute error (MAE)	${\epsilon }_{\mathit{MA}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}\left|\widehat{z}\left({\mathit{s}}_i\right)-z\left({\mathit{s}}_i\right)\right|$
Bias	${\epsilon }_{\mathit{M}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}\widehat{z}\left({\mathit{s}}_i\right)-z\left({\mathit{s}}_i\right)$
Mean absolute relative error (MARE)	${\epsilon }_{\mathit{MAR}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}\left|{\displaystyle \frac{\widehat{z}\left({\mathit{s}}_i\right)-z\left({\mathit{s}}_i\right)}{z\left({\mathit{s}}_i\right)}}\right|$
Root mean square error (RMSE)	${\epsilon }_{RMS}=\sqrt{{\displaystyle \frac{1}{N}}{{\displaystyle \sum _{i=1}^N}\left[\widehat{z}\left({\mathit{s}}_i\right)-z\left({\mathit{s}}_i\right)\right]}^2}$
Linear Correlation Coefficient	$R={\displaystyle \frac{{\sum }_{i=1}^N\left[z\left({\mathit{s}}_i\right)-m_z\right]\left[\widehat{z}\left({\mathit{s}}_i\right)-m_z\right]}{\sqrt{{\sum }_{i=1}^N{\left[z\left({\mathit{s}}_i\right)-m_z\right]}^2}\sqrt{{\sum }_{i=1}^N{\left[\widehat{z}\left({\mathit{s}}_i\right)-m_z\right]}^2}}}$

presents the LOOCV metrics used in this study. In Table 1, $\widehat{z}\left({\mathit{s}}_i\right)$ and $z\left({\mathit{s}}_i\right)$ are the predicted and observed data values at point ${\mathit{s}}_i$ and N is the number of observations.

3. Trend Modeling of Hydraulic Head in Mining Basin

Often, SRFs contain a deterministic component, the trend. Thus, an SRF can be given as $Z\left(s\right)=Z^{\prime }\left(s\right)+m\left(s\right)$, where m(s) is the deterministic component and Z’(s), the fluctuations, are the stochastic component [2,21].

The trend of the hydraulic head in mining basins is strongly influenced by topographic variations, as groundwater levels tend to follow surface elevations. Incorporating topographical data from Digital Elevation Models (DEMs) has thus become standard practice in groundwater interpolation studies [7,22].

Two auxiliary variables were considered: (i) the DEM-derived uniform gradient approximation (DEM-UGA), describing the large-scale topographic control on groundwater, and (ii) the minimum Euclidean distance in 2D between each well and the mapped temporary riverbed (RD). The DEM was used both to extract local elevations and to construct a smoothed gradient representation for the trend. The temporary riverbed was digitized from hydrographic maps and validated against DEM-derived flow-accumulation lines; distances were computed using Equation (6) in the MATLAB 2023a environment [5].

This study introduces a novel trend model that integrates the RD auxiliary variable and the DEM-UGA. We identified a correlation coefficient of 0.74 between groundwater levels and proximity to the riverbed, indicating that groundwater levels are generally higher further from the river. This correlation reflects the basin’s typical hydrological behavior, where the riverbed lies at a lower elevation, causing groundwater to discharge into the river when the phreatic surface intersects the ground.

In the following, we will use standardized coordinates in the interval [0, 1] to avoid numerical instabilities. We propose the expression of Equation (5) for the trend modeling of the groundwater level (in mbsl):

$$m_Z\left(\mathit{s}\right)=a d\left(\mathit{s}\right)+\lambda DEM\left(\mathit{s}\right)+c,$$

(5)

where $a,\lambda ,c$ are coefficients of the 1st-order polynomial model, $d\left(\mathit{s}\right)$ is the minimum distance from point $s$ to the riverbed, and $DEM\left(\mathit{s}\right)$ is the local DEM value.

For the DEM component of the trend, we also use a linear approximation based on $m_{DEM}\left(\mathit{s}\right)=\mathit{g} · \mathit{s}+c_0$, where $m_{DEM}\left(\mathit{s}\right)$ is the smoothed topographic elevation, $\mathit{g}$ is the uniform gradient, and $c_0$ the reference elevation at the origin of the axes. In this case study, the river is modeled through a river curve [5]. In general, the distance of a point ${\mathit{s}}_0=(x_0,y_0)$ from the river curve is given by

$$d^2\left({\mathit{s}}_0\right)=(x_{\mathit{min},0}-x_0{)}^2+(y_{\mathit{min},0}-y_0{)}^2,$$

(6)

where ${\mathit{s}}_{\mathit{min},0}=(x_{\mathit{min},0},y_{\mathit{min},0})$ is the closest point to ${\mathit{s}}_0$ on the river curve.

The coefficients of the trend were obtained through linear regression using the Least Squares Method. The validation of the trend was performed using LOOCV as described in Section Spatial Model Validation.

4. Bayesian Kriging Process

The empirical Bayesian bootstrap method is employed to quantify the uncertainty of the estimations [19]. For the construction of the conditional simulations, we have selected RK method from the wider kriging family. The method used in this research belongs to the Monte Carlo simulation methods. It produces multiple realizations, ranks the prediction results and captures the range of uncertainty [23,24]. The process considers the following steps:

Step 1

First, the prior variogram parameters are utilized to produce the covariance matrix. Then, a vector of random numbers is generated from the normal distribution. This vector is multiplied with the principal matrix square root of the covariance matrix to generate the simulated values. The prior trend is then added back to the simulation.

Step 2

Estimation of the groundwater-level trend—polynomial of the same order—for the simulated realization.

Step 3

Estimation of the empirical residuals variogram and model fitting.

Step 4

Iterating the above steps N times for N simulations (N = 1000 in this research) leads to the posterior distribution of the model parameters and thus, the process replicates on average, the data mean, variance, and variogram.

Step 5

The conditional simulations are generated using RK for conditioning of the simulations created in step 4 [25,26].

Step 6

RK is then used to provide estimations of the data values in a 100 × 100 grid, leading to the distribution of the predictions. At each grid node, the cumulative distribution function (CDF) was calculated in order to obtain the median, as well as the 5% and 95% quantiles.

By applying Bayes’ theorem, prior information is updated through successive simulations to yield posterior parameter distributions. This Bayesian framework underpins the iterative RK-based simulations, ensuring that the resulting realizations capture both spatial variability and estimation uncertainty [25]. Therefore, aquifer depth and prediction uncertainty maps can be developed to present the groundwater depth distribution based on the spatial interdependence of the available data.

5. Case Study: Modeling and Results

The prediction of hydraulic head in the mining basin was conducted using multiple spatial models to identify the most accurate method for mapping groundwater levels. To evaluate model performance, we applied both trend (T) and no-trend (NT) approaches, each incorporating normalizing transformations to improve accuracy. For models including a trend, transformations were applied to the residuals, whereas in no-trend models, they were applied directly to the hydraulic head data.

5.1. Exploratory Statistics

The initial hydraulic head data exhibited mild non-Gaussian behavior, with skewness and kurtosis coefficients of 1.35 and 2.10, respectively. Statistical tests on the fluctuations of different trend models revealed similar deviations from the Gaussian distribution, necessitating normalizing transformations.

5.2. No-Trend Spatial Models (NT)

In the no-trend approach, the best variogram fit was achieved using a non-differentiable Matérn model with the following optimized parameters:

Correlation length (ξ): 300 m

Sill (σ²): 0.92

Smoothness (ν): 0.65

Cross-validation results indicated that Box–Cox ($b_1$ = 0.2, $b_2$ = 1,1) with OK provided the most accurate predictions, outperforming other methods in terms of mean absolute error (MAE). The summary of the NT model performance metrics is shown in

Table 2. NT model’s performance metrics.

Method	MAE (m)	Bias (m)	MARE (%)	RMSE (m)	R
Ordinary Kriging	5.10	0.05	19.5	6.85	0.84
Box–Cox with OK	4.90	−0.28	18.0	6.60	0.85
Mod. Box–Cox with OK	4.60	0.15	17.0	5.89	0.87
TGK	4.05	−0.24	15.0	5.64	0.89

:

5.3. Trend Spatial Models (T)

For the trend-based models, the omnidirectional experimental variogram was computed from the residuals, which were normalized using a modified Box–Cox ${(\mathrm{b}}_1$ = 2, ${\mathrm{b}}_2$ = 5) transformation. We investigated three trend options:

T-DEM-UGA: Based on a uniform-gradient approximation of the DEM.

T-RD: Using the distance from the river curve.

T-DEM-UGA-RD: A combined trend using both DEM gradient and distance from the river.

The cross-validation metrics for each trend model are presented in

Table 3. Cross-validation metrics for the tested trend models.

Model	MAE (m)	Bias (m)	MARE (%)	RMSE (m)	R
T-DEM-UGA	4.20	0.30	17.0	6.50	0.86
T-RD	4.05	−0.10	15.5	5.40	0.89
T-DEM-UGA-RD	3.80	−0.08	14.0	5.00	0.91

:

The T-DEM-UGA-RD model, which incorporates both the DEM gradient and the distance from the river, delivered the best performance among the trend models, achieving an MAE of 3.80 m. This model outperformed all other models, reducing the prediction error on average by approximately 25% compared to Ordinary Kriging without trends.

5.4. Optimal Model Selection and Mapping

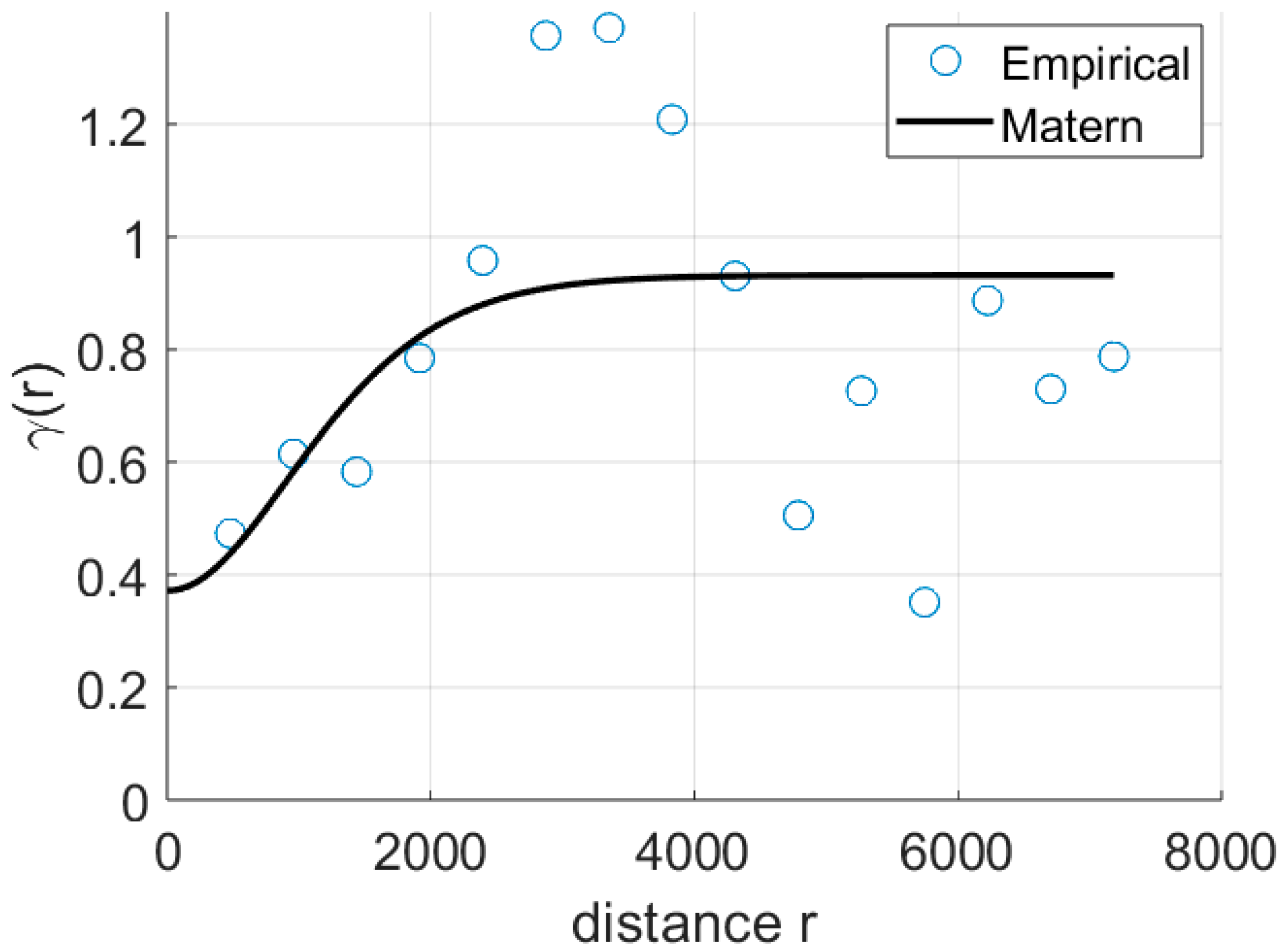
Based on the results presented in Table 3, the T-DEM-UGA-RD model was selected as the optimal spatial model. Utilizing this model, we predicted the groundwater level on a 100 × 100 grid. Estimates were restricted to points within the convex hull of sampling locations to ensure reliable predictions and minimize extrapolation errors. To model the spatial variation of residuals, a Matérn variogram was used with the refined parameters.

The optimal parameters for the Matérn variogram used in the residual interpolation were:

Range (ϕ): 2779 m

Correlation length (ξ): 366 m

Variance (σ²): 0.56

Nugget effect (c₀): 0.37

Smoothness (ν): 4.30

Where Range corresponds to the correlation range (the longest pair distance at which we consider the points correlated), and correlation length is the normalizing factor in the Matérn model. The sill is the sum of the variance and nugget.

The corresponding Matérn variogram is shown in Figure 2. As shown in Figure 1, the area has three mines, located 3–4 km from each other. The instabilities of the empirical variogram at approximately 3500 m correspond well to this distance, reflecting the change in pairs that corresponds to different mines.

A contour map of the predicted water levels was created, revealing areas of elevated groundwater levels in proximity to the river. A Bayesian uncertainty map indicated higher uncertainty levels at locations further from the sampling points.

This trend-based interpolation approach offers an enhanced method for predicting hydraulic head in mining basins, which is crucial for effective groundwater management in regions with complex topographical and hydrological conditions.

5.5. Optimal Model Results

The predicted groundwater levels (Figure 3), visualized as contour maps, revealed notable spatial patterns, particularly higher groundwater levels at locations farther from the river. These areas align with expected hydrological behavior, where groundwater tends to accumulate at elevations removed from direct drainage into the riverbed.

Additionally, a Bayesian kriging uncertainty map was generated to illustrate the confidence levels in predictions across the study area. The highest uncertainty values were found in locations further from sampling points, as expected, highlighting areas where additional sampling could improve model accuracy. This spatial uncertainty analysis offers crucial insights into targeted groundwater management efforts, highlighting where model reliability is stronger and where supplemental data collection could improve accuracy (Figure 4).

6. Discussion of Spatial Patterns

The spatial modeling of groundwater levels using the T-DEM-UGA-RD model revealed key insights into the spatial distribution and variation of groundwater levels within the mining basin. By incorporating both topographic elevation and distance from the river as trend variables, this model achieved a significant reduction in mean absolute error (MAE) to 3.80 m, representing a notable improvement over simpler models that exclude these auxiliary factors. This accuracy enhancement provides a more robust and reliable depiction of groundwater distribution, which is essential for informed groundwater management in the basin and agrees with recent studies in the area [14,21].

The observed spatial patterns of groundwater levels are closely aligned with the basin’s hydrological characteristics. Higher groundwater levels were generally found further from the river, which aligns with the natural tendency for groundwater to discharge toward lower elevations, such as the riverbed. This correlation was quantitatively supported, with a coefficient of 0.74 between groundwater levels and distance from the river, underscoring the importance of incorporating river proximity as an auxiliary variable in spatial trend modeling. The Matérn variogram was selected, as it is empirically proven to support non-Euclidean distances for certain values of the smoothness factor ν [27]. For the examined dataset, Matérn captured adequately the spatial correlations.

Bayesian kriging analysis supports more accurate spatial modeling by highlighting higher-reliability areas with significant prediction uncertainty [28]. As expected, high uncertainty is encountered in regions with sparse sampling or in areas distant from sampling locations. This spatial uncertainty map serves as a valuable tool for planning future monitoring efforts, suggesting that additional sampling in high-uncertainty zones could improve model reliability. By integrating both trend modeling and uncertainty analysis, this approach offers a comprehensive framework for groundwater assessment, supporting precise and proactive management of vulnerable areas within the basin.

7. Conclusions

This study developed an advanced spatial model for predicting groundwater levels in a mining basin, integrating topographic and hydrological variables to improve model accuracy and reliability. By incorporating both Digital Elevation Model (DEM) data and distance from a nearby river as trend variables, the T-DEM-UGA-RD model achieved a substantial improvement of the MAE to 3.80 m, a notable improvement over simpler kriging approaches. This improved model offers a more accurate spatial representation of groundwater distribution, a crucial asset for effective resource management in mining areas where groundwater levels are variable and data are often scarce.

The integration of river proximity as an auxiliary variable was particularly effective in capturing hydrological behavior within the basin, with the distance-to-river variable correlating well with observed groundwater levels. This enhanced model accurately reflects the tendency of groundwater to accumulate at higher elevations and to drain toward the riverbed, aligning with the natural topography and hydrological dynamics of the area.

Additionally, the Bayesian kriging approach enabled the explicit quantification of prediction uncertainty across the study area. High uncertainty levels were observed in locations farther from the sampling points, suggesting that these areas are priorities for future monitoring to enhance model robustness. By targeting these high-uncertainty zones for future data collection, resource managers can improve model robustness and better safeguard vulnerable groundwater reserves.

Overall, this research provides a framework for groundwater modeling in complex hydrogeological settings, demonstrating the value of integrating topographical and hydrological variables with Bayesian methods. The insights from this model can guide targeted groundwater management efforts, particularly in identifying vulnerable areas where resource management can be prioritized. Future studies should consider expanding monitoring networks in high-uncertainty regions to further refine predictions, ensuring sustainable groundwater management within the mining basin. Furthermore, spatiotemporal covariance models will be used, and the predictions will be compared with those of Deep Learning Methods.