1. Introduction
Landslides in mountain environments are a common feature all over the world, and in some areas characterized by high urbanization (like in the European Alps), infrastructure and people are often at risk. When dealing with slow and wide phenomena, as in the case of Deep Seated Gravitative Slope Deformations (DSGSDs) [
1], monitoring is often the only available instrument for risk management. In recent decades, both onsite and remote monitoring systems, coupled with geological and geomorphological knowledge as well as with numerical modeling, have significantly improved the capability of mitigating the landslide risk [
2]. In addition to these improvements, in forested and steep mountain areas, many instrumental approaches are impeded, and data series are often limited in time and space. In fact, forest cover often impedes long-term topographic landslide monitoring because of the difficulties due to tree shading masking the targets [
3]. Moreover, steep slopes make it difficult to install geotechnical instrumentation as well as to preserve the ground accuracy of satellite images and InSAR data [
4]. To overcome the limitations of instrumental monitoring especially in these areas and to provide additional information also in any more accessible, forested landslides, a strategic low-cost and low-impact alternative exists, as these landslides may be investigated through a systematic analysis of trees’ external and internal growth anomalies related to the disturbance of geomorphic processes. Analyzing the spatial distribution of external anomalies of trees (dendrometric data) or analyzing annual time series of internal growth anomalies over decades or centuries and their spatial distribution (dendrogeomorphic data) [
5] may add valuable complementary information to classical instrumental monitoring. Moreover, the dendrogeomorphic approach may provide multi-decadal information on landslide activation(s) with annual resolution [
6] and also allows to perform comparisons with meteorological inputs through time, and to date and localize environmental changes that occurred in the past in the landslide body.
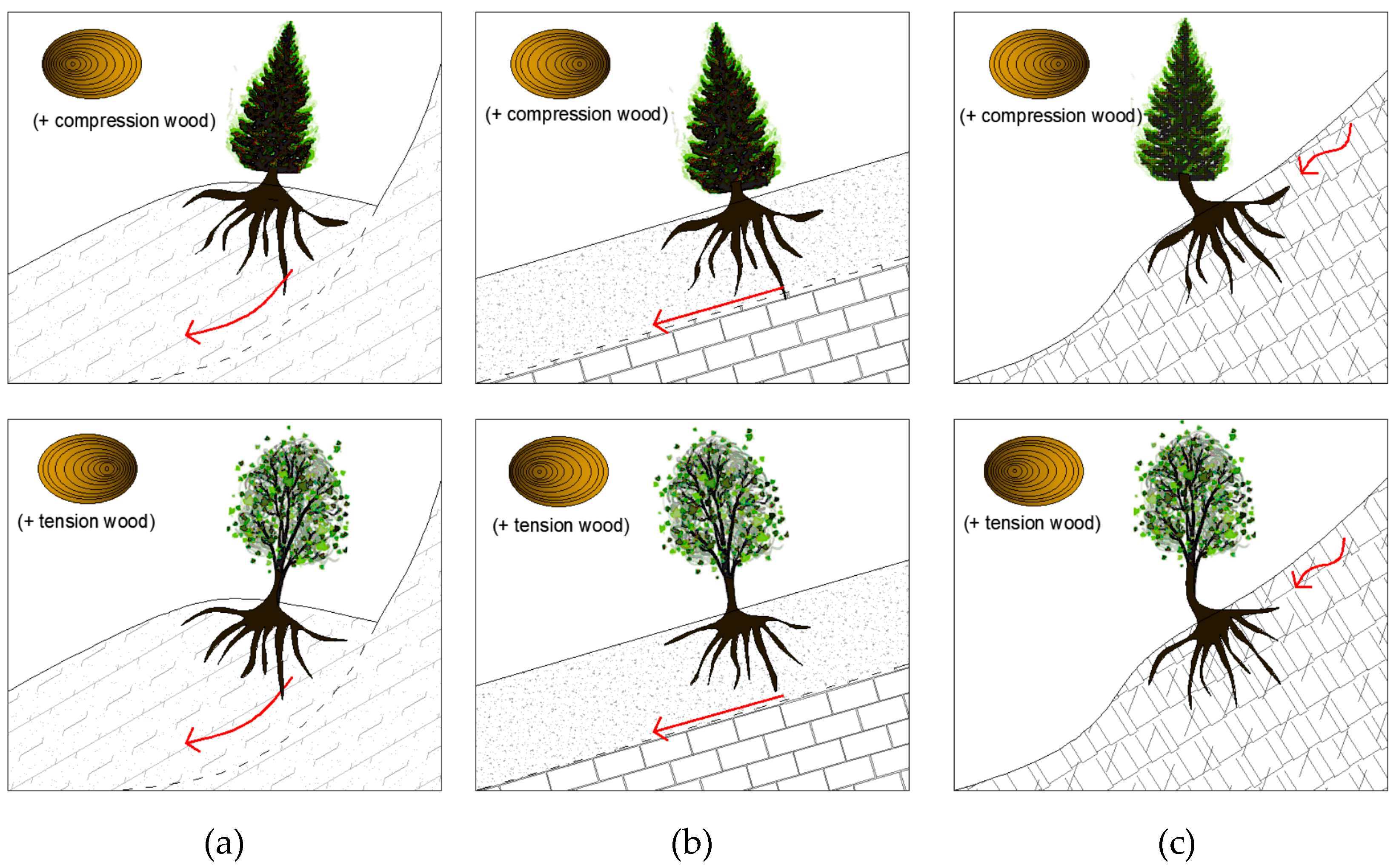
The present study aims at evaluating the potential of dendrogeomorphology for monitoring the slope dynamic in forested areas, by coupling it with a numerical modeling approach able to transform the information recorded in trees during their growth in monitoring data useful to reconstruct the stress–strain history of the slope, and therefore to define risk scenarios. In fact, dendrogeomorphology studies the tree rings for reconstructing past geomorphological events, as trees have the ability to record year by year within their structure the surface ground movements that occurred through time. Tree-ring growth anomalies, with the most common being eccentric growth, reaction wood, and abrupt growth suppression ([
7,
8,
9]), may be analysed according to the following cases:
The tilting angle can have different directions depending on the slope kinematics: in rotational sliding, the stem is titled upslope (especially close to the head scarp,
Figure 1a), whereas for planar sliding, stems are either not tilted (no eccentric growth but a growth suppression likely occurs due to root damages) or tilted downslope [
10] (
Figure 1b); if the deformation is slow enough, trees can resume their upright position, forming a peculiar J-shape at the base of the stem [
11] (
Figure 1c).
Eccentricity is an asymmetric growth of tree rings: growth develops annually, and trees may respond even to very slight tilting, and developing tree rings are wider in one direction than in the opposite direction, depending on both the slope dynamic and the tree species. Coniferous and broadleaf species show opposite directions in eccentric growth to the same geomorphic input [
12].
Reaction wood (compression wood in conifer, or tension wood in broadleaves) can originate either in the inclined side of the stem (downslope in conifers) or in the opposite side (upslope in broadleaves) as a consequence of strong mechanical stresses acting within the stem [
13].
Currently, several researchers have demonstrated that through the analysis of these growth anomalies, the following is possible:
To assess the zone of the landslide area, by identifying its perimeter as well as the most active zones [
14,
15];
To study the landslide reactivations though time, with annual resolution [
12];
To identify trigger events (i.e., by correlating the time series of anomalies with rainfall, earthquakes, or other events that may affect slope stability [
16,
17]).
In order to study the slope dynamic, and therefore the landslide evolution, other methods are commonly used, depending on the kinematics as well as the geomaterial involved in the deformative process [
18]. Among them, numerical modeling allows to simulate in 2D or 3D the behavior of the system (ground, water, and trees) taking into account in a simplified framework the different geological, hydrogeological, and vegetational issues [
19]. In general, numerical models are used to simulate the slope dynamic in complex geological settings through a system of equations with different purposes:
To predict the effects arising from a change in boundary conditions (e.g., vegetational cover, water recharge, etc.);
To analyze the influence of the different parameters affecting the behavior of a system (e.g., rock strength, root depth, etc.);
To study the pre-failure conditions in the different zones of the slope in terms of stress–strain distribution, as well as in any element modeled within or above the slope.
In this context, finite difference and finite element methods are useful tools for simulating the stress–strain behavior of complex landslides [
6,
20], by focusing on relatively recent landslide conditions, and relying on geological features, geomorphological evidence, and monitoring data usually gathered over some months or years of instrumental analysis. Generally, these methods aim at defining the landslide evolution and performing hazard assessment, but their reliability highly depends on the existing information about past events for the model calibration. When dealing with forested landslides, changes occurring at the surface over a longer time (about 50–100 years) could be an important factor to be included in these models. In fact, dendrogeomorphological data can supply long-term baseline data on landslide activity, allowing to define a possible temporality of past events as well as to delimit the affected areas. In spite of that, the possibility of incorporating in the numerical model the interaction with the vegetation cover (both in terms of roots within the ground and stem above it) is still an under researched topic. In fact, in the international literature, some authors have introduced vegetational features into numerical modeling in terms of roots affecting soil cohesion [
21] or additional weight of trees [
22]. On the other hand, some authors have analyzed the static behavior of a single tree by means of the finite element model [
23], in which the tree strain is simulated under the effect of its self-weight and the wind, in order to forecast the failure risk of the tree, but its interactions with the slope dynamic have not been investigated, yet. Indeed, the scale of analysis is very different, as well as the aim of the simulation, and the international literature does not provide examples in which a numerical analysis of the interactions between landslide and trees has been developed, in terms of stress–strain behavior of trees.
In the present study, a parametric model of the tree-slope system was first implemented to evaluate the sensitivity of the model to different parameters of tree and then to assess the reliability of modeling results in terms of stem anomalies. Afterwards, the same modeling approach was applied to a case study (the Val Roncaglia landslide in the Italian Prealps) in order to verify the consistency of modeling results with the dendrometric and dendrochronological field data. With this aim, the dendrogeomorphological signals were compared to the results of the stress–strain numerical model to evaluate the reliability of the modeling results and identify the best monitoring and management strategy for risk mitigation.
2. Materials and Methods
The numerical modeling was carried out by using a numerical modeling software package, based on the explicit Lagrangian finite difference method (FDM); the code iteratively solves the equilibrium and constitutive equations of each cell of the modeling domain to simulate the stress–strain behavior of soil and rock in presence of structural elements and groundwater flow. The numerical model has been implemented in 2D, by assuming an elastic–plastic constitutive model with a Mohr–Coulomb failure criterion in order to describe geomaterials. The modeling was first developed with a parametrical approach, on simplified case studies, by considering different reference models:
For all the case studies, the boundary and initial conditions of the numerical model were defined as follows:
Null displacements (both vertical and horizontal) at the bottom of the modeling domain;
Null horizontal displacements along the vertical borders of the modeling domain;
Self-weight and dry conditions in the whole modeling domain.
Along the slope, the trees were defined by means of an adaptive mesh refinement, in which only the trunks were reproduced (without branches) not through structural elements (like beams in [
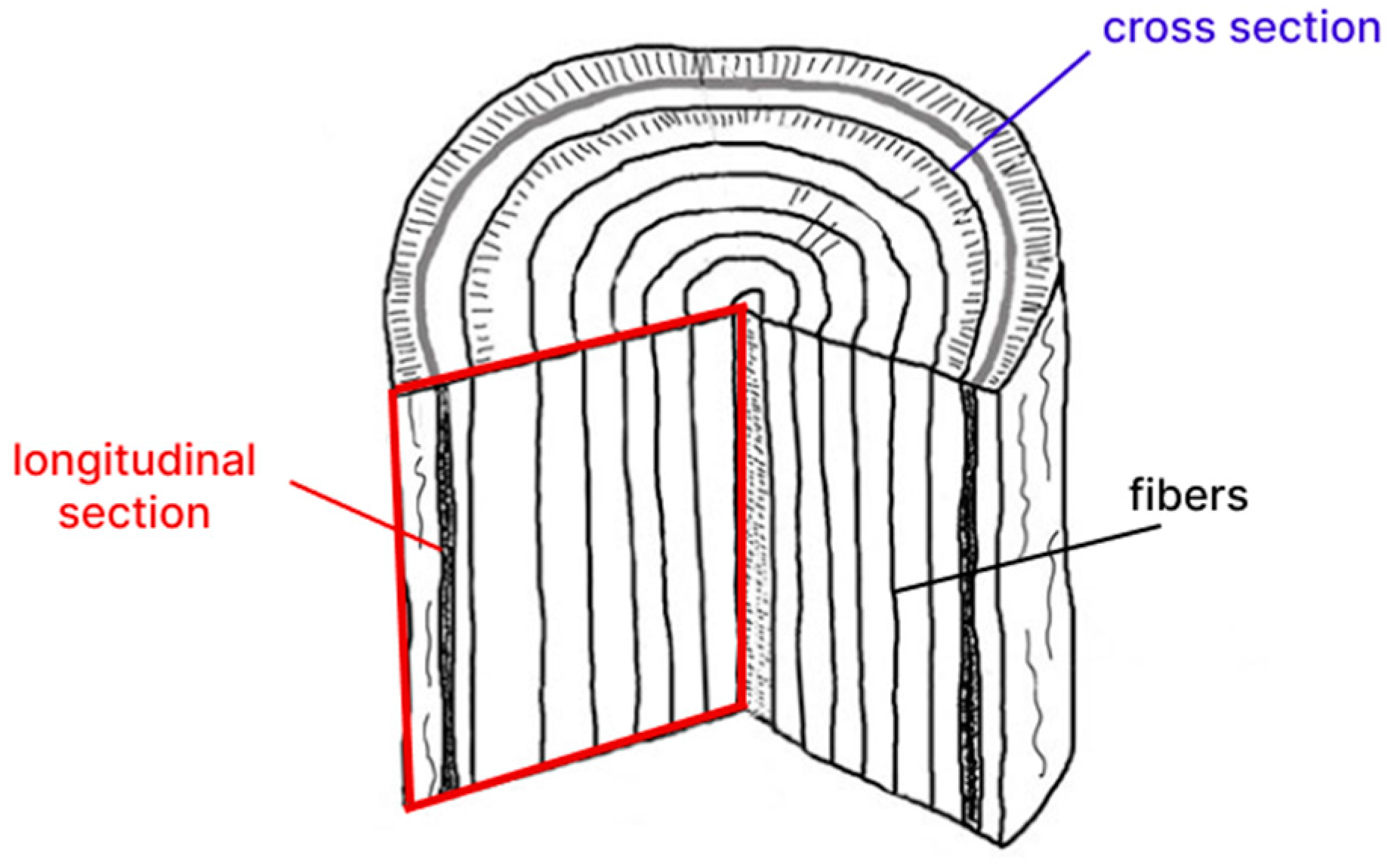
23]) but by adding finer elements to the existing mesh that reproduced the slope; in this way, the cells representing the trunks were not fixed to the ground, but they were free to deform together; moreover, no parameters describing the soil–structure interaction were needed. As the trees were implemented in the model along a longitudinal section of the stem, they were defined by using an anisotropic elastic constitutive model, able to describe the different behaviors of wood along its fibers (in the vertical section) and orthogonally to wood fibers (in the horizontal section,
Figure 2); as a consequence, the wood attributes to be added are the two moduli of elasticity (parallel and orthogonal) and the wood density; afterwards, a sensitivity analysis was carried out in order to find out the wood parameters that affect modeling results the most. In fact, even if a database of properties for several species of trees can be quite easy to find, not much data are available for green wood (which means wood having a high moisture content). Finally, the modeling approach was applied to a real case, by including data about the vegetational cover into a landslide conceptual model that had already been calibrated in a previous study [
24]. In order to analyze the behavior of the system (slope plus trees) while the failure is approaching, in the numerical modeling, a strength reduction method was used, which enabled to find out a safety factor from the stress–strain numerical simulation, and therefore to compare its results to those arising from limit equilibrium methods and stability charts regardless of the type of failure mechanism ([
25]).
2.1. Parametrical Modeling
In the parametric model, three different slope geometries were implemented to simulate different deformation conditions, both translational and rotational sliding, as well as different depths of the failure surface (
Table 1 and
Figure 3).
The modeling domains have size equal to 200 × 120 m2, with a mesh having a resolution of 0.1 m. The boundary and initial conditions applied to the parametrical models have already been described in the previous section.
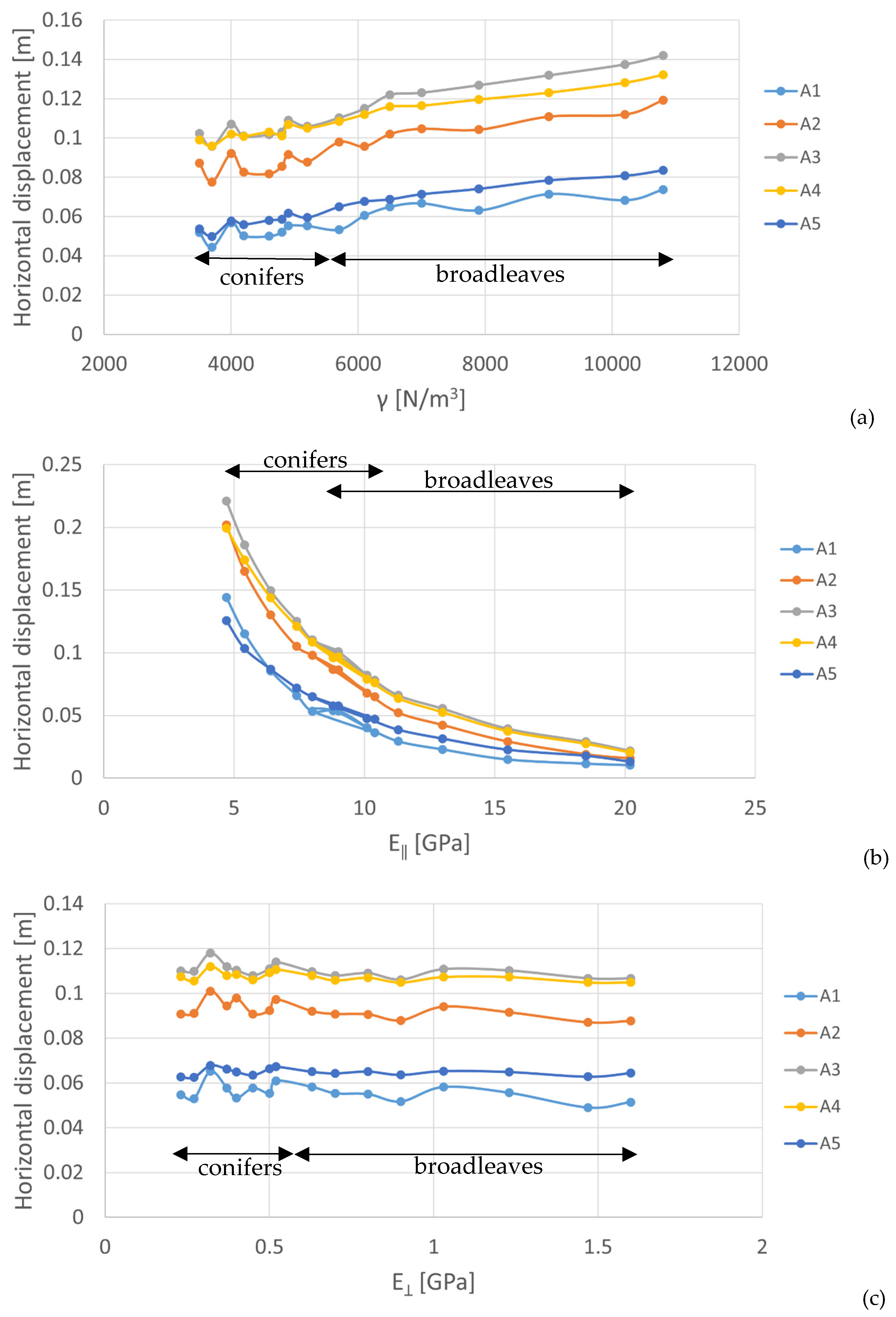
The trees were implemented considering a height equal to 2 m (outside the slope plus 1 m and within the slope for simulating the root system) and a diameter equal to 20 cm, with cells having a squared size of 10 × 10 cm. In this way, the stress–strain behavior of trees can be described at different heights of the trunk, enabling to identify and quantitively describe the following trees anomalies:
- -
The horizontal displacement at different heights, and therefore the possible J-shape of the trunk as well as the tilting angle;
- -
The internal stress state of the tree, both on the mountainside and valleyside of the trunk itself, which can be put in relation with growth disturbances.
All these parameters about trees anomalies (displacement, tilting angle, shape of the trunk, and internal stress state) were analyzed and compared in order to find out differences related to the position of trees along the slope and the possible correlation with the slope kinematics. With this aim, for geomaterials, the parameters describing the elastic–plastic model and the Mohr–Coulomb failure criterion (
Table 1) have been calibrated in order to reproduce the corresponding desired failure conditions (rotational or translational sliding).
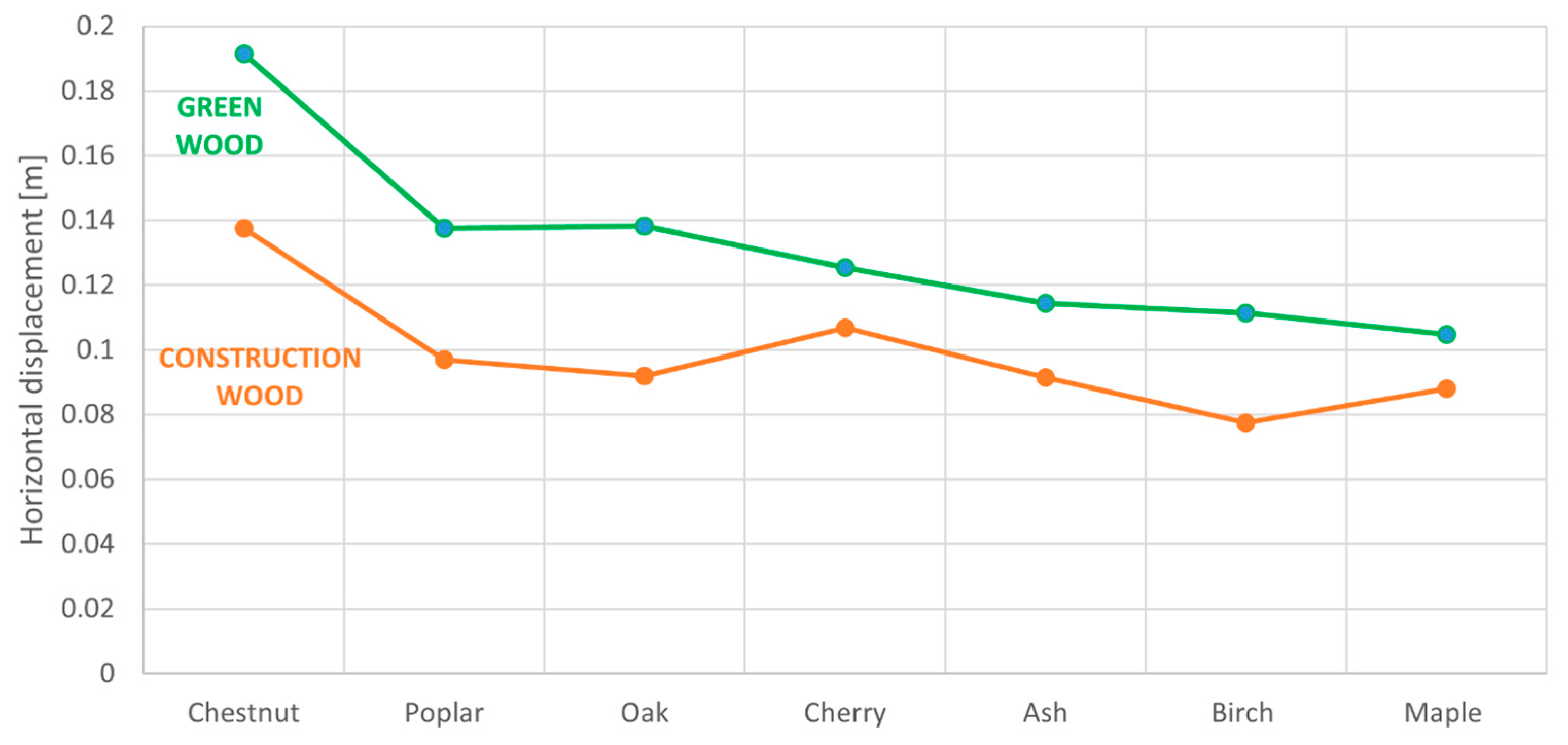
The mechanical parameters for the trees were selected based on the technical standards for construction [
26] according to two types of wood (conifers and broadleaves), which are the most common wood types in temperate forests. Because of the difficulty of properly estimating these mechanical parameters, a sensitivity analysis was carried out on them by considering the increase in the water moisture typical of the green wood, which involves a decrease in the unit weight as well as in its stiffness [
27].
2.2. Case Study of the Val Roncaglia Landslide
The Val Roncaglia landslide (Lat. 45°50′21.47″ N; Long. 10°9′38.56″ E) is located on the left side of the lower Valle Camonica (Italian Prealps, Lombardy region). This large landslide belongs to a quite complex geomorphological setting, which can be classified as a Deep Seated Gravitative Slope Deformation, with active zones at the foot of the slope (
Figure 4). The whole area is densely forested from chestnut trees (
Castanea sativa Mill.) traditionally managed as old coppice stands, mixed with broadleaves trees (up to the sub-mountain belt margin) such as ash, gray alder, birch, linden, and oaks.
Figure 4.
(
a) Geomorphological and geological map of the study area (based on data from [
28,
29]). The upper right box shows its location in Lombardy (Northern Italy). The black line A-A’ represents the cross-section line (
Figure 5), whereas the yellow rectangle identifies the sampling area for the dendrometric and dendrochronological analyses. Below the map, some photographs of the site are shown: (
b) an overview of the lowest part of the slope (photo of G.L. taken from Pian Camuno in the southeast direction in April 2021), and (
c,
d) details of the chestnut trees growing in the active portion of the slope (April 2021).
Figure 4.
(
a) Geomorphological and geological map of the study area (based on data from [
28,
29]). The upper right box shows its location in Lombardy (Northern Italy). The black line A-A’ represents the cross-section line (
Figure 5), whereas the yellow rectangle identifies the sampling area for the dendrometric and dendrochronological analyses. Below the map, some photographs of the site are shown: (
b) an overview of the lowest part of the slope (photo of G.L. taken from Pian Camuno in the southeast direction in April 2021), and (
c,
d) details of the chestnut trees growing in the active portion of the slope (April 2021).
The conceptual model of the landslide had already been defined in a previous study, based on the geological, geotechnical, hydrogeological, and the available monitoring data [
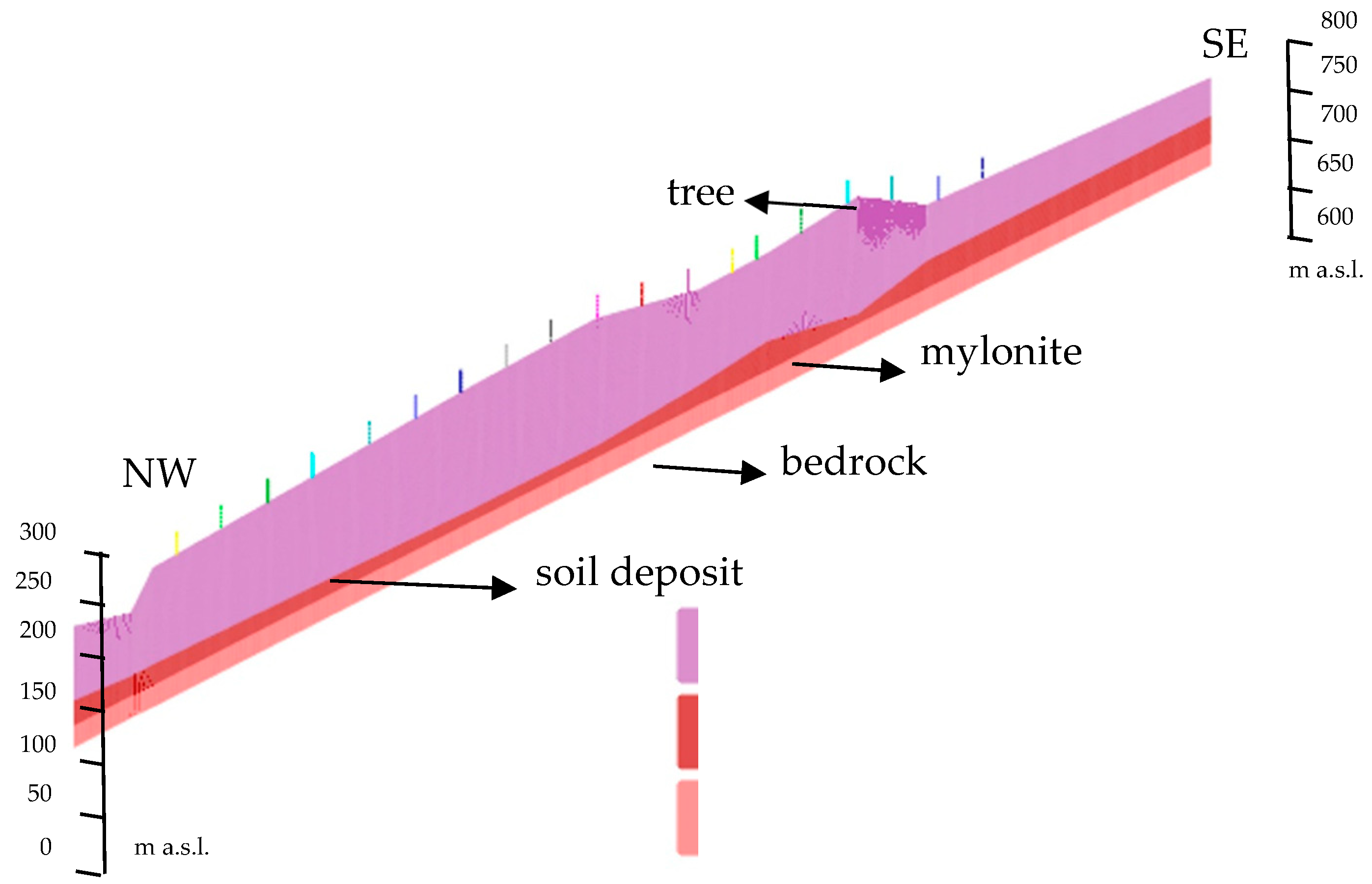
24]. From the geological point of view, the bedrock is mainly composed of micaschists, with mylonitic zones 15–30 m thick, covered by soil deposits for a thickness of about 50 m (
Figure 5). Many active, quiescent, and inactive head scarps can be identified all along the forested slope: the inactive ones are mainly located at the highest altitude (from 800 to 1000 m a.s.l.), whereas the active ones are concentrated at a lower altitude (between 400 and 700 m a.s.l.); the latter shows significantly slow deformations, with periodic reactivations, among which the most recent one occurred in 2010; after 2010, a monitoring system has been designed, with inclinometric and piezometric probes providing displacement of about 10 mm/year and water table changes of lower than 1 m (data obtained from ARPA Lombardia; protocol number: arpa_mi.2022.0029708, of 25 February 2022).
The landslide conceptual model has been implemented into a numerical model, considering a modeling domain of 1 km long that comprises the whole active zone of the slope (between 250 and 800 m a.s.l.); the mesh is composed of 1000 × 110 cells having a size equal to 1 × 1 m for the slope, whereas for the trees, a higher resolution mesh equal to 20 × 20 cm was used.
In the constitutive model for geomaterials and trees, the boundary and initial conditions are the same as those in the previously described parametric modeling. The mechanical parameters of the geomaterials involved in the landslide had already been calibrated through a trial-and-error process, based on displacement data arising from the monitoring network, and more specifically from two inclinometric probes located in the most active zone of the slope till a depth of about 100 m [
24]. Results showed a quite good capability of the model in reproducing the deep multiple-sliding kinematics of the slope, even if a residual error in the depth of the sliding surface (15%) could not be solved with the available data and no evident correlation between groundwater table and slope dynamic had been pointed out [
24].
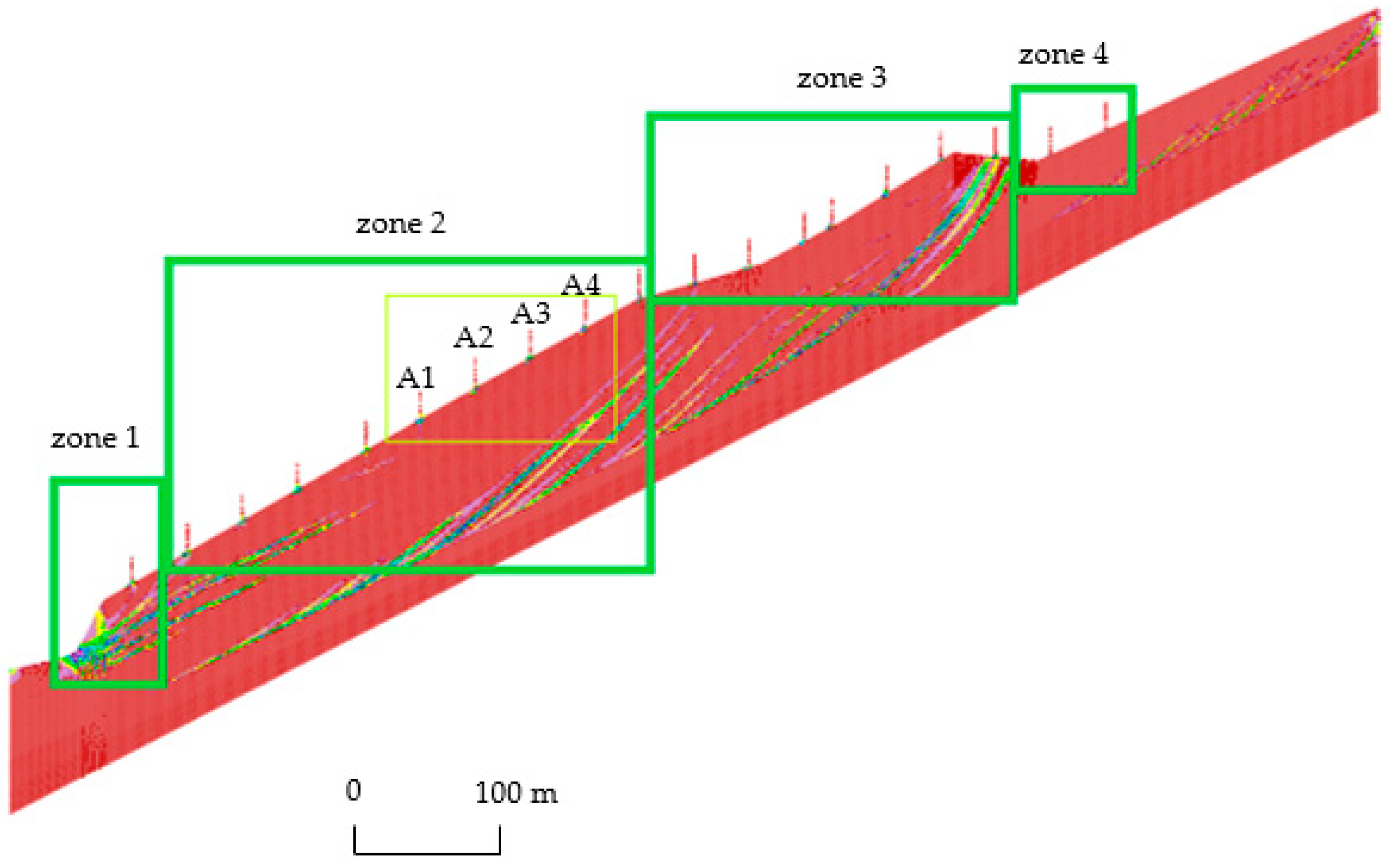
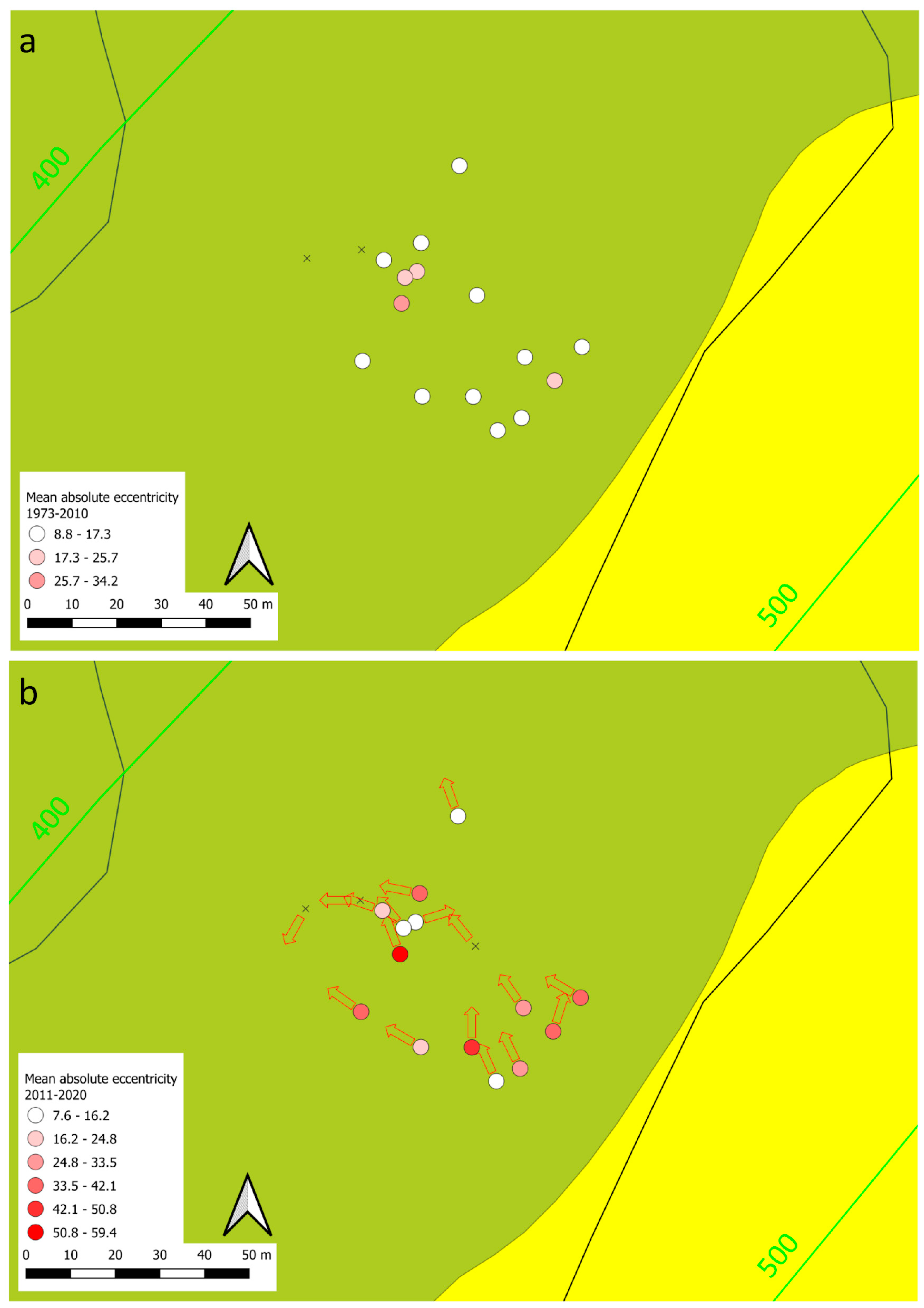
The mechanical parameters of the trees were selected based on types of wood (mainly chestnuts) and their age (
Table 2), arising from onsite dendrometric surveys. The dendrometric survey was carried out in the most active zone of the slope (altitude 400–500 m a.s.l., see
Figure 4a for location), and it involved the measurement of stem diameter (on average equal to 40 cm), external stem eccentricity, and tilting, and they were afterwards compared to the modeling results. Moreover, a dendrogeomorphological survey was performed in June and July 2021 extracting two cores (in the inclined and opposite directions) from the stems of 17 trees to reconstruct the temporal changes in tree-ring eccentricity, linked to ground displacements. Oldest-looking and most inclined, as well as J-shaped, stems were selected in the area between 400 and 500 m a.s.l., adopting an ad hoc sampling design [
30]. The samples were prepared according to standard procedures, and the tree rings were measured with a resolution of 1/100 mm using a LINTAB measurement table under a microscope (Rinntech, Germany). All growth series were visually and statistically crossdated [
31] within trees and between trees in order to check the correct dating of each tree ring. Finally, the mean absolute annual eccentricity was calculated according to the following formula [
16,
18]:
where:
Ii and Oi are the ring widths in the inclined and the opposite side of the stem, respectively, in the year i.
4. Discussion
The results obtained on simplified case studies showed that the numerical modeling can properly reproduce tilting and internal stresses of trees, by simulating different stress–strain behaviors depending on both the slope kinematics and the position of trees along the slope. For instance, in deeper rotational sliding, trees along the main body and at the foot tilt downslope, whereas close to the head scarp trees tilt upslope (
Figure 12). As far as the internal stress conditions are concerned, for rotational sliding, there is a tensile stress downslope and a compressive one upslope (
Figure 13), whereas for planal sliding an opposite stress distribution occurs (tensile stress upslope and compressive one downslope).
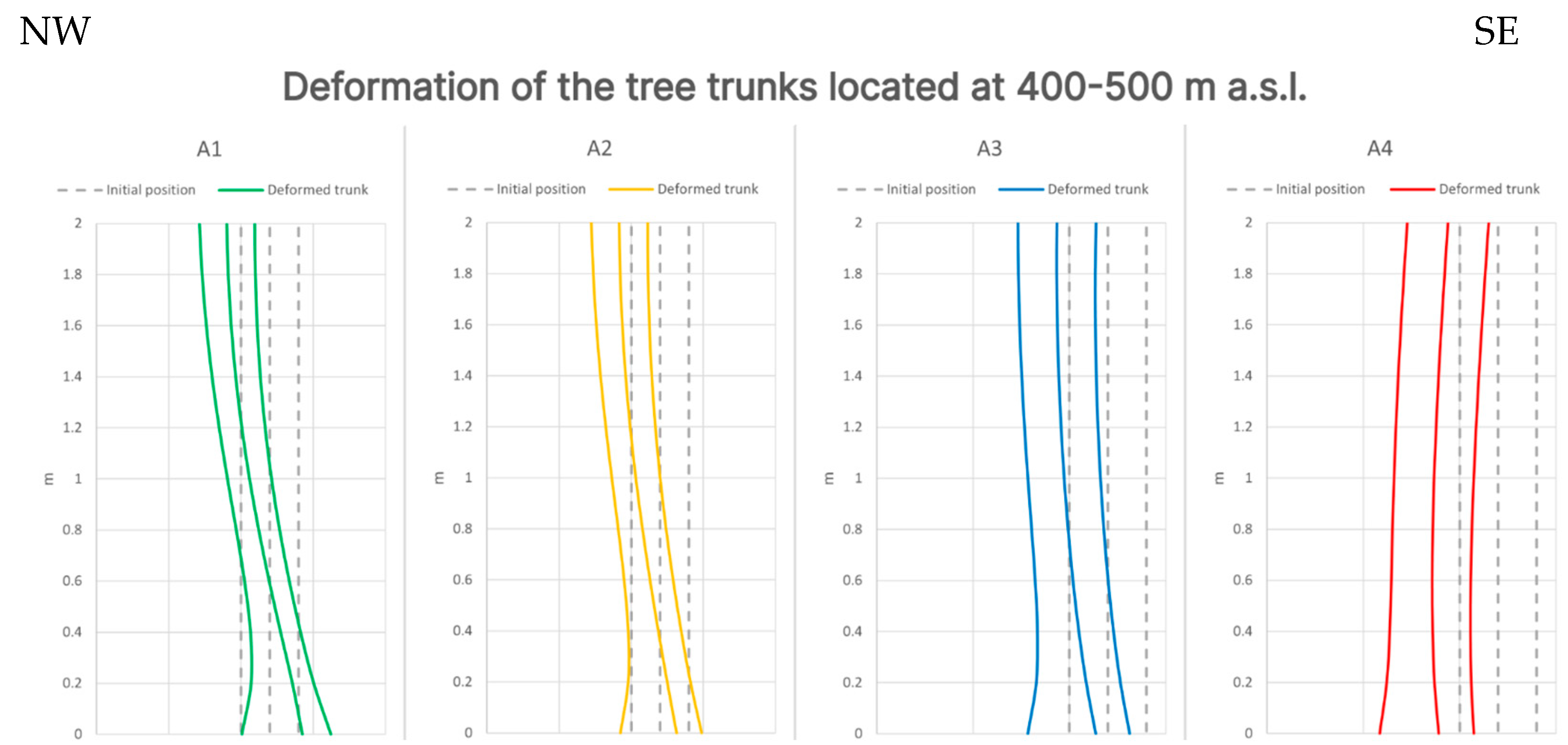
The available data on the Val Roncaglia landslide confirmed the potential of numerical models in simulating stem anomalies. In fact, stem anomalies simulated by the numerical model were compared to the observed ones, gathered during the onsite dendrometric survey (
Supplementary Materials), showing a good agreement for the tilting angles, as well as for the J-shape feature of some trees (
Figure 14 and
Table 3).
So far, no back analysis has been conducted on tree behavior due to insufficient data availability, as internal stress state and tilting angle of trunks at different time intervals would be required, involving observation periods of trees much longer than those currently available. In spite of this limitation, modeling results and their comparison to observed data allowed to identify the following opportunities arising from the proposed approach:
It is possible to effectively simulate tilting angles and internal stresses of trees, as well as their trend when failure is approaching;
The different responses of trees along the slope can provide insights about the landslide kinematics and zoning;
Multiple sliding surfaces can be detected based on stem anomalies;
Tree-ring growth anomalies such as reaction wood and eccentricity can be inferred based on numerical results on tilting and internal stresses.
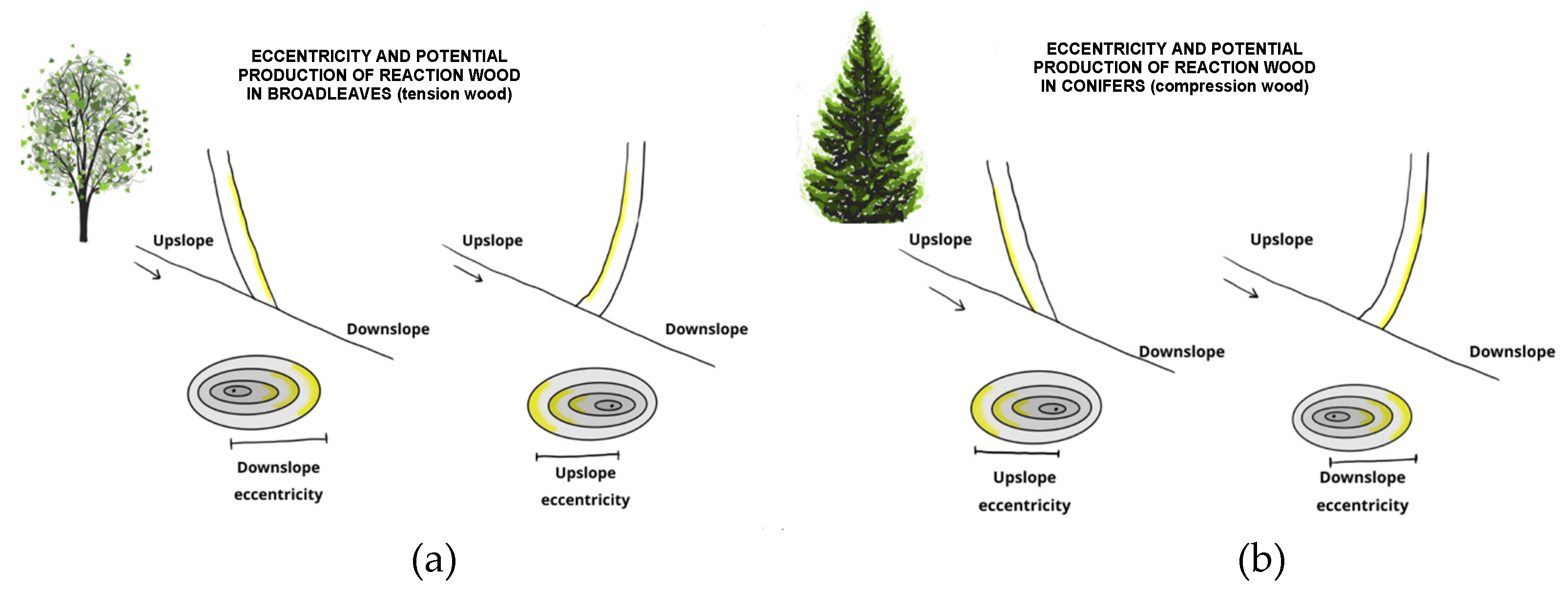
As far as the very last point is concerned, based on modeling results, a relation between tilting and internal stress simulated by the numerical model and the other tree-ring growth anomalies (eccentricity and potential production of reaction wood) can be defined (
Figure 15). In fact, there is a relationship between tilting and eccentricity, as well as between strong internal stresses and possible reaction wood production [
9,
10,
32]. For example, for broadleaves species, the trees that tilted upslope develop a downslope eccentricity exactly on the same side where tensile stress is simulated; since reaction (tension) wood in broadleaves develops where a strong tensile stress is acting, we hypothesize that the contemporary occurrence of eccentricity and strong internal tensile stresses can bring about the development of reaction wood.
These results can be applied for two main purposes. First, the numerical model provides a preliminary assessment of the behavior of tree stems, therefore facilitating the planning of a subsequent dendrometric survey. For example, for the Val Roncaglia landslide, the numerical model allowed to identify a reference site, where the stems are modeled as undisturbed, at altitudes higher than 700 m a.s.l. Moreover, trees aged 47 ± 10 years allowed to extend back in time the year-by-year eccentricity analysis up to the 1970s. Therefore, dendrometric data of stems can supply information for the numerical model calibration, even with this aim, a correlation between eccentric growth and tilting angle is required, in order to integrate the evolutive process of tree tilting simulated by the numerical model with the time series of eccentricity representative of the landslide evolution through time.
This kind of integrated model, able to describe the evolution in time of the tree-slope system, presents valuable opportunities for improving landslide monitoring and risk management strategies. In fact, it enhances the understanding of the slope dynamic: the model can be used to simulate various scenarios (involving factors like rainfall intensity and vegetation cover changes), and the integration with dendrogeomorphological data would provide monitoring data correlated to the approaching of critical conditions, even where geotechnic or topographic monitoring is not applicable due to forest cover or socioeconomic conditions. This knowledge can be used to identify areas susceptible to landslides to a wider extent than the modeled one, by considering the presence of specific conditions which comprise not only geological and geomorphological evidence (i.e., large-scale slope stability assessment methods, like geomechanical classifications or kinematic analysis [
33]) but also vegetational indices, therefore allowing the identification of landslide hotspots even in very large and relatively remote areas.
Moreover, because of its ability to replicate observed stem anomalies, the integrated modeling approach could allow the development of early warning indicators by analyzing the model response to different triggering factors, specific patterns in stem anomalies preceding actual landslide events could be identified, and these patterns could then be translated into quasi real-time monitoring strategies.
On the other hand, dendrometric and dendrogeomorphic approaches that could be integrated in surveying–monitoring systems are evidently limited by the presence of trees growing on landslides or in their vicinities and may present different applicability and limitations.
Dendrometric data refer to external features of trees (such as stem inclination, stem curvature, stem diameters, external eccentricity, etc.). These data if properly treated and precisely georeferenced may provide the spatial distribution of external anomalies in trees related to the landslide movements and also the information on the velocity of the movement with respect to the annual biological process of tree growth. In case of J-shaped stems, trees indicate the presence of persisting slow slope movements; in case of stems that are inclined but straight because trees could not efficiently react to inclination, trees indicate fast landslide movements or movements that occurred only recently (e.g., with respect to old and big standing trees). By analyzing the upslope or downslope inclination of stems in the different portions of the landslide body, it is possible to identify the type of movement (rotational or planar slide). Finally, the stem falling direction may be the same for all the trees in the analyzed portion of landslide or may be in different directions, indicating a uniform slope surface movement in the first case or a movement that locally presents anomalous directions (due to deposit deformations, local waviness or undulation of ground surface, trenches, etc.) in the second case. There are no geographic limitations for this approach from equatorial forests to sub-boreal environments. Finally, the dendrometric analysis may also indicate from where to sample trees for more efficient dendrogeomorphic reconstructions.
Dendrogeomorphic data are by definition related to dating and spatializing the geomorphic events through time. This approach is limited to regions with contrasted climate, where trees form a tree ring each year, and it is not applicable to equatorial forests. Where applicable, from subtropical to mid and high latitudes, up to the boreal tree line, this approach, although always limited by tree age, creates the opportunity to analyze with annual resolution decadal to centennial time series of growth anomalies related to landslide surface movements. Tree-ring anomalies such as eccentric growth, compression or tension wood (depending on tree species), abrupt growth suppressions, and traumatic resin ducts may all be dated to a calendar year, therefore dating geomorphic events through time and space. When dealing with time series, it is then possible to evaluate trends in tree-ring anomalies, evaluate correlations with meteorological inputs and climatic trends, and evaluate the correspondences with environmental changes that occurred on or close to the landslide body (e.g., a load increase and changes in surface water distribution) or underground (e.g., tunneling and changes in underground waters).
Finally, in spite of many opportunities offered by dendrogeomorphology for monitoring landslide processes and developing multi-decadal reconstructions of landslide movements, the approach proposed here is still affected by some limitations, mainly arising from the simplifications in modeling trees, and are given below:
- -
Canopy was not considered, even if it can affect the acting load, both in terms of weight and because of the effect of wind;
- -
Roots were considered in terms of a single anchoring (1 m in depth), but so far, no branches were modeled, which may affect the stem reaction;
- -
The elastic modulus of wood depends on the age of trees, which at present was not considered, and it can change because of the growth of reaction wood, therefore affecting the stem behavior; this parameter would require a calibration (carried out based on dendrochronological data) in order to ensure the reliability of modeling for the predictive analysis of landslide hazard.
These breakthrough issues will be investigated in future research in order to achieve a comprehensive modeling of the interactions between slope dynamic and dendrogeomorphology.
5. Conclusions
The present study is the first attempt to integrate tree responses into stress–strain numerical models at the slope scale. Even if the research still needs significant insights (i.e., the influence of branches and roots, wind action on canopy, biomechanical considerations, etc.), this effort can effectively improve knowledge and therefore risk management in forested landslide-prone areas. In fact, nowadays, land management is a matter of increasing relevance, especially in mountain areas that are often affected by unavoidable geomorphological hazards, and the related risk has to be managed.
Once the reliability of the proposed low-cost approach for landslide monitoring has been confirmed at the local scale, its application could be extended to wider scales (regional, national and even international), thus improving prediction, prevention and mitigation strategies for geomorphological hazard in forested areas and contributing to risk mitigation to a broad extent.
In conclusion, the study provides the first interdisciplinary insight in the numerical modeling of above and below ground interactions, leading to the possibility of exploiting trees in order to investigate landslide processes at a multi-decadal scale. In fact, the proposed use of dendrochronological data for model calibration, particularly regarding tree tilt and eccentricity, is a promising advancement in landslide risk management, as the long historical data arising from dendrogeomorphology integrated into the numerical model could provide a more comprehensive representation of the slope response to past triggering events. For example, for the Val Roncaglia landslide, where trees aged 47 ± 10 years, the integrated numerical model allowed to extend back in time the year-by-year eccentricity analysis up to the 1970s, in order to identify the triggering events of past landslides for which no instrumental monitoring data are available. Moreover, the integrated model could be used to predict future behavior under similar conditions and therefore design a possible early-warning system. Based on the obtained preliminary results, further analysis will be carried out in collaboration with different scientific disciplines to implement a methodology for assessing and managing landslide hazard in forested slopes, by taking into account data availability and interpretation challenges.