Abstract
Bathymetry data is indispensable for a variety of aquatic field studies and benthic resource inventories. Determining water depth can be accomplished through an echo sounding system or remote estimation utilizing space-borne and air-borne data across diverse environments, such as lakes, rivers, seas, or lagoons. Despite being a common option for bathymetry mapping, the use of satellite imagery faces challenges due to the complex inherent optical properties of water bodies (e.g., turbid water), satellite spatial resolution limitations, and constraints in the performance of retrieval models. This study focuses on advancing the remote sensing based method by harnessing the non-linear learning capabilities of the machine learning (ML) model, employing advanced feature selection through a meta-heuristic algorithm, and using image extraction techniques (i.e., band ratio, gray scale morphological operation, and morphological multi-scale decomposition). Herein, we validate the predictive capabilities of six ML models: Random Forest (RF), Support Vector Machine (SVM), CatBoost (CB), Extreme Gradient Boost (XGB), Light Gradient Boosting Machine (LGBM), and KTBoost (KTB) models, both with and without the application of meta-heuristic optimization (i.e., Dragon Fly, Particle Swarm Optimization, and Grey Wolf Optimization), to accurately ascertain water depth. This is achieved using a diverse input dataset derived from multi-spectral Landsat 9 imagery captured on a cloud-free day (19 September 2023) in a shallow, turbid lagoon. Our findings indicate the superior performance of LGBM coupled with Particle Swamp Optimization (R2 = 0.908, RMSE = 0.31 m), affirming the consistency and reliability of the feature extraction and selection-based framework, while offering novel insights into the expansion of bathymetric mapping in complex aquatic environments.
1. Introduction
Bathymetry mapping, the measurement and study of underwater depth, is critical for various applications, such as marine navigation, coastal management, the monitoring of environmental and aquatic resources, and hydrographic scanning [1,2]. Field water depth collection and further data processing have recently been carried out using the common ship-, air-, and space-borne approaches [3]. The former uses single and multi-beam echo sounding systems [3,4] to gather accurate and timely water depth datasets. Multi-beam-based equipment transmits multiple, simultaneous sonar beams to collect depth data across a wide scope and in different directions, while a single-beam sonar provides the measured depth at points along the scanning line [5]. Despite the high accuracy of field data measurement, these approaches are costly in operation and timely in field collection [3,6], leading to a gap in bathymetry map data in several regions [1,7]. The remote estimation of biological and physical parameters using satellite images has become essential to a variety of research domains in recent decades [8]. This approach is cost-effective compared to other survey techniques, is a well-developed sensing technology, is easy to integrate with artificial intelligence (AI) models, and is accurate in thematic mapping [9]. More importantly, remote sensing-based mapping requires only a limited number of field data points to train and validate the retrieval models, which confers great advantages, such as long-term and wide geographical observation, very low cost, reliability, and flexibility in retrieval computation. Hence, the use of remotely based approaches is becoming more popular for bathymetry mapping with a special focus on air-borne (e.g., UAV image [10], air-borne LiDAR [11]) and space-borne datasets, such as LiDAR data (e.g., IceSat-2 [12] and satellite images (e.g., Landsat, Sentinel, WorldView [13,14,15,16], Pléiades [17], SPOT [18], and Planet [19]). Of the satellite sensors in operation, Landsat is a common remotely sensed dataset used for bathymetry mapping with different levels of success and certainty. This satellite has been operating since 1972 at a spatial resolution of 30 m with an 8-day temporal coverage [20,21], which has increased the number of available Landsat images worldwide and has made it a valuable data source for any long-run temporal mapping projects. Landsat 9 inherits the successful design of Landsat 8 with a significant improvement in radiometric resolution of the OLI-2 (14 bits compared to the 12 bits of Landsat 8) and in straight light reduction, which enables a stronger detection of shade numbers and more accurate atmospheric correction [21]. Despite this, we have observed a very limited number of studies [22] that leverage the state-of-the-art Landsat 9 for water depth estimation.
Observing with other sensors in the Landsat family, retrieval models for Landsat images of shallow and clear coastal and oceanic regions have been developed using traditional linear band ratio approaches [19,23,24], while other studies included band ratios together with machine learning (ML) models - a modern and advanced approach for non-linear data learning and over/underfit avoidance [25] using Support Vector Machine (SVM) [26], Neural Network (NN), Random Forest (RF), Extreme Gradient Boost (XGB), NN, and deep learning Convolution Neural Network (CNN) [27]. Given the optical properties of clear coastal sites, the accuracy (R2) was observed to range between 0.85 and 0.95. Fewer studies were found for bathymetry mapping in turbid water (i.e., rivers and lagoons) using Landsat imagery. We found an optimal band ratio approach coupled with Landsat 9 [22] and a fused model of Adaboost and XGB (Adaboost-XGB) integrated into Landsat 8 [28] to derive the depth map in turbid water, all of which enhanced but varied the model confidence to R2 = 0.86 and 0.97, respectively. Liang et al. 2024 [28] implemented the fused Adaboost-XGB in a mixed area of clear and turbid water, while Niroumand-Jadidi et al. 2021 [22] deployed the retrieval model in different turbidity conditions but with a large variation in the coefficient of determination (0.44 - 0.86), leaving uncertainty in estimated depth in shallow and turbid waters. This accuracy variation may be attributed to the limited number of input features (i.e., only original bands and band ratios) used in the published models, leaving a gap where popular image feature extraction is not utilized [29], such as gray scale morphological operation (GSMO) and morphological multi-scale decomposition (MMSD), to improve the accuracy using multi-dimensional estimation models.
On the other hand, the designed framework for bathymetry retrieval assumed a similar contribution of the input bands, and a regression approach was deployed with a lower concentration in feature selection, leading to important variables being overlooked and the loss in retrieval accuracy improvement. In this domain, different techniques have been adapted for several optimization problems in different domains (e.g., meta-heuristic optimization using a natural behavior-based algorithm) [30,31,32]; however, we found no studies that applied these methods to optimize the input features for bathymetry mapping.
Given the gaps identified in the literature, this study aims to develop a general but advanced remote sensing-based method for bathymetry mapping in shallow and turbid water. We developed a novel approach using the feature extraction GSMO and MMSD to create the diverse input variables extracted from Landsat 9 imagery coupled with meta-heuristic-based feature selection to select the most important features feeding the retrieval models. We conducted a comparison of the performance of a wide range of ML models, including Random Forest (RF), Support Vector Machine (SVM), Extreme Gradient Boost (XGB), CatBoost (CB), Light Gradient Boosting Machine (LGBM), and the new candidate KTBoost (KTB) for water depth estimation in a turbid lagoon (Sam Chuon-Ha Trung lagoon, Vietnam) from 53 variables attributed to original bands, band ratios, GSMO, and MMSD image extraction. The best model was then combined with state-of-the-art meta-heuristic algorithms (i.e., Dragon Fly (DF), Particle Swamp Optimization (PSO), and Grey Wolf Optimization (GWO)) to improve the certainty of depth retrieval in the study site. The objectives of this study were to (i) validate the performance of Landsat 9 imagery; (ii) compare the estimation capability of different ML models; and (iii) examine the feature selection ability of meta-heuristic algorithms for the development of an efficient workflow for water depth estimation, which is comprehensive, reliable, and scalable for bathymetry mapping globally.
2. Material and Methods
The study workflow includes several processing steps for original image processing, image transformation and extraction, and image feature selection using meta-heuristic algorithms to optimize input bands for water depth estimation with ML models (Figure 1).
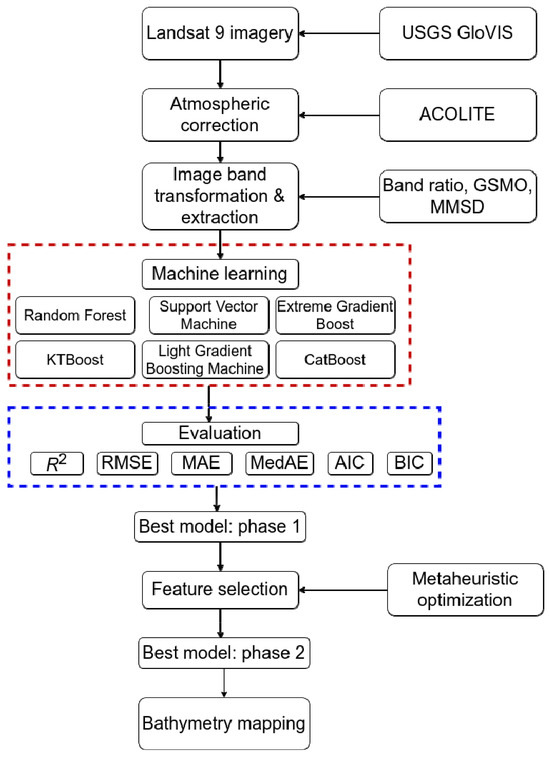
Figure 1.
Study framework (the dash lines in red and blue colors indicating the name of machine learning models and the metrics used in this study).
In the subsequent subsections, we offer detailed insights into satellite image acquisition and atmospheric correction (Section 2.2), as well as image transformation and extraction techniques employing gray scale morphological operation (GSMO) and morphological multi-scale decomposition (MMSD) methods (Section 2.2). Machine learning implementation with meta-heuristic based feature selection is elaborated in Section 2.3 using standard evaluation metrics, including the coefficient of determination (R2), root mean square error (RMSE), mean absolute error (MAE), median absolute error (MedAE), Akaike information criterion (AIC) and Bayesian information criterion (BIC).
2.1. Study Site
We selected the Sam Chuon-Ha Trung lagoon (Figure 2), located on the central coast of Thua Thien Hue province, Vietnam, as our study site. The lagoon holds vital ecological and socio-economic importance, with a high density of aquaculture ponds, fishing traps, fishing boats and tourism activity [33]. The bathymetry chart, however, is not available as either a printed bathymetry map or field measurements, making it a high-potential site for bathymetry study due to a demanding of quick and accurate method for water depth mapping for navigation, tourism and fisheries management [34]. The hydrology and water flow are characterized by tidal movements, balancing freshwater input from nearby rivers (such as the Huong) and streams, with saline intrusion from the Thuan An mouth. This dynamic interplay of brackish water creates a unique ecosystem supporting diverse flora and fauna of highly economically important aquatic species [35,36].
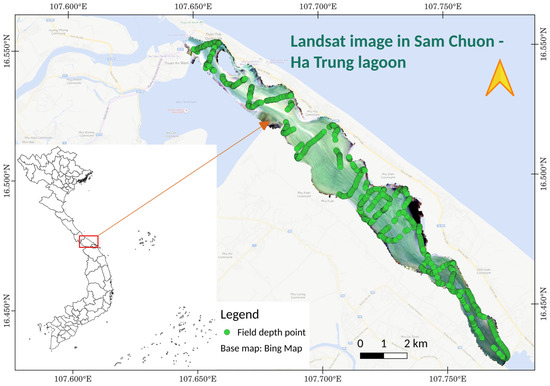
Figure 2.
Sam Chuon—Ha Trung lagoon, Vietnam, with field depth points (green circles, above), Landsat 9 image (below), and red rectangular indicates the study site in Vietnam.
The Sam Chuon-Ha Trung lagoon experiences a seasonal weather pattern impact of monsoons and tropical storms during the rainy season, which has different levels of influence on precipitation levels, wind intensity, temperature, and water dynamics, thereby affecting ecological processes. Meanwhile, meteorological conditions are typical characterized by calm winds, clear skies and stable water levels during the dry season [37].
Field Survey
We measured the water depth under clear skies, calm winds and gentle waves alongside the Sam Chuon-Ha Trung lagoon in August 2023 (Figure 2). A single beam Garmin GPSMAP 585 Plus equipment (https://www.garmin.com.my/products/onthewater/gpsmap-585-plus/, accessed on 3 February 2023) with ClearVü scanning sonar technology was used to record the water depth, deriving a dataset consisting of longitude, latitude, and water depth for each given points. This dataset fulfills the requirements for an input dataset necessary for training and validating remotely sensed models for bathymetry mapping. The team included two trained staff members to operate the boat and the Garmin equipment, recorded 1070 points within a depth range of −0.3 m to −5.52 m (Table 1).

Table 1.
Measured depth statistics.
It should be noted that, in this study, the term “bathymetry” refers to the mean water level, which represents the average between high and low tides. According to the tide measurement station located at the study site, the tide variation is below 0.3 m through the year [34], a finding corroborated by our tidal calculations (Figure 3) for the month of the satellite image acquisition. This variation is even smaller than our acceptable error rate (10%) [38]. Therefore, tidal correction does not significantly contribute to improving the results.
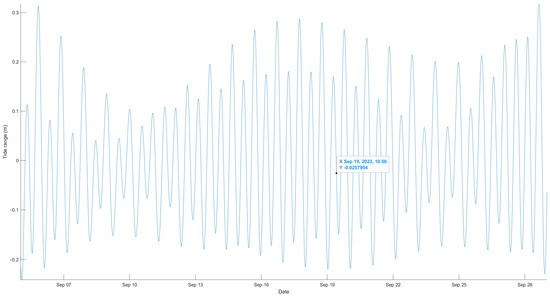
Figure 3.
Tidal variation during the time of Landsat image acquisition.
After obtaining the satellite derived bathymetry data, we proceeded to acquire the corresponding tide levels at the time of the Landsat 9 image acquisition. This was accomplished using the Tide Model Driver Matlab code developed by Greene et al. (2024) [39] in conjunction with global ocean tide models established by Hart-Davis et al. (2021) [40]. Subsequently, we employed these tide elevations to correct the water depth derived from the bathymetry data, resulting in a correction value of −0.017 m.
We also provide here the details of turbidity variation (Table 2), which was measured using a EXO3 multi-parameter sonde (https://www.ysi.com/exo3, accessed on 12 March 2023) during the field survey of water depth, indicating a turbid water environment of the study site. Among the 104 turbidity measurements taken, we observed a minimum value of 5.17 NTU and a maximum turbidity level of approximately 32 NTU. The high turbidity levels have the potential to reduce light attenuation at greater water depths, necessitating a novel approach to achieving sufficient accuracy in depth estimation from satellite imagery.

Table 2.
Measured turbidity statistics.
2.2. Satellite Image Acquisition and Transformation
2.2.1. Image Acquisition
Landsat 9 data was freely downloaded from GLOVIS (https://glovis.usgs.gov/app, accessed on 15 November 2023) (Table 3) at level 1, which underwent geo-correction and radiometric correction. Landsat 9 originally had 11 spectral bands, but only 6 spectral bands, comprising surface reflectance bands of , , , , , , were used for water depth estimation. This selection was made due to stronger light attenuation in the water column at longer wavelengths, following atmospheric correction. Given the challenges of high cloud coverage and sun glint phenomena, we found only the image on the date 19 September 2023 (Landsat 9), closest to the date of the field survey implementation. Sun glint was observed in a small area of the southern part of the image but was removed during the atmospheric correction phase.

Table 3.
Landsat image details.
2.2.2. Image Atmospheric Correction
We used the advanced ACOLITE [41] with dark spectrum algorithm [42] to complete the atmospheric correction, converting pixels from physical unit to surface reflectance () at , , , , , and . The process was executed using the command line interface in the Python environment with the most considerable parameters exhibited in Table 4. The source code for ACOLITE is available at https://github.com/acolite/acolite (accessed on 28 November 2023).

Table 4.
ACOLITE parameters used for Landsat 9 atmospheric correction.
2.2.3. Image Transformation
The sixth (6) original bands were first transformed using a natural logarithm () and subsequently renamed as , , , , , . Following this, three methods of image transformation and extraction, band ratio, GSMO, and MMSD were conducted for , , , , , .
Band Ratio
Band ratio was applied to augment the number of input features for water depth retrieval. We established ratios for different pairs of , , , , , and , resulting in 29 band ratios in the dataset.
Gray Scale Morphological Operation (GSMO)
Gray scale morphological operations (GSMO) are common approach in image processing, providing powerful techniques for analyzing and information extraction using gray scale images. Unlike binary morphological operations, which only work with black and white images, gray scale operations consider varying intensity levels within an image [43]. A diverse options of dilation, erosion, opening, and closing is essential and efficient for image noise reduction, edge detection, and feature extraction. Dilation expands the boundaries of objects, erosion shrinks them, while opening and closing combinations are effective for smoothing and filling gaps in images. GSMO is widely applied in different research fields of medical imaging, computer vision, and remote sensing [44,45], and is very efficient and practical in enhancing image quality and extracting unique information from complex visual data (i.e., satellite image of water body). In this study, the open-source Orfeo Toolbox software (https://www.orfeo-toolbox.org/, accessed on 20 December 2023), module Gray Scale Morphological Operation was used to generate twelve (12) GSMO transformed variables leveraging both the dilation and erosion approaches.
Morphological Multi-Scale Decomposition (MMSD)
Morphological multi-scale decomposition (MMSD) is a sophisticated image processing technique, in which image is decomposed into multiple scales or layers based on morphological operations. This approach is different from the single scale technique and considers a diverse scale of shades and information dimensions, enabling a more comprehensive analysis [46]. Similar to the GSMO approach, MMSD implements dilation, erosion, opening, and closing morphological operations but at different levels of scale, which has great potential for feature, edge, and texture extraction across a range of spatial resolutions. This decomposition facilitates tasks like image segmentation, texture analysis, and object recognition, where capturing details at multiple scales is crucial. MMSD is popular in remote sensing image analysis and pattern recognition to extract –dimensions of desired information while preserving structural characteristics at different levels of granularity [47,48].
Similar to the GSMO, we used the open-source Orfeo Toolbox software (https://www.orfeo-toolbox.org/, accessed on 20 December 2023), module Morphological MultiScale Decomposition, to create 6 MMSD extracted features. In total, there were a dataset of 53 input features created for this work, involving 6 original bands, 29 band ratios, and 18 GMSO-MMSD bands.
2.3. Machine Learning (ML) Model and Feature Selection Implementation
2.3.1. Selected ML Models
CatBoost
CatBoost (CB) [49] is a powerful ML model, which stands out for boosting structure improvement and the processing of categorical features. The model employs gradient boosting to build a sequence of decision trees in a given number of iterations. CB is capable of working seamlessly with text and noncontinuous features by introducing a novel algorithm to compute target statistics during the construction of the decision tree, which in turn helps to prevent data leakage, resulting in more accurate and reliable predictions. In addition, the CB model incorporates advanced features, such as robust controlling of overfitting, offering parallel and GPU training, and built-in visualization tools for model interpretation. CB has been deployed in a variety of research works for bio-physical parameters’ estimation and classification [50,51]. The CB package was sourced from https://pypi.org/project/catboost/ (accessed on 30 December 2023) with an application programing interface (API) wrapped in the scikit-learn [52].
Random Forest
Random Forest (RF) [53] is the most popular ML model, applied for diverse classification and regression tasks since first introduction in 2001. The algorithm builds multiple decision trees during training and merges their predictions to improve accuracy and robustness. Given the algorithm structure, denote as the input feature matrix with samples and features. Each decision tree in the forest is created by recursively partitioning the feature space. For a given node, a random subset of input features is chosen and Gini impurity/obtained information is used to split the samples in a round of iteration until meeting the stopping criteria (i.e., a maximum depth or minimum number of samples per leaf node). During the RF implementation, category or numerical prediction is produced for each tree and final prediction is obtained by aggregating the individual predictions (i.e., majority vote). RF is well known for simplicity, scalability in model deployment and robust prediction, making the model a priority in various research domains. The scikit-learn library supports the API for RF implementation in the Python environment.
Support Vector Machine
Support Vector Machine (SVM) [54] is another supervised learning algorithm using a strategy of searching for optimal hyperplane dividing group clusters with the maximum margin. Considering a classification dataset (xi, yi), for instance, where xi represents the feature vectors and yi represents the class labels, SVM aims to find the hyperplane that maximizes the margin between the closest points (support vectors) of different classes.
For linearly separable data, the optimization problem can be mathematically built in the following form for the linear problem:
and subject to:
We used the scikit-learn library to execute the SVM model in this study.
KTBoost
The KTBoost (KTB) algorithm was first released in 2019 [55] and the KTB implementation code was published in 2021. KTB is different from other members of the boosting family in combining the advantage of kernel and the strength of tree ensemble methods. The authors claim a more robust and consistent prediction with the integration of kernels, denoted as , into the boosting framework. The KTB code was sourced from https://pypi.org/project/KTBoost/ (accessed on 30 December 2023) using the scikit-learn API to build the model for water depth estimation.
Following the learning strategy for the boosting algorithm, weak learners were iteratively constructed under the forms of decision trees to minimized a given loss function . For an iteration , the model searches for a minimizer using the empirical risk function :
in which is the appropriately chosen loss function, and is the span of a set of base learners.
During the learning process, a matrix (i.e., kernels) can be introduced tp discriminate the differences between training instances, and hence to handle complex patterns in the dataset. Despite a promising algorithm structure, the application of KTB is modest in the literature.
Extreme Gradient Boost
Extreme Gradient Boosting (XGB) [56] employs a gradient boosting structure to define weak learners (i.e., decision trees) in the ensemble, of which the new learner improve prediction accuracy and reduce the errors from the past (i.e., previous learner). XGB is different from other traditional gradient boosting methods by providing a regularization parameter to avoid overfitting in prediction and deploying a second-order Taylor series approximation to reach the minimum value of a given loss function.
Let denote the training dataset, where represents the feature vector and represents the corresponding target label. XGB sequentially adds the new model , where is a weak learner, by minimizing the objective function:
where is the loss function and is the regularization term. XGB shows good versatility and scalability for various dataset scales and complex computation, yet produces a robust prediction, hence a wide deployment of the model in the literature. XGB source was retrieved from https://pypi.org/project/xgboost/ (accessed on 30 December 2023) using similar API in the scikit-learn library.
Light Gradient Boosting Machine
Light Gradient Boosting Machine (LGBM) is a high-performance gradient boosting framework developed and released by Microsoft company in 2017 [57]. The name of the model indicates a boosting based algorithm but has the advantage of in light computation, and hence improves the convergence speed for complex problems. The LGBM package was installed from https://pypi.org/project/lightgbm/ (accessed on 30 December 2023) and shares a similar API for model implementation in the scikit-learn library.
Similar to other boosting algorithms, LGBM optimizes the objective function by adding decision trees in a forward and greedy manner. For a given iteration, LGBM determines the best split for the leaves (i.e., num_leaves parameter in the model) to minimize the loss function by gradient descent methods with regularization terms. In addition, LGBM applies a histogram-based technique to construct histograms of feature values, which has great potential in reduction of memory consumption and increase the computation speed. LGBM is among the most popular models used in both industry and academic research.
2.3.2. Meta-Heuristic Optimization Algorithms
Dragon Fly
The Dragonfly (DF) algorithm [58] is a nature-inspired meta-heuristic algorithm that mimics the swarming behavior of dragonflies to find a solution for complex optimization problems. Each of the particles (i.e., dragonflies) presents a potential solution to reach the optimal solution using swamp behaviors. A motility of the dragonflies is simulated in the following form:
of which is the separation weight, as the separation of -th individual, is the alignment weight, is the alignment of -th individual, determines the cohesion weight, is the cohesion of -th individual, is the food factor, is the food source of -th individual, is the enemy factor, is the position of enemy of -th individual, indicates the inertia weight, and is the iteration. The DF is characterized by the most important parameters of swamp population, number of iterations, and the simulated method (e.g., random or sinusoidal).
Particle Swamp Optimization
Particle Swarm Optimization (PSO) [59] is a meta-heuristic optimization algorithm inspired by the social behavior of bird flocking or fish schooling. PSO is well known for various optimization problems in classification, numerical modeling, and machine learning. In PSO, a population of candidate solutions, called particles, moves through the search space to find the optimal solution using a given loss function. Each particle is simulated by a position vector and a velocity vector . The movement of the particle and new updated position feature a local best-known position and the global best-known position . Position is updated after each of iteration for the particle until reaching the stopping criteria (i.e., a maximum number of iterations or minimum value of the loss function), which is expressed as the following equation:
where is the inertia weight, and are acceleration coefficients, and generates a random number between 0 and 1.
PSO is capable of working with noisy data and has proven reliability, consistency and scalability for different complex problems.
Grey Wolf Optimization
Grey Wolf Optimization (GWO) [58] is a meta-heuristic algorithm inspired by the social hierarchy and hunting behavior of grey wolves in a pack. GWO develops the concept of alpha, beta, and delta parameters to simulate the elite wolves of the hunting group. Similar to the DF and PSO, each wolf updates its position after each iteration and this simulation is developed under the following equation:
Here, determines the current iteration, and are formed as coefficient vectors, is position vector of the prey, and is position vector of a grey wolf.
GWO is known for fast speed of convergence, consistency and robust optimization for diverse loss functions, therefore making it a good choice for this study.
2.3.3. ML Model Optimization and Implementation
Here, we outline the steps involved in deploying ML models in the Python environment for water depth estimation in the study.
- Step 1: Setting up the running environment
We used the Python programing environment in conjunction with Anaconda for library management. Python version 3.11 and Anaconda version 3.0 were employed to install and configure the ML models and required libraries for this study.
- Step 2: Model hyper-parameters optimization
ML models encompass various hyper-parameters that require an optimization to determine the best combination for model performance. An automatic grid search with five-fold cross validation was applied using the scikit-learn library to identify the optimal combination of different hyper-parameters (Table 5). The grid search offers a number of metrics, among which we selected the minimum square error (MSE) as a metric to halt the search when the MSE reached its minimum value.

Table 5.
ML model hyper-parameters.
- Step 3: ML model implementation
We inputted a dataset of 1070 points with 53 input features into the six ML models (Table 5) to validate their performance in estimating water depth from Landsat 9 imagery. The data were randomly divided into 70% for training (approximately 986 points) and 30% for testing (approximately 423 points) using the module in scikit-learn.
- Step 4: ML model evaluation: Phase 1
All ML models were evaluated using all 53 input features with standard metrics described in Section 2.3.4 to compare the model skills in water depth estimation at the study site. The model demonstrating the highest accuracy for water depth estimation in Step 4 (phase 1) was selected to undergo feature selection and evaluation in phase 2 (Figure 1).
Step 5: Image feature selection and ML model evaluation (Phase 2)
The most accurate model identified in Step 4 was combined with different meta-heuristic algorithms, including the DF, the PSO, and the GWO, to select the most influential features for the water depth retrieval model. We adapted the library (https://github.com/jaswinder9051998/zoofs, accessed on 30 December 2023) [60] in Python environment to implement DF, PSO, and GWO. Similar hyper-parameters were inherited for the ML model from Step 4, whilst the meta-heuristic algorithm’s hyper-parameters (Table 6) were optimized after several iterations to minimize the RMSE of water depth retrieval. DF and GWO share similar parameters of number of iterations (n_iterations), population (population_size), and simulation method, whilst the PSO requires a range number for , , and parameters.

Table 6.
DF, PSO, and GWO hyper-parameters used for feature selection.
A comparison was made using similar metrics in Step 4 to find the best model in Step 5 for water depth estimation in this study.
2.3.4. Model Evaluation
We applied standard metrics to validate the model performance, including the coefficient of determination (R2), root mean squared error (RMSE), mean absolute error (MAE), median absolute error (MedAE), Akaike information criterion (AIC) and Bayesian information criterion (BIC) (Equations (9)–(14)).
where and .
in which is the number of observations or data points; represents the observed values; represents the values predicted by the model.
in which is the number of parameters in the model; is the number of observations in the dataset; is the maximum likelihood estimate of the model.
In the next section, we present the results for water depth estimation using different single ML models (Section 3.1) and the ML model combined with meta-heuristic algorithms (Section 3.2).
3. Results
3.1. Bathymetry Retrieval from Landsat 9 Using Machine Learning
We explored the model performance using different metrics (Table 7) to validate the prediction skill in water depth retrieval from Landsat 9 imagery. Accordingly, the LGBM gained the highest accuracy in depth estimation (R2 = 0.88) with the lowest RMSE of 0.35 m. Despite a MedAE value similar to those of CB and RF, LGBM yielded lower AIC and BIC values, indicating a superior prediction capability compared to other ML models. The newly introduced KTB shared a similar performance to the CB models (R2 = 0.86); however, it obtained lower values of RMSE (0.38 m), AIC (−511), and BIC (−311). The boosting ML group (CB, LGBM, XGB, and KTB) produced a higher confidence than the bagging RF and SVM (R2 = 0.84). We noted a good fit of the SVM to the measured dataset at an RMSE of 0.41 m and a lower MedAE (Table 7).

Table 7.
ML model performance comparison using Landsat 9 image.
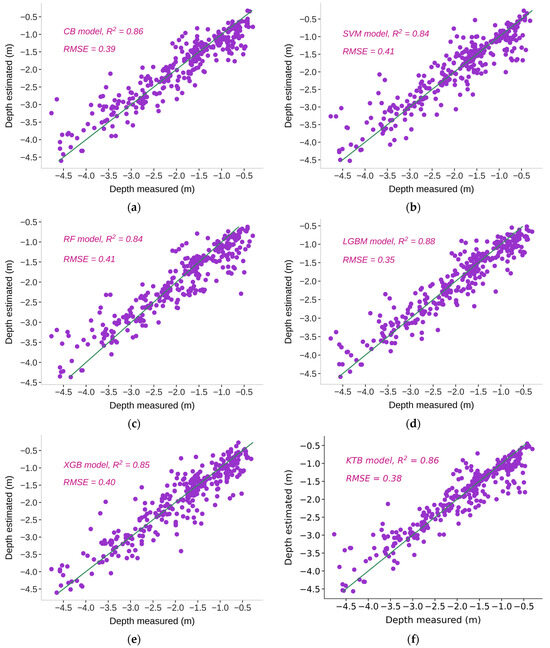
Figure 4.
ML model performance for water depth estimation from Landsat 9: (a) CB, (b) SVM, (c) RF, (d) LGBM, (e) XGB, and (f) KTB models.
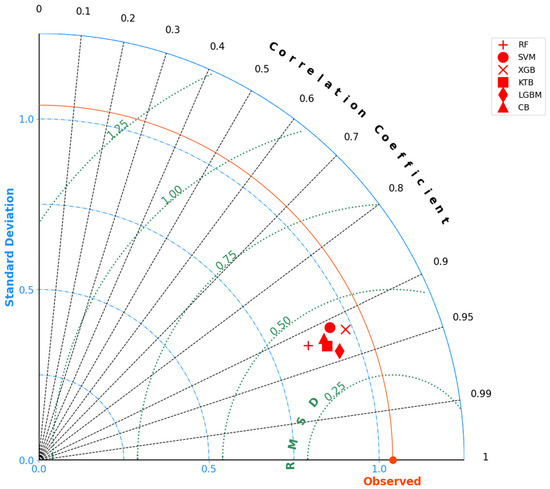
Figure 5.
ML comparison in Taylor plot for RF, SVM, XGB, CB, LGBM, and KTB models.
At various levels of the coefficient of determination (R2 ranging from 0.84 to 0.88), all the models demonstrate proficiency in handling and forecasting water depth. Nevertheless, data points exhibited a more pronounced convergence along the standard line in the case of LGBM. The scatter plot further revealed a dispersion of validation points across depth ranges, confirming the enduring performance of the LGBM model.
We provided additional illustration to validate the skills of the selected model in Taylor space with the correlation coefficient (CC), standard deviation (SD), and root mean squared deviation (RMSD) (Figure 5) in addition to the metrics provided in Table 7 and Figure 4. As seen in the Taylor space, LGBM was closest to the CC line (CC = 0.94) and the RMSD curve (RMSD = 0.35 m), which indicates that the depth derived from LGBM was closer to the measured depth than other ML models with a lower RMSD (Figure 5). Following LGBM, the Taylor plot validated the order of the KTB, CB, XGB, and RF, as shown in Table 7. Similar to the results obtained in Table 7, SVM had the lowest confidence of water depth estimation as observed at the highest location in the Taylor space.
3.2. Bathymetry Retrieval Using Machine Learning and Meta-Heuristic Optimization
The former analysis indicated a promising estimation of water depth in the turbid water of Sam Chuon-Ha Trung lagoon at the highest R2 and RMSE of 0.88 and 0.35 m, respectively. To improve the model accuracy, we adopted feature selection using different meta-heuristic algorithms coupled with the best ML model, LGBM (Table 8). DF and GWO were able to improve R2 by 1.47% and 1.59%, respectively, while PSO increased this number to 3.18%. We observed approximately 2.85% as an amendment of RMSE when LGBM was combined with DF and GWO, but an impressive value of 11.4% was obtained for PSO (Table 8). Given the selected metrics, LGBM-PSO yielded the highest confidence at the lowest RMSE of 0.31 m and MedAE of 0.16 m. The LGBM-DF shared a similar RMSE (0.34 m) with LGBM-GWO; however, it had a lower MAE (0.24 m) and MedAE (0.17 m).

Table 8.
Meta-heuristic algorithms performance.
The employment of meta-heuristic algorithms aids in extracting diverse input features, consequently enhancing the convergence of data points around the standard lines (Figure 6). Notably, LGBM-PSO exhibited a better prediction of water depth, with validation points clustering closer to the line at the lower RMSE (0.34 m) compared to LGBM-DF and LGBM-GWO.
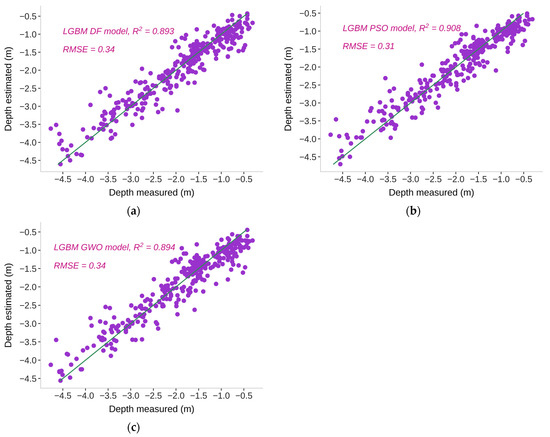
Figure 6.
LGBM model performance with (a) DF, (b) PSO, and (c) GWO.
To validate the superior predictive capability of LGBM-PSO, we compared the performance of the three model across the domains of CC, RMSE, and SD (Figure 7). While LGBM-DF and LGBM-GWO exhibited similar performance and were closely aligned (Figure 7), LGBM-PSO occupied a lower position in terms of RMSD and aligned closely with the CC line (0.95), indicating lower prediction errors and a stronger correlation with the true depth compared to LGBM-DF and LGBM-GWO. In essence, LGBM-PSO demonstrated more consistent and robust estimation of water depth in the Sam Chuon-Ha Trung lagoon.
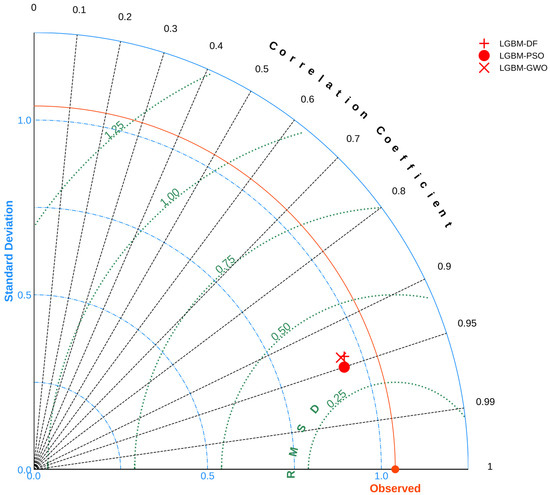
Figure 7.
LGBM models with meta-heuristic optimization comparison in Taylor plot.
Next, we extracted the importance score to elucidate the contribution of input features to the superior performance of LGBM-PSO (Figure 8). The built-in function of LGBM revealed significant contributions from three groups: single bands, image-based feature extraction, and band ratios. With the exception of single bands like , the remaining groups (band ratio, GSMO, and MMSD transformations) demonstrated substantial contributions across a wider spectral range of 443–654 nm. Given a threshold of 1.0, then the variables (1.36), (1.31), (1.19), (1.13), (1.03) exhibited a significant impact on the performance of LGBM-PSO, while other features ranged in importance from 0.19 to 0.95. Single band accumulated a score of 1.16, band ratio obtained a value of 8.96, and imaged-based feature extraction garnered the highest accumulated value of 10.68, underscoring its substantial contribution and pivotal role in the successful operation of LGBM-PSO.
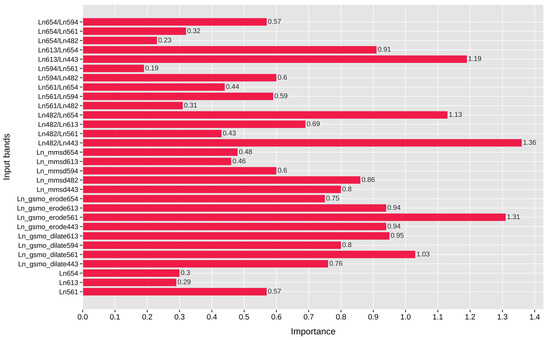
Figure 8.
Feature importance derived from LGBM-PSO.
The GSMO and MMSD extracted information at different levels among the input bands. The former shared the highest score with (1.31) and (1.03), while the latter found the most informative features from (0.86) and (0.80). Figure 8 indicates the important rank of the band with a larger contribution score in different forms of the single band (), extracted features (, ), and the number of band ratios, followed by bands at the peaks of 654, 613, and 443 nm.
As the most accurate retrieval model, we employed LGBM-PSO for the entire study site to produce the final bathymetry map with tidal correction (Figure 9), as mentioned in Section 2.1. A large area of Sam Chuon-Ha Trung has shallow water with the two deeper regions in the northern and southern parts of the lagoon, which fit our field survey as well as the color pattern in the surface reflectance image of Landsat 9 (Figure 2).
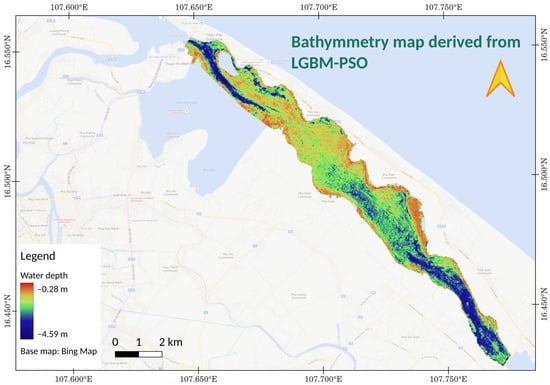
Figure 9.
Bathymetry map derived from LGBM-PSO with tidal correction.
We selected three elevation profiles from the bathymetry map derived from LGBM-PSO and Landsat 9 imagery (Figure 10a) to elucidate the overall topography, revealing a diverse and intricate landscape within the study site. Located in the northern and central regions, the first profile traversed both the shallow and deep channels, while the second profile encompassed the shallow areas of the lagoon. Deliberately focusing on the southern part, we extracted the depth profile to trace the movement through the deeper regions of the water body.
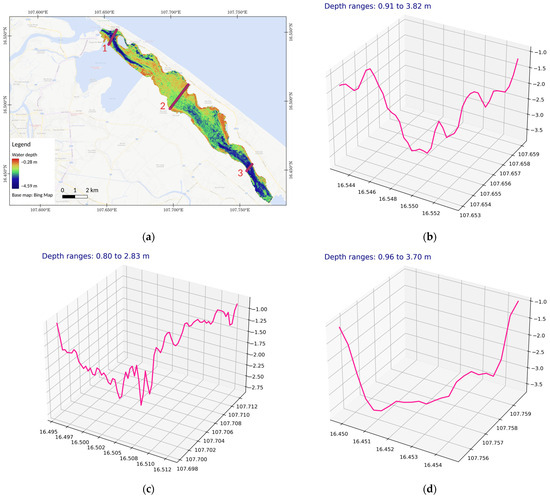
Figure 10.
Bathymetry profiles in Sam Chuon-Ha Trung lagoon: (a) three elevation profiles in the northern, central, and southern parts of the lagoon, including profile 1 (number 1), profile 2 (number 2), and profile 3 (number 3); (b) profile 1; (c) profile 2; (d) profile 3.
Accordingly, the retrieved topography was shallow at the two banks of the lagoon and increased in depth to the central point horizontally. The second profile (Figure 10c) shows a complex elevation surface, which ranges between the shallow and deep points at depths ranging from 0.80 to 2.83 m. The first profile (Figure 10b) presents another complex form of bathymetry topography, in which the water depth sharply decreases to a magnitude of 3.82 m and then gradually moves to the bank, reaching a shallow depth of 0.91 m. As a deeper region, profile 3 (Figure 10d) is determined as a deep but simple topography with two high-slope banks and deep regions in the central areas of the profile at depth ranges from 0.96 to 3.70 m.
4. Discussion
This study is the first operation and integration of diverse approaches for bathymetry mapping in coastal turbid water. Extracted data from the latest generation Landsat 9 image were combined with the state-of-the-art ML models and meta-heuristic algorithms to derive the water depth with an accuracy R2 of 0.908 and RMSE of 0.31 m using a fused model of LGBM and PSO (LGBM-PSO). Of the selected ML models, the boosting algorithms achieved superior performance compared to the bagging and the hyperplane-based SVM. LGBM gained the highest confidence in depth estimation (R2 = 0.88, RMSE = 0.35 m), followed by CB (R2 = 0.86) and XGB (R2 = 0.85). The KTB, a new boosting ML model introduced in 2021, presented a high potential in learning and predicting complex data with similar performance to the CB model (R2 = 0.86). Boosting was found to outperform the bagging and SVM groups in the retrieval of both classification and bio-physical parameters [27,50,51,61] with advancements in algorithm structures and the creative workflow in the decision making of the final model [62,63].
Following the proposed workflows, a significant improvement was gained when using both approaches of feature extraction and feature selection. Feature importance analysis (Figure 8) indicated the highest number of contributed variables (46%) of the band ratio, followed by the image extraction (44%) and original band (10%) groups, and the accumulated scores derived from LGBM-PSO were higher than those of the other variables. Of the 44% contribution, we discovered 27% and 17% of the information derived from the GSMO and the MMSD variables, respectively. There were only three original bands at the wavelengths of 561, 613, and 654 nm, while a larger contribution in the range of 443–654 nm was found for the band ratio and image extraction, implying the importance and necessity of feature extraction during the learning process of ML models. The working range of Landsat bands (443-654 nm) also fits the model performances found in other studies [23,24,27,64]. In addition to the successful retrieval of LGBM was the support of feature selection attributed to the DF, PSO, and GWO meta-heuristic algorithms. PSO produced the highest improvement in RMSE (~11%), while DF and GWO enhanced the RMSE by approximately 3% compared to the original LGBM. We do not claim here an absolute outperformance of the PSO to DF and GWO, due to a variation in the algorithm’s performance by the study sites and dataset [50,65,66]. Rather, we motivated the integration of feature selection using nature-inspired algorithms during the building of the retrieval framework, not only for bathymetry mapping but also for other studies that have great accuracy improvement potential. However, a better convergence of PSO in our study may be assumed for the velocity adjustment (i.e., acceleration coefficients and parameters) of particle trajectories based on personal and global best solutions, which enables an efficient exploration of the search space and convergence to optimal solutions. Given a -dimensional space, the inertial weight controls the velocities and to balance exploration (searching for new potential regions) with exploitation (tuning the current searching area). The bird flock structure of PSO algorithms updates the next potential position of each particle using not only the experience itself but diverse experiences from other particles in the swamp, which increases the speed of convergence and the handling of noisy datasets [67,68].
Using the turbid water in Sam Chuon-Ha Trung lagoon as an example, our results derived from Landsat 9 imagery are more promising and have higher accuracy compared to similar studies in clear water and in rivers. Most of the published studies involving Landsat images use simple approaches of either original bands or the band ratio coupled with linear models (i.e., Stumpf model [24], Generalized additive model (GAM) [23], Lyzenga optical model [19] or common ML models [27]). While this approach showed promising confidence in water depth estimation in clear coastal and ocean waters, there was a great variation in accuracy in inland turbid waters (e.g., river [22], estuary [28]).
In addition to the reliability and consistency of the proposed methods, we emphasize the leveraging of open-source remotely sensed data (i.e., Landsat image), open-source algorithms (e.g., GSMO, MMSD feature extraction, ML, and meta-heuristic optimization) and the open Python programing environment, which enable our study to be replicated and the proposed framework to be expanded to a diverse environment at different scales. This can be claimed as another valuable contribution of the current study to the research community worldwide for both bathymetry mapping and the estimation of other parameters.
Despite reliable and promising results, this study comes with an unavoidable limitation. Due to the high cloud coverage, the number of available multi-spectral satellite images is reduced to a few scenes per year, which can make the comparison between field survey data and satellite image acquisition challenging. In addition, the appearance of private fish traps along the lagoon partly prevented a full observation of water depth to be made during the field survey. Discussion was raised with many local fishermen to obtain the information for water depth from these private areas. Ongoing studies are expanding the proposed methods to other turbid water bodies in river, estuary, and coastal regions. Drone images will be validated for bathymetry mapping together with other multi-spectral sensors and will be coupled with a deep learning model. Additional feature extraction techniques will be integrated with diverse meta-heuristic feature selection models (e.g., Harris Hawk Optimization, Genetic Algorithm) to improve the confidence of water depth estimation in the future.
5. Conclusions
We present an innovative approach for bathymetry mapping in turbid water using Landsat 9 image, leveraging state-of-the-art feature extraction techniques, such as GSMO and MMSD, alongside feature selection through DF, PSO, and GWO-based meta-heuristic optimization, coupled with ML-based learning employing RF, SVM, XGB, CB, LGBM, and KTB models. Among these, LGBM demonstrated superior performance in estimating water depth using all derived features (R2 = 0.88, RMSE = 0.35 m). This model was further enhanced by integrating PSO for feature selection in the second phase of prediction, resulting in the highest accuracy for bathymetry mapping (R2 = 0.908, RMSE = 0.31 m).
Of the 30 selected variables within the spectral range of 443-654 nm, band ratios accounted for 46% of the variance, while image extraction techniques (GSMO, MMSD) contributed 44% to the number of selected bands in the LGBM-PSO model. Feature importance analysis revealed that image extraction had the highest accumulated contribution score (10.68), followed by band ratios (8.96) and single-band groups (1.16).
The DF, PSO, and GWO algorithms exhibit significant potential in selecting the optimal combination of input variables for ML models, facilitating the derivation of accurate bathymetry maps across various turbidity conditions. This study underscores the superior learning capabilities of boosting compared to bagging and SVM techniques, with LGBM and KTB models showing promise for further deployment in water depth estimation and bio-physical parameter retrieval across different regions of the world.
Author Contributions
H.T.T.T. and T.N.H. developed the research concepts and methods, writing and revising the manuscript; H.T.T.T., G.T.H.N. and T.N.H. designed and conducted the field surveys; T.N.H., Q.H.N., T.H.P. and N.T.D.P. coded, built and validated ML models and optimization; T.H.P., T.G.P. and C.T.M.T. edited and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partially supported by the Hue University under both the grant number DHH2022-02-165 and the Core Research Program, grant number NCTB.DHH.2024.06.
Data Availability Statement
Dataset available on request from the corresponding author (T.N.H.).
Acknowledgments
We express our gratitude to Hue University, acknowledging the support provided under grant number DHH2022-02-165 and grant number NCTB.DHH.2024.06. These funds were instrumental in facilitating our field trip and conducting research at the study site. Special thank is extended to An, Nguyen Van (https://orcid.org/0000-0001-5492-8558) for his advices throughout the implementation of this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hell, B.; Broman, B.; Jakobsson, L.; Jakobsson, M.; Magnusson, Å.; Wiberg, P. The Use of Bathymetric Data in Society and Science: A Review from the Baltic Sea. AMBIO 2012, 41, 138–150. [Google Scholar] [CrossRef] [PubMed]
- Duplančić Leder, T.; Baučić, M.; Leder, N.; Gilić, F. Optical Satellite-Derived Bathymetry: An Overview and WoS and Scopus Bibliometric Analysis. Remote Sens. 2023, 15, 1294. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z.; Zhang, Z.; Chu, Y.; Xu, C.; Yao, S.; García-Fernández, Á.F.; Zhu, X.; Yue, Y.; Levers, A.; et al. Exploring Modern Bathymetry: A Comprehensive Review of Data Acquisition Devices, Model Accuracy, and Interpolation Techniques for Enhanced Underwater Mapping. Front. Mar. Sci. 2023, 10, 1178845. [Google Scholar] [CrossRef]
- Mohammadloo, T.H.; Snellen, M.; Simons, D.G. Assessing the Performance of the Multi-Beam Echo-Sounder Bathymetric Uncertainty Prediction Model. Appl. Sci. 2020, 10, 4671. [Google Scholar] [CrossRef]
- Ni, H.; Wang, W.; Ren, Q.; Lu, L.; Wu, J.; Ma, L. Comparison of Single-Beam and Multibeam Sonar Systems for Sediment Characterization: Results from Shallow Water Experiment. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019; pp. 1–4. [Google Scholar]
- Hassan, R.; Saber, A.; ElKafrawy, S.B.; Rabah, M. Bathymetry Retrieval from Remote Sensing Data in Shallow Water of Marsa Alam, Egypt, Based on Multispectral Satellite Imagery. In Applications of Remote Sensing and GIS Based on an Innovative Vision; Gad, A.A., Elfiky, D., Negm, A., Elbeih, S., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 345–357. [Google Scholar]
- Klein, E.; Hadré, E.; Krastel, S.; Urlaub, M. An Evaluation of the General Bathymetric Chart of the Ocean in Shoreline-Crossing Geomorphometric Investigations of Volcanic Islands. Front. Mar. Sci. 2023, 10, 1259262. [Google Scholar] [CrossRef]
- Oregon State University; Kavanaugh, M.; Bell, T.; Catlett, D.; Cimino, M.; Doney, S.; Klajbor, W.; Messié, M.; Montes, E.; Muller Karger, F.; et al. Satellite Remote Sensing and the Marine Biodiversity Observation Network: Current Science and Future Steps. Oceanog 2021, 34, 62–79. [Google Scholar] [CrossRef]
- Sudha, S.K.; Aji, S. A Review on Recent Advances in Remote Sensing Image Retrieval Techniques. J. Indian Soc. Remote Sens. 2019, 47, 2129–2139. [Google Scholar] [CrossRef]
- Rossi, L.; Mammi, I.; Pelliccia, F. UAV-Derived Multispectral Bathymetry. Remote Sens. 2020, 12, 3897. [Google Scholar] [CrossRef]
- Eren, F.; Pe’eri, S.; Rzhanov, Y.; Ward, L. Bottom Characterization by Using Airborne Lidar Bathymetry (ALB) Waveform Features Obtained from Bottom Return Residual Analysis. Remote Sens. Environ. 2018, 206, 260–274. [Google Scholar] [CrossRef]
- Van An, N.; Quang, N.H.; Son, T.P.H.; An, T.T. High-Resolution Benthic Habitat Mapping from Machine Learning on PlanetScope Imagery and ICESat-2 Data. Geocarto Int. 2023, 38, 2184875. [Google Scholar] [CrossRef]
- Cao, B.; Fang, Y.; Jiang, Z.; Gao, L.; Hu, H. Shallow Water Bathymetry from WorldView-2 Stereo Imagery Using Two-Media Photogrammetry. Eur. J. Remote Sens. 2019, 52, 506–521. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A. Optimal Band Ratio Analysis of Worldview-3 Imagery for Bathymetry of Shallow Rivers (Case Study: Sarca River, Italy). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016; XLI-B8, 361–364. [Google Scholar] [CrossRef]
- da Silveira, C.B.L.; Strenzel, G.M.R.; Maida, M.; Araújo, T.C.M.; Ferreira, B.P. Multiresolution Satellite-Derived Bathymetry in Shallow Coral Reefs: Improving Linear Algorithms with Geographical Analysis. J. Coast. Res. 2020, 36, 1247–1265. [Google Scholar] [CrossRef]
- Chénier, R.; Faucher, M.-A.; Ahola, R. Satellite-Derived Bathymetry for Improving Canadian Hydrographic Service Charts. ISPRS Int. J. Geo-Inf. 2018, 7, 306. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, L.; Li, L.; Zhang, Q.; Zhang, P. A Generic Method to Derive Coastal Bathymetry From Satellite Photogrammetry for Tsunami Hazard Assessment. Geophys. Res. Lett. 2021, 48, e2021GL095142. [Google Scholar] [CrossRef]
- Sánchez-Carnero, N.; Ojeda-Zujar, J.; Rodríguez-Pérez, D.; Marquez-Perez, J. Assessment of Different Models for Bathymetry Calculation Using SPOT Multispectral Images in a High-Turbidity Area: The Mouth of the Guadiana Estuary. Int. J. Remote Sens. 2014, 35, 493–514. [Google Scholar] [CrossRef]
- Gabr, B.; Ahmed, M.; Marmoush, Y. PlanetScope and Landsat 8 Imageries for Bathymetry Mapping. JMSE 2020, 8, 143. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; C.e., W.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Ihlen, V. Landsat 8 (L8) Data Users Handbook; U.S. Geological Survey: Reston, VA, USA, 2019.
- Niroumand-Jadidi, M.; Legleiter, C.J.; Bovolo, F. River Bathymetry Retrieval From Landsat-9 Images Based on Neural Networks and Comparison to SuperDove and Sentinel-2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5250–5260. [Google Scholar] [CrossRef]
- Duan, Z.; Chu, S.; Cheng, L.; Ji, C.; Li, M.; Shen, W. Satellite-Derived Bathymetry Using Landsat-8 and Sentinel-2A Images: Assessment of Atmospheric Correction Algorithms and Depth Derivation Models in Shallow Waters. Opt. Express 2022, 30, 3238. [Google Scholar] [CrossRef]
- Jagalingam, P.; Akshaya, B.J.; Hegde, A.V. Bathymetry Mapping Using Landsat 8 Satellite Imagery. Procedia Eng. 2015, 116, 560–566. [Google Scholar] [CrossRef]
- Charilaou, P.; Battat, R. Machine Learning Models and Over-Fitting Considerations. WJG 2022, 28, 605–607. [Google Scholar] [CrossRef] [PubMed]
- Misra, A.; Vojinovic, Z.; Ramakrishnan, B.; Luijendijk, A.; Ranasinghe, R. Shallow Water Bathymetry Mapping Using Support Vector Machine (SVM) Technique and Multispectral Imagery. Int. J. Remote Sens. 2018, 39, 4431–4450. [Google Scholar] [CrossRef]
- Gülher, E.; Alganci, U. Satellite-Derived Bathymetry Mapping on Horseshoe Island, Antarctic Peninsula, with Open-Source Satellite Images: Evaluation of Atmospheric Correction Methods and Empirical Models. Remote Sens. 2023, 15, 2568. [Google Scholar] [CrossRef]
- Liang, Y.; Cheng, Z.; Du, Y.; Song, D.; You, Z. An Improved Method for Water Depth Mapping in Turbid Waters Based on a Machine Learning Model. Estuar. Coast. Shelf Sci. 2024, 296, 108577. [Google Scholar] [CrossRef]
- Saeidi, V.; Seydi, S.T.; Kalantar, B.; Ueda, N.; Tajfirooz, B.; Shabani, F. Water Depth Estimation from Sentinel-2 Imagery Using Advanced Machine Learning Methods and Explainable Artificial Intelligence. Geomat. Nat. Hazards Risk 2023, 14, 2225691. [Google Scholar] [CrossRef]
- Ha, N.-T.; Pham, T.-D.; Pham, H.-T.; Tran, D.-A.; Hawes, I. Total Organic Carbon Estimation in Seagrass Beds in Tauranga Harbour, New Zealand Using Multi-Sensors Imagery and Grey Wolf Optimization. Geocarto Int. 2023, 38, 2160832. [Google Scholar] [CrossRef]
- Akbari, E.; Darvishi Boloorani, A.; Neysani Samany, N.; Hamzeh, S.; Soufizadeh, S.; Pignatti, S. Crop Mapping Using Random Forest and Particle Swarm Optimization Based on Multi-Temporal Sentinel-2. Remote Sens. 2020, 12, 1449. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Nguyen, T.T.T.; Le, N.N.; Ha, N.T.; Xia, J.; Takeuchi, W.; Pham, T.D. Improvement of Mangrove Soil Carbon Stocks Estimation in North Vietnam Using Sentinel-2 Data and Machine Learning Approach. GIScience Remote Sens. 2021, 58, 68–87. [Google Scholar] [CrossRef]
- Tran, D.-T. Tam Giang—Cau Hai: Lagoon Resources Potential and Orientation for Management. J. Mar. Sci. Technol. 2007, 7, 53–62. [Google Scholar]
- Nghiem, L.; Stive, M.; Verhagen, H.; Wang, Z.B. Morphodynamics of Hue Tidal Inlets, Vietnam. In Proceedings of the Asian and Pacific Coasts Conference, Nanjing, China, 21–24 September 2007. [Google Scholar]
- Ha, H.D.; Thang, T.N. Chapter 8—Fishery Communities’ Perception of Climate Change Effects on Local Livelihoods in Tam Giang Lagoon, Vietnam. In Redefining Diversity & Dynamics of Natural Resources Management in Asia, Volume 3; Thang, T.N., Dung, N.T., Hulse, D., Sharma, S., Shivakoti, G.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 111–124. ISBN 978-0-12-805452-9. [Google Scholar]
- Tuan, T.H.; Van Xuan, M.; Nam, D.; Navrud, S. Valuing Direct Use Values of Wetlands: A Case Study of Tam Giang–Cau Hai Lagoon Wetland in Vietnam. Ocean Coast. Manag. 2009, 52, 102–112. [Google Scholar] [CrossRef]
- Open-Meteo Historical Weather API Home Page. Available online: https://open-meteo.com/en/docs/historical-weather-api (accessed on 17 October 2023).
- Tang, K.; Mahmud, M. The Accuracy of Satellite Derived Bathymetry in Coastal and Shallow Water Zone. Int. J. Built Environ. Sustain. 2021, 8, 1–8. [Google Scholar] [CrossRef]
- Greene, C.A.; Erofeeva, S.; Padman, L.; Howard, S.L.; Sutterley, T.; Egbert, G. Tide Model Driver for MATLAB. J. Open Source Softw. 2024, 9, 6018. [Google Scholar] [CrossRef]
- Hart-Davis, M.G.; Piccioni, G.; Dettmering, D.; Schwatke, C.; Passaro, M.; Seitz, F. EOT20: A Global Ocean Tide Model from Multi-Mission Satellite Altimetry. Earth Syst. Sci. Data 2021, 13, 3869–3884. [Google Scholar] [CrossRef]
- Vanhellemont, Q. ACOLITE For Sentinel-2: Aquatic Applications of MSI Imagery. In Proceedings of the 2016 ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; ESA Special Publication: Prague, Czech Republic, 2016; p. 8. [Google Scholar]
- Vanhellemont, Q. Adaptation of the Dark Spectrum Fitting Atmospheric Correction for Aquatic Applications of the Landsat and Sentinel-2 Archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Aptoula, E.; Lefèvre, S. Chapter 1—Morphological Texture Description of Grey-Scale and Color Images. In Advances in Imaging and Electron Physics; Hawkes, P.W., Ed.; Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2011; Volume 169, pp. 1–74. [Google Scholar]
- Zhang, B. Reconfigurable Morphological Processor for Grayscale Image Processing. Electronics 2021, 10, 2429. [Google Scholar] [CrossRef]
- Kavitha, A.V.; Srikrishna, A.; Satyanarayana, C. A Review on Detection of Land Use and Land Cover from an Optical Remote Sensing Image. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1074, 012002. [Google Scholar] [CrossRef]
- Bangham, J.A.; Chardaire, P.; Ling, P. The Multiscale Morphology Decomposition Theorem. In Mathematical Morphology and Its Applications to Image Processing; Serra, J., Soille, P., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 179–184. ISBN 978-94-011-1040-2. [Google Scholar]
- Schmitt, O.; Hasse, M. Morphological Multiscale Decomposition of Connected Regions with Emphasis on Cell Clusters. Comput. Vis. Image Underst. 2009, 113, 188–201. [Google Scholar] [CrossRef]
- Pei, Y.; Liu, C.; Lou, R. Multi-Scale Edge Detection Method for Potential Field Data Based on Two-Dimensional Variation Mode Decomposition and Mathematical Morphology. IEEE Access 2020, 8, 161138–161156. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2019, arXiv:1706.09516. [Google Scholar]
- Ha, N.T.; Manley-Harris, M.; Pham, T.D.; Hawes, I. The Use of Radar and Optical Satellite Imagery Combined with Advanced Machine Learning and Metaheuristic Optimization Techniques to Detect and Quantify above Ground Biomass of Intertidal Seagrass in a New Zealand Estuary. Int. J. Remote Sens. 2021, 42, 4712–4738. [Google Scholar] [CrossRef]
- Ha, N.T.; Manley-Harris, M.; Pham, T.-D.; Hawes, I. Detecting Multi-Decadal Changes in Seagrass Cover in Tauranga Harbour, New Zealand, Using Landsat Imagery and Boosting Ensemble Classification Techniques. IJGI 2021, 10, 371. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gholami, R.; Fakhari, N. Support Vector Machine: Principles, Parameters, and Applications. In Handbook of Neural Computation; Elsevier: Amsterdam, The Netherlands, 2017; pp. 515–535. ISBN 978-0-12-811318-9. [Google Scholar]
- Sigrist, F. KTBoost: Combined Kernel and Tree Boosting. arXiv 2019, arXiv:1902.03999. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’16, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 November 2017; Volume 2017-Decem, pp. 3147–3155. [Google Scholar]
- Mirjalili, S. Dragonfly Algorithm: A New Meta-Heuristic Optimization Technique for Solving Single-Objective, Discrete, and Multi-Objective Problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Singh, J. Zoofs Home Page. Available online: https://github.com/jaswinder9051998/zoofs (accessed on 23 December 2023).
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating Mangrove Above-Ground Biomass Using Extreme Gradient Boosting Decision Trees Algorithm with Fused Sentinel-2 and ALOS-2 PALSAR-2 Data in Can Gio Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Khan, S.M.; Shafi, I.; Butt, W.H.; Diez, I.d.l.T.; Flores, M.A.L.; Galán, J.C.; Ashraf, I. A Systematic Review of Disaster Management Systems: Approaches, Challenges, and Future Directions. Land 2023, 12, 1514. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A Review of Ensemble Learning Algorithms Used in Remote Sensing Applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Yunus, A.P.; Dou, J.; Song, X.; Avtar, R. Improved Bathymetric Mapping of Coastal and Lake Environments Using Sentinel-2 and Landsat-8 Images. Sensors 2019, 19, 2788. [Google Scholar] [CrossRef]
- Parmaksiz, H.; Yuzgec, U.; Dokur, E.; Erdogan, N. Mutation Based Improved Dragonfly Optimization Algorithm for a Neuro-Fuzzy System in Short Term Wind Speed Forecasting. Knowl.-Based Syst. 2023, 268, 110472. [Google Scholar] [CrossRef]
- Wang, J.-S.; Li, S.-X. An Improved Grey Wolf Optimizer Based on Differential Evolution and Elimination Mechanism. Sci. Rep. 2019, 9, 7181. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Ghosh, K.K.; De, R.; Cuevas, E.; Sarkar, R. Learning Automata Based Particle Swarm Optimization for Solving Class Imbalance Problem. Appl. Soft Comput. 2021, 113, 107959. [Google Scholar] [CrossRef]
- Choi, K.P.; Kam, E.H.H.; Tong, X.T.; Wong, W.K. Appropriate Noise Addition to Metaheuristic Algorithms Can Enhance Their Performance. Sci. Rep. 2023, 13, 5291. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).