Abstract
While geodetic measurements have long been used to assess landslides, seismic methods are increasingly recognized as valuable tools for providing additional insights into subsurface structures and mechanisms. This work aims to characterize the subsurface structures of the deep-seated gravitational slope deformation (DSGSD) at Heinzenberg through the integration of active and passive seismic measurements. Seismic techniques can hereby deliver additional information on the subsurface structure and mechanisms involved, e.g., the degree of rock mass degradation, the resonant frequencies of the potentially unstable compartments, and the local fracture network orientations that are influenced by wavefield polarization. By employing advanced methods such as H/V analysis, site-to-reference spectral ratios, polarization analysis, surface wave analysis, and the joint multizonal transdimensional Bayesian inversion of velocity structures, we establish a comprehensive baseline model of the landslide at five selected sites. This baseline model shall help identify potential changes after the refilling of Lake Lüsch, which started in 2021. Our results reveal the rupture surface of the DSGSD at various depths ranging from 30 m at the top to over 90 m in the middle of the slope. Additionally, we estimate key parameters including the shear wave velocities of the different rock masses. The 2D geophysical profiles and rock mass properties contribute to the understanding of the subsurface geometry, geomechanical properties, and potential water pathways. This study demonstrates the significance of integrating seismic methods with traditional geodetic measurements and geomorphologic analysis techniques for a comprehensive assessment of landslides, enhancing our ability to monitor and mitigate hazardous events.
1. Introduction
Deep-seated gravitational slope deformations (DSGSDs) often affect entire relief slopes, show slow displacement rates, typically consist of large rock volumes, and frequently lack sharp boundaries [1,2,3]. These slow gravitational movements may affect the whole slope from the ridge crest (and beyond) down to the valley floor, and present typical morphologies like double-crested ridges (also mountain splitting), ridge-top graben structures, uphill-facing scarps (also counterscarps), scarps, ridge-parallel trenches, morpho-structures controlling the drainage network (e.g., ponds, lakes), undulating extensional zones, tension cracks, and toe bulging or dislocation of the slopes’ toe [1,2,4].
The Heinzenberg landslide in eastern Switzerland (9°23′ E, 46°43′ N) is a typical example of a DSGSD in metamorphic rocks [5,6,7,8]. Usually, such large slope instabilities result from a complex interaction of factors like lithology, topography, and climate, and, in some cases, they can even be influenced by human activity [1,9,10,11,12]. Human activity in particular, since the 14th century, seems to have influenced the Heinzenberg landslide, namely by removing its protecting surface cover of vegetation for agricultural purposes [13]. Even if slope movements are likely to have occurred previously at Heinzenberg, no indications of dangerous slope deformations were observed at the time of early settlements. But from 1585 on, many torrent outbreaks of the Nolla river were recorded, which are strongly connected to landslide movement caused by a loss of stability at the landslide toe due to torrent erosion, resulting in increased surface displacements within the Heinzenberg slope. In the 18th and 19th centuries, debris flows were triggered by high-precipitation events and caused catastrophic floods in the plains and villages of the valley of the Rhine Posterior. Torrent control systems, control of surface water runoff, recultivating vegetation, and surface displacement measurements were initiated and have been conducted since then at Heinzenberg [6,8,14,15,16].
In the context of landslide reconnaissance, conventional surface displacement measurements are supplemented by advanced geophysical techniques, including ambient vibration measurements and active seismic refraction surveys. Burjanek et al. [17] and Kleinbrod et al. [18] applied ambient vibration measurements as a convenient, rapid, and reliable technique for the characterization of (potential) landslides. Ambient vibration measurements are mostly conducted with lightweight seismic instruments and need no active source. They represent a supplemental resource for characterizing damaged rock masses and differentiating between damaged and intact rock. From ambient vibration measurements, resonant frequencies and related volumes of instable rock masses can also be estimated [19,20,21,22]. In addition, the internal slope, damaged by gravitational processes or weathering, can be studied through its dynamic response by frequency-dependent ground-motion features [18,23]. Shear-wave (S-wave) velocity profiles can be received from surface wave dispersion curves measured by passive seismic arrays [24,25]. The technique of horizontal-to-vertical spectral ratio (H/V or HVSR) shows an increased use in the context of slope failure characterization [26,27,28]. The HVSR method can be used for the detection of buried structural interfaces (e.g., rupture surfaces), especially where two overlying materials have a strong impedance contrast, such as between slope failure deposits and undamaged bedrock [29]. Another way to measure the velocity of seismic waves in the subsurface is by examining active seismic refraction surveys, such as seismic refraction tomography (SRT). SRT can be used to map the velocity of P-compressional waves (P-wave) in the ground or to analyze surface-wave properties over depth with the multichannel analysis of surface waves (MASW) [30,31,32,33,34].
This paper presents the prospective combination of active and passive seismic surveys to better comprehend the Heinzenberg landslide’s sliding surface geometry. The results of this analysis are used to derive a geophysical baseline model of the Heinzenberg landslide. This multi-methodological approach allows us to capture details of its sliding surface geometry, enabling a more accurate representation of the complex interactions between lithological factors, topography, and historical human activities that contribute to the ongoing evolution of the Heinzenberg landslide [5,16]. Our emphasis on combining these advanced geophysical techniques underscores the significance of a holistic methodology in contemporary landslide research [35,36], aligning with global efforts to enhance the robustness of landslide characterization.
2. Description of the Heinzenberg Landslide
2.1. Geography and Geology
The Heinzenberg landslide is located in the Canton Grisson in Switzerland in the valley of the Rhine Posterior called Domleschg, about 10 km SW of Chur. The western slope of this valley between Rothenbrunnen and Thusis is called Heinzenberg. Heinzenberg is flanked to the south by the steeply incised Nolla Valley and Piz Beverin (2998 m a.s.l.). To the west, it ascends to the ridges of Glaser Grat, Lüschgrat, and Tguma, reaching an elevation up to 2119 m a.s.l. at Präzer Höhi. It gradually descends with an average slope of 15–20° towards the east, reaching the valley floor of the Rhine Posterior at about 630 m a.s.l. (Figure 1a). The soft morphology of the Heinzenberg surface is caused by the susceptibility to weathering of a series of metamorphic schists and shales. On its southern border, the mountain stream Nolla causes the incision of deep gouges; consequently, slopes are considerably steeper there (>45°).
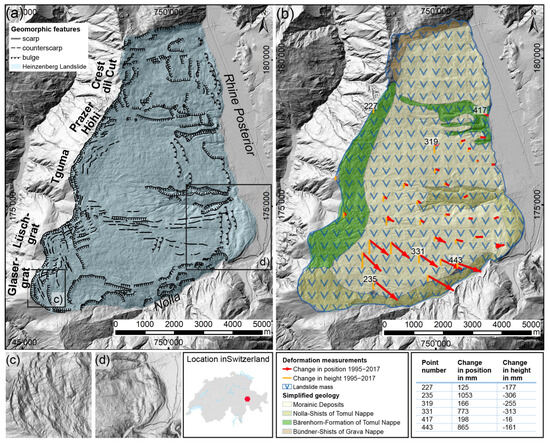
Figure 1.
Characterization of the Heinzenberg landslide. (a) Geomorphic features of the Heinzenberg landslide on the western slope of the Rhine Posterior, bounded to the south by the steeply incised Nolla river and to the west by Glasergrat, Lüschgrat, Tguma, Prazer Höhi, and Crest dil Cut. (b) Very simplified geology of the Heinzenberg landslide (modified after [7]) and results of deformation measurements from 1995 to 2017; number represent the point numbers as listed in the table, the length of the red vectors represent the change in position and of the orange vectors the change in height (after [16]). (c) Details of the head scarp area around Glasergrat with typical structures of mountain splitting and uphill-facing scarps. The direction of the splitting follows (i) the dominant strike of the SW–NE layers and (ii) the dominant fracture system which is NNW–SSE, causing the curvature of the main scarps. (d) Detail of the slopes’ toe with convex toe bulging of the mass pushing into the valley of Rhine Posterior.
Tectonically, the area covered by the Heinzenberg is dominated by the lower Penninic sedimentary cover nappes called the Grava and Tomul Nappes [7]. Two units of the Tomul Nappe cover most of Heinzenberg, the Bärenhorn formation with its sandy–clayey calcareous phyllites and typical black clay layers and the Nolla formation with clay mica schists and shales (Figure 1b). Only in the north of Heinzenberg the lowermost tectonic element (Grava Nappe) crops out with monotonous Cretaceous shaly metasedimentary rocks called Bündner Schists. Having experienced a wide variation in tectonic stress, the degree of metamorphism and weathering within the schists varies. The overall foliation is parallel to the bedding and dips about 15–35° towards the SE [7,8]. Only in the northern Heinzenberg the foliation dips steeper, almost vertically, into the slope. Inhibiting a high percentage of phyllosilicates, the Bündner Schists often react plastically to mechanical stress, and fracture systems are not well pronounced. Ziegler [8] found a dominant fracture set striking NNW–SSE, causing steep rock walls with the same orientation. It can be assumed that the Heinzenberg slope was completely covered in ice during the Last Glacial Maximum (LGM), dating between ~28 ky and ~18 ky [37,38,39]. Thus, morainic deposits (with a thickness of a few meters) cover most of the Heinzenberg slope (Figure 1b). In the uppermost part of the slope, these morainic deposits are partly covered by landslide deposits and are meanwhile transported downslope from the landslide movement.
2.2. Geomorphology
The Heinzenberg landslide can be divided into four slabs, originating each from different main scarps, namely, Glaser Grat, Luschgrat, Tguma–Prazer Höhi, and Crest dil Cut, comprising an area of about 45 km2 (Figure 1a). The main scarps follow, on one hand, the direction of strike of the bedding planes (SW–NE), and on the other hand, the dominant fracture set (NNW–SSE) [8]. This causes the curved crests of Heinzenberg (Figure 1a) and overlaps with several intersections between the different slabs. The upper zone of the Heinzenberg slope shows mountain splitting with double ridges. These uphill-facing scarps are characterized by extension, which can be seen in the extensional cracks and several secondary scarps (Figure 1c) formed. Within these zones, drainless sinks developed and little lakes like Lake Lüsch or Lake Bischol formed (Figure 2a). The middle zone of the Heinzenberg slope features lateral cracks and compressive bulges, forming an undulating terrain with ponds and many terrain waves (Figure 1a). This sagging area causes the degradation of the rock mass. Further downslope, the Heinzenberg slope can be split into the zone dewatering into the Nolla Valley (mainly the southern part of Heinzenberg) and into the zone of the remaining slope, dewatering into the Rhine Posterior. The zone dewatering into the Nolla Valley is attributed to steep (>25°) to very steep (>45°) slopes, the dominance of erosional processes at the slope’s toe, and material removal through fluviatile transport. In contrast, the part of Heinzenberg dewatering into the Rhine Posterior is not eroded by the river, but it is characterized by typical toe bulging where the landslide mass mounds up at the toe and forms large lobes (Figure 1d).
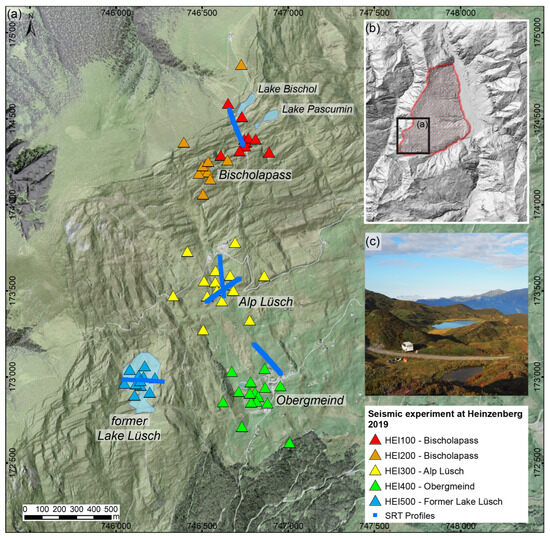
Figure 2.
Installation and array setup of the seismic experiment at Heinzenberg. (a) The five SRT profiles (blue lines) and the passive seismic array setups (triangles) at the southeastern Heinzenberg; (b) the elevation model of the Heinzenberg surroundings with the landslide area marked in red and the area of (a) highlighted; (c) photo of Lake Pascumin looking downwards towards the south.
2.3. Historic Documentation and Monitoring of the Landslide Movement
The eastern Heinzenberg slope has been known for many decades to be an active mass movement marked by a clear landslide morphology. Even though slope movements likely happened before the first settlements were established in the 14th century, no signs of dangerous slope deformations were seemingly visible. Towns like Thusis are located at the foot of a debris cone formed like a bulged slope toe of a slow-moving landslide (Figure 1d). Indeed, the landslide morphology of Heinzenberg (Figure 1a) points to a slow DSGSD, which was probably activated post-glacially. When the first settlers started cultivating the Heinzenberg slope, they cleared out forest and bushes to create exploitable ground and to receive pastures and farmland, construction wood, and firewood for heating [13,40]. At Heinzenberg, the human-caused deforestation comprised the entire slope. Thus, the early settlers deprived the mountain of its natural water retention and evaporation system built from vegetation.
The oldest reports of landslide movements date back to the 16th century. Focusing on torrent outbreaks and debris flows of the Nolla river, they describe an over-steepening of the river banks [40]. Outbreaks of the Nolla river are blamed for intensifying and activating the southern part of the Heinzenberg landslide by regressive slope destabilization of the slope’s foot. The disastrous debris flow of August 1585 was reportedly triggered by heavy rainfalls over the summer period. This debris flow destroyed the town of Thusis and ran down the Rhine Posterior to the town of Rothenbrunnen. At the beginning of the 18th century, historic documents reported six torrent outbreaks between 1705 and 1719. Another seven outbreaks were documented between 1802 and 1834, and another five outbreaks were recorded between 1868 and 1877. The torrent outbreaks were caused by the loss of cohesion of the schist outcroppings on the Nolla river banks. The over-steepened river banks were loaded with a mix of debris and unconsolidated soil and collapsed once their water content was high enough to set down the friction angle. Thus, the river banks of Nolla incised deeper and there was a slope regression developing in the uphill Heinzenberg, which caused large compartments of the southern Heinzenberg to move en bloque downwards for several meters per year [13,40].
After the numerous disasters in the 18th and 19th centuries, local engineers recognized the connection between torrent control and landslide movement. In 1870, the construction of retention dams within the Nolla valley had already started, slowing down the undercutting of the slopes and reducing the power of the torrent outbreaks in the following years. In 1884, the first drainage systems within the Heinzenberg landslide were installed, and in 1899, reforestation projects started. To further slow down these movements, Lake Lüsch, located close to Lüschgrat (Figure 2a), was drained in 1910 [5,8,13,41]. The remedial measures constructed between 1870 and 1910 led to a steady decline in displacement rates, as known from geodetic measurements [6,14,15,16]. The first geodetic measurements in 1810 showed average displacements of 4 m/a [41]. Landslide monitoring from 1910 to 1931 already indicated a reduction in movement down to 0.15 m/a [40]. Further deceleration was measured from 1929 to 1974 with 0.05 m/a and from 1976 to 1996 down to 0.04 m/a [6,14,15]. Since 2018, geodetic measurements have been complemented by three permanent GNSS stations recording continuous data, showing displacements of 0.02 m/a. In June 2022, a permanent seismic station recording seismic data was also installed to investigate potential slope movements during the reactivation of Lake Lüsch.
The overall displacement direction in the southern Heinzenberg area is mainly towards SE, and in the northern Heinzenberg, it is mainly towards the east, which corresponds more or less to the direction and dip of the slope. When looking at dip angles calculated from vertical and horizontal displacements (1929–1974), it can be noted that in the top part of the instability, i.e., in the scarp area (e.g., at former Lake Lüsch), large dip angles (29–42°) occur. In the middle part of the slope, i.e., in the sagging zone of the landslide (e.g., around Tschappina), medium dip angles of around 11–16° exist, which corresponds well with the dip of the slope and the dip of the dominant foliation. At the toe of the slope, even partially positive dips occur (e.g., west of Thusis), pointing to the mechanism of toe bulging (Figure 1b).
3. Methods
At Heinzenberg, from the year 1870 onward, several different remedial measures were applied in a short time frame to slow the downslope movements. Thus, it is not known which measures really had the largest impact or an impact at all on landslide activity. Several geological models of the Heinzenberg landslide exist [5,7,8], but they all rely on surface investigations and interpolations. Since the Heinzenberg landslide is locally greater than 100 m with a heterogeneous subsurface geology marked by intense fracturing, much is unknown about the subsurface structures. Thus, we applied different geophysical prospection methods to the Heinzenberg landslide to better characterize the subsurface.
3.1. H/V Analysis
Ambient vibration measurements with just one station were used for the horizontal-to-vertical spectral ratio analysis (H/V; [27]). We computed horizontal and vertical Fourier amplitude spectra ratios of the ambient vibration recordings for site characterization purposes. If the measurement shows a pronounced impedance contrast between the surface layer and underlying stiffer rock formation, H/V spectral curves produce a clear resonance peak with a site-characteristic frequency [26]. In particular, two methods are applied to the Heinzenberg passive seismic array data: (1) the classical H/V spectral ratio [42] and (2) the Raydec method to estimate the Rayleigh wave ellipticity curve [43].
3.2. Polarization Analysis
The frequency-dependent motion of the mass particle of the soil or rock can have a linear or, more often, elliptical pattern. We therefore analyzed the ambient vibration data with the time-frequency polarization analysis (TFPA) introduced by Burjanek et al. [23]. Polarization is described by the strike and the dip of the major axis of the particle motion ellipse and value of ellipticity. The strike is frequently observed as perpendicular to the prevailing fractures, indicating the alignment of the semi-major axis with respect to the north. A dip angle approaching zero implies a horizontally oriented major axis of the ellipse. The dip angle indicates the degree to which the major axis of the ellipse tilts in relation to the horizontal plane. A positive or negative dip indicates a tilt in the structure. The shape of the ellipse is described by the ellipticity and is defined as the ratio of the semi-minor axis to the semi-major axis. An ellipticity nearing 0 shows straight-line ground motion, whereas a ratio of 1 indicates circular ground movement. The usual range of ellipticity for hard-rock sites falls between 0.3 and 0.4 [44]. Unstable rock slopes generally show small values of the ellipticity at the resonant frequencies of the structure.
3.3. Site-to-Reference Spectral Ratios (SRSR)
It is possible to compare the ambient vibration signal from an intact rock site near the instability with the signal obtained from within the instability. Through this comparisson, it becomes feasible to approximate the relative amplification of the signal using the site-to-reference spectral ratio (SRSR, [26,45,46]). By relating the signal at the instability to a stable reference site, only characteristics of the site related to the local rock mass remain, and source- and path-specific effects are eliminated (assuming distant sources). However, this necessitates the proximity of the test and reference sites. The frequency-dependent amplification functions can also reveal resonant frequencies originating from local geological conditions. The most substantial amplification values typically appear along the primary polarization direction, as determined by the TFPA method (see Section 3.2). The extent of fissuring within the rock mass is directly expressed in the amplification factors [47]. These amplification factors contribute pivotal metrics for assessing the condition of a specific rock-slope instability [25]. Kleinbrod et al. [25] categorized rock slopes with amplification factors of around 4 as notably weakened and potentially unstable, whereas values of 8 or higher indicate a significantly disrupted rock structure.
3.4. Surface-Wave Analysis with Array Methods (3CFK)
We employed either one-component or three-component high-resolution beamforming (3CFK) in the frequency–wavenumber (f-k) domain, a technique that has demonstrated its functionality in extracting dispersion curves from geological structures with lateral heterogeneity [48,49,50,51]. Since seismic ambient noise is usually mainly composed of surface waves, 3CFK analyses the seismic signal of the three component motion and retrieves dispersion curves within the transverse, vertical, and radial space independently. With this analysis, it is possible to identify Rayleigh waves on the vertical and radial components and Love waves on the transverse component. Kleinbrod et al. [25] used the approach exclusively at depth-controlled sites, as pure volume-controlled sites do not exhibit surface-wave propagation due to the presence of open cracks. In the case of depth-controlled sites, it is typically feasible to discern only small segments of Rayleigh and Love wave dispersion curves. The low-frequency resolution is constrained by the necessity for a 1D velocity profile and the size of the array, which is often geomorphologically limited on unstable slopes. The high-frequency limit for observing surface wave propagation varies significantly based on the extent of lateral heterogeneity in the near-surface structure.
3.5. Seismic Refraction Tomography (SRT)
The data obtained from the active seismic experiments were processed using seismic techniques such as seismic refraction tomography and the multichannel analysis of surface waves (MASW, see below). Both methods are designed to characterize the subsurface in terms of elastic properties. The seismic refraction method maps velocities of actively triggered compressional body waves (P-waves) along the propagation path in the ground, employing travel-time inversion. Initial travel-time curves are established by picking the first arrival times of body waves at each receiver, allowing the system to compare the iteratively calculated travel times by ray-tracing them to the observed values until a minimized root-mean-square (RMS) error is reached [52]. In this study, SRT profiles were generated with the software package Seisimager 2DTM developed by Geometrics. As an initial model, we used a one-layer model with a P-wave velocity of 3000 m/s (typical velocity for the hard schists that represent the bedrock on this slope), and with a minimum 50 m (for some profiles up to 100 m) depth for the inversion process.
3.6. Multichannel Analysis of Surface Waves (MASW)
In order to estimate the 1D shear-wave velocity profiles of the ground, the Rayleigh-wave energy triggered by the active experiments was interpreted using the multichannel analysis of surface waves (MASW) method [53,54,55,56]. The surface waves were analyzed in terms of their dispersion, specifically their Rayleigh-wave phase velocity in relation to frequency. Dispersion curves were picked using the SurfSeis software [57], employing the wavefield transformation method developed by Park, Miller, and Xia [54] to generate phase-velocity frequency images from the seismic shots gathered. The further analysis of the picked dispersion curves was conducted through a joint inversion scheme, using a multilayer initial model, as described in detail below.
3.7. Combination and Inversion of Dispersion Curves (Neopsy)
The dispersion curves of the Rayleigh and Love surface waves, retrieved from the passive array (3CFK) and active measurements (MASW), can be inverted to create a local 1D velocity model. For this purpose, we used a joint inversion method formulated in the Bayesian probabilistic framework by Hallo et al. [58]. The inversion method relates observed dispersion curves and model parameters using an abstract multidimensional parameter space [59], which allows for a proper evaluation of uncertainties. Also, the parameter space is formulated as transdimensional [60], in which the number of layers of the velocity model is the subject of inversion itself. The sampling of the parameter space was performed with the Metropolis–Hastings algorithm [61] with the implemented parallel tempering technique [62]. The outcome from the inversion was the posterior probability density function (PDF) that expresses the most probable values and uncertainty of S- and P-wave velocities, the depth of the layer interfaces, and the optimal number of layers. The depths of the 1D velocity model with a sharp posterior PDF were inferred precisely, as a very wide posterior PDF signifies uncertain seismic velocities. This feature is useful for interpretation purposes. The S-wave velocity profiles are the main result of the inversion because of the primary influence on surface wave properties. The P-wave velocity profiles are only complementary; they have much larger uncertainties, and they can be retrieved if both the Rayleigh and Love dispersion curves are available and by using a priori plausible values for the Poisson ratio (0.2–0.42 is used in this study). The set of models was generated through the implementation of 300 Markov chains of the parallel tempering framework, consisting of 285 exploration chains and 15 sampling chains. Each individual chain underwent burn-in and production phases, with the former lasting 5000 steps and the latter extending to approximately 40,000 steps. This configuration involved the testing of around 13,500,000 models and drawing approximately 600,000 random samples from the posterior PDF.
3.8. Description of the Seismic Experiment at Heinzenberg
Previous monitoring of the Heinzenberg landslide focused on the ground-surface displacements. Subsurface structures like the thickness of the moraine cover, the degree of rock mass degradation, or the possible depths of the instability motivated us to use several seismic techniques. With these techniques, subsurface information from active and passive seismic measurements can be combined with the existing surface-displacement data to create a baseline model for the Heinzenberg landslide. We conducted a large seismic experiment in September 2019. Two different device sets were available for the acquisition of ambient noise data; 21 identical three-component portable seismometers with a natural period of 5 s and lower cut-off frequency of 0.2 Hz (Lennartz Le-3D/5s) with Centaur digitizers (Nanometrics) and seven seismometers GURALP (CMG-6TD) with a lower cut-off frequency of 0.033 Hz were used. The Lennartz sensors were placed in shallow holes on metal trihedrons for better coupling with the ground, and the GURALP sensors were completely buried in the soil. For the seismic refraction measurements, a set of 48 geophones (4.5 Hz, 5 m spacing) was deployed together with two 24-bit, 24-channel digitizers (DAQLinkIV). The required seismic energy for the seismic refraction measurements was triggered with sledgehammer shots on a nylon plate at several equidistant points along the linear profiles.
Both methods, the passive and the active seismic method, were simultaneously deployed in five different array configurations using both sets of seismometers, together with recordings of actively triggered seismic waves along nearby profiles. The configurations and locations of the seismic experiment conducted in September 2019 are shown in Figure 2, and raw and processed data are available [63]. At former Lake Lüsch (HEI500), a seismic profile of 240 m length in the E–W direction was measured as well as a passive array with a central station, four inner stations with a 30 m radius from the central station, and one hexagon with a 90 m long median (see Figure 2a and Figure 3a). The record duration of the seismic stations was synchronized to at least 90 min. At Alp Lüsch (HEI300), a passive seismic array with medians of 30 m, 90 m, and 195 m with 15 stations and a seismic profile 230 m in length were deployed in the N–S and SW–NE directions (Figure 2a and Figure 4a). The same configuration with 15 seismic stations and the same three medians up to 195 m was used at Obergmeind (HEI400), where two seismic profiles, each 230 m in length, were also deployed, running in the NW–SE direction, respectively (Figure 2a and Figure 5a). At Bischolapass (HEI100 and HEI200), a different array configuration with 10 (HEI100) and 11 (HEI200) stations was used and deployed at two sites, creating a spiral-like configuration (Figure 2a). The seismic profile installed at Bischolapass has a length of 220 m, running NW–SE.
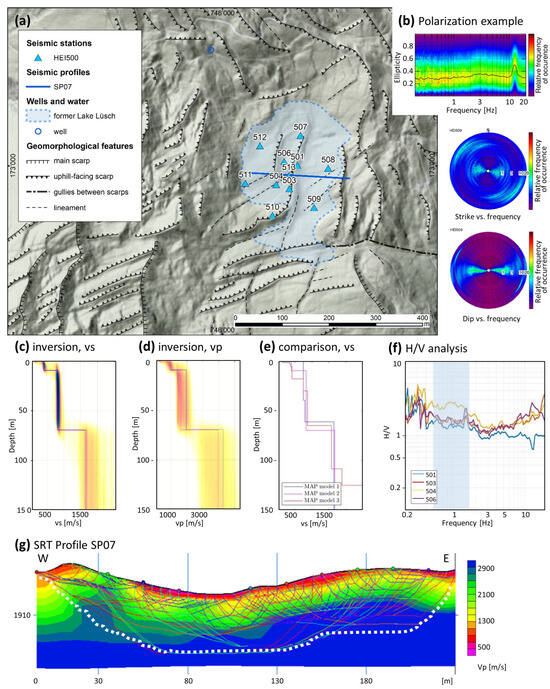
Figure 3.
Details of the results for the area around former Lake Lüsch. (a) Map of the surroundings of the seismic array within the lake basin with geomorphic structures and location of sensors with numbers indicating array station names, coordinate system in CH1903; (b) an example of polarization analysis results for station HEI509. (c) Inversion results of HEI500 for model 2 (R0R1) with the color scale representing probability increasing from light yellow to dark brown; the blue line is the maximum-likelihood model (ML) and the pink line is the maximum a posteriori model (MAP) of vs; (d) same as (c) for vp. (e) Comparison of inversion results for MAP model 1 (R0), MAP model 2 (R0R1), and MAP model 3 (R0R1R2). (f) Raydec H/V analysis of the Rayleigh wave ellipticity for selected stations of HEI500. (g) results of the SRT of the profile SP07 with the white dashed line marking the area of coverage and colored lines indicating the different ray paths used for the inversion process.
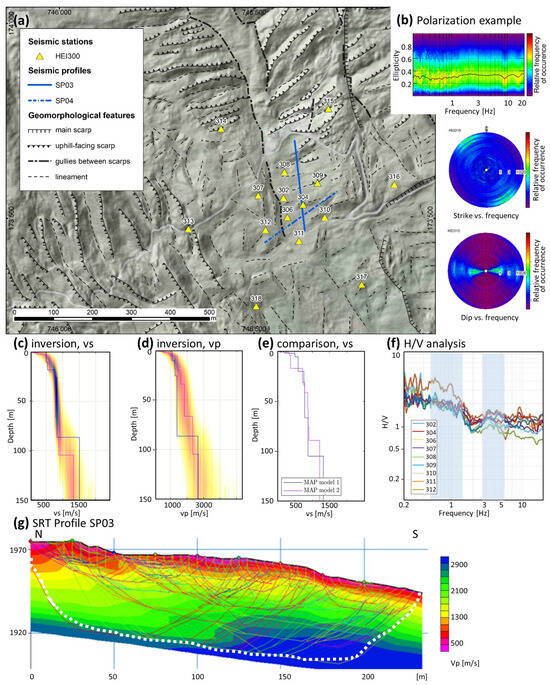
Figure 4.
Details of the results for array HEI300 at Alp Lüsch. (a) Geomorphological map of the surroundings of the seismic array with numbers indicating array station names with coordinates in CH1903. (b) example of polarization analysis results for the station HEI310. (c) Inversion results of HEI300 for model 1 (R0) with the color scale representing probability increasing from light yellow to dark brown; the blue line is the maximum-likelihood model (ML) and the pink line is the maximum a posteriori model (MAP) of vs. (d) same as (c) for vp. (e) Comparison of inversion results for MAP Model 1 (R0 passive and active) and MAP Model 2 (R0R1). (f) Raydec H/V analysis of the ellipticity for all HEI300 stations. (g) results of the SRT of the profile SP03 with the white pointed line marking the area of coverage and colored lines indicating the different ray paths used for the inversion process.
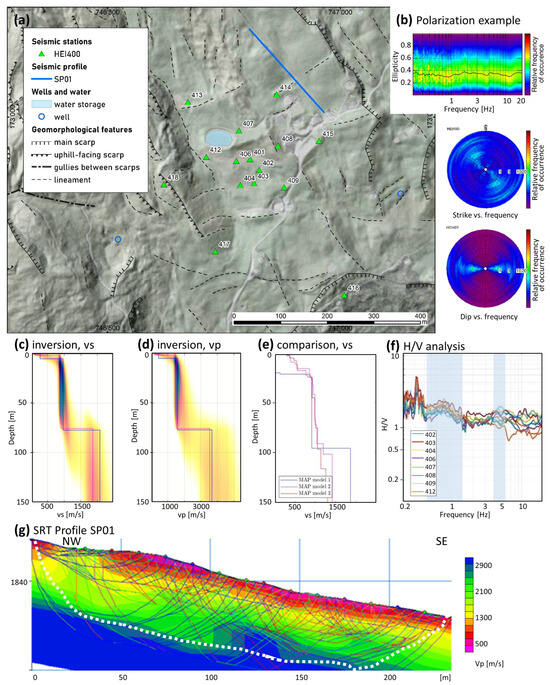
Figure 5.
Details of the results for the area with the HEI400 array around Obergmeind. (a) Geomorphological map of the surroundings of the seismic array with numbers indicating array station names between Obergmeind and the water storage basin with the coordinate system in CH1903. (b) example of polarization analysis results for the station HEI401. (c) Inversion results of HEI400 Model 1(R0 and L0) with the color scale representing probability increasing from light yellow to dark brown; the blue line is the maximum-likelihood model (ML) and the pink line is the maximum a posteriori model (MAP) of vs. (d) same as (c) for vp. (e) Comparison of inversion results for MAP Model 1 (R0L0), MAP Model 2 (R0R1), and MAP Model 3 (R0R1R2) by approximately correcting Model 1 for the lower elevation of the array. (f) Raydec H/V analysis of the ellipticity for all stations of the inner array of HEI400. (g) results of the SRT of the profile SP01 with the white pointed line marking the area of coverage and colored lines indicating the different ray paths used for the inversion process.
4. Results
4.1. Former Lake Lüsch: Within-Lake Sediments (HEI500)
This array (HEI500) is located within the former Lake Lüsch at 1930 m a.s.l. The southern border of former Lake Lüsch is also the border between the rocks of the older Bärenhorn Formation and the Nolla Schists on top. The area is characterized by the interaction between the direction of the strike of the bedding planes (SW–NE) and the dominant fracture set (NNW–SSE; [8]). This interplay results in the typical curvatures of Glaser Grat and Lüschgrat (Figure 1a). The former Lake Lüsch is located exactly between these two curved ridges and on the border between the two geologic layers. The surroundings of the array are characterized by two sets of uphill-facing scarps facing N to NW and W to SW. In the surrounding of the seismic experiment at former Lake Lüsch, uphill-facing scarps occur within 5 m to 80 m, orthogonally to each other, and can be traced over lengths of 15 m to 200 m. The seismic experiments in this zone involve one passive seismic array (HEI500) of 11 sensors and one active seismic line 230 m in length running E–W (Figure 2a).
The H/V analysis of the HEI500 stations shows a fundamental frequency between 0.7 Hz and 2 Hz (Figure 3f). The analysis of the polarization unveils a weak directional ground motion present in all array stations in the direction striking towards NW for frequencies larger than 5 Hz, which is perpendicular to the existing structures in the surroundings (e.g., station 509 in Figure 3b and Supporting Information Figure S5). For frequencies below 1 Hz, the strike is more in the E–W direction. The dip is planar to the surface and the ellipticity levels are around 0.25. No rock reference site was available for HEI500 because the compact rock was too far away from the array, and SRSR was not performed.
Inversion of dispersion curves of surface waves was performed for three different sets of input data (all data and results are presented in the Supporting Information Figures S19 and S28–S30): Model 1 (R0), Model 2 (R0 and R1), and Model 3 (R0, R1, and R2), where R0 corresponds to the fundamental-mode Rayleigh wave and R1 and R2 correspond to the first and second higher modes. Three different sets of input data were used in order to provide robust and well-validated results. For Model 2, the fundamental mode of the Rayleigh waves (R0) retrieved by the passive and active experiment are combined between 3.9 and 12.3 Hz (phase velocities between 700 m/s and 1275 m/s). The first higher mode, R1, from the MASW data is between 15.8 and 19.6 Hz, with velocities around 775 m/s to 700 m/s (Supporting Information Figure S29). Selecting R0 and R1, the inferred shear-wave velocity profile (vs; Figure 3c) shows very clear interfaces at 10 m and 70 m depth. At 10 m, vs jumps from 400 m/s to 800 m/s, and at 70 m, vs jumps from 800 m/s to 1675 m/s (Figure 3c). The P-wave velocity (vp) of the landslide block between 10 – 70 m is estimated to be 1550–2000 m/s, and that of the intact rock is estimated to be larger than 3200 m/s (Figure 3d). The latter was inferred from the MASW profiles and supported by the complementary P-wave velocity profiles from the surface-wave inversion.
Since the seismic data were also interpreted as only showing the fundamental mode R0 (Model 1) and also R0, R1, and R2 together (Model 3), all three resultant models from the different data interpretations are compared in Figure 3e. The maximum a posteriori (MAP) models from the inversion process (i.e., the most probable models) were used for the geological interpretation of the subsurface structure, along with uncertainty estimates from the posterior probability density function (PDF). The three interpretations differ in the way that the superficial sediments are visible: R0R1 (Model 2) and R0R1R2 (Model 3) cover a 5 m to 20 m surface layer, whereas R0 (Model 1) does not, due to the reduced frequency band of the used dispersion curve. The interface between landslide mass and intact rock was located for all interpretations between 60 m and 70 m (see posterior histograms of interface depth shown in the bottom-middle panels of Supporting Material Figures S28–S30), which is within the accuracy of 1 sigma through all three inversions. The shear-wave velocities of the landslide mass were, for all models, in the range of 750 m/s to 900 m/s, and for the intact rock, they were larger than 1575 m/s (Figure 3e). In order to explain that peak in H/V at around 1.4 Hz, though, a deeper interface than what is seen in the velocity profiles is necessary. We expect another velocity contrast for depths greater than 150 m.
The seismic vp refraction tomography at former Lake Lüsch indicates a superficial layer of lake sediments with an average vp of the SRT of 1000 m/s and a thickness between 0 m and 10 m (Figure 3g), followed by the landslide mass with a vp larger than 1500 m/s. The profile shows a layer of lake sediments, except close to its western end, where the landslide block outcrops the surface. The resolution of the SRT refraction tomography only covers a depth range up to about 30 m (white dotted lines in Figure 3g); thus, the basal plane of the landslide, which was detected due to the inversion at around 70 m, cannot be seen.
4.2. Alp Lüsch: Within the Water-Saturated Horizon (HEI300)
The area of Alp Lüsch at around 1975 m a.s.l. is characterized by a gentle topography. While the area uphill at Bischolapass is characterized by pronounced uphill-facing scarps, the zone around Alp Lüsch shows soft meadows and only diffuse lineaments (Figure 4a). At 1960 m a.s.l, a natural well is found, and at 1940 m a.s.l, a pumping station for the local water supply exists. Both are located in the SW of the center of the array called HEI300 (Figure 4a). The geomorphologic mapping of the surroundings of this array reveals an interesting setting—the array is located in an area with lineaments striking NW–SE and NE–SW (with a scatter). There are no clear uphill-facing scarps as they exist east, north, and west of Alp Lüsch. Only a gully running north–south crosses the array. At the end of the gully, the mentioned pumping station is located. A hexagonal configuration was deployed at Alp Lüsch. The seismic experiment setup in this area was a triangle with a 30 m median, and two hexagons with 90 m and 270 m long medians from the center. The active seismic measurements were two lines with a length of 230 m each running N–S (SP03) and NE–SW (SP04; Figure 4a).
The H/V analysis of most HEI300 stations showed a weak peak between 3 Hz and 5 Hz, which displayed a relatively homogeneous 1D subsurface of near-surface layers (Figure 4f). A second unclear peak was present below about 1.5 Hz, similar to HEI500 but at a slightly lower frequency. Polarization analysis exposed a faintly directional ground motion observed across all array stations above 10 Hz. Ground motion polarization was visible mainly in the strike, which seemed to be oriented orthogonal to the surficial lineaments resp. the dominant fracture sets in the area towards the NW direction, whereas the dip was horizontal and the ellipticity showed a constant level of around 0.3 (Figure 4b and Supporting Information Figure S3). No rock reference site was available for HEI300 because the compact rock was too far away from the array, and SRSR was not performed.
For the inversion of the dispersion curves of surface waves, two different interpretations of dispersion curves were found to be reliable. A version with the fundamental mode R0 based on active and passive data between 2.9 Hz and 16 Hz (Model 1) was tested. Another version with the fundamental mode R0 and the first higher mode R1 covering the frequency bands between 2.9 Hz and 7.0 Hz for R0 and 8.7 Hz and l3.5 Hz for R1 with surface-wave velocities between 525 m/s and 1075 m/s (R0) and 550 m/s and 675 m/s (R1) represent Model 2 (Supporting Information Figure S24). The selected inversion results presented in Figure 3c,d are based on Model 1. We assigned the entire dispersion curve to the fundamental-mode Rayleigh wave by interpreting the decrease in the velocity above 10 Hz as an effect of the variable near-surface layer. The inferred vs profile (Figure 4c) showed three layers with different velocity gradients, one near-surface layer down to approximately 15–20 m, one layer down to 110 m, and one layer at depths greater than 110 m. The 15–20 m thick near-surface layer might explain the unclear peak in the H/V ratio around 3–5 Hz. The landslide mass between 20 and 110 m showed a shear-wave velocity (vs) around 700 m/s to 900 m/s and a P-wave velocity (vp) of about 1700 m/s. The intact rock mass below 110 m showed a vs larger than 1300 m/s and a vp larger than 2400 m/s (Figure 4c,d). The velocity profile of Model 2 is similar to that of Model 1, with lower velocities in the surficial 15–20 m thick layer, but with a similar velocity contrast at about a 90 m depth. We can conclude that the interface between the landslide mass and the intact rock is located between 90 m and 110 m, 30 m deeper than at HEI500, and consistent with the low-frequency peak in H/V at a slightly lower frequency in HEI300.
The seismic vp refraction tomography at Alp Lüsch shown in Figure 4g covers the profile of SP03 between 1980 m a.s.l. and 1940 m a.s.l., striking N to S and agreeing with the complementary vp profiles from the inversion of the dispersion curves. The SRT profile SP03 shows a velocity gradient in the superficial weathered layer with a thickness range between 20 m (N) and 10 m (S) with P-wave velocities from 500 m/s to 1100 m/s. This agrees with the layer thickness defined from the inversion of the dispersion curves (Figure 4c,d). The refraction tomography covers a depth range with reliable vp values up to a ~40 m depth depending on the location of the cross-section. A similar conclusion can be drawn from section SP04 (Supporting Information Figure S11).
4.3. Obergmeind: Results from the Sagging Zone (HEI400)
The seismic experiment HEI400 was installed in the surroundings of the settlement of Obergmeind, located at 1812 m a.s.l. In this area, the sagging zone of Heinzenberg starts, featuring a gentle, undulating terrain with ponds (SE of Obergmeind) and many terrain waves due to the horizontal extension of the landslide in this area (Figure 5a). The mountain slope falls at an average of 15° towards the Rhine Posterior. There is an artificial water storage for snow production on the slopes in winter just west of Obergmeind, in the middle of the array. This pond is fed by water running down the small brook called Lüschbach, which has its artificial origin at the bottom of former Lake Lüsch. The subsurface was built from the schists of the Bärenhorn Formation. The seismic experiment in this zone involved one array called HEI400 and one profile called SP01. The seismic experiment setup in this area was three hexagons with 30 m, 90 m, and 270 m long medians around a center. The morphology is special since the first two hexagons of 30 m and 90 m lie within a depression (sensors 401, 402, 403, 404, 406, 407, 408, 409, and 412). These sensors are called an inner array and were analyzed separately. The entire array together with the six stations of the 270 m long median also covers the flanks beside the depression, with changing elevations of up to a 40 m height, with an average of 20 m. The conducted active seismic profile was also located at a higher, level following the road NE of the array in the NW direction, covering a length of 230 m using 48 geophones (SP01).
The H/V analysis of most HEI400 stations showed a dominant peak between 0.5 and 1.1 Hz, lower than that at HEI300 and HEI500, indicating that the interface between the landslide mass and the intact rock is located deeper than 110 m. The very unclear peak at 4–5 Hz indicates a shallow near-surface layer of unconsolidated material (Figure 5f). The polarization analysis indicated a weak directional ground motion observed among all array stations. Polarization is visible mainly in the strike, which seems to be oriented orthogonal to the surficial lineaments resp. the dominant fracture sets in the area in the NW direction, the dip being more or less horizontal and the ellipticity levelling around 0.35 (Figure 5b and Supporting Information Figure S4). No rock reference site was available for HEI400, and SRSR was not performed.
We tested various versions of the interpretation of the dispersion curves, covering different frequency bands using both active and passive data, and both the Rayleigh and Love fundamental modes. In the first model (Model 1), we used the fundamental mode R0 and the Love mode L0 derived from the inner passive array, between 3.1 and 11.0 Hz for R0 and 3.6 and 10.8 Hz for L0, respectively. This analysis represents the inner array at a lower elevation (Model 1). The second model (Model 2) uses R0 and R1. The dispersion curve for R0 was between 2.4 and 9.4 Hz, combining results from the large passive array and the active MASW of SP01. The R1 between 5.8 and 10.6 Hz was derived from the passive array. In addition, the third model (Model 3) uses fundamental mode R0, again combing the results from the passive and active experiment together with the first higher mode R1 from the passive measurements and the second higher mode R2 between 12.0 and 13.2 Hz from the active MASW (all data in Supporting Information Figures S18 and S25–S27). Models 2 and 3 represent a structure that is located about 20 m of elevation above the inner array of Model 1.
The inferred vs and vp velocity profiles for Model 1 are presented in Figure 5c,d and show three layers: the thin superficial layer (0–5 m), the rock mass of the DSGSD (5–75 m), and the intact rock (>75 m; Figure 5c,d). Seismic shear-wave velocities (vs) for the rock mass of the DSGSD were around 900 m/s and for the intact rock mass below 75 m larger than 1800 m/s. P-wave velocities for the landslide mass were around 1500 m/s, and for the intact rock, they were larger than 3000 m/s (Figure 5c,d).
Since the seismic data were also interpreted for the modes R0 and R1 (Model 2), respectively, R0, R1, and R2 (Model 3), all MAP models of the different interpretations are shown in Figure 5e. Note that the profile of Model 1 only starts 20 m below that of Model 2 and Model 3 due to the elevation difference. This way, it is possible to directly compare the three models with each other. The three interpretations differ in the way that the superficial sediments are visible: Models 2 and 3 cover up to 20 m of superficial ruptured material and sedimentary fillings, whereas Model 1 (R0L0) covers only the top 5 m. The interface between landslide mass and intact rock is located 75 m below the free surface for Model 1 (meaning 95 m in Figure 5e), and 90 m to 110 m for Models 2 and 3. The shear-wave velocities of the landslide mass are in the range of 800 m/s to 1050 m/s, and those of the intact rock are between 1300 m/s and 1800 m/s (Figure 5e). The low-frequency peak in H/V is at lower frequencies than that for HEI300 and HEI500. If we select Models 2 and 3, the interface between the landslide mass and the intact rock is located at a depth larger than about 90 m below the surface.
In Figure 5g, the seismic vp refraction tomography of SP01 at Obergmeind is displayed, showing P-wave velocities between 5 m and 25 m and between 900 m/s and 1600 m/s. The refraction tomography covers a reliable depth of around 25 m with similar vp values of the inversion, mostly covering the surficial layer with ruptured material.
4.4. Bischolapass: Mountain Splitting and Uphill-Facing Scarps (HEI100/HEI200)
The uppermost approximately 100 m of elevation around arrays HEI100 and HEI200 are characterized by pronounced uphill-facing scarps, with ridges and depressions on both sides of the slope crest (Figure 6a). The uphill-facing scarps in this area form a doubled ridge and ridge-top depressions as morphostructural features of a typical deep-seated gravitational slope deformation (DSGSD, [1]). The depressions are prone to water accumulation, and little ponds and swamps develop in the surroundings of the terrain, e.g., Lake Bischol (1996 m a.s.l.) or Lake Pascumin (1968 m a.s.l.). In the surrounding of the seismic experiment at Bischolapass, uphill-facing scarps occur within a 5 m to 50 m orthogonal distance from each other and can be traced over lengths of 20 m to 400 m. They mainly run NE/SW and are partly dissected through gullies running NNW–SSE. The seismic experiment in this zone involved two arrays, HEI100 and HEI200, with their center shifted around 300 m towards SW. In total, 10 sensors were deployed for HEI100 and 11 for HEI200, with the same reference station (station 115/215; see Figure 6a). Due to the close distance of the reference station, the arrays were suitable for site-to-reference spectral analysis (SRSR). The conducted active seismic measurements cross the ridge, leaving Lake Bischol and Lake Pascumin to the east, with a total length of 230 m using 48 geophones (SP02; Figure 6a).
The H/V spectral ratios at the two arrays are similar, but the SRSRs show distinct differences. At HEI100, the H/V analysis of the stations shows unclear peaks for most stations between 1 and 2 Hz, and between 5 and 10 Hz (Figure 7a). When using the Raydec method (Figure 7c), the peaks are slightly more pronounced. SRSR values, relative to the reference station 115, show amplification values up to a factor of 5 in the frequency range between 5 and 10 Hz (Figure 7e), indicating a shallow layer of disrupted material above the bedrock. From the absence of a strong H/V peak, we can conclude that shear-wave velocity in this layer increases with depth, without a strong velocity contrast to the underlying material. From the de-amplification in SRSR for frequencies below 3 Hz, we might expect a harder material at a depth below this surface layer than for reference station 115. From the variability in the SRSR curves above 5 Hz, we conclude that this shallow layer has a high variability in both average vs and thickness. We can confirm this observation from the SRT results (Figure 6g). Therefore, for frequencies above 5 Hz, surface waves in this layer do not propagate efficiently over longer distances, and this might be the reason they could not be measured with the array measurements of ambient vibrations in array HEI100 as well as with MASW in the active experiment.
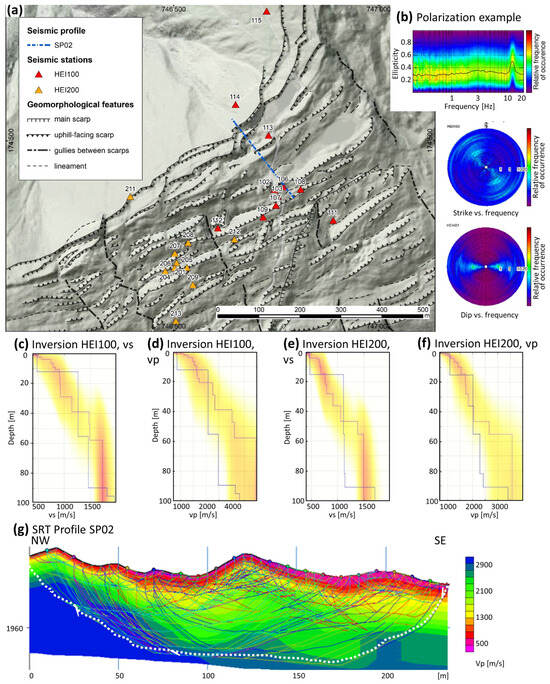
Figure 6.
Details of the results for the area around Bischolapass. (a) geomorphologic features and location of sensors of arrays HEI100, HEI200, and SP02 with numbers indicating array station names and coordinates in CH1903. (b) example of polarization analysis results for station HEI207. (c) inversion results of HEI100 with the color scale representing probability (the blue line is the maximum-likelihood model (ML) and the pink line is the maximum a posteriori model (MAP) of vs). (d) same as (c) for vp. (e) inversion results of HEI200 with the color representing probabilities between 0 and 0.8, the blue line representing the maximum-likelihood model (ML), and the pink line representing the maximum a posteriori model (MAP) for vs. (f) the same as (e) for vp. (g) SRT for the seismic profile (SP02) with the dashed white line representing the depth with reliable vp values and colored lines indicating the different ray paths used for the inversion process.
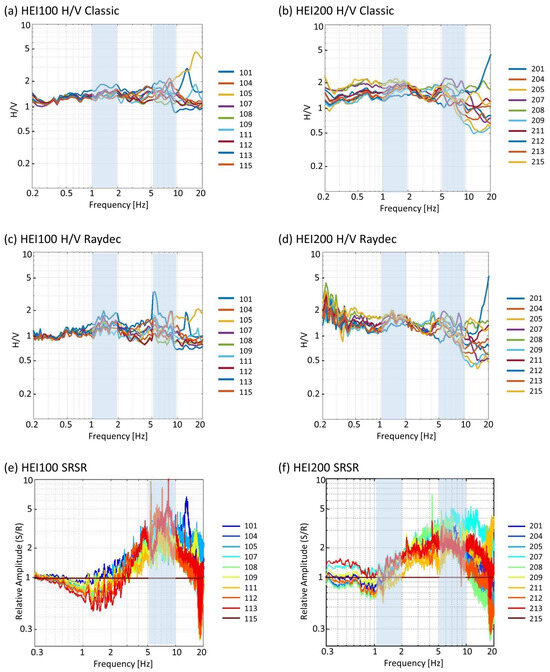
Figure 7.
H/V analysis and SRSR at arrays HEI100 (left) and HEI200 (right). (a) H/V ratios obtained for the stations in array HEI100 calculated with the classical method. (b) H/V ratios obtained for the stations in array HEI200 calculated with the classical method. (c) H/V ratios obtained for the stations in array HEI100 using Raydec. (d) H/V ratios obtained for the stations in array HEI200 using Raydec. (e) SRSR for stations in array HEI100 using station 115 as reference site. (f) SRSR for stations in array HEI200 using station 215 as reference site.
The H/V for the stations in array HEI200 show two peaks at 1–2 Hz and 5–10 Hz (Figure 7b,d). In SRSR for array HEI200, a low-frequency peak around 1–2 Hz is seen, with the SRSR amplifications around 1.5 (Figure 7f). The high-frequency peak above 5 Hz with its variation from station to station is very similar to what was observed at HEI100, with amplifications up to a factor of 5. The amplifications observed in SRSR between 1 Hz and 5 Hz indicate a relatively homogeneous 1D subsurface with vs velocities lower than those observed for HEI100 for the structure below the shallow surface layer. The measured surface-wave dispersion curves on array H200 show lower values than on HEI100, which is expected from the amplifications in the frequency range of 1–5 Hz (Supporting Information Figures S21 and S22).
The polarization analysis revealed a weak directional ground motion present in all array stations (Figure 6b for station HEI207 and other details in Supporting Information Figures S1 and S2), and often, polarization is only traced within frequencies larger than 10 Hz, covering superficial structures. For some stations, the direction of polarization strikes towards NE (e.g., stations 102, 106, 111, and 114), which is orthogonal to the dominant fracture set in the area. For other stations, the strike of the ellipse shows that it moves towards the NW direction (e.g., stations 207, 211, and 213), which is perpendicular to the existing uphill-facing scarps.
The array analysis of the ambient vibrations on HEI100 resulted in a dispersion curve of the fundamental-mode Rayleigh wave (R0) only between 3.4 Hz and 5.2 Hz, with velocities ranging from 1210 m/s to 1680 m/s. The fundamental-mode Love wave (L0) was resolved between 3.5 Hz and 6.9 Hz, with velocities ranging from 1140 m/s and 1700 m/s (Supporting Information Figure S20). The inversion results (Figure 6c,d) are not well constrained due to the lack of dispersion curves above 7 Hz, defining the properties of the near-surface layers. Inverted vs velocities in the first 20–30 m showed a wide range with a velocity gradient. The shallow superficial ruptured rock is expected to have a thickness of 5 m to 10 m, with vs velocities smaller 900 m/s. The rock mass of the DSGSD reaches a depths of 30 m to 40 m, with vs velocities between 900 m/s and 1150 m/s (Figure 6c). The intact rock below 30–40 m displays vs velocities larger than 1500 m/s.
The analysis of the HEI200 array resulted in a dispersion curve of the fundamental-mode Rayleigh wave (R0) between 3.6 Hz and 4.5 Hz, with velocities between 1150 m/s and 1425 m/s. The fundamental-mode Love wave (L0) was resolved to be between 3.5 Hz and 6.6 Hz, with velocities between 1025 m/s and 1275 m/s (Supporting Information Figures S21 and S22). Also for HEI200, the inversion results are not well constrained in the near-surface area with dispersion curves below 6.6 Hz (Figure 6e,f). For HEI200, the first 5 m to 15 m of weathered rock show shear-wave velocities smaller than 800 m/s. The interlayer between the disrupted material of the DSGSD and the intact rock can be placed at around a 40 m to 50 m depths. They show a wide range, with a changing velocity gradient and a vs between 800 m/s and 950 m/s. The compact rock is reached at about 40 m to 50 m of depth, with shear-wave velocities larger than 1500 m/s.
The seismic vp refraction tomography at Bischolapass indicates a layer thickness of the shallow superficial rock between 10 m (NW of SP02) and 25 m (SE of SP02), with a vp smaller than 1500 m/s (Figure 6g). This agrees with the velocity profiles from the inversion of the dispersion curves with velocities of the shallow superficial rock smaller than 1600 m/s (Figure 6d,f). The layer thickness of the DSGSD with vp velocities between 1650 m/s and 2100 m/s can be estimated in the refraction tomography with a 5 m thickness in the upper NW part of the profile and up to 30 m in the SE part of the SRT profile SP02 (Figure 6g). The pointed white line in the refraction tomography represents the depth with reliable vp values.
5. Discussion: Formation of a Baseline Model of Selected Sites at Heinzenberg Using Seismic Results
The seismic experiments at Heinzenberg, detailed in Table 1, offer depth and velocity information for each layer. The results were individually interpreted for each site and integrated into a schematic profile of the Heinzenberg landslide (Figure 8a). The analysis of both passive seismic experiments and active seismic profiles yielded significant insights into the subsurface characteristics of the Heinzenberg area. The investigation revealed the presence of a superficially weathered rock mass in the initial few meters beneath the surface, followed by sedimentary fillings extending up to 20 m. These structures exhibit various shear-wave velocities, generally below 900 m/s, and P-wave velocities lower than 1600 m/s. Underneath the topmost layer, the rock mass of the deep-seated gravitational slope deformation (DSGSD) can be found. It reaches depths ranging between 30 and 50 m at HEI100/HEI200, up to 70 m at former Lake Lüsch and Obergmeind (HEI400), and between 90 and 110 m at Alp Lüsch (HEI300). Shear-wave velocities (vs) for the DSGSD range from 700 to 1150 m/s. The intact rock mass underneath the landslide mass exhibits shear-wave velocities greater than 1300 m/s and P-wave velocities exceeding 2400 m/s.

Table 1.
Overview of the results from passive seismic experiments at Heinzenberg with seismic vs and vp velocities and depths below the surface of the different layers. Numbers marked with * represent the entire array HEI300 being located 20 m of elevation above the inner array of HEI300.
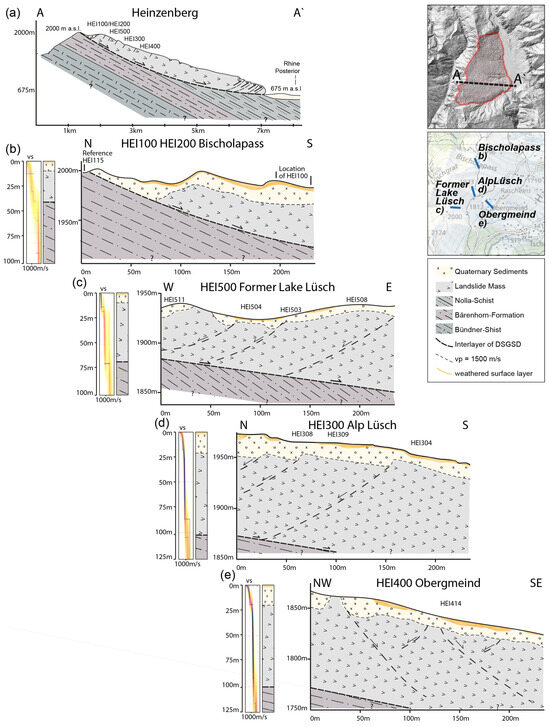
Figure 8.
Interpretation of the results of the seismic experiment at Heinzenberg. (a) Schematic profile of the Heinzenberg DSGSD with the location of the passive seismic arrays (HEI100 to HEI500). (b) geologic profile of Bischolapass (HEI100, HEI200) with a typical double-crested ridge and sedimentary filling. (b–e) detailed profiles in the direction of the SRT sections combining all data and a velocity profile to the left. Inserted legends represent the location of the schematic profile within the Heinzenberg (top), the location of the detailed profiles (b–e) (middle), and the legend of the drawn profiles (bottom).
For HEI100 and HEI200 at Bischolapass, a distinct double-crested ridge is observed (Figure 8b). The northern end of this ridge indicates a rapid increase in P-wave velocities in the SRT profile, suggesting that the highlighted rupture surface of the Heinzenberg DSGSD is situated behind the crest. The expected inclination of the rupture surface is around 25° [8], which is consistent with the superficial measurements in the vicinity [7]. The double crest is filled with sediments, creating drainless sinks where water is temporarily stored (e.g., Lake Bischol at 46.70636° N, 9.35805° E). However, due to the limited frequency range (3.5 Hz to 7 Hz) covered by the surface-wave dispersion analysis in the active seismic data, the velocity structure near the surface remains unconstrained. The inversion resolution is restricted to the first 40 m, resulting in a significant scatter of velocity profiles. Passive seismic data, on the other hand, reveal the interface between the DSGSD and intact rock at depths up to 40 m. This aligns with the interpreted headscarp of the DSGSD located just behind the crest of Bischolapass (Figure 8b).
The presence of wells has been noted at Alp Lüsch (HEI300), and insights from both SRT and inversion analyses offer valuable information about the subsurface structure. The data reveal a sedimentary layer extending from 15 to 20 m, alongside the interlayer of the DSGSD at depths exceeding 90 m. The relatively flatter morphology of the area might explain the occurrence of wells, as the flatter slope results in the accumulation of water from the steeper slopes above. Additionally, the water retention in this region could be influenced by the accumulation of fine-grained materials.
At Obergmeind (HEI400), sedimentary material extends to a depth of 20 m, and, similar to Alp Lüsch, the interlayer of the DSGSD is identified at depths exceeding 90 m. The partial lack of sedimentary cover at Obergmeind is likely attributed to superficial water runoff, which transports sedimentary material from these areas and redistributes it elsewhere, resulting in an uneven distribution of sediments across the region. The morphology of Obergmeind is characterized by NW–SE striking bedding planes. Notably, the array zone does not exhibit uphill-facing scarps. Instead, the formation of troughs forms depressions or channels filled with material originating from the DSGSD. This suggests that the unstable rock mass in Obergmeind primarily manifests through the lateral movement and spreading of material, as opposed to the creation of vertical scarps.
Situated just 80 m in elevation below the primary scarp of the DSGSD is former Lake Lüsch (HEI500), which might explain the shallower depth of the interface between the landslide mass and the intact rock (60–70 m). The prevailing NW–SE structures shaping the area’s morphology substantiate this association, resulting in uphill-facing scarps—a characteristic feature of the DSGSD’s upper part. In SRT profile SP07 (Figure 3g), a notable absence of sedimentary material in the western part indicates the substantial role played by superficial water runoff in transporting sedimentary material away from the surface. This runoff likely deposits sediment into the lake basin. Despite this, the SRT data for former Lake Lüsch reveal a slightly thinner sedimentary cover compared to other observed areas (Figure 8c). This discrepancy may be attributed to the proximity of former Lake Lüsch to the crest, limiting the sediment input from surrounding areas and resulting in a thinner sedimentary layer. The thinner sedimentary cover in the basin of former Lake Lüsch underscores the significance of considering spatial variations and local conditions when studying well formation, water accumulation, and groundwater conditions in the Heinzenberg region.
In summary, the seismic experiments and analyses conducted in Heinzenberg yield valuable insights into the subsurface structures and geological processes at the specified sites. The schematic profile of the Heinzenberg landslide illustrates a distinctive double-crested ridge at Bischolapass, signaling the presence of the DSGSD rupture surface behind the crest. This double crest, filled with sediments, forms drainless sinks that temporarily store surface water. The estimated inclination of the rupture surface varies, approximately 25° at the top and around 15° in the middle of the slope. The inversion analysis, while constrained by limitations in depth resolution, indicated that the rupture surface of the DSGSD at Heinzenberg extends from approximately 30 m at the upper part to well over 100 m in depth further downslope.
6. Conclusions
The seismic experiments conducted at four different sites on the Heinzenberg landslide have provided valuable insights into the subsurface structure and geological characteristics of the area. The results reveal the presence of superficial weathered rock layers and sedimentary fillings up to the first 20 m, with shear-wave velocities (vs) below 900 m/s and P-wave velocities (vp) below 1600 m/s. These shallow layers have clearly different and spatially varying seismic properties than the underlying layers. These layers are underlain by the rock mass of the deep-seated gravitational slope deformation (DSGSD), which varies in depth below the surface from 30 m to over 90 m at different sites. The shear-wave velocities (vs) of the DSGSD range from 700 m/s to 1150 m/s. The intact rock velocities underneath the DSGSD reach up to more than 1300 m/s for vs and more than 2400 m/s for vp. The seismic vp refraction tomography results support the interpretations of the shallow surface structure, showing distinct velocity gradients and interfaces between the different layers in the near-surface structure.
The seismic data also revealed the presence of uphill-facing scarps, lineaments, and morphostructural features associated with the DSGSD, such as ridge-top depressions and undulating terrains. The polarization analysis of ground motion indicates weak directional characteristics, mainly in the strike direction perpendicular to the existing structures or dominant fracture sets in the area. Comparisons between different inverted models and interpretations of dispersion curves highlight the uncertainties of the characteristics of superficial sediments and the depth of the interface between the landslide mass and the intact rock. The models consistently indicate the presence of distinct interfaces and velocity contrasts below the shallow superficial layers and the DSGSD. Overall, the seismic results contribute to the development of a baseline model for the selected sites in the Heinzenberg region, enhancing our understanding of the subsurface structure and geological processes associated with the DSGSD. These findings provide valuable information for further studies and assessments of the landslide dynamics and potential hazards in the area. In particular, this baseline model shall help identify potential changes after the refilling of Lake Lüsch, which started in 2021. Further research and analysis based on these results can provide additional insights and contribute to future geological studies in similar settings.
Emphasizing the broader significance of this research, it is important to recognize the global relevance of advancing our understanding of landslide dynamics through combining geophysical methodologies. Comparable studies conducted worldwide [36,64,65,66] underscore the universal importance of unraveling subsurface complexities for effective hazard assessment and mitigation strategies [35]. By aligning our efforts with a global context, we contribute to the collective knowledge that integrates geophysical and geodetic methods in landslide research and management on an international scale.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences14020028/s1, Figures S1–S30.
Author Contributions
Conceptualization, D.F. and F.G.; methodology, F.G., A.-S.M., L.C., H.-B.H., P.B., M.H. and D.F.; validation, D.F.; formal analysis, F.G., A.-S.M. and L.C.; investigation, F.G., A.-S.M., L.C., H.-B.H., P.B., M.H. and D.F..; resources, D.F. and H.-B.H.; data curation, F.G.; writing—original draft preparation, F.G.; writing—review and editing, F.G., A.-S.M., L.C., H.-B.H., P.B., M.H. and D.F.; visualization, F.G.; supervision, D.F.; project administration, D.F. and H.-B.H.; funding acquisition, D.F. and H.-B.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the projects “4D seismic response and slope failure” Swiss National Science Foundation SNF 200021E 177586 and Belgium National Science Foundation F.R.S.–FNRS 31230499, “quantification of the seismic response of instable slopes and its time variability: an important indicator for potential mass movements” SNF 200020_214916, and “Erkennung, Charakterisierung und Überwachung von Instabilitäten mit seismischen Technologien” Swiss Federal Office for the Environment FOEN 00.5032.PZ/EC049A5A7.
Data Availability Statement
Data generated in this study and their corresponding metadata are available on the ETH Research Collection via https://www.research-collection.ethz.ch/handle/20.500.11850/632639.
Acknowledgments
We thank S. Gartmann (commune of Tschappina) and A. Handke (SC¦H Chur) for their collaboration and organization of the permit for our permanent station. We thank A. Largiader (Amt für Wald und Naturgefahren, GR) for connecting us with the local parties. We thank our technician (U. Fässler, ETH) and field helpers from ETH Zurich (M. Studer, J. Junker, and P. Janusz) and from Liege (M. Julémont, C. Baudinet, and Ph. Cerfontaine) for their efforts in the field. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by ETH Zurich or the Swiss government.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Agliardi, F.; Crosta, G.B.; Zanchi, A. Structural constraints on deep-seated slope deformation kinematics. Eng. Geol. 2001, 59, 83–102. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P.; Agliardi, F. Deep seated gravitational slope deformations in the European Alps. Tectonophysics 2013, 605, 13–33. [Google Scholar] [CrossRef]
- Varnes, D. Slope movement types and processes. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- Agliardi, F.; Crosta, G.B.; Frattini, P. Slow rock-slope deformation. In Landslides: Types, Mechanisms and Modeling; Cambridge University Press: Cambridge, UK, 2012; pp. 207–221. [Google Scholar] [CrossRef]
- Osten, J.; Küppers, J.; Dufresne, A.; Huwiler, A.; Amann, F. Deep seated gravitational slope deformation of the southern Heinzenberg (Grison, Switzerland). Geomech. Tunn. 2020, 13, 74–87. [Google Scholar] [CrossRef]
- Stähli, W. Bericht zur Triangulation IV. Ordnung Heinzenberg: Diplomvermessungskurs 1976; Eidgenössische Technische Hochschule Zürich, Institut für Geodäsie und Photogrammetrie: Zürich, Switzerland, 1977. [Google Scholar]
- Wyss, R.; Jäckli, H.; Burla, S.; Streiff, V.; Wyss, R.; Wiederkehr, M. Thusis, Karte 1215, Geologische Karte des Bundesamt für Landestopografie swisstopo, Erläuterungen. In 1215 Thusis; Federal Office of Topography: Wabern, Switzerland, 2017. [Google Scholar]
- Ziegler, H. Die Hangbewegungen im Lugnez, am Heinzenberg und bei Schuders (Graubünden). Geologie und Geomechanik. Ph.D. Dissertation, Universität Bern, Bern, Switzerland, 1982. [Google Scholar]
- Evans, S.G.; Clague, J.J. Recent climatic change and catastrophic geomorphic processes in mountain environments. Geomorphology 1994, 10, 107–128. [Google Scholar] [CrossRef]
- Heim, A. Bergsturz und Menschenleben; Beer & Co.: Zürich, Switzerland, 1932. [Google Scholar]
- Savage, W.Z.; Swolfs, H.S.; Powers, P.S. Gravitational stresses in long symmetric ridges and valleys. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 291–302. [Google Scholar] [CrossRef]
- Zangerl, C.; Eberhardt, E.; Perzlmaier, S. Kinematic behaviour and velocity characteristics of a complex deep-seated crystalline rockslide system in relation to its interaction with a dam reservoir. Eng. Geol. 2010, 112, 53–67. [Google Scholar] [CrossRef]
- Romegialli, G. Das Ende des Lüschersees: Tschappina Heinzenberg; Desertina: Chur, Switzerland, 2012. [Google Scholar]
- Conzett, R. Verschiebungsmessungen am Heinzenberg; Photogrammetrisches Testfeld Heinzenberg; Verifikation von VPV-Operaten am Heinzenberg; Eichung der EDM-Distanzmesser: Diplomvermessungskurs (DVK)/Institut für Geodäsie und Photogrammetrie ETHZ 1986; Eidgenössische Technische Hochschule Zürich, Institut für Geodäsie und Photogrammetrie: Zürich, Switzerland, 1987. [Google Scholar]
- Ingensand, H. Diplomvermessungskurs Heinzenberg 1995—Neubestimmung der Landesfixpunkte; Diplomvermessungskurs Thusis 1995—Erstellen eines Grundlagennetzes; Institut für Geodäsie und Photogrammetrie an der Eidg. Technischen Hochschule Zürich: Zürich, Switzerland, 1997. [Google Scholar]
- Knechtel, S. Gefahrenkarte Heinzenberg Deformationsmessung 2018. HMQ AG 2017, 11. [Google Scholar]
- Burjanek, J.; Cauzzi, C.; Fäh, D.; Bard, P.-Y.; Cornou, C.; Pitilakis, K.; Massa, M.; Theodulidis, N.; Bertrand, E. Toward reliable characterization of sites with pronounced topography and related effects on ground motion. In Proceedings of the 15th World Conference on Earthquake Engineering (15WCEE), Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Kleinbrod, U.; Burjanek, J.; Fah, D. On the seismic response of instable rock slopes based on ambient vibration recordings. Earth Planets Space 2017, 69, 126. [Google Scholar] [CrossRef]
- Colombero, C.; Jongmans, D.; Fiolleau, S.; Valentin, J.; Baillet, L.; Bièvre, G. Seismic Noise Parameters as Indicators of Reversible Modifications in Slope Stability: A Review. Surv. Geophys. 2021, 42, 339–375. [Google Scholar] [CrossRef]
- Häusler, M.; Gischig, V.; Thöny, R.; Glueer, F.; Fäh, D. Monitoring the changing seismic site response of a fast-moving rockslide (Brienz/Brinzauls, Switzerland). Geophys. J. Int. 2022, 229, 310. [Google Scholar] [CrossRef]
- Havenith, H.-B.; Jongmans, D.; Faccioli, E.; Abdrakhmatov, K.; Bard, P.-Y. Site Effect Analysis around the Seismically Induced Ananevo Rockslide, Kyrgyzstan. Bull. Seismol. Soc. Am. 2002, 92, 3190–3209. [Google Scholar] [CrossRef]
- Mreyen, A.-S.; Cauchie, L.; Micu, M.; Onaca, A.; Havenith, H.-B. Multiple geophysical investigations to characterize massive slope failure deposits: Application to the Balta rockslide, Carpathians. Geophys. J. Int. 2021, 225, 1032–1047. [Google Scholar] [CrossRef]
- Burjanek, J.; Gassner-Stamm, G.; Poggi, V.; Moore, J.R.; Fäh, D. Ambient vibration analysis of an unstable mountain slope. Geophys. J. Int. 2010, 180, 820–828. [Google Scholar] [CrossRef]
- Danneels, G.; Bourdeau, C.; Torgoev, I.; Havenith, H.B. Geophysical investigation and dynamic modelling of unstable slopes: Case-study of Kainama (Kyrgyzstan). Geophys. J. Int. 2008, 175, 17–34. [Google Scholar] [CrossRef]
- Kleinbrod, U.; Burjanek, J.; Fah, D. Ambient vibration classification of unstable rock slopes: A systematic approach. Eng. Geol. 2019, 249, 198–217. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S.; Cotton, F.; Bard, P.-Y. The nature of noise wavefield and its applications for site effects studies: A literature review. Earth-Sci. Rev. 2006, 79, 205–227. [Google Scholar] [CrossRef]
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railw. Tech. Res. Inst. Q. Rep. 1989, 30, 9. [Google Scholar]
- Rezaei, S.; Shooshpasha, I.; Rezaei, H. Evaluation of landslides using ambient noise measurements (case study: Nargeschal landslide). Int. J. Geotech. Eng. 2020, 14, 409–419. [Google Scholar] [CrossRef]
- Pazzi, V.; Tanteri, L.; Bicocchi, G.; D’Ambrosio, M.; Caselli, A.; Fanti, R. H/V measurements as an effective tool for the reliable detection of landslide slip surfaces: Case studies of Castagnola (La Spezia, Italy) and Roccalbegna (Grosseto, Italy). Phys. Chem. Earth Parts A/B/C 2017, 98, 136–153. [Google Scholar] [CrossRef]
- Grandjean, G.; Malet, J.-P.; Bitri, A.; Méric, O. Geophysical data fusion by fuzzy logic for imaging the mechanical behaviour of mudslides. Bull. Société Géologique Fr. 2007, 178, 127–136. [Google Scholar] [CrossRef]
- Hibert, C.; Grandjean, G.; Bitri, A.; Travelletti, J.; Malet, J.-P. Characterizing landslides through geophysical data fusion: Example of the La Valette landslide (France). Eng. Geol. 2012, 128, 23–29. [Google Scholar] [CrossRef]
- Louie, J. Faster, Better: Shear-Wave Velocity to 100 Meters Depth From Refraction Microtremor Arrays. Bull. Seismol. Soc. Am. 2001, 91, 347–364. [Google Scholar] [CrossRef]
- Luo, Y.; Xia, J.; Miller, R.D.; Xu, Y.; Liu, J.; Liu, Q. Rayleigh-Wave Dispersive Energy Imaging Using a High-Resolution Linear Radon Transform. Pure Appl. Geophys. 2008, 165, 903–922. [Google Scholar] [CrossRef]
- Uhlemann, S.; Hagedorn, S.; Dashwood, B.; Maurer, H.; Gunn, D.; Dijkstra, T.; Chambers, J. Landslide characterization using P- and S-wave seismic refraction tomography—The importance of elastic moduli. J. Appl. Geophys. 2016, 134, 64–76. [Google Scholar] [CrossRef]
- Calamita, G.; Gallipoli, M.R.; Gueguen, E.; Sinisi, R.; Summa, V.; Vignola, L.; Stabile, T.A.; Bellanova, J.; Piscitelli, S.; Perrone, A. Integrated geophysical and geological surveys reveal new details of the large Montescaglioso (southern Italy) landslide of December 2013. Eng. Geol. 2023, 313, 106984. [Google Scholar] [CrossRef]
- Martino, S.; Cercato, M.; Della Seta, M.; Esposito, C.; Hailemikael, S.; Iannucci, R.; Martini, G.; Paciello, A.; Scarascia Mugnozza, G.; Seneca, D.; et al. Relevance of rock slope deformations in local seismic response and microzonation: Insights from the Accumoli case-study (central Apennines, Italy). Eng. Geol. 2020, 266, 105427. [Google Scholar] [CrossRef]
- Cavargna-Sani, M.; Epard, J.-L.; Steck, A. Structure, geometry and kinematics of the northern Adula nappe (Central Alps). Swiss J. Geosci. 2014, 107, 135–156. [Google Scholar] [CrossRef]
- Ivy-Ochs, S. Glacier variations in the European Alps at the end of the last glaciation. Cuad. Investig. Geográfica/Geogr. Res. Lett. 2015, 41, 295–315. [Google Scholar] [CrossRef]
- Ivy-Ochs, S.; Kerschner, H.; Reuther, A.; Preusser, F.; Heine, K.; Maisch, M.; Kubik, P.W.; Schlüchter, C. Chronology of the last glacial cycle in the European Alps. J. Quat. Sci. Publ. Quat. Res. Assoc. 2008, 23, 559–573. [Google Scholar] [CrossRef]
- Meisser, S. Die Nolla und die Geschichte ihrer Verbauung. In Jahrbuch des Schweizer Alpenclubs; Schweizer Alpen-Club SAC: Bern, Switzerland, 1910; Volume 46, p. 29. [Google Scholar]
- Jäckli, H. Die Bodenbewegungen im Hinterrhein-Tal und Ihre bautechnischen Auswirkungen; Schweizerische Bauzeitung: Zürich, Switzerland, 1948; p. 5. [Google Scholar]
- Fäh, D.; Kind, F.; Giardini, D. A theoretical investigation of average H/V ratios. Geophys. J. Int. 2001, 145, 535–549. [Google Scholar] [CrossRef]
- Hobiger, M.; Bard, P.; Cornou, C.; Le Bihan, N. Single station determination of Rayleigh wave ellipticity by using the random decrement technique (RayDec). Geophys. Res. Lett. 2009, 36, 5. [Google Scholar] [CrossRef]
- Burjanek, J.; Edwards, B.; Fah, D. Empirical evidence of local seismic effects at sites with pronounced topography: A systematic approach. Geophys. J. Int. 2014, 197, 608–619. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Effects of local geology on ground motion near San-Francisco-Bay. Bull. Seismol. Soc. Am. 1970, 60, 29–61. [Google Scholar]
- Perron, V.; Gélis, C.; Froment, B.; Hollender, F.; Bard, P.-Y.; Cultrera, G.; Cushing, E.M. Can broad-band earthquake site responses be predicted by the ambient noise spectral ratio? Insight from observations at two sedimentary basins. Geophys. J. Int. 2018, 215, 1442–1454. [Google Scholar] [CrossRef]
- Gischig, V.; Eberhardt, E.; Moore, J.; Hungr, O. On the seismic response of deep-seated rock slope instabilities—Insights from numerical modeling. Eng. Geol. 2015, 193, 1–18. [Google Scholar] [CrossRef]
- Chieppa, D.; Hobiger, M.; Bergamo, P.; Fäh, D. Ambient Vibration Analysis on Large Scale Arrays When Lateral Variations Occur in the Subsurface: A Study Case in Switzerland. Pure Appl. Geophys. 2020, 177, 4247–4269. [Google Scholar] [CrossRef]
- Hobiger, M.; Bergamo, P.; Imperatori, W.; Panzera, F.; Lontsi, A.M.; Perron, V.; Michel, C.; Burjánek, J.; Fäh, D. Site Characterization of Swiss Strong-Motion Stations: The Benefit of Advanced Processing Algorithms. Bull. Seism. Soc. Am. 2021, 111, 1713–1739. [Google Scholar] [CrossRef]
- Wathelet, M.; Chatelain, J.L.; Cornou, C.; Giulio, G.D.; Guillier, B.; Ohrnberger, M.; Savvaidis, A. Geopsy: A User-Friendly Open-Source Tool Set for Ambient Vibration Processing. Seismol. Res. Lett. 2020, 91, 1878–1889. [Google Scholar] [CrossRef]
- Wathelet, M.; Jongmans, D.; Ohrnberger, M.; Bonnefoy-Claudet, S. Array performances for ambient vibrations on a shallow structure and consequences over Vsinversion. J. Seismol. 2008, 12, 1–19. [Google Scholar] [CrossRef]
- White, D.J. Two-Dimensional Seismic Refraction Tomography. Geophys. J. Int. 1989, 97, 223–245. [Google Scholar] [CrossRef]
- Hayashi, K.; Takahashi, T. High resolution seismic refraction method using surface and borehole data for site characterization of rocks. Int. J. Rock Mech. Min. Sci. 2001, 38, 807–813. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.; Xia, J. Imaging dispersion curves of surface waves on multi-channel record. In SEG Technical Program Expanded Abstracts 1998; Society of Exploration Geophysicists: Tulsa, OK, USA, 1998; pp. 1377–1380. [Google Scholar]
- Xia, J.; Miller, R.D.; Park, C.B.; Hunter, J.A.; Harris, J.B. Comparing Shear-Wave Velocity Profiles from MASW with Borehole Measurements in Unconsolidated Sediments, Fraser River Delta, B.C., Canada. J. Environ. Eng. Geophys. 2000, 5, 1–13. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Multichannel analysis of surface waves. Geophysics 1999, 64, 800–808. [Google Scholar] [CrossRef]
- Park, C.B. SurfSeis-Active and Passive MASW. User’s Manual V2.0; Kansas Geological Survey: Lawrence, KS, USA, 2006. [Google Scholar]
- Hallo, M.; Imperatori, W.; Panzera, F.; Fäh, D. Joint multizonal transdimensional Bayesian inversion of surface wave dispersion and ellipticity curves for local near-surface imaging. Geophys. J. Int. 2021, 226, 627–659. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar] [CrossRef]
- Green, P.J. Reversible Jump Markov Chain Monte Carlo Computation and Bayesian Model Determination. Biometrika 1995, 82, 711–732. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Sambridge, M. A Parallel Tempering algorithm for probabilistic sampling and multimodal optimization. Geophys. J. Int. 2013, 196, 357–374. [Google Scholar] [CrossRef]
- Glueer, F.; Mreyen, A.S.; Cauchie, L.; Havenith, H.; Bergamo, P.; Halló, M.; Fäh, D. Seismic data to Integrating Seismic Methods for Characterizing and Monitoring Landslides: A Case Study of the Heinzenberg Deep-Seated Gravitational Slope Deformation (Switzerland). 2023. [CrossRef]
- Del Gaudio, V.; Wasowski, J.; Hu, W.; Capone, P.; Venisti, N.; Li, Y. Ambient noise and ERT data provide insights into the structure of co-seismic rock avalanche deposits in Sichuan (China). Bull. Eng. Geol. Environ. 2021, 80, 7153–7170. [Google Scholar] [CrossRef]
- Harba, P.; Pilecki, Z.; Krawiec, K. Comparison of MASW and seismic interferometry with use of ambient noise for estimation of S-wave velocity field in landslide subsurface. Acta Geophys. 2019, 67, 1875–1883. [Google Scholar] [CrossRef]
- Klimeš, J.; Hussain, Y.; Mreyen, A.-S.; Cauchie, L.; Schlögel, R.; Piroton, V.; Petružálek, M.; Blahůt, J.; René, M.; Meletlidis, S.; et al. New Insights into the Internal Structures and Geotechnical Rock Properties of the Giant San Andrés Landslide, El Hierro Island, Spain. Remote Sens. 2023, 15, 1627. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).