Abstract
Today, concepts within the Global Geodetic Observing System (GGOS) aim a Terrestrial Reference System (TRS) with 1 mm accuracy and long-term stability of 0.1 mm/year. GETRIS (Geodesy and Time Reference In Space) is a concept that aims to realize a relativistic reference system based on satellites as an extension to the TRS. This helps with another goal of the GGOS, namely, the connection of different satellite layers with the TRS. For a valuable contribution to the GGOS’s goals, we would expect to achieve precise determined satellite orbits at the level of 1–3 mm and satellite clocks with a picosecond accuracy. The use of increasingly precise links helps to improve the satellite precise orbit determination (POD) and is necessary to synchronize the clocks in the satellite/station network. We analyze a complementary use of high-precision optical dual one-way links at the level of 1 mm precision together with the L-band. In previous studies, we analyzed the benefit for satellite POD, achieving Medium Earth Orbit (MEO) as well as geosynchronous orbit (GSO) accuracies at the low-millimeter level. In this work, we analyze the capabilities for clock synchronization. We compare two different clock types for estimation and prediction. We analyze different satellite constellations and different combinations of measurement links.
1. Introduction
The aims for the future Terrestrial Reference System (TRS) are driven by the goals of the Global Geodetic Observing System (GGOS) [1]: 1 mm accuracy and long-term stability of 0.1 mm/year. The GGOS wants to achieve these goals by the collocated use of different observation techniques such as GNSS (Global Navigation Satellite System) measurements, VLBI (Very Long Baseline Interferometry), SLR (Satellite Laser Ranging), LLR (Lunar Laser Ranging), radar observations, ISL (Inter-Satellite Links) and gravity acceleration measurements. Furthermore, it is important for the GGOS to closely connect the different satellite layers from the Low Earth Orbit (LEO), via the Medium Earth Orbit (MEO), to the geosynchronous orbit (GSO).
The concept of a Geodesy and Time Reference in Space (GETRIS) was first discussed by [2,3]. The goal of GETRIS is to extend the TRS by a space-based relativistic reference system to contribute to the GGOS for the connection of the near Earth environment and deep space—the moon and beyond. With the complementary use of GNSS L-band measurements and dual one-way high-precision optical links between GSO and MEO satellites, a 1 mm orbit precision as well as a clock synchronization at the picosecond level shall be achieved. Dual one-way links are two one-way links that simultaneously measure between two entities, where both are transmitters and receivers. From a technical perspective, the optical links are comparable to the European Data Relay System (EDRS; [4,5])’s links, which are used for data communication with geostationary (GEO) satellites. Due to its high modulation rate, the EDRS link would technically allow ranging and time transfer with high precision. To move toward a GETRIS, such optical links have to be adapted to perform calibrated ranging and time transfer.
The GENESIS satellite mission [6] has a similar approach as the one we follow with the GETRIS concept. By a collocated use of geodetic techniques in space—GNSS, SLR, VLBI and DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite)—the time and space reference systems on Earth are aimed to be improved and homogenized. GENISIS also intends to equip the satellite with a high-stability clock. The goal is to realize a TRS with accuracy of 1 mm and long-term stability of 0.1 mm/year, which also matches the GGOS’s [1] goal. A GENESIS-like concept on GNSS satellites would even enhance the contribution to the GGOS and GETRIS.
The development of high-stability clocks has been rapidly growing in the recent past. The Cesium atomic clock (frequency stability in the low 10−13 region at one day), the Rubidium Atomic Frequency Standard (RAFS) (frequency stability in the low 10−14 region at one day) and the Passive Hydrogen Maser (PHM) (frequency stability in the high 10−15 region at one day) are clock types that are already used in satellites of different GNSSs. Satellite missions to test clocks with a significantly increased precision are already in preparation. These high-stability clock concepts are, e.g., clocks based on iodine cells and using optical frequency standards with a targeted frequency stability in the low 10−15 region for sample intervals between 100 s and 10,000 s [7,8,9]. The Deep Space Atomic Clock (DSAC; [10]), a trapped-ion atomic clock developed by the National Aeronautics and Space Administration (NASA), already demonstrated stability of 2 × 10−15 at 1 day and 3 × 10−15 at 23 days [10,11]. Along with the ESA mission Atomic Clock Ensemble in Space (ACES; [12,13]), a new clock concept is tested, which combines an Active Hydrogen Maser (AHM) and a laser-cooled Cesium clock, called the Project d’Horloge Atomique à Refroidissement d’Atomes en Orbite (PHARAO) [12,13,14]. The expected frequency stability and precision is at the level of 3 × 10−15 at 300 s, 3 × 10−16 at 1 day and 1 × 10−16 at 10 days. The main challenges of such future clock types are still the high costs and the complex manufacturing to be able to be carried by a satellite. For real-time processing and, thus, for clock prediction, it is important to have stable clocks. However, with an epoch-wise clock processing, a more stable clock does not give an improvement for clock estimation. To achieve improvements in the estimation, a possibility is to optimize the algorithm for clock modeling.
Optical two-way Inter-Satellite Links (OISL) is one measurement technique to perform high-precision dual one-way satellite-to-satellite tracking with a laser [8,15,16,17]. The impact of different ISL connectivity schemes was simulated in [15,18]. An alternative to OISL is optical two-way/dual one-way ground-to-satellite links. European Laser Timing (ELT; [19]), as part of the ACES mission, and T2L2 (Time Transfer by Laser Link; [20]) are two of the ground-to-satellite ranging and time transfer techniques. BeiDou already involved an optical measurement technique for two-way ranging, named Laser Time Transfer (LTT; [21]), and a two-way microwave technique, named Two-way Satellite Time and Frequency Transfer (TWSTFT; [22]), to achieve accurate time transfer. In [16,23], we introduced the Optical Two-Way Link (OTWL) measurement concept for a future GNSS MEO satellite constellation. This concept builds on dual one-way measurements and is the ground-to-space counterpart of OISL. In [16], we compared the OISL and OTWL measurement techniques and showed the benefits of synergistically using both techniques with Galileo L-band measurements for the POD of MEO satellites. In [17], we expanded the MEO satellite constellation by using inclined geosynchronous orbit (IGSO) and GEO satellites and analyzed the orbit errors. The resulting orbit errors from [17] showed that combinations of these measurement techniques also increase the orbit accuracy of IGSO and GEO satellites to the millimeter level.
While we only analyzed the orbit errors in [16,17], in this study we focus on the analysis of the satellite clocks from the simulation scenarios, which are identical to [17]. Our target is to estimate the satellite clocks, with respect to the reference clock, with an accuracy at the picosecond level. We assumed that all satellites in the constellation each carry a PHM. The clocks were estimated epoch-wise using a least-squares adjustment. We analyzed the results of the clock estimation by the mean error and standard deviation of the estimated (apparent) clocks as well as the Allan deviation [24]. For comparison, we performed a further simulation using the ACES clock as an example of a clock with high stability for the future. Last, we performed the prediction of the estimated clocks for all scenarios up to one day. We analyzed the influence of the OTWL and/or OISL measurements being used in addition to the GNSS L-band observations as well as the expansion of the MEO constellation with either the IGSO or GEO satellites for the clocks’ estimation and prediction. We want to indicate that this work is a simulation study and is still far from a realistic project study. We take many systematic errors for the observations’ simulation and the orbit modeling into account, but the complexity of physical reality cannot be fully transported into a simulation environment.
2. Simulation Setup and Estimation
For this paper, we evaluate the impact of different high-precision observation techniques used by a future GNSS satellite constellation for the estimation of satellite clocks. The whole simulation and estimation procedure is equal to [17]. For the simulations and analysis, we used a modified version of Bernese GNSS Software 5.2 [25]. Next, we describe the satellite constellations used (Section 2.1), the simulated observation techniques (Section 2.2) and the measurement errors (Section 2.3) as well as the parameters estimated in the least-squares adjustment (Section 2.4 and Section 2.5).
2.1. Satellite Constellations and Ground Station Network
We selected the Galileo MEO satellite constellation—the satellite properties are based on the first-generation Galileo satellites—as a typical GNSS satellite constellation and expanded the constellation by either four GEO or IGSO satellites. Analogous to the scheme of the GETRIS concept, we globally distributed the GSO satellites around the Earth [2,3]. An overview of the three satellite types used in this work is given in Table 1. We analyzed the results for the MEO-only, MEO+IGSO and MEO+GEO constellations. As the ground station network used for the L-band and OTWL measurements consists of 16 ground stations (see Figure 1), the GSO satellites had a different total number of visible ground stations. This allowed for an analysis of the necessary ground station visibility as well.

Table 1.
Simulated satellite types.

Figure 1.
Ground station network used in this study.
Our analysis was based on a period of 10 days, the Galileo MEO repeat cycle. We processed 24 h observations, and the results were taken from one-day arcs. All satellites were each equipped with one clock, to which all the observations types refer to. For the first analysis, we emulated a PHM clock on each satellite. The PHM clocks were simulated with white frequency noise at the level of 1 × 10−12 and random walk at the level of 3.9 × 10−16 when integrating over one second. A quadratic phase drift was not simulated. For comparison, we performed further simulations with the ACES clocks, carried by all satellites in the constellation, representing a high-stability clock. We simulated the AHM of the ACES clock with flicker phase noise at the level of 1.4 × 10−13, white frequency noise at the level of 3 × 10−14 and flicker frequency noise at the level of 1.35 × 10−15, when integrating over one second. PHARAO was simulated with white frequency noise at the level of 1 × 10−13 when integrating over one second. The ACES clock noise is composed in such a way that the lowest noise always dominates. As PHARAO is a frequency standard, the ACES clock is expected to have no quadratic phase drift. We are aware that high-stability clock types such as the ACES clock will not be used as a standard GNSS satellite clock in the near future. Nevertheless, in this work we want to analyze the benefit when using the ACES clocks for GSO and MEO satellites.
2.2. Simulated Obervation Techniques
The simulated observation types for the study are the common GNSS L-band as well as optical ranging and time transfer measurements: OISL, as a dual one-way satellite-to-satellite measurement concept, and OTWL, as the dual one-way ground-to satellite counterpart. An overview of the different links and their simulation procedures is given in Table 2.

Table 2.
Simulated measurement techniques.
In our simulations, it is assumed that each satellite is equipped with one terminal to perform OTWL measurements in the L-band+OTWL scenario. For OTWL, a ground station can, thus, connect with one satellite per epoch. In the following epoch, the ground station tracks the nearest available satellite by its elevation and azimuth to avoid long-distance telescope movements. The OTWL scheduling algorithm is optimized to avoid a ground station connecting with the same satellite in consecutive epochs. The minimum OTWL measurement elevation, as seen from the ground stations, is 30°. A more detailed description of the OTWL scheduling algorithm is given in [16].
Furthermore, we assumed that each satellite is equipped with one terminal to perform OISL measurements in the L-band+OISL scenario. The scheduling was an any-to-any scenario. The connectivity scheme was adapted from [27]. In the case of MEO+IGSO and MEO+GEO constellations, the IGSO or GEO satellites were integrated alongside the MEO satellites in the any-to-any link connectivity scheme, such that no GSO satellite connects to another GSO satellite in successive epochs.
For the L-band+OTWL+OISL scenario, the satellites were assumed to be equipped with two optical terminals: one to exclusively perform OISL measurements and the other to exclusively perform OTWL measurements.
In this study, we combined the three observation techniques in several ways, such as the L-band+OTWL, L-band+OISL and L-band+OTWL+OISL scenarios, and compared the results to the L-band-only scenario. We also performed the optical-only measurement technique scenario OTWL+OISL; however, in this scenario the clocks are singular [17]. Therefore, we do not consider the OTWL+OISL scenario in this work. Furthermore, we neglect relativistic effects on the clocks. No full recovery of the relativistic influences of the orbit may further disturb clock synchronization.
2.3. Simulated Measurement Errors
The simulated measurement errors for the L-band are collected in Table 3 and for the optical links in Table 4. A more detailed description of the simulation of the measurement techniques and the measurement errors is given in [15,17]. For the L-band, we only simulated white noise, while for the optical measurement types, we also accounted for other noise types. Furthermore, we used different troposphere models in the simulation and the further analysis. In the case of the L-band, we simulated Phase Center Variations (PCV) as an elevation-dependent error. Table 3 and Table 4 show that we separated the inter-technique bias into a phase bias contribution and an optical bias contribution. Hence, for our simulations we assumed that these biases remain from the calibration with the optical links.

Table 3.
Simulated L-band measurement errors.

Table 4.
Simulated OTWL and OISL measurement errors. A detailed description of the different errors is given in [15].
2.4. Estimated Parameters
An overview of the estimated parameters, with respect to each measurement technique, is given in Table 5. The estimated Solar Radiation Pressure (SRP) parameters are discussed in more detail in Section 2.5. Furthermore, we estimated station-specific tropospheric wet zenith delays for the L-band (two-hour sampling), but we did not estimate troposphere parameters with respect to the OTWL measurements. We did not estimate ground station coordinates. Satellite and ground station clock parameters were estimated epoch-wise. For the optical measurements, we estimated a daily range and clock synchronization bias for each transmitter and receiver. As we also simulated variable biases for the optical links, the estimation of daily biases did not fully represent the model. The simulated inter-technique bias also had a phase bias contribution, but for the L-band we did not estimate range and clock synchronization biases. We estimated phase ambiguities (float) for the L-band. The phase biases are absorbed by the ambiguity estimation to a great extent.

Table 5.
Estimated parameters with respect to each observation technique.
Overall, the estimation of the biases leads to a rank-deficient normal equation matrix in our simulations. Therefore, we introduced constraints for the bias estimation in different scenarios: constraints within the range of the expected precision of the optical links (1 mm) and a solution with five times looser constraints.
2.5. Estimated SRP Parameters
SRP is the largest non-gravitational force disturbing the orbits of MEO and GSO satellites [33,34,35]. To include an SRP error in the procedure, we used the box-wing (BW) model from [26] when generating the orbits for the simulation. For the GNSS solutions, we used empirical SRP parameters in the least-squares adjustment. No BW parameters were estimated. ECOM2 [36], with a total of nine SRP parameters, was selected as the basic empirical SRP model. The model was defined in the DYB coordinate system: D points from the satellite to the Sun, Y is the direction along the solar panels and B completes the right-handed orthogonal system. The ECOM2 (Equation (1)) SRP parameters were estimated as constant as well as periodic sine and cosine terms, including a once per revolution term in B as well as two and four times per revolution terms in D. Δu is the argument of latitude with respect to the Sun. In the further context, the constant parameters had a subscript 0. A subscript s was used for the sine parameter and a c for the cosine parameter. The per revolution term was numbered following the corresponding directions: D, Y or B.
As discussed in [16], it is possible to estimate up to 13 SRP parameters in a POD process when using measurements of two or more different observation techniques. The L-band-only measurement scenario could not benefit from estimating more than nine SRP parameters. Therefore, for the results shown in this work, we used ECOM2 (Equation (1)) for scenarios only using the L-band.
D = D0 + D2c cos(2Δu) + D2s sin(2Δu) + D4c cos(4Δu) + D4s sin(4Δu),
Y = Y0,
B = B0 + B1c cos(Δu) + B1s sin(Δu),
Y = Y0,
B = B0 + B1c cos(Δu) + B1s sin(Δu),
For scenarios using combinations of measurement techniques, we used an extended SRP model containing more than nine parameters. While the estimated parameters for D and Y stay the same, we extended further, per the revolution terms, for B. First, we extended the ECOM2 by the B3 parameter (sine and cosine (Equation (2)).
B = B0 + B1c cos(Δu) + B1s sin(Δu) + B3c cos(3Δu) + B3s sin(3Δu),
Second, we extended Equation (2) by the B5 parameters (sine and cosine (Equation (3)). Again, the D and Y parameters are identical to ECOM2 (see Equation (1)) when using this SRP modeling.
B = B0 + B1c cos(Δu) + B1s sin(Δu) + B3c cos(3Δu) + B3s sin(3Δu) + B5c cos(5Δu) + B5s sin(5Δu),
For each simulation scenario, we used the SRP modeling that is the best in the solution.
The DYB coordinate system is optimized for MEO and IGSO satellites but not for GEO satellites. As in orbit-normal mode, the orientation of the solar panel is not perpendicular to the Sun-satellite direction, so we used a different DYB orientation for the GEO satellites, named ͟D͟Y͟B. In this frame, ͟Y is perpendicular to the orbital plane, ͟B is perpendicular to ͟Y and the Sun-satellite direction, and ͟D completes the right-handed orthogonal system. In [17], we analyzed the modeling error introduced by the parameter differences of the true and mismodeled BW parameters for the GEO satellites. The result was a further optimized model, as shown in Equation (4). The maximum number of parameters is still 13.
͟D = ͟D0 + ͟D1s sin(Δu) + ͟D2c cos(2Δu) + ͟D3s sin(3Δu) + ͟D4c cos(4Δu),
͟Y = ͟Y0 + ͟Y1s sin(Δu) + ͟Y2c cos(2Δu),
͟B = ͟B0 + ͟B1c cos(Δu) + ͟B2s sin(2Δu) + ͟B3c cos(3Δu) + ͟B4s sin(4Δu),
͟Y = ͟Y0 + ͟Y1s sin(Δu) + ͟Y2c cos(2Δu),
͟B = ͟B0 + ͟B1c cos(Δu) + ͟B2s sin(2Δu) + ͟B3c cos(3Δu) + ͟B4s sin(4Δu),
3. Results
We discuss the results of this simulation study by analyzing the clock error (true—estimated clocks) for MEO satellites as well as IGSO and GEO satellites in the constellation. While we used PHM satellite clocks for the simulations performed in [17], all scenarios in this work are completed for two different clock types—the PHM and ACES clocks—carried by all satellites in the constellation. We analyze the clock error for the estimated period and discuss the clock prediction possibilities for the different scenarios. For each scenario, we select the SRP modeling according to the overall best solution—Equations (1)–(3) in the case of MEO and IGSO satellites and Equation (4) in the case of GEO satellites. The weights between the different observation techniques are shown in Table 6 and are selected in terms of the best orbit accuracies that could be achieved with a certain weighting. A variance component estimation was analyzed in [37].

Table 6.
Weighting of OTWL and OISL observations with respect to L-band measurements σ2L-band/σ2OTWL/OISL.
In the following, we first analyze the constraining of the clock synchronization biases in the case of OTWL measurements (Section 3.1), as this gives the constraining we use for all further analyses of the clock errors in this study. Then, we analyze the clock errors (Section 3.2) by a separate detailed analysis of the mean error (Section 3.2.1) and the standard deviation of the estimated clocks (Section 3.2.2) for the different scenarios. An analysis of the Allan deviation is given in Section 3.3. All the listed analysis steps are completed for the estimated period. Last, we analyze the possibilities of the clocks’ prediction for all the simulated scenarios (Section 3.4). The results for the clock errors are mostly given in centimeters to relate to the positioning error that is analyzed in this work.
3.1. Analysis of the Constraining of the Clock Synchronization Biases
In different scenarios regarding OTWL observations, the clock synchronization biases are either hardly (at the level of the ranging precision of 1 mm) or loosely (five times looser constraints) constrained by introducing pseudo-observations. Scenarios without OTWL observations are not affected by the constraints’ variations. In the following sections, we perform a separate detailed analysis on the mean error (see Section 3.2.1) as well as the standard deviation of the estimated clocks (see Section 3.2.2), but overall the different constraining types do not affect the standard deviation of the estimated clocks. Therefore, to analyze the effect of the constraining of the clock synchronization biases, we compute the mean error of the estimated clocks per satellite and per day of the simulation period. This leads to a total of 240 realizations for the MEO-only constellation and up to 280 realizations for the MEO+GSO constellation. These realizations are arranged in ascending order and the minimum, the 5%, the mean (average), the 95% and the maximum absolute values are extracted per scenario. Figure 2 shows the mean error of the estimated clocks as a function of the L-band+OTWL and L-band+OTWL+OISL scenarios as well as hard (left plot) or loose (right plot) constraining.

Figure 2.
Analysis of the constraining of the clock synchronization biases in the case of OTWL observations. The plots show the mean error of the estimated clocks as a function of the type of observables used, and hard (left plot) or loose (right plot) constraining. The minimum, mean (average) and maximum values as well as the values bounding the 5% or 95% of the results are reported.
For the L-band+OTWL scenario, a large discrepancy between the minimum and maximum value is generally noticeable. The L-band+OTWL scenario with hard constraints gives a factor of about 10 lower mean errors than we obtain from the scenario with five times looser constraints. For the L-band+OTWL+OISL scenario, much lower maximum values as well as a much smaller discrepancy between the minimum and maximum values can be achieved. This is due to the additional use of OISL observations. With the hard constraints, the mean error of the estimated clocks is on average at a factor of about 7.5 smaller than in the scenario with looser constraints. The same behavior can be found for results regarding the MEO+IGSO and MEO+GEO constellations. For our specific simulations, this leads us to use the hard constraints for all the further results presented in this work. Our goal is to realize a time and ranging reference. Therefore, hard constraining is needed, and for the optical link it is assumed that it is calibrated as good as possible.
3.2. Results of the Estimated Clocks
In this section, we analyze the results of the estimated clocks (true—estimated). Figure 3 shows the clock errors for different scenarios and 10 days of the simulation period from the MEO-only constellation. A similar behavior for the total error of the estimated clocks is achieved for the MEO+IGSO and MEO+GEO constellations. Referring to Figure 3, we provide a separate detailed analysis on the mean error and the standard deviation of the estimated clocks in the following subsections.
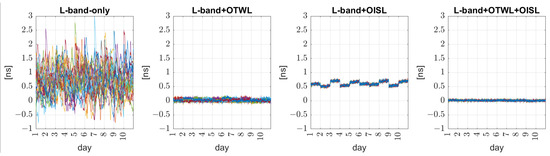
Figure 3.
Total error of the estimated clocks for the different combinations of observation techniques and for the 10 days of the simulation period. Each color represents a different clock.
3.2.1. Mean Error of the Estimated Clocks
In this section, we analyze the mean error of the estimated clocks (true—estimated) for the different scenarios. The results shown in this section refer to simulations with the PHM clocks, but almost the same results are achieved for the ACES clocks. This is expected when estimating clocks epoch-wise. The advantage of a more stable clock is then only exploited in the prediction.
For the L-band-only scenario, a substantial mean error of the estimated clocks is noticeable (see Figure 3). Due to the epoch-wise clock estimation, errors from other sources—e.g., remaining orbit errors, errors due to a wrong bias estimation and dominant troposphere errors—are shifted to the clock. The optical observations support the L-band and prevent these errors from going into the clock. OISL does not allow for errors to be put into individual satellite clocks, as all satellite clocks are strongly connected. This is the huge benefit of OISL, as all satellites are synchronized with each other. The results for the clock errors are mostly given in centimeters to relate to the positioning error, which is analyzed in this work. Hence, the scenarios including OISL show the same mean error of the estimated clocks for all satellites for each daily solution, but the mean errors are still substantial. The reason is that OISL has no direct relation to the reference station on the ground, which only allows to uniformly distribute the clock synchronization biases for an average error. For the L-band-only or L-band+OTWL scenarios, the mean error of the estimated clocks varies for each satellite. However, for the scenarios including OTWL measurements, the estimated clock synchronization bias compensates for the systematic errors to a great extent. The reason is that OTWL has a direct relation to the reference station, and OTWL forces the solution toward the optical troposphere error—no model parameters are estimated for the optical troposphere delays, which are at the level of some millimeters. In the L-band+OTWL+OISL scenario, both the arguments of OISL and OTWL apply together.
Analogous to Section 3.1, we compute the mean error of the estimated clocks per satellite and per day of the simulation period, arranging the realizations in ascending order and extract the minimum, the 5%, the mean (average), the 95% and the maximum absolute values of all realizations. Figure 4 compares the mean error of the estimated clocks for the L-band-only, L-band+OTWL, L-band+OISL and L-band+OTWL+OISL scenarios in the MEO-only constellation. On average, the L-band-only scenario achieves a mean error of the estimated clocks of around 21 cm. The scatter of the mean error of the estimated clocks for the different realizations is substantial. For the L-band+OISL scenario, the average error reduces to around 18 cm. The minimum error is at 15 cm, and the maximum error is at around 21 cm. The scatter is from the daily variation in the estimated clock synchronization biases, as all satellites achieve an almost identical mean error of the estimated clocks per daily solution (see Figure 3). The L-band+OTWL scenario achieves an average error of 0.8 cm and 3.8 cm at the maximum. The L-band+OTWL+OISL scenario achieves the best results with an average error of 0.3 cm and a maximum error of 0.7 cm.
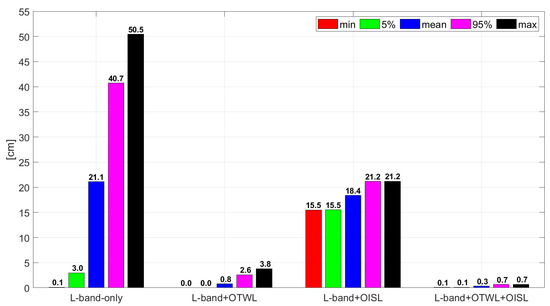
Figure 4.
Analysis of the mean error of the estimated clocks, averaged for the 24 MEO satellites in the MEO-only constellation. The plot shows the mean error of the estimated clocks as a function of the type of observables used. The minimum, mean (average) and maximum values as well as the values bounding the 5% or 95% of the results are reported.
For additional IGSO satellites in the constellation, no significant changes in the mean errors of the estimated clocks are noticeable for the MEO satellites for all the scenarios compared to the MEO-only constellation.
For IGSO satellites, the mean errors of the estimated clocks behave similarly overall to the MEO satellites. However, due to the varying number of visible ground stations for each of the four IGSO satellites and, hence, the varying numbers of L-band observations, the scatter between the minimum and maximum values of the mean error of the estimated clock is much larger in the L-band-only scenario than for the MEO satellites. For L-band-only the best realization is at around 2 cm and the worst at around 70 cm. Although the number of OTWL observations varies with the number of visible ground stations for each IGSO, no significant degradation of the mean error of the estimated clocks shows up for the L-band+OTWL scenario, when analyzing the different realizations, compared to the results achieved for the MEO satellites. The same behavior is noticeable for the L-band+OISL scenario. However, the L-band+OTWL+OISL scenario shows about 1 cm worse mean errors of the estimated clocks for some realizations for the IGSO satellites. When averaging the mean errors of the estimated clocks per satellite over 10 days (see Figure 5), it is noticeable for the L-band+OTWL and L-band+OTWL+OISL scenarios that one IGSO satellite has a larger mean error of the estimated clock than the other IGSO satellite or all the MEO satellites.
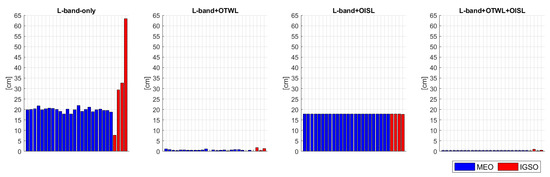
Figure 5.
Analysis of the mean error of the estimated clocks by computing the mean per satellite per day and then averaging over the 10 days of the simulation period per satellite. Each blue bar is related to one of the 24 MEOs; the red bars relate to the IGSO satellites in the MEO+IGSO constellation.
For the MEO+GEO constellation, the L-band-only scenario achieves worse mean errors of the estimated clocks for the MEO satellites, compared to the MEO-only constellation. The degradation in the L-band-only scenario is at around 3 cm for the mean and the 95% values and 9 cm for the maximum value. For the scenarios with combinations of observation techniques, the mean errors of the estimated clocks are similar to the results from the MEO-only constellation.
For the GEO satellites, the coverage by the ground stations largely affects the results of the L-band-only and L-band+OTWL scenarios. While each IGSO satellite has visibility of at least four ground stations, some GEO satellites see less: GEO-1 sees two stations, GEO-2 sees five stations, GEO-3 sees one station, and GEO-4 sees three stations. Due to this, the normal equation matrix in the estimation is singular for some GEO satellites in the L-band-only and L-band+OTWL scenarios, as we estimate the orbit parameters in parallel to the clock parameters. Therefore, we have to exclude GEO-1, -3 and -4 from the L-band-only analysis. Due to the additional two-way observations in the L-band+OTWL scenario, the clocks can be synchronized with only three ground stations when estimating the orbit and clock parameters in parallel. Hence, we only exclude GEO-1 and -3 for the L-band+OTWL scenario. The mean clock errors of the estimated clocks, averaged over 10 days, are shown in Figure 6. For the GEO satellites, similar mean errors of the estimated clocks can be achieved compared to the MEO satellites, for all scenarios.
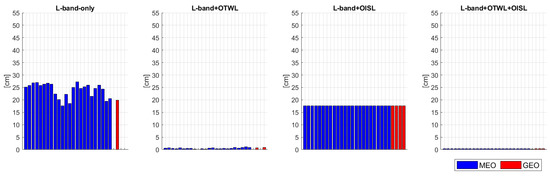
Figure 6.
Analysis of the mean error of the estimated clocks by computing the mean per satellite per day and then averaging over the 10 days of the simulation period per satellite. Each blue bar is related to one of the 24 MEO; the red bars relate to the GEO satellites in the MEO+GEO constellation.
For MEO, IGSO and GEO satellites, the main outcome is that the OISL measurements homogenize the mean errors of the estimated clocks for all satellites, which is especially noticeable when averaging the results per satellite over several days. This is expected from OISL and underlines the advantage of having steady clock synchronizations between satellites at different altitudes. Although the OTWL observations in addition to the L-band measurements cannot synchronize satellite clocks to each other, the overall mean error of the estimated clocks is much smaller compared to the L-band+OISL scenario, as OTWL has a direct relation to the reference clock and, hence, helps to reduce the L-band’s systematic errors. The L-band+OTWL+OISL scenario combines the advantages of OISL and OTWL.
3.2.2. Standard Deviation of the Estimated Clocks
In this section, we analyze the standard deviation of the estimated clocks. The results shown in this section refer to the simulations with the PHM clocks but are analogous to the mean errors of the estimated clocks; the estimation results are similar when using the ACES clocks.
For the MEO satellites, the standard deviations of the estimated clocks are similar for the MEO-only and MEO+IGSO constellations. The results according to 240 realizations is shown in Figure 7 as an example for the MEO+IGSO constellation. The L-band-only scenario still has cm level standard deviations and a remarkable discrepancy between the minimum (around 2.7 cm) and maximum (around 18 cm) values. On the other hand, the standard deviations of the estimated clocks are at the mm level for the scenarios that include optical links (see also Figure 3). In addition, when the daily standard deviations per satellite are averaged over 10 days, the scatter of the results between the satellites is negligibly small with mean values of around 4–7 mm. The L-band-only scenario has a maximum scatter of about 4 cm and a mean of around 8 cm.
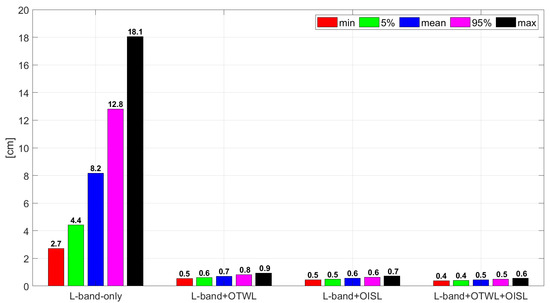
Figure 7.
Analysis of the standard deviation of the estimated clocks for the 24 MEO satellites in the MEO+IGSO constellation. The plot shows the standard deviation of the estimated clocks as a function of the type of observables used. The minimum, mean (average) and maximum values as well as the values bounding the 5% or 95% of the results are reported.
For the MEO satellites in the MEO+GEO constellation, the daily results for the standard deviation of the estimated clocks are similar to the results of the MEO-only and MEO+IGSO constellations for the scenarios that include optical links. The L-band-only scenario shows worse results. Compared to the MEO-only and MEO+IGSO constellations, the degradation factor is around 1.8 for the mean value and around 2.7 for the 95% and the maximum value. The reason for the degradation in the L-band-only scenario is the correlation between the troposphere (visible in the estimated parameters of the tropospheric wet zenith delay) and clock parameters, as the final MEO orbit errors are rather smaller when adding the GEO satellites to the constellation (compare [17]).
Analyzing the scenarios with GSO satellites in the constellation, in the L-band-only scenario the best realization (minimum value) for the IGSO satellites is at around 5.7 cm, while the worst (maximum value) is at around 44 cm. Averaged over 10 days, the best IGSO achieves a standard deviation of the estimated clocks of around 15 cm and around 32 cm for the worst. The GEO satellite with good ground station coverage achieves around 26 cm for the best realization and around 114 cm for the worst. Averaged over 10 days, the standard deviation is at around 58 cm. Hence, the IGSO satellites achieve smaller standard deviations of the estimated clocks than the GEO satellites when having only L-band measurements. However, this can be traced back to the total number of visible ground stations.
For the scenarios with optical links included, the standard deviations of the estimated clocks for all IGSO satellites in the MEO+IGSO constellation as well as for all GEO satellites in the MEO+GEO constellation are at a similar level as for the MEO satellites. Hence, the optical links stabilize the clock errors of the MEO as well as the GSO satellites overall, to a great extent.
3.3. Allan Deviation
In this section, we analyze the frequency stability of the estimated clocks for the different scenarios. The frequency stability is defined as the variation in the frequency between two consecutive periods. Computing an Allan variance, the frequency stability is shown in the time spectrum. The square root of the Allan variance gives the Allan deviation. With the simulation period of 10 days, it is possible to determine the Allan deviation up to about 1 day.
Figure 8 (left) shows the Allan deviation for the estimated PHM clocks with respect to the true clocks for the L-band-only, L-band+OTWL, L-band+OISL and L-band+OTWL+OISL scenarios. The given results apply to the MEO satellite, as an example. The estimated clock from the L-band-only scenario does not reach the stability of the true clocks for the interval up to one day. On the other hand, the estimated clocks from the L-band+OISL, L-band+OTWL and L-band+OTWL+OISL scenarios are close to each other and reach the stability of the PHM for time intervals larger than about 1000 s. This indicates that the PHM is still limiting the potential of the combination of observation techniques. With a much more stable clock, the real potential of the combination of observation techniques can be investigated. The ACES clock is such a clock, which we use as an alternative clock in this work. While the L-band-only scenario mainly shows white noise, the downward slope of the L-band+OISL, L-band+OTWL and L-band+OTWL+OISL scenarios is larger for time intervals up to around 500 s. This is quantization noise, as the current International GNSS Service (IGS) clock’s Receiver INdependent EXchange (RINEX) file—the file type we use to load our simulated clocks into the Bernese software—is primarily developed for GNSS, and, hence, the file accuracy is not quite sufficient for combinations of the observation techniques.
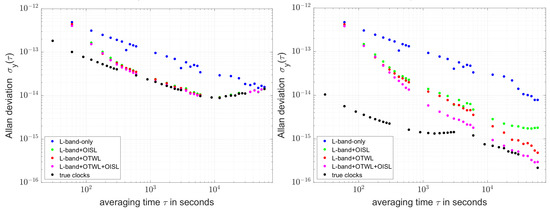
Figure 8.
Allan deviation using PHM (left) and ACES (right) clocks in the simulation study. Results are for the MEO satellite with respect to the different combinations of observation techniques. The black dots refer to the true PHM and ACES clocks.
Figure 8 (right) shows the Allan deviation of the estimated clocks when using the ACES clocks in the simulation. For the L-band-only scenario, no improvement in frequency stability can be achieved compared to the use of the PHM clocks. In the L-band+OISL scenario, the frequency stability of the estimated clocks further improves but does not reach the frequency stability of the true clocks. The L-band+OTWL scenario behaves similarly to the L-band+OISL scenario up to intervals of 5000 s but achieves a minimal better frequency stability. For larger intervals, the L-band+OTWL scenario can gain from the long-term stability of the ACES clock. The L-band+OTWL+OISL scenario now achieves a far higher frequency stability compared to the estimated clocks from the L-band+OISL and L-band+OTWL scenarios. The estimated clocks even reach the stability of the true ACES clocks for intervals larger than about 20,000 s. This means that the L-band+OTWL+OISL scenario can completely benefit from the long-term stability of the ACES clock. On the other hand, there might still be potential for further improvements in the long-term stability when using even more stable clocks.
3.4. Clock Prediction
In this section, we analyze the possibilities for the prediction of clocks when using the different combinations of observation techniques. The prediction is performed for up to one day. The PHM clocks we use in this work are simulated from the noise taken from an Allan deviation (see the true clocks shown in Figure 8). We did not simulate a quadratic phase drift for the PHM clocks. We are aware that in reality the PHM also shows a quadratic phase drift, but for short prediction periods of up to about one day the effect of a quadratic phase drift is barely noticeable, as tested in a pre-analysis using the true clocks. On the other hand, the ACES clock is expected to have no quadratic phase drift, as PHARAO is a frequency standard. Hence, our clock prediction model reduces to a linear fitting model of the estimation interval of one day. We optimize the fit length for each scenario to achieve the overall best prediction results. For each scenario, we compute the 95the percentile from all realizations at different prediction times. As a comparative value, we also include the prediction results related to the true clocks. This value can also be seen as the best possible clock prediction value.
Figure 9 shows the 95% prediction values for the MEO satellites in the MEO-only constellation when using the PHM clocks in the simulation. Similar results can be achieved for the MEO satellites in the MEO+IGSO or MEO+GEO constellations. For the L-band-only scenario, a fit length of 12 h gives the best results, while the scenarios including optical observation techniques as well as the true clocks achieved the best results for a fit length of 6 h.
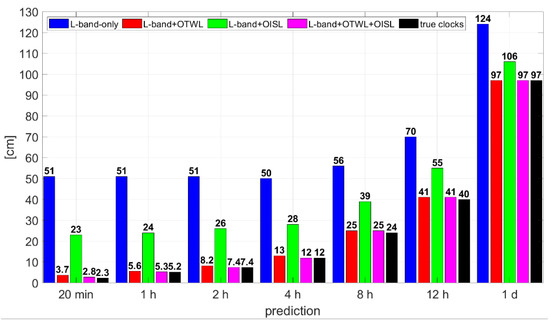
Figure 9.
The 95th percentile at certain prediction times using PHM clocks. Results are for MEO satellites in the MEO-only constellation and for the different combinations of observation techniques. The black bars refer to the true PHM clocks.
After 20 min of prediction, the values are mainly dominated by the remaining mean errors of the estimated clocks. With the L-band+OISL scenario, around 51–55% of improvement was noticeable compared to the L-band-only scenario. The L-band+OTWL and L-band+OTWL+OISL scenarios achieve the best results by far, with an improvement of around 93–94% with respect to the L-band-only scenario and of around 84–88% in relation to the L-band+OISL scenario. The L-band+OTWL+OISL scenario is almost at the level of the true clock prediction errors. This is noticeable for all the prediction times shown and again underlines that the PHM is limiting the potential of the L-band+OTWL and L-band+OTWL+OISL scenarios for the clocks’ prediction.
For longer prediction times, the percentage discrepancy between the different scenarios decreases. After a prediction of 8–12 h, the linear fitting starts to dominate the clock prediction errors. At a prediction time of one day, the L-band-only scenario achieves around 124 cm. The improvement when using the L-band+OISL scenario is at around 15% in relation to the L-band-only scenario. With a clock error of around 97 cm, the L-band+OTWL and L-band+OTWL+OISL scenarios improve by 22% compared to the L-band-only scenario.
For GSO satellites, the results concerning the L-band-only and L-band+OTWL scenarios are highly dependent on the number of ground stations each of the satellites can see. For the L-band-only scenario, the results are statistically not reliable. Furthermore, in the case of the L-band+OTWL scenario, there is a huge spread in the clock error of the prediction that does not give a reliable analysis foundation. Therefore, we only analyze the scenarios including OISL measurements, as those deliver more balanced prediction errors for the clocks and a better statistic. Almost the same results for the clock prediction are obtained for the IGSO and GEO satellites. The results are also quite similar to those of the MEO satellites for short prediction times. For long prediction times of around 12 h to one day, the clock error does not increase as much as for the MEO satellites, resulting in around a 22–27% lower clock error.
For the ACES clocks in the simulation, the fitting of a constant bias gives the best prediction results up to one day overall, as shown in Figure 10. The clock error barely decreases for the different combinations of observation techniques. Hence, all scenarios can benefit from the high stability of the ACES clock. For the 20 min prediction, the clock errors from the different scenarios improve by about 1 cm compared to the scenarios with the PHM clocks. This is expected as, for short prediction times, the results are still dominated by the mean errors of the estimated clocks, which are similar to the ones from the scenarios with the PHM clocks in the simulation (see Section 3.2.1). For comparisons, the clock prediction errors at 20 min are at the low mm level for the true ACES clocks. After one day, the L-band-only scenario improves by a factor of around 2.4, and the L-band+OISL scenario improves by a factor of around 4–5, compared to the scenarios using the PHM clock. While the clock errors decrease by only a few millimeters for the different combinations of observation techniques, the true clock prediction error at one day is at around 1.7 cm. The L-band+OTWL scenario achieves a clock prediction error of 3.5 cm at one day. This is an improvement by a factor of about 28 compared to the scenario with the PHM clock. The L-band+OTWL+OISL scenario, which gives the best results, is at around 2.1 cm. This indicates that for this prediction interval, the L-band+OTWL+OISL scenario is approaching the stability of the ACES clock. Analogous to the PHM analysis, for the ACES clocks we only analyze the L-band+OISL and L-band+OTWL+OISL scenarios for the GSO satellites. Here, the IGSO and GEO satellites achieve almost the same clock prediction errors as the MEO satellites throughout the analyzed prediction interval.
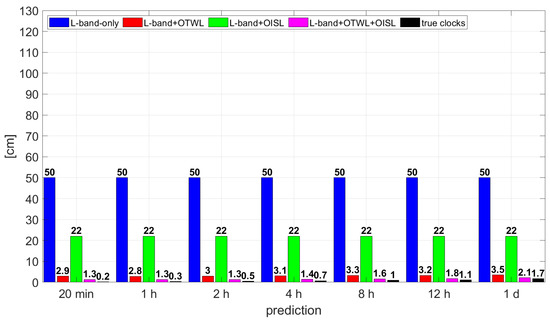
Figure 10.
The 95th percentile at certain prediction times using ACES clocks. Results are for MEO satellites in MEO-only constellation and for the different combinations of observation techniques. The black bars refer to the true ACES clocks.
For today’s procedures, performing clock synchronization from ground to space, the prediction results can be reduced by the mean, which is known from the last epoch of the estimated clocks. The mean clock error is still present when comparing the MEO system time with external time systems, but it cancels within the MEO system time and, hence, is irrelevant for the user. This leads to 35% lower clock prediction errors for the L-band-only scenario for short prediction times. The L-band+OTWL scenario only improves by about 13%. This indicates that the mean clock errors are already well-determined from the collocated use of the L-band and OTWL measurements. The L-band+OISL scenario achieves about the same results as the L-band+OTWL+OISL scenario. In the case of the PHM clocks, both scenarios reach the true clock prediction errors. For the ACES clocks, the L-band+OISL scenario’s clock prediction errors are at around 10 mm, and the L-band+OTWL+OISL scenario’s clock prediction errors are at around 6 mm, for short prediction times. Hence, the additional OTWL measurements help with further improvement, compared to the L-band+OISL scenario, when having the ACES clocks.
However, when a time system should be realized in space instead of on the Earth’s surface, then the mean does not cancel, so having a small mean error of the estimated clocks is important.
4. Conclusions
In this simulation study, we analyzed the impact of optical dual one-way measurements—Optical Inter-Satellite Links (OISL) and ground–space-oriented Optical Two-Way Links (OTWL)—in addition to L-band measurements for clock estimation. We analyzed the capabilities for a pure Medium Earth Orbit (MEO) constellation as well as the MEO+IGSO (Inclined Geosynchronous Orbits) and MEO+GEO (Geostationary Orbit) constellations by the mean error of the estimated clocks, the standard deviation and the Allan deviation. Furthermore, we predicted the estimated clocks and analyzed the capabilities for predictions up to one day. All scenarios were computed for two different clock types: Passive Hydrogen Maser (PHM) and Atomic Clock Ensemble in Space (ACES). While the PHM clock represents a current standard clock type, the ACES clock is an example of a future high-stability clock.
We want to indicate that this work is a simulation study. Generally, the complexity of physical reality cannot be fully emulated in a simulation environment. Therefore, all the results discussed in this study are to be regarded as indicative and are not absolute performance results. With real data in the future, the presented results may be confirmed or need further tuning.
As we estimated a range bias and a clock synchronization bias for each transmitter and receiver, which led to a rank-deficient normal equation matrix, we had to introduce constraints in the case of the OTWL observations. In the analysis, we had to use hard constraints for the clock synchronization biases at the level of measurement precision of 1 mm. This allowed to achieve the clock error of the estimated clocks that need a time and ranging reference in space to be implemented. Five times looser constraints already led to 7–10 times worse clock errors.
In the case of the L-band+OISL scenario, the clock error is mainly dominated by the remaining mean errors of the estimated clocks. A collocated use of the L-band and OTWL in scenarios showed that the mean error of the estimated clocks can be estimated to a great extent. The L-band+OTWL scenario shows a smaller mean error of the estimated clocks on average than the L-band+OISL scenario by far. This is due to the direct relation of OTWL to the reference station, which allows for reducing the systematic effects from the L-band measurements. While the L-band-only and L-band+OTWL scenarios show a variation in the mean error for the different satellites, scenarios including the OISL measurements help to compensate for this discrepancy. This is the benefit of OISL: not only do all MEO satellites achieve about the same mean errors of the estimated clocks but also IGSO or GEO satellites do when included in the constellation. Achieving around 3 mm of the mean error of the estimated clocks on average, the L-band+OTWL+OISL scenario gives the best results by far, combining the advantages of OTWL and OISL. We could show that the L-band, OTWL and OISL are complementary. Moreover, all scenarios that include optical observations achieve the standard deviations of the estimated clocks at the mm level for the MEO, IGSO and GEO satellites.
Hence, concerning positioning accuracy, the clock error from the L-band+OTWL+OISL scenario is at a similar level as the orbit error, with 1–3 mm being achievable for the L-band+OTWL+OISL scenario (compare with [17]). The use of a high-stability clock does not give an improvement for the clock estimation as long as the clocks are estimated epoch-wise. Clock modeling in the estimation procedure helps to gain from a higher frequency stability, but this is not shown in this work. Furthermore, a common troposphere estimation for the L-band and OTWL might improve the results.
As the Allan deviation analysis shows, the potential of clock estimation is limited by the use of the PHM clocks for the scenarios using combinations of observation techniques. The use of the ACES clocks offers the possibility of the further improvement of the frequency stability of the estimated clocks. The clocks’ prediction profits as well. After one day of prediction, the clock error is at around 2.1 cm for the L-band+OTWL+OISL scenario when using the ACES clocks—compared to around 1.7 cm when using the true ACES clocks. With the PHM clocks, the clock prediction error worsens to around 97 cm—about the same as is achievable with the true clocks. This underlines the huge capability and potential of the combination of observation techniques with high-precision links in connection to a high-stability clock, as foreseen by the GETRIS (Geodesy and Time Reference In Space) concept.
Author Contributions
Conceptualization, S.M. and A.S.; methodology, S.M.; software, S.M.; validation, S.M., A.S. and U.H.; formal analysis, S.M.; investigation, S.M. and A.S.; data curation, S.M.; writing—original draft preparation, S.M.; writing—review and editing, S.M., A.S. and U.H.; visualization, S.M.; supervision, U.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Plag, H.-P.; Pearlman, M. (Eds.) Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-642-02686-7. [Google Scholar] [CrossRef]
- Schäfer, W.; Flechtner, F.; Nothnagel, A.; Bauch, A.; Hugentobler, U. Geodesy and Time Reference in Space—GETRIS. ESA Study AO/1-6311/2010/F/WE Final Report GETRIS-TIM-FR-0001. 2013. [Google Scholar]
- Schlicht, A.; Hugentobler, U.; Stetter, M.; Schäfer, W. Concept for a Geodetic and Time Reference in Space. In Proceedings of the International Laser Ranging Service, Annapolis, MD, USA, 27–31 October 2014. [Google Scholar]
- Hauschildt, H.; Mezzasoma, S.; Moeller, H.L.; Witting, M.; Herrmann, J. European data relay system goes global. In Proceedings of the IEEE International Conference on Space Optical Systems and Applications (ICSOS), Naha, Japan, 14–16 November 2017; pp. 15–18. [Google Scholar] [CrossRef]
- Calzolaio, D.; Curreli, F.; Duncan, J.; Moorhouse, A.; Perez, G.; Voegt, S. EDRS-C—The second node of the European Data Relay System is in orbit. Acta Astronaut. 2020, 177, 537–544. [Google Scholar] [CrossRef]
- Delva, P.; Altamimi, Z.; Blazquez, A.; Blossfeld, M.; Böhm, J.; Bonnefond, P.; Boy, J.-P.; Bruinsma, S.; Bury, G.; Chatzinikos, M.; et al. GENESIS: Co-location of geodetic techniques in space. Earth Planets Space 2023, 75, 5. [Google Scholar] [CrossRef]
- Schuldt, T.; Döringshoff, K.; Kovalchuk, E.; Keetman, A.; Pahl, J.; Peters, A.; Braxmaier, C. Development of a compact optical absolute frequency reference for space with 10−15 instability. Appl. Opt. 2017, 56, 1101–1106. [Google Scholar] [CrossRef]
- Giorgi, G.; Schmidt, T.D.; Trainotti, C.; Mata-Calvo, R.; Fuchs, C.; Hoque, M.M.; Berdermann, J.; Furthner, J.; Günther, C.; Schuldt, T.; et al. Advanced technologies for satellite navigation and geodesy. Adv. Space Res. 2019, 64, 1256–1273. [Google Scholar] [CrossRef]
- Schmidt, T.D.; Schlüter, S.; Schuldt, T.; Gohlke, M.; Calvo, R.M.; Lüdtke, D.; Dauth, M.; Lezius, M.; Michaelis, C.; Brzoska, A.; et al. COMPASSO: In-orbit Verification of Optical Key Technologies for Future GNSS. In Proceedings of the 53rd Annual Precise Time and Time Interval Systems and Applications Meeting, Long Beach, CA, USA, 25–27 January 2022; pp. 158–182. [Google Scholar] [CrossRef]
- Tjoelker, R.L.; Prestage, J.D.; Burt, E.A.; Chen, P.; Chong, Y.J.; Chung, S.K.; Diener, W.; Ely, T.; Enzer, D.G.; Mojaradi, H.; et al. Mercury Ion Clock for a NASA Technology Demonstration Mission. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
- Burt, E.A.; Prestage, J.D.; Tjoelker, R.L.; Enzer, D.G.; Kuang, D.; Murphy, D.W.; Robison, D.E.; Seubert, J.M.; Wang, R.T.; Ely, T.A. Demonstration of a trapped-ion atomic clock in space. Nature 2021, 595, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Cacciapuoti, L.; Salomon, C. Space clocks and fundamental tests: The ACES experiment. Eur. Phys. J. Spec. Top. 2009, 172, 57–68. [Google Scholar] [CrossRef]
- Cacciapuoti, L.; Armano, M.; Much, R.; Sy, O.; Helm, A.; Hess, M.P.; Kehrer, J.; Koller, S.; Niedermaier, T.; Esnault, F.X.; et al. Testing gravity with cold-atom clocks in space. Eur. Phys. J. D 2020, 74, 164. [Google Scholar] [CrossRef]
- Laurent, P.; Massonnet, D.; Cacciapuoti, L.; Salomon, C. The ACES/PHARAO space mission. Comptes Rendus Phys. 2015, 16, 540–552. [Google Scholar] [CrossRef]
- Schlicht, A.; Marz, S.; Stetter, M.; Hugentobler, U.; Schäfer, W. Galileo POD using optical inter-satellite links: A simulation study. Adv. Space Res. 2020, 66, 1558–1570. [Google Scholar] [CrossRef]
- Marz, S.; Schlicht, A.; Hugentobler, U. Galileo precise orbit determination with optical two-way links (OTWL): A continuous wave laser ranging and time transfer concept. J. Geod. 2021, 95, 85. [Google Scholar] [CrossRef]
- Marz, S.; Schlicht, A.; Hugentobler, U. Geosynchronous satellites expanding a future GNSS satellite constellation: A precise orbit determination study. Adv. Space Res. 2023, 71, 624–644. [Google Scholar] [CrossRef]
- Kur, T.; Kalarus, M. Simulation of Inter-Satellite Link schemes for use in precise orbit determination and clock estimation. Adv. Space Res. 2021, 68, 4734–4752. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Prochazka, I.; Lauber, P.; Hugentobler, U.; Schäfer, W.; Cacciapuoti, L.; Nasca, R. Ground-based demonstration of the European Laser Timing (ELT) experiment. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 728–737. [Google Scholar] [CrossRef]
- Samain, E.; Vrancken, P.; Guillemot, P.; Fridelance, P.; Exertier, P. Time transfer by laser link (T2L2): Characterization and calibration of the flight instrument. Metrologia 2014, 51, 503–515. [Google Scholar] [CrossRef]
- Meng, W.; Zhang, H.; Huang, P.; Wang, J.; Zhang, Z.; Liao, Y.; Ye, Y.; Hu, W.; Wang, Y.; Chen, W.; et al. Design and experiment of onboard laser time transfer in Chinese Beidou navigation satellites. Adv. Space Res. 2013, 51, 951–958. [Google Scholar] [CrossRef]
- Tang, C.; Hu, X.; Zhou, S.; Guo, R.; He, F.; Liu, L.; Zhu, L.; Li, X.; Wu, S.; Zhao, G.; et al. Improvement of orbit determination accuracy for Beidou Navigation Satellite System with Two-way Satellite Time Frequency Transfer. Adv. Space. Res. 2016, 58, 1390–1400. [Google Scholar] [CrossRef]
- Schlicht, A.; Hugentobler, U.; Marz, S.; Seel, S.; Biller, P. Concept for continuous wave laser ranging and time transfer to Galileo using optical two-way links. In Proceedings of the 7th International Colloquium on Scientific and Fundamental Aspects of GNSS, Zurich, Switzerland, 4–6 September 2019. [Google Scholar]
- Allan, D.W. Time and frequency (time-domain) characterization, estimation, and prediction of precision clocks and oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2, User Manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I. The adjusted optical properties for Galileo/BeiDou-2/QZS-1 satellites and initial results on BeiDou-3e and QZS-2 satellites. Adv. Space Res. 2019, 63, 1803–1812. [Google Scholar] [CrossRef]
- Fernández, F.A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data. Adv. Space Res. 2011, 47, 786–801. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111, B02406. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Marini, J.W.; Murray, C.W. Correction of Laser Range Tracking Data for Atmospheric Refraction at Elevations above 10 Degrees; NASA Technical Rep. X-591-73-351; NASA/Goddard Space Flight Center: Greenbelt, Maryland, USA, November 1973. [Google Scholar]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, L14602. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A Global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Fliegel, H.F.; Gallini, T.E.; Swift, E.R. Global positioning system radiation force model for geodetic applications. J. Geophys. Res. 1992, 97, 559–568. [Google Scholar] [CrossRef]
- Springer, T.A.; Beutler, G.; Rothacher, M. A New Solar Radiation Pressure Model for GPS. Adv. Space Res. 1999, 23, 673–676. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits—Models, Methods, Applications; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 3-540-67280-X. [Google Scholar]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sosnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef]
- Kur, T.; Liwosz, T. Simulation of the Use of Variance Component Estimation in Relative Weighting of Inter-Satellite Links and GNSS Measurements. Remote Sens. 2022, 14, 6387. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).