Abstract
In recent years, it has become a common understanding among researchers that one of the significant agents for forming a variety of submarine geomorphologies is turbidity currents that travel long distances, so-called long-runout turbidity currents. In this study, we present a mathematical model of the formation of cyclic steps due to long-runout turbidity currents based on the assumption that the highly concentrated layer near the bottom of the turbidity currents achieves an equilibrium state. The model uses the four governing equations: the momentum equation, the continuity equation, the diffusion/dispersion equation of suspended sediment, and the continuity equation of sediment on the bed (the Exner equation). We simplify the governing equations by ignoring the entrainment from ambient water since there is a distinct density interface above the highly concentrated lower layer of long-runout turbidity currents. We determine the dimensions of cyclic steps based on the solution. Agreement between the predictions and field observations turns out to be reasonable.
1. Introduction
Cyclic steps are a series of upstream migrating steps bounded by hydraulic jumps. The flow is subcritical at the stoss side, where the slope is gentle, and the flow accelerates on the lee side to become supercritical flow. Taki and Parker [1] performed detailed experiments, regenerated the cyclic steps in the laboratory, and found the steps migrate upstream while preserving their form. We observe cyclic steps on the ocean floor [2,3], at river deltas [4], and on ice [5], classified into three types: transportational [1,6], net-erosional [7], and net-depositional [8]. In our study, we focus on submarine transportational cyclic steps, such as cyclic steps within the South Taiwan Shoal and West Penghu submarine canyons of the South China Sea [9].
The increased research interest in cyclic steps is due to their effect on geomorphology and a new awareness of the vital role in sediment transport efficiency. There are many models proposed previously for describing the formation of cyclic steps. Parker and Izumi [7] presented a model to analyze purely erosional cyclic steps on cohesive soil in open channel flow. Sun and Parker [6] developed an analytical model for transportational cyclic steps formed in open channel flow with abundant suspended sediment. Izumi and Yokokawa [10] performed a theoretical analysis to explain the formation of cyclic steps in mixed bedrock–alluvial channels. As for cyclic steps formed due to turbidity currents in submarine environments, Dias et al. [11] have proposed the first analytical model, to the authors’ knowledge. Their model used variables in the critical regime in the Froude sense to normalize all the main variables, such as the layer thickness of turbidity currents. Therefore, it is not easy to interpret their results in reality and compare the dimensions of cyclic steps predicted by their model with those in the field.
In many cases, turbidity currents lead to the formation of cyclic steps. Turbidity currents are sediment gravity flows triggered by slumping, earthquakes, and various other types of soil disturbances. Many analytical models have been presented in the endeavor to understand turbidity currents. Parker et al. [12] proposed a three-equation model and a four-equation model, which includes the turbulent kinetic energy equation to describe the behavior of turbidity currents. The entrainment from ambient water included in the two models leads to the thickening of currents. Izumi [13] combined the model of turbidity currents and the Exner equation to reproduce the formation of submarine gullies due to turbidity currents.
A remarkable feature of submarine turbidity currents is that they can run over 1000 km without dissipation. The models proposed by Parker et al. [12] have a limitation: they cannot explain this feature of long-runout turbidity currents. The physical mechanism of why turbidity currents can travel long distances had long been left unsolved. Luchi et al. [14] are the first to suggest a solution to this problem. In the process of deriving the velocity distribution of turbidity currents in the layer thickness direction using the k- model, they found that the turbidity current separates into two layers: a lower layer with high suspended sediment concentration and an upper layer with low suspended sediment concentration. This separation creates a density interface between the upper and lower layers where there are very little friction, momentum exchange, and diffusion. Since there is very little friction between the two layers, the lower layer has little interaction with the upper layer and can run long distances. The recent field observations by Paull et al. [15] and Pope et al. [16] partly support this assumption that a turbidity current is composed of two layers.
Earlier models designed to generate submarine morphologies failed to describe the characteristic of long-runout turbidity currents. Hence, in our study, one of the objectives was to capture the features of these currents. We derive the governing equations for long-runout turbidity currents in a manner consistent with that used by Parker et al. [12]. However, we establish the governing equations by integrating over the highly concentrated lower layer of turbidity currents based on the model of Luchi et al. [14] rather than from the bottom to infinity. We coupled with the governing equations of long-runout turbidity currents and the Exner equation as in the model by Dias et al. [11] and Izumi [13]. Taki and Parker [1] have studied the subaqueous equivalent of submarine cyclic steps and found that cyclic steps migrate upstream without changing their forms. We referred to the method presented by Sun et al. [6] to solve this problem of cyclic steps formed by long-runout turbidity currents in submarine environments.
Models proposed so far to describe cyclic steps, e.g., ref. [6] have not explained the actual scale of cyclic steps. Therefore, we normalize all the variables by the fundamental quantities in the absence of steps such as the equilibrium thickness of the highly concentrated lower layer and then calculate the actual dimensions of cyclic steps using the results of the analysis performed by Izumi [17]. We then compare these results with observations in the field to determine the reliability of our model.
2. Materials and Methods
2.1. Formulation
2.1.1. Governing Equations
Turbidity currents continually entrain ambient water. As a result, increased layer thickness results in the dilution of suspended sediment concentration. Some turbidity currents can run incredibly long distances without dissipating. As already mentioned, Luchi et al. [14] found that this feature of turbidity currents results from the fact that the flow separates into two layers, as shown in Figure 1.
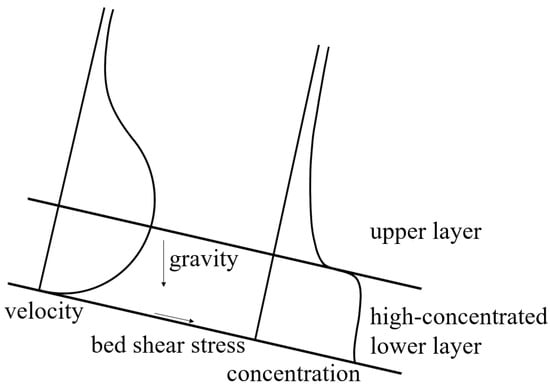
Figure 1.
Sketch of the model.
The lower driving layer has the invariant suspended sediment concentration, flow thickness, and velocity profiles, while the upper driven layer continues to entrain neighboring water and become diluted.
There is a distinct density interface between the two layers, where the velocity gradient and the shear stress are almost zero. The gravity drives the upper layer and balances the shear stress at the bottom of the lower layer. We can assume that the highly concentrated lower layer is in the equilibrium state in this configuration.
We adopt the derivation of the layer-averaged equations in the model by Parker et al. [12] in this study. However, the integration approach of the governing equations is slightly different: in this study, we integrate the governing equations over the highly concentrated lower layer. Even after this manipulation, however, the layer-averaged momentum equation has the same form as that achieved in the model presented by Parker et al. [12]
where is the streamwise coordinate, is the layer-averaged flow velocity in the direction, is the layer-averaged suspended sediment concentration, is the highly concentrated layer thickness of turbidity currents, R is the submerged specific gravity, g is the gravity acceleration, is the deviation from the bed elevation without steps, S is the average slope, is the density of water, and is the bed shear stress (=), and is the drag coefficient. In addition, we denote dimensional variables by the tilde and drop it to denote non-dimensional or normalized equivalents.
The layer-averaged continuity equation is
Note that the right-hand side of Equation (2) vanishes, whereas it does not in the model proposed by Parker et al. (1986), that is , where is the entrainment rate of water. Since we only consider the highly concentrated layer of turbidity currents, the entrainment from ambient water is assumed to be negligible.
The layer-averaged dispersion/diffusion equation of suspended sediment is described by
where is the falling velocity of suspended sediment, is the deposition rate of suspended sediment (, is the ratio of the deposition rate to the layer-integrated suspended sediment concentration ). The parameter is close to unity, assuming it is unity for simplicity in this study. The entrainment rate of sediment from the bottom is assumed in the form
where is the threshold bed shear stress below which erosion does not occur, and the parameters and are empirical constants determined by experiments. The Exner equation describing the mass balance between sediment transported and sediment on the bed takes the form
where is the porosity of the ocean floor, and is time.
In the above formulation, we apply the quasi-steady approximation and drop the temporal terms in Equations (1)–(3). The time change of the flow is much swifter than the bed elevation due to sediment transport. Therefore, we can assume that the flow adjusts immediately compared to the bed morphology. Thus, we can assume that the flow is steady and consider the time derivative only in the Exner Equation (5). This approximation is justified in the case of cyclic steps formed by turbidity currents considered in this study.
2.1.2. Normalization
We introduce the normalizations of the form
where the subscript n denotes variables in the equilibrium normal flow condition in the absence of steps. With the aid of Equations (6a) and (6b), the governing Equations (1)–(3) and (5) are rewritten, respectively, in the form
where is a non-dimensional parameter representing the suspendability of sediment, is the normalized slope, and is the Richardson number in the normal flow condition in the absence of steps, which read, respectively
In the equilibrium normal flow condition, since the gravity force is in balance with the bed shear stress (), there is a relationship between the Richardson number and , where .
The normalized erosion rate of suspended sediment is
where is the non-dimensional threshold velocity for entrainment (=), and is the dimensional threshold velocity for entrainment (=).
As reported by Taki and Parker et al. [1], the cyclic steps can reach an equilibrium state at which a periodic wave train migrates upstream without changing its form. We introduce the moving coordinates of the form
where f is the migration speed. Once the cyclic steps reach equilibrium, the average bed slope, wavelength, wave height, and wave migration speed attain constant values. When viewed in the moving coordinates, the deviation of the bed elevation becomes a function of alone. We apply the coordinate transformation described by the above equations to the governing Equations (7)–(10) and drop the hat for simplicity. The Exner Equation (10) reduces to
The dispersion/diffusion equation of suspended sediment takes the form
2.1.3. Boundary Conditions
The Richardson number is the key to the emergence of cyclic steps. The Richardson critical point stands for a location where the Richardson number is unity. This point divided the flow into the supercritical and subcritical regimes. A hydraulic jump occurs when the currents transit from the supercritical flow to the subcritical one, as shown in Figure 2. If the flow velocity does not reduce to the threshold value for bed erosion, bed erosion will continue, and the periodic cyclic steps will not form. We thus have the additional boundary condition written in the form
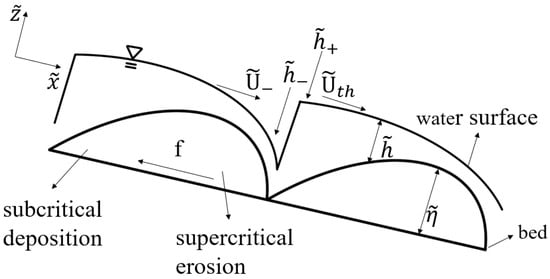
Figure 2.
Conceptual sketch of cyclic steps.
The momentum conserves between the upstream and downstream of a hydraulic jump, such that
where the subscripts − and + denote variables, respectively, at the upstream and downstream of a hydraulic jump. The suspended sediment concentration is continuous between the upstream and downstream of a hydraulic jump, such that.
2.2. Solution
Solution Method
The governing Equations (15) and (16) with the boundary conditions (19) and (20) form a two-point boundary value problem, which we solve by the shooting method with the Newton–Raphson scheme. Since the problem is similar to that solved by Sun and Parker [6], we follow their solution method to some extent.
The denominator of Equation (15) vanishes at the Richardson critical point. In order to avoid this singularity, the numerator should also vanish at the Richardson critical point. Applying this additional condition, we find the relationship among the critical velocity, the critical suspended sediment concentration, and the migration speed in the form
where the subscript c denotes variables at the Richardson critical point.
Moreover, L’Hopital’s rule is applied to Equation (15) to calculate at the Richardson critical point. Since the flow is accelerating from the subcritical to supercritical regimes via the Richardson critical point, should always be positive in order to achieve a physically realistic flow. This condition and some other restrictions allow us to find the solution domain, but since our concern is to find the actual scales of cyclic steps in this paper, we will not go further into this problem. Sun and Parker [6] have further discussed the solution domain. Readers can refer to their study for further information.
Using the Runge–Kutta method, we integrate Equations (15) and (16) in the upstream and downstream directions from the Richardson critical point. Since it is impossible to start a calculation from exactly the Richardson critical point, we use and to calculate from the vicinity of the Richardson critical point. We guess as the initial value at the Richardson critical point in the integration. Then is determined from Equation (23). While, in the downstream direction, we calculate up to the point where Equation (17) is satisfied, in the upstream direction, we calculate up to the point where Equation (20) is satisfied. These points are where the hydraulic jump takes place, and Equation (19) must be satisfied. We adjust the guessed value of using the Newton–Raphson scheme for Equation (19) to be satisfied and obtain the correct .
For the calculation, it is necessary to specify the parameters and . The parameter represents the suspendability of sediment in the absence of steps (=), where is the friction velocity in the absence of steps (=). Akiyama and Stefan [18] reported that is larger than unity when suspension starts to occur and takes a value between 50 and 100 when the suspension is saturated. The drag coefficient ranges from 0.002 to 0.02 according to Parker et al. [19]. It follows that the parameter ranges from 0.04 to 17.32. According to Sun and Parker [6], the flatbed becomes unstable only when the flow is in the supercritical regime. Therefore, the Richardson number has to be smaller than unity. Thus, the possible range of the Richardson number is from zero to unity.
3. Results
The Wavelength as a Function of and
Figure 3 shows the wavelength of cyclic steps as a function of the Richardson number and the suspendability . The wavelength of cyclic steps defines as the distance between two adjacent hydraulic jumps. In the analysis in this study, we obtain the wavelength as the sum of the distances from the Richardson critical point to the downstream and upstream hydraulic jumps, respectively.
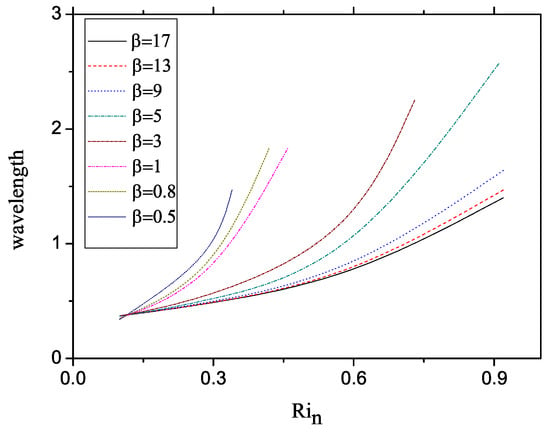
Figure 3.
The relationships among typical parameters.
In the calculation, if is greater than a specific value or is smaller than a particular value, the numerator of the equation vanishes at another point other than the Richardson critical point. It is impossible to avoid the two singularities simultaneously. In this sense, we can see that the model proposed here has no solution when is smaller than 0.12. It means that if is smaller than a certain threshold, a cyclic step will not form regardless of the value of , since the large suspendability and the generation of abundant suspended sediment are essential for the formation of cyclic steps.
In addition, we find that, as the suspendability decreases, steps will not form unless the slope is considerably steep, and if the suspendability is sufficiently large, cyclic steps can appear even on mild slopes. The analysis also shows that cyclic steps with relatively long wavelengths appear on mild slopes, while those with short wavelengths form on steep slopes. This tendency may be because, on steep slopes, the flow variation is generally rapid, and the intervals between hydraulic jumps decrease. We also find that large suspendability leads to short wavelengths. The reason may be that when the suspendability is more prominent, fewer suspended particles settle out of the fluid to form cyclic steps.
4. Discussion
Application
The non-dimensional step wavelength and wave height are obtained as functions of and . These two parameters can be calculated by the drag coefficient , bed slope S, and the value of . The wave height is the distance between the highest point of a crest and the bed. Since the wave height is normalized by the dimensional layer thickness of turbidity currents in the absence of steps and the wavelength is normalized by , is estimated to obtain the actual scales of cyclic steps.
Typical values for parameters were taken from cyclic steps within the South Taiwan Shoal canyon [9] to reproduce the submarine cyclic steps (Figure 4). We assume is 0.003. can be calculated with the aid of an average slope of 0.27 in the upper segment and 0.66 in the lower segment (). The value of is assumed to be 10, and thus is 0.55 ().
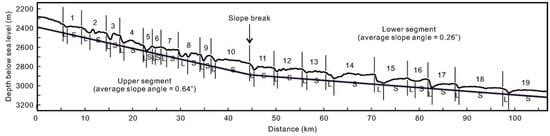
Figure 4.
Cyclic steps within the South Taiwan Shoal canyon. Redrafted from Zhong et al. [9]. 1–10 cyclic steps are in the upper segment and 11–19 cyclic steps are in the lower segment; L indicates the lee sides and S indicates the stoss sides.
To achieve the estimation of the layer thickness of long-runout turbidity currents in the absence of steps, we employ the following relation proposed by Izumi [17]:
Here is the falling velocity normalized by the sediment diameter (=), is the sediment diameter, is the suspended sediment concentration near the bottom normalized by the layer averaged suspended sediment concentration, and is the falling velocity normalized by the friction velocity (). Assuming that is 0.4 mm herein, we find 0.4. As for the entrainment rate of sediment from the bottom in the equilibrium condition in the absence of steps , Izumi and Fujii [20] proposed a formula of the form
where K and m are constants that need to be determined empirically, and assumed to be and 2, respectively. Assuming to be 10 as already mentioned, we find to be 0.2. With the use of the above assumptions, we find that the thickness of the highly concentrated layer is 20.05 m and 49.36 m in the upper and lower segment, respectively.
We can calculate the real scales of wavelength and wave height with the aid of Equation (6b). It should note that the wavelength and wave height of cyclic steps obtained in the analysis are in good agreement with the field observations. According to Zhong et al. [9], the range of wave heights is 15 m to 81 m within the South Taiwan Shoal canyon. The wavelengths of cyclic steps range from 1800 m to 8414 m in the upper segment and 4078 m to 10,452 m in the lower segment. Our model results show that the wavelength is 2135.17 m, and the wave height is 25.57 m in the upper segment. In the lower segment, the wavelength is 5686.29 m, and the wave height is 26.30 m.
The steps in the lower segment are relatively longer than those in the upper segment, and it also concurs with observations within the South Taiwan Shoal canyon. Additionally, the wavelength of cyclic steps is some orders of magnitude larger than the layer thickness, so the long wave assumption is satisfied.
Using the present model, we obtain the bed profiles over a one-step wavelength in both the upper and lower segments within the South Taiwan Shoal canyon. Figure 5 and Figure 6 show the bed and water surface profiles of one step with the aid of Equation (22), where and the Richardson critical point is at . Observed appearances bear a good agreement with the steps reproduced by the model.
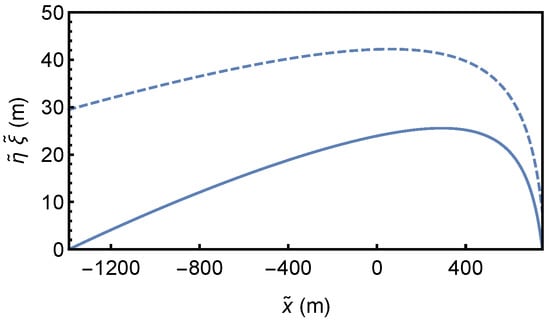
Figure 5.
The distributions of non-normalized bed elevation and water surface over one step wavelength, in the upper segment.
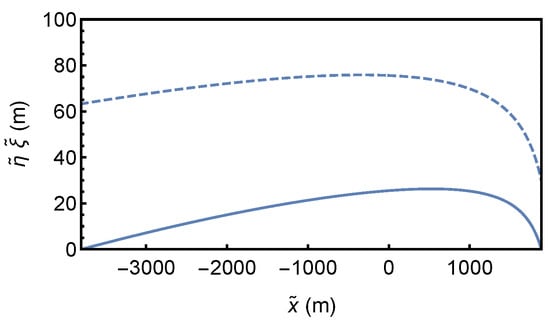
Figure 6.
The distributions of non-normalized bed elevation and water surface over one step wavelength, in the lower segment.
5. Conclusions
We present an analytical model to reproduce the cyclic steps of long-runout turbidity currents. Since the lower layer is the focus of this analysis, the entrainment from ambient seawater is considered negligible. Using the model proposed in this study, we can predict the dimensions of cyclic steps observed in the field. The analytical results show that cyclic steps cannot form when (suspendability) or the average slope divided by the drag coefficient is smaller than some threshold. Furthermore, the wavelengths of cyclic steps on mild slopes were relatively long, while the larger slope angle facilitates the formation of relatively short wavelengths. The results of the analysis are consistent with field observations.
Author Contributions
Conceptualization, Z.W. and N.I.; methodology, Z.W. and N.I.; writing—original draft preparation, Z.W.; writing—review and editing, N.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hokkaido University Ambitious Doctoral Fellowship (SDGs), grant number JPMJFS2101.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank all the members of the River and Watershed Laboratory for their support and helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| B | empirical constant (=) |
| C | suspended sediment concentration (–) |
| suspended sediment concentration near bed (–) | |
| D | deposition rate of suspended sediment (–) |
| sediment size (mm) | |
| E | entrainment rate of suspended sediment (–) |
| K | empirical constant (=) |
| R | submerged specific gravity (–) |
| S | average slope (–) |
| U | mean velocity in x direction (–) |
| threshold velocity below which erosion does not occur (–) | |
| empirical constant determined by experiments (–) | |
| entrainment of water (–) | |
| f | migration speed (–) |
| g | gravity acceleration (m s) |
| h | highly concentrated layer thickness of turbidity currents (–) |
| m | empirical constant (=2) |
| t | time (–) |
| friction velocity (–) | |
| falling velocity (–) | |
| x | streamwise coordinate (–) |
| z | upward coordinate (–) |
| normalized fall velocity (–) | |
| Richardson number (–) | |
| particle Reynolds number (–) | |
| a nondimensional parameter representing the suspendability of the turbidity currents (–) | |
| the bed elevation referenced to the average bed slope (–) | |
| porosity of sediment (–) | |
| empirical constant determined by experiments (–) | |
| the ratio between the suspended sediment concentrations and (–) | |
| density of water (kg m) | |
| bed shear stress (–) | |
| water surface elevation (–) | |
| for the case of normal flow in the absence of steps | |
| dimensional variables |
References
- Taki, K.; Parker, G. Transportational cyclic steps created by flow over an erodible bed. Part 1. Experiments. J. Hydraul. Res. 2005, 43, 488–501. [Google Scholar] [CrossRef]
- Fildani, A.; Normark, W.R.; Kostic, S.; Parker, G. Channel formation by flow stripping: Large-scale scour features along the Monterey East Channel and their relation to sediment waves. Sedimentology 2006, 53, 1265–1287. [Google Scholar] [CrossRef]
- Pirmez, C.; Imran, J. Reconstruction of turbidity currents in Amazon Channel. Mar. Pet. Geol. 2003, 20, 823–849. [Google Scholar] [CrossRef]
- Urgeles, R.; Cattaneo, A.; Puig, P.; Liquete, C.; De Mol, B.; Amblas, D.; Sultan, N.; Trincardi, F. A review of undulated sediment features on Mediterranean prodeltas: Distinguishing sediment transport structures from sediment deformation. Mar. Geophys. Res. 2011, 32, 49–69. [Google Scholar] [CrossRef] [Green Version]
- Smith, I.B.; Holt, J.W.; Spiga, A.; Howard, A.D.; Parker, G. The spiral troughs of Mars as cyclic steps. J. Geophys. Res. Planets 2013, 118, 1835–1857. [Google Scholar] [CrossRef]
- Sun, T.; Parker, G.; Izumi, N. Transportational cyclic steps created by flow over an erodible bed. Part 2. Theory and numerical simulation. J. Hydraul. Res. 2005, 43, 502–514. [Google Scholar] [CrossRef]
- Parker, G.; Izumi, N. Purely erosional cyclic and solitary steps created by flow over a cohesive bed. J. Fluid Mech. 2000, 419, 203–238. [Google Scholar] [CrossRef]
- Spinewine, B.; Sequeiros, O.E.; Garcia, M.H.; Beaubouef, R.T.; Sun, T.; Savoye, B.; Parker, G. Experiments on wedge-shaped deep sea sedimentary deposits in minibasins and/or on channel levees emplaced by turbidity currents. Part II. Morphodynamic evolution of the wedge and of the associated bedforms. J. Sediment. Res. 2009, 79, 608–628. [Google Scholar] [CrossRef]
- Zhong, G.; Cartigny, M.J.; Kuang, Z.; Wang, L. Cyclic steps along the South Taiwan Shoal and West Penghu submarine canyons on the northeastern continental slope of the South China Sea. Bulletin 2015, 127, 804–824. [Google Scholar] [CrossRef]
- Izumi, N.; Yokokawa, M.; Parker, G. Incisional cyclic steps of permanent form in mixed bedrock-alluvial rivers. J. Geophys. Res. Earth Surf. 2017, 122, 130–152. [Google Scholar] [CrossRef] [Green Version]
- Dias, D.; Izumi, N.; Yokokawa, M. Cyclic steps formed by turbidity currents. J. Jpn. Soc. Civ. Eng. Ser. A2 (Appl. Mech. (AM)) 2011, 67, 503–510. [Google Scholar] [CrossRef] [Green Version]
- Parker, G.; Fukushima, Y.; Pantin, H.M. Self-accelerating turbidity currents. J. Fluid Mech. 1986, 171, 145–181. [Google Scholar] [CrossRef]
- Izumi, N. The formation of submarine gullies by turbidity currents. J. Geophys. Res. Ocean. 2004, 109, C03048. [Google Scholar] [CrossRef]
- Luchi, R.; Balachandar, S.; Seminara, G.; Parker, G. Turbidity currents with equilibrium basal driving layers: A mechanism for long runout. Geophys. Res. Lett. 2018, 45, 1518–1526. [Google Scholar] [CrossRef]
- Paull, C.K.; Talling, P.J.; Maier, K.L.; Parsons, D.; Xu, J.; Caress, D.W.; Gwiazda, R.; Lundsten, E.M.; Anderson, K.; Barry, J.P.; et al. Powerful turbidity currents driven by dense basal layers. Nat. Commun. 2018, 9, 4114. [Google Scholar] [CrossRef] [Green Version]
- Pope, E.L.; Cartigny, M.J.; Clare, M.A.; Talling, P.J.; Lintern, D.G.; Vellinga, A.; Hage, S.; Acikalin, S.; Bailey, L.; Chapplow, N.; et al. First source-to-sink monitoring shows dense head controls sediment flux and runout in turbidity currents. Sci. Adv. 2022, 8, eabj3220. [Google Scholar] [CrossRef] [PubMed]
- Izumi, N. Equilibrium thickness of the highly concentration layer formed at lower turbidity currents. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, 811–816. [Google Scholar]
- Akiyama, J.; Stefan, H.; Henry, M. Turbidity current with erosion and deposition. J. Hydraul. Eng. 1985, 111, 1473–1496. [Google Scholar] [CrossRef]
- Parker, G.; Garcia, M.; Fukushima, Y.; Yu, W. Experiments on turbidity currents over an erodible bed. J. Hydraul. Res. 1987, 25, 123–147. [Google Scholar] [CrossRef]
- Izumi, N.; Fujii, K. Channelization on plateaus composed of weakly cohesive fine sediment. J. Geophys. Res. Earth Surf. 2006, 111, F01012. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).