Stereolithography 3D Printer for Micromodel Fabrications with Comprehensive Accuracy Evaluation by Using Microtomography
Abstract
:1. Introduction
2. Materials and Methods
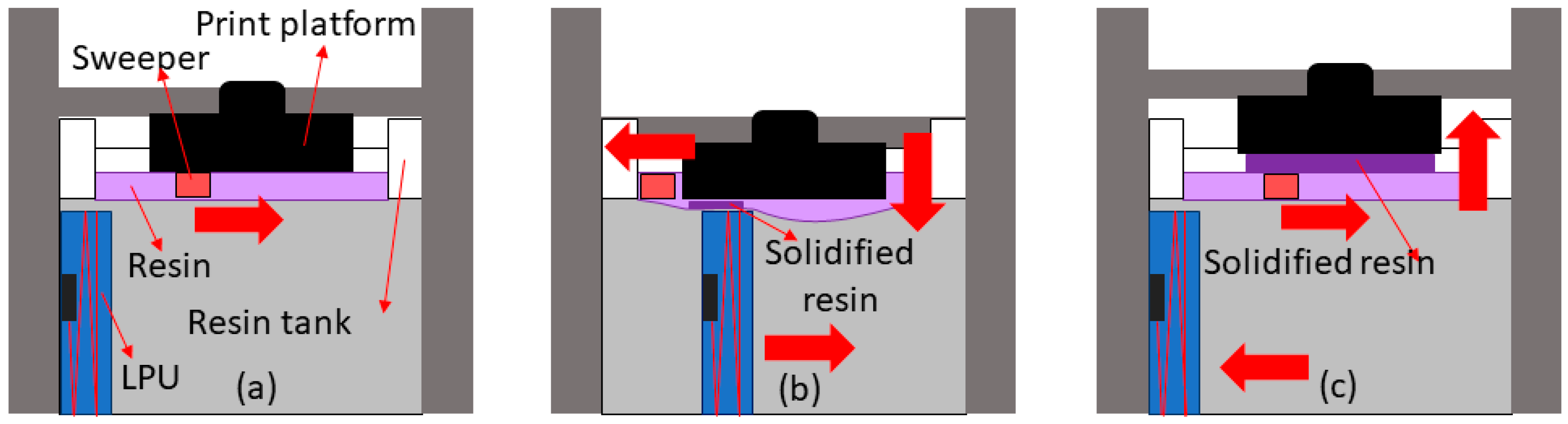
2.1. Printing with an SLA 3D Printer
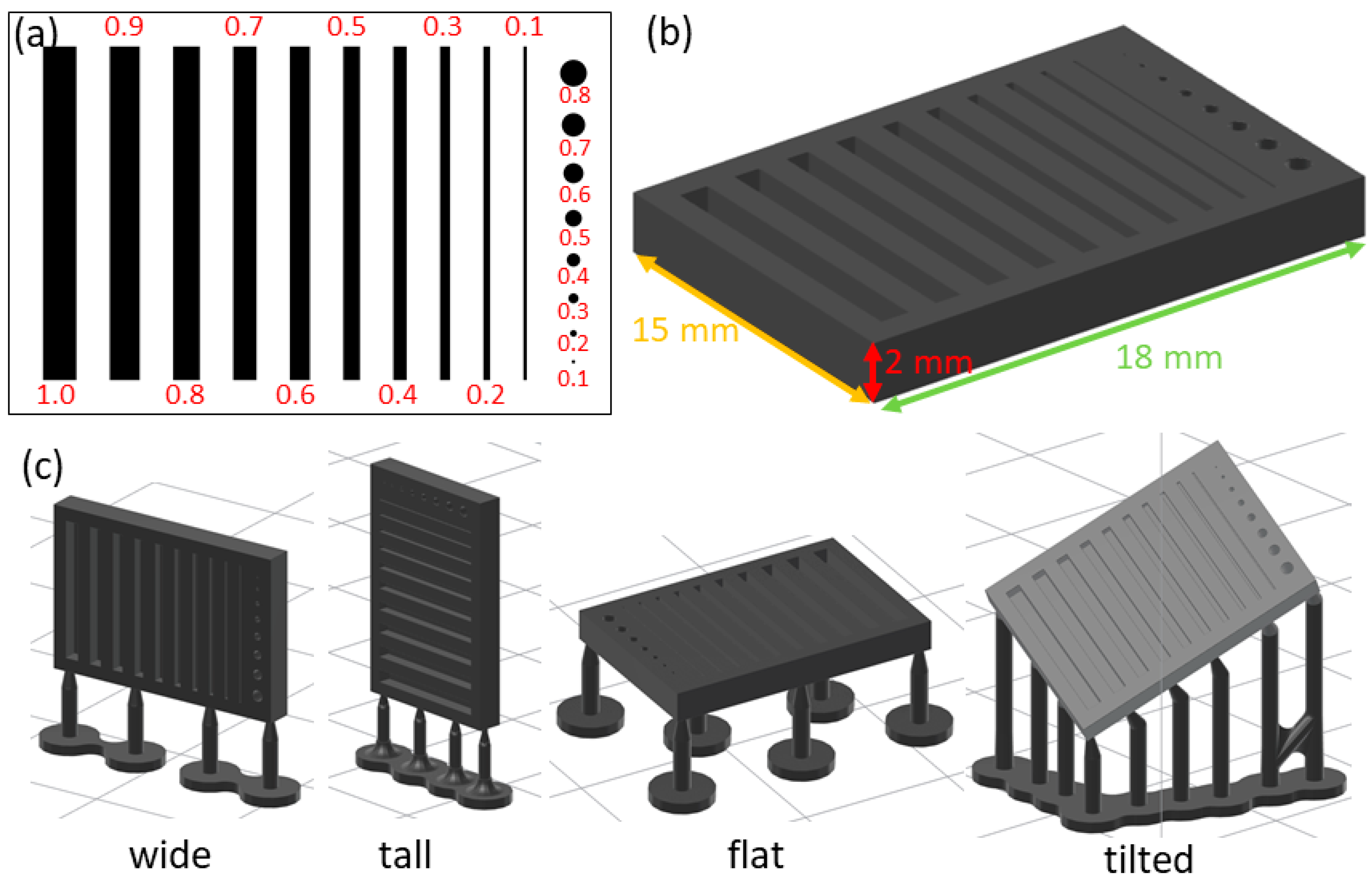
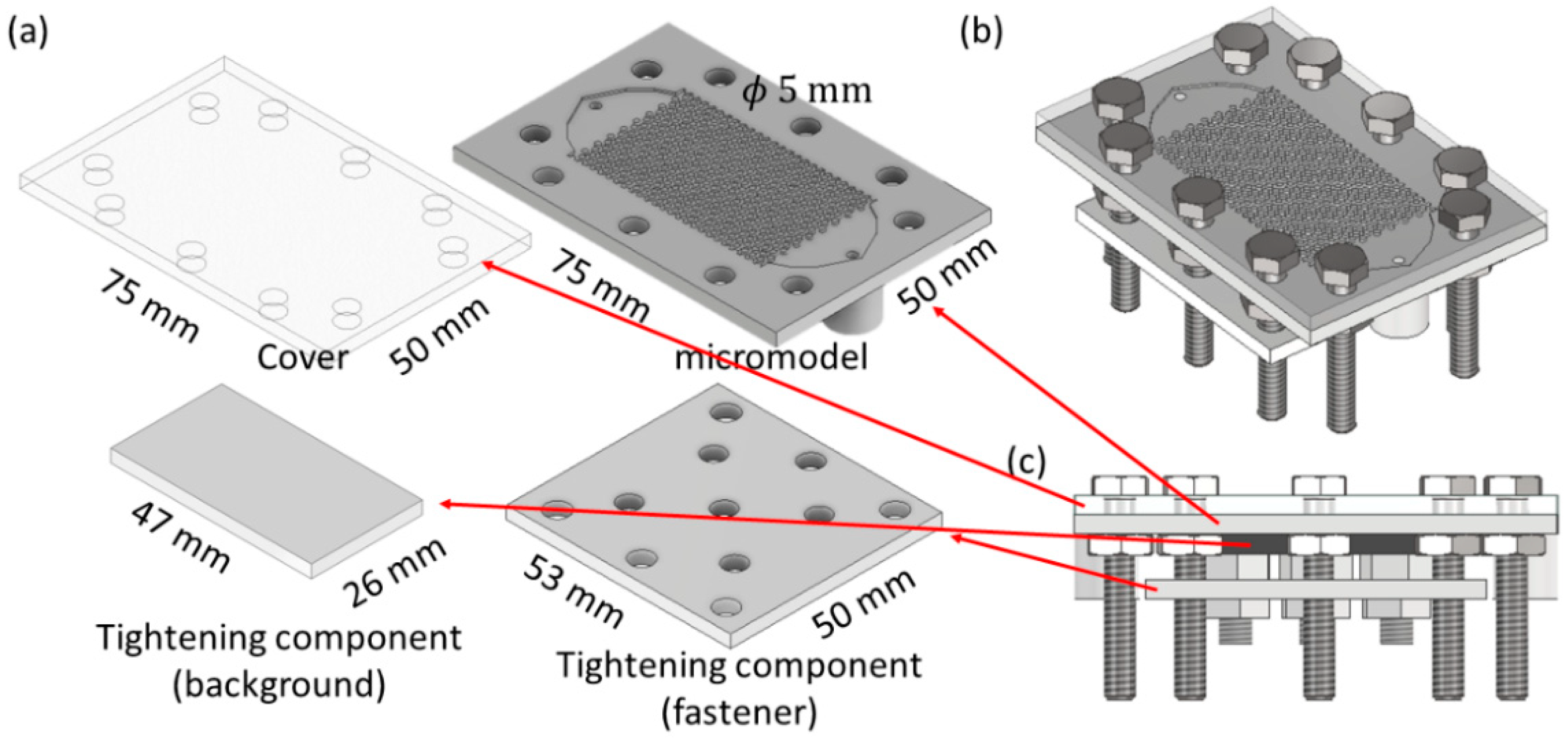
2.2. Printed Design
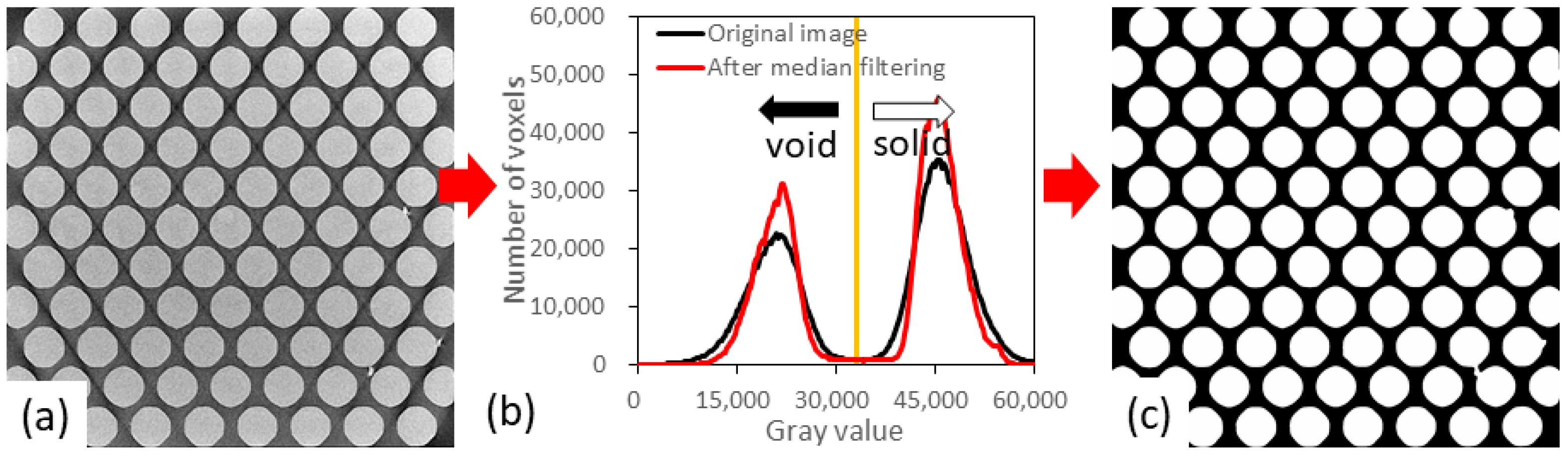
2.3. Measuring Accuracy with Microtomography
3. Results and Discussions
3.1. Accuracy Check
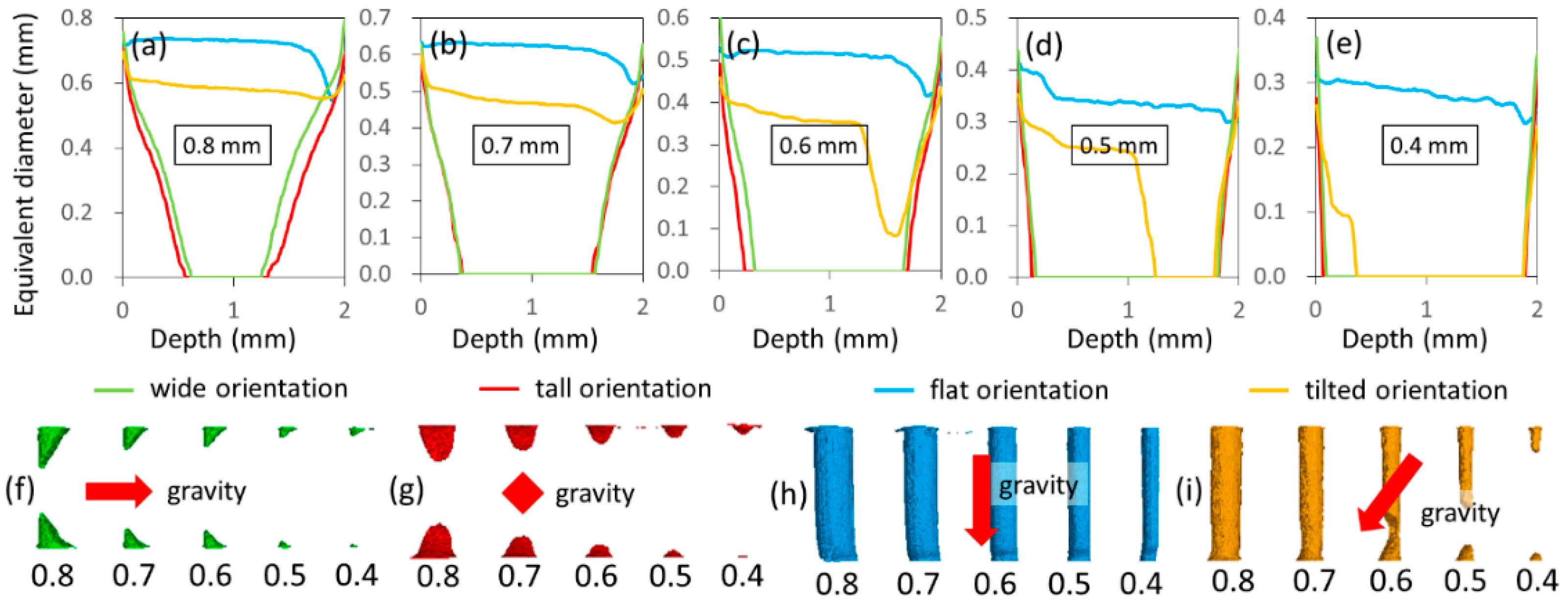
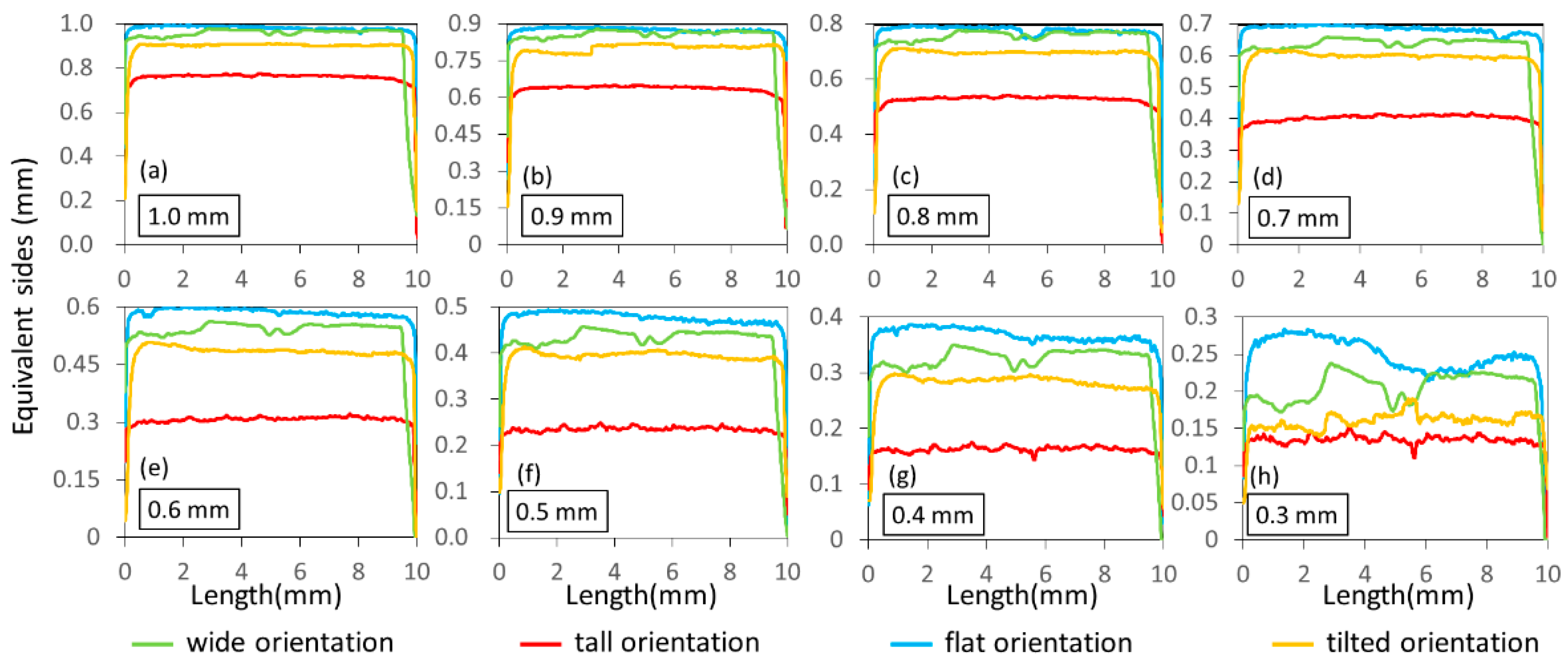
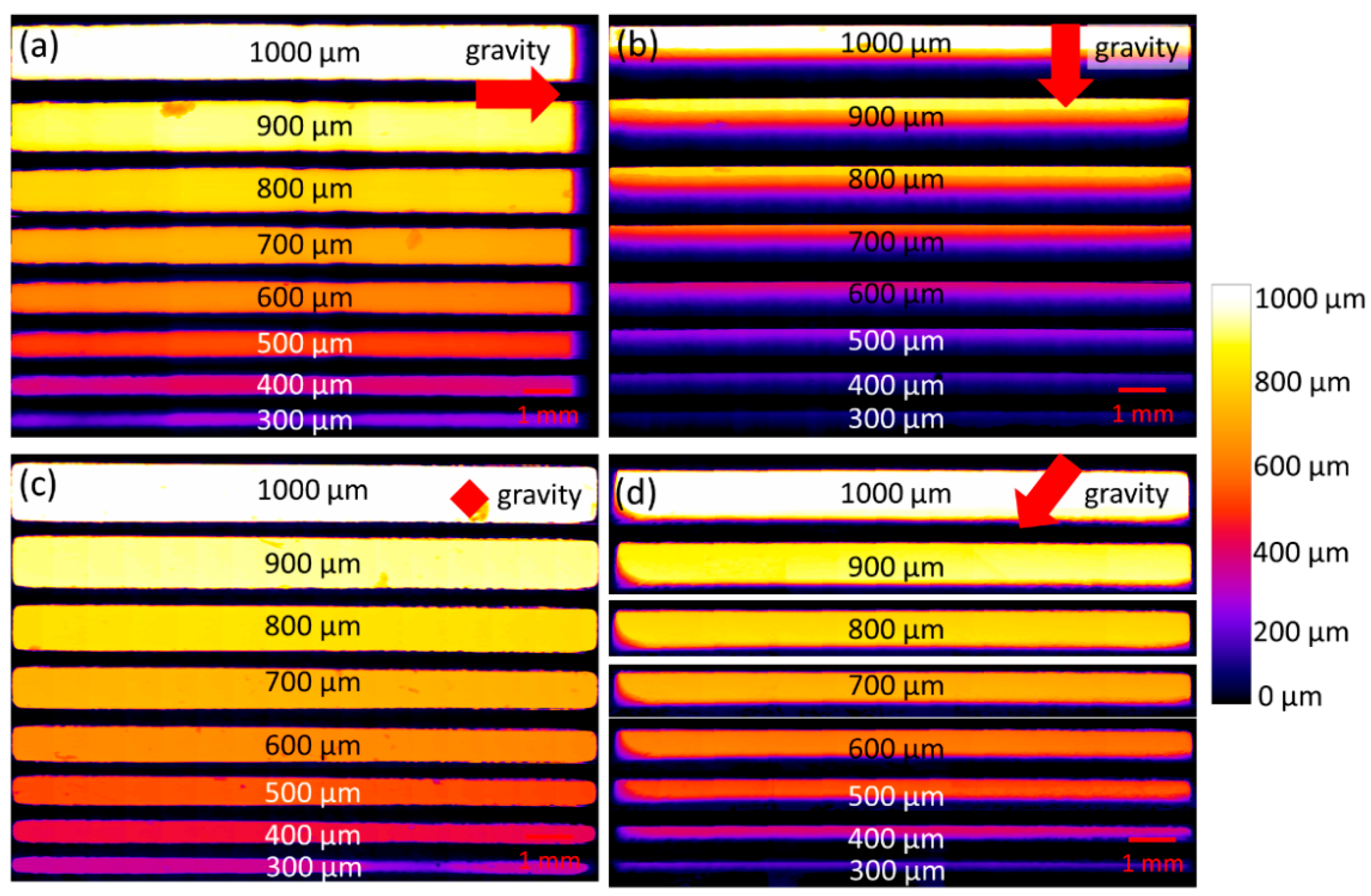
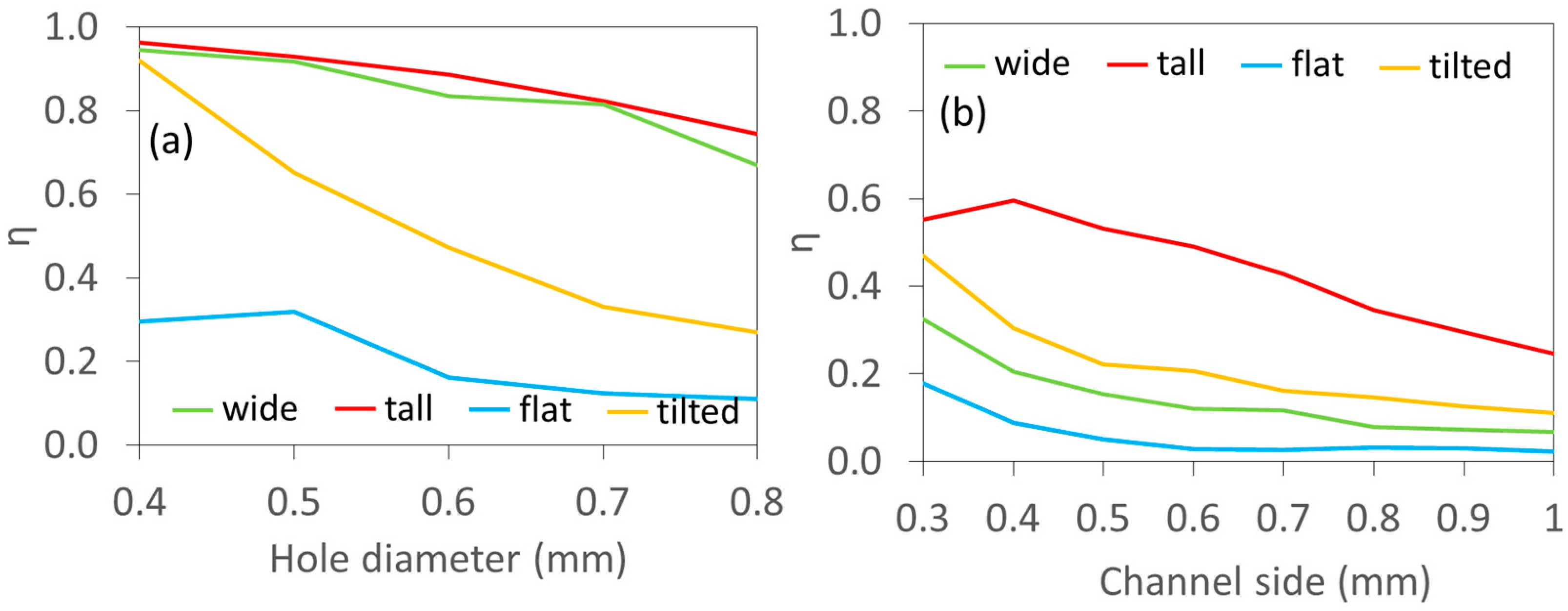
3.1.1. Holes and Channel Rows
3.1.2. Uniform Porous Media Pattern
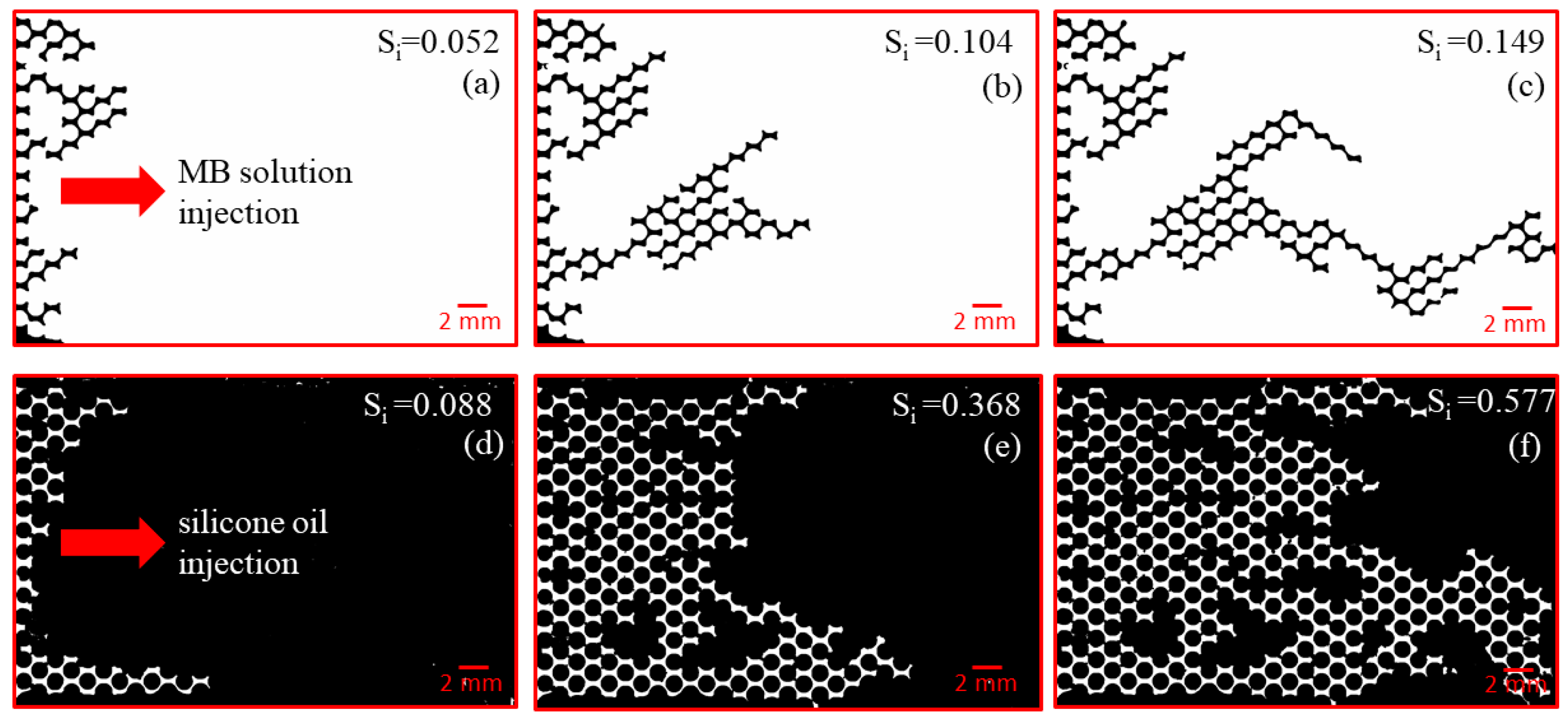
3.2. Fluid Displacement Experiments in the Fabricated Micromodel
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- She, Y.; Zhang, C.; Mahardika, M.A.; Patmonoaji, A.; Hu, Y.; Matsushita, S.; Suekane, T. Pore-scale study of in-situ surfactant flooding with strong oil emulsification in sandstone based on X-ray microtomography. J. Ind. Eng. Chem. 2021, 98, 247–261. [Google Scholar] [CrossRef]
- Wang, J.; Dong, M. Optimum effective viscosity of polymer solution for improving heavy oil recovery. J. Pet. Sci. Eng. 2009, 67, 155–158. [Google Scholar] [CrossRef]
- Osei-Bonsu, K.; Shokri, N.; Grassia, P. Fundamental investigation of foam flow in a liquid-filled Hele-Shaw cell. J. Colloid Interface Sci. 2016, 462, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Patmonoaji, A.; Xu, H.; Kaito, K.; Matsushita, S.; Suekane, T. Pore-scale investigation on nonaqueous phase liquid dissolution and mass transfer in 2D and 3D porous media. Int. J. Heat Mass Transf. 2021, 169, 120901. [Google Scholar] [CrossRef]
- Imhoff, P.T.; Jaffé, P.R.; Pinder, G.F. An experimental study of complete dissolution of a nonaqueous phase liquid in saturated porous media. Water Resour. Res. 1994, 30, 307–320. [Google Scholar] [CrossRef]
- Zhang, C.; Werth, C.J.; Webb, A.G. A magnetic resonance imaging study of dense nonaqueous phase liquid dissolution from angular porous media. Environ. Sci. Technol. 2002, 36, 3310–3317. [Google Scholar] [CrossRef]
- Johns, M.L.; Gladden, L.F. Magnetic resonance imaging study of the dissolution kinetics of octanol in porous media. J. Colloid Interface Sci. 1999, 210, 261–270. [Google Scholar] [CrossRef]
- Johns, M.; Gladden, L. Probing ganglia dissolution and mobilization in a water-saturated porous medium using MRI. J. Colloid Interface Sci. 2000, 225, 119–127. [Google Scholar] [CrossRef]
- Corapcioglu, M.Y.; Yoon, S.; Chowdhury, S. Pore-scale analysis of NAPL blob dissolution and mobilization in porous media. Transp. Porous Media 2009, 79, 419–442. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Zhang, Y.; Xue, Z.; Park, H.; Suekane, T. Experimental and numerical simulation of supercritical CO2 microbubble injection into a brine-saturated porous medium. Int. J. Greenh. Gas Control. 2019, 91, 102830. [Google Scholar] [CrossRef]
- Chang, C.; Zhou, Q.; Xia, L.; Li, X.; Yu, Q. Dynamic displacement and non-equilibrium dissolution of supercritical CO2 in low-permeability sandstone: An experimental study. Int. J. Greenh. Gas Control. 2013, 14, 1–14. [Google Scholar] [CrossRef]
- Chang, C.; Zhou, Q.; Oostrom, M.; Kneafsey, T.J.; Mehta, H. Pore-scale supercritical CO2 dissolution and mass transfer under drainage conditions. Adv. Water Resour. 2016, 100, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.; Zhou, Q.; Kneafsey, T.J.; Oostrom, M.; Wietsma, T.W.; Yu, Q. Pore-scale supercritical CO2 dissolution and mass transfer under imbibition conditions. Adv. Water Resour. 2016, 92, 142–158. [Google Scholar] [CrossRef] [Green Version]
- Heinemann, N.; Alcalde, J.; Miocic, J.M.; Hangx, S.J.T.; Kallmeyer, J.; Ostertag-Henning, C.; Hassanpouryouzband, A.; Thaysen, E.M.; Strobel, G.J.; Schmidt-Hattenberger, C.; et al. Enabling large-scale hydrogen storage in porous media-the scientific challenges. Energy Environ. Sci. 2021, 14, 853–864. [Google Scholar] [CrossRef]
- Lysyy, M.; Ersland, G.; Fernø, M. Pore-scale dynamics for underground porous media hydrogen storage. Adv. Water Resour. 2022, 163, 104167. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Muharrik, M.; Hu, Y.; Zhang, C.; Suekane, T. Three-dimensional fingering structures in immiscible flow at the crossover from viscous to capillary fingering. Int. J. Multiph. Flow 2020, 122, 103147. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Wei, N.; Oostrom, M.; Wietsma, T.W.; Li, X.; Bonneville, A. Experimental study of crossover from capillary to viscous fingering for supercritical CO-water displacement in a homogeneous pore network. Environ. Sci. Technol. 2013, 47, 212–218. [Google Scholar] [CrossRef]
- Zhang, C.; Oostrom, M.; Wietsma, T.W.; Grate, J.W.; Warner, M.G. Influence of Viscous and Capillary Forces on Immiscible Fluid Displacement: Pore-Scale Experimental Study in a Water-Wet Micromodel Demonstrating Viscous and Capillary Fingering. Energy Fuels 2011, 25, 3493–3505. [Google Scholar] [CrossRef]
- Lenormand, R.; Touboul, E.; Zarcone, C. Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 1988, 189, 165. [Google Scholar] [CrossRef]
- Lin, W.; Xiong, S.; Liu, Y.; He, Y.; Chu, S.; Liu, S. Spontaneous imbibition in tight porous media with different wettability: Pore-scale simulation. Phys. Fluids 2021, 33, 032013. [Google Scholar] [CrossRef]
- Zhang, C.; Suekane, T.; Minokawa, K.; Hu, Y.; Patmonoaji, A. Solute transport in porous media studied by lattice Boltzmann simulations at pore scale and x-ray tomography experiments. Phys. Rev. E 2019, 100, 063110. [Google Scholar] [CrossRef] [PubMed]
- Al Mansoori, S.K.; Iglauer, S.; Pentland, C.H.; Blunt, M.J. Three-phase measurements of oil and gas trapping in sand packs. Adv. Water Resour. 2009, 32, 1535–1542. [Google Scholar] [CrossRef]
- Al-Raoush, R.I. Experimental investigation of the influence of grain geometry on residual NAPL using synchrotron microtomography. J. Contam. Hydrol. 2014, 159, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Patmonoaji, A.; Hu, Y.; Nasir, M.; Zhang, C.; Suekane, T. Effects of Dissolution Fingering on Mass Transfer Rate in Three-Dimensional Porous Media. Water Resour. Res. 2021, 57, e2020WR029353. [Google Scholar] [CrossRef]
- Miri, R.; Hellevang, H. Salt precipitation during CO2 storage—A review. Int. J. Greenh. Gas Control. 2016, 51, 136–147. [Google Scholar] [CrossRef]
- Vogel, H. Scale Issues in Soil Hydrology. Vadose Zone J. 2019, 18, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore Scale Perspective; Cambridge University Press: London, UK, 2017. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Roman, S.; Abu-Al-Saud, M.O.; Tokunaga, T.; Wan, J.; Kovscek, A.R.; Tchelepi, H.A. Measurements and simulation of liquid films during drainage displacements and snap-off in constricted capillary tubes. J. Colloid Interface Sci. 2017, 507, 279–289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Z.; Santamarina, J.C. Haines jumps: Pore scale mechanisms. Phys. Rev. E 2019, 100, 023115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitra, S.K.; Chakraborty, S. Microfluidics and Nanofluidics Handbook: Fabrication, Implementation, and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Beauchamp, M.J.; Nordin, G.P.; Woolley, A.T. Moving from millifluidic to truly microfluidic sub-100-μm cross-section 3D printed devices. Anal. Bioanal. Chem. 2017, 409, 4311–4319. [Google Scholar] [CrossRef] [PubMed]
- Gyimah, N.; Scheler, O.; Rang, T.; Pardy, T. Can 3d printing bring droplet microfluidics to every lab?—a systematic review. Micromachines 2021, 12, 339. [Google Scholar] [CrossRef] [PubMed]
- Behm, J.M.; Lykke, K.R.; Pellin, M.J.; Hemminger, J.C. Projection Photolithography Utilizing a Schwarzschild Microscope and Self-Assembled Alkanethiol Monolayers as Simple Photoresists. Langmuir 1996, 12, 2121–2124. [Google Scholar] [CrossRef]
- Love, J.C.; Wolfe, D.B.; Jacobs, H.O.; Whitesides, G.M. Microscope projection photolithography for rapid prototyping of masters with micron-scale features for use in soft lithography. Langmuir 2001, 17, 6005–6012. [Google Scholar] [CrossRef]
- Comina, G.; Suska, A.; Filippini, D. Low cost lab-on-a-chip prototyping with a consumer grade 3D printer. Lab Chip 2014, 14, 2978–2982. [Google Scholar] [CrossRef] [PubMed]
- Comina, G.; Suska, A.; Filippini, D. PDMS lab-on-a-chip fabrication using 3D printed templates. Lab Chip 2014, 14, 424–430. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Sentanu, D.A. Characteristics and performance of carabiner remodeling using 3D printing with graded filler and different orientation methods. Eng. Fail. Anal. 2021, 130, 105795. [Google Scholar] [CrossRef]
- Alfarisi, N.A.S.; Santos, G.N.C.; Norcahyo, R.; Sentanuhady, J.; Azizah, N.; Muflikhun, M.A. Model optimization and performance evaluation of hand cranked music box base structure manufactured via 3D printing. Heliyon 2021, 7, e08432. [Google Scholar] [CrossRef]
- Daly, A.C.; Pitacco, P.; Nulty, J.; Cunniffe, G.M.; Kelly, D.J. 3D printed microchannel networks to direct vascularisation during endochondral bone repair. Biomaterials 2018, 162, 34–46. [Google Scholar] [CrossRef]
- Watson, F.; Maes, J.; Geiger, S.; Mackay, E.; Singleton, M.; McGravie, T.; Anouilh, T.; Jobe, T.D.; Zhang, S.; Agar, S.; et al. Comparison of Flow and Transport Experiments on 3D Printed Micromodels with Direct Numerical Simulations. Transp. Porous Media 2019, 129, 449–466. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Zhang, D.; Lei, G. Experimental study on multiphase flow in fracture-vug medium using 3D printing technology and visualization techniques. J. Pet. Sci. Eng. 2020, 193, 107394. [Google Scholar] [CrossRef]
- Dimou, A.P.; Menke, H.P.; Maes, J. Benchmarking the Viability of 3D Printed Micromodels for Single Phase Flow Using Particle Image Velocimetry and Direct Numerical Simulations. Transp. Porous Media 2021, 141, 279–294. [Google Scholar] [CrossRef]
- Osei-Bonsu, K.; Grassia, P.; Shokri, N. Investigation of foam flow in a 3D printed porous medium in the presence of oil. J. Colloid Interface Sci. 2017, 490, 850–858. [Google Scholar] [CrossRef] [PubMed]
- Ahkami, M.; Roesgen, T.; Saar, M.O.; Kong, X.Z. High-Resolution Temporo-Ensemble PIV to Resolve Pore-Scale Flow in 3D-Printed Fractured Porous Media. Transp. Porous Media 2019, 129, 467–483. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Sadeghnejad, S.; Ostadhassan, M. Evaluation of 3D printed microfluidic networks to study fluid flow in rocks. Oil Gas Sci. Technol. 2021, 76, 50. [Google Scholar] [CrossRef]
- Ishutov, S. Establishing Framework for 3D Printing Porous Rock Models in Curable Resins. Transp. Porous Media 2019, 129, 431–448. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [Green Version]
- Patmonoaji, A.; Tsuji, K.; Suekane, T. Pore-throat characterization of unconsolidated porous media using watershed-segmentation algorithm. Powder Technol. 2020, 362, 635–644. [Google Scholar] [CrossRef]
- Lindquist, W.B.; Lee, S.-M.; Coker, D.A.; Jones, K.W.; Spanne, P. Medial axis analysis of void structure in three-dimensional tomographic images of porous media. J. Geophys. Res. Solid Earth 1996, 101, 8297–8310. [Google Scholar] [CrossRef] [Green Version]
- Gostick, J.T. Versatile and efficient pore network extraction method using marker-based watershed segmentation. Phys. Rev. E 2017, 96, 023307. [Google Scholar] [CrossRef] [Green Version]
- Rabbani, H.S.; Or, D.; Liu, Y.; Lai, C.Y.; Lu, N.B.; Datta, S.S.; Stone, H.A.; Shokri, N. Suppressing viscous fingering in structured porous media. Proc. Natl. Acad. Sci. USA 2018, 115, 4833–4838. [Google Scholar] [CrossRef] [Green Version]
- Lu, N.B.; Browne, C.A.; Amchin, D.B.; Nunes, J.K.; Datta, S.S. Controlling capillary fingering using pore size gradients in disordered media. Phys. Rev. Fluids 2019, 4, 084303. [Google Scholar] [CrossRef] [Green Version]
- Haitjema, H.M.; Anderson, M.P. Darcy velocity is not a velocity. Ground Water 2016, 54, 1. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man. Cybern. 1979, 6, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Ishutov, S.; Hasiuk, F.J.; Jobe, D.; Agar, S. Using Resin-Based 3D Printing to Build Geometrically Accurate Proxies of Porous Sedimentary Rocks. Groundwater 2018, 56, 482–490. [Google Scholar] [CrossRef]
- Ju, Y.; Xi, C.; Zheng, J.; Gong, W.; Wu, J.; Wang, S.; Mao, L. Study on three-dimensional immiscible water–Oil two-phase displacement and trapping in deformed pore structures subjected to varying geostress via in situ computed tomography scanning and additively printed models. Int. J. Eng. Sci. 2022, 171, 103615. [Google Scholar] [CrossRef]
- Fee, C. 3D-printed porous bed structures. Curr. Opin. Chem. Eng. 2017, 18, 10–15. [Google Scholar] [CrossRef]
- Fee, C.; Nawada, S.; Dimartino, S. 3D printed porous media columns with fine control of column packing morphology. J. Chromatogr. A 2014, 1333, 18–24. [Google Scholar] [CrossRef]



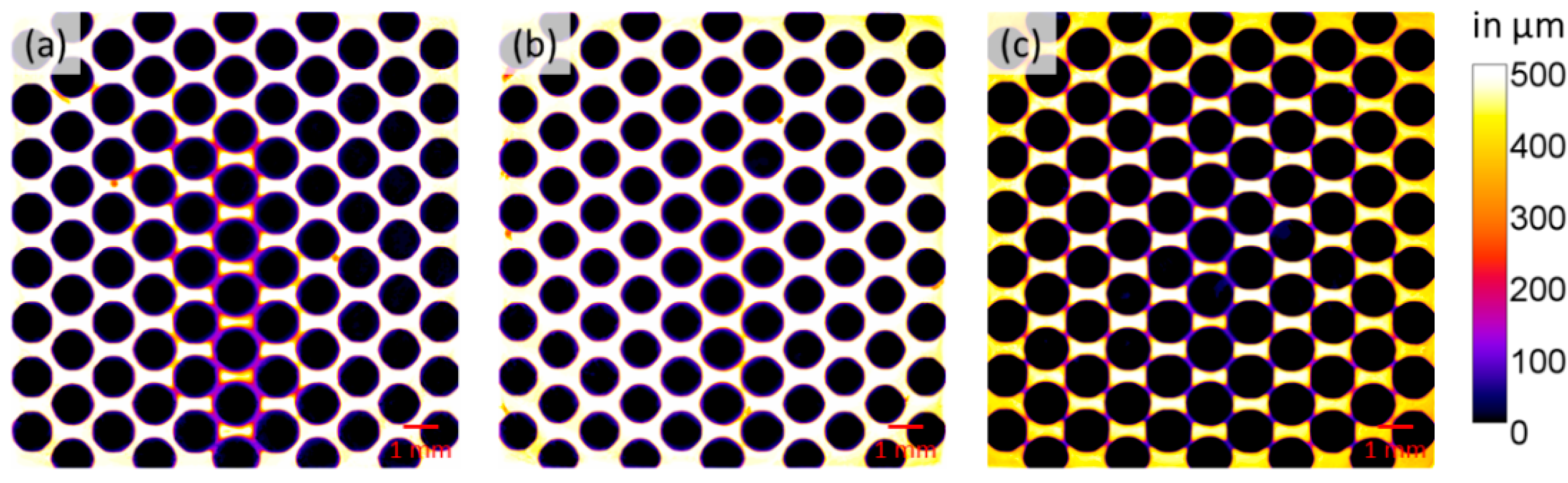
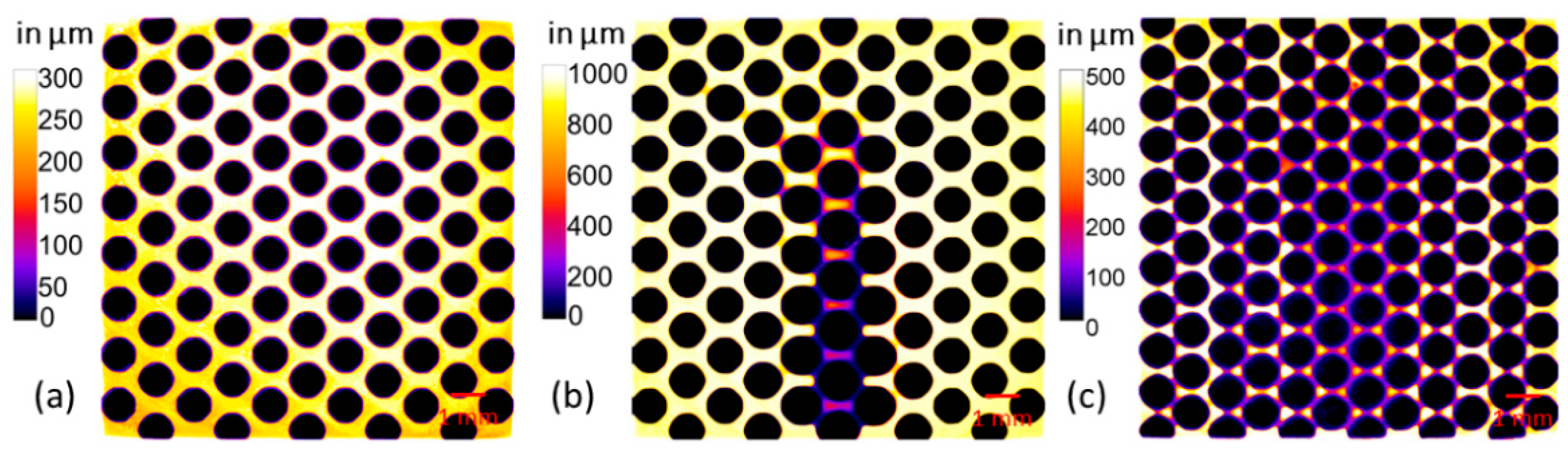
| Printing Design | Overall Volume Error | Throat Blockages | Pillar Average Diameter (μm) |
|---|---|---|---|
| Thickness resolution 25 μm | 0.316 | 0 | 1378 |
| Thickness resolution 50 μm | 0.163 | 29 | 1278 |
| Thickness resolution 100 μm | 0.517 | 126 | 1431 |
| Pattern depth 300 μm | 0.199 | 0 | 1270 |
| Pattern depth 1000 μm | 0.315 | 25 | 1303 |
| GapX 300 μm GapR 274 μm | 0.442 | most | 1305 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patmonoaji, A.; Mahardika, M.A.; Nasir, M.; She, Y.; Wang, W.; Muflikhun, M.A.; Suekane, T. Stereolithography 3D Printer for Micromodel Fabrications with Comprehensive Accuracy Evaluation by Using Microtomography. Geosciences 2022, 12, 183. https://doi.org/10.3390/geosciences12050183
Patmonoaji A, Mahardika MA, Nasir M, She Y, Wang W, Muflikhun MA, Suekane T. Stereolithography 3D Printer for Micromodel Fabrications with Comprehensive Accuracy Evaluation by Using Microtomography. Geosciences. 2022; 12(5):183. https://doi.org/10.3390/geosciences12050183
Chicago/Turabian StylePatmonoaji, Anindityo, Mohammmad Azis Mahardika, Muhammad Nasir, Yun She, Weicen Wang, Muhammad Akhsin Muflikhun, and Tetsuya Suekane. 2022. "Stereolithography 3D Printer for Micromodel Fabrications with Comprehensive Accuracy Evaluation by Using Microtomography" Geosciences 12, no. 5: 183. https://doi.org/10.3390/geosciences12050183
APA StylePatmonoaji, A., Mahardika, M. A., Nasir, M., She, Y., Wang, W., Muflikhun, M. A., & Suekane, T. (2022). Stereolithography 3D Printer for Micromodel Fabrications with Comprehensive Accuracy Evaluation by Using Microtomography. Geosciences, 12(5), 183. https://doi.org/10.3390/geosciences12050183








