Abstract
This study introduces a new energy dissipation device with a high damping capacity for the seismic protection of buildings. The device exploits the friction losses between a movable shaft and a lead core to dissipate the seismic energy and takes advantage of the prestressing of the lead material to control the friction force. Numerical analyses are introduced to evaluate the influence of prestressing on the axial force of the device. Cyclic tests performed on a prototype demonstrate the high damping capability, with an equivalent damping ratio ξeff of approximately 55%, a robust and stable response over repeated cycles and a low sensitivity of the mechanical properties to the frequency, suggesting that the proposed device may be a potentially effective solution for providing supplementary energy dissipation to structures in seismic areas. Moreover, the device is able to endure multiple cycles of motion at the basic design earthquake displacement, ensuring maintenance-free operation even in presence of repeated ground shakes.
1. Introduction
Supplementary energy dissipation has extensively proven, through research studies and practical applications, to be a viable strategy for protecting new and existing structures against nonstructural and structural damage caused by earthquakes [1,2,3,4]. In buildings, this strategy is often implemented by providing the structure with dissipative bracing systems, consisting of steel braces equipped with dissipation devices, or dampers, which aim at achieving two effects, namely increasing the structural stiffness, with a consequent reduction in displacement, and dissipating much of the seismic energy, leading to a decrease in acceleration [5]. Steel hysteretic dampers, which exploit the plastic deformation of a mild steel core to dissipate the seismic energy, are today the most frequently used devices in ordinary structures, such as school, residential and industrial buildings, owing to their good damping capacity, predictable behavior and low cost.
Nowadays, enhancing the community resilience, i.e., the community’s ability to prepare for, respond to and recover after a disaster within the shortest possible time [6], is becoming a priority for modern societies, influencing the work in fields such as civil engineering dealing with seismic hazards. However, most current energy dissipation devices appear not to be suitable to meet this target. In fact, the design of dissipative bracing systems is performed respecting the “structural safety requirement” at the ultimate limit state only [2,3,4,7], and the dissipative devices are designed to be engaged under extreme events only and not under weak seismic excitations [8]. Consequently, under low-intensity earthquakes, a structure equipped with dissipative braces may be subjected to greater accelerations and thereby suffer higher damage than the bare configuration due to an increase in stiffness introduced by the bracing system [9]. Another issue hampering the achievement of resilience concerns the steel hysteretic dampers, which generally need to be replaced after a major earthquake because of low resistance to low-cycle fatigue and accrual of permanent deformation. This carries a potential threat to the safety of the structure that, until the replacement of the dissipative system, is left exposed to aftershocks which may occur in a short time after the main event [10].
The design of energy dissipation devices meeting the needs of a resilient community should indeed fulfill multiple objectives [11,12]: (i) they should not require maintenance after a major earthquake, in order to guarantee a high safety level in case of aftershocks; (ii) they should not be at risk of low-cycle fatigue fracture, which is a typical issue for current steel hysteretic devices; (iii) they should ensure the recentering of the structure at the end of a seismic event; (iv) they should be a compact and architecturally lowly invasive in order to reduce the impact on the building layout; and (v) the cost of manufacturing and installation should be economically appealing compared with alternative design solutions such as structural strengthening.
This study introduces a novel damper designed for increased resilience. The damper dissipates the input energy through the friction activated between a lead core and a steel shaft and achieves high specific dissipation capability through prestressing the working material. Differently from lead dampers proposed in the past [13,14,15,16,17,18], the operation of the novel device, which is called the prestressed lead damper with straight shaft (or PS-LED), is based on friction solely and does not exploit the extrusion of lead through an orifice, which mitigates the cyclic degradation of the response, eases the design and the construction and reduces production costs. The performance of the damper is assessed experimentally to evaluate the damping capability and the robustness during repeated cycles and to verify the compliance with the requirements of the European standard EN 15129 for displacement-dependent devices [19].
2. Design and Construction of the PS-LED
2.1. Lead Extrusion Dampers
The idea of dissipating energy by exploiting the plastic deformation of a lead core was conceived by Robinson and Greenbank [20,21], who proposed dampers where the lead is confined into a steel tube crossed by a moving shaft (Figure 1). In the configuration shown in Figure 1a, the shaft is provided with two heads, which force the lead to flow through an orifice created by an annular constriction of the tube wall. In the configuration shown in Figure 1b, the orifice is created by the clearance between a bulge on the shaft and the internal wall of the tube; as the shaft moves, the orifice travels through the lead core and pushes the material to flow through. Two mechanisms contribute to the dissipation of energy, namely the plastic deformation of the lead material forced to flow through the annular orifice and the friction force activated between the lead core and the shaft [21,22]. Both mechanisms were demonstrated to be only weakly rate-dependent, so the energy dissipation capacity has a weak dependence on velocity too [11,23]. In the lead extrusion damper, part of the energy required to produce the plastic deformation of lead is dissipated as heat, while the other part is stored and used to promote the recrystallization of the deformed lead, by which the material regains its original properties; this mechanism results in consistent force across multiple cycles of response without any loss of strength or stiffness, or any other low-cycle fatigue effect [21].
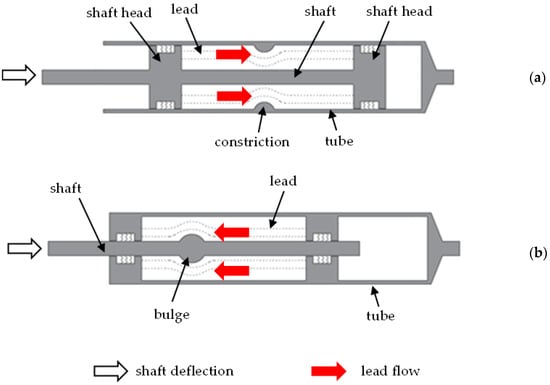
Figure 1.
Longitudinal section of lead extrusion dampers: constricted tube type (a); bulged shaft type (b). Adapted from [24].
The main issue affecting the Robinson damper was related to the voids that formed within the working material during the extrusion of lead: due to its compressibility, when forced to flow through the orifice, the lead is compressed plastically into a smaller volume leading to the formation of a “trailing void” which reduces the extrusion resistance and the amount of dissipation as the number of cycles of deflection increases. Lead extrusion dampers used in the first structural applications were therefore large, in order to provide sufficient dissipation capability, but their size was considered an impediment, preventing their implementation in most of the possible applications [13].
A substantial improvement that rekindled the interest in this technology was introduced by Rodgers [13,25] with the high force-to-volume (HF2V) damper. In this version, whose design resembled the bulged shaft version shown in Figure 1a, a notable increase in the specific force and the dissipation capability of the damper was achieved by preloading the lead core during the assembly. Compressing the lead reduced the formation of trailing voids and boosted the force-to-volume ratio, allowing a more compact design [25,26,27]. HF2V dampers were assessed both experimentally and numerically, providing an amount of energy dissipation larger than that of mild steel devices designed for the same yield force, without encountering any fatigue problem [12,21,23,28,29,30,31,32,33,34,35,36]. The HF2V technology was practically employed in the Kilmore Street Medical Center in New Zealand, where the HF2V devices were used to develop a hybrid system, called the “Advanced-Flag Shape” system, to allow controlled rocking of the structure [27]. Further research on this technology was carried out by Soydan [14,15,16,17], Patel [36,37], Yang [37,38] and Quaglini [10,11]. The application of HF2V devices in structural connections of both precast structures and steel structures was studied in [29,33,35]. The results showed that this system can provide a level of energy dissipation comparable to, or in excess of, that of mild steel hysteretic dampers designed for the same yield force, without encountering any fatigue problem experienced by the alternative solutions [39]. Moreover, because of low-cycle fatigue and residual stresses, mild steel energy dissipation systems need to be replaced after an earthquake, while the lead damper does not need any maintenance, and thanks to its ability to creep out over time, it does not prevent the self-centering of the structure [39,40]. However, analyses and experiments showed that the huge amount of energy dissipated in form of heat causes a substantial rise in the temperature of the lead core, producing the melting of the working material and the ensuing decrease in its yield strength. The consequence is a continuous decrease in the extrusion force and therefore unpredictable behavior of the damper during repeated cycles of motion, e.g., during strong earthquakes.
2.2. Structure of the PS-LED
The PS-LED is composed of four main parts: the straight shaft, the tube, the cap and the lead core (Figure 2). The tube, shaft and cap are made of high strength steel, and the shaft is plated with hard chromium. A bushing provided in the cap drives the linear motion of the shaft and prevents leakage of lead outside the device.
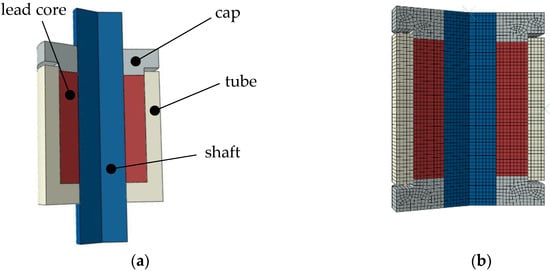
Figure 2.
The PS-LED: (a) longitudinal section and (b) finite element model.
The assembly of the PS-LED consists of four main steps: (i) the lead core is cast in a hollow cylindrical mold with the outer and inner diameters resembling the diameters of the tube wall and the shaft, respectively; (ii) the lead core is fitted within the tube and the shaft is gently forced to pass through the lead core; (iii) the cap is locked to the tube wall by means of screws; by tightening the screws the lead core is prestressed and voids and clearances are removed, resulting in a perfect fit to the tube and the shaft; (iv) hinges are fitted to one end of the shaft and the opposite end of the tube to connect the damper to the structure. Possible configurations for installation of the PS-LED in a structural frame are based on placing the device within diagonal braces (Figure 3a), where the damper develops resistive forces against the brace elongation [41], or at both sides of the web (Figure 3b), where the device develops resistive forces against the beam rotation [35].
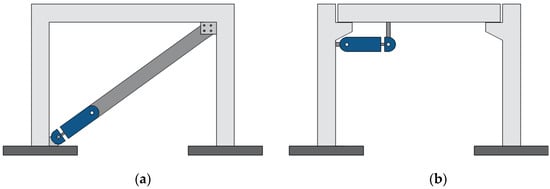
Figure 3.
Possible configurations of installation of the PS-LED on frame structures: (a) brace configuration; (b) beam–column joint configuration.
The damper is placed in conventional damped braced systems and connected at one end of the shaft and at the opposite end of the tube. When the structure oscillates under the effects of the ground motion, the shaft moves relative to the tube, activating a friction force at the interface with the lead core, through which energy is dissipated. Since the coefficient of friction between lead and chromium-plated steel is noted to remain almost steady once sliding is triggered [11], the damper provides a constant force over its entire stroke and an ensuing essentially rectangular hysteretic curve, which maximizes the amount of energy dissipation. The theoretical amount of energy dissipated in a full cycle of amplitude db indeed amounts to EDC = 4 F0 db, where F0 is the resisting force developed by friction during deflection of the shaft. During the assembling, the lead core is prestressed by tightening the locking screws of the cap (Figure 4); increasing the bulk stress within the lead core boosts the friction force between the core and the shaft, allowing high levels of energy dissipation, compact dimensions and low manufacturing cost to be achieved. Moreover, relying on friction force only is expected to reduce the influence of heating (which indeed has a major effect on the extrusion resistance of lead) on the output force and increase the stability of the damping characteristic during repeated cycles. In addition to the high damping-to-volume ratio achieved by prestressing, another favorable feature of the PS-LED is that the straight shaft does not require complex and expensive machining operation as its bulged counterpart does, permitting the use of commercial chromed shafts and reducing manufacturing costs.
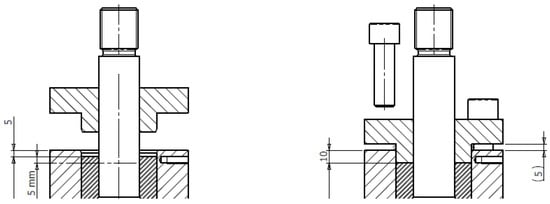
Figure 4.
Prestressing of the lead core during the assembly of the PS-LED [41].
In order to investigate the effect of prestressing the lead, a simplified numerical model of the PS-LED was formulated in the general-purpose software Abaqus/CAE 6.14-2 [38,42], using 4-node bilinear axisymmetric elements type C4X4. By taking advantage of the symmetry of the system about its longitudinal axis, only half of the prototype was modeled. The model includes the four parts of the damper: the shaft, the tube, the plug and the working material (Figure 2b). A fine mesh (3.3 mm maximum element size) was used to represent the volume of working material, in order to allow a realistic simulation of the lead around the shaft without severe distortion of the elements that may cause abortion of analysis. Lead is modeled as an elastic–almost perfectly plastic material (a small hardening is introduced in order to avoid convergence issues), and S450 steel is assumed for the shaft, tube and cap. The modeling parameters of the FE model are tabulated in Table 1 [11,36]. Hard contact is introduced at the interfaces between shaft and tube and between the shaft and cap, while hard contact in the normal direction and penalty friction formulation in the shear direction are assigned at the interfaces between the lead and shaft and between the lead and tube, where the relevant friction coefficients are µ1 = 0.15 and µ2 = 0.30, respectively [12]. The analyses were performed in two steps. In the first step, prestressing of the working material was simulated by applying an increasing force, uniformly distributed on the upper surface of the cap, until a deflection ΔL of the cap, corresponding to an assigned axial strain ε = ΔL/L of the lead bulk, was achieved, where L is the initial height of the bulk. In the second step, the prestressing load imposed in the previous step was held constant, and dynamic implicit analysis was performed by imposing a cyclic displacement history to the shaft with a displacement amplitude of 20 mm.

Table 1.
Material properties used in the FE model [12].
Figure 5 reports the axial force F0 of the PS-LED calculated for different values of axial strain ε imposed on the lead core and for different diameters of the shaft (the outer diameter of the core is 70 mm). The force increases almost proportionally with ε until a certain threshold is achieved, beyond which no further increase occurs. The strain threshold corresponds to the yielding of lead and determines the maximum stress that can be induced in the material bulk, which is in turn proportional to the friction force. As a first approximation, the axial force of the damper can indeed be calculated as the product of the friction coefficient µ1 between the shaft and lead times the bulk stress in the lead times the area of the shaft–lead interface. Though very simple, this analytical model justifies the linear dependence of F0 on the diameter of the shaft and the achievement of a steady force level beyond a certain strain observed in the finite element analyses. Eventually, it is worth noting that the steady value F0 = 200 kN of the PS-LED with 32.5 mm diameter predicted numerically is close to the experimental value of 220 kN measured on a prototype of a lead damper with a bulged shaft reported in [11], thereby proving the effectiveness of the preload in controlling the friction force and the viability of the proposed design to achieve force and damping capabilities equivalent to the ones of the bulged shaft counterpart.
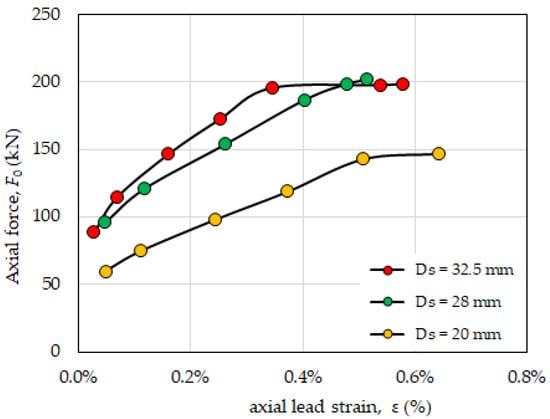
Figure 5.
Axial load F0 of the PS-LED vs. axial strain ε of the prestressed lead core for different diameters of the shaft Ds.
3. Experimental Assessment
3.1. Description of the Prototype
A prototype of the PS-LED has been experimentally assessed in this study. The exploded drawing of the prototype is shown in Figure 6, while the materials are according to the description given in Section 2.2. All components are made of 42CrMo4 quenching and tempering steel, except for the core which is made of 99.99% pure lead. The cap is fixed to the tube wall by means of eight M16 screws. The operational dimensions of the device are as follows: the shaft diameter Ds = 32 mm, the external diameter of the lead core Dl = 60 mm, and the length of lead core L = 80 mm. The design deflection of the prototype calculated for the basic design earthquake (corresponding to the life-safety limit state according to the Italian Building Code (IBC) [43]) is dbd = 20 mm in either direction. In order to avoid off-axis load, self-lubricating spherical hinges with a minimum rotation capacity of ±2° are provided at the two connection points, namely the bottom of the tube and the far end of the shaft. The total length of the prototype is 568 mm (433 mm between the center axes of the joints), and the external dimensions of the tube (with square cross-section) are 110 mm × 125 mm. During assembling, the lead core was prestressed by tightening the fixing screws of the cap to a torque of 212 Nm.
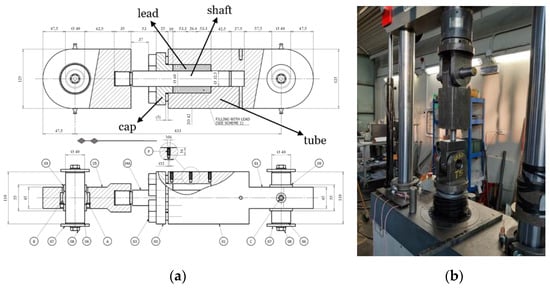
Figure 6.
PS-LED experimentally assessed in the study: (a) shop drawing; (b) prototype on the testing machine [41].
3.2. Experimental Protocol
The experimental campaign was performed at the Materials Testing Laboratory of Politecnico di Milano, using a servohydraulic testing machine (MTS Systems, Eden Prairie, MN) with a load capacity of 500 kN (Figure 6b).
The prototype was subjected to the type testing protocol prescribed in the European standard on antiseismic devices, EN 15129 [18] for assessment of displacement-dependent devices (labeled as tests #1 and #2 in Table 2). The hysteretic force–deflection response was evaluated by imposing harmonic cycles of increasing amplitude at 25%, 50% and 100% of the design deflection dbd at a frequency f = 0.5 Hz. Five cycles for each intermediate amplitude and ten cycles for the maximum amplitude were applied. Then, the deflection capacity of the prototype was assessed in a ramp test consisting in the application of an increasing deformation up to the limit γb γx dbd, where γb = 1.1 and γx = 1.2 are the amplification factor and the reliability factor given in the product standard [18]. It is worth noting that the quantity γx dbd is denoted as d2 and represents the deflection of the damper evaluated at the collapse ultimate limit state according to IBC [43].

Table 2.
Testing protocol.
In order to investigate the dependence on the velocity, three additional tests were performed, consisting in the application of harmonic cycles to the design deflection dbd at three distinct frequencies (test #3 in Table 2).
Eventually, the dedicated test prescribed by IBC [43] for displacement-dependent devices and consisting in the application of five harmonic cycles with amplitude d2 = γx dbd was performed (test #4 in Table 2). Before each test, the tightening of the cap fixing screws was checked and restored to 212 Nm if necessary.
At the end of the testing protocol, for direct assessment of the effect of prestressing, the cap fixing screws were loosened and then tightened to either 165 Nm (first run) or 100 Nm (second run), and then the cyclic test with amplitude equal to dbd = 20 mm (test #2) was repeated.
3.3. Results
The force–displacement behavior of the PS-LED prototype observed in a fully reversed cycle with the maximum deflection dbd is illustrated in Figure 7. Figure 7a shows the hysteretic response of the prototype with fixing screws tightened to 212 Nm. An elastic deflection of the whole damper is initially observed until the breakaway friction resistance of the working material is overcome and sliding of the shaft relative to the lead core is eventually engaged. From this point on, the force–displacement curve shows a plastic branch characterized by an almost steady force independently of the accommodated deflection, and the same behavior occurs after each motion reversal. It is worth noting that owing to the high elastic stiffness of the steel members, which provide a high initial stiffness, the hysteresis loop has an essentially rectangular shape. The behavior of the device is symmetric in tension and compression, with similar values of the axial force F0 both in tension (N > 0, shaft mowing outwards) and in compression (N < 0, shaft moving inwards). The small changes in the output force at motion reversals suggest that the friction between the shaft and the lead has a shallow dependence on the velocity, though this dependency does not affect the overall response too much. The idle displacement observed after the motion reversal and highlighted in Figure 7a by the red arrows is ascribed to the clearance of the spherical hinges.
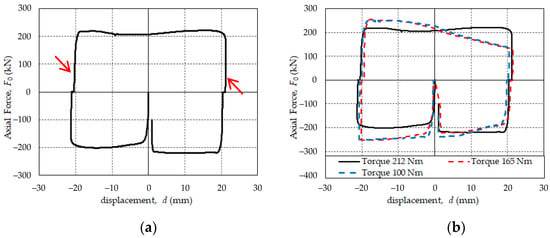
Figure 7.
Hysteresis loops of the PS-LED prototype: (a) regular loop of the prototype with fixing screws tightened to 212 Nm [41]; (b) deformed loop with trailing void for low tightening torque.
Figure 7b compares the cyclic responses assessed at three different levels of prestressing of the lead core. Preloading the core below the yield stress of the material seems to be ineffective to prevent the occurrence of “trailing voids”, due to the loosening of prestressing. Though the resulting force–displacement curve is asymmetric, the dissipated energy per cycle (i.e., the area enclosed in the hysteresis cycle) looks close to the one observed when the prototype is tightened to the preset torque of 212 Nm.
Two quantities were calculated at each test cycle and used to characterize the response of the PS-LED:
- Effective stiffness:
- Equivalent damping ratio:
In order to prove a repeatable and stable cyclic response, the European standard [18] prescribes that both quantities Keff and ξeff shall remain essentially constant during a sequence of cycles of same amplitude:
where i is the cycle number (i ≥ 2), and Keff,3 and ξeff,3 are the effective stiffness and the equivalent damping ratio evaluated at the third cycle.
Figure 8 shows the effective stiffness and equivalent damping assessed in test #1 for different amplitudes. The diagrams highlight the stable and predictable behavior of the prototype. Disregarding the first cycle, both Keff,3 and ξeff,3 fulfill the stability requirements, with the maximum changes of 9.9% in the effective stiffness and of 2.4% in the equivalent damping in the most challenging test sequence at the design deflection dbd. The average value of ξeff,3 over 10 cycles performed at the design seismic displacement dbd is 0.55, i.e., 86% of the equivalent damping of an ideally rectangular loop, confirming the excellent dissipation capacity of the PS-LED. It is worth observing that, differently from the stiffness, the equivalent damping ratio is almost independent of the maximum displacement achieved during the cycle (Figure 8b). Since the PS-LED provides a constant force F0 independent of the displacement, the hysteretic force–displacement curve has a nearly rectangular shape (Figure 7a), and the energy dissipated in a cycle of amplitude db is EDC = 4 F0 db; hence, by recalling Equation (2), an equivalent damping ratio ξeff = 2/π follows regardless of the maximum deflection. For standard buckling-restrained steel hysteretic dampers made of mild steel, the equivalent damping ratio generally lies in the range of 20% to 40%, depending on the geometry and the design deflection [44,45,46]. In the ramp test, the prototype was able to sustain the amplified design deflection γx γb dbd without any cracking, and after the peak value due to the breakaway friction the force–deflection curve presented a nondecreasing behavior (Figure 9), demonstrating the ability of the device to accommodate the capacity demand without any deterioration of its stiffness.
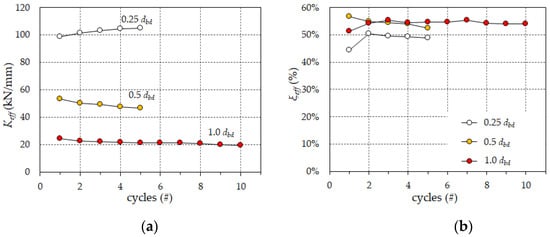
Figure 8.
Variation of the properties of the PS-LED prototype in cyclic tests at different amplitudes: (a) the effective stiffness Keff; and (b) the equivalent damping ratio ξeff.
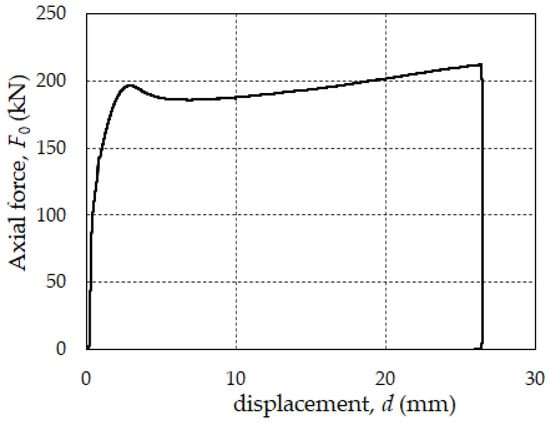
Figure 9.
Ramp test of the PS-LED prototype subjected to deformation increasing to the amplified seismic deflection γx γb dbd.
Figure 10 illustrates the variations in the effective stiffness and the equivalent damping ratio due to the strain rate assessed in test #3 with reference to a frequency variation of ±50%. After each series of cycles at a given frequency, the prototype was left to recover at ambient temperature for a short time (between 45 and 90 min) and then subjected to a new series of cycles at a higher frequency. The effective stiffness of the device exhibits a shallow dependence on the frequency, while the equivalent damping ratio is virtually unaffected. The provision of the European standard [18] requiring a ±10% maximum variation due to strain rate with reference to the properties evaluated at the third cycle is therefore fulfilled. Eventually, in test #4, the prototype demonstrated its ability to resist a series of cycles to the maximum deflection evaluated at the collapse ultimate limit state according to IBC 43]. The results, shown in Figure 10, confirmed the suitability of the prototype to resist up to five cycles performed to its displacement capacity with no substantial degradation of stiffness and damping characteristics.
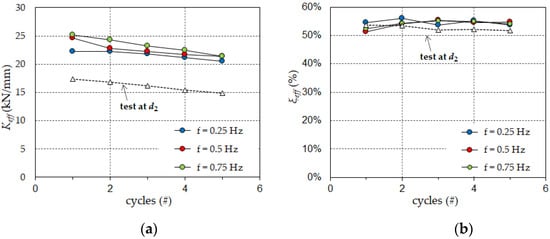
Figure 10.
Variation of the properties of the PS-LED prototype in cyclic tests at different frequencies f with maximum deflection d2 (design deflection at the collapse ultimate limit state): (a) the effective stiffness Keff and (b) the equivalent damping ratio ξeff.
4. Conclusions
The prestressed lead damper with straight shaft, a novel energy dissipation device with behavior mainly dependent on the displacement, has been introduced by this study. The device dissipates energy through the friction losses that occur at the interface between the lead core and the metal shaft and achieves high specific force and damping capability through preloading of the working material. Differently from other versions of lead dampers with bulged shafts, the present device employs a straight shaft, which eases the production and reduces the manufacturing costs, while it disregards the plastic deformation of lead as a means to dissipate energy. This design is aimed at enhancing the stability of the mechanical response of the damper during repeated cycles since heating of the lead core caused by the dissipation of energy can affect the yield strength of lead and reduce the extrusion force.
The main outcomes of the study are recalled as follows:
- A prototype of the PS-LED was experimentally assessed according to the provisions of the European standard EN 15129 [18] for displacement-dependent devices. The damper exhibits an essentially rigid–plastic behavior, with an equivalent damping ratio ξeff = 55%, independent of the maximum cyclic displacement.
- Prestressing the lead core according to the procedure developed in this study is a viable means to control the axial force and the energy dissipation of the device, allowing the achievement of damping capability similar to that obtained with lead dampers with bulged shafts of the same size.
- The mechanical response of the damper over a series of cycles with an amplitude equal to the design seismic displacement is stable and predictable and fulfills the limits of variation prescribed in the European standard [18]. The changes in the equivalent damping ratio over 10 cycles at the design deflection are less than 3%, ensuring a consistent energy dissipation capability even in case of severe seismic demand. The response is not substantially affected by the frequency of loading.
- The damper prototype afforded several sequences of cycles with amplitudes equal to the basic design earthquake displacement and then a final set of five cycles to the maximum displacement evaluated for the collapse ultimate limit state without being damaged or exhibiting substantial changes in its mechanical properties.
The damper proves to be able to fulfill two basic requirements, i.e., robust and stable mechanical behavior and maintenance-free operation even in presence of repeated excitations occurring within a short time, as may happen, e.g., in the case of aftershock sequences, thereby representing a viable system for the development of resilient structural solutions. The main limit of the device is the lack of restoring capability to recenter the structure in the aftermath of an earthquake. A possible solution, consisting in coupling the PS-LED with steel springs, will be investigated in a future study.
Author Contributions
Conceptualization, V.Q.; Investigation, V.Q., C.P., E.B.; Methodology, V.Q.; Software, C.P.; Supervision, V.Q.; Validation, E.B.; Writing—Original Draft, V.Q.; Writing—Review and Editing, C.P. and E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Department of the Italian Civil Protection (DPC) in the Frame of the National Research Project DPC, ReLUIS (National Network of Laboratories of Seismic Engineering) 2019–2021, Work Package 15 “Regulatory Contributions for Isolation and Dissipation”.
Data Availability Statement
Data supporting reported results can be found by writing to the corresponding author: virginio.quaglini@polimi.it.
Acknowledgments
The authors wish to thank Roberto Minerva and the Materials Testing Laboratory of Politecnico di Milano for making available the experimental facilities and Giacomo Vazzana for assisting in the execution of the tests.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aliakbari, F.; Garivani, S.; Aghakouchak, A.A. An energy based method for seismic design of frame structures equipped with metallic yielding dampers considering uniform inter-story drift concept. Eng. Struct. 2020, 205, 110114. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Di Cesare, A.; Ponzo, F.C. Seismic retrofit of reinforced concrete frame buildings with hysteretic bracing systems: Design procedure and behaviour factor. Shock Vib. 2017, 2017, 2639361. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Displacement-Based Design procedure of damped braces for the seismic retrofitting of RC framed buildings. Bull. Earthq. Eng. 2015, 13, 2121–2143. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Displacement-Based seismic Design of hysteretic damped braces for retrofitting in-elevation irregular RC framed buildings. Soil Dyn. Earthq. Eng. 2015, 69, 115–124. [Google Scholar] [CrossRef]
- Bruschi, E.; Macobatti, F.; Pettorruso, C.; Quaglini, V. Characterization and numerical assessment of Lead Extrusion Damper with adaptive behavior. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 27 September–2 October 2020. [Google Scholar]
- Manyena, S.B. The concept of resilience revisited. Disasters 2006, 30, 434–450. [Google Scholar] [CrossRef]
- Bruschi, E.; Quaglini, V.; Calvi, P.M. A simplified design procedure for seismic upgrade of frame structures equipped with hysteretic dampers. Eng. Struct. 2022, 251, 113504. [Google Scholar] [CrossRef]
- Martínez-Rueda, J.E. On the evolution of energy dissipation devices for seismic design. Earthq. Spectra 2002, 18, 309–346. [Google Scholar] [CrossRef]
- Gandelli, E.; Taras, A.; Disti, J.; Quaglini, V. Seismic retrofit of hospitals by means of hysteretic braces: Influence on acceleration-sensitive non-structural components. Front. Built Environ. 2019, 5, 100. [Google Scholar] [CrossRef]
- Pettorruso, C.; Bruschi, E.; Quaglini, V. Supplemental energy dissipation with prestressed Lead Extrusion Dampers (P-LED): Experiments and modeling. In Proceedings of the COMPDYN 2021, the 8th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Athens, Greece, 28–30 June 2021. [Google Scholar]
- Quaglini, V.; Pettorruso, C.; Bruschi, E. Experimental and numerical assessment of prestressed lead extrusion dampers. Int. J. Earthq. Eng. 2021, XXXVIII, 46–69. [Google Scholar]
- Rodgers, G.W.; Solberg, K.M.; Chase, J.G.; Mander, J.B.; Bradley, B.A.; Dhakal, R.P.; Li, L. Performance of a damage-protected beam-column subassembly utilizing external HF2V energy dissipation devices. Earthq. Eng. Struct. Dyn. 2008, 37, 1549–1564. [Google Scholar] [CrossRef]
- Rodgers, G.W.; Chase, G.J.; Mander, J.B.; Leach, N.C.; Denmead, C.S. Experimental development, tradeoff analysis and design implementation of high force-to-volume damping technology. Bull. N. Z. Nat. Soc. Earthq. Eng. 2007, 40, 35–48. [Google Scholar] [CrossRef][Green Version]
- Soydan, C.; Yüksel, E.; İrtem, E. Numerical modeling of single-storey precast frame’s pinned connections with a special damper. In Proceedings of the COMPDYN 2013, the 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Kos Island, Greece, 12–14 June 2013. [Google Scholar]
- Soydan, C.; Yüksel, E.; İrtem, E. The behavior of a steel connection equipped with the lead extrusion damper. Adv. Struct. Eng. 2014, 17, 25–40. [Google Scholar] [CrossRef]
- Soydan, C.; Yüksel, E.; İrtem, E. Determination of the characteristics of a new prestressed Lead Extrusion Damper. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Soydan, C.; Yüksel, E.; İrtem, E. Retrofitting of pinned beam–column connections in RC precast frames using lead extrusion dampers. Bull. Earthq. Eng. 2018, 16, 1273–1292. [Google Scholar] [CrossRef]
- EN 15129; Anti-Seismic Devices. CEN (European Committee for Standardization): Brussels, Belgium, 2009.
- Robinson, W.H.; Greenbank, L.R. Properties of an extrusion energy absorber. Bull. N. Z. Nat. Soc. Earthq. Eng. 1975, 8, 187–191. [Google Scholar] [CrossRef]
- Robinson, W.H.; Greenbank, L.R. An extrusion energy absorber suitable for the protection of structures during an earthquake. Earthq. Eng. Struct. Dyn. 1976, 4, 251–259. [Google Scholar] [CrossRef]
- Vishnupriya, V.; Rodgers, G.W.; Mander, J.B.; Chase, J.G. Precision design modelling of HF2V devices. Structures 2018, 14, 243–250. [Google Scholar] [CrossRef]
- Rodgers, G.W.; Chase, J.G.; Mander, J.B. Repeatability and high-speed validation of supplemental lead-extrusion energy dissipation devices. Adv. Civ. Eng. 2019, 2019, 7935026. [Google Scholar] [CrossRef]
- Golodrino, J.C.; Chase, J.G.; Rodgers, G.W.; MacRae, G.A.; Clifton, C.G. Velocity dependence of HF2V devices using different shaft configurations. In Proceedings of the Annual Conference of the New Zealand Society for Earthquake Engineering, Christchurch, New Zealand, 13 April 2012; p. 99. [Google Scholar]
- Cousins, W.J.; Porrit, T.E. Improvements to lead-extrusion damper technology. Bull. N. Z. Nat. Soc. Earthq. Eng. 1993, 26, 342–348. [Google Scholar] [CrossRef]
- Rodgers, G.W.; Mander, J.B.; Chase, J.G.; Dhakal, R.P.; Leach, N.C.; Denmead, C.S. Spectral analysis and design approach for high force-to-volume extrusion damper-based structural energy dissipation. Earthq. Eng. Struct. Dyn. 2008, 37, 207–223. [Google Scholar] [CrossRef]
- Rodgers, G.W.; Chase, J.G. Testing of Lead Extrusion Damping devices undergoing representative earthquake velocities. In Proceedings of the Annual Conference of the New Zealand Society for Earthquake Engineering, Wellington, New Zealand, 26–28 April 2013. [Google Scholar]
- Latham, D.A.; Reay, A.M.; Pampanin, S. Kilmore Street Medical Centre: Application of an advanced flag-shape steel rocking system. In Proceedings of the Annual Conference of the New Zealand Society for Earthquake Engineering, Wellington, New Zealand, 26–28 April 2013. [Google Scholar]
- Rodgers, G.W.; Mander, J.B.; Chase, J.G.; Dhakal, R.P.; Solberg, K.M. DAD post-tensioned concrete connections with lead dampers: Analytical models and experimental validation. In Proceedings of the 8th Pacific Conference on Earthquake Engineering, Singapore, 5–7 December 2007. [Google Scholar]
- Rodgers, G.W.; Mander, J.B.; Chase, J.G.; Dhakal, R.P.; MacRae, G.A. Steel beam-column connections designed for damage avoidance utilizing high force-to-volume dampers. In Proceedings of the Australasian Conference on Mechanics of Structure and Materials (ACMSM20), Toowoomba, Australia, 2–5 December 2008. [Google Scholar]
- Rodgers, G.W.; Chase, J.G.; MacRae, G.A.; Bacht, T.; Dhakal, R.P.; Desombre, J. Influence of HF2V damping devices on the performance of the SAC3building subjected to the SAC ground motion suites. In Proceedings of the 9th US National and 10th Canadian Conference on Earthquake Engineering, Toronto, ON, Canada, 25–29 June 2010; Curran Associates, Inc.: Red Hook, NY, USA, 2010. [Google Scholar]
- Rodgers, G.W.; Solberg, K.M.; Mander, J.B.; Chase, J.G.; Bradley, B.A.; Dhakal, R.P. High-Force-to-Volume seismic dissipators embedded in a jointed precast concrete frame. J. Struct. Eng. 2012, 138, 375–386. [Google Scholar] [CrossRef]
- Desombre, J.; Rodgers, G.W.; MacRae, G.A.; Rabczuk, T.; Dhakal, R.P.; Chase, J.G. Experimentally validated FEA models of HF2V damage free steel connections for use in full structural analysis. Struct. Eng. Mech. 2011, 37, 385–389. [Google Scholar] [CrossRef][Green Version]
- Bacht, T.; Chase, J.G.; MacRae, G.; Rodgers, G.W.; Rabczuk, T.; Dhakal, R.P.; Desombre, J. HF2V dissipator effects on the performance of a 3-story moment frame. J. Constr. Steel Res. 2011, 67, 1843–1849. [Google Scholar] [CrossRef]
- Mander, T.J.; Rodgers, G.W.; Chase, J.G.; Mander, J.B.; MacRae, G.A. A damage avoidance design steel beam-column moment connection using high-force-to-volume dissipators. J. Struct. Eng. 2009, 135, 1390–1397. [Google Scholar] [CrossRef]
- Vishnupriya, V.; Rodgers, G.W.; Chase, J.G. Finite Element Modelling of HF2V lead extrusion dampers for specific force capacities. In Proceedings of the Pacific Conference on Earthquake Engineering and Annual Conference of the New Zealand Society for Earthquake Engineering, Auckland, New Zealand, 4–6 June 2019; p. 133. [Google Scholar]
- Patel, C.C. Seismic analysis of parallel structures coupled by lead extrusion dampers. Int. J. Adv. Struct. Eng. 2017, 9, 177–190. [Google Scholar] [CrossRef][Green Version]
- Yang, M.F.; Xu, Z.D.; Zhang, X.C. Experimental study on lead extrusion damper and its earthquake mitigation effects for large-span reticulated shell. Steel Comp. Struct. 2015, 18, 481–496. [Google Scholar] [CrossRef]
- Rodgers, G.W. Next Generation Structural Technologies: Implementing High Force-to-Volume Energy Absorbers. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2009. [Google Scholar]
- Solberg, K.M.; Bradley, B.A.; Mander, J.B.; Dhakal, R.P.; Rodgers, G.W.; Chase, J.G. Multi-level seismic performance assessment of a damage-protected beam-column joint with internal lead dampers. In Proceedings of the New Zealand Society for Earthquake Engineering Annual Conference, Palmerston North, New Zealand, 30 March–1 April 2007. [Google Scholar]
- Bruschi, E. Seismic Retrofit of RC Framed Buildings with Supplementary Energy Dissipation: Modelling and Application of a Novel Lead Damper. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2021. [Google Scholar]
- Dassault Systemes Simulia Corp. Abaqus/CAE User’s Guide; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2017. [Google Scholar]
- CSLLPP (Consiglio Superiore dei Lavori Pubblici). D.M. 17 Gennaio 2018 in Materia di “norme Tecniche Per le Costruzioni”. Gazzetta Ufficiale n.42 del 20 Febbraio 2018, Supplemento Ordinario n.8. Ministero Delle Infrastrutture e dei Trasporti, Rome, Italy. 2018. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 20 April 2022). (In Italian).
- Sina, F.; Amir, H.A.; Lars, D. Equivalent viscous damping for buckling-restrained braced RC frame structures. Structures 2021, 34, 1229–1252. [Google Scholar]
- Tonon, E.; Forte, M.; Mammino, A.; Moro, S. Protezione sismica degli edifici mediante dissipatori d’energia: Applicazione pratica della nuova sede della prefettura de L’Aquila. In Proceeding of the XV Conference of the Italian Association of Seismic Engineering ANIDIS, Padua, Italy, 30 June–4 July 2013. [Google Scholar]
- Sitler, B.; Takeuchi, T.; Matsui, R.; Terashima, M.; Terazawa, Y. Experimental investigation of a multistage buckling-restrained brace. Eng. Struct. 2020, 213, 110482. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).