Numerical Modelling of Reactive Flows through Porous Media
Abstract
:1. Introduction
2. Lattice Boltzmann Model
Boundary Conditions
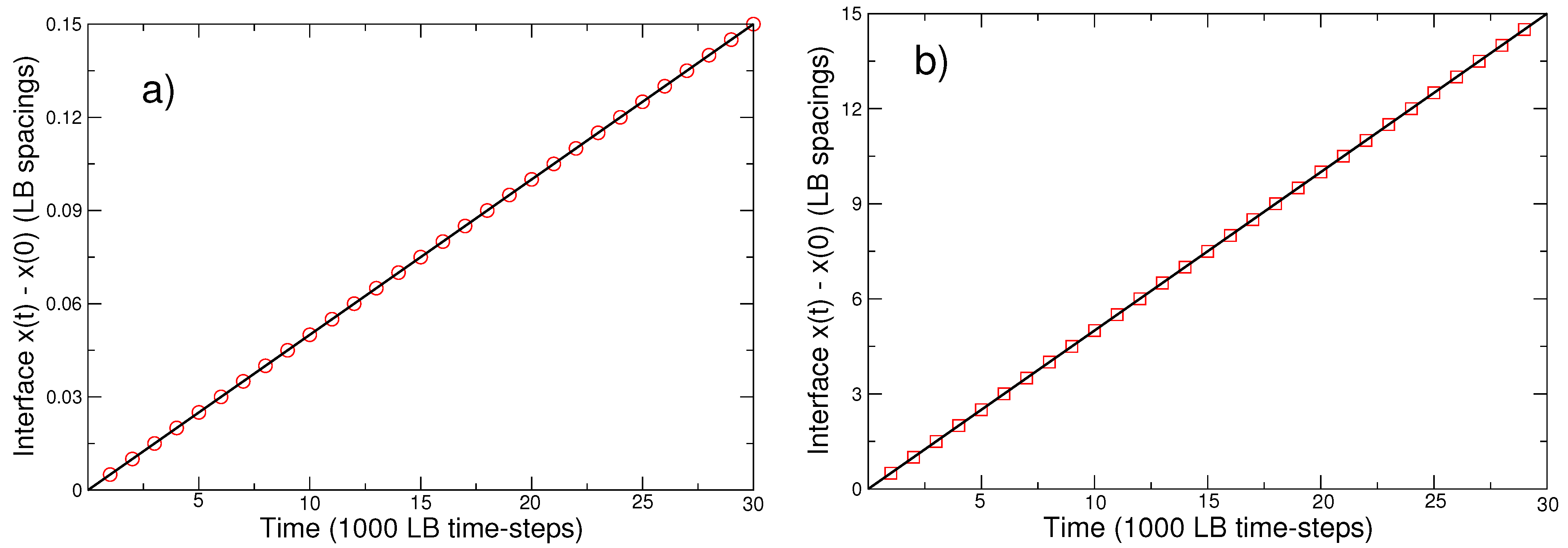
3. Comparison between LB and Analytical Results
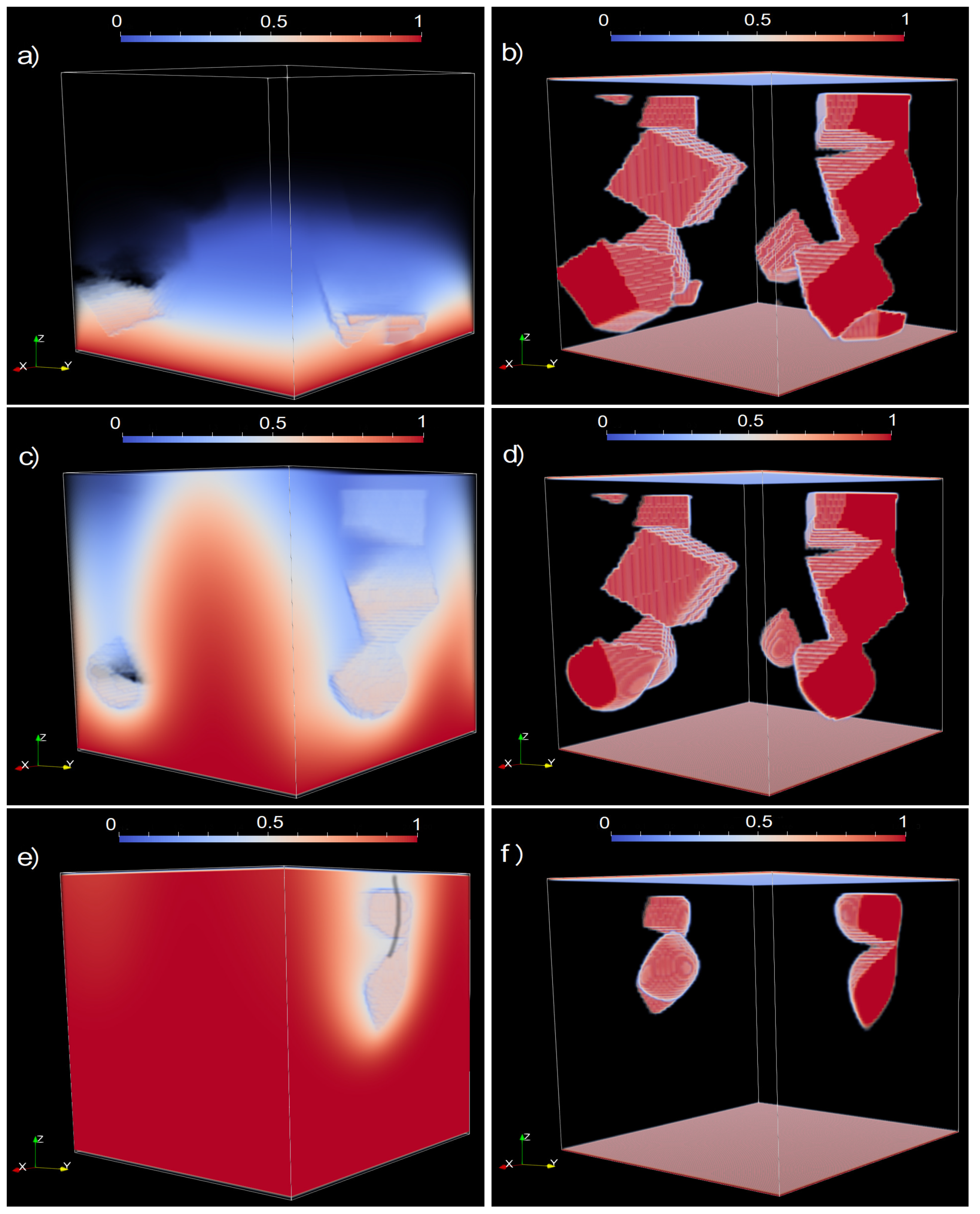
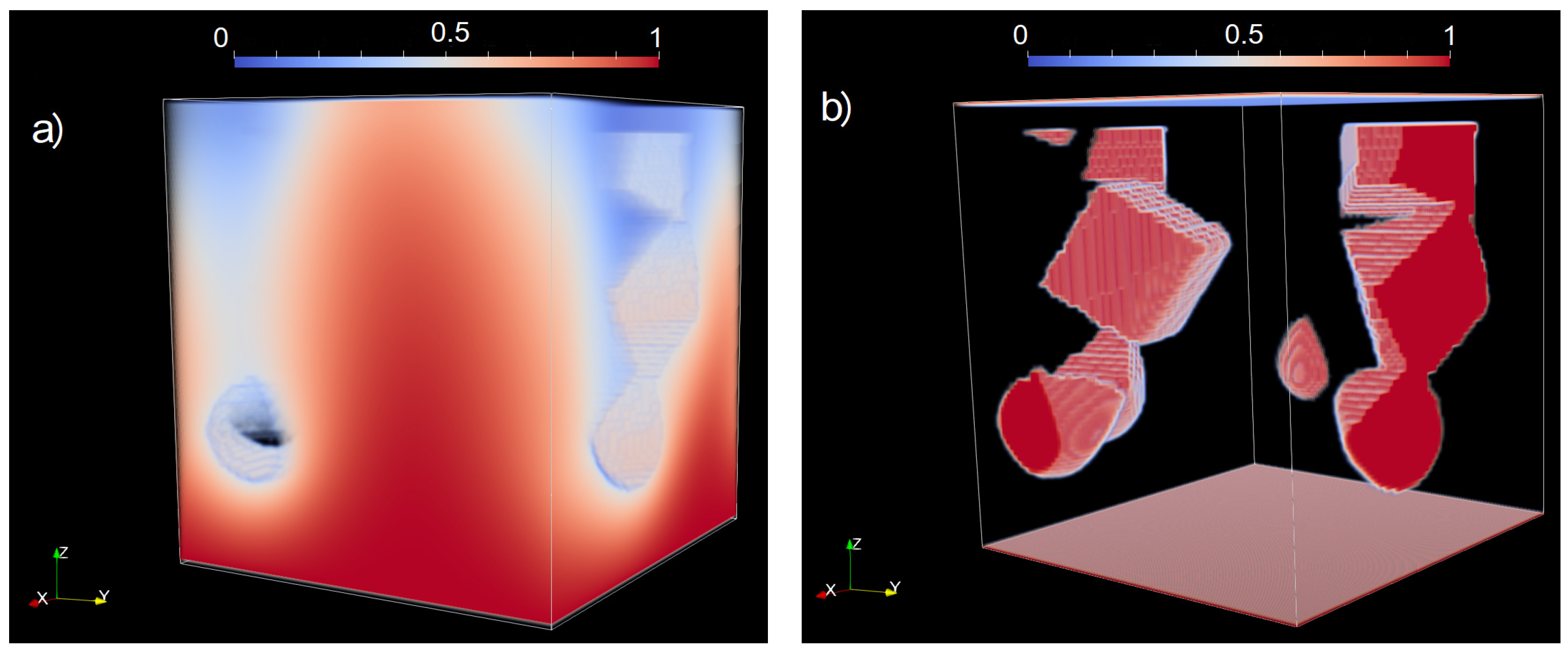
4. Three-Dimensional Flow, Diffusion, and Reaction
Non-Trivial Pore-Scale Geometry
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cross, M.; Bennett, C.R.; Croft, T.N.; Mcbride, D.; Gebhardt, H. Computational modeling of reactive multi-phase flows in porous media: Applications to metals extraction and environmental recovery processes. Min. Eng. 2006, 19, 1098–1108. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.J.; Robinson, B.A.; He, Y.-L.; Tao, W.-Q. Pore-scale modelling of multiphase reactive transport with phase transitions and dissolution-precipitation processes in closed systems. Phys. Rev. E 2013, 87, 043306. [Google Scholar] [CrossRef] [Green Version]
- Molins, S.; Trebotich, D.; Steefel, C.I.; Shen, C.-P. An investigation of the effect of pore scale flow on average geochemical reaction rates using direct numerical simulation. Water Resour. Res. 2012, 48, W03527. [Google Scholar]
- Patel, R.A.; Phung, Q.T.; Seetharam, S.C.; Perko, J.; Jacques, D.; Maes, N.; De Schutter, G.; Ye, G.; Van Breugel, K. Diffusivity of saturated ordinary Portland cement-based materials: A critical review of experimental and analytical modelling approaches. Cem. Concr. Res. 2016, 90, 52–72. [Google Scholar] [CrossRef]
- Voronov, R.; VanGordon, S.; Sikavitsas, V.I.; Papavassiliou, D.V. Computational modelling of flow-induced shear stresses with 3D salt-leached poeour scaffolds imaged via micro-CT. J. Biomech. 2010, 43, 1279–1286. [Google Scholar] [CrossRef] [PubMed]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Clarendon Press: Oxford, UK, 2001. [Google Scholar]
- Kruger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E. The Lattice Boltzmann Method. Principles and Practice, 1st ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Ann. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1996, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.-H.; Kang, Q.-J.; Leornardi, C.R.; Schmiechek, S.; Narvez, A.; Jones, B.D.; Williams, J.R.; Valocchi, A.J.; Harting, J. Multiphase lattice-Boltzmann simulations for porous media applications. Computat. Geosci. 2016, 20, 777–805. [Google Scholar] [CrossRef] [Green Version]
- Talon, L.; Bauer, D.; Gland, N.; Youseff, S.; Auradou, H.; Ginzburg, I. Assessment of the two relaxation Lattice Boltzmann scheme to simulate Stokes flow in porous media. Water Resour. Res. 2012, 48, W04526. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Hayot, F.; Saam, W.F. Darcy’s law from lattice-gas hydrodynamics. Phys. Rev. A 1987, 36, 2248–2253. [Google Scholar] [CrossRef]
- Gao, Y.; Sharma, M.M. A LGA model for fluid-flow in heterogeneous porous media. Transp. Porous Media 1994, 17, 1–17. [Google Scholar] [CrossRef]
- Dardis, O.; McCloskey, J. Lattice Boltzmann scheme with real numbered solid density for the simulation of flow in porous media. Phys. Rev. E 1998, 57, 4834–4837. [Google Scholar] [CrossRef]
- Thorne, D.T.; Sukop, M.C. Lattice Boltzmann approach to Richard’s equation. Dev. Water Sci. 2004, 55, 1549. [Google Scholar]
- Zhu, J.J.; Ma, S. An improved gray lattice Boltzmann model for simulating fluid flow in multi-scale porous media. Adv. Water Resourc. 2013, 56, 61–76. [Google Scholar] [CrossRef]
- Li, R.R.; Yang, S.; Pan, J.-X.; Pereira, G.G.; Taylor, J.A.; Clennell, B.; Zou, C. Lattice Boltzmann modelling of permeability of porous materials with partially percolating voxels. Phys. Rev. E 2014, 90, 033301. [Google Scholar] [CrossRef] [PubMed]
- Pereira, G.G.; Wu, B.; Ahmed, A. Lattice Boltzmann heat transfer model for permeable voxels. Phys. Rev. E 2017, 96, 063108. [Google Scholar] [CrossRef]
- Pereira, G.G. Fluid flow, relative permeabilities and capillary pressure curves through heterogeneous porous media. Appl. Math. Model. 2019, 75, 481–493. [Google Scholar] [CrossRef]
- Bhatnager, P.I.; Gross, E.P.; Krook, M. A model for collision processes in gases. 1. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- D’Humieres, D.; Ginzburg, I.; Krafczyk, M.; Lallem, P.; Luo, L.-S. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Ginzbourg, I.; Adler, P.M. Boundary flow condition analysis for the three-dimensional lattice Boltzmann model. J. Phys. II Fr. 1994, 4, 191–214. [Google Scholar] [CrossRef]
- Inamuro, T.; Yoshino, T.M.; Inoue, H.; Mizuno, R.; Ogino, F. A lattice Boltzmann method for a binary miscible fluid mixture and its application to a heat-transfer problem. J. Comput. Phys. 2002, 179, 201–215. [Google Scholar] [CrossRef] [Green Version]
- Noble, D.R.; Torczynski, J.R. A lattice Boltzmann method for partially saturated computational cells. Int. J. Mod. Phys. 1998, 9, 1189–1201. [Google Scholar] [CrossRef]
- Bouzidi, M.; Firdaouss, P. Lallemand, Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 2001, 13, 3452–3459. [Google Scholar] [CrossRef]
- Verhaeghe, F.; Arnout, S.; Blanpain, B.; Wollants, P. Lattice-Boltzmann modelling of dissolution phenomena. Phys. Rev. 2006, 73, 036316. [Google Scholar]
- Walsh, S.D.C.; Saar, M.O. Interpolated lattice Boltzmann boundary conditions for surface reaction kinetics. Phys. Rev. 2010, 82, 066703. [Google Scholar] [CrossRef] [Green Version]
- Aaron, H.B.; Fainstein, D.; Kotler, G.R. Diffusion limited phase transformations: A comparison and critical evaluation of the mathematical approximations. J. Appl. Phys. 1970, 41, 4404–4410. [Google Scholar] [CrossRef]
- Habashi, F. Principles of Extractive Metallurgy; Gordon and Breach: New York, NY, USA, 1969. [Google Scholar]
- Seta, T. Implicit temperature-correction-based immersed-boundary thermal lattice Boltzmann method for the simulation of natural convection. Phys. Rev. 2013, 87, 063304. [Google Scholar] [CrossRef] [Green Version]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, G.G. Numerical Modelling of Reactive Flows through Porous Media. Geosciences 2022, 12, 153. https://doi.org/10.3390/geosciences12040153
Pereira GG. Numerical Modelling of Reactive Flows through Porous Media. Geosciences. 2022; 12(4):153. https://doi.org/10.3390/geosciences12040153
Chicago/Turabian StylePereira, Gerald G. 2022. "Numerical Modelling of Reactive Flows through Porous Media" Geosciences 12, no. 4: 153. https://doi.org/10.3390/geosciences12040153
APA StylePereira, G. G. (2022). Numerical Modelling of Reactive Flows through Porous Media. Geosciences, 12(4), 153. https://doi.org/10.3390/geosciences12040153





