Coseismic Ground Displacement after the Mw6.2 Earthquake in NW Croatia Determined from Sentinel-1 and GNSS CORS Data
Abstract
1. Introduction
2. Geodynamic Framework
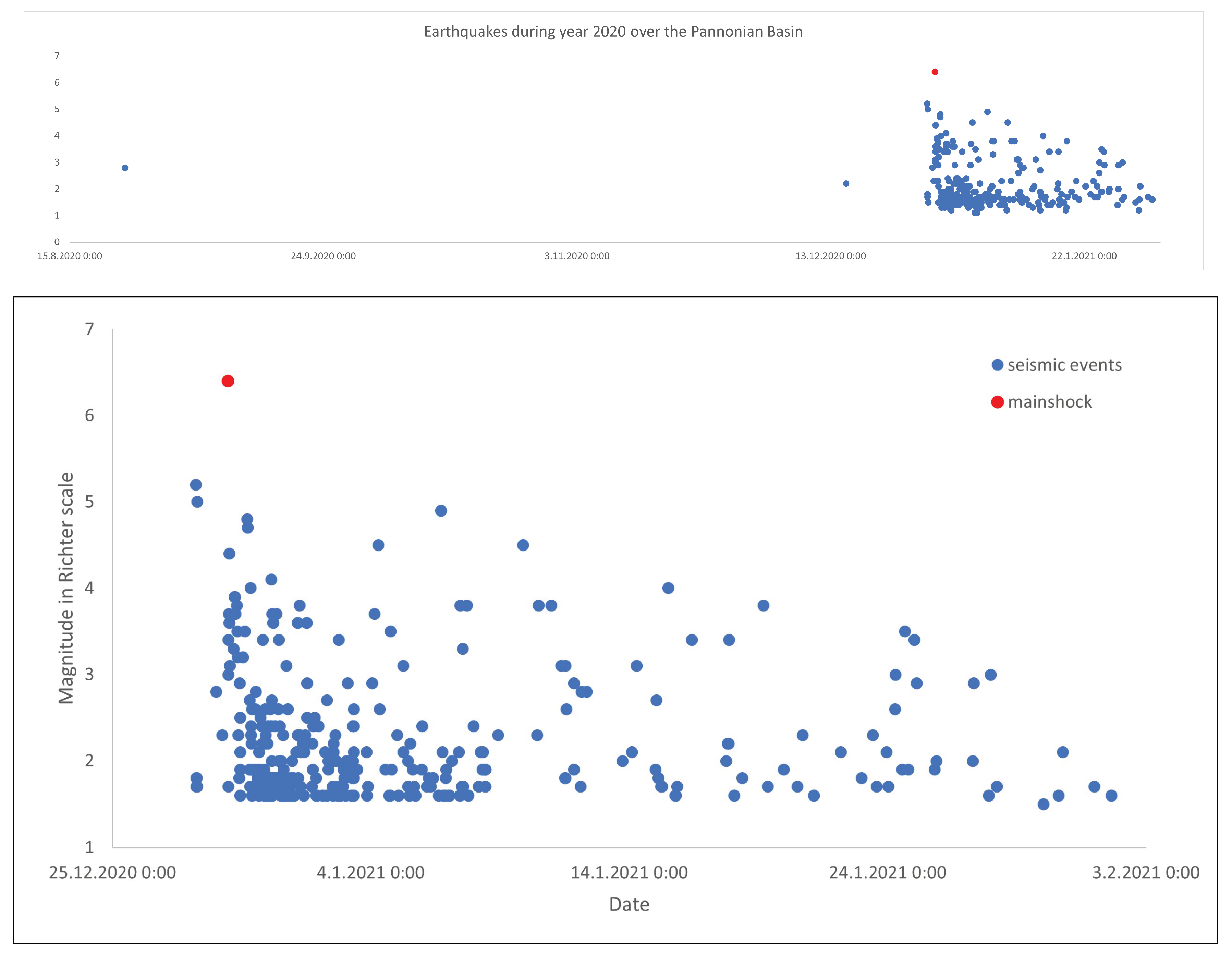
Seismicity of Croatia
3. Study Area
4. Data and Methodology
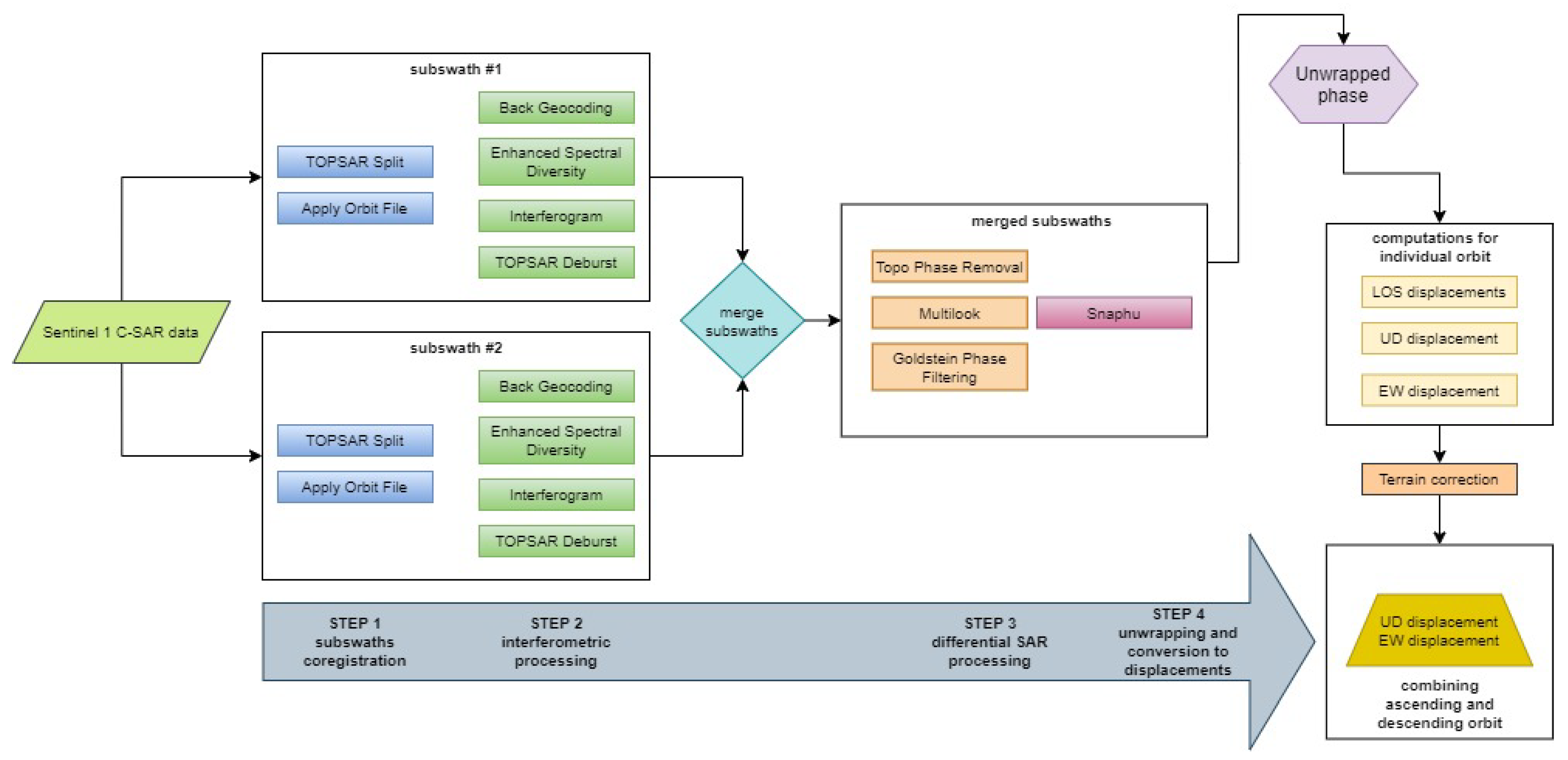
4.1. SAR Data
4.2. GNSS CORS Data
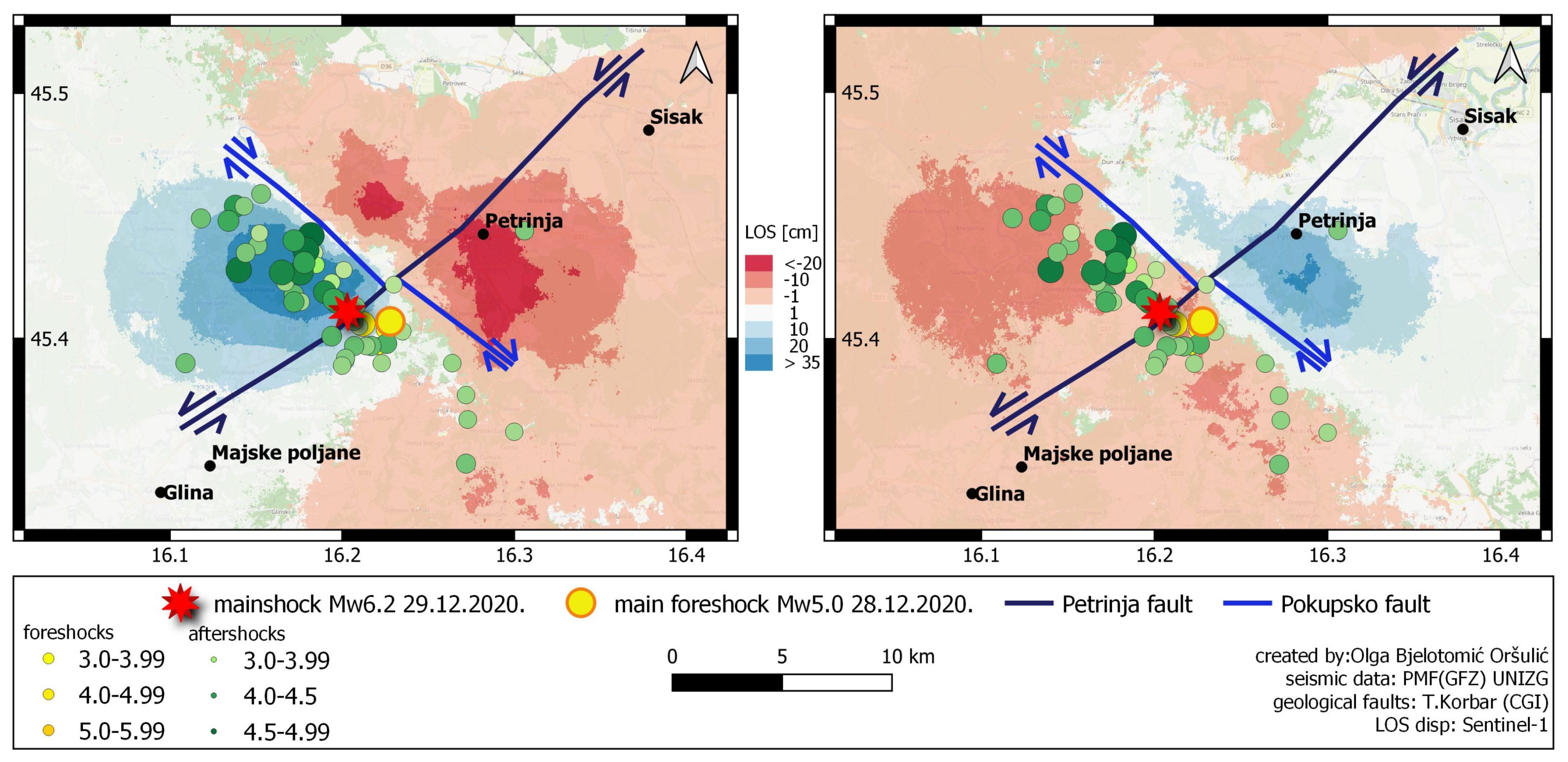
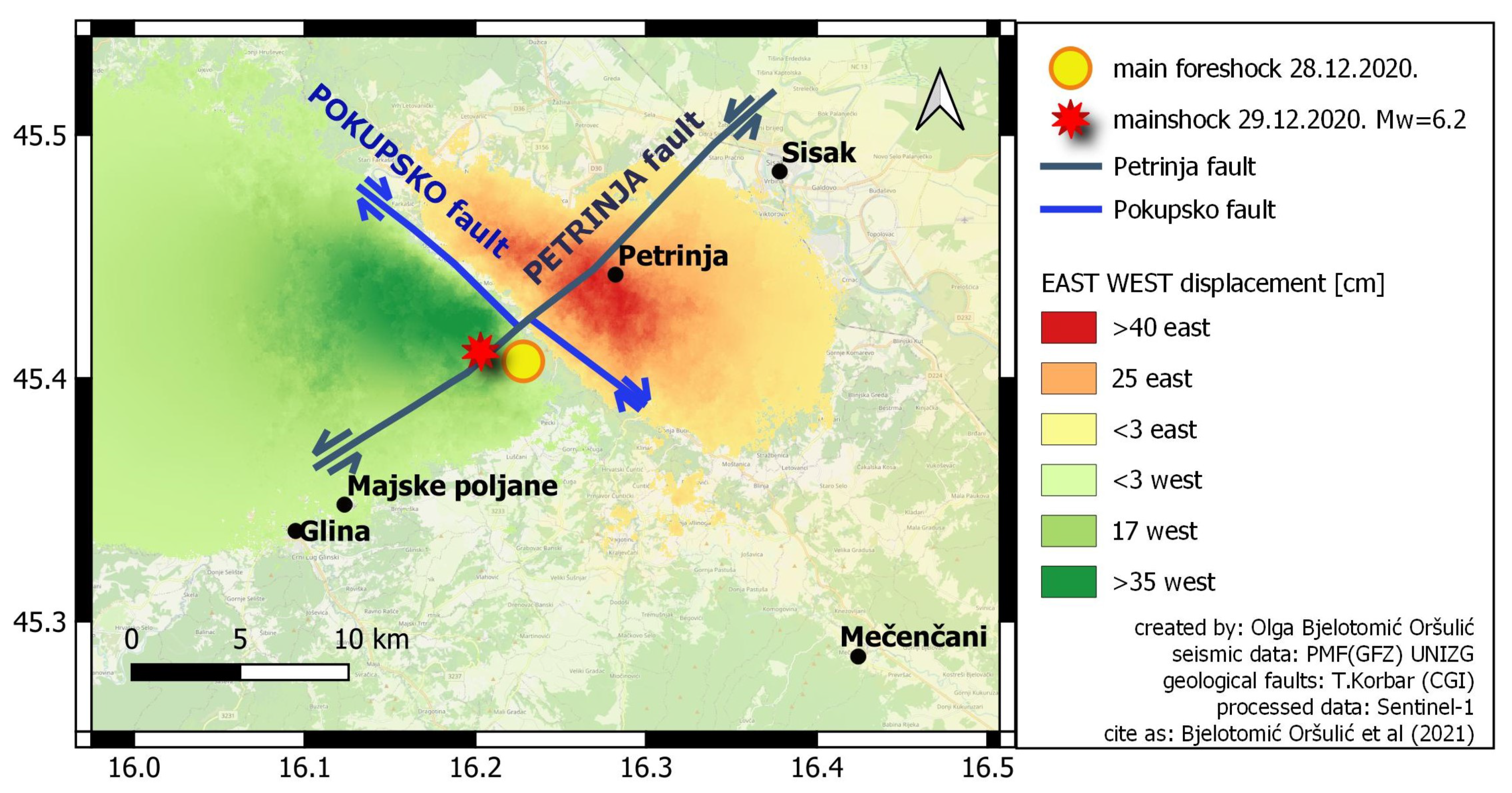
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, K.; Liu, G.; Li, Z.; Li, T.; Yu, B.; Wang, X.; Singleton, A. Extracting Vertical Displacement Rates in Shanghai (China) with Multi-Platform SAR Images. Remote Sens. 2015, 7, 9542–9562. [Google Scholar] [CrossRef]
- Bovenga, F. Special Issue “Synthetic Aperture Radar (SAR) Techniques and Applications”. Sensors 2020, 20, 1851. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, Y.; Jin, M.; Jing, Y.; Liu, Y.; Liu, Y.; Sun, W.; Wei, J.; Chen, Y. Monitoring Land Subsidence in Wuhan City (China) using the SBAS-InSAR Method with Radarsat-2 Imagery Data. Sensors 2019, 19, 743. [Google Scholar] [CrossRef]
- Mora, O.; Ordoqui, P.; Iglesias, R.; Blanco, P. Earthquake Rapid Mapping Using Ascending and Descending Sentinel-1 TOPSAR Interferograms. Procedia Comput. Sci. 2016, 100, 1135–1140. [Google Scholar] [CrossRef]
- Goorabi, A. Detection of landslide induced by large earthquake using InSAR coherence techniques—Northwest Zagros, Iran. Egypt. J. Remote Sens. Space Sci. 2020, 23, 195–205. [Google Scholar] [CrossRef]
- Jo, M.J.; Jung, H.S.; Yun, S.H. Retrieving Precise Three-Dimensional Deformation on the 2014 M6.0 South Napa Earthquake by Joint Inversion of Multi-Sensor SAR. Sci. Rep. 2017, 7, 5485. [Google Scholar] [CrossRef]
- Xing, X.; Chen, L.; Yuan, Z.; Shi, Z. An Improved Time-Series Model Considering Rheological Parameters for Surface Deformation Monitoring of Soft Clay Subgrade. Sensors 2019, 19, 3073. [Google Scholar] [CrossRef]
- Raspini, F.; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Solari, L.; Novali, F.; Del Conte, S.; Rucci, A.; Ferretti, A.; Casagli, N. Continuous, semi-automatic monitoring of ground deformation using Sentinel-1 satellites. Sci. Rep. 2018, 8, 7253. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Garthwaite, M.C. Resolving Three-Dimensional Surface Motion with InSAR: Constraints from Multi-Geometry Data Fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef]
- Aslan, G.; Cakir, Z.; Lasserre, C.; Renard, F. Investigating Subsidence in the Bursa Plain, Turkey, Using Ascending and Descending Sentinel-1 Satellite Data. Remote Sens. 2019, 11, 85. [Google Scholar] [CrossRef]
- Malmgren-Hansen, D.; Sohnesen, T.; Fisker, P.; Baez, J. Sentinel-1 Change Detection Analysis for Cyclone Damage Assessment in Urban Environments. Remote Sens. 2020, 12, 2409. [Google Scholar] [CrossRef]
- Delgado Blasco, J.M.; Foumelis, M.; Stewart, C.; Hooper, A. Measuring Urban Subsidence in the Rome Metropolitan Area (Italy) with Sentinel-1 SNAP-StaMPS Persistent Scatterer Interferometry. Remote Sens. 2019, 11, 129. [Google Scholar] [CrossRef]
- Kovács, I.P.; Bugya, T.; Czigány, S.; Defilippi, M.; Lóczy, D.; Riccardi, P.; Ronczyk, L.; Pasquali, P. How to avoid false interpretations of Sentinel-1A TOPSAR interferometric data in landslide mapping? A case study: Recent landslides in Transdanubia, Hungary. Nat. Hazards 2019, 96, 693–712. [Google Scholar] [CrossRef]
- Thomas, A. Mapping of surface deformation associated with the 5.2 magnitude Stilfontein earthquake of 3 April 2017 using radar interferometry. Egypt. J. Remote Sens. Space Sci. 2020, 24, 85–108. [Google Scholar] [CrossRef]
- Tzouvaras, M.; Danezis, C.; Hadjimitsis, D.G. Differential SAR Interferometry Using Sentinel-1 Imagery-Limitations in Monitoring Fast Moving Landslides: The Case Study of Cyprus. Geosciences 2020, 10, 236. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.V.; Brovelli, M.A.; Manzoni, M.; Mariotti d’Alessandro, M.; Molinari, M.E.; Oxoli, D. Coherent Change Detection for Multipass SAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6811–6822. [Google Scholar] [CrossRef]
- Burrows, K.; Walters, R.J.; Milledge, D.; Spaans, K.; Densmore, A.L. A New Method for Large-Scale Landslide Classification from Satellite Radar. Remote Sens. 2019, 11, 237. [Google Scholar] [CrossRef]
- Uemoto, J.; Moriyama, T.; Nadai, A.; Kojima, S.; Umehara, T. Landslide Detection Based on Height and Amplitude Differences Using Pre- and Post-Event Airborne X-Band SAR Data. Nat. Hazards 2019, 95, 485–503. [Google Scholar] [CrossRef]
- Jung, J.; Yun, S.-H. Evaluation of Coherent and Incoherent Landslide Detection Methods Based on Synthetic Aperture Radar for Rapid Response: A Case Study for the 2018 Hokkaido Landslides. Remote Sens. 2020, 12, 265. [Google Scholar] [CrossRef]
- Park, S.-E.; Jung, Y.T. Detection of Earthquake-Induced Building Damages Using Polarimetric SAR Data. Remote Sens. 2020, 12, 137. [Google Scholar] [CrossRef]
- Jiang, G.; Wen, Y.; Li, K.; Fang, L.; Xu, C.; Zhang, Y.; Xu, X. A NE-trending oblique-slip fault responsible for the 2016 Zaduo earthquake (Qinghai, China) revealed by InSAR data. Pure Appl. Geophys. 2018, 175, 4275–4288. [Google Scholar] [CrossRef]
- Jiang, G.; Xu, C.; Wen, Y.; Liu, Y.; Yin, Z.; Wang, J. Inversion for coseismic slip distribution of the 2010 Mw 6.9 Yushu Earthquake from InSAR data using angular dislocations. Geophys. J. Int. 2013, 194, 1011–1022. [Google Scholar] [CrossRef]
- Wen, Y.; Li, Z.; Xu, C.; Ryder, I.; Bürgmann, R. Postseismic motion after the 2001 Mw 7.8 Kokoxili earthquake in Tibet observed by InSAR time series. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Wen, Y.; Yin, Z.; Jiang, G.; Fang, L. Slip model for the 25 November 2016 Mw 6.6 Aketao earthquake, western China, revealed by sentinel-1 and ALOS-2 observations. Remote Sens. 2017, 9, 325. [Google Scholar] [CrossRef]
- Golshadi, Z.; Rezapour, M.; Atzori, S.; Salvi, S. Multiple source analysis from InSAR data and new insights into fault activation The 2005 Zarand, Iran, earthquake. Terra Nova. 2020. [Google Scholar] [CrossRef]
- Béjar-Pizarro, M.; Álvarez Gómez, J.A.; Staller, A.; Luna, M.P.; Pérez-López, R.; Monserrat, O.; Chunga, K.; Lima, A.; Galve, J.P.; Martínez Díaz, J.J.; et al. InSAR-Based Mapping to Support Decision-Making after an Earthquake. Remote Sens. 2018, 10, 899. [Google Scholar] [CrossRef]
- Ganas, A.; Elias, P.; Briole, P.; Cannavo, F.; Valkaniotis, S.; Tsironi, V.; Partheniou, E.I. Ground Deformation and Seismic Fault Model of the M6.4 Durres (Albania) Nov. 26, 2019 Earthquake, Based on GNSS/INSAR Observations. Geosciences 2020, 10, 210. [Google Scholar] [CrossRef]
- Valkaniotis, S.; Briole, P.; Ganas, A.; Elias, P.; Kapetanidis, V.; Tsironi, V.; Fokaefs, A.; Partheniou, H.; Paschos, P. The Mw = 5.6 Kanallaki Earthquake of 21 March 2020 in West Epirus, Greece: Reverse Fault Model from InSAR Data and Seismotectonic Implications for Apulia-Eurasia Collision. Geosciences 2020, 10, 454. [Google Scholar] [CrossRef]
- Battaglia, M.; Murray, M.H.; Serpelloni, E.; Bürgmann, R. The Adriatic region: An independent microplate within the Africa-Eurasia collision zone. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Kalman Šipoš, T. Insights from existing earthquake loss assessment research in Croatia. Earthq. Struct. 2017, 13, 365–375. [Google Scholar]
- Markušić, S.; Herak, M. Seismic zoning of Croatia. Nat. Haz. 1999, 18, 269–285. [Google Scholar] [CrossRef]
- Basili, R.; Kastelic, V.; Demircioglu, M.B.; Garcia Moreno, D.; Nemser, E.S.; Petricca, P.; Sboras, S.P.; Besana-Ostman, G.M.; Cabral, J.; Camelbeeck, T.; et al. The European Database of Seismogenic Faults (EDSF) Compiled in the Framework of the Project SHARE. 2013. Available online: http://diss.rm.ingv.it/share-edsf/ (accessed on 3 January 2021).
- Ustaszewski, K.; Le Breton, E.; Balling, P.; Handy, M.R.; Molli, G.; Tomljenović, B. One microplate-three orogens: Alps, Dinarides, Apennines and the role of the Adriatic plate. In Proceedings of the EGU General Assembly Conference Abstracts, EGU, Vienna, Austria, 23–28 April 2017. Abstract Number 16444. [Google Scholar]
- Prelogović, E.; Cvijanović, D.; Aljinović, B.; Kranjec, V.; Skoko, D.; Blašković, I.; Zagorac, Ž. Seismotectonic activity along the coastal area of Yugoslavia. Geološki Vjesn. 1982, 35, 195–207. [Google Scholar]
- Aljinović, B.; Blašković, I.; Cvijanović, D.; Prelogović, E.; Skoko, D.; Brdarević, N. Correlation of geophysical, geological and seismological data in the coastal part of Yugoslavia. Boll. Oceanol. Teor. Appl. 1984, 2, 77–90. [Google Scholar]
- Horváth, F.; Musitz, B.; Balázs, A.; Végh, A.; Uhrin, A.; Nádor, A.; Koroknai, B.; Pap, N.; Tóth, T.; Wórum, G. Evolution of the Pannonian basin and its geothermal resources. Geothermics 2015, 53, 328–352. [Google Scholar] [CrossRef]
- Farr, T.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- McKenzie, D.P. Active tectonics of the Mediterranean region. Geophys. J. Int. 1972, 30, 109–185. [Google Scholar] [CrossRef]
- Ward, S. Constraints on the seismotectonics of the central Mediterranean from Very Long Baseline Interferometry. Geophys. J. Int. 1994, 117, 441–452. [Google Scholar] [CrossRef]
- Calais, E.; Nocquet, J.M.; Jouanne, F.; Tardy, M. Current strain regime in the Western Alps from continuous global positioning system measurements, 1996–2001. Geology 2002, 30, 651–654. [Google Scholar] [CrossRef]
- Grenerczy, G.; Sella, G.; Stein, S.; Kenyeres, A. Tectonic implications of the GPS velocity field in the northern Adriatic region. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Serpelloni, E.; Anzidei, M.; Baldi, P.; Casula, G.; Galvani, A. Crustal velocity and strain-rate fields in Italy and surrounding regions: New results from the analysis of permanent and non-permanent GPS networks. Geophys. J. Int. 2005, 161, 861–880. [Google Scholar] [CrossRef]
- D’Agostino, N.; Avallone, A.; Cheloni, D.; D’Anastasio, E.; Mantenuto, S.; Selvaggi, G. Active tectonics of the Adriatic region from GPS and earthquake slip vectors. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Devoti, R.; Riguzzi, F.; Cuffaro, M.; Doglioni, C. New GPS constraints on the kinematics of the Apennines subduction. Earth Planet. Sci. Lett. 2008, 273, 163–174. [Google Scholar] [CrossRef]
- Marjanović, M.; Bačić, Ž.; Bašić, T. Determination of Horizontal and Vertical Movements of the Adriatic Microplate on the Basis of GPS Measurements. In Geodesy for Planet Earth, International Association of Geodesy Symposia; Kenyon, S., Pacino, M., Marti, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 136. [Google Scholar]
- Weber, J.; Vrabec, M.; Pavlovčič-Prešeren, P.; Dixon, T.; Jiang, Y.; Stopar, B. GPS-derived motion of the Adriatic microplate from Istria Peninsula and Po Plain sites, and geodynamic implications. Tectonophysics 2010, 483, 214–222. [Google Scholar] [CrossRef]
- Ollier, C.; Pain, C. The apennines, the dinarides, and the adriatic sea: Is the Adriatic microplate a reality? Geogr. Fis. Din. Quat. 2009, 32, 167–175. [Google Scholar]
- Handy, M.R.; Schmid, S.M.; Bousque, R.; Kissling, E.; Bernoulli, D. Reconciling plate-tectonic reconstructions of Alpine Tethys with the geological–geophysical record of spreading and subduction in the Alps. Earth Sci. Rev. 2010, 102, 121–158. [Google Scholar] [CrossRef]
- Le Breton, E.; Handy, M.R.; Molli, G.; Ustaszewski, K. Post-20 Ma Motion of the Adriatic Plate: New Constraints From Surrounding Orogens and Implications for Crust-Mantle Decoupling. Tectonics 2017, 36, 3135–3154. [Google Scholar] [CrossRef]
- Medak, D.; Pribičević, B.; Prelogović, E. Recent geodynamical GPS-project in Croatia, raziskave s področja geodezije in geofizike 2006. In Proceedings of the 12th Strokovno Srečanje Slovenskega Združenja za Geodezijo in Geofiziko, Ljubljana, Slovenija, 18 January 2007. [Google Scholar]
- Kišpatić, M. Earthquakes in Croatia; Yugoslavia Academy of Science and Arts: Zagreb, Croatia, 1892; Volume 1, pp. 1–79. (In Croatian) [Google Scholar]
- Mohorovičić, A. Earthquake of 8 October 1909 (Potres od 8. X. 1909). In Annual Report of Zagreb Meteorological Observatory; Yearly Report of the Zagreb Meteorological Observatory for the Year 1909; Zagreb Meteorological Observatory: Zagreb, Croatia, 1909; pp. 1–63, (In Croatian and German). [Google Scholar]
- Markušić, S. Seismicity of Croatia. In Earthquake Monitoring and Seismic Hazard Mitigation in Balkan Countries; Springer: Dordrecht, The Netherlands, 2008; pp. 81–98. [Google Scholar]
- Markušić, S.; Stanko, D.; Penava, D.; Ivančić, I.; Bjelotomić Oršulić, O.; Korbar, T.; Sarhosis, V. Destructive M6.2 Petrinja Earthquake (Croatia) in 2020—Preliminary Multidisciplinary Research. Remote Sens. 2021, 13, 1095. [Google Scholar] [CrossRef]
- Ivančić, I.; Herak, D.; Herak, M.; Allegretti, I.; Fiket, T.; Kuk, K.; Markušić, S.; Prevolnik, S.; Sović, I.; Dasović, I.; et al. Seismicity of Croatia in the period 2006–2015. Geofizika 2018, 35, 69–98. [Google Scholar] [CrossRef]
- Herak, M.; Herak, D.; Markušić, S. Revision of the earthquake catalogue and seismicity of Croatia, 1908–1992. Terra Nova 1996, 8, 86–94. [Google Scholar] [CrossRef]
- Herak, D.; Herak, M.; Tomljenović, B. Seismicity and earthquake focal mechanisms in North-Western Croatia. Tectonophysics 2009, 465, 212–220. [Google Scholar] [CrossRef]
- European-Mediterranean Seismological Centre. Available online: https://www.emsc-csem.org/ (accessed on 5 January 2021).
- Markušić, S.; Stanko, D.; Korbar, T.; Belić, N.; Penava, D.; Kordić, B. The Zagreb (Croatia) M5.5 Earthquake on 22 March 2020. Geosciences 2020, 10, 252. [Google Scholar] [CrossRef]
- Herak, M. Croatian map of seismic risk. In Proceedings of the IV Conference of Croatian Platform for Decreasing the Risk of Catastrophe, Zagreb, Croatia, 13 December 2012. (In Croatian). [Google Scholar]
- Atalić, J.; Šavor Novak, M.; Uroš, M. Seismic risk for Croatia: Overview of research activities and present assessments with guidelines for the future. Građevinar 2019, 10, 923–947. [Google Scholar]
- Michetti, A.M.; Esposito, E.; Guerrieri, L.; Porfido, S.; Serva, L.; Tatevossian, R.; Vittori, E.; Audemard, F.; Azuma, T.; Clague, J.; et al. Memorie Descrittive Della Carta Geologica D’Italia, Intensity Scale ESI 2007; Guerrieri, L., Vittori, E., Eds.; ISPRA: Roma, Italy, 2007.
- Seismological Service. Available online: https://www.pmf.unizg.hr/geof/seizmoloska_sluzba/ (accessed on 4 January 2021). (In Croatian).
- National Institute of Geophysics and Vulcanology (INGV). Available online: https://ingvterremoti.com/2020/12/29/terremoto-mw-6-2-in-croazia-29-dicembre-2020-ore-1219/ (accessed on 14 March 2021). (In Italian).
- USGS’s Earthquake Hazards Program. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us6000d3zh/executive (accessed on 14 March 2021).
- European Union. Regulation (EU) No 377/2014 of the European Parliament and of the Council of 3 April 2014 Establishing the Copernicus Programme and Repealing Regulation (EU) No 911/2010; European Union: Brussels, Belgium, 2014; Retrieved 04 January 2021. [Google Scholar]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain Observation by Progressive Scans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Copernicus Data Hub. Available online: https://scihub.copernicus.eu/ (accessed on 2 January 2021).
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science and Business Media: Dordrecht, The Netherlands, 2001; Volume 2. [Google Scholar]
- Veci, L. Interferometry Tutorial. In Sentinel Toolbox; ESA; Array Systems Computing Inc.: North York, ON, Canada, 2015; pp. 1–21. [Google Scholar]
- Aobpaet, A.; Cuenca, M.C.; Hooper, A.; Trisirisatayawong, I. InSAR time-series analysis of land subsidence in Bangkok, Thailand. Int. J. Remote Sens. 2013, 34, 2969–2982. [Google Scholar] [CrossRef]
- Chaussard, E.; Amelung, F.; Abidin, H.; Hong, S.H. Sinking cities in Indonesia: ALOS PALSAR detects rapid subsidence due to groundwater and gas extraction. Remote Sens. Environ. 2013, 128, 150–161. [Google Scholar] [CrossRef]
- CROPOS- Croatian National Positioning Reference Frame. Available online: https://www.cropos.hr/ (accessed on 31 January 2021).
- Croatian Geological Institute—Press Release on Petrinja Earthquake. Available online: https://www.hgi-cgs.hr/press-release-of-the-croatian-geological-survey-hgi-cgs/ (accessed on 9 January 2021).
- State Geodetic Administration—Press Release on First Official Results of GNSS Field Measurements over Petrinja Earthquake Area. (In Croatian). Available online: https://dgu.gov.hr/vijesti/prvi-sluzbeni-rezultati-satelitskih-mjerenja-na-potresom-pogodjenom-podrucju/5645 (accessed on 16 February 2021).
- Croatian Geological Institute—Press Release on Petrinja Earthquake. Available online: https://www.hgi-cgs.hr/urusavanje-tla-u-mecencanima-i-okolici-izazvano-potresom-magnitude-6-2-kod-petrinje-te-prethodnim-i-naknadnim-potresima/ (accessed on 17 March 2021).
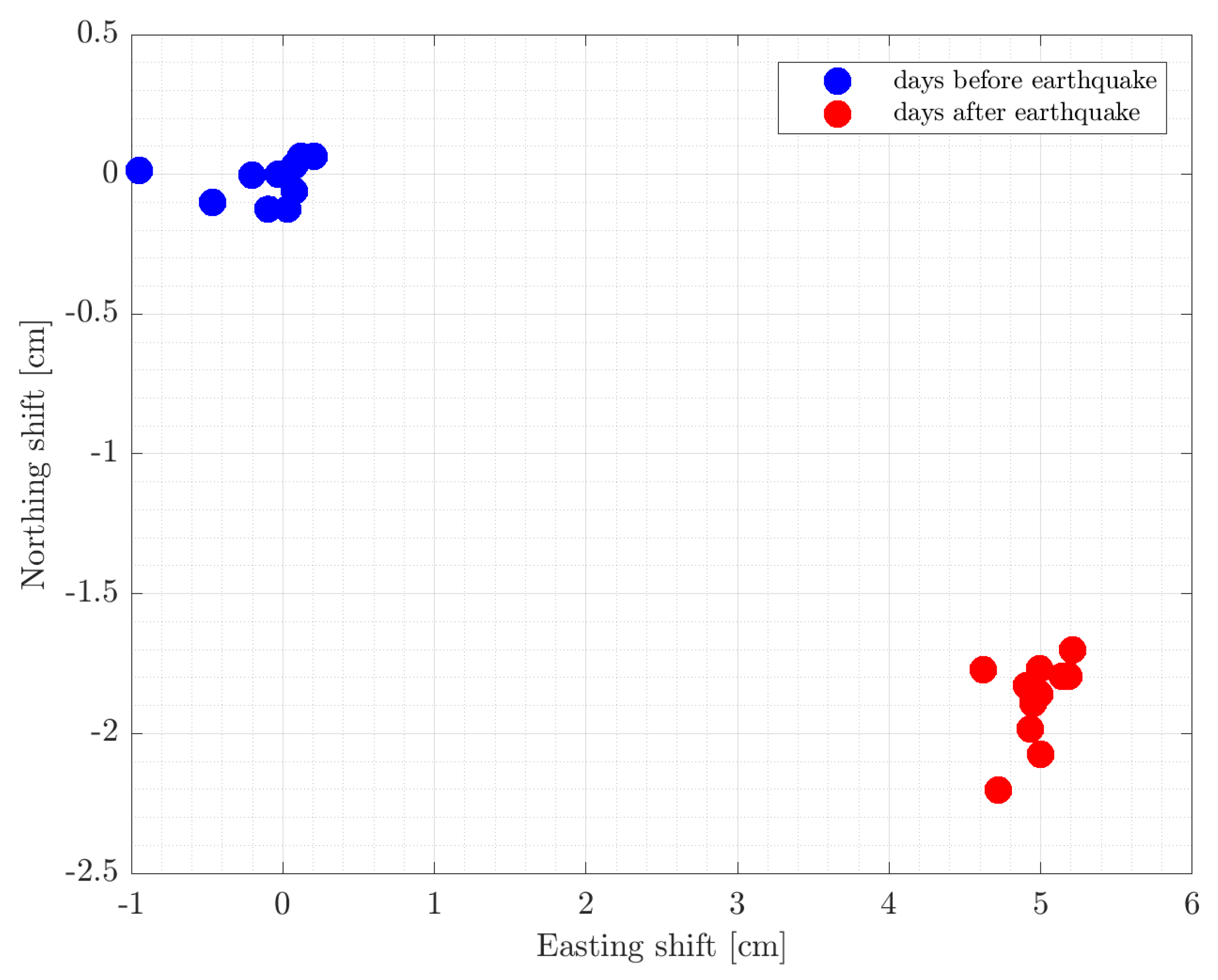
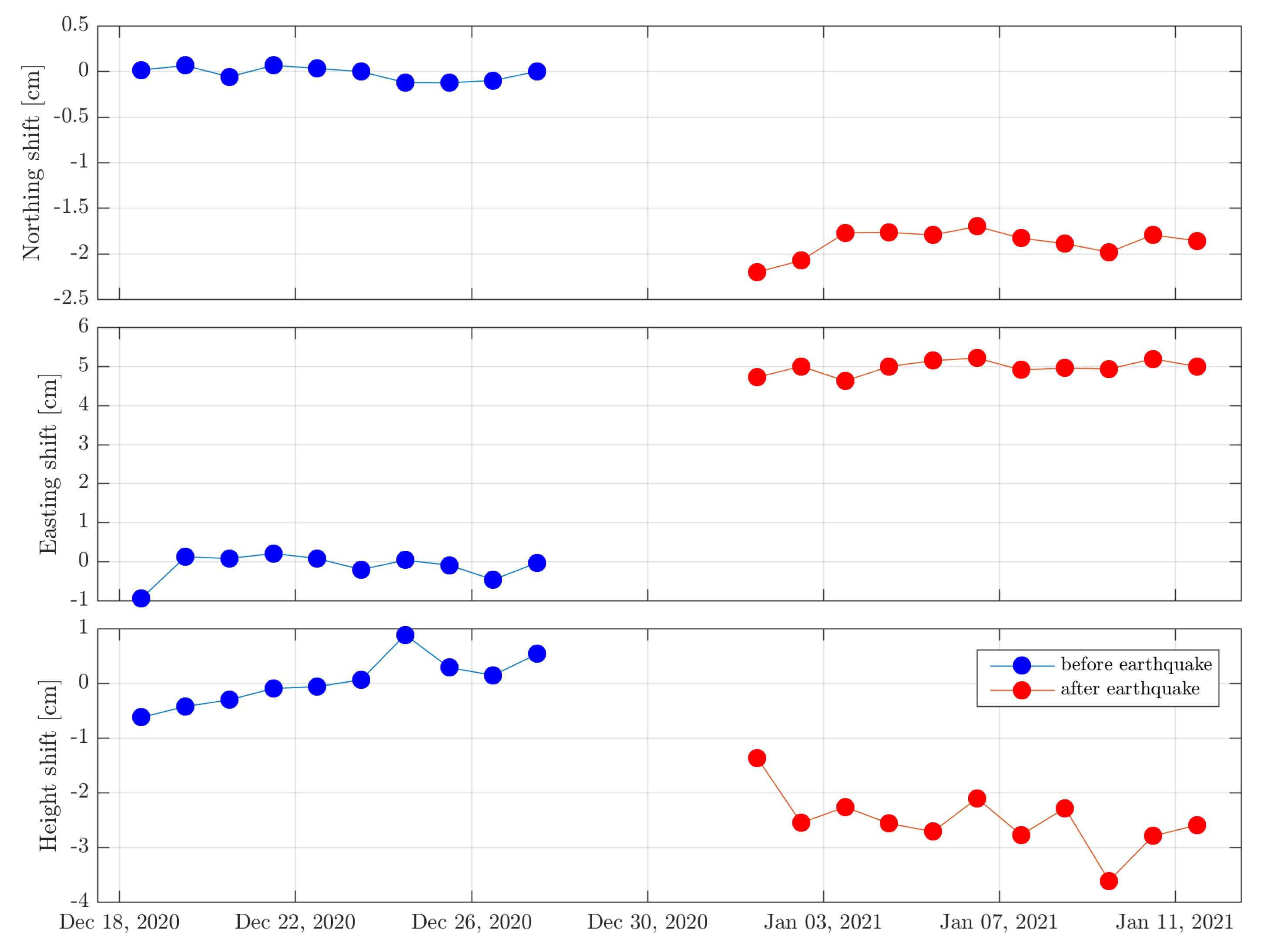
| Sentinel | Acquisition Date | Relative Orbit Track | Subswath | Initial Burst | Last Burst |
|---|---|---|---|---|---|
| 1A-SLC | 18 December 2020 | T146 | IW2, IW3 | 6 | 8 |
| 1A-SLC | 30 December 2020 | T146 | IW2, IW3 | 6 | 8 |
| 1A-SLC | 11 January 2021 | T146 | IW2, IW3 | 6 | 9 |
| 1A-SLC | 23 January 2021 | T146 | IW2, IW3 | 6 | 9 |
| 1B-SLC | 23 December 2020 | T124 | IW2 | 5 | 7 |
| 1B-SLC | 4 January 2021 | T124 | IW2 | 5 | 7 |
| 1B-SLC | 16 January 2021 | T124 | IW2 | 5 | 7 |
| 1B-SLC | 28 January 2021 | T124 | IW2 | 5 | 7 |
| Satellite | LOS Displ. | UP-DOWN Displ. | EAST-WEST Displ. |
|---|---|---|---|
| min/max | min/max | min/max | |
| 1A-IW-SLC | −30.6/43.0 | −40.8/57.0 | −46.0/65.6 |
| 1B-IW-SLC | −17.7/35.4 | −23.3/46.0 | −27.2/55.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bjelotomić Oršulić, O.; Markovinović, D.; Varga, M.; Bašić, T. Coseismic Ground Displacement after the Mw6.2 Earthquake in NW Croatia Determined from Sentinel-1 and GNSS CORS Data. Geosciences 2021, 11, 170. https://doi.org/10.3390/geosciences11040170
Bjelotomić Oršulić O, Markovinović D, Varga M, Bašić T. Coseismic Ground Displacement after the Mw6.2 Earthquake in NW Croatia Determined from Sentinel-1 and GNSS CORS Data. Geosciences. 2021; 11(4):170. https://doi.org/10.3390/geosciences11040170
Chicago/Turabian StyleBjelotomić Oršulić, Olga, Danko Markovinović, Matej Varga, and Tomislav Bašić. 2021. "Coseismic Ground Displacement after the Mw6.2 Earthquake in NW Croatia Determined from Sentinel-1 and GNSS CORS Data" Geosciences 11, no. 4: 170. https://doi.org/10.3390/geosciences11040170
APA StyleBjelotomić Oršulić, O., Markovinović, D., Varga, M., & Bašić, T. (2021). Coseismic Ground Displacement after the Mw6.2 Earthquake in NW Croatia Determined from Sentinel-1 and GNSS CORS Data. Geosciences, 11(4), 170. https://doi.org/10.3390/geosciences11040170








