Abstract
Geomathematics is extremely important in geosciences, particularly in the geology. The key for any geomathematical analysis is the definition of a typical model to be applied for further prognosis, either through deterministic or stochastic approaches. The selection of the appropriate procedure is presented in this paper. Two different geomathematical subfield datasets were used in subsurface geological mapping and palaeontology and different biostatistics applications, representing important geomathematical subfields in the Croatian geology. The different subsurface interpolation methods tested, validated and recommended for application were used to obtain the best possible outcome in reservoir modelling, in the cases with small datasets. Cross-validation may be chosen as the main selection criteria, applied to the Croatian part of the Pannonian Basin System (CPBS). Recent advances in biostatistics applied in palaeontology and case studies from Croatia are also presented, where biometric studies are of significant importance in fossil biota. Data, methods and problems in geosciences are vast subjects, and address a wide spectrum of fundamental science. Because geology includes subsurface and surface geology, and very different datasets regarding variable and number of data, we have chosen here two representative case study groups with original samples from Northern Croatia. Subsurface mapping has been presented on limited petrophysical datasets from the Northern Croatian, Miocene, hydrocarbon reservoirs. Biostatistics have been presented on very different samples, allowing us to achieve paleoenvironmental reconstructions of the size of relevant fossils, such as dinosaurs or other species and their paleoenvironments. All examples highlight examples of the valuable application of geomathematical tools in geology. The results, cautiously validated and correlated with other, non-numerical (indicator, categorical) geological knowledge, are of enormous assistance in creating better geological models.
1. Introduction
The development of geomathematics in the past was a very dynamic and non-linear process. In the early days (until the 1980s) geomathematics and geostatistics were considered as synonymous, so pioneer works in geostatistics were considered as breakthroughs in the entire geomathematics applied in geosciences. The first results of geostatistical research (different from research in the field of “spatial statistics”) had been published by [1,2,3] where kriging was described for the first time. The same algorithm had already been applied earlier by [4] for estimation of gold nuggets concentrations in South African mines. Matheron’s foundation has been based on the least square method and linear Gaussian model, which stayed as a base until the present day. Following the linear models, authors such as [5] and [6] also developed non-parametric and non-linear geostatistics. In parallel, geostatistics was developed together with applied statistics by [7]. Cressie [8] made an important step toward unification of geostatistics and other data analysis methods in geology, describing three main branches of spatial statistics-geostatistics, spatial variations and spatial point processes. That is what we today call geomathematics.
Here it is also worth mentioning some pioneer works that preceded Matheron’s development of early geostatistics. Frits Agterberg published some early papers crucial for later development of spatial statistics. He used numerical analysis of depositional and structural data to interpret sedimentation rates [9] as well as divergent structural trends [10] and single structural events. In Agterberg [11] the origin of skewed distributions of ore minerals was discussed and spatial dependence recognized using Fourier analysis. Krumbein [12,13,14] developed and published several statistical models in geological mapping. Approximating simulations with Matheron works, Vistelius [15] published important studies in mathematical geology, and Merriam [16] undertook the early application of computers in geology.
Here, it is important to mention that the use of geostatistics (even statistics) is closely related with exploration and the production of hydrocarbon reservoirs (e.g., [17,18]). In the late 1980s, geostatistics offered new algorithms, allowing much better reservoir characterisation to be obtained, in particular visualisation. However, from the early days in geostatistics and later geomathematics, the main factor in the selection of a method was the number and distribution of data elements. Those two problems are often intertwined, although distribution of data is considered as fundamental for any later analysis.
As in any data-based analysis, geomathematics is highly dependent on hard data, i.e., measurements, aiming to predict values in non-sampled volumes (Figure 1). The problem had been solved differently. As geological variables are mostly presented in deterministic ways, knowledge about (sub)surface is always partial. In fact, the models are stochastic but too complex so that available mathematical approximations, restricted with limited data, could be presented in such a way. Geomathematics offered the approaches designed for object-based models, where objects are datasets analysed and visualised with different spatial methods (e.g., [19,20]). Most of them are deterministic (kriging) but some approaches could be stochastic (simulations).
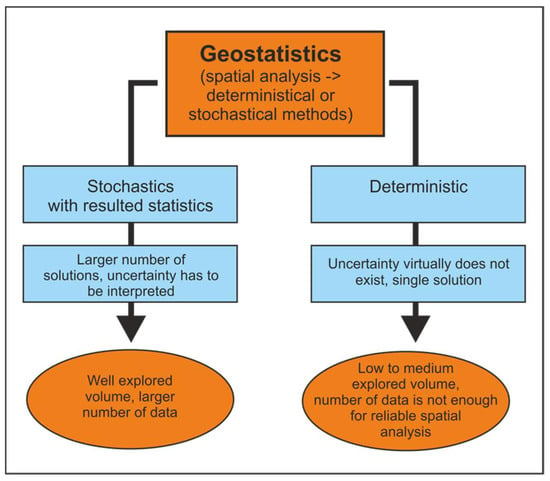
Figure 1.
Relation between geostatistical approach and number of data elements.
Any classification of such models can be categorised. Here we decided to divide them into:
- Full deterministic, models where volume is well known, without uncertainties, possible correlated, and settings are known and established. Such knowledge is rare, but many areas are approximated in such a way.
- Stochastic volumes, where uncertainties cannot be full described and permanently exists. However, the probability model allows predictions and estimations to be made with different geomathematical algorithms. This is mostly done with analysed (sub)surface volumes, but the stochastic approach asks for more experiences and, contradictorily, more data than the deterministic approach.
- Unpredictable volumes, where analysed variables could not be described by any algorithm or just the number of data elements is not high enough so that any observation is valid and general.
The key goal for any geomathematical analysis is the definition of a typical model that can be applied for further prognosis in similar or the same conditions. Any such prognosis needs to be based on valid choices, grounded on previous case studies where decision trees are made. Such choices are always based on the number of inputs, regarding variables and dataset size. Generally, the explored geological volume is researched longer so that the object of researching could be improved more easily with both deterministic or stochastic approaches. The decision depends on experience, knowledge and readiness to accept uncertainties in future estimations. Any multivariable approach is beneficial (like co-kriging) but needs well-documented connections among dependent variables. Significant inherited (measurements limitations, equipment error) and man-made (biased sampling) uncertainties forced stochastics, but limitation of such an approach is a must-have spatial model. However, it is not a condition at all for simpler algorithms like inverse distance weighting (IDW), the modified Shepard’s method (MSM), nearest neighbourhood (NN) or similar. The largest limitation is the number of data elements (Figure 2), especially if the primary variable is to be defined in the entire dataset. The sparse or non-representative dataset greatly limits the application of statistics. Even statistical representative sets (e.g., n > 30) are much easier when analysed with parametric statistics that require Gaussian distribution. By contrast, non-parametric statistics are only a choice, which can limit the number of tests and mapping, in particular.
Figure 2.
Simple decision tree for geomathematical analysis.
However, and despite all limitations, geomathematics has many favourable and robust tools and algorithms for analysis of almost all geological datasets. It is especially valid if geomathematics is considered as a field divided into three sub-fields: geostatistics, statistics applied to geosciences and neural networks applied to geoscientific data.
The main challenge is the selection of an appropriate procedure. How to find such tools, but only in a very tiny spectre of geomathematics and geosciences, has been presented in this work, through the examples of two different geomathematical subfield datasets. The first one refers to the subsurface geological mapping, as described above, and the second one refers to palaeontology and biostatistics.
The starting point in paleontological research is the assumption presented by day biota and processes which are the key to understanding Earth’s history. Therefore, the biological research methods and facts, such as biostatistics (biological statistics or biometry), are common in taxonomical and palaeoecological studies in palaeontology due to the assumption that species can be defined by morphology, including the measurable parameters.
The development of biostatistics dates back to the 19th century, with Francis Galton (1822−1911), “the father of biostatistics and eugenics”. His methodology, used in the analysis of biological variation, is considered as the foundation for the application of statistics to biology [13]. The term “biometry” was coined by the zoologist W.F.R. Wilson (1860−1906), who was working with Karl Pearson on the application of statistical methods in biology [21]. The application of biometry in the systematic description of plants and animals was pointed out by [22], where he describes the necessity of specific descriptions of taxon characteristics, in order to precisely describe the specimen. The rising impact of biometry resulted in the establishment of the Biometric Society on 6 September 1947 at Woods Hole, USA, as described by [23]. The first president of the Biometric Society was Sir Ronald Aylmer Fisher (1890−1962). The society was later renamed the International Biometric Society. The Biometric Section of the American Statistical Association started publishing the Biometrics Bulletin in 1945, which was renamed Biometrics in 1947.
Two significantly different datasets and applications in geological subsurface mapping and biostatistics (biometrics) presented in this paper, represent, in the last decade, as well as currently, the most progressive and publicised geomathematical subfields in Croatian geology.
2. Mathematical Basics of Algorithms Applied in the Presented Case Studies
2.1. Kriging Method
Kriging (as well as the co-kriging and stochastic simulations) is a group of statistical estimation methods. The specificity of kriging (e.g., [5,24,25]) is the definition as the best linear unbiased estimator (BLUE), although it is valid only for specific datasets. The strength of the kriging approach is due to the weighting coefficient calculation, the procedure based on the minimisation of kriging variance. The linear method means that estimation has been done by the combination of hard data; the unbiased character makes sure that the estimation’s expected value is as real as for the entire possible population. The estimator defines the applied methodology. The linear estimation is shown in Equation (1):
where:
- Zk
- value of the regionalised variable (variable that described some geological property in a selected space with clear structure and known statistics) calculated at location “k”;
- Zi
- value of the regionalised variable measured at location “I”;
- λi
- weighting coefficient calculated by kriging matrices for location “I”.
The necessary condition for the kriging estimation is that the measured Zi values are characterised with normal distribution or, at least, that such property is assumed for that variable in the case of a large number of measurements. Compared with simpler estimation algorithms, kriging is a more time-consuming interpolation method, but also better tool for handling with highly clustered data. By contrast, the kriging results in very weak works with small datasets (n < 20), unable to give an origin to meaningful spatial models. The spatial (variogram, co-variance or madogram) tools are powerful when applied with enough data and background knowledge. The variogram is the most often applied among them. It is defined as squared difference between two pints at some distance.
As mentioned earlier, the main advantage of kriging is the weighting coefficient calculation. After the spatial model has been set up, the calculation of the coefficient is not dependent on their value, but exclusively on the distance between measured points and location where the value is not known. Such a value is also called “statistical distance” or “semivariogram distance”, referring to their derivation from the variogram (value of variance for any data-pair, which is function of their distance; once variogram model is calculated, the variogram for new measurements can be calculated only from the distance itself, regardless of their value). The kriging equations (Equation (2)) are calculated using matrices. In two of them (W, B), the values are given with variogram values, which depend on distances among observed locations:
There are numerous kriging techniques, each of them differenced by some modification in matrices. The most used in Croatian case studies are herein designated by simple, ordinary, indicator and universal kriging. Simple kriging is the basis for all the other available techniques. The matrix is presented in Equation (3):
where γ—variogram value, Z1…Zn—known measured values in spatial points (hard data), x—location where value is estimated from known values, λ—weighed coefficients for location 1…n.
Although the basic technique, it is the only one that do not satisfy the condition of unbiased estimation, because it is the only equation without constraint. Such constraint(s) could be linear or non-linear.
The technique used most often is presented in Equation (4) with an additional constraint, the Lagrange multiplier (μ), aiming to find the local minima and maxima of the function, subjected to equality constraints, i.e., to minimise the kriging variance.
2.2. Inverse Distance Weighting (IDW) Interpolation Method
IDW is a widely used interpolation method, both for small and large datasets. The unknown value is calculated based on all known points and inversely proportional to their distances, weighted by power exponent (Equation (5), e.g., [26,27,28]) and is defined as:
where:
- ZIU
- estimated value,
- d1…dn
- distance between locations (points) with measurements (1…n) and estimated location (IU),
- p
- power (distance) exponent,
- z1…zn
- known values at locations 1…n.
The mapping results are greatly influenced by the power exponent, which could stress the influence of more distance points and smooth the map (for p <= 2) or force very local estimation (p > 2) and even, for large “p”, result in zonal estimation, i.e., in map like Voronoi polygons. This method has been proved for mapping problems in the Croatian part of the Pannonian Basin System (CPBS) for all datasets where clustering was not largely imposed, and for datasets smaller than 15 points too (e.g., [29,30]).
2.3. Basics of the Nearest Neighbourhood (NN) Estimation Method
NN is the simplest statistical estimation method when an unknown point is estimated only from the closest known value. The results are valued polygons, like the Voronoi diagram. The distance between the points is Euclidean (Equation (6)):
where:
- d
- distance,
- n
- n-th pair of points,
- x and T
- unknown and measured point,
- X and T
- length of line segment in Euclidean space connecting the points X and T for pairs 1…n, in the Euclidian n-space.
The method is meaningful to apply only for very small datasets, like 5 or fewer points. The output is not a map, but a schematic polygon view.
2.4. Basics of the Natural Neighbourhood (NaN) Estimation Method
NaN is the modification of the NN and results are also shown as Voronoi diagrams (polygons). The unknown point is estimated from several nearest points (e.g., [31,32,33]) using Equation (7):
where:
- X(x,y)
- estimated value in point (x,y),
- A(Xi,Yi)
- known value in point (Xi,Yi),
- wi
- proportion of polygon, i“ in total area.
2.5. Modified Shepard’s Method (MSM)
The MSM interpolation is a modification of the IDW method, with the aim of reducing the expressive local values (outliers, extremes) that could cause “bull’s-eyeing” or “butterfly shape” effects. The method was developed by [34] and it is why is named as Shepard’s method. The modification of the method was carried out in the works of, e.g., [35,36]. The estimation is done by Equation (8):
where:
- F
- MSM function,
- W
- relative weights,
- Qk
- bivariate quadratic function,
- x, y
- data coordinates,
- n
- number of data elements.
MSM used so called relative weights determined (Equation (9)):
where:
- dk
- Euclidean distance between points at locations (x, y) and (xk, yk),
- Rω
- radius of influence around node (xk, yk).
2.6. Cross-Validation as Numerical Estimation of Mapping Error
Cross-validation is a numerical procedure which can be applied also as error-based comparison tool for several maps with the same input, but sequentially interpolated with two or more methods. The procedure is repeated as many times as there are measured (hard) values, dropping one known point out and calculating the estimation in the same location from the rest of the hard data (Equation (10)). One of the measures that can be calculated based on cross-validation are mean square error (MSE, e.g., [29,37,38,39]). This value is often used as criteria for the most appropriate map selection in the case of small datasets in the CPBS (e.g., [40,41]).
where:
- MSE
- mean square error value,
- n
- number of known values,
- SV
- measured value in point “i”,
- P
- estimated value in point “i”,
- i
- i-th point.
2.7. Shannon–Wiener Index or Shannon Diversity Index (H)
In paleoecological analyses, one of the goals is to explore species richness and diversity in the analysed data sets, and to compare biological diversity between the samples with an uneven number of species and individuals. In the examples presented in this paper (e.g., see here Figure 6), authors showed part of the research on the biodiversity of microfossils Foraminifera, where the Shannon–Wiener or Shannon diversity index (H) (called also Shannon entropy in informatics) is used as one of the measures of species diversity in one sample, and between samples [34]. The “H” is calculated by Equation (11) [42]:
where:
- pi
- a proportion of individuals belonging to the ith species in the sample,
- ln
- a natural logarithm,
- R
- total number of species in the community (richness).
Equation (11) shows dependence of H (Shannon index) on pi (proportion of individuals, and if all species in the sample are equally represented, H is at its maximum [42].
3. Recent Advances in Geomathematical Mapping in Small Datasets and Case Studies from Croatia
During 2019 and 2020, broad testing of small datasets mapping has been applied [41,43] to the CPBS. A small subsurface sample set is considered to be a set of measurements which includes [41] less than 20 inputs data. Furthermore, such datasets could be subdivided in groups with respect to the number of data inputs: a) 1–5, b) 6–10 and c) 11–19. One example is selected here when the reservoir mapping is done by mathematically simpler methods (compared with previously widely used kriging) and results are accepted as the best possible outcomes for further reservoir development. The permeability maps of the Lower Pontian “K” reservoir (Lower Pontian age, 18 data) of the field “B” are shown in Figure 3.
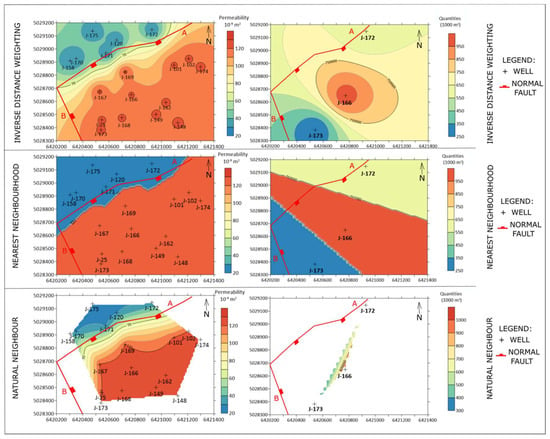
Figure 3.
Results of inverse distance weighting (IDW), nearest neighbourhood (NN) and natural neighbourhood (NaN) methods (from top to bottom) of the permeability (left) and injected volumes (right) in the “K” reservoir [41].
All maps obtained with different methods (Figure 3) are validated with a cross-validation (Table 1) and visual assessment (where the larger “bull’s-eyes” areas mean worse interpolation).

Table 1.
Summary results of cross-validation (mean square error, MSE) for IDW, NN, NaN and modified Shepard’s method (MSM) methods [41].
Two interpolation (IDW, NaN) methods and one zonal (NN) method, gave different mapping results as well as cross-validation errors, as expected. Interestingly, each of them led to at least one useful information about analysed reservoirs, i.e., about connection between permeability and injected water volumes, including the role of some fault zone. The IDW method algorithm remains the main interpolation method of mapping for a small reservoir dataset in Northern Croatia. Other interpolation methods, NN, NaN, may be additional information. But the main advantage was that such datasets could be divided into three classes regarding their mapping, as follows: (a) 1–5, (b) 6–10 and (c) 11–19 inputs. The “class a” could not be analysed with the NaN method because it is often not possible to calculate the cross-validation and the interpolated area is very small regarding unit margins. In the “class b” and “class c”, all three methods gave results, and the main selection criteria could be cross-validation.
Malvić et al. [40] also analysed the possibility of artificially increasing the input data set using the “jack-knifed” method. That is a resampling statistical technique, later upgraded into, e.g., bootstrapping. It is useful for statistics estimation, sequentially leaving out each value from datasets and calculating the statistical parameters of remaining data. For example, if the estimated parameter is the population mean (x), using jack-knifing it is possible to calculate the mean of each sub-dataset that includes all but the i-th measurement (xi) using Equation (12):
where:
- mean of sub-dataset, where i-th data is skipped,
- n
- number of data points,
- j
- data currently analysed.
The presented analysis is the first of such a kind in the Sava Depression (Northern Croatia). It represents the continuation of previous geostatistical analyses conducted in that depression and the entire CPBS. The “jack-knifed” method was applied on porosity of reservoir “K” (19 data) of the “B” field (Figure 4).
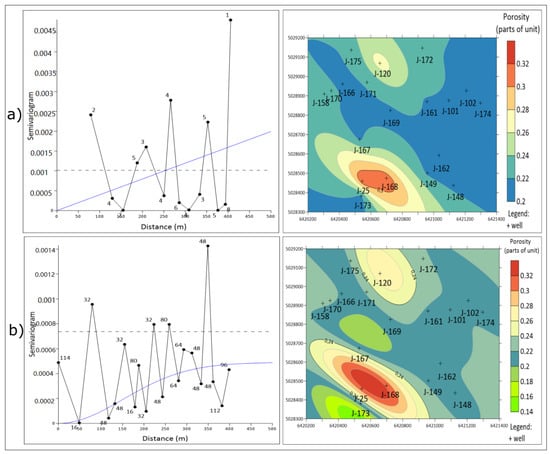
Figure 4.
Experimental semivariograms and porosity maps for the “K” reservoir obtained by the ordinary kriging (OK) method: (a) without the “jack-knifed” method and (b) with the “jack-knifed” method [40].
The porosity maps obtained were analysed by comparing the cross-validation values and expression of the “bull’s-eyes” effect. The results of the analysis of the “jack-knifing” method are summarized in Table 2.

Table 2.
Comparison of cross-validation (MSE) values for OK maps based on original and “jack-knifed” semivariograms [40].
The results in Table 2 confirm the possibility of applying the “jack-knifing” method to reservoirs with small data input and should be compared with the maps obtained by the IDW method. By contrast, in another analysed reservoir, the OK was not accepted as the interpolation method, but IDW has been accepted. It was the case when jack-knifing did not yield any progress in spatial modelling and the kriging has been abandoned as an approach.
The permanent problem of small datasets could be oversized with new data. Such data can be obtained with new sampling, but also with the creation of new artificial data, based on the statistical properties of original dataset. The jack-knifing is one such method, appropriate for datasets of 15–30 points, where the basic, descriptive statistics are more or less representative (variance and mean), and the Gaussian distribution can be assumed or verified with use of the Shapiro-Wilk test. In the presented analysis, the original semivariogram results were highly uncertain, with large oscillations, a small number of data pairs per class and unknown nugget. Consequently, the linear model was the only acceptable theoretical model to use. Due to fact that a small dataset could not be statistically representative, the new kriged maps interpolated from “jack-knifed” semivariograms has been tested (a) visually (maps without the “bull-eye” or “butterfly” effects are better) and (b) numerically, using cross-validation and comparing with the simpler method of the IDW. Obviously, the results were better in one of the two cases where such validation has been applied.
The next examples are taken from [43] and compare the differences between the results obtained with the IDW and MSM methods. The IDW does not use weighting coefficient, i.e., each value is “weighted” by a simple (powered) inversely proportional distance from the measured point. The MSM (Modified Shepard’s Method) uses relative weights. The porosity, permeability and thickness maps, interpolated with IDW and MSM are given in Figure 5. They show the oil reservoir “K” of the Lower Pontian age in the Sava Depression.
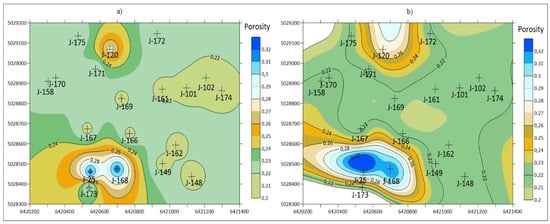
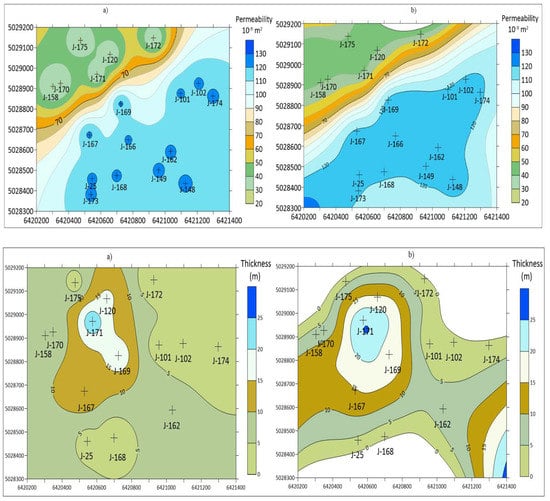
Figure 5.
The mapping of the Lower Pontian “K” reservoir, the Sava Depression, Northern Croatia. Left—IDW results, right—MSM results. Top—porosity, middle permeability, down—thickness [43].
The maps obtained by the IDW and MSM methods could be assessed in two ways. One is numerical, using cross-validation. The another is quick-look searching for observable feature of highly expressed local value, i.e., bull’s-eye or butterfly shape effects. The expected advantage of the MSM is the larger smoothing of the shapes, which is confirmed in that analysis (Figure 5). The numerical cross-validation strongly favoured the IDW (Table 3).

Table 3.
Cross-validation (MSE) of the IDW and MSM methods applied in reservoir “K” [43].
The difference resulted from the different mathematical backgrounds of those two methods [43], because the IDW takes into account all measured points or work with general searching radius (or radii for ellipsoid), but the MSM works with local searching by default. This is why cross-validation was higher for MSM—for porosity 289%, permeability 7%, and thickness 49%.
Both methods, obviously led to appropriate quick assessment of the reservoir. However, it was also shown that visual assessment is sometimes the more important criteria than purely numerical cross-validation, what is a crucial conclusion for subsampled reservoirs of the CPBS, and stressed the importance of human and geological expertise, and not purely the application of interpolation algorithms. Consequently, [43] recommended the MSM for subsurface geological mapping of Neogene reservoirs in Northern Croatia in (a) number of samples smaller than 20 measured values, and/or (b) for early exploration phase or later development phase when the number of measurements of the selected property is small, but a quick insight in the spatial distribution of such variables is necessary.
4. Recent Advances in Biostatistics Applied in Palaeontology and Case Studies from Croatia and the Wider Region
Paleontological studies published by numerous authors, including those from Croatia, almost always include basic numerical analyses in recognizing the different taxa. In Croatia, [44] measured the dimensions of the bivalve shells (length, width, length/width ratio of the shell, apical angle) in order to recognize the bivalve subspecies. In her dissertation and several published papers (e.g., [45]), A. Sokač applied biometry in order to present the differences in growth pattern of male and female ostracods. One of the earliest graphically substantiated biometric analysis on the fossil assemblage from Croatia was published by [46], who studied the taxonomy and biometry of Eocene corals. The authors distinguished two coral species based on the biometric analyses of the smallest and the largest diameter of the calyx, and the height of the coral calyx plotted in a scatter diagram. Looking at the dispersal of the measured parameters, two areas of dispersal could be recognized, indicating the existence of different species between measured specimens.
During the last decades, a number of global researches were focused on the paleoecology of terrestrial, fresh-water or marine biota. In Northern Croatia, Miocene deposits from the Paratethys epicontinental Sea comprise the marine invertebrate fauna, mostly foraminifers, mollusks and ostracods, which were often subject to biostatistics analyses (e.g., [47,48,49,50]). The following data, common in palaeoecological studies, are presented in the referred papers: plankton/benthos ratio, number of species, relative abundance of benthic species within the community, species diversity of benthic foraminifera estimated by the Shannon–Wiener index (H), dominance (D), Fisher α index (α), oxygen index and the infauna/epifauna ratio. The Shannon–Wiener index or Shannon diversity index (H) estimate the species diversity in the assemblage, as described in Section 2.6 of this paper (after [42]). Dominance (D) reflects a distribution of a particular species in the assemblage, and the dominant species are those presented with >10% in the sample [42]. The Fisher α index (α) shows the relation of the number of species to the number of the individuals, and to explore the number of species by each individual, a log series distribution is used [42]. This index is used for palaeoecological determinations, because specific values are characteristic for each environment. Depending on the index value range, we can analyse the palaeoecological changes in the environment.
The aforementioned analyses were enhanced by defining and comparing the benthic foraminiferal fauna from different localities conducting the Cluster Analysis and Non-metric Multidimensional Scaling by means of the PAST (PAlaeontology STatistic) Program (https://folk.uio.no/ohammer/past/; e.g., [48]; Figure 6).
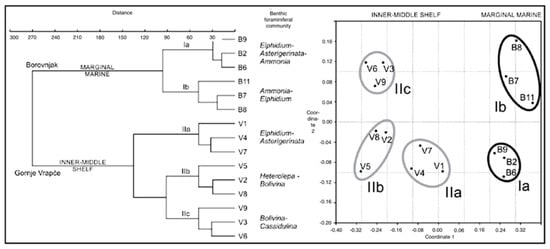
Figure 6.
Example of statistical comparison of fauna from different localities using cluster analysis and non-metric multidimensional scaling analyses (after [48]).
There are a number of other papers dealing with paleoenvironmental reconstructions of fossil communities based on the biometry of benthic foraminifera. Growth characteristics are used as a parameter for the palaeoecological and phylogenetical studies in the wider region (e.g., [51,52]). For example, [53] calibrated test flattening of the foraminifera species Heterostegina depressa as a bathymetric signal (Figure 7), using its growth functions and thickness. Similar study can be applied to the Miocene large nummulitids from Northern Croatia.
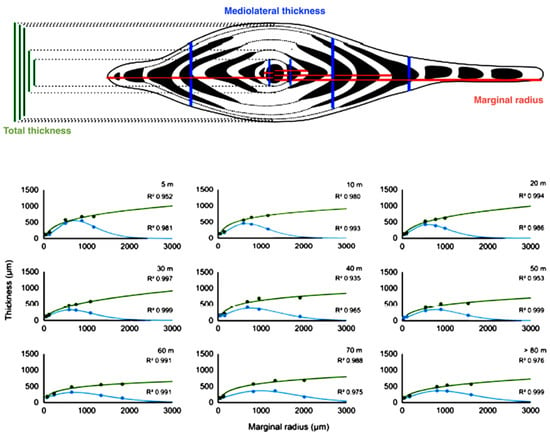
Figure 7.
Example of using growth characteristics as an indicator of the bathymetry [53].
Biometric studies are also commonly applied in taxonomic study of mollusks. For example, a thorough revision based upon this method was made by [54] on gastropod families Conidae and Conorbidae from the Paratethys Sea. The authors measured several shell parameters (shell length, maximum diameter, aperture height, height of maximum diameter, spire angle, apertural length, the angle of the last whorl, length width ratio, relative diameter ratio, position of maximum diameter ratio, relative height of spire ratio, subsutural flexure, mean and standard deviation), analysed by principal component analysis (PCA). Applying this analysis, authors compared similar species of Conidae and showed the separation of the species and morphospace occupied by genera (Figure 8).
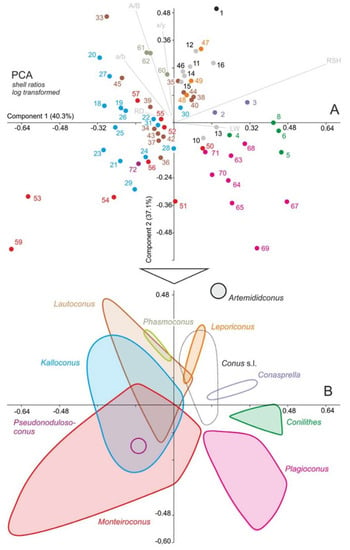
Figure 8.
Separation of the species and morphospace occupied by genera as shown by principal component analysis (after [54]).
Studies from Croatia were mostly focused on gastropods and scaphopods (e.g., [55,56,57]). Several parameters are measured (height and length of the shell, apical angle), defining the basic numerical data useful in species determination, morphometric characteristics of the group, correlation with recent species, comparison with other localities and palaeoecological interpretations.
Bošnjak et al. [55] studied the Miocene planktic gastropods from northern Croatia and, based on the measured shell elements, compared their data with the available published measures of that fossil group found in the Miocene deposits of the neighbouring areas (Figure 9).
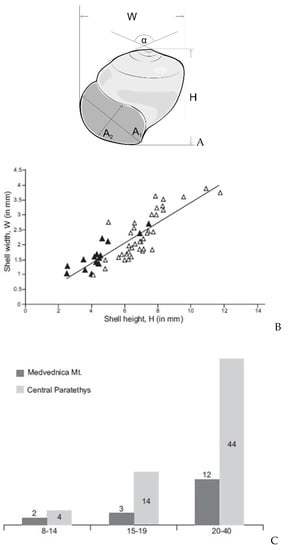
Figure 9.
Morphometric characteristics and comparison of the planktic gastropods between different localities based on the measured morphometric elements of the shell (after [55]). (A): Measured parameters on the gastropod shell: H (height of the shell), W (width of the shell), α (apical angle), A1 and A2 (aperture diameters). (B) Comparison of planktic gastropod from different areas (black and white triangles) based on the measured values of the shell height and width. (C) Comparison of planktic gastropod species from different areas (dark and light grey columns) based on the measured values of the apical angle of the gastropod shells.
Bioerosive traces on skeletal remains, in most cases traces of predation, are also rather common topic in biostatistical analyses. Measures and shapes of the drill-holes can indicate the possible predator and help to gain a better insight into the predator–prey relationship, as described in numerous papers (e.g., [58] and references therein).
One more example of biostatistics analysis is presented in [59]. The authors measured the orientations of oyster attachments on ammonite shells, concluding that the oysters attached themselves while the ammonites were living (Figure 10). The results are helpful in palaeoecological studies of fauna in oxygen-depleted environments.
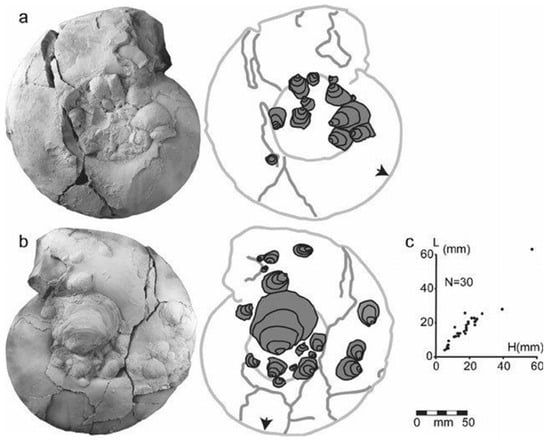
Figure 10.
Analysis of oyster attachments positions on the ammonite shell [59].
Biostatistical analyses are also common in studies of vertebrates. In Croatia, research included the study of dinosaur footprints. The measured parameters of footprints included width and length of the footprint, and length of the second, third and fourth finger (e.g., [60] and references therein). These studies give an insight on the dimensions of the animal (height) and type of their movement (walking) based on the calculations of the movement speed (e.g., [60,61,62,63] and references therein), which gives a better insight into the biodynamics of the animal. Costa-Pérez et al. [64] demonstrated the application of geometric morphometrics as a tool for the shape analysis of the dinosaur footprints and trackways geometric differences (Figure 11).
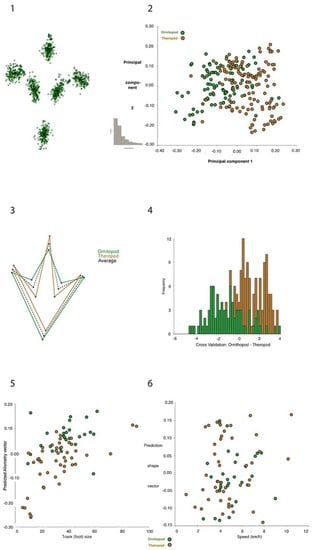
Figure 11.
Application of geometric morphometrics on the dinosaur footprints analysis [64].
We can conclude that biostatistical analyses generally occurred very early in paleontological studies. In Croatia, their number exhibits the pattern of periodicity. Basic numeric analyses of fossil assemblages were published in the mid-1990s, marking the first peak of biometric studies in Croatia. The second peak was during the first decade of the 2000s, with most research done on microfossils (foraminifers and accompanying ostracods). We can say that the third pulse is happening from 2016 onwards, considering the various groups of fossil biota.
The analyses are mostly made to give more insight in the paleoecology of populations or fossil assemblages, and to help in the species determination. To present the analysed parameters, common statistical tools are used, mostly MS Office Excel and PAST (PAlaeontological STatistics) programs.
5. Discussion and Conclusions
The topic “Advances in Geosciences” is so broad that any publication would hardly cover only the small portion of significant milestones that shaped and led the progress in geosciences in general. The spectre of geosciences includes so many “fundamental” sciences that the means of progress are very different, regarding data, methods and problems. Geosciences could be found in social (e.g., geography), technical (e.g., geodesy) and natural (e.g., geology) sciences. This is why the authors selected only one science (geology) with only one small segment (subsurface and surface geology) and tiny analytical, numerical methods (small datasets in mapping, larger in biostatistics). Even in such a case, the presented cases are given mostly from the researching area where authors worked mostly in the last decade, i.e., original samples taken from the surface and subsurface of the Northern Croatia.
However, both examples present the areas where, at least in Croatia, huge progress was made and referencing methods for later researchers were set up. After more than 15 years of extensive and successful application of the different Kriging techniques in the subsurface mapping of the CPBS, the problem of a small dataset where geostatistics cannot be reliable applied has been solved. Several simpler algorithms are tested, validated and recommended for application, namely inverse distance weighting, nearest neighbourhood, natural neighbourhood and the modified Shepard method. For such small datasets, the importance of mutual application for cross-validation and visual assessment had been stressed. Additionally, the Kriging was simultaneously tested as an alternative to such algorithms, even in cases when variogram model cannot be calculated as reliable value, even an omnidirectional one. The extensive experiments with the jack-knifing method have been done on variogram, creating artificial data from original dataset. In some cases, jack-knifed variograms gave competitive value to the kriging results, but geostatistics was eliminated as the first choice in mapping analysis of small subsurface datasets.
The application of biostatistics has been presented on very different samples, collected from shallow subsurface or surface outcrops. Here the numerical values characterised not petrophysics, but morphological variables of different fossil groups (foraminifers, molluscs, vertebrates). In the presented examples on molluscs, parameters like the height and length of the shell are measured giving a set of numerical values for determination of morphometrics and consequently species which gave more insight into Miocene palaeoecological conditions and environments in Northern Croatia, especially during the existence of the Paratethys Sea. On a larger scale, biostatistical analysis in Croatia helped to reconstruct the size and height of, e.g., dinosaurs, using footprint measurements. Two periods of the Croatian biostatistical (biometric) analyses, presented with relevant publications, are noted. The first was in the mid-1990s, and the second was during the first decade of the 2000s, with most research done on microfossils (foraminifers and accompanying ostracods). Croatian researchers entered the third fruitful period from 2016 onwards, currently analysing the various marine fossil biota aiming to determine species and their paleoenvironments.
Both examples showed the useful application of geomathematical tools in geology. The first group showed how small datasets (n < 10 data) of different geological variables collected in the Neogene sandstones in the Northern Croatia can be reliably mapped with the IDW and MSM methods. The second presented how morphometric and surface features could be collected, numerically analysed and applied in paleoenvironmental reconstructions. Uncertainties, of course, remained due to the data properties. The most problematic is clustering, which can be hardly handled when datasets are small and/or spatially noisy. In such cases, two crucial statistical properties cannot be reliably checked or established. That are proof of the normal distribution and statistical representativeness of a dataset (mean, variance of population). However, the results, carefully validated and correlated with other, non-numerical (indicator, categorical) geological knowledge, are of great help in creating better geological models.
Author Contributions
Conceptualization, T.M., M.B., J.V. and J.S.; Formal analysis, M.B., J.I. Investigation, U.B., M.A.P.D., M.B..; Software, J.I. and M.B.; Supervision, T.M., J.V. and J.S.; Validation, T.M.; Visualization, M.B. and J.I.; Writing—original draft, T.M., M.B., J.I., J.S., U.B., M.A.P.D.; Writing—review and editing, T.M. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
The authors are grateful for partial support from the project “Mathematical methods in geology IV” (led by T.M.). Funds were given from the University of Zagreb, for the year 2019. Also, great help was offered by Mr. Renato Drempetić in drawing the final figures for biostatistical examples.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Matheron, G. Traité de géostatistique appliquée; Editions Technip: Paris, France, 1962; Volume 1, p. 334. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Matheron, G. Les Variables Régionalisées et leur Estimation; Masson & Cie: Paris, France, 1965; p. 306. [Google Scholar]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. Chem. Metall. Min. Soc. S. Afr. 1951, 52, 119–139. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978. [Google Scholar]
- Ripley, B.D. Spatial Statistics; Wiley & Sons Ltd.: New York, NY, USA, 1981; p. 272. [Google Scholar]
- Davis, J.C.; Sampson, R.J. Statistics and Data Analysis in Geology; John Wiley & Sons Inc.: New York, NY, USA, 1973. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley & Sons Ltd.: New York, NY, USA, 1991. [Google Scholar]
- Agterberg, F.P. An undulation of the rate of sedimentation in southern Gotland. Geol. Mijnb. 1958, 20, 253–260. [Google Scholar]
- Agterberg, F.P. On the measuring of strongly dispersed minor folds. Geol. Mijnb. 1959, 21, 133–137. [Google Scholar]
- Agterberg, F.P. The skew frequency distribution of some ore minerals. Geol. Mijnb. 1961, 23, 149–162. [Google Scholar]
- Krumbein, W.C. Regional and local components in facies maps. AAPG Bull. 1956, 40, 2163–2194. [Google Scholar]
- Krumbein, W.C. Trend-surface analysis of contour type maps with irregular control-point spacing. J. Geophys. Res. 1959, 64, 823–834. [Google Scholar] [CrossRef]
- Krumbein, W.C.; Graybill, F.A. An Introduction to Statistical Models in Geology; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Vistelius, A.B. Studies in Mathematical Geology (Translated from Russian by George V. Keller); Consultants Bureau: New York, NY, USA, 1967. [Google Scholar]
- Merriam, D.F. Geologic use of the computer. In Symposium on Recently Developed Geologic Principles and Sedimentation of the Permo-Pennsylvanian of the Rocky Mountains—Wyoming Geologists’s Association 20th Annual Conference; Petroleum Inf.: Casper, WY, USA, 1967; pp. 109–112. [Google Scholar]
- Isaaks, E.; Srivastava, R. An Introduction to Applied Geostatistics; Oxford University Press Inc.: New York, NY, USA, 1989. [Google Scholar]
- Jensen, J.L.; Lake, L.W.; Corbett, P.W.M.; Goggin, D.J. Statistics for Petroleum Engineers and Geoscientists; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Dubrule, O. Geostatistics in Petroleum Geology; AAPG Education Course Note, Series #38; AAPG and Geological Society Publishing House: Tulsa, Oklahoma, 1998. [Google Scholar]
- Kelkar, M.; Perez, G. Applied Geostatistics for Reservoir Characterization; Society of Petroleum Engineers: Richardson, TX, USA, 2002. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Introduction to Biostatistics, 2nd ed.; Dover Publications Inc.: Dover, DE, USA, 2009; pp. 1–363. [Google Scholar]
- Lincoln Edwards, C. Biometry as a Method in Taxonomy. Am. Nat. 1908, 42, 537–540. [Google Scholar] [CrossRef]
- Billard, L. Sir Ronald A. Fisher and The International Biometric Society. Biometrics 2014, 70, 259–265. [Google Scholar] [CrossRef]
- Hohn, M.E. Geostatistics and Petroleum Geology; Van Nostrand Reinhold: New York, NY, USA, 1988. [Google Scholar]
- Liebhold, A.M.; Rossi, R.E.; Kemp, W.P. Geostatistics and Geographic Information System in Applied Insect Ecology. Annu. Rev. Entomol. 1993, 38, 303–327. [Google Scholar] [CrossRef]
- Balić, D.; Velić, J.; Malvić, T. Selection of the most appropriate interpolation method for sandstone reservoirs in the Kloštar oil and gas field. Geol. Croat. 2008, 61, 27–35. [Google Scholar]
- Medved, I.; Pribičević, B.; Medak, D.; Kuzmanić. Usporedba metoda interpolacije batimetrijskih mjerenja za praćenje promjena volumena jezera (Comparison of Interpolation Methods of Bathymetry Data Used for Monitoring of Lake Volume Change—In Croatian). Geod. List 2010, 2, 71–86. [Google Scholar]
- Ly, S.; Charles, C.; Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Husanović, E.; Malvić, T. Review of deterministic geostatistical mapping methods in Croatian hydrocarbon reservoirs and advantages of such approach. Nafta 2014, 65, 57–63. [Google Scholar]
- Ivšinović, J. Deep mapping of hydrocarbon reservoirs in the case of a small number of data on the example of the Lower Pontian reservoirs of the western part of Sava Depression. In Proceedings of the 2nd Croatian Congress on Geomathematics and Geological Terminology, Zagreb, Croatia, 6 October 2018; Malvić, T., Velić, J., Rajić, R., Eds.; University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2018; pp. 59–65. [Google Scholar]
- Traversoni, L. Natural neighbour finite elements. Trans. Ecol. Environ. 1994, 8, 291–297. [Google Scholar]
- Boissonnat, J.-D.; Cazals, F. Natural neighbor coordinates of points on a surface. Comput. Geom. 2001, 19, 155–173. [Google Scholar] [CrossRef]
- Tsidaev, A. Parallel Algorithm for Natural Neighbor Interpolation. In Proceedings of the 2nd Ural Workshop on Parallel, Distributed, and Cloud Computing for Young Scientists, Yekaterinburg, Russia, 6 October 2016; Sozykin, A., Akimova, E., Ustalov, D., Eds.; Ural-PDC: Yekaterinburg, Russia, 2016; pp. 78–83. [Google Scholar]
- Shepard, D. A two-dimensional interpolation for irregularly spaced data function. In Proceedings of the 1968 ACM National Conference, New York, NY, USA, 27–29 August 1968; Blue, R.B., Rosenberg, A.M., Eds.; Association for Computing Machinery: New York, NY, USA, 1968; pp. 517–523. [Google Scholar]
- Franke, R.; Nielson, G. Smooth Interpolation of Large Sets of Scattered Data. Int. J. Numer. Methods Eng. 1980, 15, 1691–1704. [Google Scholar] [CrossRef]
- Renka, R.J. Multivariate Interpolation of Large Sets of Scattered Data. ACM Trans. Math. Softw. 1988, 14, 139–148. [Google Scholar] [CrossRef]
- Davis, B. Uses and Abuses of Cross Validation in Geostatistics. Math. Geol. 1987, 19, 241–248. (In Dordrecht) [Google Scholar] [CrossRef]
- Rodrıguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 3, 569–575. [Google Scholar] [CrossRef]
- Arlot, S.; Lerasle, M. Choice of V for V-Fold Cross-Validation in Least-Squares Density Estimation. J. Mach. Learn. Res. 2016, 17, 7256–7305. [Google Scholar]
- Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Kriging with a Small Number of Data Points Supported by Jack- Knifing, a Case Study in the Sava Depression (Northern Croatia). Geosciences 2019, 9, 36. [Google Scholar] [CrossRef]
- Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Interpolation of Small Datasets in the Sandstone Hydrocarbon Reservoirs, Case Study of the Sava Depression, Croatia. Geosciences 2019, 9, 201. [Google Scholar] [CrossRef]
- Murray, J.W. Ecology and Applications of Benthic Foraminifera; Cambridge—University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Malvić, T.; Ivšinović, J.; Velić, J.; Sremac, J.; Barudžija, U. Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia. Stats 2020, 3, 68–83. [Google Scholar] [CrossRef]
- Kochansky-Devidé, V. O fauni marinskog miocena i o tortonskom šliru Medvednice (Zagrebačke gore) [Ueber die Fauna des marinen Miozäns und über den Tortonischen “Schlier” von Medvednica (Zagreber Gebirge)]. Geološki Vjesnik 1957, 10, 39–50. [Google Scholar]
- Sokač, A. Panonska fauna ostrakoda Donjeg Selišta jugozapadno od Gline (Pannonische Ostrakodenfauna von Donje Selište südwestlich von Glina). Geološki Vjesnik 1963, 15, 391–401. [Google Scholar]
- Prlj Šimić, N.; Sremac, J.; Ćosović, V. Taxonomy and Biometry (Applied to the Eocene Corals from the Island of Krk –Croatia). 1st Croatian Geological Congress; Abstracts Book. 1995, pp. 495–498. Available online: http://geol.pmf.hr/~jsremac/radovi/znanstveni/1995_opat_koralji.pdf (accessed on 14 May 2020).
- Pezelj, Đ.; Sremac, J.; Sokač, A. Palaeoecology of the Late Badenian foraminifera and ostracoda from the SW Central Paratethys (Medvednica Mt., Croatia). Geol. Croat. 2007, 60, 139–150. [Google Scholar]
- Pezelj, Đ.; Sremac, J.; Bermanec, V. Shallow-water benthic foraminiferal assemblages and their response to the palaeoenvironmental changes—example from the Middle Miocene of Medvednica Mt. (Croatia, Central Paratethys). Geol. Carpathica 2016, 67, 329–345. [Google Scholar] [CrossRef]
- Pezelj, Đ.; Sremac, J. Badenian Marginal Marine Environment in the Medvednica Mt. (Croatia). Joannea Geol. Paläont. 2007, 9, 83–84. [Google Scholar]
- Pezelj, Đ.; Drobnjak, L. Foraminifera-based estimation of water depth in epicontinental seas: Badenian deposits from Glavnica Gornja (Medvednica Mt., Croatia), Central Paratethys. Geol. Croatica 2019, 72, 93–100. [Google Scholar] [CrossRef]
- Hohenegger, J. Growth-invariant Meristic Characters Tools to Reveal Phylogenetic Relationships in Nummulitidae (Foraminifera). Turk. J. Earth Sci. 2011, 20, 655–681. [Google Scholar] [CrossRef]
- Hohenegger, J.; Torres-Silva, A.I. Growth-invariant and growth-independent characters in equatorial sections of Heterostegina shells relieve phylogenetic and paleobiogeographic interpretations. Palaios 2017, 32, 30–43. [Google Scholar] [CrossRef]
- Eder, W.; Hohenegger, J.; Briguglio, A. Test flattening in the larger foraminifer Heterostegina depressa: Predicting bathymetry from axial sections. Paleobiology 2018, 44, 76–88. [Google Scholar] [CrossRef]
- Harzhauser, M.; Landau, B. A revision of the Neogene Conidae and Conorbidae (Gastropoda) of the Paratethys Sea. Zootaxa 2016, 4210, 001–178. [Google Scholar] [CrossRef]
- Bošnjak, M.; Sremac, J.; Vrsaljko, D.; Aščić, Š.; Bosak, L. The Miocene “Pteropod event” in the SW part of the Central Paratethys (Medvednica Mt., northern Croatia). Geol. Carpathica 2017, 68, 329–349. [Google Scholar] [CrossRef]
- Derežić, I.; Bošnjak, M.; Sremac, J. Biostatistic analyses of newly found pteropods (Mollusca, Gastropoda) in the Middle Miocene (Badenian) deposits from the southeastern Medvednica Mt. (Northern Croatia). In Mathematical Methods and Terminology in Geology; Malvić, T., Velić, J., Rajić, R., Eds.; Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb: Zagreb, Croatia, 2018; pp. 95–102. [Google Scholar]
- Šeparović, A. Miocene Deposits with Scaphopods South from Veternica Cave (Medvednica). Master’s Thesis, University of Zagreb, Faculty of Science, Zagreb, Croatia, 2019; pp. 1–66. [Google Scholar]
- Kowalewski, M. The Fossil Record of Predation: An Overview of Analytical Methods. In The Fossil Record of Predation; Kowalewski, M., Kelley, P.H., Eds.; Paleontological Special Papers, 8; Yale University: New Haven, CT, USA, 2002; pp. 3–42. [Google Scholar]
- Zell, P.; Beckmann, S.; Stinnesbeck, W. Liostrea roemeri (Ostreida, Bivalvia) attached to Upper Jurassic ammonites of northeastern Mexico. Palaeobio Palaeoenv 2014, 94, 439–451. [Google Scholar] [CrossRef]
- Curman, D. Digital Model Analysis of Theropod Footprints from Solaris Tracksite (Istria). Master’s Thesis, University of Zagreb, Faculty of Science, Zagreb, Croatia, 2017; pp. 1–72. [Google Scholar]
- Dalla Vecchia, F.M. Remains of Sauropoda (Reptilia, Saurischia) in the Lower Cretaceous (Upper Hauterivian/Lower Barremian) limestones of SW Istria (Croatia). Geol. Croat. 1998, 51, 105–134. [Google Scholar]
- Mezga, A.; Cvetko Tešović, B.; Bajraktarević, Z.; Bucković, D. A new dinosaur tracksite in the late Albian of Istria, Croatia. Riv. Ital. Paleontol. Stratigr. 2007, 113, 139–148. [Google Scholar]
- Mezga, A.; Cvetko Tešović, B.; Pretković, V.; Jovanović, N.; Bajraktarević, Z. Dinosaur footprints in the Lower Hauterivian deposits of Palud Cove in Istria, Croatia. Geol. Croat. 2015, 68, 113–122. [Google Scholar] [CrossRef]
- Costa-Pérez, M.; Joaquín Moratalla, J.; Marugán-Lobón, J. Studying bipedal dinosaur trackways using geometric morphometrics. Palaeontol. Electron. 2019, 22, 1–13. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).