Abstract
Shear tests on quartz rocks and single quartz crystals have been conducted to understand the possible relationship between the intensity of detectable stress in fault areas and the energy released in the form of electromagnetic waves in the range 30 KHz-1 MHz (LF–MF). For these tests, a new type of piston-cylinder has been developed, instrumented to collect the electromagnetic signals generated by the quartz during shear stress tests and that allows energy measurements on electromagnetic emissions (EMR) to be performed. The data obtained indicate that shear-stressed quartz crystals can generate electromagnetic emissions in the LF–MF range. These emissions represent a tiny fraction of the total energy dissipated in the fracturing process. The spectrum of radio emissions consists of continuous radiation and overlapping peaks. For the first time, a characteristic migration of peak frequencies was observed, proportional to the evolution of the fracturing process. In particular, the continuous recording of the radio emission spectra shows a migration of the peaks toward higher frequencies, as stress continues over time and smaller and larger fractures form. This migration could be used to distinguish possible natural signals emitted by quartz in tectonically active environments from possible signals of other geophysical and possibly anthropogenic origin.
1. Introduction
Electromagnetic emission monitoring (EMR) has long been proposed for earthquake forecasting–oriented research [1]. However, there is a possibility that the recorded signals are not of tectonic origin but may be produced by other processes of geophysical [2,3] or anthropogenic [4] origin, so it seems appropriate to develop investigation techniques that allow us to distinguish the origin of the signal by tracing, where possible, any signatures characteristic of signals of a different origin from the tectonic one. Research of this type is made possible by laboratory simulations of natural phenomena [5,6,7,8]. In particular, previous laboratory experiments have allowed us to verify that EMR induced by mechanical stress on rocks and single crystals are emitted over a very wide energy spectrum, with frequencies ranging from a few Hz to heat emissions in thermal infrared and optical band emissions in visible and UV [2,9,10] and, for some solids, in the X-ray range [11]. These emissions bring with them a series of useful information to understand, in a remote and non-invasive way, what happens inside rocky bodies and crystals and, in particular, the state and size of the fractures, the degree of plastic deformation suffered, and more [12,13]. Consequently, it is crucial to understand which fingerprints are from EMR from stress, connected with deformation processes of the earth’s crust, even of a possible precursor of seismic events, discriminating them from other emissions of natural and human origin. The solid compounds are broken down by the extension of the microfractures, already present inside the gratings, through relaxing efforts, until they are separated into smaller fragments. In general, to obtain the reduction of crystals, the application of a tensile stress is more effective than that of a compressive nature [14,15]. In order to cause the reduction of minerals, the energy supplied is consumed not only in the opening of new crack surfaces, through the breaking up of atomic bonds, but also in the plastic deformation of the reticular regions around the crack tip: part of the fracture energy is dissipated to create a permanent deformation of the crystal lattice, with the consequent formation of amorphous zones around the crack tip [14,15,16,17] and, in part, re-emitted as EMR.
2. Experimental Study
The aim of this work is to improve our understanding of the spectral characteristics of the signals generated by quartz crystals subjected to shear stresses, in order to correlate the intensity of the stress with the morphological quantities and the electromagnetic radiation emitted during the formation of the new fracture surfaces. In the same period, other minerals were also tested in order to verify the difference in intensity and spectral characteristics of the triboemissions of quartz and other solid phases subjected to the same stresses. An image illustrating some preliminary results has been included in the Supplementary materials (Figure S2 of Supplementary Materials). For these purposes, equipment capable of crushing mineral samples has been developed, together with a system for the detection and recording of electromagnetic emissions. The system developed to analyze the signals coming from the fracturing of minerals is a “piston-cylinder” consisting of a Teflon cylinder and two steel pistons. Tensile stresses are produced on the crystals by the effect of the different strength of Teflon compared to steel. Pistons and Teflon form a 100 pF capacitor, where the dielectric is made up of the Teflon, the material under test and the air. The prevalence of Teflon compared to the material inserted in the cylinder (quartz powder) and to the air leads to a high stability of the electric capacity of the piston cylinder (Table 1). The measurement system has been developed taking into account similar systems published in the past by different authors—for example, the ultrafast load cell (UFLC) system that was designed to investigate the effects of an impact on individual particles and on the fracturing energy of individual crystals [18,19,20]. The non-invasive measurement system of electromagnetic emissions from the piston cylinder has already been described in the paper [21]. A 580 μH inductance is wound around the Teflon cylinder and connected in parallel to the pistons, thus forming an “LC” resonant circuit. A second 580 μH inductance, wound on the first, forms the receiving circuit. The receiving circuit is connected to the recording circuit, consisting of three devices: an external professional sound card for low frequency, from 20 Hz to 96 kHz, (Steinberg UR 242, Steimberg Media Technology Gmbh, Germany); two software-defined radio (SDR) cards for the reception of the LF, MF, and HF bands, from 0.096 to 10 MHz (AIRSPY MF+ and SDR1A) (Figure S1 of Supplementary Materials). The different impedances between the low and high-frequency recording circuit were decoupled through a MOSFET stage with unitary gain (source follower). In this circuit, the input impedance is very high, higher than MΩ, while the output impedance is very low, around 50 Ω. Signal analysis, such as amplitude and frequency analysis, was carried out using Sigview 2.8 software (SignalLab e.K.: Berlin, Germany). The piston-cylinder was previously characterized from the electrical point of view through the analysis of capacitive and inductive impedance, both vacuum and loaded with 1 g of quartz, using a measuring bridge (LCR Philips Fluke PM 6304, Fluke Corp. Washington, USA); the frequency response of the coil and electrical data of the piston-cylinder are summarized in Figure 1 and Table 1. Spectral response correction was performed by software, using the characteristic curve obtained during calibration. Quartz samples were selected in the weight range from 0.05 g to 1.5 g by weight. The test products (powders) were analyzed by shape, size, area, and volume using the Malvern Morphology G3ID (Malvern Panalytical, Malvern UK), image analysis system based on scanning optical microscopy. The measurement of the stresses obtained in the experimental device was performed using a pressure-sensitive film (Pressurex Sensor film, Sensor Products Inc. USA) [21]. The number of charges involved is first calculated:
where Q is the number of charges, R is the input impedance of the measuring system, integrated in the t1 – tn measuring interval. The energy emitted as electromagnetic radiation (Em), expressed in J is
where Em is the energy emitted in the t1-tn measuring interval, V is the amplitude of peaks read one by one and Q is the number of charges. This energy is subdivided by the weight of the sample and then expressed as specific radiated energy, expressed in J/g. The energy fed into the measuring system is expressed as compression work,
where P is the weight force exerted on the crystal [kg] and h is the height of the crystal or of the material placed between the two pistons, calculated from the morphometric data of the samples as they are. The free surface energy of the fractures, Efr, is calculated using the product between the new area produced by the cracks, analyzed by the observation of the particles and the free surface energy of the quartz, equal to 2678 J/m2 [14]. The shredding efficiency is equal to the percentage ratio between the surface energy and the total energy input,
where η is the efficiency of comminution in percentage [16]. Data on electrical signals and energy parameters collected from measurements are collected in Table S1 of Supplementary Materials.
Etot = P × Δh [J]
η =100 × Efr/Etot, [%]

Table 1.
Electrical parameters of piston cylinder apparatus at different frequencies. L—inductance, C—electrical capacity.
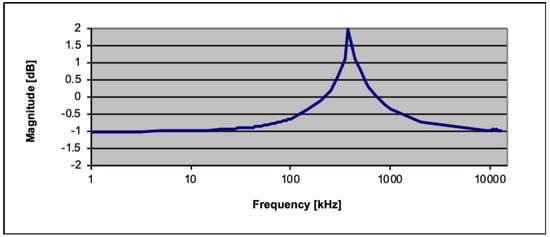
Figure 1.
Frequency response of antenna coil vs. frequency from 1 kHz to 10 MHz.
3. Results
The crushing of the quartz in the piston-cylinder generates pulses, which have a frequency spectrum dispersed from a few Hz to tens of MHz. We have been able to verify that quartz is tens of times more active in triboemissions than calcite and silica glass (Figure S2 in Supplementary Materials).The spectral analysis of the quartz signals, obtained by Fast Fourier Transform (FFT), shows a spectrum composed of “bursts” of various frequencies and their corresponding harmonics superimposed on a continuous noise (Figure 2). In LF and MF recordings, there are dozens of events of varying intensity, and the most intense of these correspond to the early stages of compression and fracture, when the fractures are still of centimeter lenghts. In FFT graphics, the X axis is time and the Y axis is frequencies. Signal strength is marked by a more or less bright color. These images show vertical traces, which represent the multifrequency pulses corresponding to the fracture moments and horizontal traces which represent particular frequencies at which the signal is more intense, which tend to migrate during the fracture. Migration is due to the change in the width of the fracture due to the fragmentation of the crystals into increasingly smaller portions.
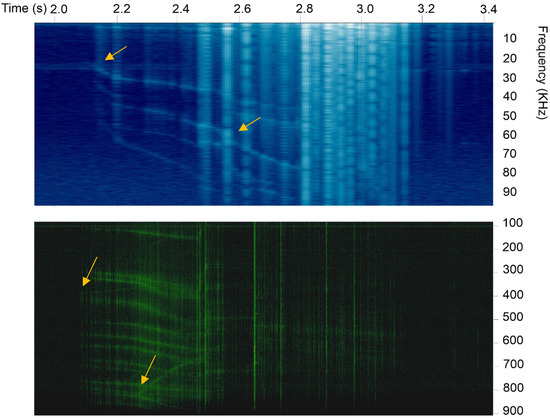
Figure 2.
Fast Fourier Transform (FFT) of LF signal (up) and MF signal (down) from quartz under stress; arrows indicate the dichotomies of fractures.
The frequency spectrum generated by these events, analyzed by FFT, propagates from a few Hz to over 10 MHz. A subdivision of the peaks into two and more orders is also observed (Figure 2).
In Figure 3, the quantities of energy emitted in the LF and MF ranges are compared with the surface of the granules generated by the fractures. From the energy analysis of the signals, it can be easily deduced that the primary emissions are concentrated in the MF range. Emissions in LF express energies that are, on average, two orders of magnitude lower than those in MF and may be due to harmonics of the primary emissions. We compared the energy fed into the piston-cylinder as compression work with the values of radiant energy and the values of fracture surface free energy. We evaluated the fracturing performance of the piston-cylinder between 0.03% and 0.4% of the energy input; the energy emitted as EMR radiation in the LF bands is eight orders of magnitude lower than the energy input, while the EMR radiation in the MF band is seven orders of magnitude lower than the energy input.
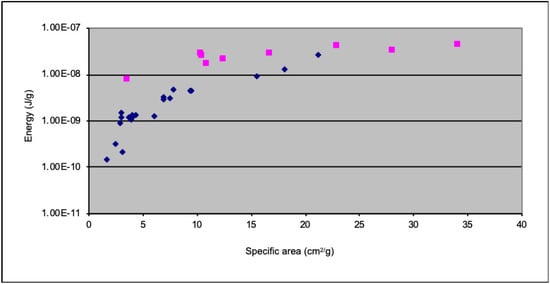
Figure 3.
Low frequency (blue) and medium frequency (pink) emission energy (J/g) vs. specific surface area of quartz samples (cm2/g).
4. Discussion of Data
Electromagnetic emissions in LF and MF bands were analyzed in frequency and amplitude and correlated with various physical parameters of the material, detected by the image analysis of quartz granules. EMRs consist of a spectrum of lines superimposed on a continuous spectrum consisting of electronic noise. The line spectrum is measured over a range from a few Hz to at least 30 MHz, with a decreasing energy trend, but with maximum energy placed in the range MF, from 100 kHz to 1 MHz. Rapid migration of the central frequencies of the emission peaks has been noted as the fracture proceeds. According to references [12,13], the emission frequencies expressed as pulsations (rad/sec) ω, are inversely correlated to the width of the fracture “b” [m], according to the relation
where vel is the speed of Rayleigh, which has a value of 3158 m/s (for quartz [14]). Given the relationship between the emission frequency and the size of the fractures, it can be easily deduced that the shift of the emission frequencies towards higher frequencies is due to the reduction in the size of the fractures and therefore of the granules generated. As the granules become smaller, the width of the fractures tends to decrease, as does their length. As a result, the frequency increases, and the amplitude of peak emissions decreases. Using the model developed by [17], we can assimilate fractures to capacitors placed in series and parallel to each other. In this model, the signal is born from the resonance created by the individual capacitors (single fractures) that generate oscillations at high frequencies (from 100 kHz up to a few MHz) and one or more peaks at lower frequencies that result from the harmonics and some resonance of the overall capacity that is created (< 100 kHz). In the tests carried out on the single crystals, the extension of the stress determines the fracturing into smaller and smaller granules, detached from each other, and this determines a rapid migration of the frequencies of the peaks towards higher. The intensity of the EM emissions gradually decreases as the particle size (and the structural order) decreases until it disappears.
ω = πvel/b
In EM signal recordings from quartz crystals, we have frequently verified the multiplication of signals during the fracturing process. These peak multiplications derive directly from subdivisions of fractures; from a first fracture (first order) two or more shorter fractures are generated and so on.
Under the electron microscope, we have shown that the subdivisions of the fractures are marked by angles between the mother fracture and the daughters’ fractures of about 27°, as foreseen by [14] for quartz (Figure 4). Finally, the amplitudes of the electric fields available between the walls of the fractures of the various monocrystals were calculated, which we can estimate from a few thousand V/m (for 250 μm of fracture width) to hundreds of thousands of volts/m (for a few μm of fracture width). An electric field of this magnitude could also be responsible for the luminescence that quartz can generate when rubbed, ground, or fractured [22,23]. The frequencies of EM fracture emissions, produced here by stressed and crushed quartz crystals, are compatible with the electromagnetic radiation ranges that can be transmitted through low conductivity rocks [24,25,26,27,28].

Figure 4.
Dicotomies of fractures on quartz particles (Composite image 2500 X) SEM—Zeiss EVO MA 10, Zeiss Germany.
On the other hand, in order to understand if these signals can actually travel for tens of kilometers and be received on the earth’s surface, important insights will be needed, in particular on the role that rocks with different conductivity can play as a “waveguide” for these ranges of electromagnetic signals.
Finally, we want to talk about the piezoelectric effect of quartz. As is known, alpha quartz is a mineral that has the ability to generate extremely intense electric fields due to mechanical deformations. The effect occurs on the crystals as long as it remains in an elastic regime; when the crystal exceeds this condition because it breaks, or deforms to the point of considerably reducing crystallinity, or exceeds the alpha-beta inversion point at 573 °C and becoming beta quartz, these effects weaken and disappear [29,30,31]. In the case we have studied, triboelectric signals are independent of the piezoelectric effect, in that they are electrical signals that occur during and immediately after the crystal fracture. This is the reason why, in discussing the data obtained, we cannot invoke the piezoelectric effect to justify the signals emitted in the fracture. In any case, the role of the piezoelectric effect will have to be studied in order to understand the pre-fracture effects, which we plan to do in the near future. As regards the applicability of the detection of triboemission signals to the analysis of the fracture process, the creation of a protocol that uses only quartz is limiting, since this mineral is very frequent, but not ubiquitous. For now, the only applicability for the technique we have developed is the remote detection of stress in quartz-rich rocks, such as in granites, gneiss, and in all rocks that contain more than 10% of quartz.
About the discussion on the fracture process down to the microscopic level, we want to mention a phenomenon which can be of great use in understanding connected phenomena. It concerns what happens to solid and brittle material with the advancement of fractures. The “breaking point” advances estimated at around 1297 m/s [14]. Fractures such as those shown in Figure 4 of the work have an average length, before at a speed approaching, from 50% to 70%, at the maximum critical speed, which for quartz has been the bifurcations, of about 25 μm. This means that the advance lasted 3.8 × 10−8 s. In this very short period, the advancement of the crack tip could not have generated anything but an adiabatic transformation and the temperature inside the fracture reached extraordinarily high levels, so as to melt the interposed material. This has been observed by several authors on various minerals. Some Authors [32,33] observed the propagation of the fracture in quartz crystals with optical spectrometers; calculated the final temperature, which exceeded 1700 °C. As a consequence of this heating, a melting flash is generated and the density of the molten material decreases, corresponding to an increase in volume. In fact, from the SEM images (Figure 4) it is noted that the fractures form a ridge with respect to the surface: in Figure 4 particle of about 100 × 100 μm is observed, with a thickness of about 15 μm, on whose surface there are various fractures, which they tend to bifurcate several times, forming ridges between a few tens of nm in height, up to 0.7 μm at the first bifurcation. These micro-melting determine the formation of new materials, which could influence the sliding in a still unknown way.
5. Conclusions
Experience has shown that quartz crystals generate electromagnetic emissions in the LF–MF range, linked in intensity and frequency to the surface created by the fractures and to the distance between the walls of the fractures. The energy balance indicates that the amount of energy emitted as electromagnetic radiation in the LF–MF range represents a small fraction of the energy intake (between seven and eight orders of magnitude less). The continuous recording of the emission signals shows a migration of the frequencies of the peaks towards higher values, as the stress is prolonged over time. This phenomenon may be due to the decrease in granule size and fractures as stress increases. It is still premature to say whether these phenomena can be used as premonitory for seismic events, although the electric fields generated by the electromagnetic emissions of quartz are very intense, and their frequencies could, in principle, be compatible with the transmission through geological barriers of tens of kilometers in depth. Furthermore, we still do not know if all or only a part of the minerals that make up the rocks are subject to the same phenomenon. For the moment we have highlighted that quartz translates stress in the form of electromagnetic impulses in an extremely efficient way and this makes it a natural “sensor” that can be used in the determination of the states of tension of rocks, as well as in building structures or in monitoring landslides. Furthermore, the spectral characteristics of the triboemissions from quartz could help to discriminate these signals from any other signal of other geophysical origin or even of possible anthropogenic origin.
Supplementary Materials
The Supplementary Material for this article can be found online at: https://www.mdpi.com/2076-3263/10/4/140/s1.
Author Contributions
G.M. supervised the experimental procedures and interpreted data. P.P. engineered the utilized equipment and interpreted the data. E.T. obtained the experimental data and improved the utilized equipment. All authors have read and agreed to the published version of the manuscript.
Funding
Present research was supported by Project FESR 2007-2013 RECAT (recovery of spent catalyst) (P.P. and E.T.). GM was partially supported by the Chinese Academy of Sciences visiting Professorship for Senior International Scientists (2018VMA0007).
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could result in a potential conflict of interest.
Data Availability
All data discussed in this study are supplied in the main text and in Supplementary Tables.
References
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Carpinteri, A.; Borla, O. Fracto-Emissions as seismic precursors. Eng. Fract. Mech. 2017, 177, 239–250. [Google Scholar] [CrossRef]
- Hayakawa, M.; Asano, T.; Rozhnoi, A.; Solovieva, M. Very-Low to Low-Frequency Sounding of Ionospheric Perturbations and Possible Association with Earthquakes. In Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; Geophysical Monograph 234; Wiley-AGU: Hoboken, NJ, USA, 2018; pp. 273–304. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Minadakis, G.; Eftakias, K. Analysis of electromagnetic pre-seismic emissions using Fisher information and Tsallis entropy. Phys. A Stat. Mech. Appl. 2012, 391, 300–306. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D.; Tzanis, A.; Anastasiadis, C.; Stavrakas, I. Electric earthquake precursors: From laboratory results to field observations. Phys. Chem. Earth Parts A/B/C 2004, 29, 339–351. [Google Scholar] [CrossRef]
- Di Toro, G.; Hirose, T.; Nielsen, S.; Pennacchioni, G.; Shimamoto, T. Natural and Experimental Evidence of Melt Lubrication of Faults during Earthquakes. Science 2006, 311, 647–649. [Google Scholar] [CrossRef]
- Freund, F.T.; Takeuchi, A.; Lau, B.W.S. Elastic currents streaming out of stressed igneous rocks- A step towards understanding pre-earthquake low frequency EM emissions. Phys. Chem. Earth 2006, 31, 389–396. [Google Scholar] [CrossRef]
- Cress, G.O.; Brady, B.T.; Rowell, G.A. Sources of electromagnetic radiation from fracture of rock samples in the laboratory. Geophys. Res. Lett. 1987, 14, 331–334. [Google Scholar] [CrossRef]
- Enomoto, Y.; Hashimoto, H. Emission of charged particles from indentation fracture of rocks. Nature 1990, 346, 641–643. [Google Scholar] [CrossRef]
- O’Keefe, S.G.; Thiel, D.V. Mechanism for the production of electromagnetic radiation during fracture of brittle materials. Phys. Earth Planet. Inter. 1995, 89, 127–135. [Google Scholar] [CrossRef]
- Camara, C.G.; Escobar, J.V.; Hird, J.R.; Putterman, S.J. Correlation between nanosecond X-ray flashes and stick–slip friction in peeling tape. Nature 2008, 455, 1089–1092. [Google Scholar] [CrossRef]
- Rabinovitch, A.; Frid, V.; Bahat, D.; Goldbaum, J. Fracture area calculation from electromagnetic radiation and its use in chalk failure analysis. Int. J. Rock Mech. Min. Sci. 2000, 37, 1149–1154. [Google Scholar] [CrossRef]
- Goldbaum, J.; Frid, V.; Bahat, D.; Rabinovitch, A. An analysis of complex electromagnetic radiation signals induced by fracture. Meas. Sci. Technol. 2003, 14, 1839–1844. [Google Scholar] [CrossRef]
- Tromans, D.; Meech, J.A. Fracture toughness and surface energies of minerals: Theoretical estimates. Miner. Eng. 2002, 17, 1–15. [Google Scholar] [CrossRef]
- Tromans, D. Mineral comminution: Energy efficiency considerations. Miner. Eng. 2008, 21, 613–620. [Google Scholar] [CrossRef]
- Fuerstenau, D.W.; Abouzeid, A.Z.M. The energy efficiency of ball milling in comminution. Int. J. Min. Process. 2003, 67, 161–185. [Google Scholar] [CrossRef]
- Rumpf, H. Physics aspects of comminution and new formulation of a law of comminution. Powder Technol. 1973, 7, 21–26. [Google Scholar] [CrossRef]
- Tavares, L.M.; King, R.P. Single particle fracture under impact loading. Int. J. Miner. Process. 1998, 54, 1–28. [Google Scholar] [CrossRef]
- Tavares, L.M. Optimum routes for particles breakage by impact. Powder Technol. 2004, 142, 81–91. [Google Scholar] [CrossRef]
- Tugcam Tuzcu, E.; Rajamani, R.K. Modeling breakage rates in mills with impact energy spectra and ultra fast load cell data. Miner. Eng. 2011, 24, 252–260. [Google Scholar] [CrossRef]
- Plescia, P.; Tempesta, E. Analysis of Friction coefficient in a vibrating cup mill (ring mill) during grinding. Tribol. Int. 2017, 114, 458–468. [Google Scholar] [CrossRef]
- Aman, S.; Tomas, J.; Chaikina, M. Structure modification and Mechanoluminescence of Quartz. Chem. Sustain. Dev. 2005, 2, 125–130. [Google Scholar]
- Thériault, R.; St-Laurent, F.; Freund, F.T.; Derr, J.S. Prevalence of Earthquake Lights Associated with Rift Environments. Seismol. Res. Lett. 2014, 85, 159–178. [Google Scholar] [CrossRef]
- Bremmer, H. Terrestrial Radio Waves; Elsevier: Amsterdam, The Netherlands, 1949. [Google Scholar]
- Field, F.C.; Dore, M. Electromagnetic Communication in the Earth’s Crust, Pacific-Sierra Research Corp. Santa Monica, California. Available online: https://pdfs.semanticscholar.org/e89c/d0080beeb48d686bc66cece92372154e9fef.pdf (accessed on 11 April 2020).
- Hermance, J.F. Electrical Conductivity Models of the Crust and mantle. In Global Earth Physics A Handbook of Physical Constants; American Geophysical Union: Washington, DC, USA, 1995; Volume 1. [Google Scholar] [CrossRef]
- Wheeler, H. Radio-Wave propagation in the Earth’s Crust. J. Res. Natl. Bur. Stand. Sect. D Radio Propag. 1961, 65, 189. [Google Scholar] [CrossRef]
- Safari, A.; Akdoğan, K.A. Piezoelectric and Acoustic Materials for Transducer Applications; Springer: Boston, MA, USA, 2008. [Google Scholar]
- Brice, J.C. Crystals for quartz resonators. Rev. Mod. Phys. 1985, 57, 105–146. [Google Scholar] [CrossRef]
- Cambon, O.; Haines, J.; Keen, D.A.; Tucker, M.G.; Dove, M.T. Structural disorder and loss of piezoelectric properties in a-quartz at high temperature. Appl. Phys. Lett. 2002, 81, 2968–2970. [Google Scholar]
- Cambon, O.; Haines, J.; Fraysse, G.; Keen, D.A.; Tucker, M.G. Piezoelectric properties at high temperature in a-quartz materials. J. Phys. Colloq. 2005, 126, 27–30. [Google Scholar] [CrossRef]
- Weichert, R.; Schonert, K. Heat generation at the tip of a moving crack. J. Mech. Phys. Solids 1978, 26, 151–161. [Google Scholar] [CrossRef]
- Pandey, K.N.; Chand, S.N. Analysis of temperature distribution near the crack tip under constant amplitude loading. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 316–326. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).