Abstract
In this paper an elastic settlement analysis method for rigid rectangular footings applicable to both clays and sands is proposed. The proposed method is based on the concept of equivalent shape, where any rectangular footing is suitably replaced by a footing of elliptical shape; the conditions of equal area and equal perimeter are satisfied simultaneously. The case of clay is differentiated from the case of sand using different contact pressure distribution, whilst, additionally, for the sands, the modulus of elasticity increases linearly with depth. The method can conveniently be calibrated against any set of settlement data obtained analytically, experimentally, or numerically; in this respect the authors used values which have been derived analytically from third parties. Among the most interesting findings is that sands produce “settlement x soil modulus/applied pressure” values approximately 10% greater than the respective ones corresponding to clays. Moreover, for large Poisson’s ratio (v) values, the settlement of rigid footings is closer to the settlement corresponding to the corner of the respective flexible footings. As v decreases, the derived settlement of the rigid footing approaches the settlement value corresponding to the characteristic point of the respective flexible footing. Finally, corrections for the net applied pressure, footing rigidity, and non-elastic response of soil under loading are also proposed.
1. Introduction
The problem of settlement of shallow foundations is among the more important ones in classical soil mechanics. During the last several decades a great number of approaches has been proposed in the literature for the title problem, an exact solution of which is still not available. In this respect, solutions have been provided by various authors [1,2,3,4,5,6,7,8,9,10,11]. Numerical results for perfectly smooth, uniformly loaded rectangular rafts, of any rigidity resting on a homogeneous elastic layer which is underlain by a rough rigid base, were presented in graphical form by Fraser and Wardle [12]. Semi-empirical approaches combining the theory of elasticity with experimental and/or numerical results also exist in the literature [13,14,15,16,17]. Schiffman and Aggarwala [18] and Mayne and Poulos [15] used the concept of equivalent ellipse and circle respectively (equivalency as for the footprint area).
In this paper an elastic settlement analysis method for rigid rectangular footings applicable to both clays and sands is proposed. The proposed method is based on the concept of equivalent shape, where any rectangular footing is suitably replaced by a footing of elliptical shape. The suitability of the equivalent shape concept is deeply investigated aiming at the production of analytical expressions for the elastic settlement analysis of rigid rectangular footings on sands and clays. As shown, this concept is only valid when the equivalent shape satisfies both the condition of equal area and equal perimeter length at the same time. The case of clay is differentiated from the case of sand using different contact pressure distribution, whilst the modulus of elasticity for the case of sands additionally increases linearly with depth.
2. Settlement of Rigid Elliptical Footing
Boussinesq [19] solved the problem of stresses produced at any point in a homogenous, elastic, isotropic, and semi-infinite medium as the result of a point load applied on the surface. Following the notation of Figure 1, the increase in normal stresses caused by the point load P is
where , and ν is the Poisson’s ratio (see [20,21,22]).
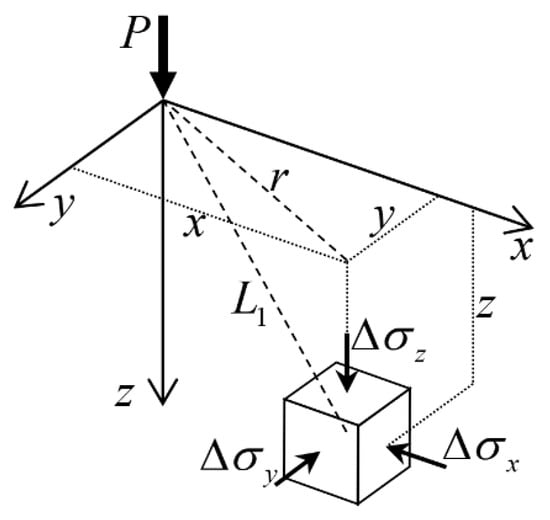
Figure 1.
Stresses in an elastic medium caused by a point load acting on the surface of a semi-infinite mass [23].
The above equations along with the equation effectively representing the contact pressure distribution leads to the elastic settlement of footing following a standard procedure (see [19,24]). In this respect, by using the following contact pressure distribution (see [18]):
The settlement of a rigid elliptical footing can be obtained in a way similar to the case of Boussinesq’s [19] rigid circular footing (see also [24]); where is the total load on the elliptical rigid footing (the origin of the axes lies on the centroid of the elliptical disc), whilst a and b are the two radii defining the ellipse.
The infinitesimal point load P at any point (x,y) inside the ellipse is, thus, given by
where
is the load per unit area of the footing.
Hence, the increase in the normal stress in the i-axis due to loading over the elliptical surface area can be found by integrating the respective stress increase (i = x, y or z) (see Equations (1)–(3)) over this area using Equation (5). That is:
Note that the differentials dx and dy are included in P (see Equation (5)). The integration can conveniently be done by changing to polar variables r and θ, setting and , where the ranges of the radial and angular variables, respectively, are and . For the area element in the polar variables then it stands that .
The unit vertical strain is, then, calculated from the constitutive relationship of Hooke’s Law:
and finally, the footing settlement, , corresponding to a layer of thickness H is
where
with and ; is the strain influence factor. The integration as for z can easily be implemented numerically in spreadsheet so that the effect of varying soil modulus with depth to be taken into account in a way similar to Schmertmann’s method [14].
In the case of homogenous semi-infinite mass, the settlement becomes:
where is the eccentricity of the ellipse and is the complete elliptic integral of the first kind [25]. Due to the fact that in the circular case (because and also, ), Equation (11) goes over to the well-known expression of Boussinesq [19,24]:
3. Elastic Settlement of the Equivalent Rectangular Footing
From the theory of elasticity for flexible footings over semi-infinite media, it is well known that the settlement at the center of a uniformly loaded square footing having edge B is approximately equal to the respective settlement of a circular footing of equal area (radius of footing equal to ) [26]; the percentage difference in settlement between these two special cases is only 0.53%.
The concept of shape equivalency has been used in the past by Mayne and Poulos [15], where any rectangular footing is reduced to a circular footing of equal area. The radius of Mayne and Poulos’ [15] equivalent circle is
Several years earlier, Schiffman and Aggarwala [18] suggested that the two radii defining the equivalent elliptical footing of a rectangular footing be
Schiffman and Aggarwala [18] considered the problem of an elastic half-space loaded on the surface by a rigid elliptical footing. They developed general formulae for the stresses and displacements within and on the surface of the solid. It is noted that Equation (14) derives from the condition of equal area and from ; the condition of equal perimeter is not satisfied.
Sovinc [8] worked analytically on the problem of settlement of smooth, rectangular footing resting on the surface of a finite layer with ν = 0.5, providing a “calibration platform” for the proposed method. He expressed the settlement of footing with respect of the long footing dimension, , as follows:
Unfortunately, Sovinc published vs. curves and not a closed-form expression for ; for readers’ convenience, these curves can be found in the freely available book of Poulos and Davis [27] (www.usucger.org/PandD/complete_book.pdf). Sovinc’s [8] values were compared by the authors against the respective values given by Butterfield and Banerjee ([10]; also in Poulos and Davis [27]) providing, in turn, the necessary validation of the “calibration platform” mentioned above. The results of these studies are in full agreement.
From the vs. comparison chart of Figure 2 it is clear that Schiffman and Aggarwala’s [18] equivalent shape (see Equation (14)) is not a reliable choice.
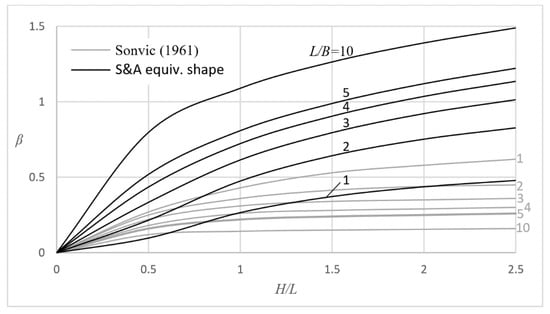
Figure 2.
Comparison chart between Sovinc’s [8] factor for rigid rectangular footing (ν = 0.5) and the respective one based on Schiffman and Aggarwala ([18]; denoted as S&A on the figure) equivalent ellipse.
The authors also considered the case of equivalent ellipse satisfying both the condition of area and perimeter. The area of the ellipse is exact and given by the expression . The perimeter is exactly given by , where is the complete elliptic integral of second kind [25]. This is a transcendental expression which can be calculated explicitly through infinite series. Instead, one may use Ramanujan’s approximate formula giving values very close to the exact perimeter values:
The two radii of the equivalent ellipse are then:
with .
The new equivalent shape gave vs. curves close to those given by Sovinc indicating the need for calibration with respect of the footing shape. The new factor referring to the equivalent rectangular footing is a function of the aspect ratio of footing, . The calibration against Sovinc’s [8] chart gave:
where
and = 1 m (unit width). The notation denotes the use of Equation (10) but replacing with
The expression for the settlement, thus, becomes
or, in the more familiar form,
with
and
The integral in Equation (23) requires numerical evaluation, which can be easily done using one of the numerous proprietary and non-proprietary mathematical programs available.
As shown is Figure 3, the new factor compares very well with Sovinc’s factor. Although, the proposed method was calibrated manually against Sovinc’s [8] dimensionless values, any set of relevant data could be used instead, while the procedure could be facilitated by the use of a statistical analysis program. The use of elastic settlement values derived from 3D finite element analysis is subject matter of work by the authors.
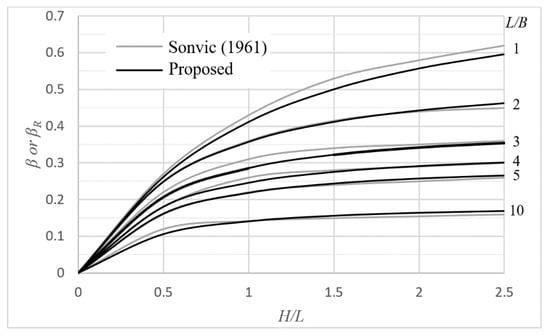
Figure 3.
Comparison chart between Sovinc’s [8] factor for rigid rectangular footing and the proposed ; all curves refer to ν = 0.5.
It is interesting that, Equations (19) and (20) contain the term , best known from the influence depth of footings proposed by Terzaghi et al. [28], i.e., zl = 2B(1 + log(L/B))
The effect of footing shape on the modulus of elasticity has not yet been considered in the analysis. In this respect, Terzaghi et al. [28] suggested that
with , where, the triaxial modulus of elasticity of soil. For , the ratio ranges between 1 and 1.4 for the axisymmetric and plane strain condition, respectively. Very recently, Pantelidis [29,30] showed that the correct relationship is
Thus, including the effect of footing shape on the modulus of soil, the footing settlement will be
The triaxial modulus of soil, , can be obtained by the triaxial compression test or continuous probing tests.
4. Elastic Settlement Analysis of Rigid Footings on Sands
The above formulations were based on the contact pressure distribution of Equation (4). This contact pressure of parabolic form, where the minimum and the maximum pressure value is found at the center and the edges of footing respectively (Figure 4a), is, however, more suitable for clays. For smooth rigid footings on clean sand, the minimum and maximum contact pressure are observed at the edges and the center of the footing respectively, as shown in Figure 4b [28,31].
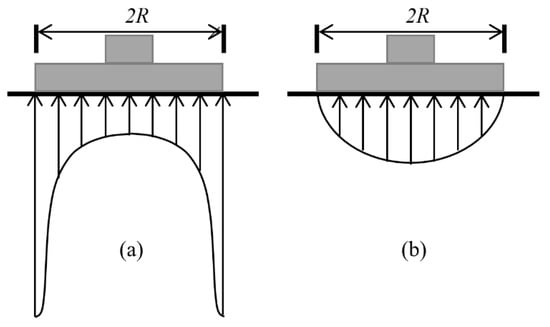
Figure 4.
Assumed contact pressure distribution of smooth rigid footing on (a) cohesive soil and (b) cohesionless soil.
Referring to an elliptical rigid footing over sand, the contact pressure distribution can be effectively represented by a half spheroid attached under the footing. The infinitesimal point load P in Equations (1)–(3) can, then, be expressed as follows:
In addition, as known sands are compacted under their own weight, where their modulus of elasticity usually appears to increase linearly with depth obeying Gibson’s law [32]:
where = the soil modulus directly beneath the foundation base (z = 0), = the rate of increase of modulus with depth (units of E per unit depth) and z = the depth having modulus . This has also been proved experimentally by the first author [29] performing a series of Dynamic Probing Light (DPL) tests on clean quarry sand. Indeed, this phenomenon occurs immediately after deposition and it is due to the increase of the density caused by the overburden mass in combination with the increased confinement at greater depths. In a similar manner, any surcharge on the surface of the sand material will have an analogous impact. In this respect, it was suggested [29] that
where γ is the unit weight of soil, σz = γz + qIσ and Iσ is the well-known stress influence factor; Iσ values for various footing shapes can be found in any soil mechanics book (e.g., [26]). Therefore, the settlement is given as follows:
The factor is calculated using the following equation (recall Equation (10))
with
and
whilst ζ must again be replaced by ζR (recall Equation (20)) as indicated in Equation (31). It is reminded that is given by Equation (19). The integral of Equation (34) has been transformed to polar variables with and for the sake of convenience. Unfortunately, the integral in Equation (34) requires numerical evaluation. For avoiding such a procedure, the term is given in chart form in Figure 5.
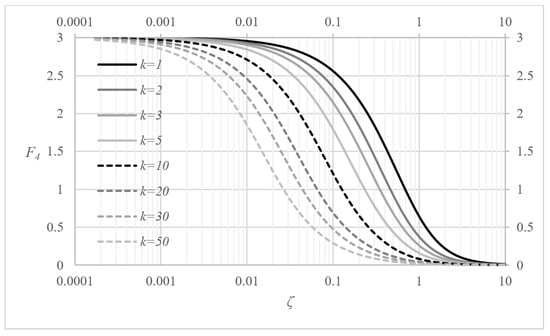
Figure 5.
Chart giving the factor with respect to ζ.
It is finally mentioned that, for the special case of and kE = 0 the factor can be obtained fully analytically (see Appendix A).
5. Other Factors Affecting Elastic Settlement of Shallow Foundations
The modulus of elasticity and in turn, the elastic settlement of shallow foundations may seriously be affected by various factors, such as the shape of the footing [29,30,33], the footing load (phenomenon occurring in sands; [29]), the embedment depth of footing [15,34,35,36,37,38], and a possible water table rise into the influence depth of footing [39,40,41,42,43,44,45,46,47,48]. Creep in sands may also affect the settlement of shallow foundations (see [13,28]). The rigidity of footing, the net applied pressure and the non-elastic response of the ground are also factors affecting settlement of shallow foundations for which corrections are suggested below.
5.1. Correction for Footing Rigidity
According to ACI Committee 336, DIN 4018 and IS 2950-1 [49,50,51], whether a foundation behaves as a rigid or a flexible structure depends on the relative stiffness of the structure and the foundation soil. The relative stiffness factor, , is given as follows:
where is the flexural rigidity of the superstructure and foundation per unit length at right angles to and is the modulus of concrete. An approximate value of per unit width of building can be determined by summing the rigidity of foundation, , the rigidity of beams, , and the rigidity of shearwalls, :
where and are the thickness and height of the shearwalls respectively (e.g., see [49,50,51,52]. Ignoring the effect of superstructure, the relative stiffness factor simplifies to
because , where, d is the thickness of foundation.
Alternatively, the expression including the Poisson’s ratio values can be used (e.g., see [53]):
Generally, the foundation is considered to be rigid when and flexible when (e.g., [51]). Based on the finite element analysis carried out by Brown [54] (see also [15]), however, a footing can be regarded as flexible if , rigid if and of intermediate rigidity if . Indeed, between the limits defining the intermediate condition, a linear relationship exists between and settlement [15]. In this respect, the following linear interpolation for calculating the settlement of footings (at the center) of intermediate rigidity is suggested:
where
is calculated using Equation (A7) (see Appendix B).
5.2. Correction for the Net Applied Pressure
When the structure lies at the bottom of excavation of depth , as usually this is the case, the settlement should be better calculated according to the following equation:
where the first resilient modulus of soil (it refers to the first reloading). An empirical relationship connecting E with the overconsolidation ratio (OCR) of soils could be used for the estimation of , e.g., Duncan and Buchignani’s [55] - - OCR chart for undrained clays (where and are the undrained modulus and the undrained cohesion respectively, and the plasticity index of soil; see also [56]) or Bowles’s [42] multiplier. According to Mayne and Kulhawy [57], the square-root of OCR is applicable for both sands and clays. In addition, for saturated overconsolidated clays subjected to unloading, Mesri et al. [58] observed that, in every case, the excess negative pore pressures is dissipated faster than predicted from the Terzaghi’s one dimensional consolidation theory; thus, Equation (41) could be used in every case.
The overconsolidation, here, is due to , which is excavated for placing the construction at depth . Alternatively, adopting the square root rule of Bowles [42], the first resilient modulus will be
and thus, Equation (41) simplifies to
with
By ignoring the term in brackets, that is, if is equal to , the calculated settlement is on the unfavorable side.
5.3. Non-Elastic Response of Soil under Loading
In reality, the soil medium response to loading is not elastic, even at low working stresses. Based on parametric finite element analysis, D’Appolonia et al. [59] proposed a correction factor to the settlement of perfectly flexible footings on saturated clays . An alternative and more general procedure is proposed below.
First, a load-settlement response is assumed, relying on the initial gradient of this relationship and the ultimate bearing capacity of the soil medium, , which are both known; a third (calibration) parameter is also necessary (this is discussed later). In a - diagram, the initial gradient of the curve is (with being a factor for taking into account e.g., the influence of the embedment depth, a possible water table rise etc.), whilst is calculated based on a well-established theory (in this respect, the formulations given in EN 1997-1 [60] could be used). In the case of stratified soil mediums, the equivalent modulus of soils concept shall be used (see [61]). Mathematically, the load-settlement response can be approximated by an equation of the form:
where is the plastic settlement of footing.
Equation (45) presents maximum at
Relating the plastic settlement at with the respective elastic one, i.e.,
from Equations (46) and (47)
where is the calibration parameter denoting how many times the plastic settlement at is greater than the respective elastic one (see Figure 6); takes values greater than or equal to 2.
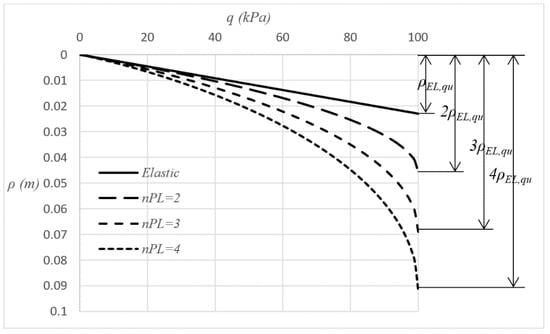
Figure 6.
Proposed approach for non-elastic response of soil; can be any positive real number greater than 2.
At the ultimate loading, from Equations (45), (46), and (48):
and solving the latter as for :
The parameter can be estimated based on (a) local experience, i.e., known measured settlements of neighbor structures, (b) plate bearing test data given that the soil and soil conditions are relatively homogenous with depth, or (c) 2D plastic finite element analysis by interpolating between the load-settlement response of the respective axisymmetric and plane strain problem (circular and strip footing both having radius and width respectively equal to B). The calibration should refer to similar loading conditions, i.e., drained or undrained.
The plastic settlement, , corresponding to q is, finally, obtained from Equation (45). The latter has two solutions, from which the smaller one is adopted. Depending on the value used, numerical approximation may be required.
An example q - chart referring to a 1 m × 2 m rigid footing lying on the surface of a semi-infinite homogenous clay soil with E = 5000 kPa and ν = 0.1 (drained conditions) is given in Figure 6. In this respect, four q - relationships were drawn, i.e., for perfectly elastic medium and for plastic medium with = 2, 3 and 4. The ultimate bearing capacity value (qu) is equal to 100 kPa. Moreover, the correction regarding the effect of footing shape on the modulus of soil (recall Equation (26)) was ignored in this example.
6. Comparison Examples
6.1. Comparison with Existing Methods and Approaches
The proposed method is compared with Mayne and Poulos’ [15] method, as well as with the “characteristic point” approach [62,63]. Third factors affecting settlement, such as the embedment depth, soil creep, are ignored, whilst the mass is considered to be semi-infinite and homogenous.
Since Mayne and Poulos’ method deals with footings of any rigidity, both the cases of perfectly flexible and perfectly rigid footing will be presented. The settlement values obtained from the theory of elasticity for both the center and the corner of footing, considering that the latter is perfectly flexible are presented as boundary values (the elastic settlement of the respective rigid footing should be an intermediate value). The average settlement of perfectly flexible footing is also given. All settlement expressions used are given in the Appendix B.
Regarding the so-called “characteristic point”, at this point the settlement of a flexible loaded area is considered to be the same as the uniform settlement of a rigid area, both having the same area and shape and bearing the same total load. In an ideally elastic soil, the characteristic point at a rectangular footing is located at distance and from the center [62,63,64,65]. What is not widely known, however, is that the above distances refer to the simple case of ν = 0 [62,63,66].
vs. curves are given for ν = 0.1 and 0.5; see Figure 7. These values were selected because, based on accurate measurements using local strain devices mounted midlevel on soil specimens and measured internally to the triaxial cell, the appropriate value of ν to use in elastic continuum solutions for drained loading is 0.1 < ν < 0.2 for all soil types [15,67,68,69]. For undrained conditions involving short-term loading of clays, it remains appropriate to use the value from isotropic elastic theory of ν = 0.5.
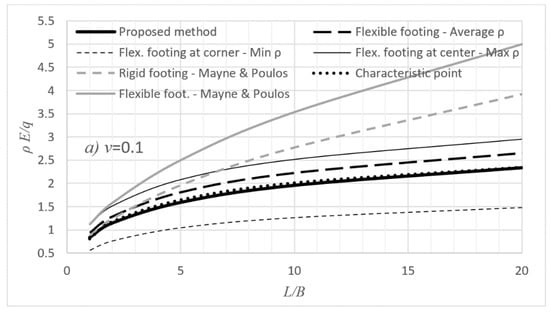
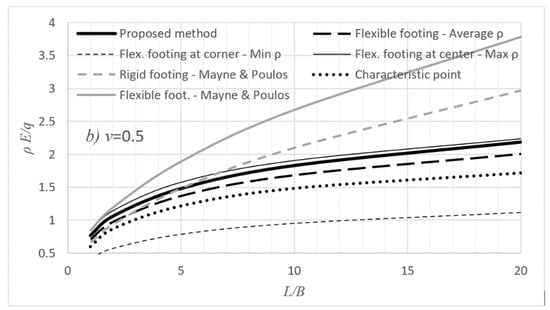
Figure 7.
Comparison example: (a) v = 0.1 and (b) v = 0.5.
From Figure 7 it is inferred that, Mayne and Poulos’ [15] method largely overestimates settlement (see also [70]); indeed, it gives settlement values for the rigid footing greater than the values corresponding to the center of the respective flexible footing (upper boundary). On the other hand, the vs. curves derived from the proposed method lie between the two boundary curves derived from the theory of elasticity, whilst moreover, they are parallel to these boundaries. In addition, the proposed − curve for ν = 0.1 compares well with the respective curve corresponding to the characteristic point. The latter can also be considered indicative of the success of the calibration of the proposed method. Furthermore, as shown in Figure 7, the average settlement curve overestimates settlement for small ν values and underestimates settlement for great ν values.
In addition, from Figure 8 it is inferred that for the same ν value, the term for the rigid footing on sand is greater than the respective one for the same footing on clay. The goal of Figure 8 is to compare the effect of the different contact pressure distributions, assuming the same E value, which is also constant with depth. In reality, E may vary with depth; this is usually observed in sands, where E increases with depth (Gibson profile [32]), even immediately after deposition [29]. It is also very interesting that, as shown in Figure 9, when the effect of footing shape on the modulus of elasticity of soil is considered in the analysis, the ratio of footing has, practically, minor effect on the derived settlement. In this respect, revisiting existing experimental and theoretical studies, Pantelidis [29,30] draw the conclusion that the elastic settlement appears to be independent of the aspect ratio of footing; it seems that the adverse effect of the second dimension of footing, which is responsible for the iso-stress bulbs to dive deeper into the ground, is compensated by the increase in E due to the increased confinement induced by the longer (and thus, greater) footprint of the footing. In this respect, he suggested that, the elastic settlement of a B × L footing be calculated considering a circular footing with diameter equal to B (or better, 2B/) and the bearing pressure q of the original problem. A problem, however, arises when soil medium is stratified. This can be solved by replacing the original stratified medium with an equivalent homogenous one having the same elastic constant values throughout its body. A reliable procedure for that is given by Pantelidis [33,61].
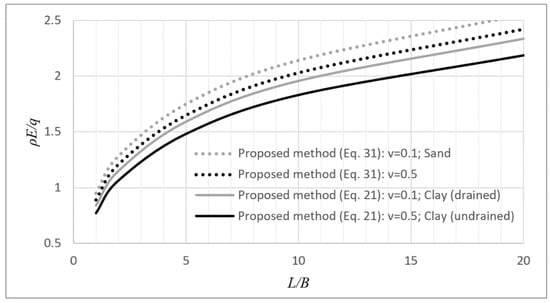
Figure 8.
Effect of the contact pressure distribution (simulating rigid footing on sands and clays) on .
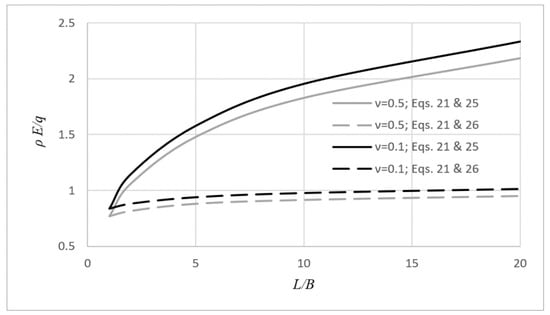
Figure 9.
Effect of footing shape on the modulus of soil and, in turn, on .
6.2. Comparison against 3D Finite Element Elastic Settlement Analysis
Fraser and Wardle [12] gave a complete elastic settlement example using 3D numerical analysis. They considered a square raft foundation with edge 10 m and thickness d = 0.5 m, lying on a soil medium of thickness 40 m. The raft is subjected to a uniform load of 0.1 MPa. The elastic constants of raft are Eb = 15,000 MPa and vb = 0.2, whilst the elastic constants of soil are E = 83.2 MPa and v = 0.3.
Following the proposed approach, the settlement of the raft considering that it is perfectly rigid is = 8.728 mm, whilst following Harr [71], the settlement at the center of the respective flexible footing is = 10.796 mm. Based on Equation (38), = 1.78, thus, the footing is of intermediate rigidity () with IF = 1.154 (Equation (40)). Therefore, the corrected settlement value is = 10.07 mm (Equation (39)), which compares very well with the 10.7 mm given by Fraser and Wardle. Applying Mayne and Poulos’ method, the settlement of the same footing is 8.71 mm (Mayne and Poulos’ factors: IE = 1, IF = 0.792 and IG = 0.89).
7. Summary and Conclusions
In this paper an elastic settlement analysis method for rigid rectangular footings applicable to both clays and sands has been proposed. The case of clay is differentiated from the case of sand using different contact pressure distribution, whilst, moreover, the modulus of elasticity for the case of sands increases linearly with depth. The proposed method is based on the concept of equivalent shape, where, any footing is suitably replaced by a footing of elliptical shape. The analysis showed that an equivalent ellipse returns satisfactory results only if the conditions of equal area and equal perimeter length are satisfied simultaneously. The equivalent area condition alone, as it has been shown, gives elastic settlement values that greatly differ from the respective values referring to the mother rectangular footing.
Herein, the derived equations were calibrated manually against Sovinc’s [8] dimensionless values. However, any set of relevant data could be used, while the procedure could be facilitated by the use of a statistical analysis program. The use of elastic settlement values derived from 3D finite element analysis is subject matter of work by the authors.
Among the most interesting findings is that sands produce “settlement x soil modulus/applied pressure” values approximately 10% greater compared to the respective ones corresponding to clays. Moreover, for large Poisson’s ratio (v) values, the settlement of a rigid footing is closer to the settlement corresponding to the center of the respective flexible footing. On the other hand, as v decreases, the derived settlement of the rigid footing approaches the settlement value corresponding to the characteristic point of the respective flexible footing; it is also noted that, the derived settlement value for small v values is smaller than the average settlement of the footing considering that the latter is perfectly flexible. Last but not least is that, considering the effect of footing shape on the modulus of soil, the settlement of rigid footings is rather insensitive to the L/B ratio. In this respect, it seems that the adverse effect of the second dimension of footing (the length L), which is responsible for the iso-stress bulbs to dive deeper into the ground, is compensated by the increase in the modulus of soil due to the increased confinement induced by the longer (and thus, greater) footprint of the footing. Thus, it is suggested that, the elastic settlement of a B × L footing be calculated considering a circular footing with diameter equal to 2B/ and the bearing pressure q of the original problem.
Finally, corrections for the net applied pressure, footing rigidity and non-elastic response of soil under loading are also offered. Regarding the net applied pressure, it has been shown that when the bearing pressure is used, the calculated settlement is on the unfavorable side; instead a new, yet simple expression is suggested, allowing for the first resilient modulus of the soil to be taken into account for structure loading equal to .
Author Contributions
Conceptualization, L.P.; methodology, L.P. and E.G.; software, L.P. and E.G.; validation, L.P. and E.G.; formal analysis, L.P. and E.G.; writing—original draft preparation, L.P. and E.G.; writing—review and editing, L.P. and E.G.; visualization, L.P. and E.G.; supervision, L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In spite of the difficulty to evaluate analytically F4 that would provide the β factor for arbitrary H, the β factor for can be obtained fully analytically by first integrating with respect to ζ and then with respect to θ:
where is the complete elliptic integral of the first kind, and i is the imaginary unit. Hence,
For the case of circular footing (k = 1) over sand, Equation (33) simplifies to
and by integrating the latter from z = 0 to H, we get the factor β
For Equation (A4) gives
and, thus, the settlement expression becomes
meaning that the term for a circular rigid footing on sands is by 50% greater than the respective one for clays.
Appendix B
Settlement under the corner and center of a (flexible) rectangular footing [71]
with , , and for the corner of the footing, whilst , , and for the center; z = 0 (and thus, n = 0) for the settlement on the surface of a homogenous, semi-infinite mass. For the settlement of footing underlain by a layer of finite thickness H, the principle of superposition stands, i.e., .
Average settlement of a (flexible) rectangular footing on semi-infinite homogenous mass [72]
with m as defined above.
Mayne and Poulos [15] expressed the settlement as follows:
where and 1 for perfectly rigid and perfectly flexible footing respectively, for foundation on the surface and for homogenous, semi-infinite mass. For more about the I-factors, please see the original publication [15].
References
- Noble, B. The numerical solution of the singular integral equation for the charge distribution on a flat rectangular plate. In Proceedings of the PICC Symposium on Differential and Integral Equations, Rome, Italy, 20–24 September 1960; Birkhäuser: Basel, Switzerland; Stuttgart, Germany, 1960; pp. 530–543. [Google Scholar]
- Borodachev, N.M.; Galin, L.A. Contact problem for a stamp with narrow rectangular base: PMM vol. 38, n≗ 1, 1974, pp. 125–130. J. Appl. Math. Mech. 1974, 38, 108–113. [Google Scholar] [CrossRef]
- Gorbunov-Possadov, M.; Serebrjanyi, R. Design of Structures on Elastic Foundations. In Proceedings of the Fifth International Conference on Soil Mechanics and Foundation Engineering, 17–22 July, 1961; Dunod: Paris, France, 1961; pp. 643–648. [Google Scholar]
- Borodachev, N.M. Contact problem for a stamp with a rectangular base: PMM vol. 40, n≗ 3, 1976, pp. 554–560. J. Appl. Math. Mech. 1976, 40, 505–512. [Google Scholar] [CrossRef]
- Mullan, S.J.; Sinclair, G.B.; Brothers, P.W. Stresses for an elastic half-space uniformly indented by a rigid rectangular footing. Int. J. Numer. Anal. Methods Geomech. 1980, 4, 277–284. [Google Scholar] [CrossRef]
- Brothers, P.W.; Sinclair, G.B.; Segedin, C.M. Uniform indentation of the elastic half-space by a rigid rectangular punch. Int. J. Solids Struct. 1977, 13, 1059–1072. [Google Scholar] [CrossRef]
- Panek, C.; Kalker, J.J. A solution for the narrow rectangular punch. J. Elast. 1977, 7, 213–218. [Google Scholar] [CrossRef]
- Sovinc, I. Displacements and inclinations of rigid footings resting on a limited elastic layer on uniform thickness. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering; Sociedad Mexicana de Mecanica: Mexico City, Mexico, 1961; pp. 385–389. [Google Scholar]
- Dempsey, J.P.; Li, H. A rigid rectangular footing on an elastic layer. Géotechnique 1989, 39, 147–152. [Google Scholar] [CrossRef]
- Butterfield, R.; Banerjee, P.K. A rigid disc embedded in an elastic half space. Geotech. Eng. 1971, 2, 35–52. [Google Scholar]
- Fabrikant, V.I. Flat punch of arbitrary shape on an elastic half-space. Int. J. Eng. Sci. 1986, 24, 1731–1740. [Google Scholar] [CrossRef]
- Fraser, R.A.; Wardle, L.J. Numerical analysis of rectangular rafts on layered foundations. Géotechnique 1976, 26, 613–630. [Google Scholar] [CrossRef]
- Schmertmann, J.H. Static cone to compute static settlement over sand. J. Soil Mech. Found. Div. 1970, 96, 1011–1043. [Google Scholar]
- Schmertmann, J.H.; Hartman, J.P.; Brown, P.R. Improved strain influence factor diagrams. J. Geotech. Geoenviron. Eng. 1978, 104, 1131–1135. [Google Scholar]
- Mayne, P.W.; Poulos, H.G. Approximate displacement influence factors for elastic shallow foundations. J. Geotech. Geoenviron. Eng. 1999, 125, 453–460. [Google Scholar] [CrossRef]
- Foye, K.C.; Basu, P.; Prezzi, M. Immediate Settlement of Shallow Foundations Bearing on Clay. Int. J. Geomech. 2008, 8, 300–310. [Google Scholar] [CrossRef]
- Lee, J.; Salgado, R. Estimation of footing settlement in sand. Int. J. Geomech. 2002, 2, 1–28. [Google Scholar] [CrossRef]
- Schiffman, R.L.; Aggarwala, B.D. Stresses and displacements produced in a semi-infinite elastic solid by a rigid elliptical footing. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; Dunod: Paris, France, 1961; Volume 1, pp. 795–801. [Google Scholar]
- Boussinesq, J. Application des Potentiels à L’étude de L’équilibre et du Mouvement des Solides Élastiques: Principalement au Calcul des Déformations et des Pressions que Produisent, dans ces Solides, des Efforts Quelconques Exercés sur une Petite Partie de Leur Surface; Gauthier-Villars: Paris, France, 1885; Volume 4. [Google Scholar]
- Das, B.M. Fundamentals of Geotechnical Engineering, 3rd ed.; Thomson-Engineering: Mobile, AL, USA, 2007; ISBN 10:0-495-29572-8. [Google Scholar]
- Hudson, J.A.; Harrison, J.P. Engineering Rock Mechanics: An Introduction to the Principles; Elsevier: Amsterdam, The Netherlands, 2000; ISBN 0080530966. [Google Scholar]
- Sadd, M.H. Elasticity: Theory, Applications, and Numerics; Academic Press: Cambridge, MA, USA, 2009; ISBN 0080922414. [Google Scholar]
- Pantelidis, L. Strain Influence Factor Charts for Settlement Evaluation of Spread Foundations based on the Stress–Strain Method. Appl. Sci. 2020, 10, 3822. [Google Scholar] [CrossRef]
- Kézdi, Á.; Rétháti, L. Soil Mechanics of Earthworks, Foundations and Highway Engineering, Handbook of Soil Mechanics; Elsevier: New York, NY, USA, 1988; Volume 3, ISBN 0-444-98929-3. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: North Chelmsford, MA, USA, 1965; Volume 55, ISBN 0486612724. [Google Scholar]
- Das, B.M. Shallow Foundations: Bearing Capacity and Settlement, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781315163871. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Elastic Solutions for Soil and Rock Mechanics; John Wiley: New York, NY, USA, 1991; ISBN 0471695653. [Google Scholar]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice; John Wiley: New York, NY, USA, 1996; ISBN 0471086584. [Google Scholar]
- Pantelidis, L. Elastic Settlement Analysis for Various Footing Cases Based on Strain Influence Areas. Geotech. Geol. Eng. 2020, 38, 4201–4225. [Google Scholar] [CrossRef]
- Pantelidis, L. The effect of footing shape on the elastic modulus of soil. In Proceedings of the 2nd Conference of the Arabian Journal of Geosciences (CAJG), Sousse, Tunisia, 25–28 November 2019; Springer Nature: Sousse, Tunisia, 2019. [Google Scholar]
- Barnes, G. Soil Mechanics: Principles and Practice; Palgrave Macmillan: London, UK, 2016; ISBN 1137512210. [Google Scholar]
- Gibson, R.E. Some Results Concerning Displacements and Stresses in a Non-Homogeneous Elastic Half-space. Géotechnique 1967, 17, 58–67. [Google Scholar] [CrossRef]
- Pantelidis, L. On the modulus of subgrade reaction for shallow foundations on homogenous or stratified mediums. In Proceedings of the 3rd International Structural Engineering and Construction Conference (EURO-MED-SEC-03), Limassol, Cyprus, 3–8 August 2020; Vacanas, Y., Danezis, C., Yazdani, S., Singh, A., Eds.; ISEC Press: Limassol, Cyprus, 2020. [Google Scholar]
- Fox, L. The mean elastic settlement of a uniformly loaded area at a depth below the ground surface. In Proceedings of the Second International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, The Netherlands, 21–30 June 1948; Volume 1, p. 129. [Google Scholar]
- Janbu, N.; Bjerrum, L.; Kjaernsli, B. Veiledning ved lo/sniffing av fundamenterings oppgaver. In Norwegian with English Summary; Soil Mechanics Applied to Some Engineering Problems; Norwegian Geotechnical Institute, Publication: Oslo, Norway, 1956. [Google Scholar]
- Burland, J.B. Discussion of session A. In Proc. of the Conf. on In Situ Investigations in Soils and Rocks; British Geotechnical Society: London, UK, 1970; pp. 61–62. [Google Scholar]
- Christian, J.; Carrier, D. Janbu, Bjerrum and Kjaernsli’s chart reinterpreted. Can. Geotech. J. 1978, 15, 123–128. [Google Scholar] [CrossRef]
- Díaz, E.; Tomás, R. Revisiting the effect of foundation embedment on elastic settlement: A new approach. Comput. Geotech. 2014, 62, 283–292. [Google Scholar] [CrossRef]
- Teng, W.C. Foundation Design; Prendice-Hall Inc.: New York, NY, USA, 1962. [Google Scholar]
- Alpan, I. Estimating the settlements of foundations on sands. Civ. Eng Public Work. Rev. UK 1964, 59, 1415–1418. [Google Scholar]
- Bazaraa, A.R. Use of the Standard Penetration Test for Estimating Settlements of Shallow Foundations on Sand; University of Illinois: Champaign, IL, USA, 1967. [Google Scholar]
- Bowles, L.E. Foundation Analysis and Design; McGraw-Hill: New York, NY, USA, 1996; ISBN 0079122477. [Google Scholar]
- Peck, R.B.; Hanson, W.E.; Thornburn, T.H. Foundation Engineering; Wiley: New York, NY, USA, 1974; Volume 10. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John and Wiley and Sons: Hoboken, NJ, USA, 1967; ISBN 0471852732. [Google Scholar]
- Agarwal, K.B.; Rana, M.K. Effect of ground water on settlement of footings in sand. In Proceedings of the 9th European Conference on Soil Mechanics and Foundation Engineering, Dublin, Ireland, 31 August–3 September 1987; Balkema: Rotterdam, The Netherlands, 1987; pp. 751–754. [Google Scholar]
- NAVFAC. Soil Mechanics Design Manual (NAVFAC DM 7.1); Naval Facilities Engineering Command: Alexandria, VA, USA, 1982. [Google Scholar]
- Shahriar, M.A.N.; Sivakugan, N.; Das, B.M. Settlement correction for future water table rise in granular soils: A numerical modelling approach. Int. J. Geotech. Eng. 2013, 7, 214–217. [Google Scholar] [CrossRef]
- Shahriar, M.A.; Sivakugan, N.; Das, B.M.; Urquhart, A.; Tapiolas, M. Water Table Correction Factors for Settlements of Shallow Foundations in Granular Soils. Int. J. Geomech. 2015, 15, 06014015. [Google Scholar] [CrossRef]
- Ulrich, E.J.; Shukla, S.N.; Baker, C.N., Jr.; Ball, S.C.; Bowles, J.E.; Colaco, J.P.; Davisson, T.; Focht, J.A., Jr.; Gaynor, M.; Gnaedinger, J.P.; et al. Suggested analysis and design procedures for combined footings and mats. J. Am. Concr. Inst. 1988, 86, 304–324. [Google Scholar]
- DIN 4018 Berechnung der Sohldruckverteilung unter Flächengründungen Einschl; Deutsche Normen: Berlin, Germany, 1974.
- IS 2950-1 Code of Practice for Design and Construction of Raft Foundations, Part 1: Design IS 1904:1986 Code for Practice, Design and Construction of Foundations in Soil; Bureau of Indian Standards: New Delhi, India, 1981.
- Varghese, P.C. Foundation Engineering; PHI Learning Pvt. Ltd.: Delhi, India, 2005; ISBN 8120326520. [Google Scholar]
- Milovic, D. Stresses and Displacements for Shallow Foundations; Elsevier: Amsterdam, The Netherlands, 1992; ISBN 0-444-88349-5. [Google Scholar]
- Brown, P.T. Numerical analyses of uniformly loaded circular rafts on deep elastic foundations. Geotechnique 1969, 19, 399–404. [Google Scholar] [CrossRef]
- Duncan, J.M.; Buchignani, A.L. An Engineering Manual for Settlement Studies; Department of Civil Engineering, University of California: Berkley, CA, USA, 1976. [Google Scholar]
- US Army Corps of Engineers. Engineering and Design-Settlement Analysis, EM 1110-1904; U.S. Army Corps of Engineers: Washington, DC, USA, 1990.
- Mayne, P.W.; Kulhawy, F.H. K0-OCR relationships in soil. J. Geotech. Eng. 1982, 108, 851–872. [Google Scholar]
- Mesri, G.; Ullrich, C.R.; Choi, Y.K. The rate of swelling of overconsolidated clays subjected to unloading. Géotechnique 1978, 28, 281–307. [Google Scholar] [CrossRef]
- D’Appolonia, D.J.; Poulos, H.G.; Ladd, C.C. Initial settlement of of structures on clay. J. Soil Mech. Found. Div. ASCE 1971, 97, 1359–1377. [Google Scholar]
- EN 1997-1. Eurocode 7 Geotechnical Design—Part 1: General Rules; European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- Pantelidis, L. The equivalent modulus of elasticity of layered soil mediums for designing shallow foundations with the Winkler spring hypothesis: A critical review. Eng. Struct. 2019, 201, 109452. [Google Scholar] [CrossRef]
- Kany, M. Berechnung von Flächengründungen, 2nd ed.; Ernst u. Sohn: Berlin, Germany, 1974. [Google Scholar]
- Grasshoff, H. Setzungsberechnungen starrer Fundamente mit Hilfe des kennzeichnenden Punktes. Bauingenieur 1955, 30, 53–54. [Google Scholar]
- Kaniraj, S.R. Design Aids in Soil Mechanics and Foundation Engineering; Tata McGraw-Hill: New York, NY, USA, 1988; ISBN 0074517147. [Google Scholar]
- Fellenius, B.H. Basics of Foundation Design; BC BiTech Publishers Limited: Richmond, BC, Canada, 2006. [Google Scholar]
- Kempfert, H.-G.; Gebreselassie, B. Excavations and Foundations in Soft Soils; Springer Science & Business Media: Berlin, Germany, 2006; ISBN 3540328955. [Google Scholar]
- Tatsuoka, F.; Teachavorasinskun, S.; Dong, J.; Kohata, Y.; Sato, T. Importance of Measuring Local Strains in Cyclic Triaxial Tests on Granular Materials. In Dynamic Geotechnical Testing II; ASTM International: West Conshohocken, PA, USA, 1994; pp. 288–302. [Google Scholar]
- Jamiolkowski, M.; Lancellotta, R.; LoPresti, D.C.F. Remarks on the stiffness at small strains of six Italian clays. In Proceedings of the Int. Symp. on Pre-Failure Deformation of Geomaterials, Sapporo, Japan, 12–14 September 1994; Balkema: Rotterdam, The Netherlands, 1995; pp. 817–836. [Google Scholar]
- Pincus, H.; Lo Presti, D.; Pallara, O.; Puci, I. A Modified Commercial Triaxial Testing System for Small Strain Measurements: Preliminary Results on Pisa Clay. Geotech. Test. J. 1995, 18, 15. [Google Scholar] [CrossRef]
- Cho, H.; Kim, N.; Park, H.; Kim, D. Settlement Prediction of Footings Using VS. Appl. Sci. 2017, 7, 1105. [Google Scholar] [CrossRef]
- Harr, M.E. Foundations of Theoretical Soil Mechanics; McGraw-Hill Inc.: New York, NY, USA, 1966; ISBN 10:0070267413. [Google Scholar]
- Schleicher, F. Schleicher Zur Theorie der Baugrundes. Bauingenieur 1926, 48, 931–935. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).