Seismic Density Model of the White Sea’s Crust
Abstract
1. Introduction
2. Materials and Methods
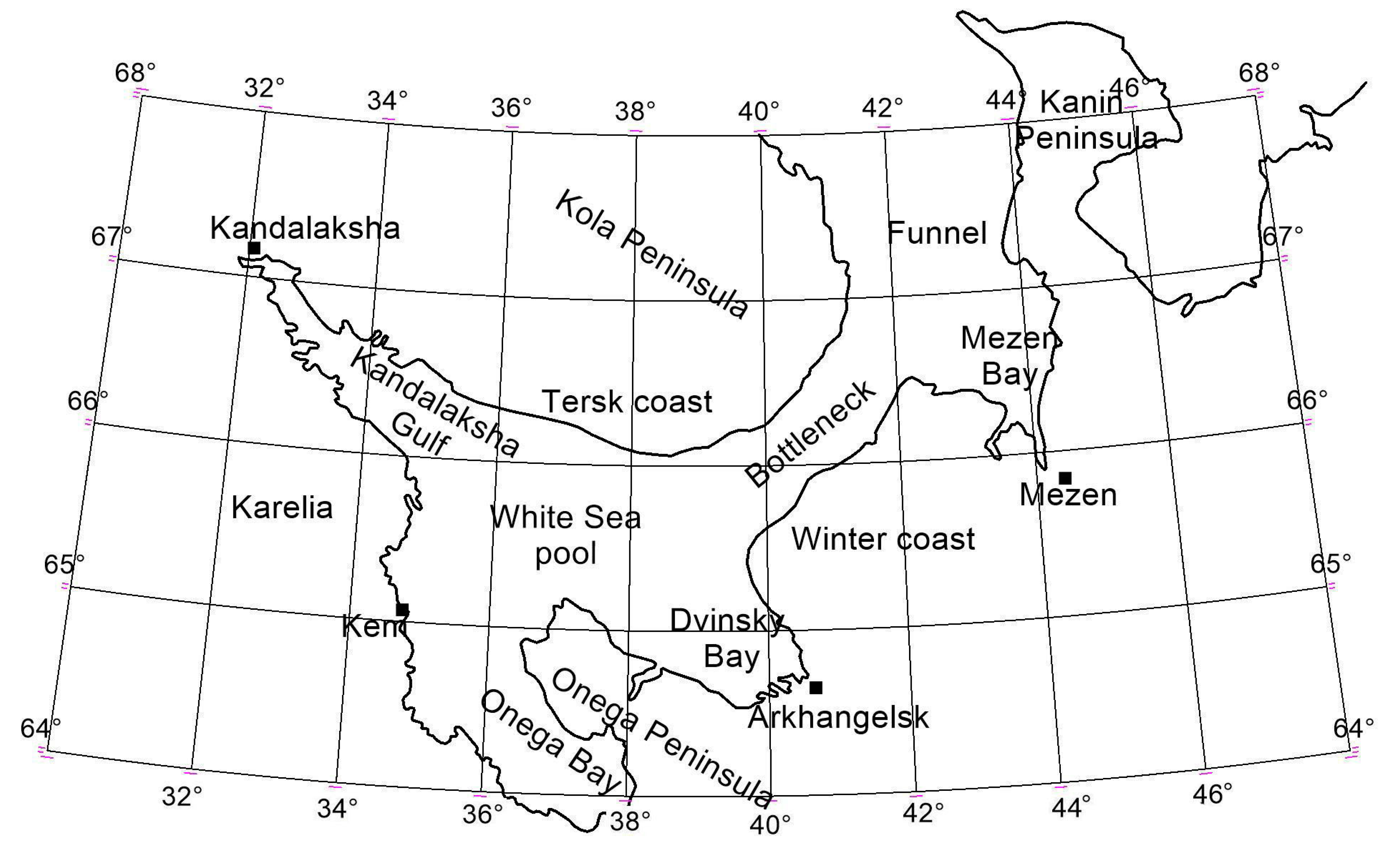
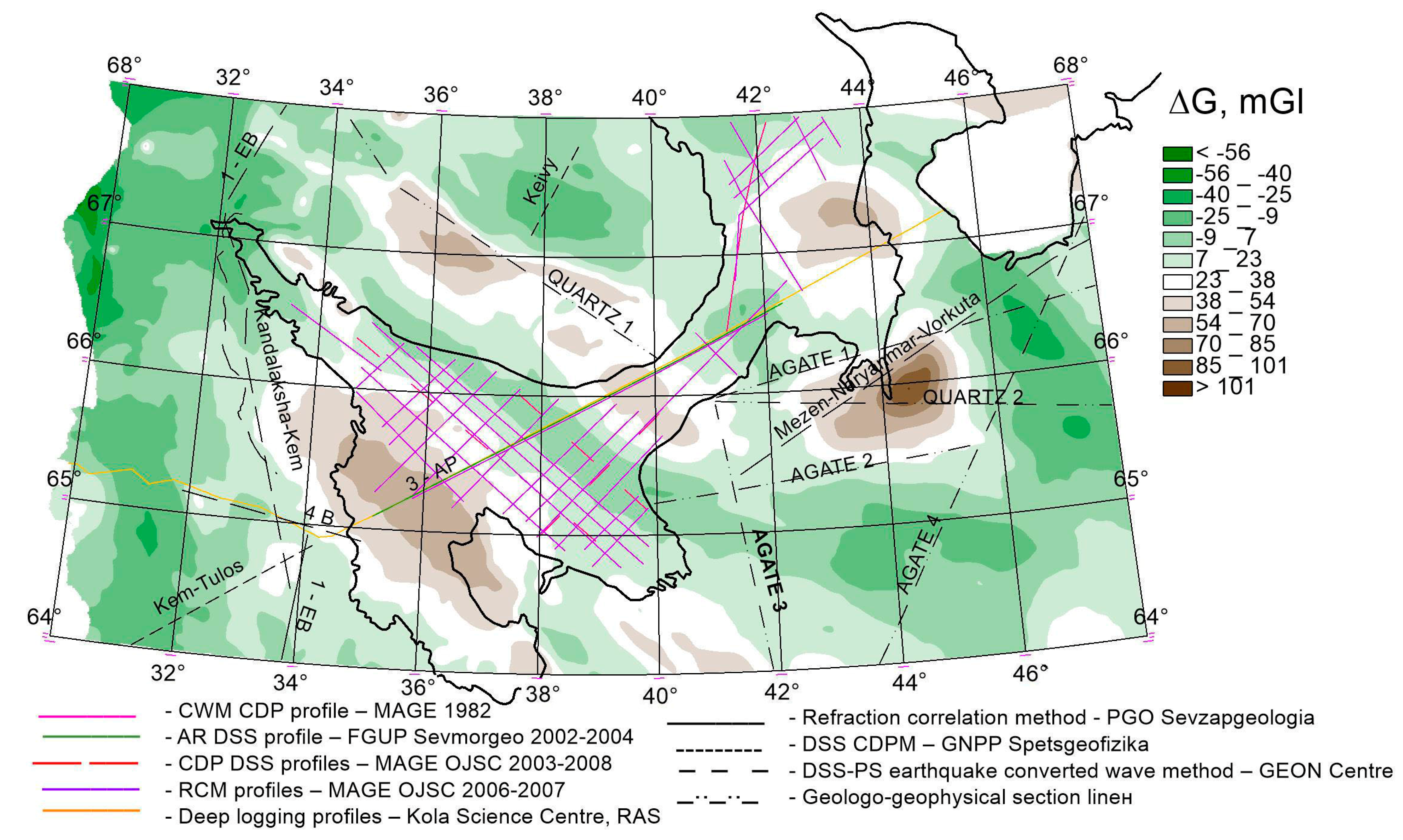
2.1. Initial Data
2.2. Methods of Data Processing
3. Results
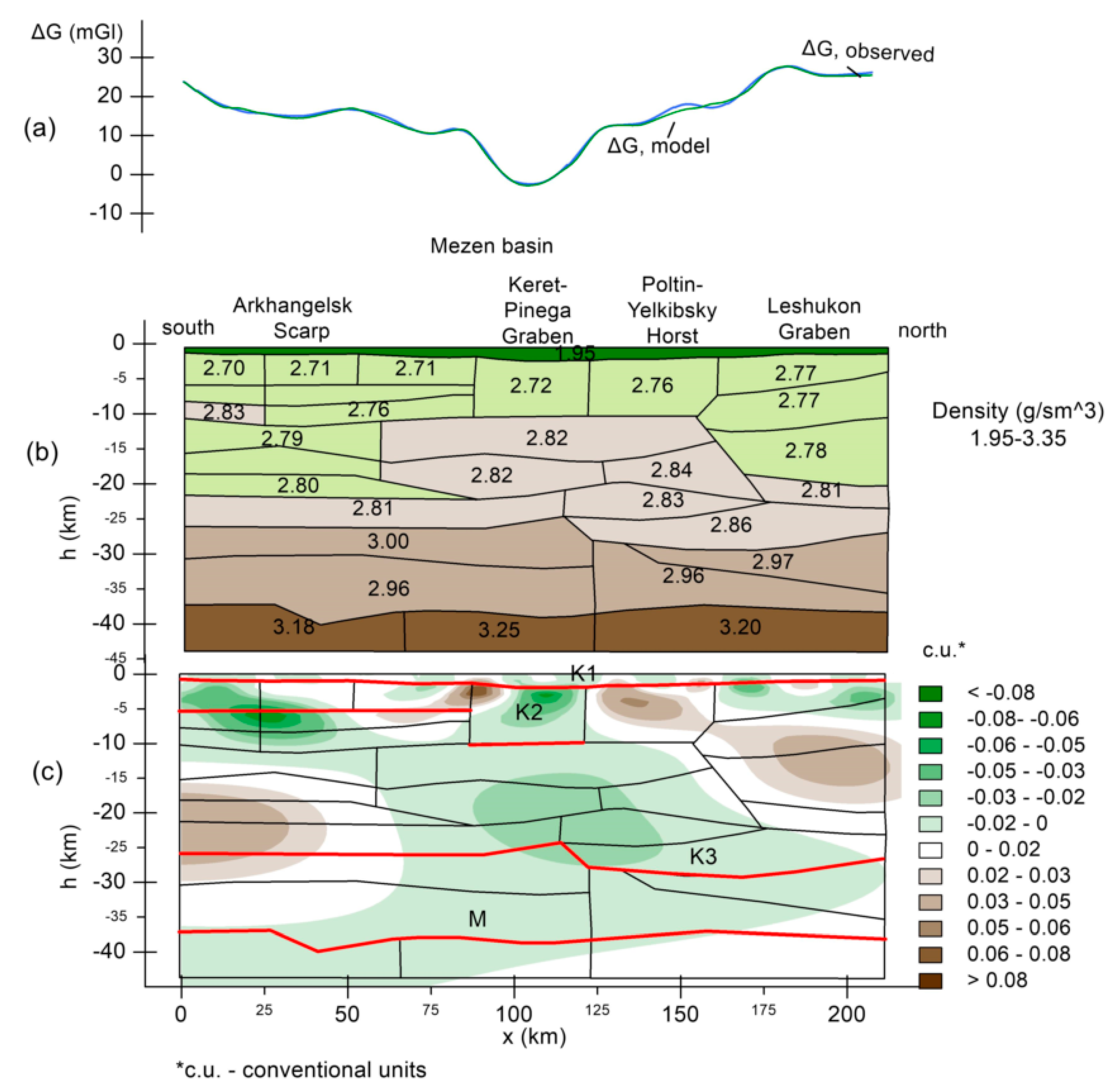
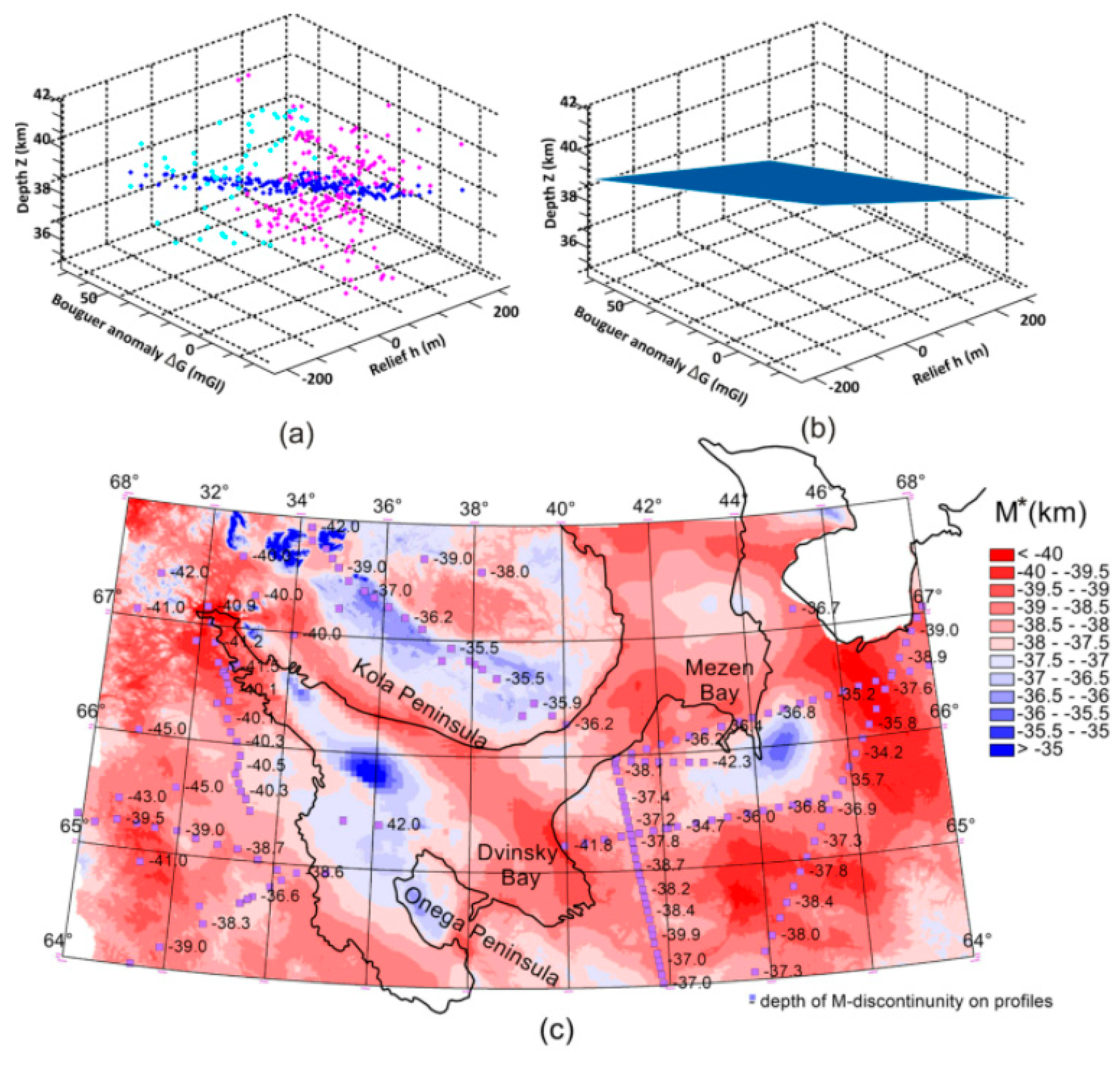
3.1. 2D Modelling Example
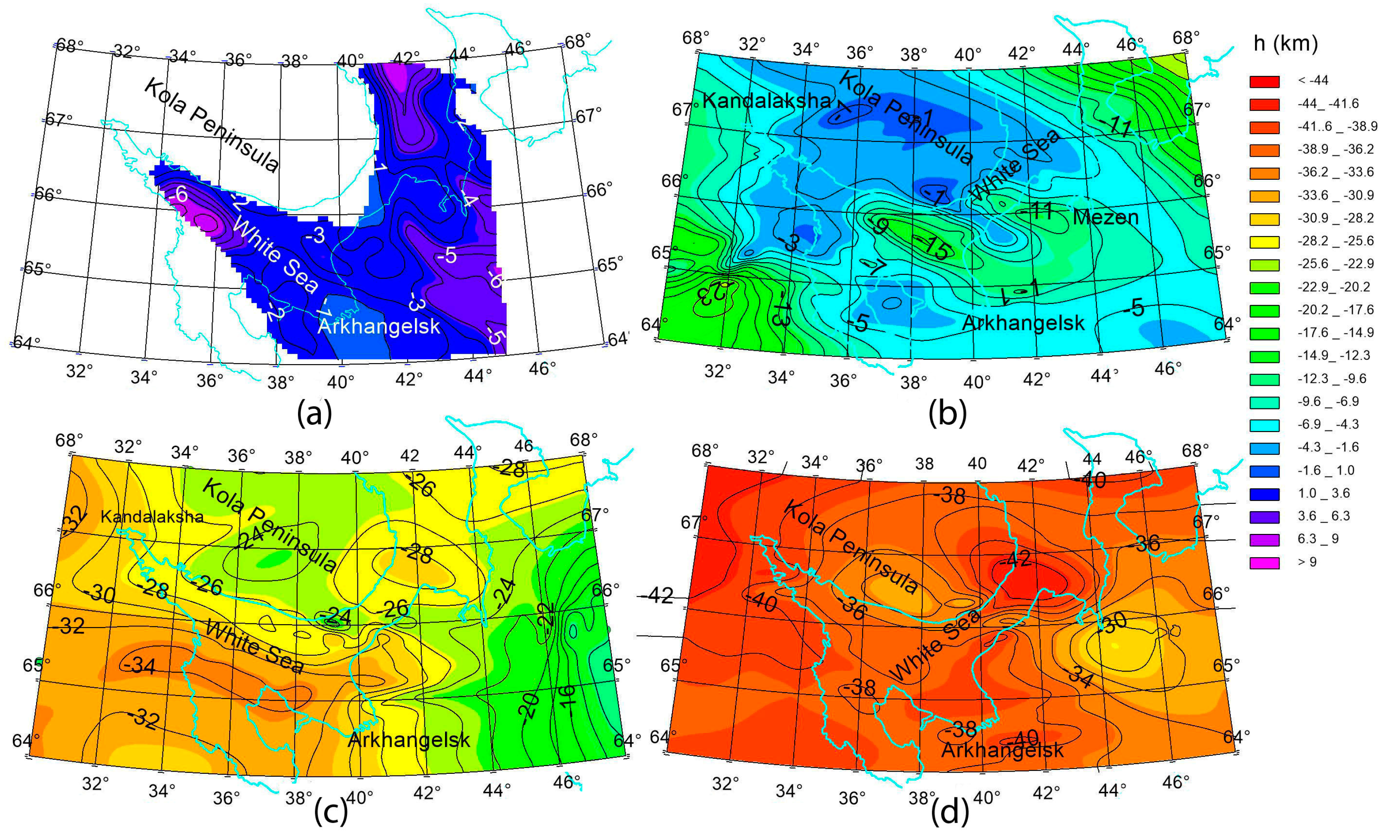
3.2. 3D Density Model of the White Sea Region
3.3. Alternative Map of the M-Border
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baluev, A.S.; Brusilovskii, Y.V.; Ivanenko, A.N. The crustal structure of Onega-Kandalaksha paleorift identified by complex analysis of the anomalous magnetic field of the White Sea. Geodyn. Tectonophys. 2018, 9, 1293–1312. [Google Scholar] [CrossRef]
- Konstantinovsky, A.A. Rifeisky Onega-Kandalakshsky graben of the East European Platform. Geotectonics 1977, 3, 38–45. (In Russian) [Google Scholar]
- Dobrynina, M.I. Riftogenesis in the Geological History of the Precambrian of the Northern part of the Russian Plate. Deep Structure and Geodynamics of Crystal Shields of the European Part of the USSR; Mitrofanov, F.P., Bolotov, V.I., Eds.; Publishing House of the KSC RAS: Apatites, Russia, 1992; pp. 71–78. (In Russian) [Google Scholar]
- Sim, L.A.; Postnikov, A.V.; Postnikova, O.A.; Poshibaev, V.V. Influence of the latest geodynamics on the gas content of the Irkineyevo-Chadobetsky riftogenic deflection. Expo. Oil Gas 2016, 6, 8–12. (In Russian) [Google Scholar]
- Kazanin, G.S.; Zhuravlev, V.A.; Pavlov, S.P. The structure of the sedimentary cover and the White Sea’s oil and gas potential. Buren. Neft. 2006, 2, 26–28. (In Russian) [Google Scholar]
- Kheraskova, T.N.; Sapozhnikov, R.B.; Volozh, Y.A.; Antipov, M.P. Late Precambrian geodynamics and evolution of the northern East European Platform, as shown by regional seismic profiling. Geotektonika 2006, 6, 33–51. (In Russian) [Google Scholar]
- Aplonov, S.V.; Fedorov, D.L. (Eds.) Geodynamics and Oil and Gas Potential of the Mezen Sedimentary Basin; Nauka: Sant Petersburg, Russia, 2006; 319p. (In Russian) [Google Scholar]
- Zhuravlev, V.A. Earth crust structure of the White Sea Region. Razved. i Okhrana Nedr. 2007, 9, 22–26. (In Russian) [Google Scholar]
- Zhuravlev, V.A.; Shipilov, E.V. Structure of basins in the White Sea rift system. Okeanologia 2008, 48, 123–131. (In Russian) [Google Scholar] [CrossRef]
- Baluev, A.S.; Zhuravlev, V.A.; Terekhov, A.N.; Przhiyalgovsky, E.S. Tectonics of the White Sea and Adjacent Areas (Explanatory Note to a “1: 500 000 Tectonic Map of the White Sea and Adjacent Areas” 1:500000); GEOS: Moscaw, Russia, 2012; 104p. (In Russian) [Google Scholar]
- The White Sea System. Sedimentation, Geology and History; Nauch. Mir: Moscaw, Russia, 2017; Volume 4, 1030p. (In Russian)
- Kutinov, Y.G.; Chistova, Z.B.; Polyakova, E.V.; Mineyev, A.L. Digital modelling of relief for forecasting of areas with oil and diamonds. Acute Oil Gas Probl. 2019, 24. (In Russian) [Google Scholar] [CrossRef]
- Sharov, N.V.; Mitrofanov, F.P.; Verba, M.L.; Gillen, C. (Eds.) Lithospheric structure of the Russian Barents Sea Region; KarRC. RAS: Petrozavodsk, Russia, 2005; 318p. (In Russian) [Google Scholar]
- Sharov, N.V.; Slabunov, A.I.; Isanina, E.V.; Krupnova, N.A.; Roslov, Y.V.; Shchiptsova, N.I. Seismic section of the earth crust along the DSS-CDP profile «Land-Sea» Kalevala-Kem-White Sea Throat. Geofiz. Zhurn. 2010, 32, 21–34. (In Russian) [Google Scholar]
- Glaznev, V.N.; Raevsky, A.B.; Skopenko, G.B. A three-dimensional integrated density and thermal model of the Fennoscandian lithosphere. Tectonophysics 1996, 258, 15–33. [Google Scholar] [CrossRef]
- Glaznev, V.N.; Mints, M.V.; Muravina, O.M.; Raevsky, A.B.; Osipenko, L.G. Complex geological—Geophysical 3D model of the crust in the southeastern Fennoscandian sheild: Nature of density layering of the crust and the crust—Mantle boundary. Geodyn. Tectonophys. 2015, 6, 133–170. [Google Scholar] [CrossRef][Green Version]
- Konanova, H.B. Volumetric models of the gravimetric field of the Timan-North Uralian Region and adjacent areas. Bull. Inst. Geol. Komi Sci. Cent. Ural Branch Russ. Acad. Sci. 2010, 9, 8–14. (In Russian) [Google Scholar]
- Mints, M.; Suleimanov, A.; Zamozhniaya, N.; Stupak, V. A 3-D model of the Early Precambrian crust under the south-eastern Fennoscandian Shield: Karelia Craton and Belomorian tectonic province. Tectonophysics 2009, 472, 323–339. [Google Scholar] [CrossRef]
- Pospeyeva, E.V.; Vitte, L.V. Structural characteristics of the earth crust of the White Sea block and part of the Karelian block, as shown by magnetotelluric studies. Geofizika 2011, 3, 64–72. (In Russian) [Google Scholar]
- Cheremisina, E.N.; Finkelstein, M.Y.; Lyubimova, A.V. GIS INTEGRO—An import-replacing software-technological complex for solving geologo-geophysical problems. Geoinformatika 2018, 3, 8–17. (In Russian) [Google Scholar]
- Sharov, N.V.; Zhuravlev, A.V. Crustal structure of the White Sea and adjacent areas. Arct. Ecol. Econ. 2019, 3, 62–72. (In Russian) [Google Scholar] [CrossRef]
- Sharov, N.V.; Bakunovich, L.I.; Belashev, B.Z.; Zhuravelev, A.V.; Nilov, M.Y. Geologo-geophysical models of the earth crust of the White Sea Region. Geodyn. Tectonophys. 2020, 11, 566–582. (In Russian) [Google Scholar] [CrossRef]
- Mitrofanov, F.P.; Sharov, N.V.; Zagorodny, V.G.; Glaznev, V.N.; Korja, A.K. Crustal Structure of the Baltic Shield along the Pechenga-Kostomuksha-Lovisa Geotraverse. Intern. Geol. Rev. 1998, 40, 990–997. [Google Scholar] [CrossRef]
- Sharov, N.V. Lithosphere of Northern Europe, as Shown by Seismic Data; KarRC RAS: Petrozavodsk, Russia, 2017; 173p. (In Russian) [Google Scholar]
- Pimanova, N.N.; Spiridonov, V.A.; Sharov, N.V.; Lyubimova, A.V.; Senner, A.E. Distribution of density heterogeneities in the earth crust and mantle of the southeastern Fennoscandian Shield, as shown by geological and geophysical data. Geoinformatika 2018, 1, 43–51. (In Russian) [Google Scholar]
- Sapozhnikov, R.B. Efficiency of EWM DP seismic prospecting for the study of the geological structure of the Mezen syneclise. Razved. Okhrana Nedr. 2003, 5, 32–35. (In Russian) [Google Scholar]
- 1:1000000 Scale State Geological Map of the Russian Federation (Third Generation). Baltic Series. Sheet Q-(35), 36—Apatity. Explanatory Note; VSEGEI Cartographic Factory: Murmansk/Sant Peterburg, Russia, 2009; 487p. (In Russian)
- 1:1000000 Scale State Geological Map of the Russian Federation (Third Generation). Baltic Series. Sheet Q-37- Arkhangelsk. Explanatory Note; VSEGEI Cartographic Factory: Murmansk/Sant Peterburg, Russia, 2009; 338p. (In Russian)
- 1:1000000 State Geological Map of the Russian Federation (Third Generation). Mezen Series. Sheet Q-38- Mezen. Explanatory Note; VSEGEI Cartographic Factory: Murmansk/Sant Peterburg, Russia, 2009; 350p. (In Russian)
- Sharov, N.V. (Ed.) Deep Structure and Seismicity of the Karelian Region and Surrounding Areas; KarRC RAS: Petrozavodsk, Russia, 2004; 353p. (In Russian) [Google Scholar]
- Erinchek, Y.M. (Ed.) A Model of the Earth Crust and the Upper Mantle Based on Deep Seismic Profiling; VSEGEI: Sant Peterburg, Russia, 2007; 245p. (In Russian) [Google Scholar]
- Pimanova, N.N.; Biserkin, I.A.; Deev, K.V. Technology for constructing 3D density models in the Integro GIS environment. Geoinformatics 2013, 4, 45–48. (In Russian) [Google Scholar]
- Kobrunov, A.I. Mathematical Foundations of the Theory of Interpretation of Geophysical Data; TsentrLitNefteGaz: Moscow, Russia, 2008; 286p. (In Russian) [Google Scholar]
- Priezzhev, I.I. Construction of distributions of physical parameters of the environment according to the data of gravity prospecting, magnetometry. Geophysics 2005, 3, 46–51. (In Russian) [Google Scholar]
- Mitsyn, S.V.; Ososkov, G.A. Extrapolation of grid models of geophysical fields by the finite difference method. Geoinformatics 2016, 3, 29–34. (In Russian) [Google Scholar]
- Deev, K.V. Multilevel two-dimensional interpolation in the processing of geological and geophysical information. Geoinformatics 2003, 2, 55–59. (In Russian) [Google Scholar]
- Kashubin, S.N.; Petrov, O.V.; Androsov, E.A.; Morozov, A.F.; Kaminsky, V.D.; Poselov, V.A. A map of the crustal thickness of Circumpolar Arctic. Reg. Geol. Metallog. 2011, 46, 5–13. (In Russian) [Google Scholar]
- Golubev, Y.K.; Vaganov, V.I.; Prusakova, N.A. Principles of forecasting diamondiferous areas on the East European Platform. Rudy Met. 2005, 1, 55–70. (In Russian) [Google Scholar]

| Crustal Layer | Vp, km/s | Ρ, kg/m3 | Depth Range, km |
|---|---|---|---|
| Sedimentary layer, 0–K1 | 3.4–5.7 | 1900–2600 | 0–10 |
| Granite-metamorphic layer, K1–K2 | 5.80–6.20 | 2600–2750 | 0–20 |
| Granulite-basite layer, K2– K3 | 6.30–6.80 | 2775–2900 | 20–32 |
| Crust mantle mix layer, K3–M | 7.0–7.2 | 2950–3000 | 32–44 |
| Upper mantle | 8.00–8.20 | 3400 | >44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belashev, B.; Bakunovich, L.; Sharov, N.; Nilov, M. Seismic Density Model of the White Sea’s Crust. Geosciences 2020, 10, 492. https://doi.org/10.3390/geosciences10120492
Belashev B, Bakunovich L, Sharov N, Nilov M. Seismic Density Model of the White Sea’s Crust. Geosciences. 2020; 10(12):492. https://doi.org/10.3390/geosciences10120492
Chicago/Turabian StyleBelashev, Boris, Lyubov Bakunovich, Nikolai Sharov, and Michail Nilov. 2020. "Seismic Density Model of the White Sea’s Crust" Geosciences 10, no. 12: 492. https://doi.org/10.3390/geosciences10120492
APA StyleBelashev, B., Bakunovich, L., Sharov, N., & Nilov, M. (2020). Seismic Density Model of the White Sea’s Crust. Geosciences, 10(12), 492. https://doi.org/10.3390/geosciences10120492




