Abstract
Data on the disastrous snow avalanche that occurred on 18 January 2017 at the spa hotel Rigopiano, municipality of Farindola in the Abruzzo region of central Italy, are analyzed in different ways. The main results are the following. (i) The 2017 Rigopiano avalanche went beyond the run-out point predicted by the topographic-statistical - model with standard Norwegian calibration, while avalanches in neighboring paths appear to have run no farther than the -point of their respective paths during the same period. (ii) The curvature and super-elevation of the trimline between 1500 and 1300 m a.s.l. indicate that the velocity of the front was around 40 m s. In contrast, the tail velocity of the avalanche can hardly have exceeded 25 m s in the same segment. (iii) The deposits observed along all of the lower track and in the run-out zone suggest that the avalanche eroded essentially the entire snow cover, but fully entrained only a moderate amount of snow (and debris). The entrainment appears to have had a considerable decelerating effect on the flow front. (iv) Estimates of the degree to which different parts of the building were damaged is combined with information about the location of the persons in the building and their fates. This allows to refine a preliminary vulnerability curve for persons in buildings obtained from the 2015 Longyearbyen avalanche, Svalbard.
1. Introduction
In the evening of 18 January 2017, a large snow avalanche released at about 1900 m a.s.l. on the east flank of Monte Siella in the Abruzzo region of central Italy (Figure 1). Through the Grava dei Bruciati gully, it descended to the flat area called Rigopiano at 1100 m a.s.l. It completely destroyed the Hotel Rigopiano and killed 29 of the 40 persons waiting there for evacuation, making this one of the single most disastrous avalanche events in Europe in a century. The avalanche also destroyed or heavily damaged more than 5 ha of partly mature and partly young beech forest.
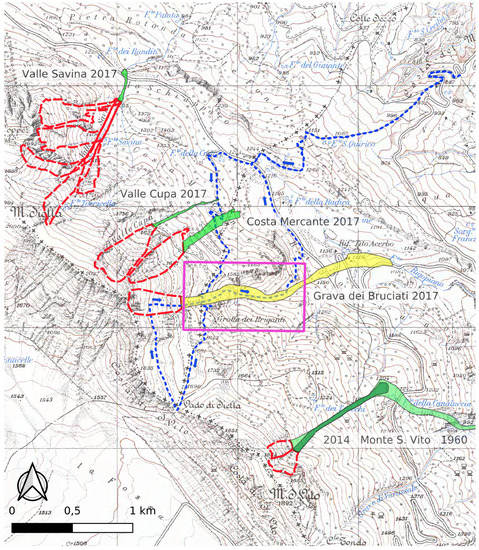
Figure 1.
Topographic map of the Monte Siella area with the largest known avalanche events in each path (lower track and run-out areas shown as yellow and green polygons, potential release and upper-track areas as red dashed polygons). From North to South: Grava di Valle Savina (2017, based on information by D. Borgheggiani), Grava di Valle Cupa and Grava di Costa Mercante (both 2017, data from author’s survey and Google Maps orthophotos), Grava dei Bruciati (2017, from Google Maps orthophoto, author’s survey, and [8]), and Monte San Vito (1963, run-out beyond map to approximately 700 m a.s.l., and 2014, communicated by D. Borgheggiani). Author’s survey itinerary on 3 June 2017 in blue dotted line. The purple rectangle indicates the area shown in Figure 5. Equidistance of isolines 25 m. Basemap downloaded from http://opendata.regione.abruzzo.it/content/dbtr-regione-abruzzo-scala-125000-edizione-2007 on 5 November 2020 under Creative Commons license CC BY-NC.
In early June 2017, the author surveyed the release area and track of this avalanche path, particularly with regard to the forest damage, and summarized the findings together with information retrieved from the Internet in a report [1]. The survey revealed also that at least two further avalanches with long run-out occurred in the same period in the two adjacent paths to the north of the Grava dei Bruciati. Aerial photos of the area [2] and a letter to the authorities in Farindola [3], published on the Internet after the disaster, show that an avalanche of similar or even larger size completely destroyed the forest in or around 1936 and a smaller one—benefiting from the absence of mature forest in the path—almost reached the location of the hotel in 1959.
Since the event, several publications have summarized the synoptic situation leading to the avalanche and the forensic investigations [4], the snow and emergency management before and after the disaster, see, e.g., in [5,6], and a reconstruction of the avalanche flow with a numerical model [7]. The inferences made in [1] are largely in agreement with those in [4], while the present paper is complementary to the study in [7].
Here, the principal aim is to use the observations from the survey together with other available information to elucidate the dynamics of this event, particularly with regard to bounds on the flow velocity (Section 3) and pressure (Section 5), the mass balance (Section 4), and the effect of the dense forest on the flow. Additionally, in Section 2, we analyze historical information on several avalanche events in the Grava dei Bruciati and three nearby paths in terms of the topographic-statistical - model [9]. Moreover, the large number of persons involved in this catastrophe and sufficient information on the degree of building damage at their respective locations allows an update of the vulnerability curve derived from the avalanche at Longyearbyen, Svalbard, on 19 December 2015 [10], see Section 6.
2. Comparison with a Topographic-Statistical Run-Out Model
As detailed in [1], some information on the run-out distances of frequent as well as rare avalanches in the Grava dei Bruciati path and four other paths nearby can be inferred from historical sources, aerial photos, and our survey observations. The reach of avalanches with return periods of approximately ten years is discernible as the boundary of dense forest consisting of shrubs and very young, flexible trees [1]. These estimates are collected in Table 1.

Table 1.
Estimated return period, path steepness , observed run-out angle , and expected run-out angle for an extreme avalanche event according to the - model for Norway. Angles are rounded to nearest degree. Values for the 1959 avalanche in Grava dei Bruciati are rough estimates. The values for avalanches with return period of approximately 10 years are estimated from the extent of stands of bushes and very young trees near the centerline of the path. The date 1936 for the first known avalanche in the Grava dei Bruciati is not certain, and the run-out data are estimates based on the extent of damage.
At the time of the field survey, the run-out area around the destroyed Hotel Rigopiano was closed off by the authorities. This prevented the author from investigating the remaining avalanche traces in the distal area and determining the run-out distance directly. However, debris visible in Figure 2 indicates that the horizontally measured run-out distance from the probable fracture line is around 2200 m, in agreement with survey notes of an Austrian rescue team [8]. It is unclear, however, whether the debris visible in the photo was deposited by the dense/fluidized part of the avalanche or carried there by the powder-snow cloud.

Figure 2.
View of the lower part of the Grava dei Bruciati gully and the run-out zone of the avalanche from a point south of the release area at approximately 1700 m a.s.l.
In the topographic-statistical - model [9], characterizes the steepness of the track; it is the mean angle between the fracture crown and the point, where the slope angle falls below 10°. is the run-out angle, measured from the fracture crown to the distal end of the deposit. The - model is a linear correlation
between the run-out angle and the path steepness . The coefficients p and q depend on the regional winter climate and the typical terrain roughness at scales that are not smoothed out by blowing snow. To the best of the author’s knowledge, no - correlation has been elaborated for the Abruzzo region yet. We will therefore use the best-fit coefficients and ° (with a standard deviation of 2.3°) from Norway for comparison purposes.
Significant events in the Grava dei Bruciati (Rigopiano) path have been recorded for close to a century since the construction of the Rifugio Rigopiano (Figure 3). Avalanches in the other four paths do not affect any buildings, and the roads they may reach under special circumstances are usually closed in winter time. The first record for the Monte San Vito path dates almost 60 years back, but there might be later events similar to the one in 2014 that have not been recorded. The observation period for the remaining paths is perhaps 10–20 years. Based on this, we estimate that the events of January 2017 in the Grava di Valle Cupa and Grava di Costa Mercante paths correspond to return periods of, respectively, 10–30 years and 20–50 years. In the Grava dei Bruciati, an event of similar or larger magnitude as the one of 1959 has likely a return period between 25 and 50 years; events like those of 1936 and 2017 or larger may correspond to a return period of 50–100 years.

Figure 3.
View of the original cabin Rifugio Rigopiano in the 1950s, with the Grava dei Bruciati and snow-covered Monte Siella in the background. Unknown photographer, image in public domain downloaded from [11] (originally uploaded from http://www.gelsumino.it/immagini/rigopiano.html).
Of the seven recorded avalanche events in five paths, about half stopped at or above the point; given the relatively short return periods estimated for those events, this is similar to the behavior that would be expected in western Norway. The exceptionally long 1963 avalanche from Monte San Vito and the 1936, 1959, and 2017 Rigopiano avalanches exceeded their respective points. Moreover, the 1936 and 2017 Rigopiano events are the only known ones that have gone beyond the point expected from the Norwegian correlation (see the last three columns of Table 1); with two events in an observation period of about one century, their most likely frequency is in the range 0.01 to 0.02 year so that they may be considered rare events in this path. Given the tenuous statistical base, the observed run-out distances thus appear compatible with the correlation for avalanches in western Norway. The data may hint at relatively higher mobility of avalanches in the Grava dei Bruciati compared to the neighboring paths. Possible explanations for this could be sought in the larger size of the potential release area, thanks to which avalanches would be less affected by the braking effect of the forest, the somewhat higher altitude of the starting zone and perhaps its easterly aspect as opposed to the northeasterly aspect of the other release areas.
It may look surprising at first that the observed run-out angles seem to be broadly compatible with the correlation from Norway, given the southerly location of the area, the relatively narrow gullies, and the dense beech forest in all paths. However, the Gran Sasso area is exposed to cold northeasterly Bora winds across the Adriatic Sea. They are forced to climb almost 2000 m, which causes intense snow storms at low temperatures. Thus, meteorological conditions conducive to avalanches with long run-out may be just as frequent in the Gran Sasso area as near the Norwegian coast, whose climate is comparatively mild due to the Gulf Stream.
3. Velocity Estimates
Four observations can be used to obtain rough estimates of the velocity of the head and the tail of the 2017 avalanche in the middle to lower track: (i) Parts of the avalanche overflowed the terrain shoulder at 1500 m a.s.l. with little deflection (Figure 4 and Figure 5). (ii) In the left bend at 1300 m a.s.l., the trimline is 20–30 m above the gully floor and has a (horizontally projected) radius close to 400 m (Figure 5). (iii) In the same bend, debris was deposited along the thalweg while trees only 5–10 m away were left unscathed. The minimum curvature radius of the flow was about 200 m. (iv) Similarly, the shoulder mentioned above deflected the tail of the avalanche, which subsequently circled around its foot at 1450–1410 m a.s.l. with a curvature radius of about 120 m (Figure 5).

Figure 4.
The shoulder at 1500 m a.s.l., seen from the northern side of the gully. Note the strong curvature of the trajectory across the ridge and the complete destruction of the forest on the downward slope.
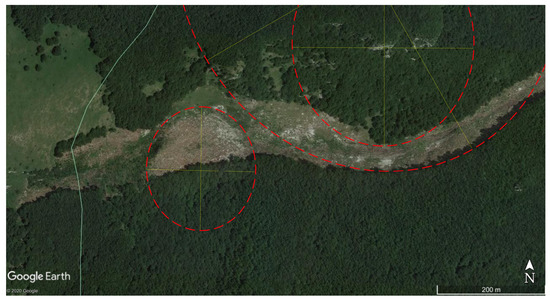
Figure 5.
Orthophoto of 25 June 2017 (©2020 Google), showing the pronounced shoulder at 1500 m a.s.l. and the bend at 1300 m a.s.l. The trimline is at the transition from light foliage to dark shadows. Contour lines (equidistance 10 m) computed from a DTM with 10 m resolution [13]. Red dotted lines are ellipses used for estimating curvature radii in bends, with major axes in yellow.
Avalanche flow in gullies with bends is a three-dimensional problem that needs to be drastically simplified in order to extract velocity estimates from flow marks in bends without detailed numerical simulations. The correct treatment of super-elevation still is a field of active research [12] and debate. In Appendix A and Appendix B, we discuss different approaches to the problem in some detail and derive the formulas used in this section. These formulas do not apply to the powder-snow cloud that most likely accompanied the (fluidized) head and (dense) body of the avalanche; we will disregard the powder-snow cloud here, assuming that it did not separate from the denser parts before the run-out zone below 1200 m a.s.l.
The simplest situation to analyze is the trajectory across the shoulder in Figure 4 and Figure 5 along the southern trim line. We can get a lower bound on the velocity by noting that the avalanche front crossed the shoulder and retained enough speed to cut down any tree that was not flexible (this includes more or less all the trees on the eastern slope). From the isolines derived from the digital terrain model (DTM, Figure 5) [13], one would infer that the avalanche did not have to climb a counter-slope. However, the survey and the photo in Figure 4 showed clearly that the avalanche had to ascend a counter-slope and that the altitude difference was 15 m or more, depending on the exact location. The downslope (approach) angle and the counter-slope angle are in the ranges 20° to 25° and 25° to 35°, respectively. If one assumes that only the fluidized part of the avalanche, with a density in the range 50–150 kg m, crossed the shoulder and that a stagnation pressure of at least 20 kPa (augmented by a hydrostatic contribution of no more than 5 kPa) is needed to break or uproot all the (young) trees on the downstream side of the shoulder (see Section 5.1), the velocity of the front had to be at the ridge.
As a first approximation, we may use the observed run-out angle of this avalanche (Section 2) to obtain the average effective friction coefficient as . With a climb height m, we can then solve the inequality (A1) for a lower bound on the approach velocity :
The higher end of this range may appear large but is close to the estimate from a compilation of experimental measurements [14], which gives 62 m s for a drop height m.
The ridge is rather sharp, with an estimated curvature radius m. An avalanche reaching the top with a speed m s will therefore lift off, jump some horizontal distance over the ridge, and land on the downstream side of the shoulder, which has a mean inclination . If we neglect air resistance and the finite width of the curved ridge, assume a lift-off speed and use , we get (see Appendix A for the derivation)
The simplifications in the derivation lead to an overestimate of , but the assumed is only a lower limit on the front speed. According to Equation (A4), the jumping snow masses would hit the ground at a velocity of 30–50 m s or more and under a blunt angle. In open terrain with a relatively soft sediment cover, such an impact may create a crater-like feature in the terrain, see, e.g., in [15]. During the survey, we did not notice such an impact feature. However, both the deep snow cover and the dense forest in the potential impact zone would dissipate most of the impact energy. Nevertheless, the speed estimate (2) suggests that the avalanche front jumped a considerable distance and that much of the forest on the downslope side of the shoulder was destroyed only after the passage of the front, when the approach velocity was 20–30 m s and the density exceeded 100 kg m.
In analyzing the information contained in the trim lines, one first needs to account for the general inclination of the path, which is in this area. In Figure 5, circles tilted by , i.e., ellipses with axes in the ratio , are fitted visually to the trimlines or the assumed trajectory of the tail of the avalanche; the major axis then corresponds to the curvature radius. For the outer trimline along the bend at 1300 m a.s.l., we obtain m. The largest altitude difference between the gully floor and the southern trim line is approximately 35 m near the downstream end of the bend. We estimate the flow width W at 60 m on average and the super-elevation , i.e., the altitude difference between corresponding flow marks on either side of the gully, at about 30 m. Using Equations (A19) and (A12) with , the speeds in the bend, , and before the bend, , are estimated from the formulas
as m s and m s. The upper values result if we assume °; more likely, however, due to full fluidization so that one should neglect the square root in the equation for and obtains the lower bounds. While this estimate is compatible with the lower bound (2) on the approach velocity to the terrain shoulder at 1500 m a.s.l., it suggests that the upper bound in (2) may be too high.
A similar analysis can be attempted for the slow tail of the avalanche flowing around the shoulder, but the uncertainty is much larger because one cannot infer the width of the flow unambiguously from vestiges of the avalanche event; moreover, the DTM is rather coarse for this purpose. A better constrained estimate can perhaps be obtained combining a high-resolution DTM with footage from drone flights shortly after the catastrophe. Here, we estimate a width based on tree debris observations (see Figure 6) and a mean curvature radius at the center line m (after correction for the mean slope angle). The super-elevation is even more uncertain, but likely at most 5 m, perhaps as low as 1–2 m. If the super-elevation angle is small, the velocity estimate becomes very sensitive to the value of . This part of the flow carried along much debris and entire trees, so may have been above the local slope angle of about 21°; we tentatively set °. Evaluating Equation (A19) with these values will give an upper bound on the velocity. If one considers that the shear rate in vertical planes parallel with the flow direction was large, one expects that little or no additional shear strength could be mobilized against shear on bed-parallel planes, ; accordingly, the term should be dropped, which provides a lower bound on u. For m and m, we obtain the ranges . We believe that a more definite estimate can only be obtained with a dynamical model that correctly predicts the flow regime and accounts for all terms of the shear stress tensor.

Figure 6.
Amassed tree debris in the center of the path. Photo taken at approximately 1350 m a.s.l. The Rigopiano area is visible in the background.
We proceed analogously for the bend at 1300 m a.s.l, estimating m, m, , ° (Figure 5). With this, we find for m and for m. If one assumes , these results are compatible—within their very large uncertainties—with earlier findings from field investigations that indicated the body/tail velocity of dry-snow avalanches to be roughly half of the front velocity [16].
4. Estimate of the Mass Balance
With the limited data available on the extent and, most importantly, the depth of the deposits, a plausible mass balance for this event can only be established by piecing together qualitative information from photos in the media, experience from investigations of other large avalanches, and by trial and error. In Table 2, we collect our best estimates for the mass balance in the different segments of the path; the reader should keep in mind, however, that each of these mass estimates has a large uncertainty. The main constraints are the limits on the size of the release area (from the lateral limits of forest damage in the upper track, see Figure 1), the amount of erodible snow in the gully (from the meteorological data), and the deposit volume.

Table 2.
Estimated snow mass balance of the 2017 Rigopiano avalanche. Length and area of the different sections are measured in horizontal projection. and are the spatial erosion and deposition rates, respectively, integrated over the path width. Integrating and over the segment length gives the changes of entrained and deposited mass, and . is the estimate for the snow mass that flowed through the cross section at the lower end of the respective path segment. Numbers in parentheses for and in the release area are used for calculating , but do not count for and in Figure 7.
With an average (vertical) slab height of 1.3–2.6 m, we estimate the release volume in the range 100,000 to 200,000 m, corresponding to a mass in the range 15 to 50 kt if the slab density is assumed in the range 150–250 kg m. The horizontal distance from the end of the Grava dei Bruciati at 1200 m a.s.l. to the distal end of the deposit is about 600 m. Figure 2 suggests that the deposit beyond the gully had approximately oval or rhomboidal shape, with a maximum width of about 100 m. This amounts to an area of 40,000–55,000 m. Near the hotel on the main axis, the deposit depth exceeded 5 m as the debris of the four-story hotel was mostly covered by snow, but the average over the entire area is more likely in the range 2 to 4 m. The difficulties of digging the victims out indicates that the snow was very hard, with a density of some 500 kg m, to judge from experience with other large avalanches [17]. From this, we estimate a deposit mass in the range 40 to 110 kt in the run-out area. In the following, we shall use central values of 30 kt for the release mass and 75 kt for the deposit mass in the run-out zone.
We expect that the avalanche deposited only an insignificant amount of snow in the upper track between 1700 and 1550 m a.s.l. In contrast, in the middle and lower track from 1550 m a.s.l. to 1200 m a.s.l., over a distance of more than 1 km and with an average width of some 20 m, voluminous tree debris was deposited on the gully bottom (Figure 6). On photos and videos from the rescue operation, the tree debris was not visible for some time after the event (this was helped by the snowfall continuing after the avalanche descent). We may therefore assume that the deposit depth was at least 2 m at the bottom of the gully, with a density in the range 300 to 500 kg m. Snow of similar density may also have been deposited along the gully sides by the fluidized part of the avalanche over a width of 30–120 m, but likely with a depth of 0.5 m or less. This gives a lower bound of 15–30 kt of deposited snow, but the actual value could exceed 50 kt as the deposit may have been significantly deeper.
Our best estimate of the total deposited snow mass is 110–120 kt, in the middle of the range 55 to 160 kt. This implies that the avalanche eroded about 80 kt of snow (with a plausible range 40 to 110 kt) or about twice the release mass. However, maybe only a fraction of this mass was fully entrained into the avalanche, i.e., accelerated to avalanche speed. At an average density of 200 kg m, this amounts to 400,000 m. If all of this extra mass were eroded in the track between 1700 and 1200 m a.s.l., which has an area of roughly 135,000 m, about 3 m of snow (or a snow water equivalent of 600 mm) would have to be eroded on average. This amounts to all of the snow precipitation of the winter 2016/2017 until then or more; also, such deep erosion over a large area has not been observed in full-scale experiments to the author’s knowledge. A more plausible closure of the mass balance is achieved if one assumes that the avalanche continued to erode a substantial part of the snow cover well into the run-out zone, without entraining much of it. By tweaking the numbers in Table 2 slightly, one could easily balance the sums of eroded and deposited mass, and , but we leave the slight discrepancy as a reminder of the very large uncertainty of these estimates.
Table 2 is graphically summarized in Figure 7 in a form that can be compared to the plots from the measurements at the Monte Pizzac test site [18]. Developing such scenarios is useful for understanding the limitations that the characteristics of the avalanche path impose on the mass balance. The erosion and deposition rates shown in the figure do not include the mass of tree debris, which would contribute substantially.
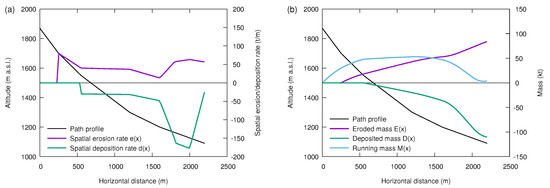
Figure 7.
Qualitative evolution of erosion, deposition and mass balance. (a) Width-integrated erosion rate and deposition rate . (b) Evolution of running mass (mass passing the cross section at x), the cumulated erosion, , and the cumulated deposition, . is the location of the stauchwall. Note that for . For , a linearly decreasing width of the release area is assumed in .
An interesting and relevant question is to which degree these snow masses were not just eroded, but properly entrained into the avalanche flow, and how far the eroded snow traveled on average. Sovilla et al. [18] dug a large number of transverse snow pits along the Monte Pizzac avalanche path and so were able to determine the total mass that flowed across the cross-section at x, , the erosion per unit distance, , and the deposition per unit distance, . Such information is invaluable for testing advanced erosion/deposition models and is not available from Light Detection and Ranging (LiDaR) scans or photogrammetry before and after the avalanche event, which only provide an estimate of the net erosion volume per unit length, , with and the mean densities of the eroded and deposited snow, respectively. A detailed reconstruction of , and is obviously not possible for this event, but the observations summarized above imply the following,
- Along most of the track and probably also in the run-out zone, most of the snow cover was eroded, including the old snow.
- There is no observational information about erosion and deposition in the upper track above 1550 m a.s.l., but based on experience from other avalanche paths (Monte Pizzac, Vallée de la Sionne, Ryggfonn), it is likely that while the net entrainment rate probably was almost equal to the erosion rate so that increased rapidly in that path segment.
- In the middle and lower track, deposition appears to have equaled or exceeded erosion. The likely causes are the diminishing slope angle and increased dissipation due to still intact or already uprooted trees.
- The deposited mass in the run-out area below 1200 m a.s.l. is much larger than the mass of the snow cover before the avalanche. It is likely that the mass increase in the run-out zone also exceeds the release mass. This would mean that and that the running mass, , of the avalanche increased, at least in the steeper parts of the path down to perhaps 1400 or 1300 m a.s.l.
- Detailed measurements at Vallée de la Sionne as well as dynamical considerations [19] indicate that deposition occurs only in the tail of an avalanche, except right before it stops. This suggests that much of the fully entrained snow—possibly stemming from the upper layers of the snow cover—traveled over a large distance, whereas older snow from near the ground was dragged along a relatively short distance and subsequently deposited when the tail of the avalanche passed over it.
- On the one hand, substantial masses of tree debris were deposited near the distal end of the avalanche, where there had been no forest. This implies that some trees were dragged at least 200–300 m by the avalanche. On the other hand, uprooted or broken trees were found a short distance below the point where the avalanche entered the forest. This suggests that the tree destruction rate (the mass of trees per unit area that were broken and/or uprooted) in a dense forest exceeds the debris deposition rate at least in the steeper reaches of the path and that it also exceeds the debris entrainment rate along the forested part of the path.
To estimate the degree of actual entrainment of snow and debris, consider the mass and momentum balances of the entire avalanche and of the fluidized front (index h) separately, with and the respective masses and mean velocities. We may set and change the independent variable from the time t to s, the center-of-mass coordinate along the path, using to obtain
is the slope angle averaged over the instantaneous extent of the avalanche. In the mass balance, we account for the different velocities of the front (), the tail (), and the center-of-mass (v); and . The last term in Equation (6) accounts for eroded snow that is not mixed into the avalanche but merely dragged along and eventually left behind while it still has some velocity ; if this is the case, mass loss is also accompanied by momentum loss. From Equations (5) and (6) one arrives at
where we estimate .
As emphasized in [20,21], when an avalanche runs over a natural snow pack with a buried layer that is weaker than the snow above it, fracture may occur first in that weaker layer, leading to a jump in the erosion depth and gradual acceleration of the eroded mass. is the effective friction coefficient in this weak layer and directly related to its residual shear strength, which will typically be in the range 0.5 to 5 kPa. The normal stress from the avalanche and slab is 3–10 kPa, therefore . If the path characteristics vary slowly with s, the entraining avalanche tends toward a dynamic equilibrium characterized by . Figure 7a suggests that over a large part of the track so that we may set . With kg, and m s, one finds an upper limit for entrainment,
which just covers the observational estimate . If one considers only the fluidized head of the avalanche, and so that the entrainment limit for the head alone is about an order of magnitude smaller. This suggests that the head destroyed the forest and deeply eroded the snow cover, but fully entrained only a small part of it. It appears likely that the body of the avalanche entrained some more snow and debris, but it also deposited large amounts.
5. Observational Limits on Impact Pressure
5.1. Limits Inferred From Forest Destruction
Information from trimlines: The forest was completely destroyed wherever the avalanche reached. The only exceptions are small islands in the upper track that are sheltered to some degree by topographical features, and the lateral edges of the path where the flow stopped a few meters inside the surviving forest without producing much damage. This is best exemplified in [1] (Figure 25), but can also be observed by enlarging Figures 12, 16, 18, and 21 of [1]. Such a damage pattern can be explained if (i) the impact pressure of the avalanche along the trimline was close to the minimum value, , for breaking or uprooting the trees; (ii) the pressure rapidly diminished near the edges of the flow; and (iii) there were no pronounced variations of along the flow direction of the avalanche.
If the three suppositions above are correct, knowing will only give information on the maximum impact pressure along two lines in the flow domain. In particular, the question remains unanswered whether the pressure is much larger close to the centerline of the flow. Nevertheless, an estimate of the pressure needed to break or uproot an average tree will be useful in understanding how much kinetic energy of the avalanche is dissipated as the forest is being destroyed.
Breakage vs. uprooting: While some trees were broken or both uprooted and broken, the majority were only uprooted. This observation can be explained consistently if (i) the root systems of the majority of beech trees could sustain a lesser bending moment than the tree trunks; (ii) the shear strength of the root system in the ground varied strongly, so that the maximum sustainable bending moment of the root system exceeded that of the trunk in some cases; and (iii) the root systems failed so quickly in most cases that the bending moment was reduced significantly as the trees toppled, so that the trunks were not broken. Requirement (i) appears plausible given the very shallow topsoil and the strongly fractured, karstic bedrock, which was pulled out in large quantities together with the root system (Figure 8). We will attempt to make this requirement more quantitative below. There is no data or pertinent observation regarding requirement (ii), but one expects local variations in topsoil depth, in the degree of weathering and in the growth conditions for the root systems of trees to be considerable in a rugged area like the Grava dei Bruciati. Requirement (iii) is also difficult to verify. One may argue, however, that the bending moment due to the avalanche increased gradually over several seconds. This makes it plausible that toppling began when the root system failed and before the modulus of rupture (MoR) of the trunk was reached.

Figure 8.
Root system of an uprooted tree, showing how the roots permeate the soil and karstic subsoil.
Minimum avalanche pressure for breaking trees: See Appendix C for the derivation of approximate formulas for calculating the bending moment exerted on a tree by an avalanche and for estimates of the maximum bending moment before a tree trunk breaks. Comparing Equations (A25) and (A28), we find the following criterion for the stagnation pressure that will break beech trees,
If we assume a flow depth m, young trees with diameter m will break at stagnation pressures of 15–60 kPa, while 60–240 kPa is needed for mature trees with m. The majority of trees in the avalanche path likely had trunk diameters of 0.3 m or less, so stagnation pressures of 35–135 kPa would have been able to break their trunks. The velocity estimates of Section 3 lead to stagnation pressures in the range of 50 to 150 kPa. One may therefore expect that some of the oldest trees in favorable locations could have withstood the avalanche if their root system provided sufficient anchoring and if they were not felled by the impact of uprooted trees swept along by the avalanche.
Minimum avalanche pressure for uprooting trees: A bending moment applied to the tree trunk is transmitted to the root system as long as the trunk does not break. According to the field observations, the failure surface of the root system can be approximated quite well by a hemisphere with a diameter in the range of 1.5 to 3 m. The soil layer is very shallow in the Grava dei Bruciati, but the karstic limestone is heavily weathered so that the beech roots penetrated into it and significant masses of rocks were pulled out together with the roots (Figure 8). The resistance against the bending moment can therefore be attributed to the shear strength of both the roots, soil, and weathered bedrock.
Assuming for simplicity that the shear strength of the root–soil system has a constant value along the hemispherical failure surface with diameter , the moment at failure is
Comparing this with Equation (A25), we find that a tree is uprooted rather than broken if
According to the observations described in [1], most trees were uprooted and . Mattheck et al. [22] (Figure 14) indicate for trees in dense stands. With the latter values, we obtain an upper limit for the shear strength of the soil–root system. This appears plausible for this type of soil. Unfortunately, we do not have other, independent ways of estimating the soil shear strength in this location, such as pulling tests on trees.
An experimental study on tree resistance in the central Amazon basin [23] found critical bending moments in the range of 50 to 400 kN m for different tree species with BHD from 0.2 to 0.4 m, but on average seemed to increase about linearly with BHD, rather than with the third power as predicted by the simple mechanical analysis. Moreover, they found comparable numbers of failure due to snapping and uprooting, with some variations between species and type of terrain.
Energetics of forest destruction and avalanche braking: It is instructive to compare the energy dissipation caused by the forest to the rate at which the avalanche converts potential energy to kinetic energy. A tree standing in an avalanche flow dissipates flow energy at the rate , where is the force acting on the tree. Most of this energy is dissipated by internal friction in the flow around the obstacle, only a small fraction is transmitted to the tree and stored as elastic deformation energy, kinetic energy (after breaking or uprooting), and/or dissipated in plastic deformation including disintegration. Once a tree has fallen, it depends on the circumstances whether it continues to dissipate flow energy or not. We will disregard this question in the following.
The time until breaking or uprooting (index bu in the following) cannot be straightforwardly calculated from the modulus of rupture of the tree or from the failure moment of the root system because the load history and maximum deformation from impact to extraction of the tree are not known. From videos of (mostly powder-snow) avalanche descents, we estimate that the shrubs and flexible young trees within the reach of frequent avalanches above 1450 m a.s.l. can be bent down in . In contrast, the root system of the more mature trees below 1400 m a.s.l. has a residual shear strength after failure that slows down the overturning of the tree. Due to their considerable moment of inertia, mature trees take about 5 s or more to fall under the action of gravity during timber harvest; under the pressure from an avalanche, this may shorten to . For the Rigopiano avalanche, we thus estimate the length of the destruction zone, where trees are standing or falling, as m above 1450 m, increasing to m between 1400 and 1200 m a.s.l.
The energy dissipation due to the forest can be expressed as
The number of trees generating energy dissipation, is the product of the stand density corrected for the obliquity of the terrain, , the width of the avalanche, W, and . We estimate , , and in the fluidized avalanche front. The forest parameters differ strongly between the mostly young forest above 1450 m a.s.l. (down to 1400 m a.s.l. on the eastern flank of the shoulder) and the mature forest below:
- Between 1550 and 1450 m a.s.l., we assume m, m s, W = 80 m, m, , and . This leads to GW.
- Between 1400 and 1200 m a.s.l., we set , m, m, , m and m s. From this, .
In comparison, the avalanche flow converts potential energy to kinetic energy at a rate , which amounts to 3–9 GW for the entire avalanche, and to about 0.2–2 GW for the flow in the forest destruction zone. Dense forest thus has a significant braking effect on the fluidized head.
Surprisingly, the large number of young trees and shrubs above 1450 m a.s.l. seem to provide a stronger braking effect than the mature forest farther down. This should be regarded with caution, however, because the trees and shrubs may well already have been bent down by the large snow load before the avalanche struck so that above 1450 m a.s.l. may be much smaller than estimated.
5.2. Limits from Damage to Hotel Rigopiano
Inferences from destruction of buildings: The complete destruction of Hotel Rigopiano may provide more substantial lower bounds on the pressure, albeit only at one location in the path. However, we do not have enough information about the structural strength of the different parts of the hotel complex to make more than an educated guess about the avalanche pressure: From period photos, it seems the original Rifugio Rigopiano was built in masonry, presumably without steel reinforcement (Figure 3). If that is the case, the analysis detailed in Appendix D suggests that a depth-averaged impact pressure in the range 50–75 kPa combined with a flow depth of 2 m would be needed to shear a free-standing wall from its foundation. The wall would, however, already topple due to the moment of an impact of about 10 kPa if the avalanche flows on a snow cover of 2 m. Side walls, interior dividing walls, and the ceilings will likely raise the minimum impact pressure to 30–50 kPa or more, depending on the number and size of windows. Due to the support from the ceiling, a wall would presumably cave in rather than topple.
From Appendix D, it can be inferred that the trunks of mature trees, transported at roughly the same speed as the avalanche, are likely to be able to penetrate the masonry wall of the old Rifugio Rigopiano if they hit axially and perpendicular to the wall. Under these conditions, the tree is stopped in the course of some tens of milliseconds, creating a localized force of 500 kN or more; this is likely to induce shear fracture in the mortar between the stones, which typically has a shear strength of the order of several hundred kPa. The same holds for the new parts of Hotel Rigopiano (except the spa area) if they were not constructed with reinforced concrete. However, oblique or non-axial tree impacts are much more likely. It remains an open question whether such impacts would be able to penetrate a masonry wall already strained close to its limit by the impacting snow masses.
Inferences from displacement of the hotel: The photos give evidence that virtually all of the western, main wing was displaced by tens of meters in the flow direction of the avalanche (Figure 9). We do not have sufficient information about the failure mode of the ground floor and what degree of shear resistance the joint between the foundation and the hotel walls had. However, a lower bound on the pressure can be obtained by estimating , the necessary pressure to overcome the friction during the displacement. Let be the effective impact area of the avalanche, the mass of the building, and the effective friction coefficient of the house debris on its foundation. Our assumptions with regard to the mass of the building are summarized in Table 3; note that these estimates were obtained purely on the basis of photos and have a large degree of uncertainty. The dense or fluidized part of the avalanche probably had a flow depth of 2–3 m, giving an impact area of 25–40 m. The friction coefficient of the debris is unknown, but in view of all iron bars and the roughness of fracture surfaces, it certainly was at least 0.5, and perhaps even larger than 1. With this, one obtains a mean avalanche pressure in the range

Figure 9.
Position of the destroyed Hotel Rigopiano (yellow lines) before (right panel) and after the avalanche (left panel) relative to the structurally stable edge of the spa area (red lines). Still image downloaded from [11] and reproduced under Creative Commons license CC-BY 3.0, extracted from Youtube video uploaded by TvSEI (https://www.youtube.com/watch?v=6La91fbpbbg).

Table 3.
Assumptions used for estimating the minimum avalanche impact pressure at the location of the hotel from the friction force of the rubble against the foundation.
This pressure range appears plausible for an avalanche of this size: One expects the velocity to be in the range for an avalanche of this size in the upper run-out zone and after mowing down the forest over a distance of 1 km. At NGI’s avalanche test site Ryggfonn in Western Norway, pressure and velocity are simultaneously recorded by load plates and Doppler radar, respectively. The measurements on dry-snow avalanches indicate that mostly is in the range (80–200) kg m [24]. The drag coefficient of the load plates is presumably somewhat smaller than that of a large wall such as the backside of the hotel. With kg m, we obtain an impact pressure
in reassuringly good agreement with the estimate (13)—albeit with very large uncertainties. These bounds are also well above the minimum pressure for caving in masonry walls inferred earlier.
6. On the Vulnerability of Buildings and Persons Hit by Snow Avalanches
In quantitative risk assessment, the risk, , associated with an event scenario S is commonly treated as the product of three factors, namely, (i) the hazard or the probability of the potentially disadvantageous scenario S occurring at a given point; (ii) the exposure as the expected number of persons or the value of objects being present when such an event happens; and (iii) the vulnerability of persons or objects, expressed as the conditional probability of, e.g., death or critical injury to a person or the probable degree of damage of an object given the scenario S:
For snow avalanches, a scenario can be defined as an avalanche reaching some given point with some given pressure p. The summation over S is then replaced by an integral over and p, and the hazard is expressed as the differential probability per unit time, .
As discussed in [10], the vulnerability function or is still poorly known, not least because it strongly depends on the type of building that is affected by the avalanche. In order to enable use of data on avalanches hitting different types of building, the work in [10] adopts the working hypothesis that the vulnerability of persons in buildings is governed by the degree of damage, , i.e., how much of the building’s protective function against avalanches is lost; in other words, the function is assumed independent of the type of building. The construction type b determines the degree of damage as a function of impact pressure and flow depth, . It is advantageous to categorize buildings into a number of classes, ranging from simple wood-frame houses over wooden block and non-reinforced brick houses to reinforced concrete buildings. The degree of damage is a number between 0 and 1; Table 4 describes the damage classes proposed in [10]. Furthermore, different classes of vulnerability may be considered, e.g., the probability of grave injury or death, or the probability of moderate injury.

Table 4.
Categorization of the degree of damage as proposed in [10].
With regard to the damage function , the Rigopiano avalanche can give us the following information.
- The main building can probably be classified as a large multi-story masonry building, whereas the newer spa complex was a one- or two-story reinforced-concrete construction. Neither of them was specifically dimensioned for avalanche impact. Note that these classifications need to be confirmed.
- The impact pressure of the avalanche can only be inferred from numerical simulations, which are fraught with large uncertainties because the initial conditions are poorly known and most models do not explicitly consider fluidization or the formation of a powder snow cloud.
- The damage to the main building was in Category 5, .
- Images in the media suggest that the spa complex collapsed only partially. Snow entered the building in large quantities and blocked the way for the children in the gaming room, but left them with enough space and air for surviving over an extended period. This points to damage in Category 3 and .
Generally, the degree of damage corresponds to the expectations, given the type of building and the probable range of impact pressure. More detailed information on the constructional details of the main building and the surface of the spa complex that was exposed to the avalanche impact would be helpful. Furthermore, for the assessment of the vulnerability function for persons, the location of, and damage to, the gaming room should be known in more detail.
To the author’s knowledge, detailed information about where uninjured, moderately injured and deceased persons were found is not released yet. Aggregating information from media reports on the rescue actions and images of the destroyed hotel (Figure 10), the following is assumed for the time being:
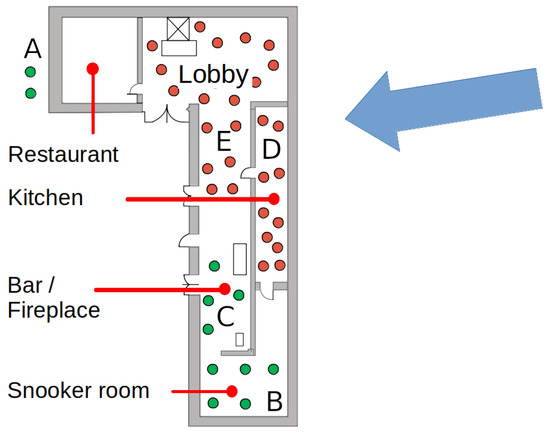
Figure 10.
Plan view of the hotel/spa complex and location of the survivors (green dots) and victims (red dots). Approximate flow direction and area of strongest impact indicated by large arrow. Based on original work by Wikimedia user Fringio published under Creative Commons license CC BY-SA 4.0, retrieved on 1st November 2020 from https://commons.wikimedia.org/w/index.php?curid=57784522.
- There were a total of 38 persons inside the hotel complex, while two persons were in the parking lot outside the devastated area and were unharmed.
- Several children were playing in a room near the spa area, which was less exposed to the avalanche. The degree of damage was presumably in Category 3, i.e., between 0.4 and 0.7, as it took up to four days to rescue some of the children.
- Five of the adults were found alive. In at least two cases, the degree of damage seems to be in Category 4, yet the persons were only lightly injured.
- The death toll was 29 adults who were gathered in the hotel lobby at the time the avalanche struck. As the entire four-story main building was displaced some 10 m and completely collapsed, one can assume the degree of damage to be in Category 5.
In Figure 11, these data are combined with those from the avalanche at Longyearbyen (Svalbard) on 19 December 2015. In the case of Longyearbyen, each house hit by that avalanche gives rise to two separate data points, one for each story. For Rigopiano, the adult victims apparently were all gathered in the lobby and most of the children in a game room, which were damaged to different degrees. Therefore, the Rigopiano data appear as two separate data points. For each data point from Longyearbyen as well as for the one from the game room at Rigopiano, the “sample size”, i.e., the number of persons exposed to the avalanche, was very small (1–5), so that the statistical uncertainty is very large; for this reason, it is not plotted in the figure. The statistical uncertainty of the data points from the Rigopiano lobby, however, is about . The reader should be aware that the lines in the plot are only meant to guide the eye—they are not the result of a rigorous statistical analysis, which does not seem to be warranted yet. The trends from this limited data set can be summarized as follows:
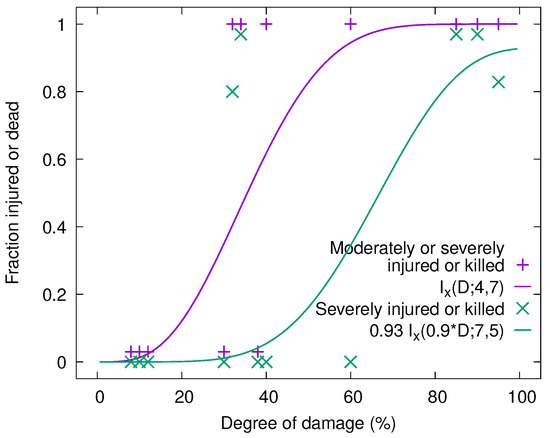
Figure 11.
Vulnerability data from two avalanche events. The data points with and are from the game room and lobby of Hotel Rigopiano, respectively, the other 11 sets of two points with equal are from each of the houses hit by the 19 December 2015 Longyearbyen avalanche [10]. Where data points would overlap, they were slightly shifted. The full curves were fitted visually with incomplete Beta functions and are only meant to guide the eye.
- The data for damage in Categories 4 and 5 appear consistent between the Longyearbyen and Rigopiano events. Somewhat surprisingly, six persons out of 35 survived building damage of degree 5 in Rigopiano, despite the long time it took to find and free them.
- Within the statistical uncertainty, the data from the Rigopiano game room is also consistent with the findings from Longyearbyen, even though the three children in Rigopiano may have survived essentially unscathed in a quite severely damaged room. The degree of damage should, however, be reassessed once more detailed information is released.
7. Conclusions
The observations on the 2017 Rigopiano avalanche described in [1] were limited by the short duration of the survey and the inaccessibility of the surroundings of the hotel ruins. Nevertheless, many interesting aspects of the dynamics of this event could be analyzed on the basis of this data, using simple yet physics-based descriptions. We summarize the main findings:
- Among the four avalanches that occurred in the vicinity of Rigopiano on or around 18 January 2017, the avalanche that destroyed the hotel had a much longer run-out than the others relative to the prediction of the - model. The reasons for this remain uncertain.
- The estimated front speeds in the range of 35 to 60 m s have a wide margin of uncertainty, but the most likely values in the range of 40 to 45 m s are of the same order as observations, measurements and numerical simulations of avalanches of similar size. The slow-moving, dense parts of the avalanche appear to have moved at about half the speed of the front. This agrees with observations and analyses in small-to-medium size avalanche paths in the Swiss Alps [16].
- Estimates of the mass balance are also fraught with large uncertainties, but a consistent picture emerges. It is probable that a large part of the snow cover was eroded, but much of this mass was only dragged along for some distance without becoming properly entrained into the flow. Tree debris contributed much to the mass growth of the avalanche.
- The observed damage patterns are consistent with the pressures derived from the velocity estimates, both with respect to the destroyed forest and the obliterated and displaced hotel. Breaking or uprooting of the forest was not a dominant factor in the energy balance of the entire avalanche, but must have had a significant braking effect on the fluidized flow in the forest destruction zone.
- When expressed as a function of the degree of building damage, the lethality curve resulting from the Rigopiano event is consistent with the one found in the 2015 Longyearbyen avalanche within the large uncertainties due to the small statistical base. This supports the usefulness of the degree of damage as the proper variable for obtaining a universal relation that does not depend on the building type.
The analyses presented here also provide a few pointers for future research. The first is that simple mechanical considerations often allow one to deduce a considerable amount of semiquantitative information from limited observational information. Each inference has a large margin of uncertainty, but if they all are consistent with each other, the probability of them being far off will be small. Thus, analysis of a large number of such observations can provide valuable insight on issues of avalanche dynamics, e.g., their scaling behavior or the conditions and frequency of specific flow regimes occurring.
The data collected in [4] and here can be used for detailed tests of dynamical avalanche models, as already attempted, e.g., in [7]. The assumed release area in those simulations, based on the work in [4], is about half of our estimate in Table 2, leading to an initial mass of 20 kt compared to our estimate of 30 kt. The authors reduced the estimated erodible snow mass of about 500 kg m in open terrain according to the crown coverage in the forested gully. The simulations with an extended variant of RAMMS [25] indicated a peak velocity of 44 m s at an altitude of 1450 m a.s.l., which is similar to our estimate of the minimum approach velocity to the shoulder at 1500 m a.s.l. We have no direct observations to compare to the simulated avalanche speed of 30 m s at Hotel Rigopiano. However, the simulated peak impact pressure of about 400 kPa at that location is at the upper end of our estimate for the minimum pressure for displacing the ruin, see Equation (13), and is thus compatible with it. The entrained mass in the model simulations was 100,000 m or 20–25 kt, which is far below our estimate of 110 kt of eroded mass, but there is no contradiction between these results: In our reconstructed mass balance (Figure 7b), the running mass peaks slightly above 50 kt, which means a net entrainment of 20 kt. According to the simulations, the maximum deposit depth near the hotel was less than 2 m; this appears at odds with photos and video clips showing a many meters deep deposit. This point deserves closer scrutiny when relevant data from the judicial investigation is made accessible. In the future, detailed analysis of tree debris distribution from drone surveys may also allow testing of comprehensive models of the braking effect and destruction of forests.
Some locals of Rigopiano have considerable knowledge about the avalanche history of the area, including release frequency and run-out distance in many avalanche paths on the eastern flank of this mountain chain. If these observations could be collected; critically analyzed; compared with a detailed dendrochronological study as presented by, e.g., the authors of [26,27]; and supplemented by numerical simulations, high-quality avalanche hazard maps could be elaborated for this little studied, rather southerly area. Such a map could contribute towards a solid and safe basis for the future touristic development of the surroundings of Farindola, which has suffered an enormous setback from this tragic event.
Funding
This work was funded by the special grant for snow avalanche research from the Norwegian Ministry of Oil and Energy, administrated by the Norwegian Water Resources and Energy Directorate (NVE). Writing of the paper was supported by the general research grant (“Grunnbevilgning”) from the Research Council of Norway to NGI.
Acknowledgments
Alessia Errera and Massimiliano Barbolini furnished valuable information about the event, the rescue operations, and the coverage in the Italian media. Jan-Thomas Fischer shared the notes of a survey by an Austrian team during the rescue operations and Betty Sovilla helped finding a digital terrain model. Thomas Scrine (Farindola) played a pivotal role for the survey by pointing out how the site could be surveyed without violating access restrictions due to the ongoing judicial investigations and bringing the author in contact with Daniele Borgheggiani, who provided a good map of the area, suggested a safe itinerary, and provided important information about avalanche activity around Rigopiano. I sincerely thank them all for their invaluable support. I am also grateful for encouraging comments from my colleagues at NGI, most notably Christian Jaedicke and Frode Sandersen, and the valuable help from three anonymous reviewers in correcting errors and making the manuscript more readable.
I dedicate this paper to the memory of my long-time friend and colleague Karstein Lied (1941–2019), who firmly believed in the importance of field observations and used them to gain deep insight into the behavior of avalanches. He also showed great interest in this event and the inferences presented here.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study or interpretation of data, in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Derivation of Flow Velocity from Run-Up
To analyze the run-up of an avalanche on a counter-slope of inclination , one should account for a number of effects: (1) conversion of kinetic energy to potential energy due to gravity, (2) bed friction along the counter-slope, (3) the tail of the avalanche “pushing” the front, and (4) energy dissipation due to internal shearing and increased bed friction in the bend at the foot of the counter-slope. For fast dry-snow avalanches, the flow velocity decreases along the avalanche body so that it seems justified to neglect the longitudinal pressure gradient. If the slope angle in the approach is , the avalanche is deflected by an angle at the foot of the counter-slope; this causes an extra frictional shear stress per unit mass of , with R the curvature radius at the foot of the slope. Throughout the hollow, the centrifugal acceleration is usually much larger than the gravitational one, , so that the equation of motion is , with s ranging from 0 to . With initial velocity , this gives the velocity at the beginning of the ascent after the hollow. Then, one readily obtains the approximate energy balance
for the velocity u after the avalanche has climbed the height . Dissipation due to internal shearing is responsible for the inequality. Note that centrifugal friction can dissipate a large part of the kinetic energy as –0.4 and often is in the range of 0.5 to 1. Formula (A1) applies to the dense and fluidized parts of an avalanche only; for an approximate treatment of run-up of powder-snow clouds, see [28].
To estimate the jump length of an avalanche flowing over a sharp ridge, we assume that (i) the ascent and descent sides of the ridge are inclined at constant angles and , respectively; (ii) the ridge itself is a circular arc with curvature radius r; (iii) we may disregard air resistance in a first approximation; and (iv) the width of the crest is negligible compared to the jump length. Lift-off occurs if the centrifugal pseudo-force exceeds the slope-normal component of gravity at the beginning of the curved crest segment, i.e., ; the lift-off angle is . We ascribe coordinates to the lift-off point. The avalanche front moves on a parabola given by . Eliminate the time t to obtain the curve
The touch-down distance is determined by the intersection of this parabola with the ground, . This evaluates to
An upper bound for the impact velocity is readily obtained from energy conservation:
Appendix B. Derivation of Flow Velocity from Super-Elevation
It is intuitively apparent that super-elevation—the height difference of flow marks on the outer and inner bank of a channel bend—contains information of high practical importance to the velocity of a past flow event. The motion of an avalanche or debris flow through a sinuous channel is, however, a complex flow-mechanical problem for which—in the author’s opinion—only numerical methods will provide a satisfactory solution. However, such an approach not only is labor-intensive but also requires specification of suitable initial conditions, which usually are not known. For this reason, several analyses with different degrees of simplification have been proposed in the literature, see, e.g., in [12,29,30,31,32]. To assess the reliability of these methods, it may be helpful to explicitly list the simplifications made in different proposals with regard to criteria that span the breadth of the physical problem at hand.
Appendix B.1. Characterization of the Topography
As convincingly demonstrated in [31], natural channels do not consist of straight-line and circle segments, but the curvature varies strongly along the curved segments. Except for the work in [12], approximate relations between super-elevation, curvature and avalanche velocity use a single value of curvature, and it is not always specified at which scale the latter was determined.
Furthermore, note that a gully bend that looks like a circular segment with horizontal radius and curvature on a map in reality is part of a screwline, provided that the inclination of the thalweg is constant, . The curvature of the screwline is then , where typically ranges from 0.5 to 1. In the literature, it is not always clear whether this geometric effect is taken into account or not. Moreover, in many estimates of flow velocity from super-elevation only the radius of the centerline of the gully is considered; this is sufficient if the curvature radius R is much larger than the channel width W; however, in many avalanche gullies where super-elevation is observed, is in the range of 0.1 to 0.5, making this approximation questionable.
Appendix B.2. Time Dependence
In mixed dry-snow avalanches such as the Rigopiano avalanche of 2017, the flow velocity decreases significantly (by roughly a factor of at least 2 [16] to as much as 10 [33]) from the fluidized front to the main avalanche body and to the decelerating and possibly stopping tail. It follows that super-elevation is a strongly time-dependent quantity. Yet, all approximate super-elevation formulas known to the author assume stationary flow to simplify the equations. This amounts to modeling the avalanche similarly to a river flow with constant discharge. For practical purposes, the maximum avalanche velocity, i.e., the front velocity, is usually of foremost interest. Therefore, if the super-elevation corresponding to the avalanche front can be determined, neglect of the time-dependent terms from the mass and momentum balances is acceptable from a practical point of view.
Field work after an event can estimate the super-elevation only from the altitude difference of the top flow marks on opposite points on the two channel flanks. It is generally assumed that the top flow marks were created by the fastest part of the avalanche, i.e., the front. However, this is not obvious for the top flow mark on the inner bend because the larger centrifugal force drives the fast front more strongly away from the inner bank than the slower parts following later. If this is the case, maximum super-elevation may be underestimated considerably. The assumption may nevertheless be correct if the front is strongly fluidized and has a much larger flow depth than the denser body. This may well have been true in the Rigopiano avalanche of 2017, and we will proceed with this assumption.
Appendix B.3. Can Inertial Effects Be Neglected?
A far-reaching simplification is obtained by neglecting spatial variations in the flow direction, which reduces the problem to a quasi-static balance between the forces acting in the cross-sectional plane. Furthermore, depth-averaging is generally applied so that the resulting equation is one-dimensional in the direction transverse to the flow (denoted r in the following).
One may try to justify this assumption by invoking the tendency of gravity mass flows to reach a (nearly) steady state on a slope of constant inclination. However, when an avalanche enters a bend and begins to climb up on the outer bank, the frictional dissipation can no longer be covered by gravitational work alone so that the kinetic energy is reduced. In this phase, the flow is not in a quasi-steady state and the velocity gradient in the flow direction s, , does not vanish. Likewise, as the flow exits the bend, it descends more steeply than and picks up speed, i.e., . If the bend is long enough, the avalanche might attain a (short-lived) new quasi-steady state with super-elevation in which, moreover, the transverse velocity so that the mass balance equation is trivially satisfied if there is no entrainment. In contrast, if the bend is too short for a new quasi-steady state to be reached, the inertial terms cannot be neglected: When the avalanche reaches the apex of its excursion from the thalweg, the super-elevation is less than what would be observed for an avalanche with the same initial conditions in a long bend.
To proceed, we assume that the avalanche indeed reaches a superelevated quasi-steady state in the bend so that we can ignore the inertial term in the momentum balance. That state is determined by a quasi-static force balance in the transverse direction through a one-dimensional ordinary differential equation; we term the force balance quasi-static because the radial pressure gradient depends crucially on the centrifugal force, which in turn depends on the (depth-averaged) azimuthal velocity . For this reason, further assumptions on are needed; we examine the most popular ones below.
If there are no other quasi-static forces than gravity and the centrifugal force (i.e., no friction or surface tension), the shape of the surface, , is determined by the requirement that it be perpendicular to the resulting force on a volume element at the surface,
with .
The free (or irrotational) vortex assumption is based on the conservation of vorticity in inviscid fluid flow: If the flow approaching the bend has zero vorticity, the vorticity has to remain zero in the bend, i.e., . In cylindrical coordinates and with , this reduces to , i.e., , where is constant across the cross section. Applying this in Equation (A5) leads to , i.e., the surface forms an upward convex hyperboloid. The two constants and can be determined by requiring that the volume discharge and the linear momentum discharge of the flow be conserved. We will not pursue this further because the free vortex assumption can hardly be justified for highly frictional flows like avalanches.
In contrast, the forced vortex assumption emphasizes that shear stresses inside a granular mass flow will tend to minimize the shear as it passes through the bend. In the limit, this leads to a quasi-rigid-body flow where the angular velocity is equal everywhere across a cross section. If frictional forces are neglected, Equation (A5) with leads to
i.e., the flow surface would be an upward concave paraboloid. The pressure per unit mass inside the flow is
in the approach part of the channel and
during the quasi-stationary phase of the flow through the bend. By direct integration of the body forces inside the wedge and the pressure on its boundary, one may verify that exactly balances the centrifugal force from all the mass in the wedge if the surface satisfies Equation (A6).
The flow depth at the inner bank, , and the angular velocity, , have to be chosen so as to fulfill additional constraints. The main candidates are the fundamental conservation laws, in this case expressed in terms of discharge of mass, linear and angular momentum, and energy. Under our idealized conditions, the flow is stationary so that the mass discharge must remain constant along the channel, providing the first constraint. Due to the normal and shear stresses exerted on the flow by the channel, none of the other three quantities is conserved for the flow itself so that the corresponding discharges are not strictly constant. If the bed and wall shear stresses are small or if they are mostly balanced by the downhill gravitational force, the discharge of both linear momentum and angular momentum about a given axis remain approximately constant. With a leap of faith, this can be used as a second constraint.
The relatively simple case of a frictionless fluid is useful for exploring the effect of different channel geometries. Consider first a rectangular channel with constant width W (Figure A1a,b). With an approach velocity and initial flow depth , one finds the volume discharge, , and the discharge of angular momentum about the center axis of the bend, before the bend. In the bend, the volume discharge is
with . From Equation (A9) one deduces
provided this is positive (negative values of indicate that the flow no longer touches the inner bank and these expressions need to be modified). In the limit one has , and .
Proceeding in the same way, one may express the angular momentum discharge as
In the limit , reduces to . The general solution to this quartic equation is not very illuminating, but if one sets , one immediately finds an approximate solution for very gently curved channels,
which allows one to relate the super-elevation not only to , the velocity in the bend, but also to the approach velocity . Furthermore, if one evaluates Equation (A6) at , one can express the super-elevation as
The first part of Equation (A13) is equivalent to Equation (8.27a) in [29], (p. 308).
Figure A1.
Simple channel geometries used in the text: (a) Normal view and (b) cross section of a rectangular channel of constant width with a circular bend. (c) Prismatic channel. Note that the bank slope angle is measured in the cross-sectional plane, which in general is inclined relative to the horizontal. The flow depth in a straight segment is drawn such that the cross-sectional area is somewhat smaller than in the superelevated state to indicate that the mean flow velocity in the bend may be lower than in the straight segments due to increased dissipation.
Prismatic channel cross section: A more relevant geometry for snow avalanches is a gully with prismatic cross section, as shown in Figure A1c. The physical principle of the transverse pressure gradient balancing the centrifugal force remains the same, and so the formulas for the surface shape (A6) and the pressure distribution (A8) are unchanged except for modifications to the domain according to Figure A1c. With this, the surface still is a paraboloid under the forced-vortex assumption. Equation (A13) carries over to this geometry if one sets and replaces W by . varies according to and is determined by the intersection of the flow surface with the outer bank: , where one is to take the smaller of the two roots of this quadratic equation. For larger than a critical value, there is no solution and, hence, no quasi-static configuration; however, substantial input of energy would be needed to reach this state. One may now proceed to calculate the mass and angular-momentum discharges and and to approximately determine and , but explicitly doing so is beyond the present scope.
In reality, flow in a channel or gully bend will not be irrotational due to viscous stresses or friction inside the flow, nor will it be like rigid-body motion because these stresses are not strong enough to prevent considerable shear in the -z plane. It is doubtful whether the assumption of a quasi-steady super-elevation state is a reasonable approximation at all since the flow is three-dimensional and non-stationary. Even if one admits this approximation, the shape of the surface will be between an upward convex hyperboloid and an upward concave paraboloid in the absence of friction. One may argue that the free-vortex approximations will be closer to reality if the flowing material has low internal viscosity or friction and if the bend is short and sharp, i.e., the channel width W is of the same order of magnitude as the mean radius and its length is short compared to the characteristic distance over which the flow adapts its velocity to new conditions. If and , the forced-vortex assumption will be closer to reality.
Appendix B.4. McClung’s Model for Super-Elevation in Granular Avalanches
Some researchers have adapted Equation (A13) with an empirical factor to account for the specific properties of granular mass flows. Not surprisingly, the values of the coefficient range over an order of magnitude because important physics is missing. McClung gave the first analysis of super-elevation based on a central property of granular materials, namely, friction [30]. The model distinguishes between basal friction, characterized by an effective friction coefficient , and the internal friction angle of the moving avalanche, . The latter contributes to the balance of forces through passive earth pressure across a longitudinal section at the foot of the outer bank slope. Basal friction acts along the outer bank slope. As a quasi-stationary flow is considered, there is no actual sliding along the bank slope transverse to the flow direction and it is not a priori clear in which direction this friction force acts. This is left to separate assessment in each specific situation, but it is argued that fast dry-snow avalanches will tend to move upslope () so that the friction force points downslope, and conversely for slow wet-snow avalanches ().
If one assumes a triangular channel cross section ( in Figure A1c) and that as well as the flow depth at the center line of the channel are known, the following velocity estimate is proposed in [30],
Here, is the passive earth pressure coefficient; it depends on the internal friction angle and is larger than 1. Usually, . is the transverse sliding velocity, or rather, sliding tendency, which determines the sign of the transverse frictional force component. The latter is proportional to the effective friction coefficient . If one sets and , Equation (8.27a) in [29], (p. 308) is recovered. If and the terms specific to granular flows are accounted for, a frictional avalanche needs higher velocity than a frictionless one to attain an observed super-elevation.
Closer scrutiny reveals a number of points to consider before applying this formula. First, the geometry suggested in [30] (Figure 2) does not allow one to connect the super-elevation to flow marks on the inner channel bank because the author assumes that the lowest point of the flow surface is in the center and that the flow surface rises towards the innermost point in some unspecified way. This means that and have to be estimated from the condition , leading to considerable ambiguity. If the flow cross section in the approach section, , can be estimated from flow marks, one may try to narrow the possible values down by setting the volume discharges and equal. However, the cross-sectional area on the inside of the center line, needs to be guessed and assumptions about the relation between and made.
A second point to note is that a uniform velocity across the cross section is tacitly assumed. This differs fundamentally from the forced-vortex assumption and is hardly more realistic in a frictional material because such motion would cause considerable shear and friction forces in planes normal to the radial direction, tending to the rigid-body motion implied by the forced-vortex assumption. Moreover, only the curvature radius at the center line, is considered; this amounts to the condition , which often does not hold in real avalanche gullies.
Third, there are some subtleties associated with the basal friction term in Equation (A14): The avalanche is moving in the azimuthal direction in the assumed quasi-steady state. This means that there is shear at the flow base, implying that the Coulomb failure criterion is met at the interface between the flow and the bed and that the maximum shear stress is mobilized against the flow direction. must hold in the quasi-steady state so that the shear stress component along the bank slope becomes approximately (with the corresponding normal stress), i.e., it goes to zero. Accordingly this term should be dropped from Equation (A14).
Appendix B.5. Alternative Treatment of Granular Effects
When attempting to remedy the shortcomings of the model in [30], one of the questions that arise concerns the shape of the superelevated flow surface when friction is present. Assume that the forced-vortex assumption is fulfilled in the limiting quasi-steady state so that the shear stress vanishes or is relatively small. An infinitesimal control volume at the flow surface is subjected to a body force per unit mass, ,
in the local cylindrical coordinate system , with the azimuth angle in the flow direction and . It must be compensated by the forces from the shear stresses and and the normal stresses and . These combine to
where , , and we assume hydrostatic normal stresses for simplicity. The coefficients and indicate the degree to which the frictional shear strength is mobilized in the respective direction; they must satisfy the condition . From the quasi-steady-state condition , one sees that two cases must be distinguished: (a) If , and . Then, the radial component of the force balance leads to the same equations for , Equation (A6), and the super-elevation, Equation (A13), as in the case of a viscous fluid. (b) If , then and . Now one obtains the differential equation
which is solved by
Thus, if the gully floor is less steep than the internal friction angle, this simplistic granular model also predicts a paraboloid surface shape, but the super-elevation is reduced:
This formula predicts the velocity of a granular flow in a gently inclined gully to be higher than the estimate from Formula (A13) for a viscous fluid. The main problem in applying Formula (A19) is the lack of measurements of the dynamic internal friction angle of avalanches, with estimates in the literature differing from about 15° to 65° (see the discussion in [30] (Section 4)). However, if there is reason to assume that the avalanche front was strongly fluidized, the dynamic internal friction angle can be set to 0 and Equation (A13) applies.
Appendix B.6. Remarks on the Pudasaini–Jaboyedoff Super-Elevation Model
In [12], a substantially different approach to estimating flow velocity from super-elevation is used. The starting point is the Pudasaini–Hutter model [34], an extension of the Savage–Hutter model adapted to flows in arbitrarily curved avalanche gullies. It is formulated in a special “tubular” coordinate system , the center line of which () parallels the talweg of the gully. s is the arc length along the center line; for each value of s, all points in the plane normal to the center line can be described by the azimuthal angle , measured from the local normal vector of the center line, and the distance r from . (In [12,34], the azimuthal angle is ; we will use instead to prevent confusion with the slope angle used elsewhere in the present paper.) As a curve in 3D space, is characterized by its curvature and torsion , from which the curvature and torsion of the coordinate lines can readily be calculated. This coordinate system is locally orthogonal, but not terrain-following so that the gully surface is not usually tangential to the s and coordinate lines and normal to the r lines. This is relevant because it induces extra gravitational force terms in the momentum balance equations (termed “topographical pressure gradient terms” in [12]).
Written in this complex coordinate system, the balance equations of mass and momentum necessarily contain many terms that account for the curvature effects. An unusual feature is that the torsion of also enters in a prominent role. This is a direct consequence of the s-dependence of the normal vector of , from which the azimuthal coordinate is measured. Statements like “In fact, super-elevation is the result of the twist of the topography that corresponds to ” [12] (p. 1385), must therefore not be interpreted as saying that other approaches to super-elevation, using substantially different coordinate systems, are wrong if they do not account for torsion. For example, in the report [35] the depth-averaged balance equations for a gravity mass flow are derived for terrain-following curvilinear coordinate systems; as no talweg or similar curve is singled out, there is no notion of torsion, yet the equations are physically equivalent to the ones presented in [34] (up to terms of higher order in an expansion in powers of small quantities).
The Pudasaini–Hutter model achieves significant simplification by a scale analysis and discarding all but the leading and next-to-leading terms. However, in this author’s opinion, some of the assumptions are poorly adapted to strongly channelized flows like the Chamoson debris flow featured in [12]. In particular, it is assumed that the curvature radii of the gully are much larger than the flow length, and it is not recognized that gullies often are more strongly curved in the cross-flow direction than in the flow direction. The assumed ordering of terms retains extra friction due to the centrifugal force associated with the main bend, , but drops similar contributions proportional to and . While typically , this may be compensated by . For example, neglecting this term will lead to significantly wrong predictions for the run-up height of an avalanche released from the side of a gently inclined straight gully.
To focus on the decisive points of the super-elevation formulas developed in [12], we set the earth-pressure coefficients to 1, assume a constant semicircular cross section of the gully (radius ) and use the variables , and instead of s, and r. In this simplified setting, the topographic gradient as well as derivatives in the z-direction vanish. We set , and . The quantity
plays an important role in this theory. The time derivatives and the inertial terms are dropped from the momentum balance equations in [12] so that the latter reduce to
Squaring this vector equation leads to an expression that can be solved for the longitudinal velocity u (equivalent to Equation (6) in [12] if the topographic pressure gradient vanishes):
However, this formula has significant limitations: (i) At some points along the gully, and/or may be zero. This causes divergence of u unless there is exact equilibrium between the gravitational driving force and the hydrostatic pressure gradient on the one hand, and the frictional resistance on the other hand. (ii) Where , the frictional force without centrifugal effects must be smaller than the driving forces for a real solution to exist. (iii) The factor should be replaced by to ensure a real solution. (iv) To calculate u, the spatial distribution of the flow depth must be known so that can be evaluated. This information is not available except in laboratory experiments. One may try to obtain a rough estimate from the super-elevation height and the width W of the channel, but the gradient of h will depend crucially on the shape of the surface. However, the discussion in Section B.5 has shown how strongly this shape depends on the transverse profile of u.
The authors then proceed to extract the transverse velocity v through the formula
where they define the so-called super-elevation number as
This formula predicts v to be non-zero unless . Near the outer edge of the avalanche , therefore , and conversely near the inner edge. Thus the Pudasaini–Jaboyedoff model predicts that the avalanche will spread sideways while rounding the bend (this may or may not be the case in reality) and that this spreading will continue (within the bend) until the avalanche becomes very thin so that . This nonphysical result is a direct consequence of neglecting the inertial terms, yet applying the truncated equations to a non-stationary situation.
Appendix C. Forces, Moments and Energetics of Tree Breaking and Uprooting
A tree trunk breaks when either the tensile stress near the outer periphery of the trunk or the compressive stress near the inner periphery exceed the modulus of rupture (MoR). The MoR has been measured by many authors, with somewhat differing results; in particular, it is about 50% higher for dried wood than for green wood. According to the work in [36] (ch. 4), the MoR for (green) beech is about 59 MPa. With some simplifying assumptions of homogeneity across the cross section, the maximum bending moment can be obtained by integration across the cross section:
where is the trunk diameter at the failing cross section. For simplicity, is often replaced by the diameter at breast height (DBH). A beech with m will thus break at a bending moment of (40–50) kN m, whereas (600–750) kN m is required to break one with m.
To estimate the bending moment due to an avalanche, we assume a local slope angle , a snow depth and a flow depth (both measured normal to the ground), flow density , flow velocity profile (with z the coordinate normal to the ground), and a constant trunk diameter . For simplicity, we neglect drag forces along the axis of the tree trunk due to the oblique impact and apply a drag formula that is appropriate for flow of cohesionless granular materials around a cylinder [37,38,39]:
with . Then, we obtain
The integral evaluates to
Our lack of knowledge of the velocity profile leads to an uncertainty of about %, and the effect of a non-uniform density profile has not been accounted for in this simple analysis. For plausible values , the integral is in the range . With typical Froude numbers in the range 3–7, one has , so that we estimate
To calculate the maximum moment that the root system of a tree can sustain, one would need detailed information about the shear strength of the root system as a function of distance from the tree foot and of depth in the soil and about the cohesion and internal friction angle of the soil as a function of depth. None of this is available for the Grava dei Bruciati, so only a summary estimate can be made in terms of some mean shear strength of the root system and the soil/bedrock combined. The observations and the literature provide an approximate value for the diameter of the root system, , out to the failure surface relative to the tree diameter, namely, from the observations and from the work in [22] (Figure 14).
With these simplifications, one can integrate the moment about the y-axis perpendicular to the flow direction over the hemisphere. In a spherical coordinate system with azimuth angle about the y-axis and elevation angle , the leverage arm is and the surface area element , which leads to
Appendix D. Estimate of the Strength of Hotel Rigopiano against Avalanche Impact
Analyzing the structural stability of a complex building under impact is far beyond the scope of the present paper. Nevertheless, to get an indication of the order of magnitude, we consider two simple load cases that should be relevant in the case of Hotel Rigopiano, namely, (i) failure of a wide solid wall under an impact lasting longer than the period of the lowest eigenmode and (ii) impact of a solid object (tree or stone) on a masonry wall. Windows and doors may reduce the structural strength significantly, but the extra support from sidewalls and ceilings will most likely more than compensate for this. The letters and will be used to denote stress and material strength, respectively, with subscripts c, s and t indicating compression, shear and tension.
When an avalanche impacts a wide solid wall of thickness b without interior support walls, the shear stress inside the wall at the level of the bottom of the flow, at , can be calculated as
where is the vertical pressure profile along the wall and H is the splashing height at the wall, limited by the building height. Similarly, the bending moment per unit width at the base of the wall is
In the calculation of , splashing can be neglected and used, giving . In the calculation of , splashing matters in that it reduces the pressure in the upper part of the flow while reaching higher than the original flow depth, with a correspondingly larger leverage arm. The analysis in [40] and the recommendations in [41] (Chapter 11) are relevant in this context, but in view of the large uncertainties we take a short-cut and use , with the depth of the flow. The area moment of inertia of the wall per unit width being , the maximum tension at the base becomes .
The strength of non-reinforced masonry walls is essentially determined by the mortar, of which there are many varieties with widely varying properties. Typical values found in the literature and on various websites are about for the shear strength, for the tensile strength and for the compressive strength, but significantly lower or higher values are also mentioned.
The impact of a tree onto a masonry wall is a complex process, both with regard to the physics and the variability of the initial conditions. Some trees are rafted by the avalanche with the crown ahead, others with the root system first. Especially the crown has a large area and is much softer than the trunk, whereas the root systems of trees in the Rigopiano avalanche often contained large quantities of limestone. If the tree trunk is not aligned with the flow direction, it will be rotated about a approximately vertical axis upon impact. Due to this variability, it does not seem possible to assess the effect of the tree debris on the damage to Hotel Rigopiano with simple means.
It may nevertheless be of some interest to consider the limiting case with the largest damage potential: Assume a tree of (constant) diameter , length , density , and Young’s modulus E (along the fibers) to hit the masonry wall in axial direction and perpendicularly with a velocity v. The stone block that is hit is assumed to transmit the impact force to the mortar along its perimeter of length ℓ and depth b. The wall is considered to be damaged if the mean shear stress in the mortar exceeds its shear strength, . This gives a lower bound on the tree velocity required for damaging the wall; under non-axial and/or oblique impact, the shear stresses are reduced and a higher impact velocity is needed.
The impact force exerted by the tree is transmitted almost instantaneously through the stone to the mortar, leading to a mean shear stress in the latter. From this, one obtains the failure condition . The value of ℓ depends on whether the tree hits one or several stones, which we assume to have mean width w and height h: for a single stone, for two stones shifted by , in the case of three stones in two layers, etc. This does not take into account that the shear stress is not uniform along the perimeter. For typical masonry (limestone blocks for the old Rifugio Rigopiano, possibly bricks in the new part of the hotel), one may assume ℓ to be about one order of magnitude larger than .
To obtain a bound on , consider that the momentum of the tree, , needs to be transmitted during the time it takes to stop the tree, thus
During the impact, a compressive shock travels along the tree with a speed c so that . This implies that does not depend on the tree length while is proportional to it. The wall will be penetrated by the tree if
The physics behind this approach is similar to the so-called water hammer effect, the main difference being the appearance of plastic deformation in a solid. This makes the problem significantly harder to treat for solids than for a Newtonian fluid, see, e.g., in [42] for a lucid account. The following simple analysis is largely guided by that work.
In the linear elastic regime, characterized by Young’s modulus E, the propagation speed of sound waves is given by (we use the engineering convention here with compressive stresses counted positive). With GPa along the grain for most tree species and kg m for beech, km s. At an impact speeds above 10 m s, the compressive stress, , exceeds the compressive strength of green beech wood along the grain (about 25 MPa according to the work in [36]). It is likely, however, that a long tree trunk will fail already at lower impact speed due to buckling. In addition, the wood begins to deform plastically well before the stress equals its compressive strength. It appears reasonable to assume wood to be hardening in the plastic regime, i.e., , which implies that the plastic shock propagates more slowly than the elastic wave. If we further suppose that the plastic shock speed is still larger than the sound speed in water, . Using this value in Equation (A33) with m, m, MPa, m, and kg m leads to a minimum impact velocity of 2.5–4 m s. However, as pointed out above, the probability of a perpendicular and axial impact without dampening effect of the crown or root system is very low.
Incidentally, the obtained minimum velocity looks plausible when comparing it to the impact velocity of battering rams used in sieges of fortified cities in antiquity and the Middle Ages: The rams were often suspended from chains so that they could be swung. To judge from images of medieval siege machines [43], the fall height during the swing was probably about 1.5 m or less, giving an impact velocity of 5–10 m s against very massive walls with .
References
- Issler, D. Field Survey of the 2017 Rigopiano Avalanche; NGI Technical Note 20170131-02-TN; Norwegian Geotechnical Institute: Oslo, Norway, 2018; Available online: https://www.ngi.no/download/file/14511 (accessed on 8 April 2020).
- Hotel Rigopiano, l’esposto del Forum H2O: “In queste foto la prova di valanghe precedenti”. 2017. Available online: https://www.repubblica.it/cronaca/2017/01/26/foto/rigopiano_forum_h2o-156964271 (accessed on 8 April 2020).
- Iannetti, P. Oggetto: Commissione Valanghe (L.R. n.47 del 18.06.92). Letter to the Mayor of Farindola. 1999. Available online: http://www.repubblica.it/static/infografica/cronaca/rigopiano/Relazione-Comune-Farindola-001.pdf (accessed on 10 November 2018).
- Chiambretti, I.; Chiaia, B.; Frigo, B.; Marello, S.; Maggioni, M.; Fantucci, R.; Bernabei, M. The 18th January 2017 Rigopiano avalanche disaster in Italy—Analysis of the applied forensic field investigation techniques. In Proceedings of the International Snow Science Workshop, Innsbruck, Austria, 7–12 October 2018; pp. 1208–1212. [Google Scholar]
- Chiambretti, I.; Sofia, S. Winter 2016–2017 snowfall and avalanche energency management in Italy (central Appennines)—A review. In Proceedings of the International Snow Science Workshop, Innsbruck, Austria, 7–12 October 2018; pp. 1445–1449. [Google Scholar]
- Tedim, F.; Leone, V. The deadly avalanche of Rigopiano (Italy): Evidences of a constructed local disaster. In The Overarching Issues of the European Space—Preparing the New Decade for Key Socio-economic and Environmental Challenges; Remoalda, P., Ed.; Faculdade de Letras da Universidade do Porto: Porto, Portugal, 2018; pp. 408–424. [Google Scholar]
- Frigo, B.; Chiaia, B.; Chiambretti, I.; Bartelt, P.; Maggioni, M.; Freppaz, M. The January 18th 2017 Rigopiano disaster in Italy—Analysis of the avalanche dynamics. In Proceedings of the International Snow Science Workshop, Innsbruck, Austria, 7–12 October 2018; pp. 6–10. [Google Scholar]
- Fischer, J.-T. BFW, Innsbruck, Austria. Personal communication to D. Issler, 2017. [Google Scholar]
- Bakkehøi, S.; Domaas, U.; Lied, K. Calculation of snow avalanche runout distance. Ann. Glaciol. 1983, 4, 24–29. [Google Scholar] [CrossRef]
- Issler, D.; Jónsson, Á.; Gauer, P.; Domaas, U. Vulnerability of houses and persons under avalanche impact—The avalanche at Longyearbyen on 2015-12-19. In Proceedings of the International Snow Science Workshop ISSW 2016, Breckenridge, CO, USA, 3–7 October 2016; pp. 371–378. [Google Scholar]
- Valanga di Rigopiano. 2017. Available online: https://it.wikipedia.org/wiki/Valanga_di_Rigopiano (accessed on 2 November 2020). (In Italian).
- Pudasaini, S.P.; Jaboyedoff, M. A general analytical model for superelevation in landslide. Landslides 2020, 17, 1377–1392. [Google Scholar] [CrossRef]
- Tarquini, S.; Isola, I.; Favalli, M.; Battistini, A. TINITALY, a Digital Elevation Model of Italy with a 10 m-Cell Size (Version 1.0). Data Set Prepared by Istituto Nazionale di Geofisica e Vulcanologia (INGV). 2007. Available online: http://tinitaly.pi.ingv.it/ (accessed on 22 October 2020). [CrossRef]
- Gauer, P. Considerations on scaling behavior in avalanche flow along cycloidal and parabolic tracks. Cold Regions Sci. Technol. 2018, 151, 34–46. [Google Scholar] [CrossRef]
- Smith, D.J.; McCarthy, D.P.; Luckman, B.H. Snow-avalanche impact pools in the Canadian Rocky Mountains. Arct. Alp. Res. 1994, 26, 116–127. [Google Scholar] [CrossRef]
- Issler, D.; Errera, A.; Priano, S.; Gubler, H.; Teufen, B.; Krummenacher, B. Inferences on flow mechanisms from snow avalanche deposits. Ann. Glaciol. 2008, 49, 187–192. [Google Scholar] [CrossRef][Green Version]
- Issler, D.; Gauer, P.; Schaer, M.; Keller, S. Supplementary Materials: Field observations of three mixed snow avalanches. Geosciences 2020, 10, 2. [Google Scholar] [CrossRef]
- Sovilla, B.; Sommavilla, F.; Tomaselli, A. Measurements of mass balance in dense snow avalanche events. Ann. Glaciol. 2001, 32, 230–236. [Google Scholar] [CrossRef]
- Rauter, M.; Köhler, A. Constraints on entrainment and deposition models in avalanche simulations from high-resolution radar data. Geosciences 2020, 10, 9. [Google Scholar] [CrossRef]
- Sovilla, B. Field Experiments and Numerical Modelling of Mass Entrainment and Deposition Processes in Snow Avalanches. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2004. [Google Scholar] [CrossRef]
- Gauer, P.; Issler, D. Possible erosion mechanisms in snow avalanches. Ann. Glaciol. 2004, 38, 384–392. [Google Scholar] [CrossRef]
- Mattheck, C.; Bethge, K.; Kappel, R.; Mueller, P.; Tesari, I. Failure modes for trees and related criteria. In ‘Wind Effects on Trees’ Proceedings of the International Conference; Ruck, B., Kottmeier, C., Mattheck, C., Quine, C., Wilhelm, G., Eds.; Laboratory of Building and Environmental Aerodynamics, Institute for Hydromechanics, University of Karlsruhe: Karlsruhe, Germany, 2003; p. P9/1. ISBN 3-00-011922-1. [Google Scholar]
- Ribeiro, G.H.P.M.; Chambers, J.Q.; Peterson, C.J.; Trumbore, S.E.; Magnabosco Marra, D.; Wirth, C.; Cannon, J.B.; Négron-Juárez, R.I.; Lima, A.J.N.; de Paula, E.V.C.M.; et al. Mechanical vulnerability and resistance to snapping and uprooting for Central Amazon tree species. For. Ecol. Mgmt. 2016, 380, 1–10. [Google Scholar] [CrossRef]
- Gauer, P.; Lied, K.; Kristensen, K. On avalanche measurements at the Norwegian full-scale test-site Ryggfonn. Cold Reg. Sci. Technol. 2008, 51, 138–155. [Google Scholar] [CrossRef]
- Bartelt, P.; Christen, M.; Bühler, Y.; Caviezel, A.; Buser, O. Snow entrainment: Avalanche interaction with an erodible substrate. In Proceedings of the International Snow Science Workshop, Innsbruck, Austria, 7–12 October 2018; pp. 716–720. [Google Scholar]
- Favillier, A.; Guillet, S.; Morel, P.; Corona, C.; Lopez Saez, J.; Eckert, N.; Ballesteros Cánovas, J.A.; Peiry, J.L.; Stoffel, M. Disentangling the impacts of exogenous disturbances on forest stands to assess multi-centennial tree-ring reconstructions of avalanche activity in the upper Goms Valley (Canton of Valais, Switzerland). Quat. Geochronol. 2017, 42, 89–104. [Google Scholar] [CrossRef]
- Oller, P.; Fischer, J.T.; Muntán, E. Multidisciplinary approach to reconstruct the historic avalanche that destroyed the village of Àrreu in 1803, Catalan Pyrenees. Geosciences 2020, 10, 169. [Google Scholar] [CrossRef]
- Issler, D.; Gauer, P.; Schaer, M.; Keller, S. Inferences on Mixed Snow Avalanches from Field Observations. Geosciences 2020, 10, 2. [Google Scholar] [CrossRef]
- Johnson, A.M.; Rodine, J.R. Debris flow. In Slope Instability; Brunsden, D., Prior, D.B., Eds.; Landscape Systems; John Wiley & Sons: Chichester, UK, 1984; Chapter 8; pp. 257–361. [Google Scholar]
- McClung, D.M. Superelevation of flowing avalanches around curved channel bends. J. Geophys. Res. 2001, 106, 16489–16498. [Google Scholar] [CrossRef]
- Prochaska, A.B.; Santi, P.M.; Higgins, J.D.; Cannon, S.H. A study of methods to estimate debris flow velocity. Landslides 2008, 5, 431–444. [Google Scholar] [CrossRef]
- Scheidl, C.; McArdell, B.W.; Rickenmann, D. Debris-flow velocities and superelevation in a curved laboratory channel. Can. Geotech. J. 2015, 52, 305–317. [Google Scholar] [CrossRef]
- Gauer, P.; Kern, M.; Kristensen, K.; Lied, K.; Rammer, L.; Schreiber, H. On pulsed Doppler radar measurements of avalanches and their implication to avalanche dynamics. Cold Regions Sci. Technol. 2007, 50, 55–71. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Hutter, K. Rapid shear flows of dry granular masses down curved and twisted channels. J. Fluid Mech. 2003, 495, 192–208. [Google Scholar] [CrossRef]
- Issler, D. Curvature Effects in Depth-Averaged Flow Models on Arbitrary Topography; NGI Report 20021048–14; Norwegian Geotechnical Institute: Oslo, Norway, 2006. [Google Scholar]
- Forest Products Laboratory. Wood Handbook. Wood as an Engineering Material; General Technical Report FPL-GTR-113; Forest Products Laboratory, Forest Service, U.S. Dept. of Agriculture: Madison, WI, USA, 1999. [Google Scholar]
- Chehata, D.; Zenit, R.; Wassgren, C.R. Dense granular flow around an immersed cylinder. Phys. Fluids 2003, 15, 1522–1531. [Google Scholar] [CrossRef]
- Wassgren, C.R.; Cordova, J.A.; Zenit, R.; Karion, A. Dilute granular flow around an immersed cylinder. Phys. Fluids 2003, 15. [Google Scholar] [CrossRef]
- Issler, D.; Gleditsch Gisnås, K.; Domaas, U. Approaches to Including Climate and Forest Effects in Avalanche Hazard Indication Maps in Norway; Technical Note 20150457-10-TN; Norwegian Geotechnical Institute: Oslo, Norway, 2020; Available online: https://www.nve.no/media/10589/20150457-10-tn.pdf.
- Kulibaba, V.S.; Eglit, M.E. Numerical modeling of an avalanche impact against an obstacle with account of snow compressibility. Ann. Glaciol. 2008, 49, 27–32. [Google Scholar] [CrossRef]
- Jóhannesson, T.; Gauer, P.; Issler, D.; Lied, K. (Eds.) The Design of Avalanche Protection Dams—Recent Practical and Theoretical Developments; Contributions by Barbolini, M., Domaas, U., Faug, T., Gauer, P., Hákonardóttir, K.M., Harbitz, C.B., Issler, D., Jóhannesson, T., Lied, K., Naaim, M., et al.; European Commission: Brussels, Belgium, 2009; p. X + 195. Volume 23339. [Google Scholar] [CrossRef]
- Cohen, T.; Durban, D. Longitudinal shock waves in solids: The piston shock analogue. Proc. R. Soc. (Lond.) Ser. A 2014, 470, 20130061. [Google Scholar] [CrossRef]
- Battering Ram. 2020. Available online: https://en.wikipedia.org/wiki/Battering_ram (accessed on 11 April 2012).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).