Prediction of Sow Farrowing Onset Time Using Activity Time Series Extracted by Optical Flow Estimation
Simple Summary
Abstract
1. Introduction
2. Materials and Dataset
2.1. Experimental Subjects and Data Collection
2.2. Dataset Construction
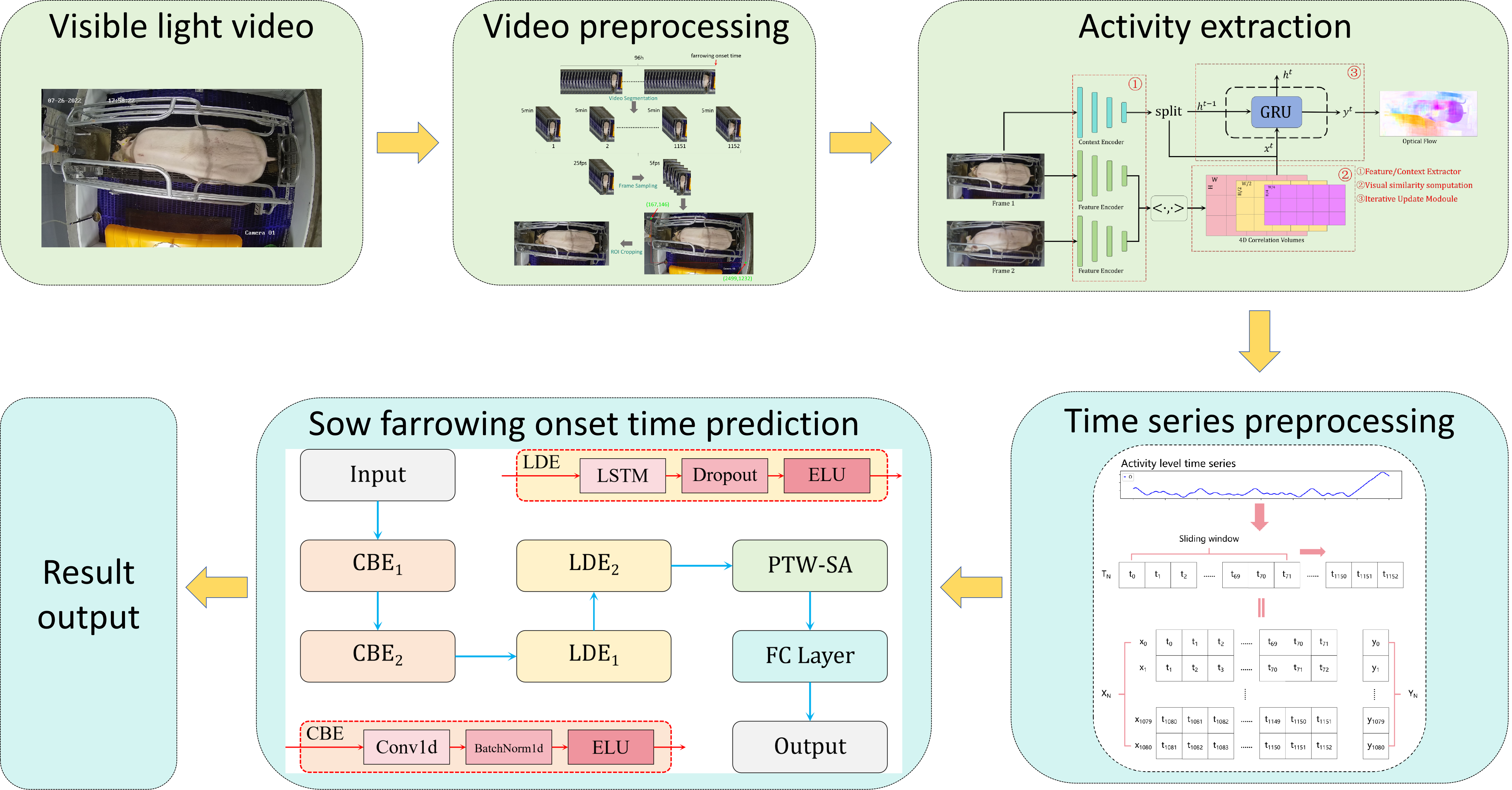
2.2.1. Visible-Light Video Preprocessing
- (1)
- Video segmentation: The onset of sow farrowing (defined as the moment the first piglet is born, determined through manual review of the visible-light video) is used as the endpoint for segmentation. Starting from this point, the video is segmented into 5-min clips by moving backward in time. For each sow, a total of 1152 video clips, each 5 min long, were generated.
- (2)
- Frame extraction: To reduce computational complexity while preserving key information, the original video frame rate of 25 frames per second (fps) was reduced to 2 fps. Specifically, the 1st and 13th frames of each second were selected.
- (3)
- Image cropping: To focus on the activity area of the sow, each video frame was cropped to exclude irrelevant regions and highlight the region of interest (ROI). A red rectangle was first used to mark the ROI in the image, with the top-left corner coordinates at (167, 146) and the bottom-right corner coordinates at (2499, 1232), resulting in a rectangle size of 2332 pixels in width and 1086 pixels in height. Based on this marked ROI, all video frames were cropped, ensuring that the dataset retained only the activity information within the target area.
2.2.2. Construction of Sow-Activity Time-Series Dataset
3. Methods
3.1. Overview of the Methodology
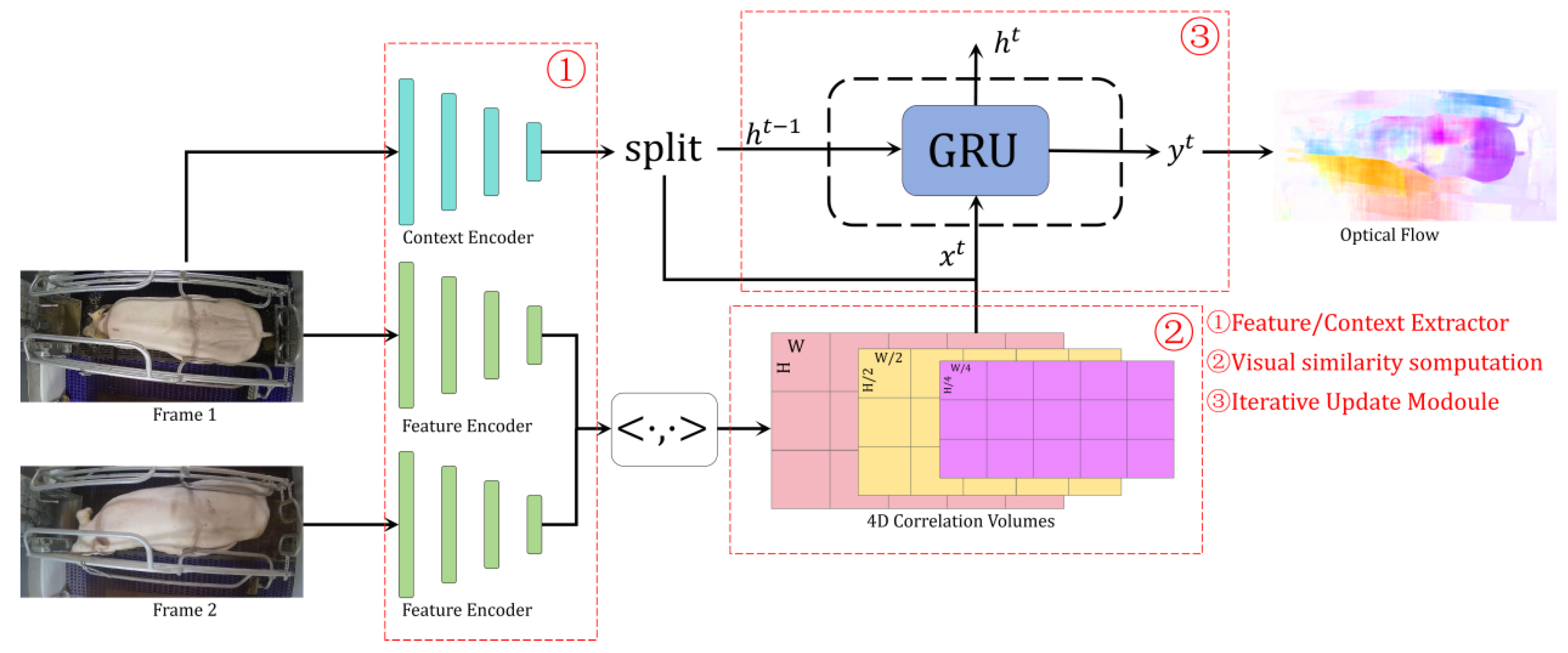
3.2. Sow Activity Extraction Algorithm Based on Optical Flow Estimation
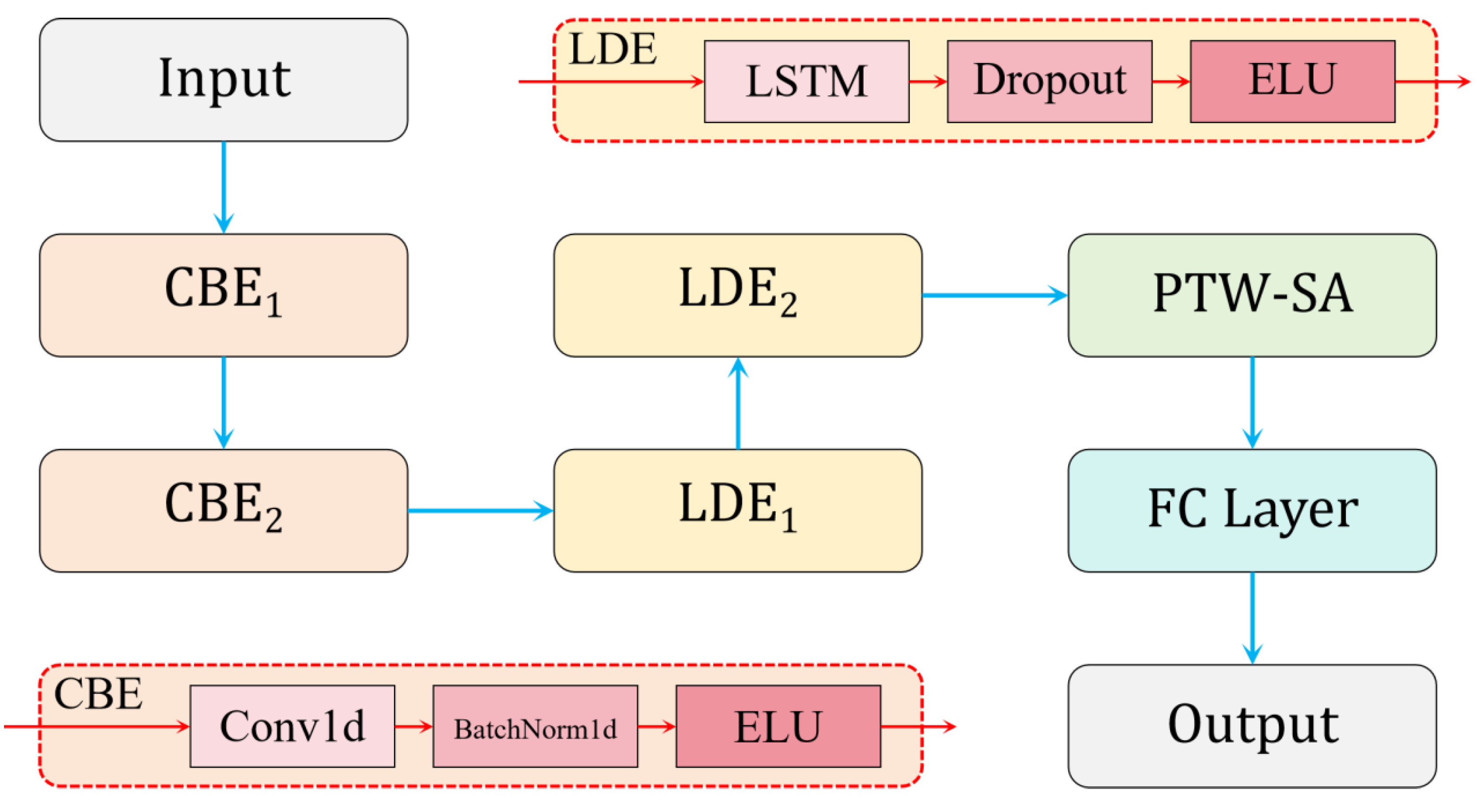
3.3. Construction of the CLA-PTNet Model
3.3.1. Structure of CLA-PTNet
3.3.2. Design of PTW-SA
4. Results and Analysis
4.1. Experimental Platform
4.2. Evaluation Metrics
4.3. Comparison of Different Optical Flow Estimation Models
4.4. Sow Activity Data Analysis
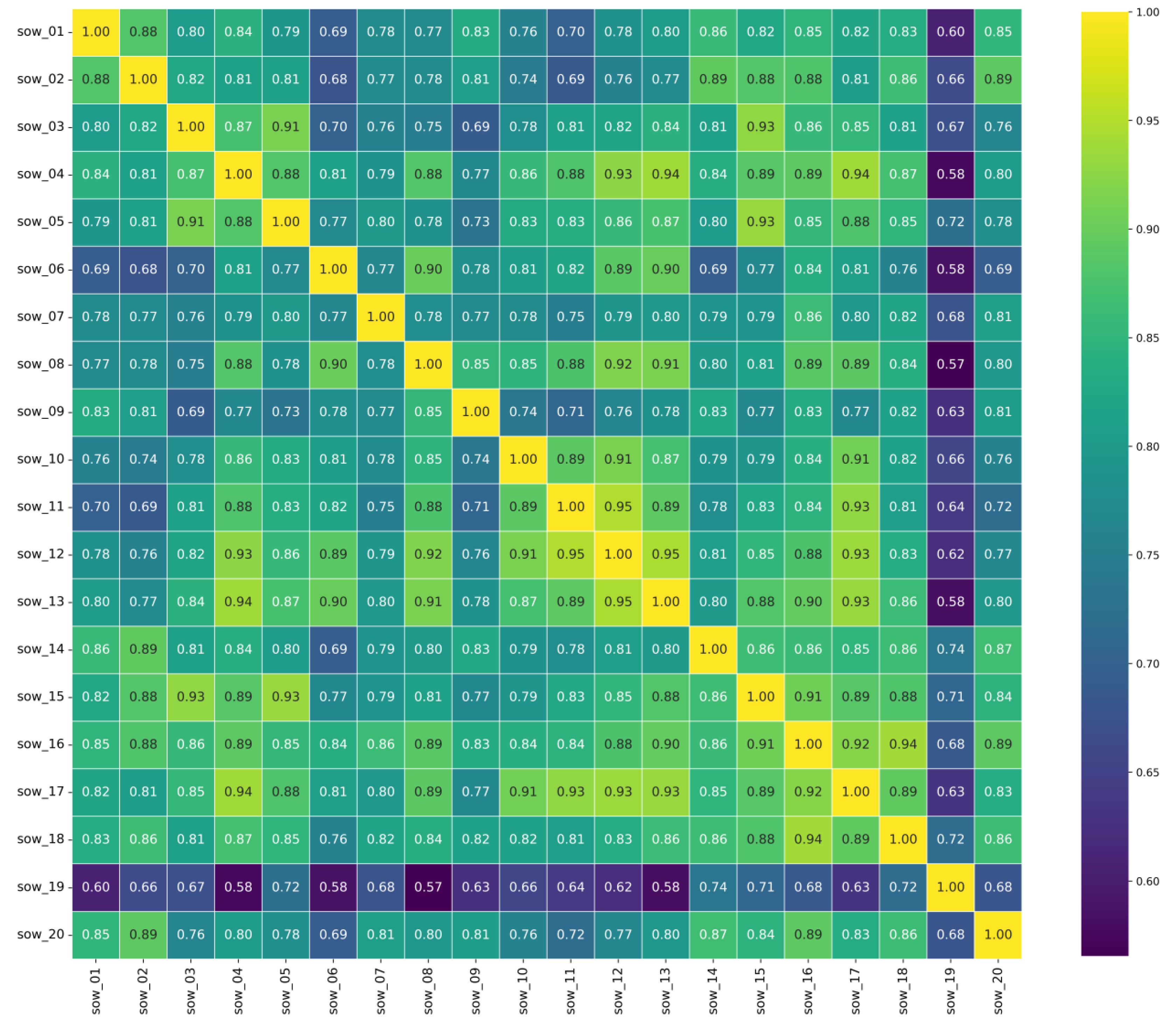
4.4.1. Correlation Analysis of Sow Activity
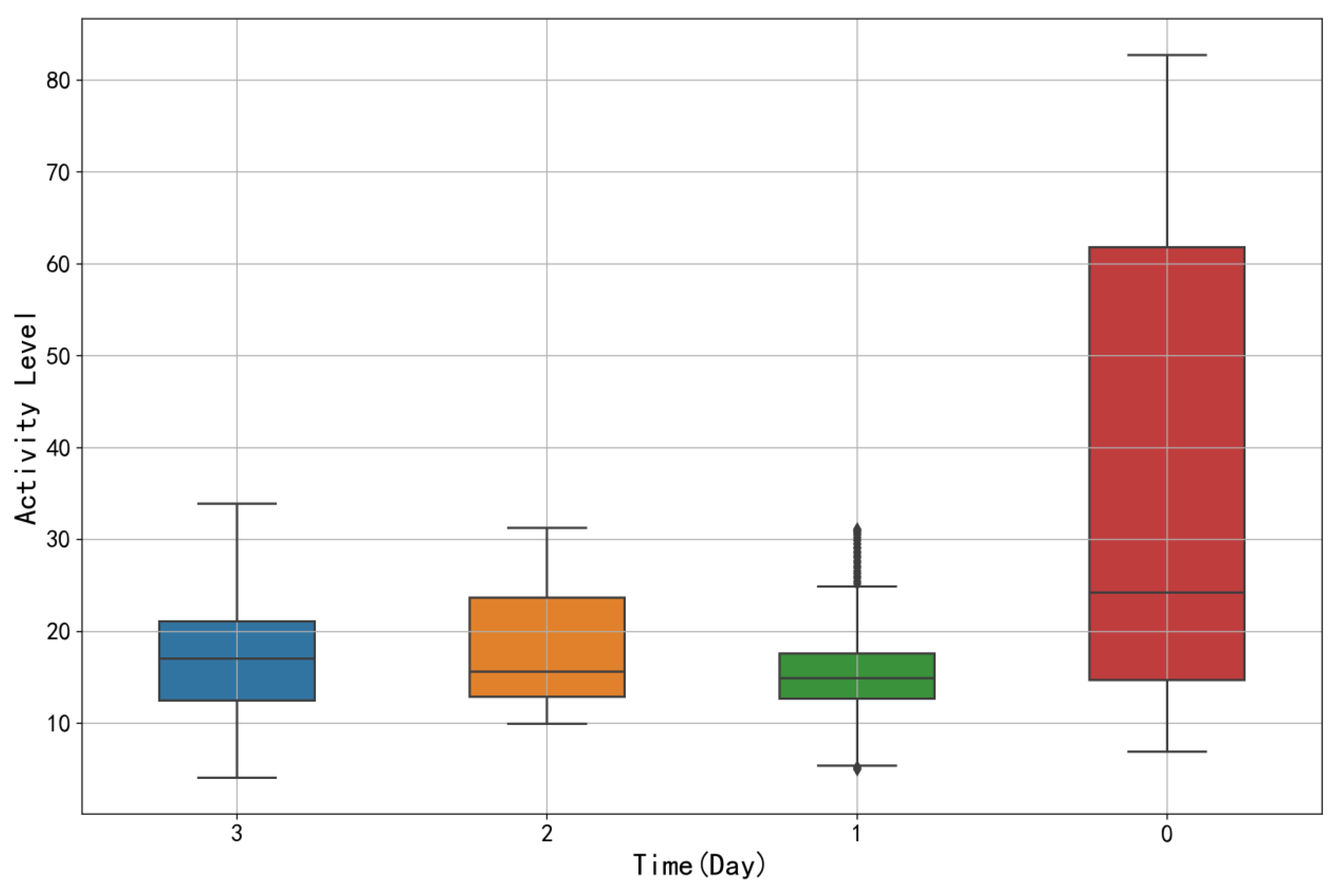
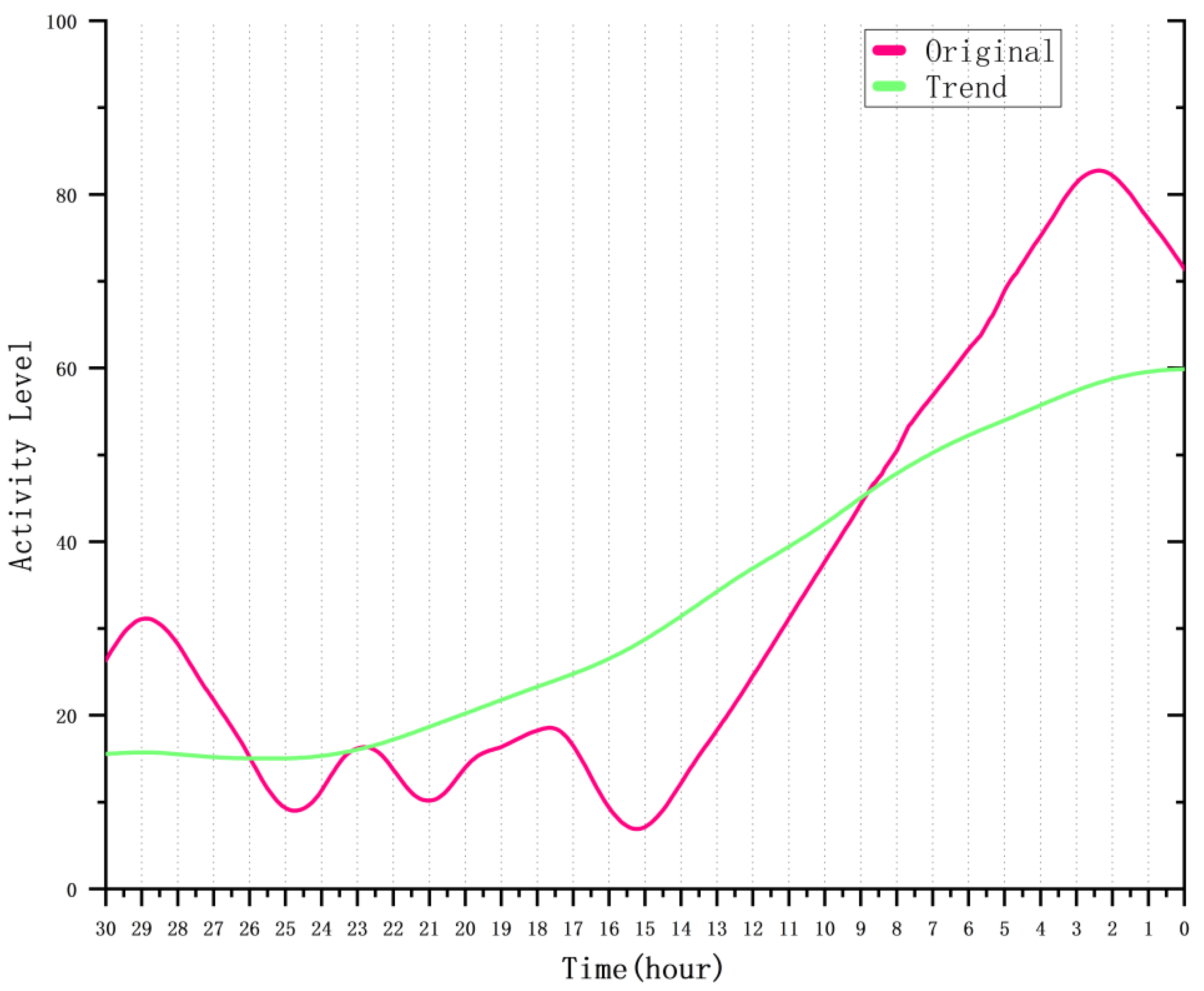
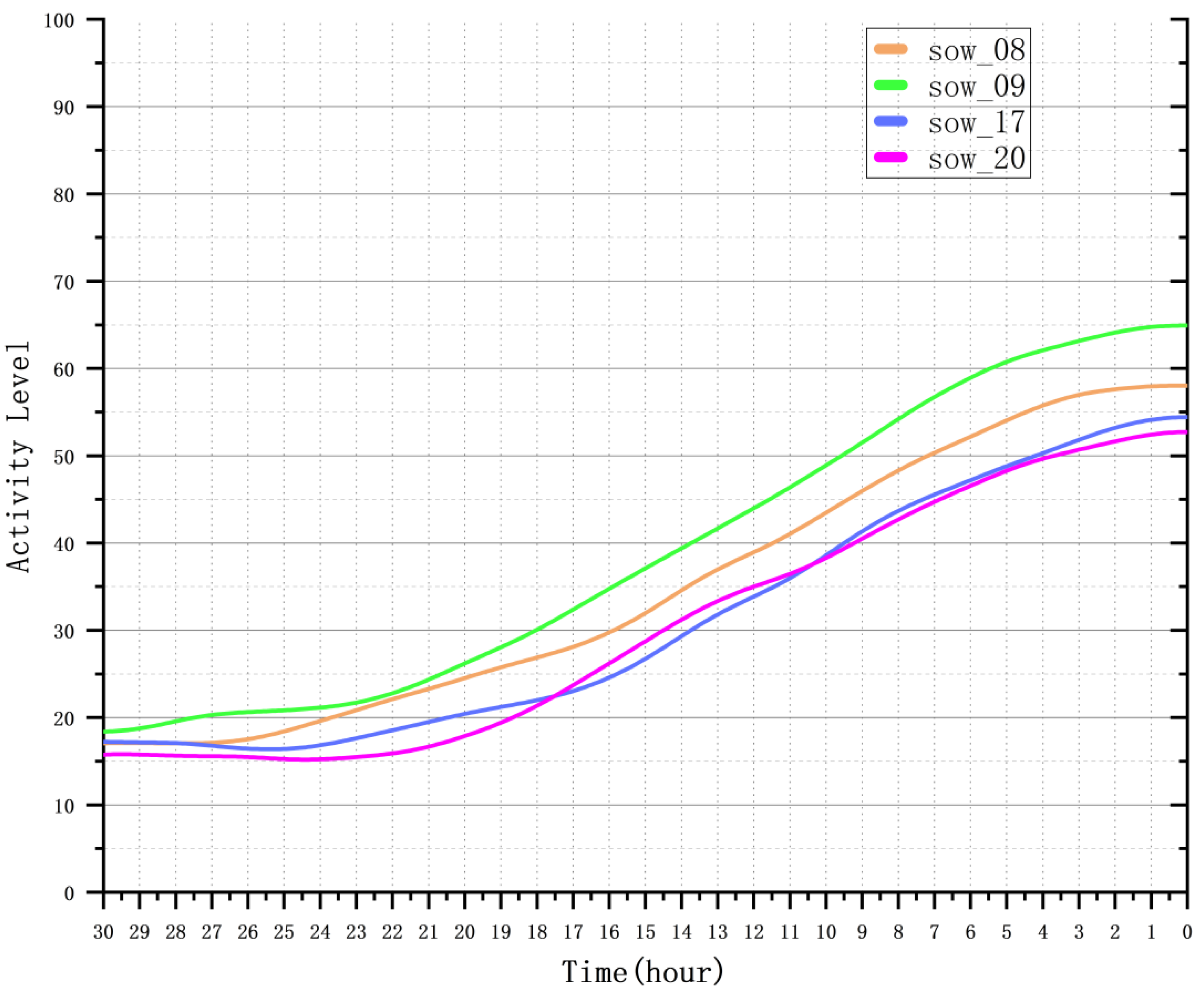
4.4.2. Analysis of Sow Activity Variation Patterns
4.5. Predictive Performance of Sow Farrowing Onset Estimation
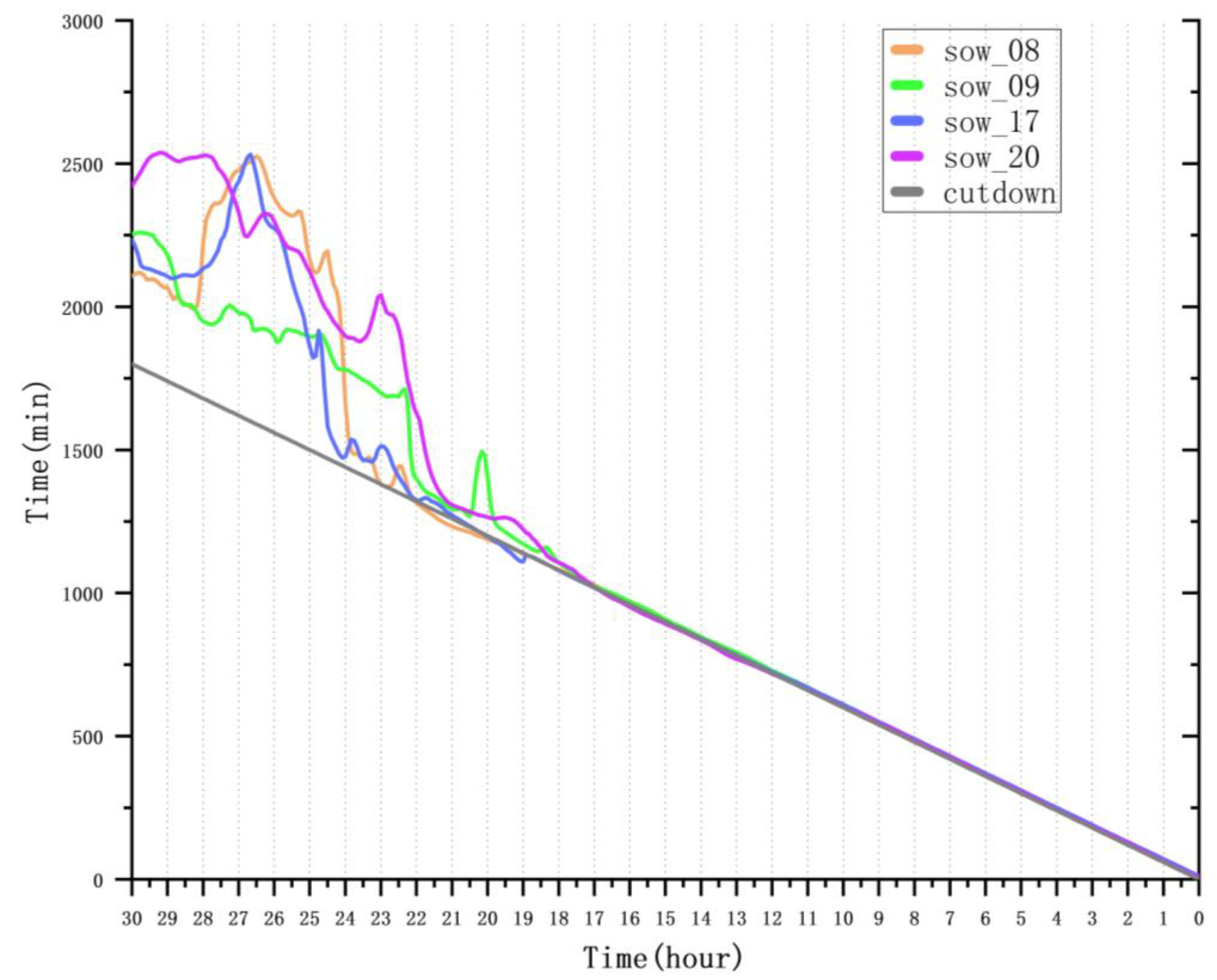
4.5.1. Analysis of Farrowing Onset Prediction Accuracy
4.5.2. Performance Comparison of CLA-PTNet with Other Models
4.5.3. Impact of Sliding Window Length on Prediction Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soare, E.; Chiurciu, I.; Apostol, C.; Stoicea, P.; Dobre, C.; Iorga, A.; Bălan, A.; Firățoiu, A. Study on the Worldwide Pork Market for the Period 2015–2021. Sci. Pap. Ser. Manag. Econ. Eng. Agric. Rural. Dev. 2024, 24, 923–928. [Google Scholar]
- Kim, S.W.; Gormley, A.; Jang, K.B.; Duarte, M.E. Current status of global pig production: An overview and research trends. Anim. Biosci. 2023, 37, 719. [Google Scholar]
- Avramescu, D.; Chirilä, C.; Petroman, I.; Mergheå, P. Food importance of pork. Lucr. Științifice Manag. Agric. 2014, 16, 151. [Google Scholar]
- Ma, X.; Jiang, Z.; Lai, C. Significance of increasing n-3 PUFA content in pork on human health. Crit. Rev. Food Sci. 2016, 56, 858–870. [Google Scholar] [CrossRef]
- Drewnowski, A. Perspective: The place of pork meat in sustainable healthy diets. Adv. Nutr. 2024, 15, 100213. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.K.; Mun, H.; Ampode, K.M.B.; Lagua, E.B.; Park, H.; Kim, Y.; Sharifuzzaman, M.; Yang, C. Transformation toward precision large-scale operations for sustainable farming: A review based on China’s pig industry. J. Adv. Vet. Anim. Res. 2024, 11, 1076. [Google Scholar]
- Tzanidakis, C.; Simitzis, P.; Arvanitis, K.; Panagakis, P. An overview of the current trends in precision pig farming technologies. Livest. Sci. 2021, 249, 104530. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, J.; Meng, Y.; You, J. Overview of ecology and automation status of pig breeding. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2023; p. 12060. [Google Scholar]
- Guanghui, T. Information sensing and environment control of precision facility livestock and poultry farming. Smart Agric. 2019, 1, 1. [Google Scholar]
- Wu, Y.; Zhao, J.; Xu, C.; Ma, N.; He, T.; Zhao, J.; Ma, X.; Thacker, P.A. Progress towards pig nutrition in the last 27 years. J. Sci. Food Agric. 2020, 100, 5102–5110. [Google Scholar]
- Dorca-Preda, T.; Kongsted, A.G.; Andersen, H.M.; Kristensen, T.; Theil, P.K.; Knudsen, M.T.; Mogensen, L. Refining life cycle nutrient modeling in organic pig production. An analysis focusing on feeding strategies in organic Danish pig farming. Livest. Sci. 2023, 272, 105248. [Google Scholar]
- Nam, N.H.; Sukon, P. Risk factors associated with dystocia in swine. Vet. World 2021, 14, 1835. [Google Scholar] [PubMed]
- Kraeling, R.R.; Webel, S.K. Current strategies for reproductive management of gilts and sows in North America. J. Anim. Sci. Biotechnol. 2015, 6, 3. [Google Scholar]
- Peltoniemi, O.; Oliviero, C.; Yun, J.; Grahofer, A.; Björkman, S. Management practices to optimize the parturition process in the hyperprolific sow. J. Anim. Sci. 2020, 98, S96–S106. [Google Scholar] [PubMed]
- Björkman, S.; Grahofer, A. Optimizing Piglet Survival and Sows’ Reproductive Health. In Animal Reproduction in Veterinary Medicine; IntechOpen: London, UK, 2021; p. 89. [Google Scholar]
- Chen, J.; Zhou, J.; Liu, L.; Shu, C.; Shen, M.; Yao, W. Sow farrowing early warning and supervision for embedded board implementations. Sensors 2023, 23, 727. [Google Scholar] [CrossRef]
- Gulliksen, S.M.; Framstad, T.; Kielland, C.; Velazquez, M.A.; Terøy, M.M.; Helland, E.M.; Lyngstad, R.H.; Delgado, A.O.; Oropeza-Moe, M. Infrared thermography as a possible technique for the estimation of parturition onset in sows. Porc. Health Manag. 2023, 9, 3. [Google Scholar]
- Vanderhaeghe, C.; Dewulf, J.; Jourquin, J.; De Kruif, A.; Maes, D. Incidence and prevention of early parturition in sows. Reprod. Domest. Anim. 2011, 46, 428–433. [Google Scholar] [PubMed]
- Shi, L.; Li, H.; Wang, L. Genetic parameters estimation and genome molecular marker identification for gestation length in pigs. Front. Genet. 2023, 13, 1046423. [Google Scholar]
- Straw, B.; Bates, R.; May, G. Influence of method of administration of prostaglandin on farrowing and relationship between gestation length and piglet performance. J. Swine Health Prod. 2008, 16, 138–143. [Google Scholar] [CrossRef]
- Rydhmer, L.; Lundeheim, N.; Canario, L. Genetic correlations between gestation length, piglet survival and early growth. Livest. Sci. 2008, 115, 287–293. [Google Scholar]
- Sasaki, Y.; Koketsu, Y. Variability and repeatability in gestation length related to litter performance in female pigs on commercial farms. Theriogenology 2007, 68, 123–127. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.; Zhou, S.; Wang, Z.; Qiao, C.; Han, J.; Li, M.; Zhou, H.; Li, X.; Xin, W. Genome-Wide Association Study Pinpoints Novel Candidate Genes Associated with the Gestation Length of the First Parity in French Large White Sows. Animals 2025, 15, 447. [Google Scholar] [CrossRef]
- Kirkden, R.D.; Broom, D.M.; Andersen, I.L. Piglet mortality: The impact of induction of farrowing using prostaglandins and oxytocin. Anim. Reprod. Sci. 2013, 138, 14–24. [Google Scholar] [CrossRef] [PubMed]
- Nam, N.H.; Sukon, P. Incidence of dystocia at piglet level in cloprostenol-induced farrowings and associated risk factors. Arch. Anim. Breed. 2022, 65, 97–103. [Google Scholar] [CrossRef]
- Damm, B.I.; Vestergaard, K.S.; Schrøder-Petersen, D.L.; Ladewig, J. The effects of branches on prepartum nest building in gilts with access to straw. Appl. Anim. Behav. Sci. 2000, 69, 113–124. [Google Scholar] [CrossRef]
- Ison, S.H.; Jarvis, S.; Hall, S.A.; Ashworth, C.J.; Rutherford, K.M. Periparturient behavior and physiology: Further insight into the farrowing process for primiparous and multiparous sows. Front. Vet. Sci. 2018, 5, 122. [Google Scholar] [CrossRef]
- Oliviero, C.; Heinonen, M.; Valros, A.; Hälli, O.; Peltoniemi, O. Effect of the environment on the physiology of the sow during late pregnancy, farrowing and early lactation. Anim. Reprod. Sci. 2008, 105, 365–377. [Google Scholar] [CrossRef] [PubMed]
- Illmann, G.; Chaloupková, H.; Melišová, M. Impact of sow prepartum behavior on maternal behavior, piglet body weight gain, and mortality in farrowing pens and crates. J. Anim. Sci. 2016, 94, 3978–3986. [Google Scholar]
- King, R.L.; Baxter, E.M.; Matheson, S.M.; Edwards, S.A. Sow free farrowing behaviour: Experiential, seasonal and individual variation. Appl. Anim. Behav. Sci. 2018, 208, 14–21. [Google Scholar] [CrossRef]
- Traulsen, I.; Scheel, C.; Auer, W.; Burfeind, O.; Krieter, J. Using acceleration data to automatically detect the onset of farrowing in sows. Sensors 2018, 18, 170. [Google Scholar] [CrossRef]
- Osterlundh, I.; Holst, H.; Magnusson, U. Hormonal and immunological changes in blood and mammary secretion in the sow at parturition. Theriogenology 1998, 50, 465–477. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, C.L. Endocrine regulation of periparturient behaviour in pigs. Reprod. Camb. Suppl. 2001, 58, 263–276. [Google Scholar] [CrossRef]
- Hendrix, W.F.; Kelley, K.W.; Gaskins, C.T.; Bendel, R.B. Changes in respiratory rate and rectal temperature of swine near parturition. J. Anim. Sci. 1978, 47, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Bressers, H.; Te Brake, J.; Jansen, M.B.; Nijenhuis, P.J.; Noordhuizen, J. Monitoring individual sows: Radiotelemetrically recorded ear base temperature changes around farrowing. Livest. Prod. Sci. 1994, 37, 353–361. [Google Scholar] [CrossRef]
- Aparna, U.; Pedersen, L.J.; Jørgensen, E. Hidden phase-type Markov model for the prediction of onset of farrowing for loose-housed sows. Comput. Electron. Agric. 2014, 108, 135–147. [Google Scholar] [CrossRef]
- Manteuffel, C.; Hartung, E.; Schmidt, M.; Hoffmann, G.; Schön, P.C. Towards qualitative and quantitative prediction and detection of parturition onset in sows using light barriers. Comput. Electron. Agric. 2015, 116, 201–210. [Google Scholar] [CrossRef]
- Pastell, M.; Hietaoja, J.; Yun, J.; Tiusanen, J.; Valros, A. Predicting farrowing of sows housed in crates and pens using accelerometers and CUSUM charts. Comput. Electron. Agric. 2016, 127, 197–203. [Google Scholar] [CrossRef]
- Oczak, M.; Maschat, K.; Baumgartner, J. Dynamics of sows’ activity housed in farrowing pens with possibility of temporary crating might indicate the time when sows should be confined in a crate before the onset of farrowing. Animals 2019, 10, 6. [Google Scholar] [CrossRef]
- Oczak, M.; Maschat, K.; Baumgartner, J. Implementation of Computer-Vision-Based Farrowing Prediction in Pens with Temporary Sow Confinement. Vet. Sci. 2023, 10, 109. [Google Scholar] [CrossRef]
- Teed, Z.; Deng, J. Raft: Recurrent all-pairs field transforms for optical flow. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 402–419. [Google Scholar]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2462–2470. [Google Scholar]
- Jiang, S.; Campbell, D.; Lu, Y.; Li, H.; Hartley, R. Learning to estimate hidden motions with global motion aggregation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9772–9781. [Google Scholar]
- Zhao, S.; Sheng, Y.; Dong, Y.; Chang, E.I.; Xu, Y. Maskflownet: Asymmetric feature matching with learnable occlusion mask. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6278–6287. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.; Kautz, J. Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8934–8943. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]




| Dataset | Number of Sows |
|---|---|
| Training set | 12 |
| Validation set | 4 |
| Test set | 4 |
| Model | Sintel Clean EPE (Pixels) | Sintel Final EPE (Pixels) | KITTI2015 EPE (Pixels) | KITTI2015 Fl-All | Parameter (M) |
|---|---|---|---|---|---|
| FlowNet2 | 1.96 | 3.69 | 8.23 | 28.28% | 162 |
| GMA | 1.48 | 2.93 | 6.73 | 19.17% | 5.9 |
| MaskFlowNet | 2.30 | 3.73 | 9.36 | 29.70% | 42 |
| PWC-Net | 2.26 | 3.79 | 9.49 | 29.85% | 9.3 |
| RAFT | 1.38 | 2.79 | 4.95 | 16.23% | 5.3 |
| Sow ID | AACC | Sow ID | AACC | Sow ID | AACC | Sow ID | AACC |
|---|---|---|---|---|---|---|---|
| sow_01 | 0.804 | sow_06 | 0.783 | sow_11 | 0.817 | sow_16 | 0.870 |
| sow_02 | 0.810 | sow_16 | 0.793 | sow_12 | 0.850 | sow_17 | 0.864 |
| sow_03 | 0.813 | sow_08 | 0.832 | sow_13 | 0.854 | sow_18 | 0.847 |
| sow_04 | 0.853 | sow_09 | 0.784 | sow_14 | 0.826 | sow_19 | 0.668 |
| sow_05 | 0.835 | sow_10 | 0.818 | sow_15 | 0.852 | sow_20 | 0.811 |
| Date | Mean | Min | Max | Q1 | Q2 | Q3 | SD |
|---|---|---|---|---|---|---|---|
| 3 | 17.21 | 4.09 | 33.90 | 12.49 | 17.04 | 21.07 | 6.93 |
| 2 | 18.31 | 9.96 | 31.27 | 12.90 | 15.60 | 23.68 | 6.70 |
| 1 | 15.75 | 5.00 | 31.15 | 12.70 | 14.92 | 17.58 | 6.10 |
| 0 | 36.83 | 6.89 | 82.75 | 14.70 | 24.26 | 61.83 | 26.26 |
| Sow ID | Hours Before Farrow | MAE (min) | RMSE (min) | R2 |
|---|---|---|---|---|
| sow_08 | 30–24 | 609.82 | 651.47 | −38.31 |
| 24–18 | 22.74 | 34.74 | 0.89 | |
| 18–12 | 3.48 | 4.34 | 0.99 | |
| 12–6 | 4.08 | 4.52 | 0.99 | |
| 6–0 | 2.53 | 2.98 | 0.99 | |
| sow_09 | 30–24 | 367.70 | 372.49 | −11.85 |
| 24–18 | 144.99 | 196.25 | −2.56 | |
| 18–12 | 9.98 | 10.68 | 0.98 | |
| 12–6 | 7.72 | 8.17 | 0.99 | |
| 6–0 | 6.36 | 6.54 | 0.99 | |
| sow_17 | 30–24 | 489.20 | 538.64 | −25.87 |
| 24–18 | 31.53 | 48.52 | 0.78 | |
| 18–12 | 4.61 | 5.18 | 0.99 | |
| 12–6 | 5.62 | 5.66 | 0.99 | |
| 6–0 | 4.97 | 5.13 | 0.99 | |
| sow_20 | 30–24 | 708.01 | 716.08 | −46.49 |
| 24–18 | 222.45 | 310.63 | −7.94 | |
| 18–12 | 8.39 | 10.21 | 0.99 | |
| 12–6 | 4.06 | 4.77 | 0.99 | |
| 6–0 | 3.35 | 3.49 | 0.99 |
| Model | MAE (min) | RMSE (min) | R2 | Parameter (M) |
|---|---|---|---|---|
| LSTM | 86.34 | 98.76 | 0.94 | 0.65 |
| CNN-LSTM | 68.66 | 70.36 | 0.96 | 0.71 |
| CLA-PTNet | 5.42 | 5.97 | 0.99 | 0.76 |
| Sliding Windows (h) | MAE (min) | RMSE (min) | Inference Time (ms) |
|---|---|---|---|
| 3 | 8.62 | 9.37 | 12.24 |
| 6 | 5.42 | 5.97 | 22.75 |
| 12 | 5.86 | 6.35 | 44.23 |
| 24 | 6.18 | 7.01 | 81.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Huang, Y.; Liu, J.; Tan, Z.; Xiao, D. Prediction of Sow Farrowing Onset Time Using Activity Time Series Extracted by Optical Flow Estimation. Animals 2025, 15, 998. https://doi.org/10.3390/ani15070998
Liu K, Huang Y, Liu J, Tan Z, Xiao D. Prediction of Sow Farrowing Onset Time Using Activity Time Series Extracted by Optical Flow Estimation. Animals. 2025; 15(7):998. https://doi.org/10.3390/ani15070998
Chicago/Turabian StyleLiu, Kejian, Yigui Huang, Junbin Liu, Zujie Tan, and Deqin Xiao. 2025. "Prediction of Sow Farrowing Onset Time Using Activity Time Series Extracted by Optical Flow Estimation" Animals 15, no. 7: 998. https://doi.org/10.3390/ani15070998
APA StyleLiu, K., Huang, Y., Liu, J., Tan, Z., & Xiao, D. (2025). Prediction of Sow Farrowing Onset Time Using Activity Time Series Extracted by Optical Flow Estimation. Animals, 15(7), 998. https://doi.org/10.3390/ani15070998





