Swimming Performance and Behavior of High-Altitude Fish in High-Flow Velocity Environments
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
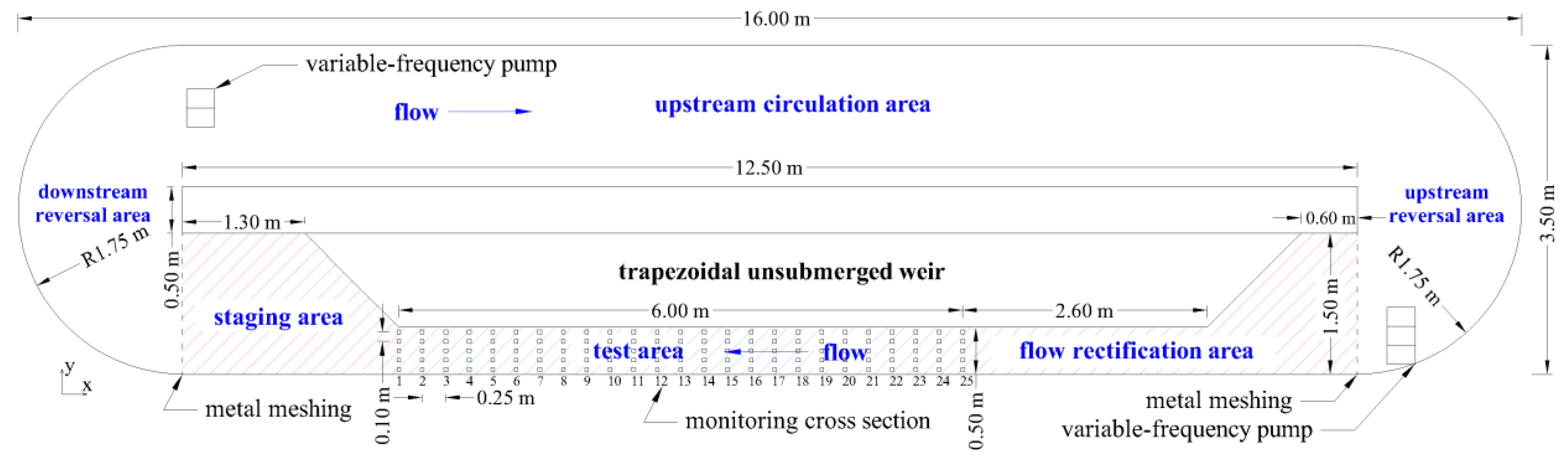
2.1. Study Apparatus
2.2. Fish Husbandry and Trials
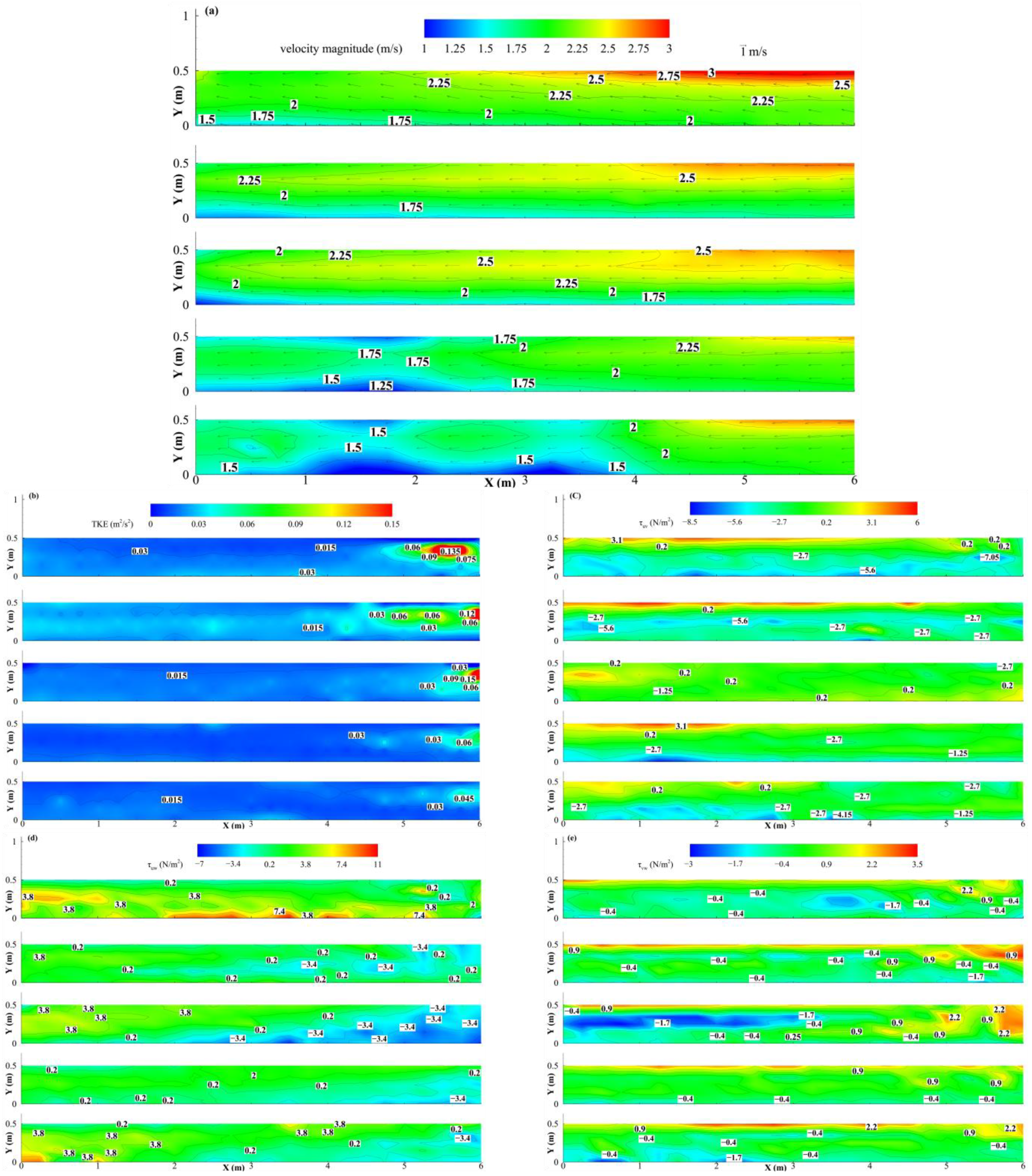
2.3. Hydraulic Characteristics
2.4. Swimming Performance
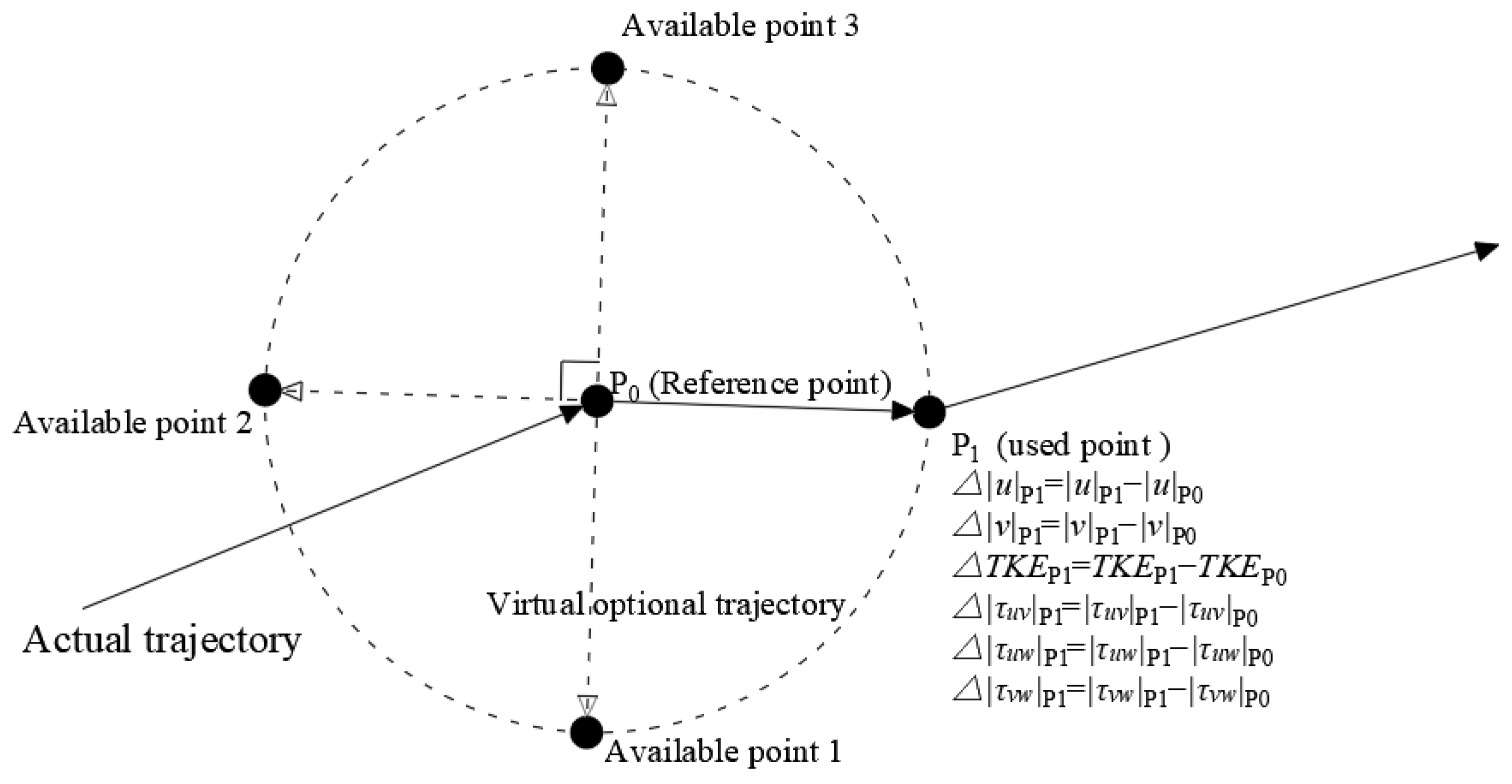
2.5. Swimming Behavior
2.6. Statistical Methods
2.6.1. Swimming Performance
2.6.2. Swimming Behavior
3. Results
3.1. Hydrodynamic Characteristics of the Flume
3.2. Swimming Performance
3.2.1. Swimming Speed
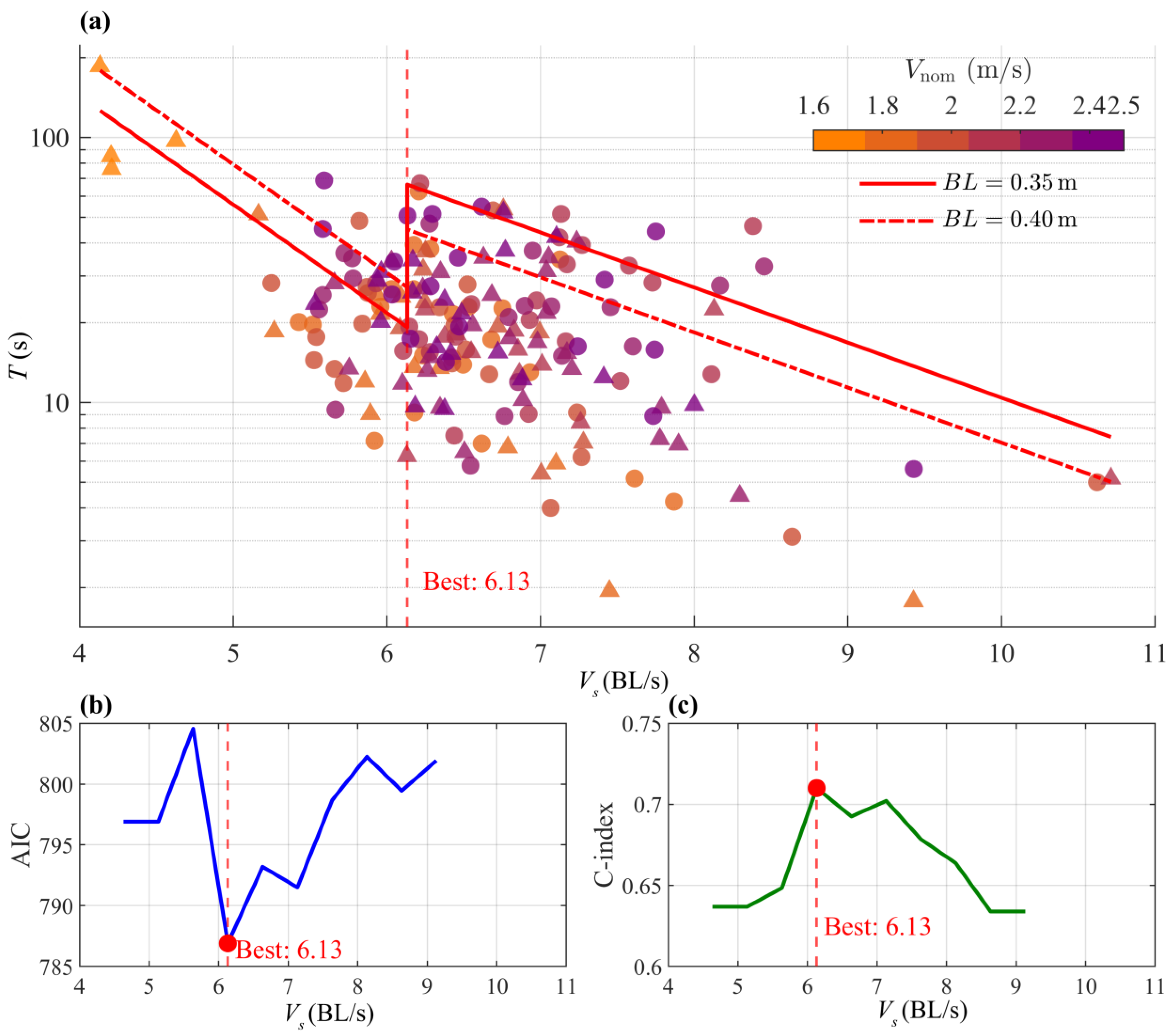
3.2.2. Endurance
3.3. Swimming Behavior
3.3.1. Relationship Between Behavioral Strategies and Movement Mode
3.3.2. Interaction Between Endurance State and Hydraulic Factors
4. Discussion
4.1. Movement Mode Dependency of Swimming Speed
4.2. High-Altitude Adaptations of S. oconnori’s Endurance
4.3. Navigation Mechanism Based on Energy Conservation and Movement Stability Objectives
4.4. Regulatory Role of Endurance State in Movement Strategy
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmutz, S.; Moog, O. Dams: Ecological Impacts and Management. In Riverine Ecosystem Management: Science for Governing Towards a Sustainable Future; Schmutz, S., Sendzimir, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 111–127. [Google Scholar]
- Waldman, J.R.; Quinn, T.P. North American diadromous fishes: Drivers of decline and potential for recovery in the Anthropocene. Sci. Adv. 2022, 8, eabl5486. [Google Scholar] [CrossRef] [PubMed]
- Verhelst, P.; Reubens, J.; Buysse, D.; Goethals, P.; Van Wichelen, J.; Moens, T. Toward a roadmap for diadromous fish conservation: The Big Five considerations. Front. Ecol. Environ. 2021, 19, 396–403. [Google Scholar] [CrossRef]
- Silva, A.T.; Lucas, M.C.; Castro-Santos, T.; Katopodis, C.; Baumgartner, L.J.; Thiem, J.D.; Aarestrup, K.; Pompeu, P.S.; O’Brien, G.C.; Braun, D.C.; et al. The future of fish passage science, engineering, and practice. Fish Fish. 2018, 19, 340–362. [Google Scholar] [CrossRef]
- Elings, J.; Bruneel, S.; Pauwels, I.S.; Schneider, M.; Kopecki, I.; Coeck, J.; Mawer, R.; Goethals, P.L.M. Finding navigation cues near fishways. Biol. Rev. 2024, 99, 313–327. [Google Scholar] [CrossRef]
- Shi, X.; Ke, S.; Tu, Z.; Wang, Y.; Tan, J.; Guo, W. Swimming capability of target fish from eight hydropower stations in China relative to fishway design. Can. J. Fish. Aquat. Sci. 2021, 79, 124–132. [Google Scholar] [CrossRef]
- Hou, Y.; Cai, L.; Wang, X.; Chen, X.; Zhu, D.; Johnson, D.; Shi, X. Swimming performance of 12 Schizothoracinae species from five rivers. J. Fish Biol. 2018, 92, 2022–2028. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, X.; Liu, K.; Pu, X.; Wang, Y. Swimming ability of Schizothoracinae fishes in Yarlung Zangbo River of China. J. Fish Biol. 2024, 105, 95–109. [Google Scholar] [CrossRef]
- Tudorache, C.; Viaenen, P.; Blust, R.; De Boeck, G. Longer flumes increase critical swimming speeds by increasing burst–glide swimming duration in carp Cyprinus carpio L. J. Fish Biol. 2007, 71, 1630–1638. [Google Scholar] [CrossRef]
- Li, M.N.; An, R.D.; Chen, M.; Li, J. Evaluation of Volitional Swimming Behavior of Schizothorax prenanti Using an Open-Channel Flume with Spatially Heterogeneous Turbulent Flow. Animals 2022, 12, 752. [Google Scholar] [CrossRef]
- Ke, S.; Yang, S.; Tu, Z.; Soomro, S.-E.-H.; Ji, H.; Li, D.; Xu, J.; Qi, H.; Shi, X. Swimming performance of a threatened native fish (Gymnocypris przewalskii) informs fishway design in Qinghai Lake. Hydrobiologia 2025, 852, 3997–4012. [Google Scholar] [CrossRef]
- Castro-Santos, T.; Haro, A. Quantifying migratory delay: A new application of survival analysis methods. Can. J. Fish. Aquat. Sci. 2003, 60, 986–996. [Google Scholar] [CrossRef]
- Sanz-Ronda, F.J.; Ruiz-Legazpi, J.; Bravo-Córdoba, F.J.; Makrakis, S.; Castro-Santos, T. Sprinting performance of two Iberian fish: Luciobarbus bocagei and Pseudochondrostoma duriense in an open channel flume. Ecol. Eng. 2015, 83, 61–70. [Google Scholar] [CrossRef]
- Arnold, G.P. Rheotropism in Fishes. Biol. Rev. 1974, 49, 515–576. [Google Scholar] [CrossRef] [PubMed]
- Delavan, S.K.; Sood, S.; Pérez-Fuentetaja, A.; Hannes, A.R. Anthropogenic turbulence and velocity barriers for upstream swimming fish: A field study on emerald shiners (Notropis atherinoides) in the Upper Niagara River. Ecol. Eng. 2017, 101, 91–106. [Google Scholar] [CrossRef]
- Plaut, I. Critical swimming speed: Its ecological relevance. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2001, 131, 41–50. [Google Scholar] [CrossRef]
- Li, G.; Kolomenskiy, D.; Liu, H.; Godoy-Diana, R.; Thiria, B. Intermittent versus continuous swimming: An optimization tale. Phys. Rev. Fluids 2023, 8, 013101. [Google Scholar] [CrossRef]
- Winger, P.D.; He, P.; Walsh, S.J. Factors affecting the swimming endurance and catchability of Atlantic cod (Gadus morhua). Can. J. Fish. Aquat. Sci. 2000, 57, 1200–1207. [Google Scholar] [CrossRef]
- Li, G.; Ashraf, I.; François, B.; Kolomenskiy, D.; Lechenault, F.; Godoy-Diana, R.; Thiria, B. Burst-and-coast swimmers optimize gait by adapting unique intrinsic cycle. Commun. Biol. 2021, 4, 40. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. The Kármán gait: Novel body kinematics of rainbow trout swimming in a vortex street. J. Exp. Biol. 2003, 206, 1059–1073. [Google Scholar] [CrossRef]
- Enders, E.C.; Boisclair, D.; Roy, A.G. A model of total swimming costs in turbulent flow for juvenile Atlantic salmon (Salmo salar). Can. J. Fish. Aquat. Sci. 2005, 62, 1079–1089. [Google Scholar] [CrossRef]
- Silva, A.T.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N.; Katopodis, C. Effects of water velocity and turbulence on the behaviour of Iberian barbel (Luciobarbus bocagei, Steindachner 1864) in an experimental pool-type fishway. River Res. Appl. 2011, 27, 360–373. [Google Scholar] [CrossRef]
- Odeh, M.; Noreika, J.F.; Haro, A. Evaluation of the Effects of Turbulence on the Behavior of Migratory Fish, Final Report 2002; Bonneville Power Administration (BPA): Portland, OR, USA, 2002.
- Baumgartner, L.J.; Thorncraft, G.; Phonekhampheng, O.; Boys, C.; Navarro, A.; Robinson, W.; Brown, R.; Deng, Z.D. High fluid shear strain causes injury in silver shark: Preliminary implications for Mekong hydropower turbine design. Fish. Manag. Ecol. 2017, 24, 193–198. [Google Scholar] [CrossRef]
- Mawer, R.; Bruneel, S.P.; Pauwels, I.S.; Elings, J.; Pickholtz, E.; Pickholtz, R.; Schneider, M.; Coeck, J.; Goethals, P.L.M. Individual variation in the habitat selection of upstream migrating fish near a barrier. Mov. Ecol. 2023, 11, 49. [Google Scholar] [CrossRef]
- Chatterjee, N.; Wolfson, D.; Kim, D.; Velez, J.; Freeman, S.; Bacheler, N.M.; Shertzer, K.; Taylor, J.C.; Fieberg, J. Modelling individual variability in habitat selection and movement using integrated step-selection analysis. Methods Ecol. Evol. 2024, 15, 1034–1047. [Google Scholar] [CrossRef]
- Dudley, P.N.; John, S.N.; Daniels, M.E.; Danner, E.M. Using decades of spawning data and hydraulic models to construct a temperature-dependent resource selection function for management of an endangered salmonid. Can. J. Fish. Aquat. Sci. 2021, 79, 73–81. [Google Scholar] [CrossRef]
- Griffin, L.P.; Casselberry, G.A.; Hart, K.M.; Jordaan, A.; Becker, S.L.; Novak, A.J.; DeAngelis, B.M.; Pollock, C.G.; Lundgren, I.; Hillis-Starr, Z.; et al. A Novel Framework to Predict Relative Habitat Selection in Aquatic Systems: Applying Machine Learning and Resource Selection Functions to Acoustic Telemetry Data From Multiple Shark Species. Front. Mar. Sci. 2021, 8, 631262. [Google Scholar] [CrossRef]
- Waller, M.J.; Queiroz, N.; da Costa, I.; Cidade, T.; Loureiro, B.; Womersley, F.C.; Fontes, J.; Afonso, P.; Macena, B.C.; Loveridge, A. Direct measurement of cruising and burst swimming speeds of the shortfin mako shark (Isurus oxyrinchus) with estimates of field metabolic rate. J. Fish Biol. 2023, 103, 864–883. [Google Scholar] [CrossRef]
- Freitas, C.; Olsen, E.M.; Knutsen, H.; Albretsen, J.; Moland, E. Temperature-associated habitat selection in a cold-water marine fish. J. Anim. Ecol. 2016, 85, 628–637. [Google Scholar] [CrossRef]
- Eguiraun, H.; Martinez, I. Non-Linear Analyses of Fish Behaviours in Response to Aquatic Environmental Pollutants—A Review. Fishes 2023, 8, 311. [Google Scholar] [CrossRef]
- Wang, J.; Qie, Z.; Li, G.; Ran, Y.; Wu, X. An efficient fish migration modeling method integrating the random forest and Eulerian–Lagrangian–agent method for vertical slot fishways. Ecol. Eng. 2023, 195, 107067. [Google Scholar] [CrossRef]
- Chen, X.; Deng, X.; Zhu, Y.; Huang, S.; Kattel, G.R.; Wu, Y.; Zahid, A.; Shi, X. Development of a hybrid CNN-GRU model for accurately predicting fish migration trajectories in fishways by integrating hydraulic and fish movement characteristics. Aquat. Sci. 2025, 88, 4. [Google Scholar] [CrossRef]
- Hinch, S.G.; Rand, P.S. Optimal swimming speeds and forward-assisted propulsion: Energy-conserving behaviours of upriver-migrating adult salmon. Can. J. Fish. Aquat. Sci. 2000, 57, 2470–2478. [Google Scholar] [CrossRef]
- Standen, E.M.; Hinch, S.G.; Rand, P.S. Influence of river speed on path selection by migrating adult sockeye salmon (Oncorhynchus nerka). Can. J. Fish. Aquat. Sci. 2004, 61, 905–912. [Google Scholar] [CrossRef]
- Hinch, S.G.; Standen, E.M.; Healey, M.C.; Farrell, A.P. Swimming patterns and behaviour of upriver-migrating adult pink (Oncorhynchus gorbuscha) and sockeye (O. nerka) salmon as assessed by EMG telemetry in the Fraser River, British Columbia, Canada. Hydrobiologia 2002, 483, 147–160. [Google Scholar] [CrossRef]
- Williams, J.G.; Armstrong, G.; Katopodis, C.; Larinier, M.; Travade, F. Thinking Like a Fish: A Key Ingredient for Development of Effective Fish Passage Facilities at River Obstructions. River Res. Appl. 2012, 28, 407–417. [Google Scholar] [CrossRef]
- Mendes, L.M.M.; Souza, G.A.R.; Santos, H.A. Downstream alterations on hydrodynamic fields by hydropower plant operations: Implications for upstream fish migration. Hydrobiologia 2022, 849, 281–307. [Google Scholar] [CrossRef]
- Silva, A.T.; Bærum, K.M.; Hedger, R.D.; Baktoft, H.; Fjeldstad, H.-P.; Gjelland, K.Ø.; Økland, F.; Forseth, T. The effects of hydrodynamics on the three-dimensional downstream migratory movement of Atlantic salmon. Sci. Total Environ. 2020, 705, 135773. [Google Scholar] [CrossRef]
- Hu, J.; Wang, P.; Chen, H.; Liu, Z.; Chen, S. Effects of the Diversity of Flow Velocity on the Upstream Migration Behavior of Grass Carp in the Reaches of Spur Dikes. Water 2023, 15, 3091. [Google Scholar] [CrossRef]
- Standen, E.M.; Hinch, S.G.; Healey, M.C.; Farrell, A.P. Energetic costs of migration through the Fraser River Canyon, British Columbia, in adult pink (Oncorhynchus gorbuscha) and sockeye (Oncorhynchus nerka) salmon as assessed by EMG telemetry. Can. J. Fish. Aquat. Sci. 2002, 59, 1809–1818. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, C. The Fishes of the Qinghai-Xizang Plateau; Sichuan Publishing House of Science & Technology: Chengdu, China, 1992. [Google Scholar]
- Ma, B.; Wei, K.; Zhao, T.; Pei, F.; Huo, B. Research progress on the systematic evolution and plateau adaptation of schizothoracine fishes. J. Lake Sci. 2023, 35, 1–18. [Google Scholar] [CrossRef]
- Zhang, C.; Tong, C.; Ludwig, A.; Tang, Y.; Liu, S.; Zhang, R.; Feng, C.; Li, G.; Peng, Z.; Zhao, K. Adaptive Evolution of the Eda Gene and Scales Loss in Schizothoracine Fishes in Response to Uplift of the Tibetan Plateau. Int. J. Mol. Sci. 2018, 19, 2953. [Google Scholar] [CrossRef]
- Cai, L.; Huang, Y.; Johnson, D.; Li, M.; Liu, R.; Hu, W.; Jin, Y.; Chen, X.; Tao, J.; Zou, X.; et al. Swimming ability of cyprinid species (subfamily schizothoracinae) at high altitude. Front. Physiol. 2023, 14, 1152697. [Google Scholar] [CrossRef]
- Sung, W.; Peiqi, Y.; Yiyu, C. China Red Data Book of Endangered Animals: Pisces; Science Press: Beijing, China, 1998. [Google Scholar]
- Liang, Y.; Hou, Y.; Hu, W.; Johnson, D.; Wang, J. Flow velocity preference of Schizothorax oconnori Lloyd swimming upstream. Glob. Ecol. Conserv. 2021, 32, e01902. [Google Scholar] [CrossRef]
- Ma, B.; Wang, S.; Shao, J.; Li, D.; Xie, C.; Liu, X.; Huo, B. Population resources and fishery conversation policies of Schizothorax oconnori in the Yarlung Zangbo River. J. Fish. Sci. China 2020, 27, 106–118. [Google Scholar]
- Tierney, K.B. Swimming performance assessment in fishes. J. Vis. Exp. JoVE 2011, 51, 2572. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics; Routledge: Oxfordshire, UK, 2017. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Brett, J.R. The Respiratory Metabolism and Swimming Performance of Young Sockeye Salmon. J. Fish. Res. Board Can. 1964, 21, 1183–1226. [Google Scholar] [CrossRef]
- Castro-Santos, T.; Kieffer, M.; Goerig, E. Sprinting performance and behavior of adult shortnose sturgeon (Acipenser brevirostrum). Can. J. Fish. Aquat. Sci. 2024, 81, 1495–1513. [Google Scholar] [CrossRef]
- Saikia, R.; Barman, M.P. A review on accelerated failure time models. Int. J. Stat. Syst. 2017, 12, 311–322. [Google Scholar]
- Castro-Santos, T. Optimal swim speeds for traversing velocity barriers: An analysis of volitional high-speed swimming behavior of migratory fishes. J. Exp. Biol. 2005, 208, 421–432. [Google Scholar] [CrossRef]
- Manly, B.F.; McDonald, L.L.; Thomas, D.L.; McDonald, T.L.; Erickson, W.P. Resource Selection by Animals: Statistical Design and Analysis for Field Studies; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: http://www.R-project.org/ (accessed on 1 April 2025).
- Wood, S.N. mgcv: GAMs and generalized ridge regression for R. R News 2001, 1, 20–25. [Google Scholar]
- Simpson, G.L. gratia: An R package for exploring generalized additive models. arXiv 2024, arXiv:2406.19082. [Google Scholar] [CrossRef]
- Team, R. RStudio: Integrated Development for R; RStudio Inc.: Boston, MA, USA, 2015; Volume 700, p. 879. [Google Scholar]
- Castro-Santos, T. Modeling the Effect of Varying Swim Speeds on Fish Passage through Velocity Barriers. Trans. Am. Fish. Soc. 2006, 135, 1230–1237. [Google Scholar] [CrossRef]
- Moosbauer, J.; Herbinger, J.; Casalicchio, G.; Lindauer, M.; Bischl, B. Explaining hyperparameter optimization via partial dependence plots. Adv. Neural Inf. Process. Syst. 2021, 34, 2280–2291. [Google Scholar]
- Katopodis, C.; Cai, L.; Johnson, D. Sturgeon survival: The role of swimming performance and fish passage research. Fish. Res. 2019, 212, 162–171. [Google Scholar] [CrossRef]
- Kern, P.; Cramp, R.; Gordos, M.; Watson, J.; Franklin, C. Measuring U crit and endurance: Equipment choice influences estimates of fish swimming performance. J. Fish Biol. 2018, 92, 237–247. [Google Scholar] [CrossRef]
- Liao, J.C. A review of fish swimming mechanics and behaviour in altered flows. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1973–1993. [Google Scholar] [CrossRef]
- Peake, S.J.; Farrell, A.P. Fatigue is a behavioural response in respirometer-confined smallmouth bass. J. Fish Biol. 2006, 68, 1742–1755. [Google Scholar] [CrossRef]
- Groot, C. Physiological Ecology of Pacific Salmon; UBC Press: Vancouver, BC, Canada, 2010. [Google Scholar]
- Peake, S.J. Swimming and Respiration. In Sturgeons and Paddlefish of North America; Springer: Dordrecht, The Netherlands, 2004; pp. 147–166. [Google Scholar]
- Kieffer, J.; Arsenault, L.; Litvak, M. Behaviour and performance of juvenile shortnose sturgeon Acipenser brevirostrum at different water velocities. J. Fish Biol. 2009, 74, 674–682. [Google Scholar] [CrossRef] [PubMed]
- Boavida, I.; Costa, M.J.; Portela, M.M.; Godinho, F.; Tuhtan, J.; Pinheiro, A. Do cyprinid fish use lateral flow-refuges during hydropeaking? River Res. Appl. 2023, 39, 554–560. [Google Scholar] [CrossRef]
- Macdonald, J. Mortality during the migration of Fraser River sockeye salmon (Oncorhynchus nerka): A study of the effects of ocean and river environmental conditions in 1997. Can. Tech. Rep. Fish. Aquat. Sci. 2000, 12, 2315. [Google Scholar]
- Holder, P.E.; Wood, C.M.; Lawrence, M.J.; Clark, T.D.; Suski, C.D.; Weber, J.M.; Danylchuk, A.J.; Cooke, S.J. Are we any closer to understanding why fish can die after severe exercise? Fish Fish. 2022, 23, 1400–1417. [Google Scholar] [CrossRef]
- Hinch, S.G.; Bratty, J. Effects of swim speed and activity pattern on success of adult sockeye salmon migration through an area of difficult passage. Trans. Am. Fish. Soc. 2000, 129, 598–606. [Google Scholar]
- Breen, M.; Dyson, J.; O’Neill, F.G.; Jones, E.; Haigh, M. Swimming endurance of haddock (Melanogrammus aeglefinus L.) at prolonged and sustained swimming speeds, and its role in their capture by towed fishing gears. ICES J. Mar. Sci. 2004, 61, 1071–1079. [Google Scholar] [CrossRef]
- Nelson, J.; Gotwalt, P.; Reidy, S.; Webber, D. Beyond Ucrit: Matching swimming performance tests to the physiological ecology of the animal, including a new fish ‘drag strip’. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2002, 133, 289–302. [Google Scholar] [CrossRef]
- Cai, L.; Chen, J.; Johnson, D.; Tu, Z.; Huang, Y. Effect of body length on swimming capability and vertical slot fishway design. Glob. Ecol. Conserv. 2020, 22, e00990. [Google Scholar] [CrossRef]
- Castro-Santos, T.; Sanz-Ronda, F.J.; Ruiz-Legazpi, J. Breaking the speed limit—Comparative sprinting performance of brook trout (Salvelinus fontinalis) and brown trout (Salmo trutta). Can. J. Fish. Aquat. Sci. 2013, 70, 280–293. [Google Scholar] [CrossRef]
- Hunt von Herbing, I.; Pan, T.C.F.; Méndez-Sánchez, F.; Garduño-Paz, M.; Hernández-Gallegos, O.; Ruiz-Gómez, M.L.; Rodríguez-Vargas, G. Chronic stress of rainbow trout Oncorhynchus mykiss at high altitude: A field study. J. Fish Biol. 2015, 87, 138–158. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. Fish Exploiting Vortices Decrease Muscle Activity. Science 2003, 302, 1566–1569. [Google Scholar] [CrossRef]
- Enders, E.C.; Castro-Santos, T.; Lacey, R.W.J. The effects of horizontally and vertically oriented baffles on flow structure and ascent performance of upstream-migrating fish. J. Ecohydraulics 2017, 2, 38–52. [Google Scholar] [CrossRef]
- Silva, A.T.; Katopodis, C.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N. Cyprinid swimming behaviour in response to turbulent flow. Ecol. Eng. 2012, 44, 314–328. [Google Scholar] [CrossRef]
- Muhawenimana, V.; Wilson, C.A.M.E.; Ouro, P.; Cable, J. Spanwise Cylinder Wake Hydrodynamics and Fish Behavior. Water Resour. Res. 2019, 55, 8569–8582. [Google Scholar] [CrossRef]
- Persson, L.; Leonardsson, K.; Alanärä, A. Manipulation of the energetic state of Atlantic salmon Salmo salar juveniles and the effect on migration speed. J. Fish Biol. 2018, 92, 961–978. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, C.; Enberg, K.; Mangel, M. Modelling and interpreting fish bioenergetics: A role for behaviour, life-history traits and survival trade-offs. J. Fish Biol. 2016, 88, 389–402. [Google Scholar] [CrossRef]
- Norin, T.; Clark, T.D. Fish face a trade-off between ‘eating big’ for growth efficiency and ‘eating small’ to retain aerobic capacity. Biol. Lett. 2017, 13, 20170298. [Google Scholar] [CrossRef]
- Zhai, C.; Li, Y.; Zhu, G.; Peng, W.; E, Q.; Zhang, Y.; Ma, B. The Effects of Water Flow Speed on Swimming Capacity and Energy Metabolism in Adult Amur Grayling (Thymallus grubii). Fishes 2024, 9, 272. [Google Scholar] [CrossRef]
- Espírito-Santo, C.; Guardiola, F.A.; Ozório, R.O.A.; Magnoni, L.J. Short-term induced swimming activity enhanced innate immune parameters and antioxidant status of European eel (Anguilla anguilla). Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2024, 296, 111680. [Google Scholar] [CrossRef]
- Hou, Q.; Fu, S.; Huang, T.; Li, X.; Shi, X. Effects of Aerobic Exercise Training on the Growth, Swimming Performance, Antipredation Ability and Immune Parameters of Juvenile Rock Carp (Procypris rabaudi). Animals 2022, 12, 257. [Google Scholar] [CrossRef]
- Zhu, T.; Li, D.; Xiang, K.; Zhao, J.; Zhu, Z.; Peng, Z.; Zhu, S.; Liu, Y.; Ye, Z. Effects of acute flow velocity stress on oxygen consumption rate, energy metabolism and transcription level of mandarin fish (Siniperca chuatsi). Aquac. Rep. 2024, 38, 102293. [Google Scholar] [CrossRef]
- Espírito-Santo, C.; Alburquerque, C.; Cavalheri, T.; Guardiola, F.A.; Ozório, R.O.A.; Magnoni, L.J. Induced swimming reduced stress and modulated immune response and antioxidant status in juvenile rainbow trout (Oncorhynchus mykiss). Fish Physiol. Biochem. 2025, 51, 151. [Google Scholar] [CrossRef] [PubMed]

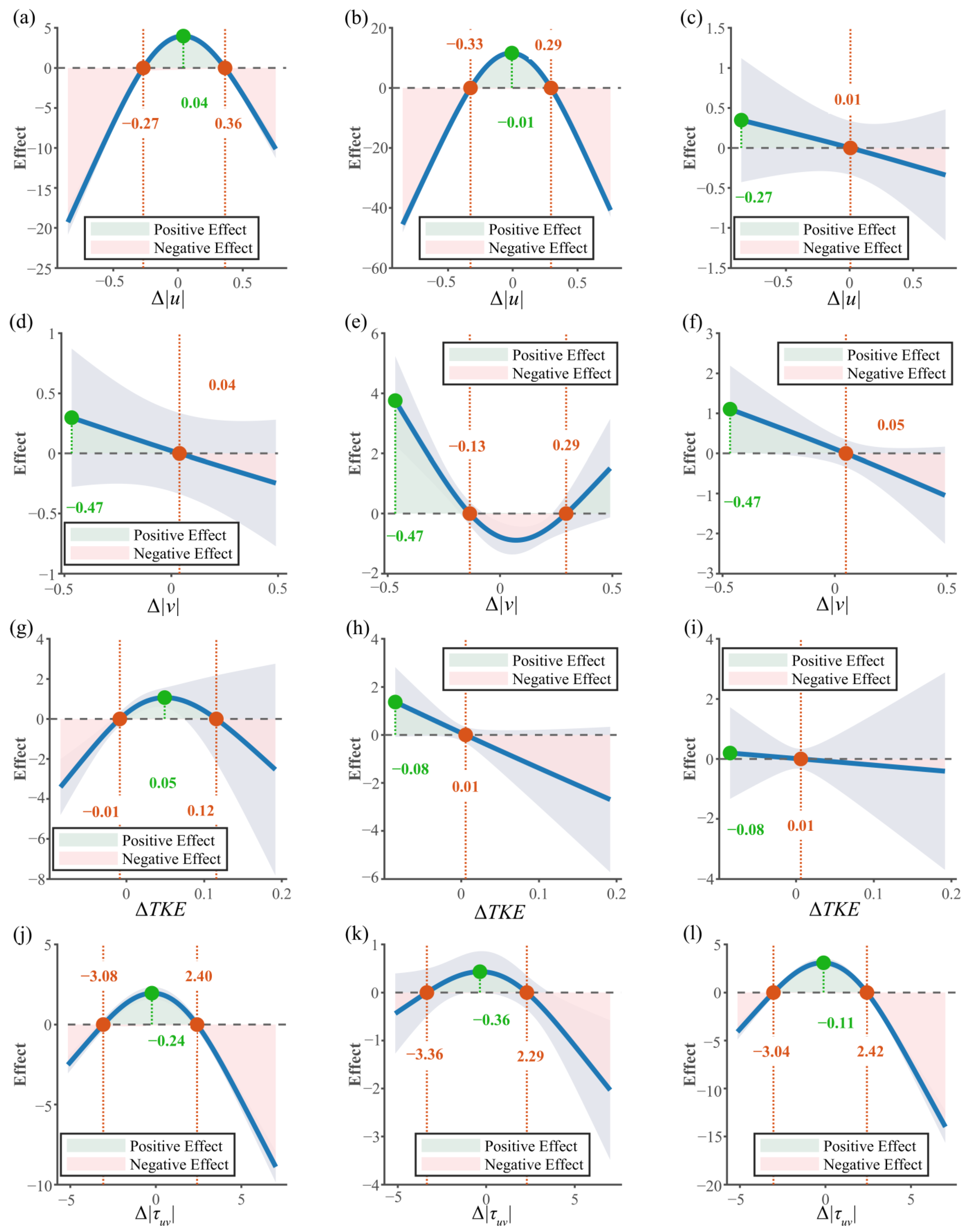
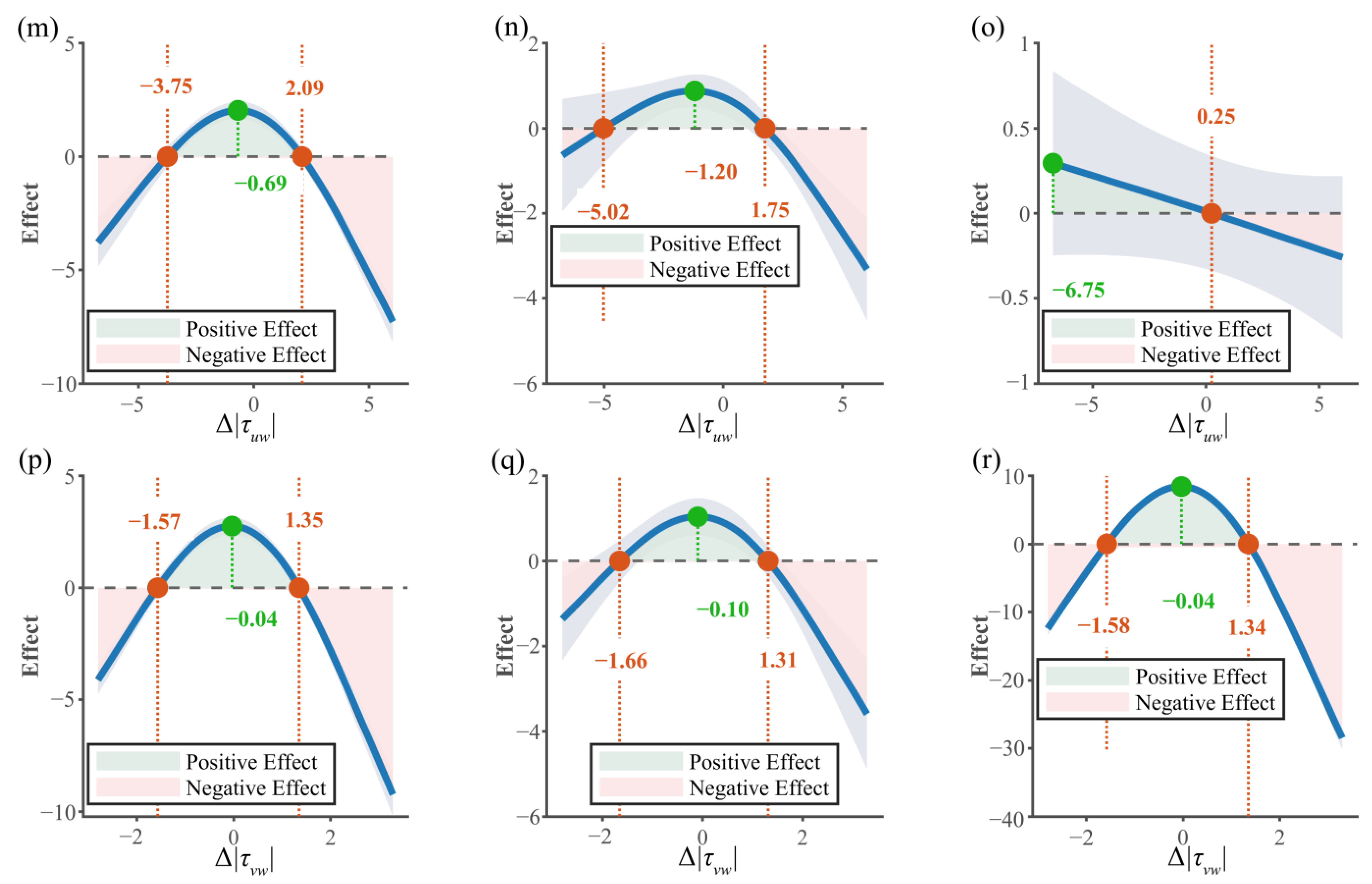
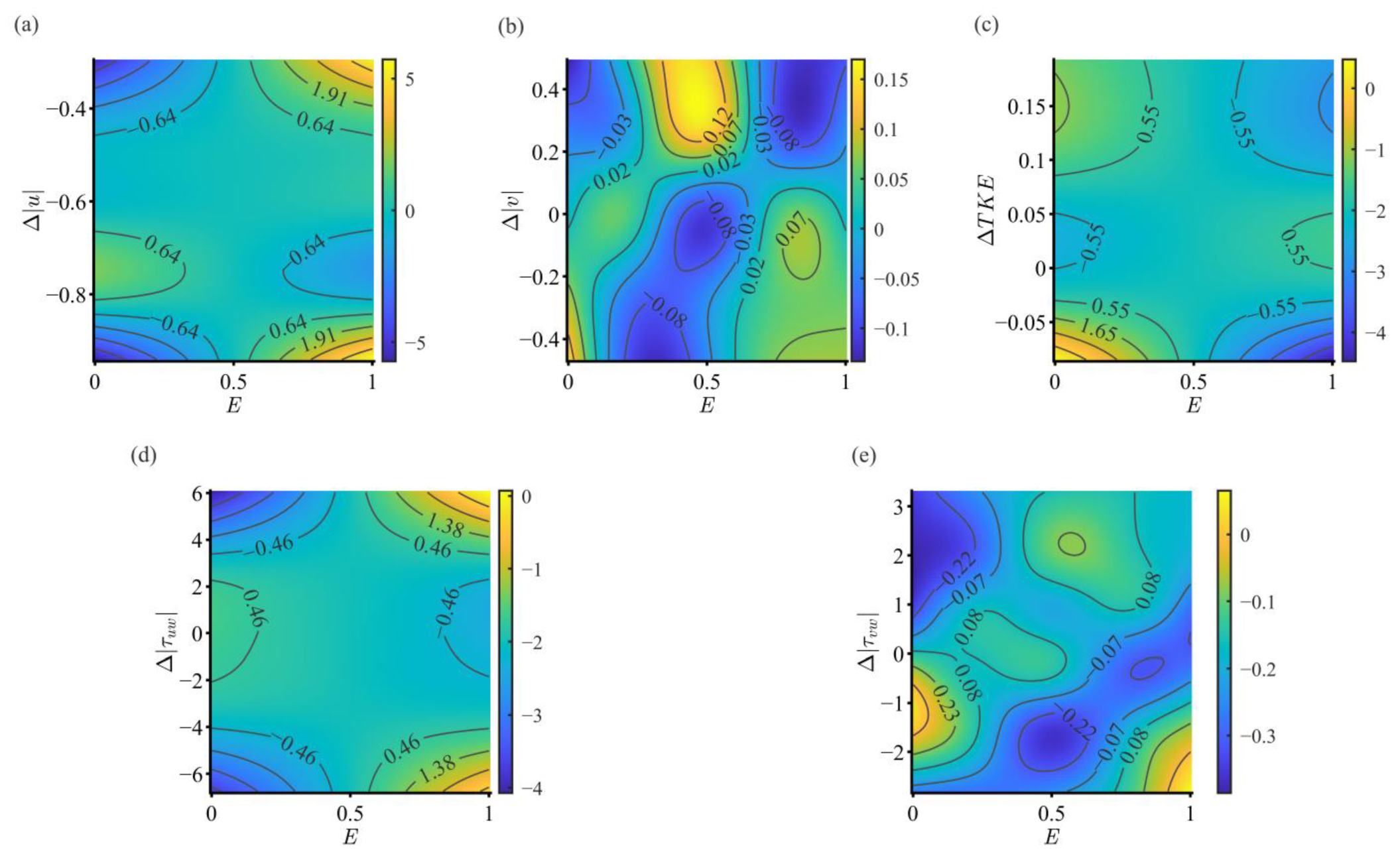
| Trial | N | BL (Mean ± SD, cm) | Weight (Mean ± SD, g) | Temp (Mean ± SD, °C) | DO (Mean ± SD, mg/L) | Vnom (m/s) | Q (m3/s) |
|---|---|---|---|---|---|---|---|
| 1 | 42 | 38.80 ± 4.57 | 939.58 ± 327.20 | 12.70 ± 0.80 | 6.19 ± 0.07 | 1.80 | 0.24 |
| 2 | 41 | 39.55 ± 4.72 | 1021.42 ± 373.49 | 12.89 ± 0.85 | 6.18 ± 0.06 | 2.00 | 0.27 |
| 3 | 40 | 38.81 ± 4.93 | 989.08 ± 368.02 | 12.75 ± 0.80 | 6.18 ± 0.06 | 2.20 | 0.28 |
| 4 | 40 | 39.66 ± 4.01 | 992.70 ± 304.00 | 12.93 ± 0.80 | 6.20 ± 0.06 | 2.40 | 0.28 |
| 5 | 40 | 38.95 ± 3.96 | 940.45 ± 320.70 | 12.94 ± 0.80 | 6.17 ± 0.05 | 2.50 | 0.29 |
| Rank | Covariates | AIC | ΔAIC | w |
|---|---|---|---|---|
| 1 | Vs + BL | 802.62 | 0 | 0.64 |
| 2 | Vs + BL + DO | 804.50 | 1.88 | 0.25 |
| 3 | Vs + BL + DO + Temp | 806.24 | 3.61 | 0.11 |
| Model | Variable | Coefficient | SE | p |
|---|---|---|---|---|
| Prolonged | Intercept | 6.29 | 1.10 | <0.0001 |
| Vs (BL/s) | −0.94 | 0.15 | <0.0001 | |
| BL (m) | 6.98 | 2.65 | 0.0086 | |
| Log(scale) | −0.86 | 0.18 | <0.0001 | |
| N (prolonged) | 47 | |||
| Sprint | Intercept | 9.87 | 1.45 | <0.0001 |
| Vs (BL/s) | −0.48 | 0.12 | <0.0001 | |
| BL (m) | −7.81 | 2.12 | 0.00024 | |
| Log(scale) | −0.50 | 0.10 | <0.0001 | |
| N (sprint) | 138 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Ding, G.; Li, Y.; He, G.; Zhou, Y.; Wang, X. Swimming Performance and Behavior of High-Altitude Fish in High-Flow Velocity Environments. Animals 2025, 15, 3327. https://doi.org/10.3390/ani15223327
Chen K, Ding G, Li Y, He G, Zhou Y, Wang X. Swimming Performance and Behavior of High-Altitude Fish in High-Flow Velocity Environments. Animals. 2025; 15(22):3327. https://doi.org/10.3390/ani15223327
Chicago/Turabian StyleChen, Kaixiao, Guanxi Ding, Yun Li, Gangwei He, Yanteng Zhou, and Xiaogang Wang. 2025. "Swimming Performance and Behavior of High-Altitude Fish in High-Flow Velocity Environments" Animals 15, no. 22: 3327. https://doi.org/10.3390/ani15223327
APA StyleChen, K., Ding, G., Li, Y., He, G., Zhou, Y., & Wang, X. (2025). Swimming Performance and Behavior of High-Altitude Fish in High-Flow Velocity Environments. Animals, 15(22), 3327. https://doi.org/10.3390/ani15223327






