Analysis of Population Structure in Hungarian Coldblood Horses Based on Pedigree Information
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Pedigree Analysis
2.2. Pedigree Completeness
- Maximum number of generations (GenMax)—the number of generations separating the individual from its furthest ancestor [7];
- Number of complete generations (GenCom)—the furthest generation where all ancestors of the individual are known [7];
- Equivalent complete generations (GenEqu)—defined as the sum of the proportion of known ancestors over all generations traced. It could be computed as the sum over all known ancestors of the terms computed as the sum of (1/2)n, where n is the number of generations separating the individual from each known ancestor [7].
2.3. Generation Interval
2.4. Probability of Gene Origin
- Number of founders (Nf)—the number of animals with unknown parents [18];
- Number of ancestors (Na)—the minimum number of individuals in the pedigree, which explains the total genetic variability in the population [18];
- Effective number of founders (fe)—the number of animals that, if mated randomly, would produce the same amount of genetic variation as the study population [15];
- Effective number of ancestors (fa)—the marginal contributions of ancestors that would be expected to produce the same genetic diversity as in the population under study [15].
2.5. Inbreeding Coefficient and Average Relatedness
- Wright method (F_Wright)—the probability that the two alleles at any locus in an individual are identical by descent [19];
- Ballou method (F_Ballou)—the probability that an individual inherits an allele which has undergone inbreeding in the past at least once [20];
- Kalinowski method (F_Kal) and Kalinowski new method (F_Kal_new)—classical inbreeding coefficient is split into two parts, alleles which had undergone inbreeding in the past (‘old’, i.e., F_Kal) and alleles identical by descent for the first time (‘new’ inbreeding coefficient, F_Kal_new). Thus, F_Kal represents the part of the genome where alleles are currently in identical by descent status and have also been identical by descent in the ancestor of the animal at least once [12,21];
- Average relatedness (AR)—the probability that an allele randomly selected from the entire population belongs to the individual [22].
3. Results
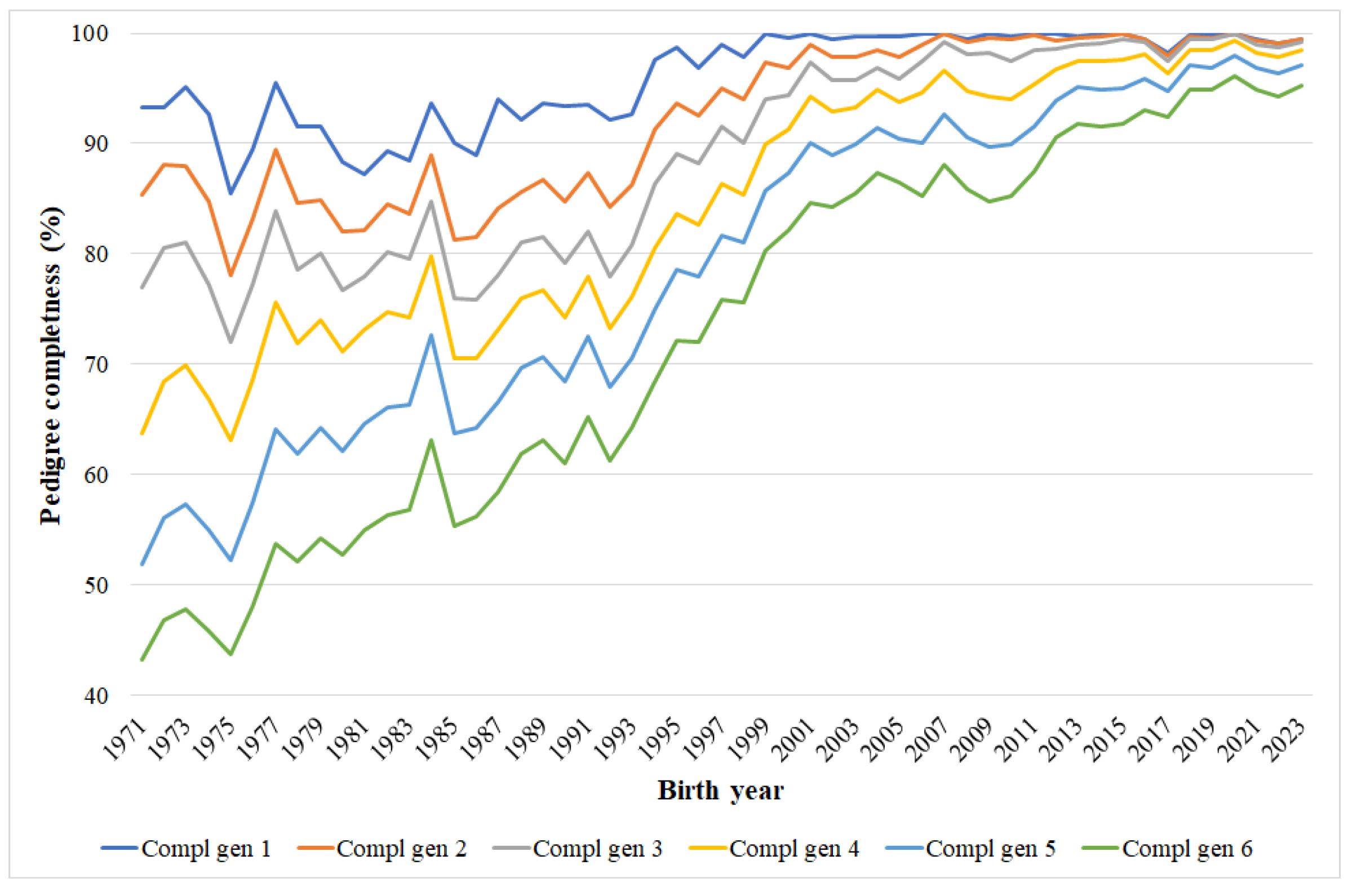
3.1. Pedigree Completeness
3.2. Generation Interval
3.3. Probability of Gene Origin Based on Parameters
3.4. Inbreeding Level and Average Relatedness
4. Discussion
4.1. Pedigree Completeness
4.2. Generation Interval
4.3. Probability of Gene Origin Based on Parameters
4.4. Inbreeding Level and Average Relatedness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bodó, I. A ló szaporítása. In Lótenyésztők Kézikönyve, 1st ed.; Bodó, I., Hacker, W., Eds.; Mezőgazda Kiadó: Budapest, Hungary, 1992; pp. 224–225. (In Hungarian) [Google Scholar]
- Magyar Hidegvérű Tenyésztők Országos Egyesülete. 30 év Magyar Hidegvérű Lótenyésztő Országos Egyesület; Magyar Hidegvérű Lótenyésztő Országos Egyesület: Lippó, Hungary, 2022; p. 157. (In Hungarian) [Google Scholar]
- Pataki, B. Magyar hidegvérű. In Ló és Szamár; Mihók, S., Ed.; Mezőgazda Kiadó: Budapest, Hungary, 2001; pp. 206–210. (In Hungarian) [Google Scholar]
- Gulyás, L.; Markos, L.; Medve, F.; Mihók, S.; Müller, J.; Pataki, B. A magyar hidegvérű ló kialakulása. In A Magyar Hidegvérű Ló; Mihók, S., Ed.; Mezőgazda Lap- és Könyvkiadó: Budapest, Hungary, 2017; pp. 31–56. (In Hungarian) [Google Scholar]
- Pongrácz, L.; Kósik, P. Sustainability Aspects of the Hungarian Horse Industry. Chem. Eng. Trans. 2023, 107, 391–396. [Google Scholar] [CrossRef]
- 32/2004. (IV. 19.) OGY Határozat a Védett Őshonos Vagy Veszélyeztetett, Magas Genetikai Értéket Képviselő Tenyésztett Magyar Állatfajták Nemzeti Kinccsé Nyilvánításáról. Available online: https://njt.hu/jogszabaly/2004-32-30-41 (accessed on 24 March 2025). (In Hungarian).
- Maignel, L.; Boichard, D.; Verrier, E. Genetic variability of French dairy breeds estimated from pedigree information. Interbull Bull. 1996, 14, 49–54. [Google Scholar]
- Nagy, I. Kvantitatív Genetikai Vizsgálatok Multipara Állatfajokban. Ph.D. Thesis, Hungarian Academy of Sciences, Budapest, Hungary, 2017. (In Hungarian). [Google Scholar]
- Gutiérrez, J.P.; Goyache, F. A note on ENDOG: A computer program for analysing pedigree information. J. Anim. Breed. Genet. 2005, 122, 172–176. [Google Scholar] [CrossRef]
- Groeneveld, E.; Westhuizen, B.D.; Maiwashe, A.; Voordewind, F.; Ferraz, J.B. POPREP: A Generic Report for Population Management. Genet. Mol. Res. GMR 2009, 8, 1158–1178. [Google Scholar] [CrossRef] [PubMed]
- Kinghorn, B.P. Pedigree Viewer-A graphical utility for browsing pedigreed data sets. In Proceedings of the 5th World Congress on Genetics Applied to Livestock Production, Guelph, ON, Canada, 7–12 August 1994; Volume 22, pp. 85–86. [Google Scholar]
- Baumung, R.; Farkas, J.; Boichard, D.; Mészáros, G.; Sölkner, J.; Curik, I. GRAIN: A computer program to calculate ancestral and partial inbreeding coefficients using a gene dropping approach. J. Anim. Breed. Genet. 2015, 132, 100–108. [Google Scholar] [CrossRef]
- Vígh, Z.; Csató, L.; Nagy, I. A pedigré analízisben alkalmazott mutatószámok és értelmezésük [Application pedigree analysis in the animal breeding programs]. Hung. J. Anim. Breed. 2008, 57, 549–564. (In Hungarian) [Google Scholar]
- Sigurdson, A.; Jonmudson, J.V. Inbreeding and its impact in the closed population of Icelandic dairy cattle. Acta Agric. Scand. 1995, 45, 11–16. [Google Scholar] [CrossRef]
- Boichard, D.; Maignel, L.; Verrier, É. The value of using probabilities of gene origin to measure genetic variability in a population. Genet. Sel. Evol. 1997, 29, 5–23. [Google Scholar] [CrossRef]
- Caballero, A.; Fernández, A.; Villanueva, B.; Toro, M.A. A comparison of marker-based estimators of inbreeding and inbreeding depression. Genet. Sel. Evol. 2022, 54, 82. [Google Scholar] [CrossRef]
- Valera, M.; Molina, A.; Gutiérrez, J.P.; Gómez, J.; Goyache, F. Pedigree analysis in the Andalusian horse: Population structure, genetic variability and influence of the Carthusian strain. Liv. Prod. Sci. 2005, 95, 57–66. [Google Scholar] [CrossRef]
- Bokor, Á.; Jónás, D.; Bart, D.; Nagy, I.; Bokor, J.; Szabari, M. Pedigree analysis of the Hungarian Thoroughbred population. Livest. Sci. 2013, 151, 1–10. [Google Scholar] [CrossRef]
- Wright, S. Systems of mating II. The effects of inbreeding on the genetic composition of a population. Genetics 1921, 6, 124–143. [Google Scholar] [CrossRef] [PubMed]
- Suwanlee, S.; Baumung, R.; Sölkner, J.; Curik, I. Evaluation of ancestral inbreeding coefficients: Ballou’s formula versus gene dropping. Conserv. Genet. 2007, 8, 489–495. [Google Scholar] [CrossRef]
- Kalinowski, S.T.; Hedrick, P.W.; Miller, P.S. Inbreeding Depression in the Speke’s Gazelle Captive Breeding Program. Conserv. Biol. 2000, 14, 1375–1384. [Google Scholar] [CrossRef]
- Colleau, J.J. An indirect approach to the extensive calculation of relationship coefficients. Genet. Sel. Evol. 2002, 34, 409–421. [Google Scholar] [CrossRef]
- Rogic, B.; Strbac, L.; Preradovic, S.; Vazic, B. Pedigree analysis of the Lipizzan horse populations from Bosnia and Herzegovina and Serbia: Structure, inbreeding and genetic variability. Czech J. Anim. Sci. 2022, 67, 483–492. [Google Scholar] [CrossRef]
- Klein, R.; Oláh, J.; Mihók, S.; Posta, J. Pedigree-Based Description of Three Traditional Hungarian Horse Breeds. Animals 2022, 12, 2071. [Google Scholar] [CrossRef]
- Bramante, G.; Pieragostini, E.; Ciani, E. Genetic Variability within the Murgese Horse Breed Inferred from Genealogical Data and Morphometric Measurements. Diversity 2022, 14, 422. [Google Scholar] [CrossRef]
- Mcmanus, C.; Santos, S.A.; Dallago, B.S.L.; Paiva, S.R.; Martins, R.F.S.; Neto, J.B.; Marques, P.R.; Abreu, U.G.P.D. Evaluation of conservation program for the Pantaneiro horse in Brazil. R. Bras. Zootec. 2013, 42, 404–413. [Google Scholar] [CrossRef]
- Klecel, W.; Kloch, M.; Wojciechowska, M.; Gajewska, M.; Martyniuk, E. Population structure and genetic diversity of Polish Arabian horses based on pedigree data. Animal 2024, 18, 101148. [Google Scholar] [CrossRef]
- Faria, R.A.S.; Maiorano, A.M.; Bernardes, P.A.; Pereira, G.L.M.; Curi, R.A. Assessment of pedigree information in the Quarter Horse: Population, breeding and genetic diversity. Livest. Sci. 2018, 214, 135–141. [Google Scholar] [CrossRef]
- Duru, S. Pedigree analysis of the Turkish Arab horse population: Structure, inbreeding and genetic variability. Animal 2017, 11, 1449–1456. [Google Scholar] [CrossRef]
- Giontella, A.; Sarti, F.M.; Cardinali, I.; Giovannini, S.; Cherchi, R.; Lancioni, H.; Silvestrelli, M.; Pieramati, C. Genetic variability and population structure in the Sardinian Anglo-Arab horse. Animals 2020, 10, 1018. [Google Scholar] [CrossRef] [PubMed]
- Polak, G. Genetic variability of cold-blooded horses participating in genetic resources conservation programs, using pedigree analysis. Ann. Anim. Sci. 2019, 19, 49–60. [Google Scholar] [CrossRef]
- Nikonova, V.; Jonkus, D.; Paura, L. Pedigree analysis of Latvian Warmblood horse heavy type population. Czech J. Anim. Sci. 2024, 69, 462–469. [Google Scholar] [CrossRef]
- Poncet, P.A.; Pfister, W.; Muntwyler, J.; Glowatzki-Mullis, M.L.; Gaillard, C. Analysis of pedigree and conformation data to explain genetic variability of the horse breed Franches-Montagnes. J. Anim. Breed. Genet. 2006, 123, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Bussiman, F.D.O.; Perez, B.C.; Ventura, R.V.; Peixoto, M.G.C.D.; Curi, R.A.; Balieiro, J.C.D.C. Pedigree analysis and inbreeding effects over morphological traits in Campolina horse population. Animal 2018, 12, 2246–2255. [Google Scholar] [CrossRef]
- Schurink, A.; Arts, D.J.G.; Ducro, B.J. Genetic diversity in the Dutch harness horse population using pedigree analysis. Livest. Sci. 2012, 143, 270–277. [Google Scholar] [CrossRef]
- Dell, A.; Curry, M.; Yarnell, K.; Starbuck, G.; Wilson, P.B. Genetic analysis of the endangered Cleveland Bay horse: A century of breeding characterised by pedigree and microsatellite data. PLoS ONE 2020, 15, e0240410. [Google Scholar] [CrossRef]
- Pjontek, J.; Kadlečík, O.; Kasarda, R.; Horný, M. Pedigree analysis in four Slovak endangered horse breeds. Czech J. Anim. Sci. 2012, 57, 54–64. [Google Scholar] [CrossRef]
- Maciel, M.D.S.; Lucena, J.E.C.; Pinto, A.P.G.; Nascimento, C.A.D.M.S.; Arandas, J.K.G.; Rocha, L.L.D.; Santiago, J.M. Analysis of the pedigree of the Mangalarga breed: Population structure and genetic diversity. R. Bras. Zootec. 2024, 53, e20230122. [Google Scholar] [CrossRef]
- Mancin, E.; Ablondi, M.; Mantovani, R.; Pigozzi, G.; Sabbioni, A.; Sartori, C. Genetic variability in the Italian heavy draught horse from pedigree data and genomic information. Animals 2020, 10, 1310. [Google Scholar] [CrossRef] [PubMed]
- Stephens, T.D.; Splan, R.K. Population history and genetic variability of the American Shire horse. Anim. Genet. 2013, 52, 31–38. [Google Scholar] [CrossRef]
- Vostrá-Vydrová, H.; Vostrý, L.; Hofmanová, B.; Krupa, E.; Zavadilová, L. Pedigree analysis of the endangered Old Kladruber horse population. Livest. Sci. 2016, 185, 17–23. [Google Scholar] [CrossRef]

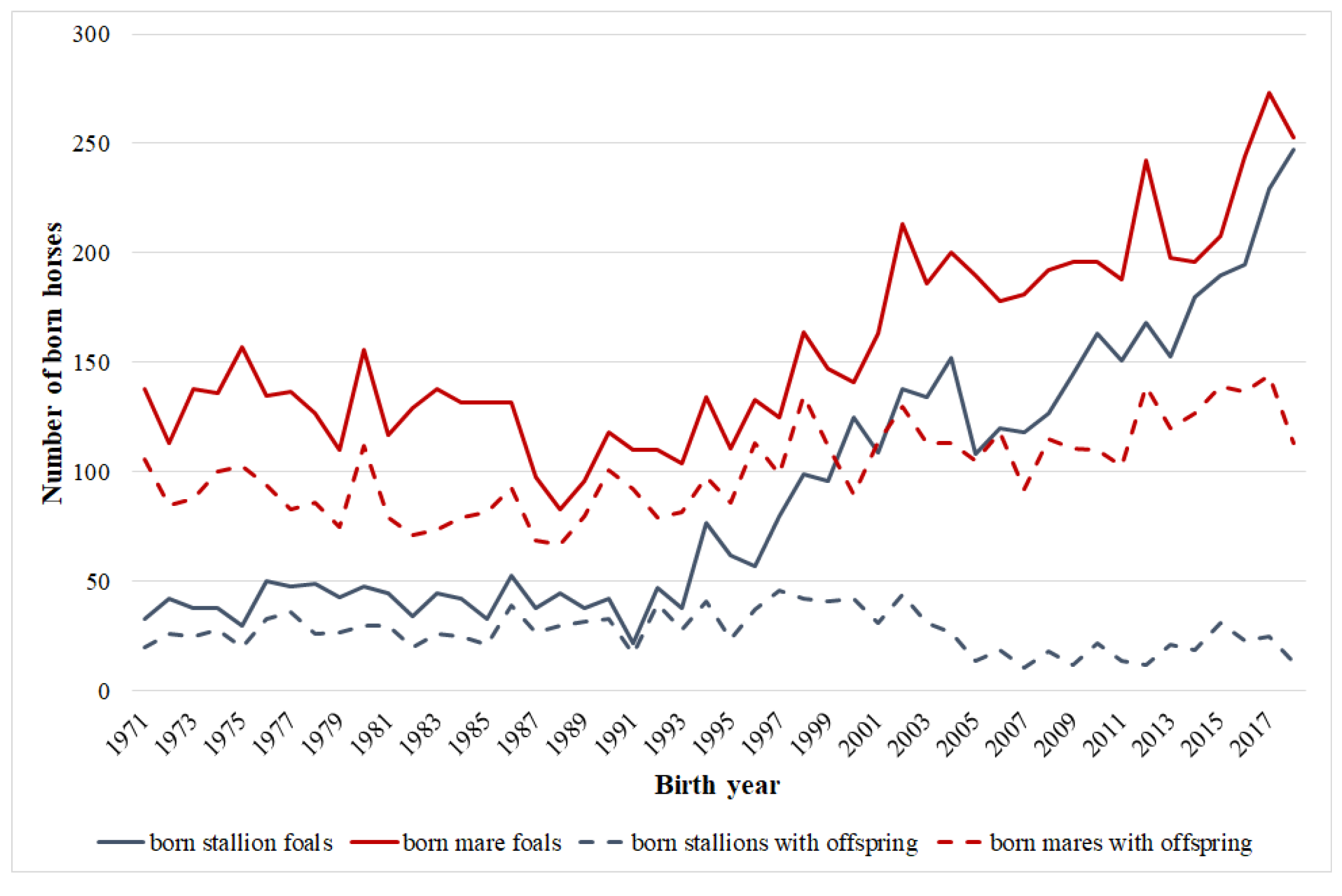

| Parameter | Total Population | Actual Breeding Stock | Breeding Stock in 1989 |
|---|---|---|---|
| Total number of horses | 21,699 | 1123 | 182 |
| Number of stallions | 8269 | 216 | 70 |
| Number of mares | 13,430 | 907 | 112 |
| Parameter | Total Population | Breeding Stock in 1989 | Actual Breeding Stock |
|---|---|---|---|
| N | 21,699 | 182 | 1123 |
| GenMax | 7.90 | 5.31 | 13.06 |
| GenCom | 2.80 | 2.18 | 4.60 |
| GenEqu | 4.64 | 3.34 | 7.72 |
| Pathways | Numbers | Generation Interval (Years) | Deviation |
|---|---|---|---|
| Sire-to-son | 1715 | 10.14 a | 4.81 |
| Sire-to-daughter | 5562 | 9.51 b | 4.45 |
| Dam-to-son | 1455 | 8.93 c | 3.82 |
| Dam-to-daughter | 4719 | 8.49 d | 3.90 |
| Average | 13,451 | 9.17 | 4.29 |
| Parameter | Total Population | Breeding Stock in 1989 | Actual Breeding Stock |
|---|---|---|---|
| Nf | 3996 | 708 | 1501 |
| Na | 3169 | 205 | 415 |
| fe | 278 | 238 | 183 |
| fa | 95 | 99 | 49 |
| fa/fe | 0.342 | 0.416 | 0.268 |
| Parameter | Total Population | Breeding Stock in 1989 | Actual Breeding Stock |
|---|---|---|---|
| Na50 | 44 | 54 | 17 |
| Na60 | 83 | 72 | 27 |
| Na70 | 168 | 91 | 42 |
| Na80 | 414 | 114 | 72 |
| Na90 | 1161 | 144 | 132 |
| Na100 | 3169 | 205 | 415 |
| Parameter | Total Population | Breeding Stock in 1989 | Actual Breeding Stock |
|---|---|---|---|
| first ancestor | 4.59 | 4.18 | 5.68 |
| second ancestor | 4.07 | 3.93 | 5.22 |
| third ancestor | 3.75 | 2.94 | 5.17 |
| first 3 ancestors | 12.41 | 11.04 | 16.07 |
| first 10 ancestors | 26.71 | 22.57 | 37.84 |
| Parameter | Total Population | Breeding Stock in 1989 | Actual Breeding Stock |
|---|---|---|---|
| F_Wright (%) | 1.13 | 0.77 | 2.35 |
| F_Kal (%) | 0.18 | 0.03 | 0.39 |
| F_Kal_new (%) | 0.95 | 0.74 | 1.96 |
| F_Ballou (%) | 2.47 | 0.73 | 4.95 |
| AR (%) | 1.32 | 1.11 | 2.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barsi, B.; Oláh, J.; Posta, J. Analysis of Population Structure in Hungarian Coldblood Horses Based on Pedigree Information. Animals 2025, 15, 1406. https://doi.org/10.3390/ani15101406
Barsi B, Oláh J, Posta J. Analysis of Population Structure in Hungarian Coldblood Horses Based on Pedigree Information. Animals. 2025; 15(10):1406. https://doi.org/10.3390/ani15101406
Chicago/Turabian StyleBarsi, Brigitta, János Oláh, and János Posta. 2025. "Analysis of Population Structure in Hungarian Coldblood Horses Based on Pedigree Information" Animals 15, no. 10: 1406. https://doi.org/10.3390/ani15101406
APA StyleBarsi, B., Oláh, J., & Posta, J. (2025). Analysis of Population Structure in Hungarian Coldblood Horses Based on Pedigree Information. Animals, 15(10), 1406. https://doi.org/10.3390/ani15101406







