Accuracies of Genomic Prediction for Growth Traits at Weaning and Yearling Ages in Yak
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Statement
2.2. Populations and Phenotypes
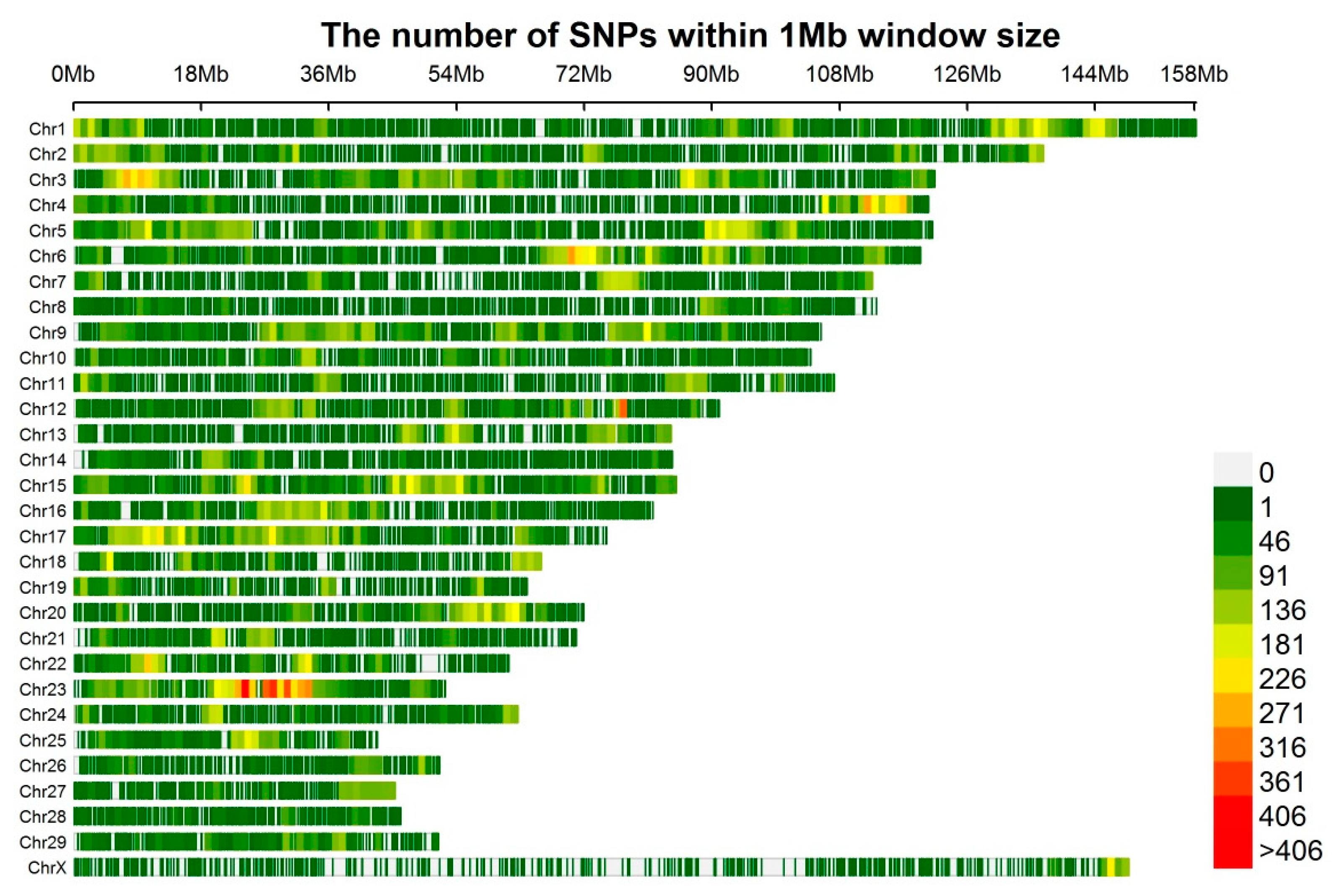
2.3. Genotypes and Quality Control
2.4. Statistical Models
2.4.1. GBLUP
2.4.2. Bayes A, Bayes B, Bayes C, and Bayes Lasso
2.5. Evaluation of Genomic Prediction Accuracy
3. Results
3.1. Estimation of Genetic Parameters
3.2. Predictive Ability and Accuracy
3.3. Correlation between Predicted Phenotype and Observation
4. Discussion
4.1. Comparison of Approaches to Genomic Prediction
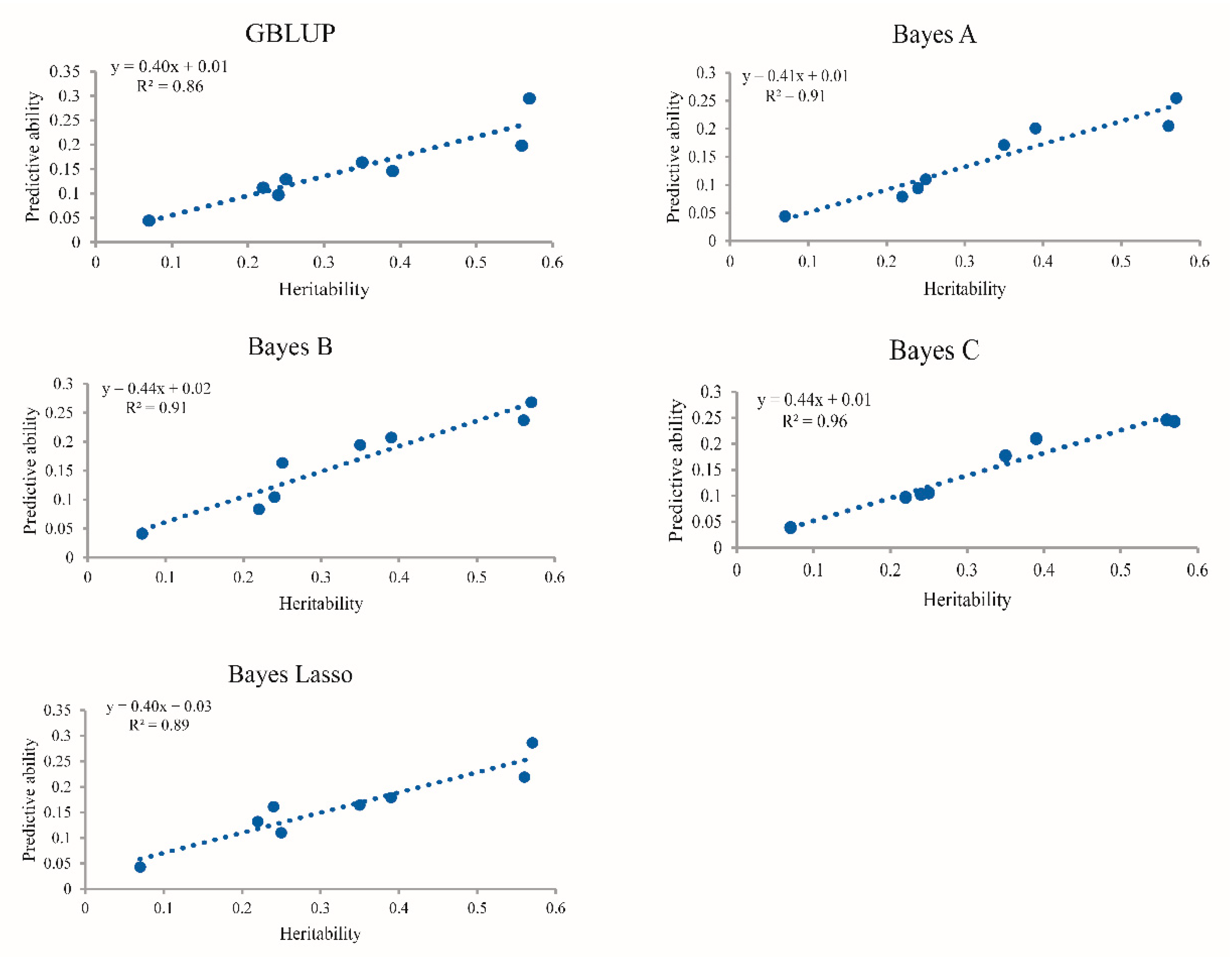
4.2. Impact of Heritability on the Accuracy of Genomic Prediction
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Genomic selection: A paradigm shift in animal breeding. Anim. Front. 2016, 6, 6–14. [Google Scholar] [CrossRef]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [PubMed]
- Hayes, B.J.; Bowman, P.J.; Chamberlain, A.C.; Verbyla, K.; Goddard, M.E. Accuracy of genomic breeding values in multi-breed dairy cattle populations. Genet. Sel. Evol. 2009, 41, 51. [Google Scholar] [CrossRef] [PubMed]
- Weller, J.I.; Ezra, E.; Ron, M. Invited review: A perspective on the future of genomic selection in dairy cattle. J. Dairy Sci. 2017, 100, 8633–8644. [Google Scholar] [CrossRef]
- VanRaden, P.; Van Tassell, C.P.; Wiggans, G.; Sonstegard, T.; Schnabel, R.D.; Taylor, J.; Schenkel, F. Invited Review: Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 2009, 92, 16–24. [Google Scholar] [CrossRef]
- Verbyla, K.; Hayes, B.J.; Bowman, P.J.; Goddard, M.E. Accuracy of genomic selection using stochastic search variable selection in Australian Holstein Friesian dairy cattle. Genet. Res. 2009, 91, 307–311. [Google Scholar] [CrossRef]
- Luan, T.; Woolliams, J.A.; Lien, S.; Kent, M.; Svendsen, M.; Meuwissen, T.H.E. The Accuracy of Genomic Selection in Norwegian Red Cattle Assessed by Cross-Validation. Genetics 2009, 183, 1119–1126. [Google Scholar] [CrossRef]
- Harris, B.; Johnson, D. Genomic predictions for New Zealand dairy bulls and integration with national genetic evaluation. J. Dairy Sci. 2010, 93, 1243–1252. [Google Scholar] [CrossRef]
- Boichard, D.; Guillaume, F.; Baur, A.; Croiseau, P.; Rossignol, M.N.; Boscher, M.Y.; Druet, T.; Genestout, L.; Colleau, J.J.; Journaux, L.; et al. Genomic selection in French dairy cattle. Anim. Prod. Sci. 2012, 52, 115. [Google Scholar] [CrossRef]
- García-Ruiz, A.; Cole, J.B.; VanRaden, P.M.; Wiggans, G.R.; Ruiz-Lopez, F.D.J.; Van Tassell, C.P. Changes in genetic selection differentials and generation intervals in US Holstein dairy cattle as a result of genomic selection. Proc. Natl. Acad. Sci. USA 2016, 113, E3995–E4004. [Google Scholar] [CrossRef]
- Piccoli, M.L.; Brito, L.F.; Braccini, J.; Cardoso, F.F.; Sargolzaei, M.; Schenkel, F.S. Genomic predictions for economically important traits in Brazilian Braford and Hereford beef cattle using true and imputed genotypes. BMC Genet. 2017, 18, 2. [Google Scholar] [CrossRef] [PubMed]
- Brito, L.F.; Clarke, S.; McEwan, J.C.; Miller, S.P.; Pickering, N.; Bain, W.E.; Dodds, K.; Sargolzaei, M.; Schenkel, F.S. Prediction of genomic breeding values for growth, carcass and meat quality traits in a multi-breed sheep population using a HD SNP chip. BMC Genet. 2017, 18, 7. [Google Scholar] [CrossRef] [PubMed]
- Ibáñez-Escriche, N.; Forni, S.; Noguera, J.L.; Varona, L. Genomic information in pig breeding: Science meets industry needs. Livest. Sci. 2014, 166, 94–100. [Google Scholar] [CrossRef]
- Lopez, M.E.; Neira, R.; Yanez, J.M. Applications in the search for genomic selection signatures in fish. Front. Genet. 2015, 5, 458. [Google Scholar] [CrossRef]
- Wolc, A.; Zhao, H.H.; Arango, J.; Settar, P.; Fulton, J.E.; O’Sullivan, N.P.; Preisinger, R.; Stricker, C.; Habier, D.; Fernando, R.L.; et al. Response and inbreeding from a genomic selection experiment in layer chickens. Genet. Sel. Evol. 2015, 47, 59. [Google Scholar] [CrossRef]
- Fu, D.; Ma, X.; Jia, C.; Chu, M.; Lei, Q.; Wen, Z.; Wu, X.; Pei, J.; Bao, P.; Ding, X.; et al. A Study of Genomic Prediction of 12 Important Traits in the Domesticated Yak (Bos grunniens). Animals 2019, 9, 927. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, H.; Tang, Z.; Xu, J.; Yin, D.; Zhang, Z.; Yuan, X.; Zhu, M.; Zhao, S.; Li, X.; et al. rMVP: A Memory-efficient, Visualization-enhanced, and Parallel-accelerated tool for Genome-Wide Association Study. bioRxiv 2020. [Google Scholar] [CrossRef]
- Hammami, H.; Rekik, B.; Soyeurt, H.; Bastin, C.; Bay, E.; Stoll, J.; Gengler, N. Accessing genotype by environment interaction using within- and across-country test-day random regression sire models. J. Anim. Breed. Genet. 2009, 126, 366–377. [Google Scholar] [CrossRef]
- VanRaden, P. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Meuwissen, T.; Solberg, T.R.; Shepherd, R.; Woolliams, J. A fast algorithm for BayesB type of prediction of genome-wide estimates of genetic value. Genet. Sel. Evol. 2009, 41, 2. [Google Scholar] [CrossRef]
- Alkan, C.; Coe, B.P.; Eichler, E.E. Genome structural variation discovery and genotyping. Nat. Rev. Genet. 2011, 12, 363–376. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, P.; Campos, G.D.L. Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Pryce, J.; Arias, J.; Bowman, P.; Davis, S.; Macdonald, K.; Waghorn, G.; Wales, W.; Williams, Y.; Spelman, R.; Hayes, B.J. Accuracy of genomic predictions of residual feed intake and 250-day body weight in growing heifers using 625,000 single nucleotide polymorphism markers. J. Dairy Sci. 2012, 95, 2108–2119. [Google Scholar] [CrossRef]
- Saatchi, M.; McClure, M.C.; McKay, S.D.; Rolf, M.M.; Kim, J.; Decker, J.E.; Taxis, T.M.; Chapple, R.H.; Ramey, H.R.; Northcutt, S.L.; et al. Accuracies of genomic breeding values in American Angus beef cattle using K-means clustering for cross-validation. Genet. Sel. Evol. 2011, 43, 40. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Guo, P.; Zhang, W.; Chen, Y.; Zhang, L.; Gao, H.; Wang, Z.; Gao, X.; Xu, L.; Li, J. Accuracies of genomic prediction for twenty economically important traits in Chinese Simmental beef cattle. Anim. Genet. 2019, 50, 634–643. [Google Scholar] [CrossRef] [PubMed]
- Garrick, D.J. The nature, scope and impact of genomic prediction in beef cattle in the United States. Genet. Sel. Evol. 2011, 43, 17. [Google Scholar] [CrossRef] [PubMed]
- Medugorac, I.; Graf, A.; Grohs, C.; Rothammer, S.; Zagdsuren, Y.; Gladyr, E.; Zinovieva, N.; Barbieri, J.; Seichter, D.; Russ, I.; et al. Whole-genome analysis of introgressive hybridization and characterization of the bovine legacy of Mongolian yaks. Nat. Genet. 2017, 49, 470–475. [Google Scholar] [CrossRef] [PubMed]
- Iheshiulor, O.O.M.; Woolliams, J.; Yu, X.; Wellmann, R.; Meuwissen, T.H.E. Within- and across-breed genomic prediction using whole-genome sequence and single nucleotide polymorphism panels. Genet. Sel. Evol. 2016, 48, 15. [Google Scholar] [CrossRef]
- Sun, X.; Habier, D.; Fernando, R.L.; Garrick, D.J.; Dekkers, J.C.M. Genomic breeding value prediction and QTL mapping of QTLMAS2010 data using Bayesian Methods. BMC Proc. 2011, 5, 1–8. [Google Scholar] [CrossRef]
- Gao, H.; Su, G.; Janss, L.; Zhang, Y.; Lund, M. Model comparison on genomic predictions using high-density markers for different groups of bulls in the Nordic Holstein population. J. Dairy Sci. 2013, 96, 4678–4687. [Google Scholar] [CrossRef]
- Cleveland, M.A.; Forni, S.; Deeb, N.; Maltecca, C. Genomic breeding value prediction using three Bayesian methods and application to reduced density marker panels. BMC Proc. 2010, 4, S6. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Vinsky, M.; Li, C. Accuracy of predicting genomic breeding values for carcass merit traits in Angus and Charolais beef cattle. Anim. Genet. 2014, 46, 55–59. [Google Scholar] [CrossRef] [PubMed]
- Hayes, B.J.; Bowman, P.; Chamberlain, A.; Goddard, M.E. Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 2009, 92, 433–443. [Google Scholar] [CrossRef]
- Heslot, N.; Yang, H.-P.; Sorrells, M.E.; Jannink, J.-L. Genomic Selection in Plant Breeding: A Comparison of Models. Crop Sci. 2012, 52, 146–160. [Google Scholar] [CrossRef]
- De Roos, A.P.W.; Hayes, B.J.; Spelman, R.J.; Goddard, M.E. Linkage Disequilibrium and Persistence of Phase in Holstein–Friesian, Jersey and Angus Cattle. Genetics 2008, 179, 1503–1512. [Google Scholar] [CrossRef]
- Jia, Y.; Jannink, J.-L. Multiple-Trait Genomic Selection Methods Increase Genetic Value Prediction Accuracy. Genetics 2012, 192, 1513–1522. [Google Scholar] [CrossRef]
- Su, G.; Madsen, P.; Nielsen, U.; Mäntysaari, E.; Aamand, G.; Christensen, O.; Lund, M. Genomic prediction for Nordic Red Cattle using one-step and selection index blending. J. Dairy Sci. 2012, 95, 909–917. [Google Scholar] [CrossRef] [PubMed]
| Trait | Number | Mean | SD | Minimum | Maximum | Trait Definition |
|---|---|---|---|---|---|---|
| BW6 | 350 | 84.18 | 10.31 | 58 | 117 | Body weight at 6 months, kg |
| WH6 | 354 | 94.37 | 5.26 | 82 | 108 | Withers height at 6 months, cm |
| BL6 | 354 | 91.89 | 7.379 | 73 | 116 | Body length at 6 months, cm |
| CG6 | 354 | 124.03 | 7.809 | 100 | 144 | Chest girth at 6 months, cm |
| BW12 | 343 | 82.57 | 10.51 | 48 | 113 | Body weight at 12 months, kg |
| WH12 | 349 | 90.49 | 4.18 | 81 | 102 | Withers height at 12 months, cm |
| BL12 | 349 | 95.93 | 4.957 | 80 | 113 | Body length at 12 months, cm |
| CG12 | 349 | 117.16 | 5.08 | 102 | 134 | Chest girth at 12 months, cm |
| BW30 | 263 | 155.42 | 15.23 | 108 | 203 | Body weight at 30 months, kg |
| WH30 | 267 | 99.55 | 4.997 | 90 | 117 | Withers height at 30 months, cm |
| BL30 | 265 | 113.17 | 5.696 | 96 | 126 | Body length at 30 months, cm |
| CG30 | 261 | 146.97 | 8.266 | 122 | 173 | Chest girth at 30 months, cm |
| Trait | |||
|---|---|---|---|
| BW6 | 37.506 | 68.848 | 0.35 ± 0.01 |
| WH6 | 15.597 | 11.558 | 0.57 ± 0.02 |
| BL6 | 30.752 | 24.181 | 0.56 ± 0.02 |
| CG6 | 23.822 | 36.526 | 0.39 ± 0.01 |
| BW12 | 26.815 | 83.298 | 0.24 ± 0.01 |
| WH12 | 3.941 | 13.511 | 0.22 ± 0.02 |
| BL12 | 1.746 | 22.812 | 0.07 ± 0.04 |
| CG12 | 6.493 | 19.171 | 0.25 ± 0.02 |
| Trait | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GBLUP | BayesA | BayesB | BayesC | Bayes Lasso | GBLUP | BayesA | BayesB | BayesC | Bayes Lasso | |
| BW6 | 0.164 | 0.171 | 0.194 | 0.177 | 0.164 | 0.277 | 0.289 | 0.328 | 0.299 | 0.277 |
| WH6 | 0.295 | 0.255 | 0.268 | 0.243 | 0.286 | 0.391 | 0.338 | 0.355 | 0.322 | 0.379 |
| BL6 | 0.198 | 0.205 | 0.237 | 0.246 | 0.219 | 0.265 | 0.274 | 0.317 | 0.329 | 0.293 |
| CG6 | 0.146 | 0.201 | 0.207 | 0.210 | 0.179 | 0.234 | 0.322 | 0.331 | 0.336 | 0.287 |
| BW12 | 0.097 | 0.094 | 0.104 | 0.103 | 0.161 | 0.198 | 0.192 | 0.212 | 0.210 | 0.329 |
| WH12 | 0.112 | 0.079 | 0.083 | 0.097 | 0.132 | 0.239 | 0.168 | 0.177 | 0.207 | 0.281 |
| BL12 | 0.044 | 0.044 | 0.041 | 0.039 | 0.043 | 0.166 | 0.166 | 0.155 | 0.147 | 0.163 |
| CG12 | 0.129 | 0.110 | 0.163 | 0.106 | 0.110 | 0.220 | 0.220 | 0.326 | 0.212 | 0.220 |
| GBLUP | BayesA | BayesB | BayesC | BayesLasso | |
|---|---|---|---|---|---|
| Pearson correlation coefficient | 0.407 | 0.422 | 0.403 | 0.405 | 0.374 |
| Significance | p < 0.001 | p < 0.001 | p < 0.001 | p < 0.001 | p < 0.001 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, F.; Jia, C.; Bao, P.; Wu, X.; Liang, C.; Yan, P. Accuracies of Genomic Prediction for Growth Traits at Weaning and Yearling Ages in Yak. Animals 2020, 10, 1793. https://doi.org/10.3390/ani10101793
Ge F, Jia C, Bao P, Wu X, Liang C, Yan P. Accuracies of Genomic Prediction for Growth Traits at Weaning and Yearling Ages in Yak. Animals. 2020; 10(10):1793. https://doi.org/10.3390/ani10101793
Chicago/Turabian StyleGe, Fei, Congjun Jia, Pengjia Bao, Xiaoyun Wu, Chunnian Liang, and Ping Yan. 2020. "Accuracies of Genomic Prediction for Growth Traits at Weaning and Yearling Ages in Yak" Animals 10, no. 10: 1793. https://doi.org/10.3390/ani10101793
APA StyleGe, F., Jia, C., Bao, P., Wu, X., Liang, C., & Yan, P. (2020). Accuracies of Genomic Prediction for Growth Traits at Weaning and Yearling Ages in Yak. Animals, 10(10), 1793. https://doi.org/10.3390/ani10101793





