Validating a Bayesian Spatio-Temporal Model to Predict La Crosse Virus Human Incidence in the Appalachian Mountain Region, USA
Abstract
1. Introduction
2. Materials and Methods
2.1. La Crosse Virus Reported Human Incidence Data for the Eastern USA and Appalachian Mountain Region
2.2. Covariates
2.3. The Model
2.4. Model Selection
2.5. Modeling Prediction and Inter-Year Accuracy
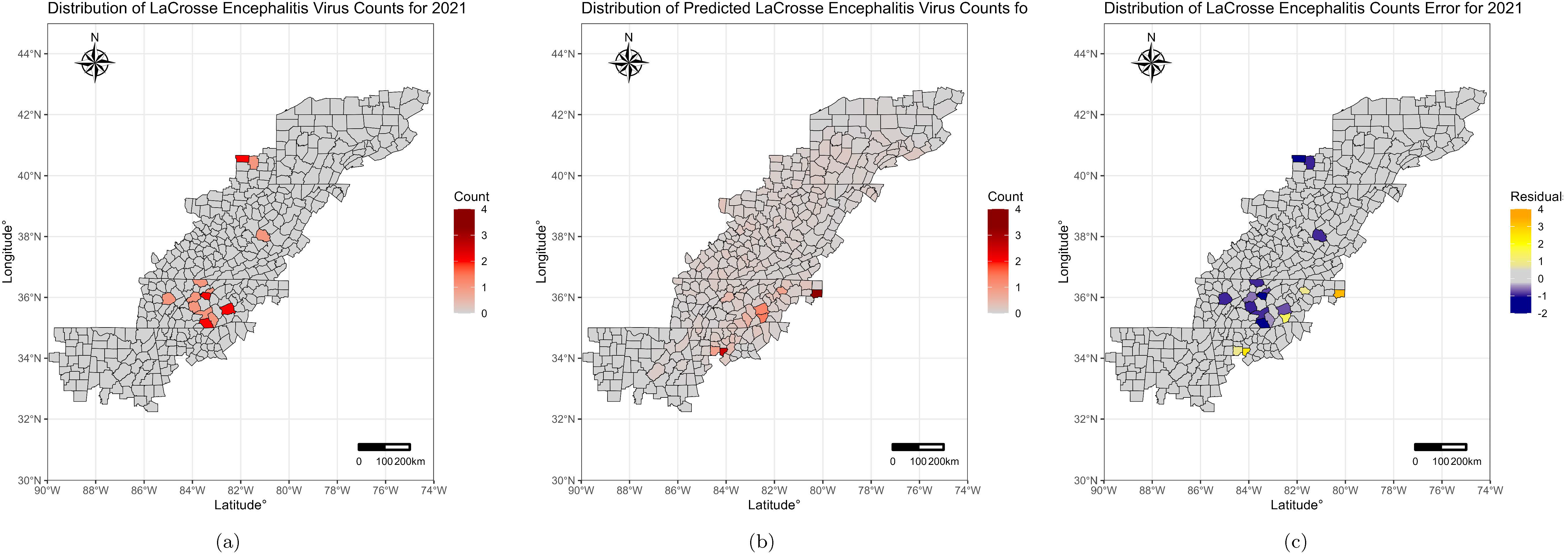
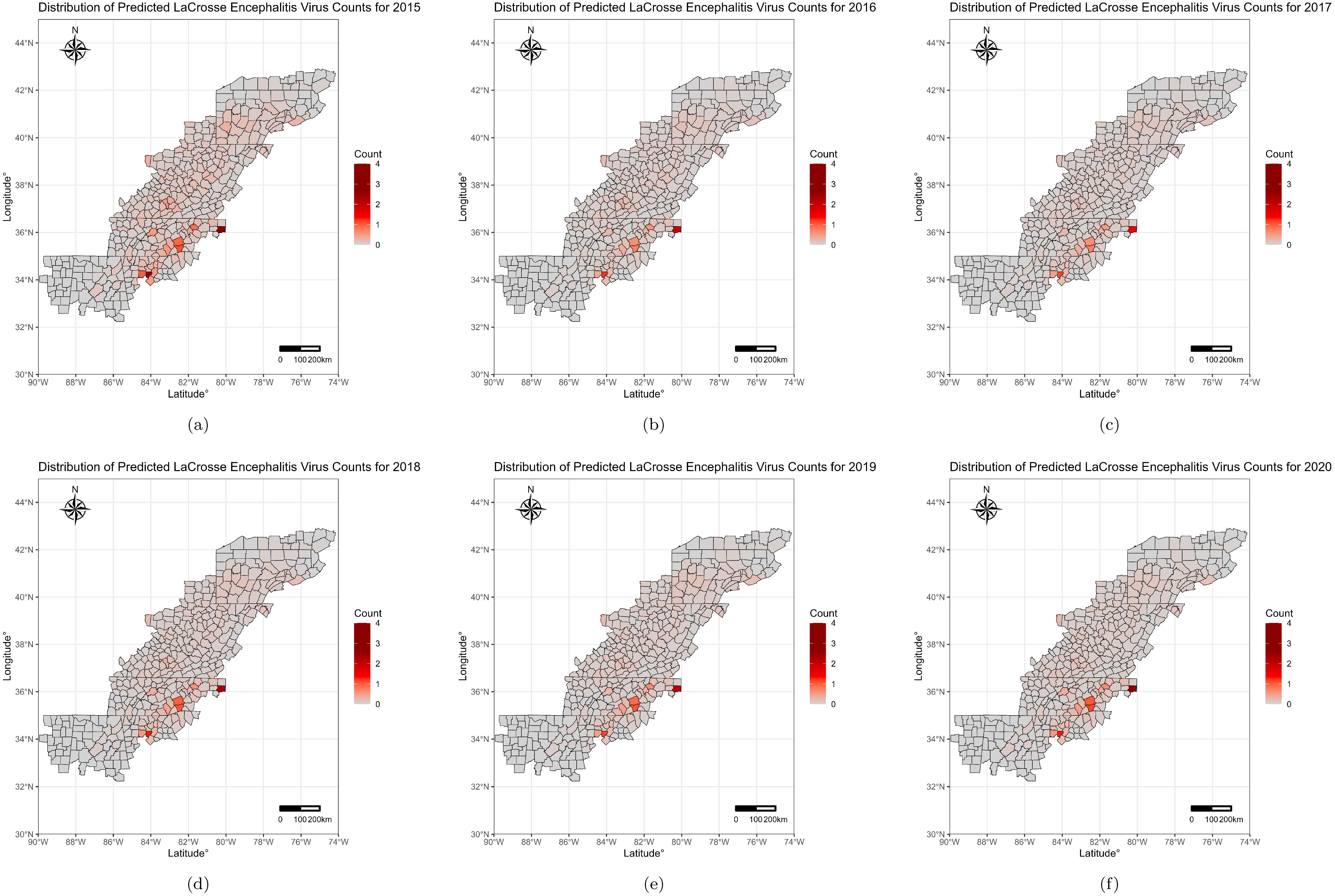
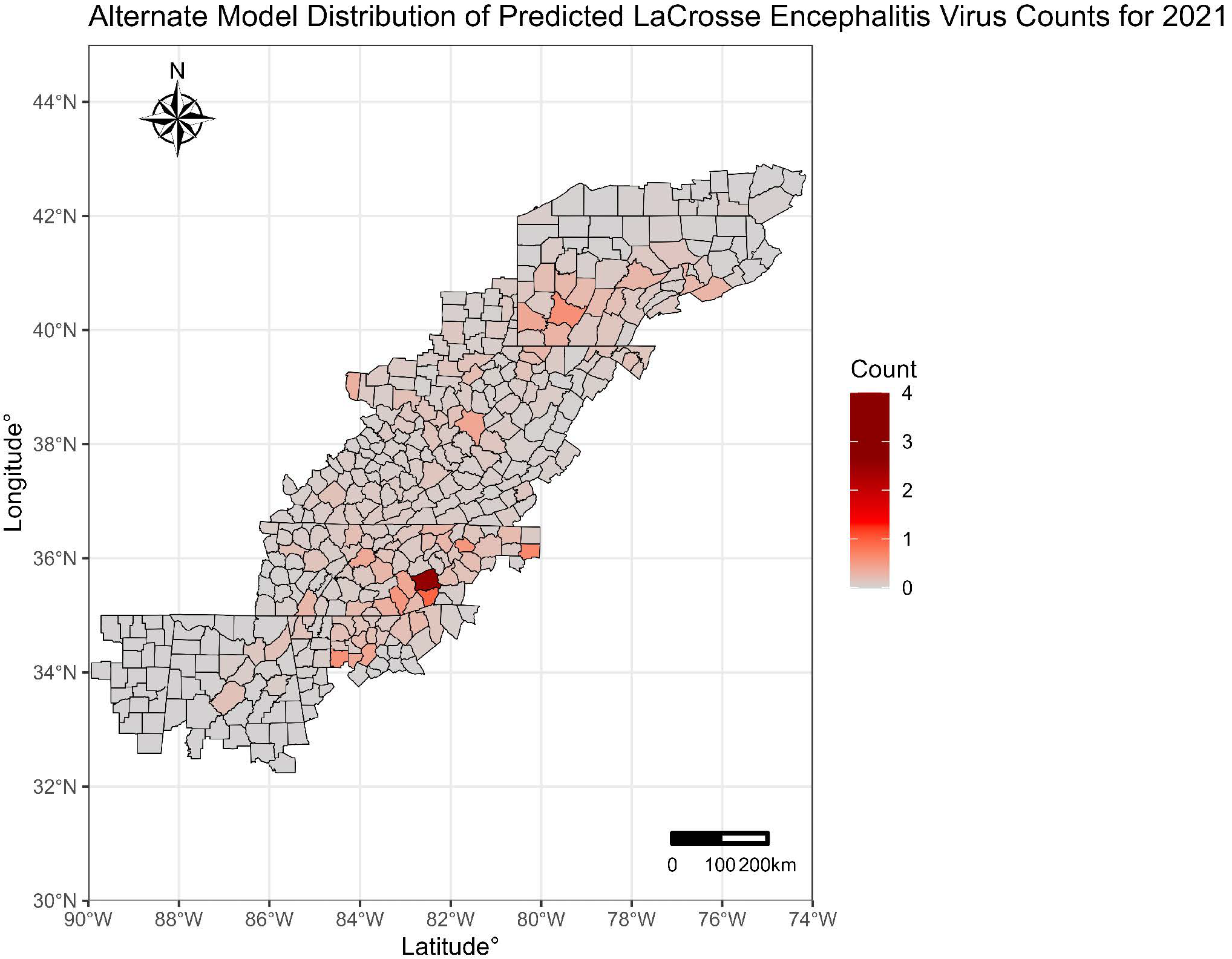
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACF | Autocorrelation factor |
| ARC | Appalachian Regional Commission |
| CDC | United States Centers for Disease Control and Prevention |
| INLA | Integrated nested Laplace approximation |
| LACV | La Crosse Virus |
| MCMC | Markov chain Monte Carlo |
| NLCD | National Land Cover Database |
| USA | United States of America |
| VIF | Variance inflation factor |
| VPD | Vapor pressure deficit |
References
- Thompson, W.H.; Kalfayan, B.; Anslow, R. Isolation of California encephalitis group virus from a fatal human illness. Am. J. Epidemiol. 1965, 81, 245–253. [Google Scholar] [PubMed]
- Sutter, R.A. West Nile Virus and Other Nationally Notifiable Arboviral Diseases—United States, 2022. MMWR Morb. Mortal. Wkly. Rep. 2024, 73, 484–488. [Google Scholar] [CrossRef] [PubMed]
- Bewick, S.; Agusto, F.; Calabrese, J.M.; Muturi, E.J.; Fagan, W.F. Epidemiology of La Crosse Virus Emergence, Appalachia Region, United States. Emerg. Infect. Dis. 2016, 22, 1921–1929. [Google Scholar] [CrossRef] [PubMed]
- Calisher, C.H. Medically important arboviruses of the United States and Canada. Clin. Microbiol. Rev. 1994, 7, 89–116. [Google Scholar]
- Grimstad, P.R.; Barrett, C.L.; Humphrey, R.L.; Sinsko, M.J. Serologic evidence for widespread infection with La Crosse and St. Louis encephalitis viruses in the Indiana human population. Am. J. Epidemiol. 1984, 119, 913–930. [Google Scholar]
- Jones, T.F.; Craig, A.S.; Nasci, R.S.; Patterson, L.E.; Erwin, P.C.; Gerhardt, R.R.; Ussery, X.T.; Schaffner, W. Newly recognized focus of La Crosse encephalitis in Tennessee. Clin. Infect. Dis. 1999, 28, 93–97. [Google Scholar] [CrossRef]
- Vahey, G.M.; Lindsey, N.P.; Staples, J.E.; Hills, S.L. La Crosse Virus Disease in the United States, 2003–2019. Am. J. Trop. Med. Hyg. 2021, 105, 807–812. [Google Scholar] [CrossRef]
- Boutzoukas, A.E.; Freedman, D.A.; Koterba, C.; Hunt, G.W.; Mack, K.; Cass, J.; Yildiz, V.O.; de Los Reyes, E.; Twanow, J.; Chung, M.G. La Crosse virus neuroinvasive disease in children: A contemporary analysis of clinical/neurobehavioral outcomes and predictors of disease severity. Clin. Infect. Dis. 2023, 76, e1114–e1122. [Google Scholar]
- McJunkin, J.E.; de los Reyes, E.C.; Irazuzta, J.E.; Caceres, M.J.; Khan, R.R.; Minnich, L.L.; Fu, K.D.; Lovett, G.D.; Tsai, T.; Thompson, A. La Crosse encephalitis in children. N. Engl. J. Med. 2001, 344, 801–807. [Google Scholar]
- Teleron, A.L.A.; Rose, B.K.; Williams, D.M.; Kemper, S.E.; McJunkin, J.E. La Crosse encephalitis: An adult case series. Am. J. Med. 2016, 129, 881–884. [Google Scholar]
- Utz, J.T.; Apperson, C.S.; MacCormack, J.N.; Salyers, M.; Dietz, E.J.; McPherson, J.T. Economic and social impacts of La Crosse encephalitis in western North Carolina. Am. J. Trop. Med. Hyg. 2003, 69, 509–518. [Google Scholar] [CrossRef] [PubMed]
- Eastwood, G.; Shepard, J.J.; Misencik, M.J.; Andreadis, T.G.; Armstrong, P.M. Local persistence of novel regional variants of La Crosse virus in the Northeast USA. Parasites Vectors 2020, 13, 1–8. [Google Scholar] [CrossRef]
- Harris, M.C.; Yang, F.; Jackson, D.M.; Dotseth, E.J.; Paulson, S.L.; Hawley, D.M. La Crosse virus field detection and vector competence of Culex mosquitoes. Am. J. Trop. Med. Hyg. 2015, 93, 461. [Google Scholar] [CrossRef] [PubMed]
- Byrd, B.D. La Crosse encephalitis: A persistent arboviral threat in North Carolina. North Carol. Med. J. 2016, 77, 330–333. [Google Scholar]
- Watts, D.M.; Pantuwatana, S.; DeFoliart, G.; Yuill, T.; Thompson, W. Transovarial transmission of LaCrosse virus (California encephalitis group) in the mosquito, Aedes triseriatus. Science 1973, 182, 1140–1141. [Google Scholar] [CrossRef] [PubMed]
- Westby, K.M.; Fritzen, C.; Paulsen, D.; Poindexter, S.; Moncayo, A.C. La Crosse encephalitis virus infection in field-collected Aedes albopictus, Aedes japonicus, and Aedes triseriatus in Tennessee. J. Am. Mosq. Control. Assoc. 2015, 31, 233–241. [Google Scholar] [CrossRef]
- Gauld, L.W.; Yuill, T.M.; Hanson, R.P.; Sinha, S.K. Isolation of La Crosse virus (California encephalitis group) from the chipmunk (Tamias striatus), an amplifier host. Am. J. Trop. Med. Hyg. 1975, 24, 999–1005. [Google Scholar] [CrossRef]
- Harding, S.; Greig, J.; Mascarenhas, M.; Young, I.; Waddell, L. La Crosse virus: A scoping review of the global evidence. Epidemiol. Infect. 2019, 147, e66. [Google Scholar] [CrossRef]
- Osorio, J.E.; Godsey, M.S.; Defoliart, G.R.; Yuill, T.M. La Crosse viremias in white-tailed deer and chipmunks exposed by injection or mosquito bite. Am. J. Trop. Med. Hyg. 1996, 54, 338–342. [Google Scholar] [CrossRef]
- Ghataka, M.; Urcuyo, J.; Wise, P.; Fryxell, R.T.; Lenhart, S. Modeling the average population of La Crosse vectors in Knox County, Tennessee. Lett. Biomath. 2019, 6, 20–31. [Google Scholar] [CrossRef]
- Murphree, R.; Dunn, J.; Schaffner, W.; Jones, T. La Crosse encephalitis surveillance using single versus paired serologic testing. Zoonoses Public Health 2012, 59, 181–183. [Google Scholar] [PubMed]
- Haddow, A.D.; Bixler, D.; Odoi, A. The spatial epidemiology and clinical features of reported cases of La Crosse virus infection in West Virginia from 2003 to 2007. BMC Infect. Dis. 2011, 11, 29. [Google Scholar] [CrossRef]
- Day, C.A.; Richards, S.L.; Reiskind, M.H.; Doyle, M.S.; Byrd, B.D. Context-dependent accuracy of the BG-Counter remote mosquito surveillance device in North Carolina. J. Am. Mosq. Control Assoc. 2020, 36, 74–80. [Google Scholar]
- Trout Fryxell, R.T.; Camponovo, M.; Smith, B.; Butefish, K.; Rosenberg, J.M.; Andsager, J.L.; Day, C.A.; Willis, M.P. Development of a community-driven mosquito surveillance program for vectors of La Crosse virus to educate, inform, and empower a community. Insects 2022, 13, 164. [Google Scholar] [CrossRef]
- Siettos, C.I.; Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 2013, 4, 295–306. [Google Scholar] [PubMed]
- Aswi, A.; Cramb, S.; Moraga, P.; Mengersen, K. Bayesian spatial and spatio-temporal approaches to modelling dengue fever: A systematic review. Epidemiol. Infect. 2019, 147, e33. [Google Scholar] [CrossRef]
- Myer, M.H.; Johnston, J.M. Spatiotemporal Bayesian modeling of West Nile virus: Identifying risk of infection in mosquitoes with local-scale predictors. Sci. Total Environ. 2019, 650, 2818–2829. [Google Scholar]
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D. Markov Chain Monte Carlo in Practice; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Martheswaran, T.K.; Hamdi, H.; Al-Barty, A.; Zaid, A.A.; Das, B. Prediction of dengue fever outbreaks using climate variability and Markov chain Monte Carlo techniques in a stochastic susceptible-infected-removed model. Sci. Rep. 2022, 12, 5459. [Google Scholar]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- CDC. ArboNET. Available online: https://www.cdc.gov/mosquitoes/php/arbonet/index.html (accessed on 23 April 2022).
- USGS. Eastern Chipmunk (Tamias striatus) Habitat Map. Available online: https://www.usgs.gov/data/eastern-chipmunk-tamias-striatus-meachxconus2001v1-habitat-map (accessed on 6 January 2022).
- USGS. Eastern Gray Squirrel (Sciurus carolinensis) Habitat Map. Available online: https://www.usgs.gov/data/eastern-gray-squirrel-sciurus-carolinensis-mebsqxconus2001v1-habitat-map (accessed on 6 January 2022).
- USGS. National Land Cover Database. Available online: https://www.usgs.gov/centers/eros/science/national-land-cover-database (accessed on 6 January 2022).
- PRISM. Climate Group at Oregon State University. Available online: https://prism.oregonstate.edu/ (accessed on 6 January 2022).
- Lütkepohl, H.; Krätzig, M. Applied Time Series Econometrics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ward, M.P.; Iglesias, R.M.; Brookes, V.J. Autoregressive Models Applied to Time-Series Data in Veterinary Science. Front. Vet. Sci. 2020, 7, 604. [Google Scholar] [CrossRef]
- Dotseth, E.; Lewis, C.; Abshire, M. West Virginia Mosquito and Tick Surveillance Report; West Virginia Department of Health and Human Resources: Charleston, WV, USA, 2019; p. 17.
- Juma, E.O.; Allan, B.F.; Kim, C.-H.; Stone, C.; Dunlap, C.; Muturi, E.J. The larval environment strongly influences the bacterial communities of Aedes triseriatus and Aedes japonicus (Diptera: Culicidae). Sci. Rep. 2021, 11, 7910. [Google Scholar]
- García-Carrasco, J.-M.; Muñoz, A.-R.; Olivero, J.; Segura, M.; Real, R. Predicting the spatio-temporal spread of West Nile virus in Europe. PLoS Neglected Trop. Dis. 2021, 15, e0009022. [Google Scholar] [CrossRef] [PubMed]
- Laporta, G.Z.; Ilacqua, R.C.; Bergo, E.S.; Chaves, L.S.; Rodovalho, S.R.; Moresco, G.G.; Figueira, E.A.; Massad, E.; de Oliveira, T.M.; Bickersmith, S.A. Malaria transmission in landscapes with varying deforestation levels and timelines in the Amazon: A longitudinal spatiotemporal study. Sci. Rep. 2021, 11, 6477. [Google Scholar] [CrossRef]
- Kutta, E.; Hubbart, J. Climatic trends of West Virginia: A representative Appalachian microcosm. Water 2019, 11, 1117. [Google Scholar] [CrossRef]
- Weterings, R.; Umponstira, C.; Buckley, H.L. Container-breeding mosquitoes and predator community dynamics along an urban-forest gradient: The effects of habitat type and isolation. Basic Appl. Ecol. 2014, 15, 486–495. [Google Scholar]
- Gleiser, R.M.; Zalazar, L.P. Distribution of mosquitoes in relation to urban landscape characteristics. Bull. Entomol. Res. 2010, 100, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Day, C.A.; Armstrong, E.G.; Byrd, B.D. Population growth rates of Aedes atropalpus (Diptera: Culicidae) are depressed at lower temperatures where Aedes japonicus japonicus (Diptera: Culicidae) are naturally abundant in rock pools. J. Med. Entomol. 2021, 58, 493–497. [Google Scholar] [CrossRef]
- Tamini, T.T.; Byrd, B.D.; Goggins, J.A.; Sither, C.B.; White, L.; Wasserberg, G. Peridomestic conditions affect La Crosse virus entomological risk by modifying the habitat use patterns of its mosquito vectors. J. Vector Ecol. 2021, 46, 34–47. [Google Scholar]
- Brown, J.J.; Pascual, M.; Wimberly, M.C.; Johnson, L.R.; Murdock, C.C. Humidity–The overlooked variable in the thermal biology of mosquito-borne disease. Ecol. Lett. 2023, 26, 1029–1049. [Google Scholar]
- Drakou, K.; Nikolaou, T.; Vasquez, M.; Petric, D.; Michaelakis, A.; Kapranas, A.; Papatheodoulou, A.; Koliou, M. The effect of weather variables on mosquito activity: A snapshot of the main point of entry of Cyprus. Int. J. Environ. Res. Public Health 2020, 17, 1403. [Google Scholar] [CrossRef]
- Ikeda, T.; Behera, S.K.; Morioka, Y.; Minakawa, N.; Hashizume, M.; Tsuzuki, A.; Maharaj, R.; Kruger, P. Seasonally lagged effects of climatic factors on malaria incidence in South Africa. Sci. Rep. 2017, 7, 2458. [Google Scholar] [CrossRef] [PubMed]
- Center for Disease Control and Prevention. La Crosse Encephalitis in West Virginia. MMWR Morb. Mortal. Wkly. Rep. 1988, 12, 79–82. [Google Scholar]
- LaBeaud, A.; Bashir, F.; King, C.H. Measuring the burden of arboviral diseases: The spectrum of morbidity and mortality from four prevalent infections. Popul. Health Metr. 2011, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
| Variable | Estimate | Standard Deviation | Lower Bound of 95% HPD Interval | Upper Bound of 95% HPD Interval |
|---|---|---|---|---|
| Intercept | −3.7310 | 0.2201 | −4.1707 | −3.3098 |
| Proportion Age 19 and under | 0.4006 | 0.0768 | 0.2504 | 0.5515 |
| Developed Open Space | 0.8503 | 0.0818 | 0.6909 | 1.0116 |
| Developed High Intensity | −0.3587 | 0.0819 | −0.5199 | −0.1986 |
| Barren Land | 0.1763 | 0.0577 | 0.0638 | 0.2901 |
| Evergreen Forest | −0.4000 | 0.1488 | −0.6938 | −0.1105 |
| Hay Pasture | −0.2931 | 0.0721 | −0.4350 | −0.1525 |
| Woody Wetland | −3.3714 | 0.5984 | −4.5671 | −2.2267 |
| Vapor Pressure Deficit index | −0.2669 | 0.0937 | −0.4511 | −0.0838 |
| Year | −0.0391 | 0.0794 | −0.1948 | 0.1162 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCarter, M.; Self, S.C.W.; Li, H.; Ewing, J.A.; Gual-Gonzalez, L.; Kanyangarara, M.; Nolan, M.S. Validating a Bayesian Spatio-Temporal Model to Predict La Crosse Virus Human Incidence in the Appalachian Mountain Region, USA. Microorganisms 2025, 13, 812. https://doi.org/10.3390/microorganisms13040812
McCarter M, Self SCW, Li H, Ewing JA, Gual-Gonzalez L, Kanyangarara M, Nolan MS. Validating a Bayesian Spatio-Temporal Model to Predict La Crosse Virus Human Incidence in the Appalachian Mountain Region, USA. Microorganisms. 2025; 13(4):812. https://doi.org/10.3390/microorganisms13040812
Chicago/Turabian StyleMcCarter, Maggie, Stella C. W. Self, Huixuan Li, Joseph A. Ewing, Lídia Gual-Gonzalez, Mufaro Kanyangarara, and Melissa S. Nolan. 2025. "Validating a Bayesian Spatio-Temporal Model to Predict La Crosse Virus Human Incidence in the Appalachian Mountain Region, USA" Microorganisms 13, no. 4: 812. https://doi.org/10.3390/microorganisms13040812
APA StyleMcCarter, M., Self, S. C. W., Li, H., Ewing, J. A., Gual-Gonzalez, L., Kanyangarara, M., & Nolan, M. S. (2025). Validating a Bayesian Spatio-Temporal Model to Predict La Crosse Virus Human Incidence in the Appalachian Mountain Region, USA. Microorganisms, 13(4), 812. https://doi.org/10.3390/microorganisms13040812






