Practical Considerations in the Modelling and Simulation of Electromechanical Actuators
Abstract
1. Introduction
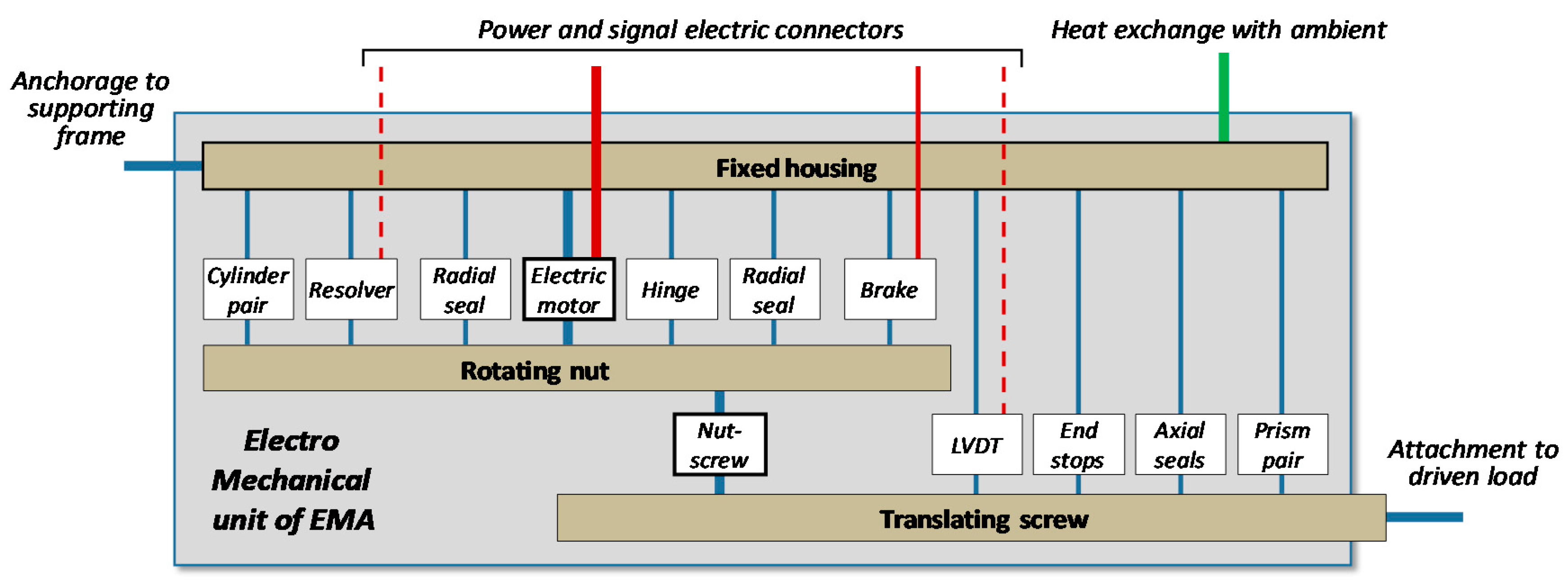
2. Electromechanical Actuator Designs and Architectures
- A Permanent Magnet Synchronous Motor (PMSM);
- A ball-screw;
- A rotor angular position sensor;
- A rod extension sensor;
- An electric-off brake;
- All sealing and bearing devices.
- The power electronics with the three legs of the inverter;
- The Pulse Width Modulation (PWM) switching to drive the power transistors of the inverter;
- The direct and inverse Park transforms to implement Field-Oriented Control (FOC) in the D-Q frame;
- The excitation and conditioning of current, speed, and position sensors;
- The current loops with limitations, flux weakening, Proportional plus Integral (PI) controller with anti-windup, and back electromotive force (BEMF) compensation;
- The motor speed and rod position loops with PI control and anti-windup;
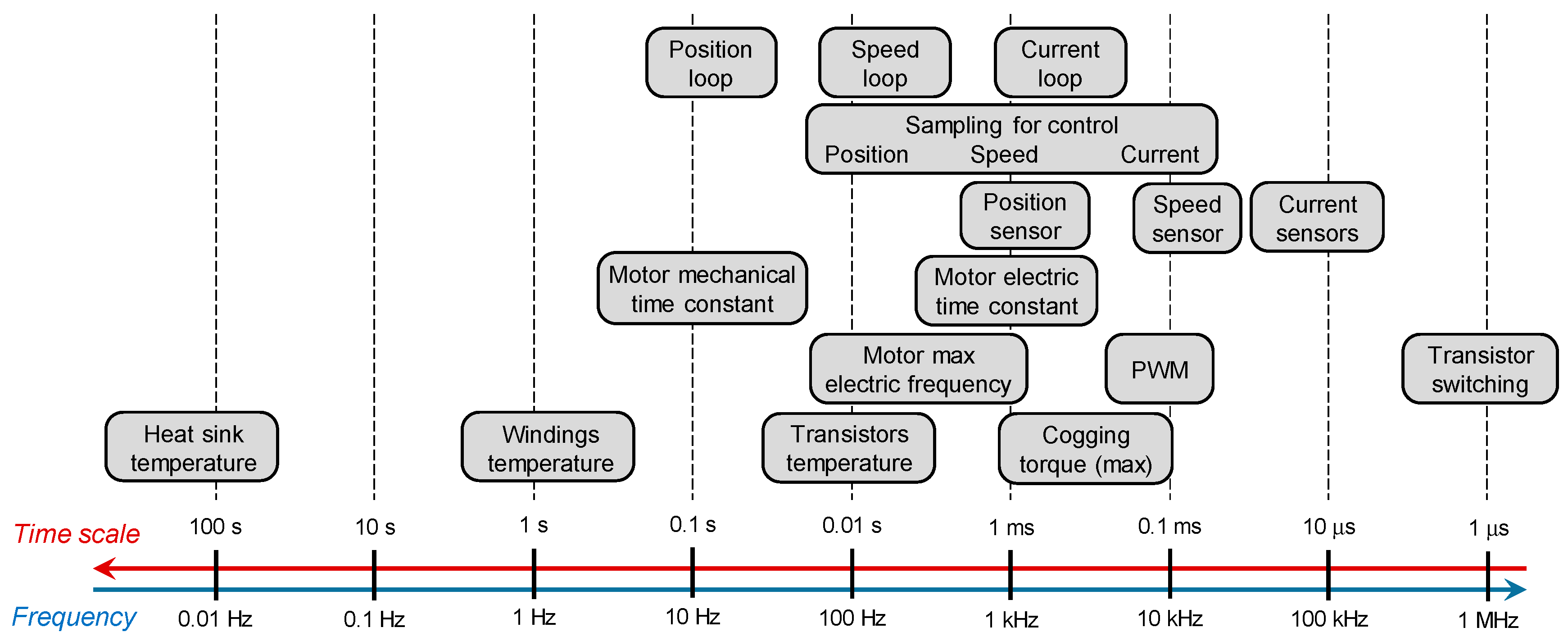
- The clocks used for each control loop, speed sensor conditioning, and PWM;
- The DC-link, including the diode, capacitance, braking resistance, and chopper.
3. Top-Level EMA Model
3.1. Proposed Model
3.2. Power Limitation Due to the Motor, Power Electronics, and Electric Supply
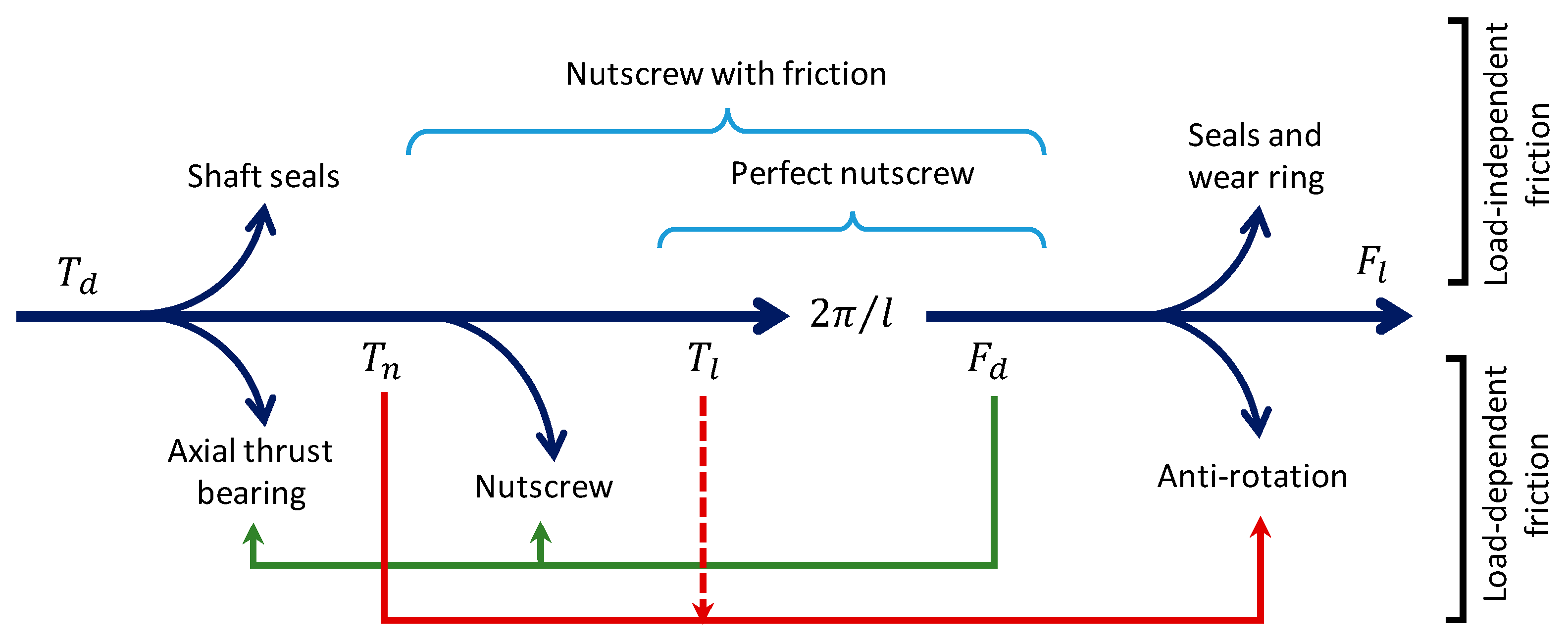
3.3. Friction Losses in the EMA Mechanical Transmission
- The load-dependent friction through direct and indirect efficiencies;
- The load-independent friction through tare losses to reproduce the no-load driving torque and the no-drive back-driving load force.
4. Detailed Models of EMA
4.1. Dynamics in Presence
4.2. Modelling Needs vs. Engineering Needs
5. Detailed Modelling of the Power Chain
5.1. Motor and Power Electronics
5.1.1. Motor Model
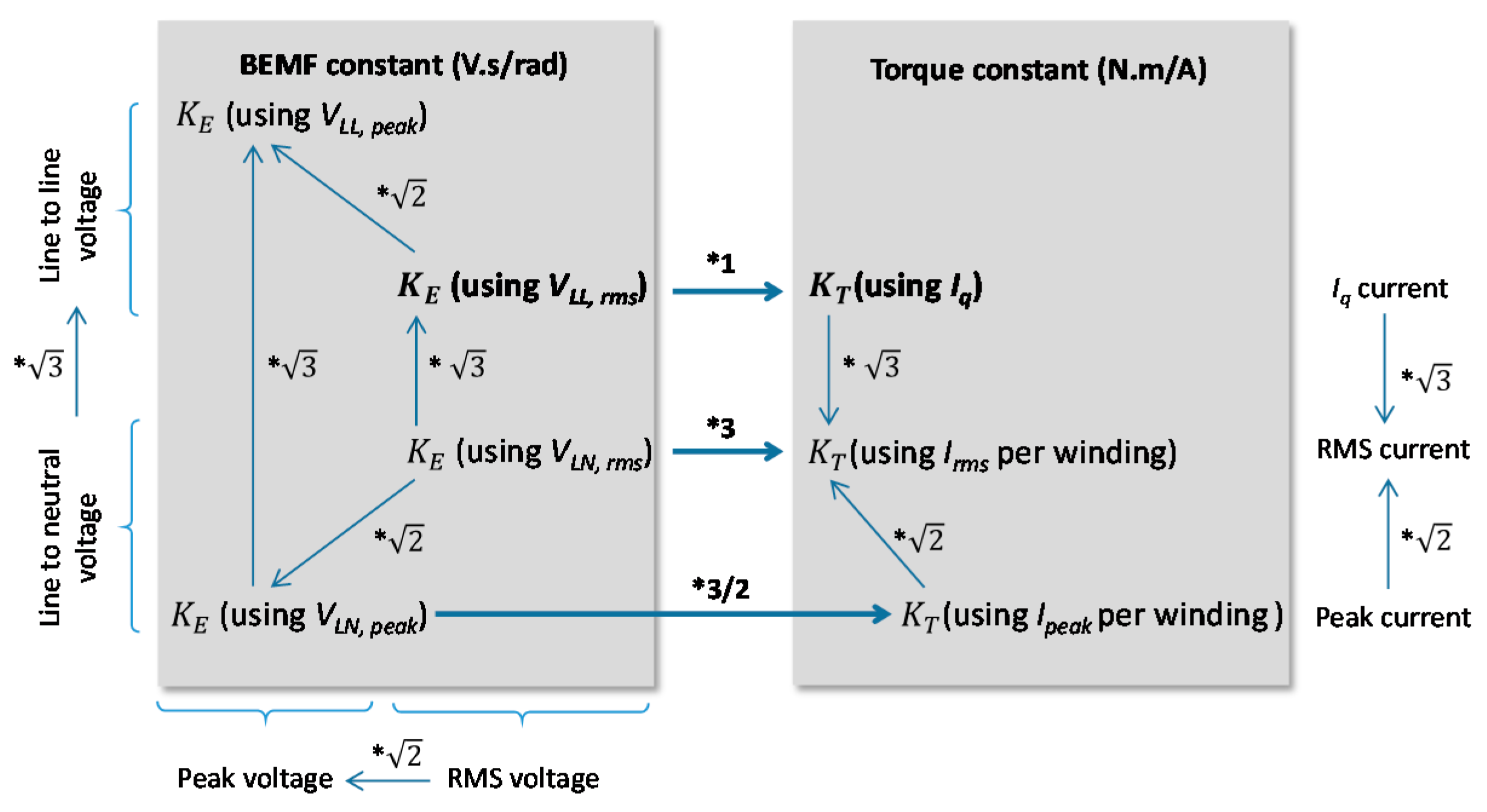
Three-Phase Model and Motor Constants
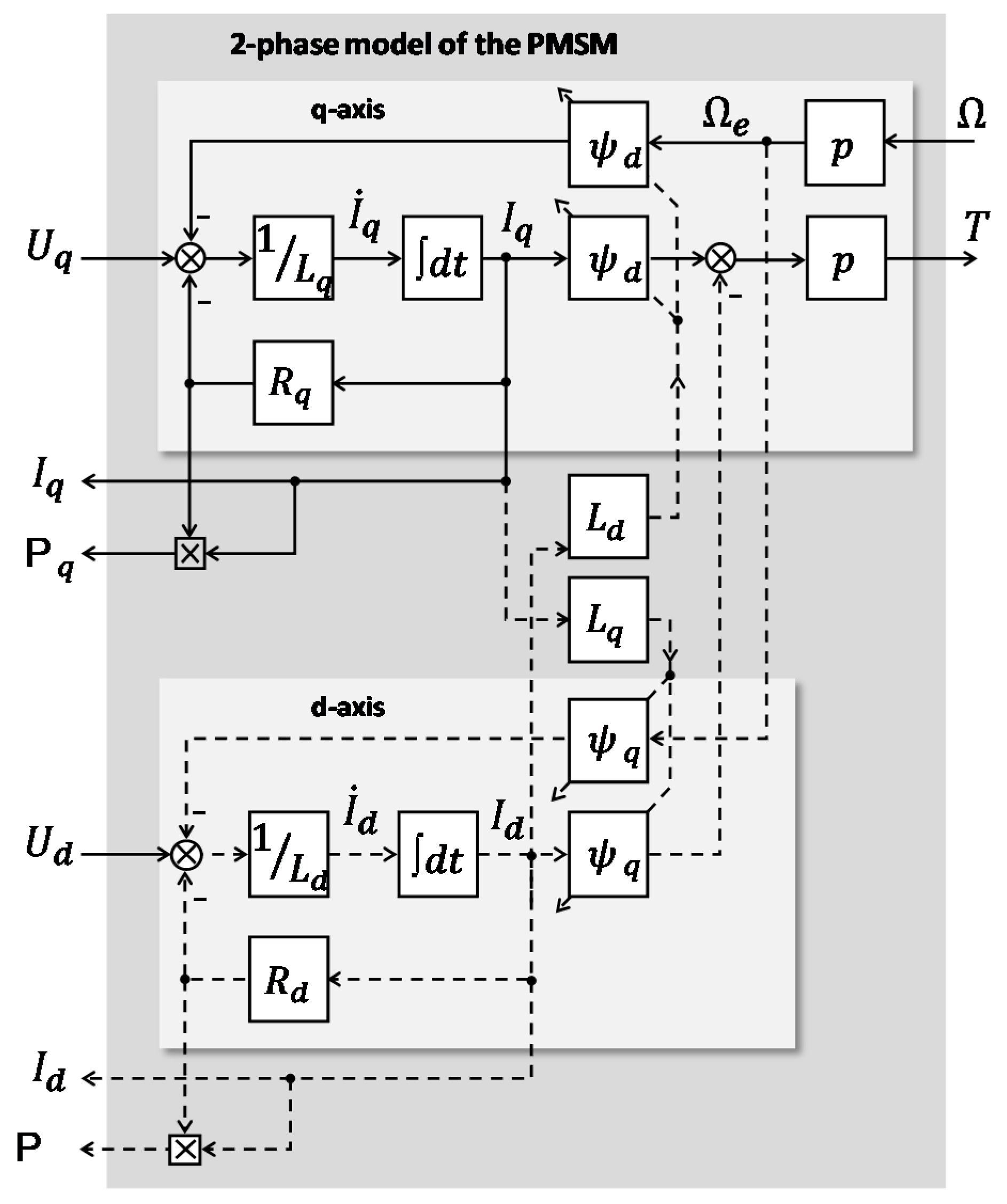
Two-PhaseMmodel
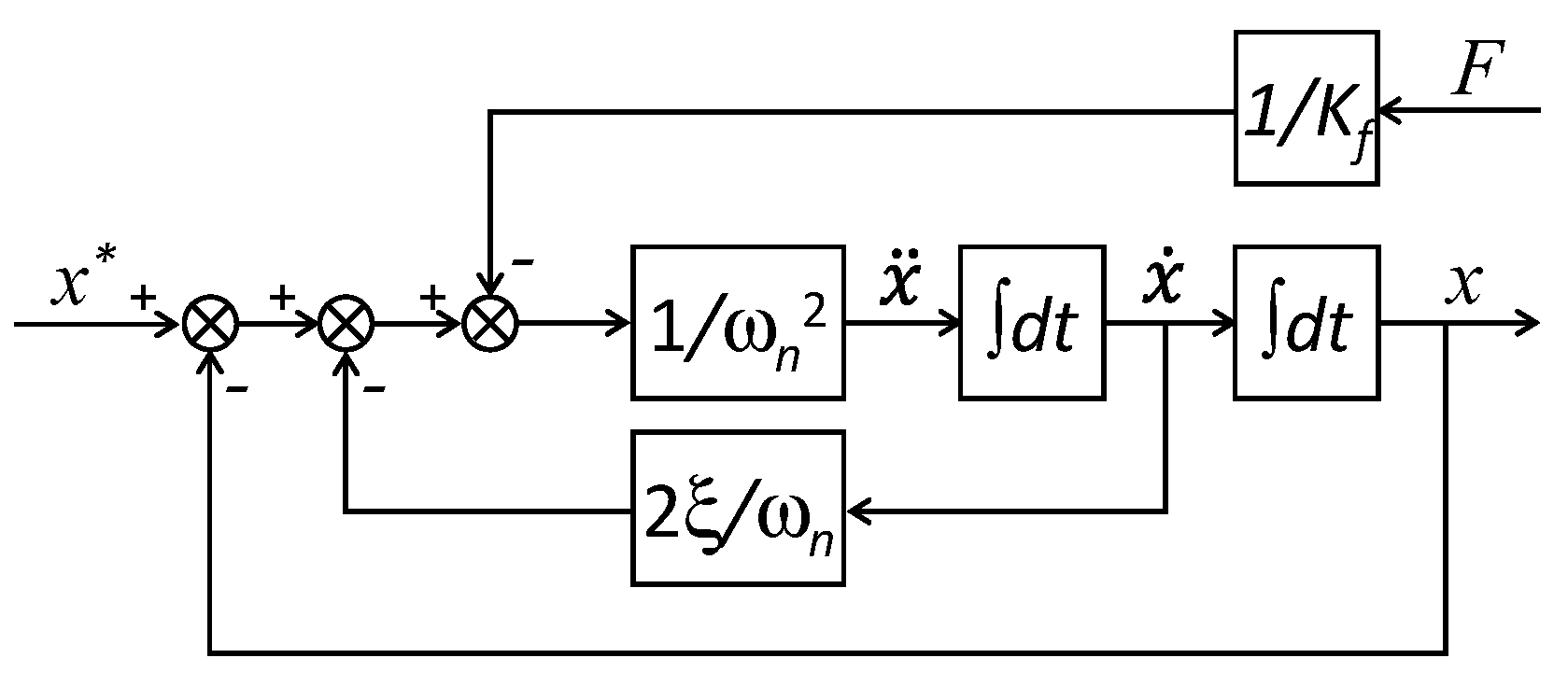
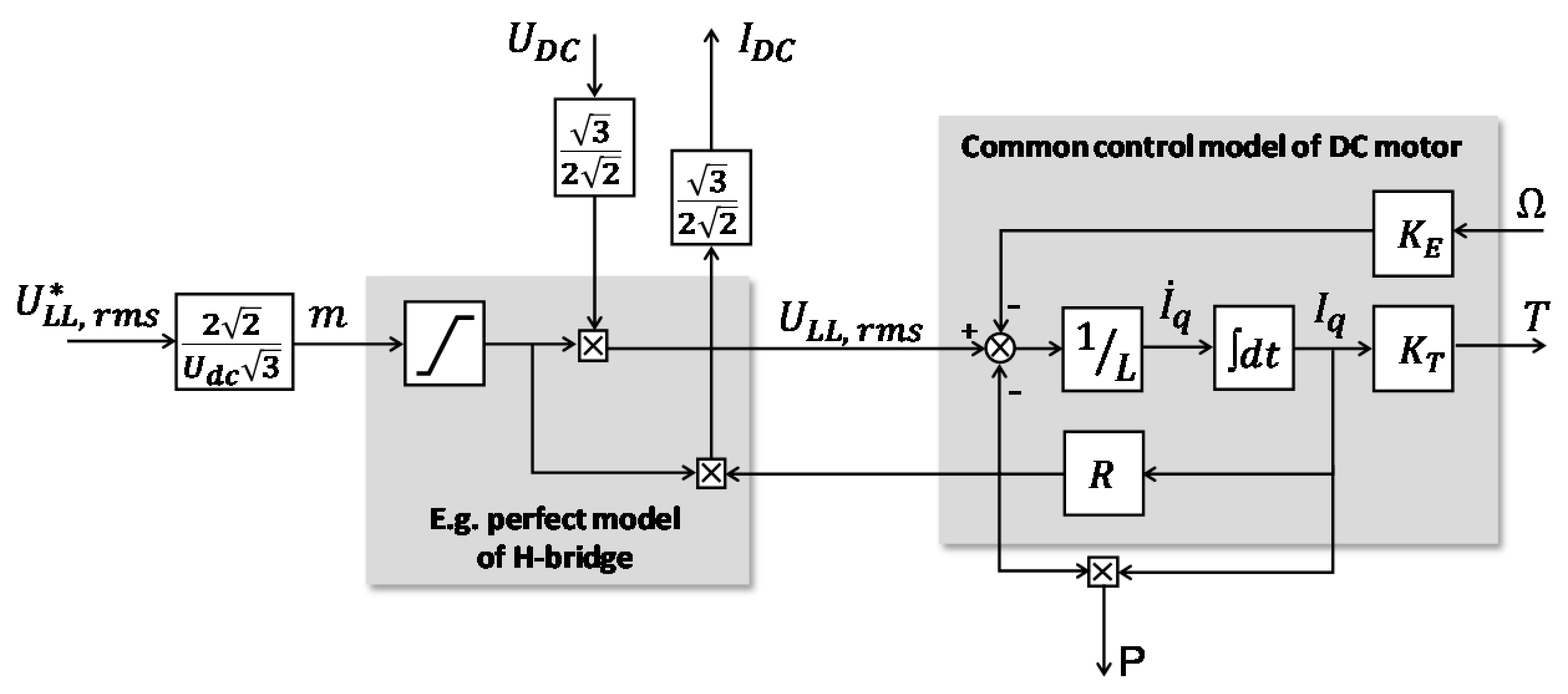
Equivalent DC Motor Model
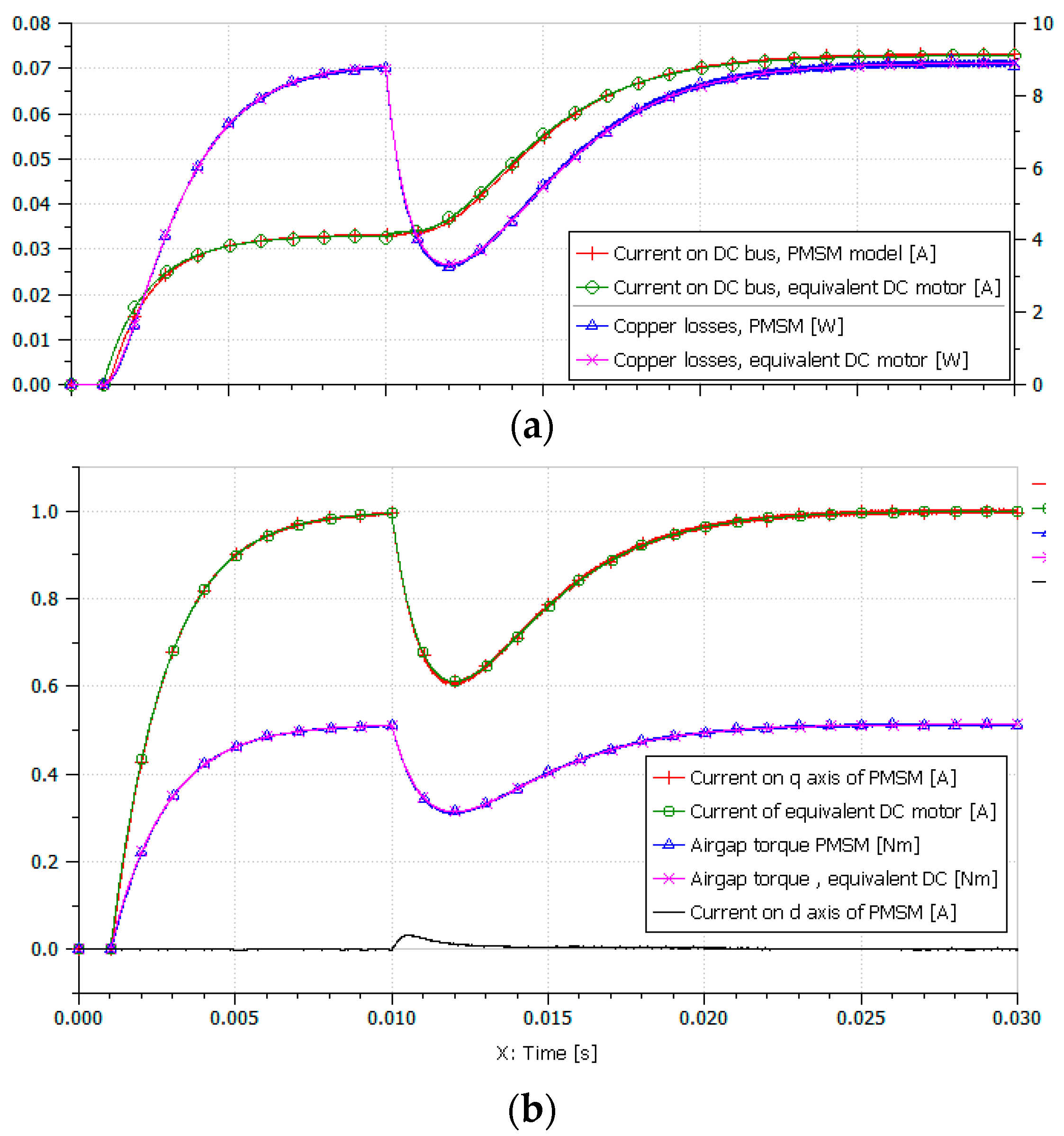
- Only a current loop is implemented with a P-I controller. The controller gains and sampling frequencies are identical for both models.
- The system is at rest at time 0 (no current demand, no rotor speed). A step current demand is applied at time , then a step motor speed is imposed at time . With these excitations, the operation remains below the saturation limits.
- Both models are supplied with the same constant DC bus voltage.
- Current sensors are perfect in both models.
- In the full model, a symmetric triangle PWM is used to drive the three-phase inverter. The * setpoint is set to null. Flux weakening and BEMF compensation are not enabled. The losses in power electronics are quasi null. The current controller makes the current loop five times faster than the one.
- Control design: same static and dynamics for current and torque.
- Thermal balance and energy losses: same motor copper losses.
- Power drawn: same current from DC voltage source, thanks to the factor in the equivalent DC motor model.
5.1.2. Model of Power Electronics
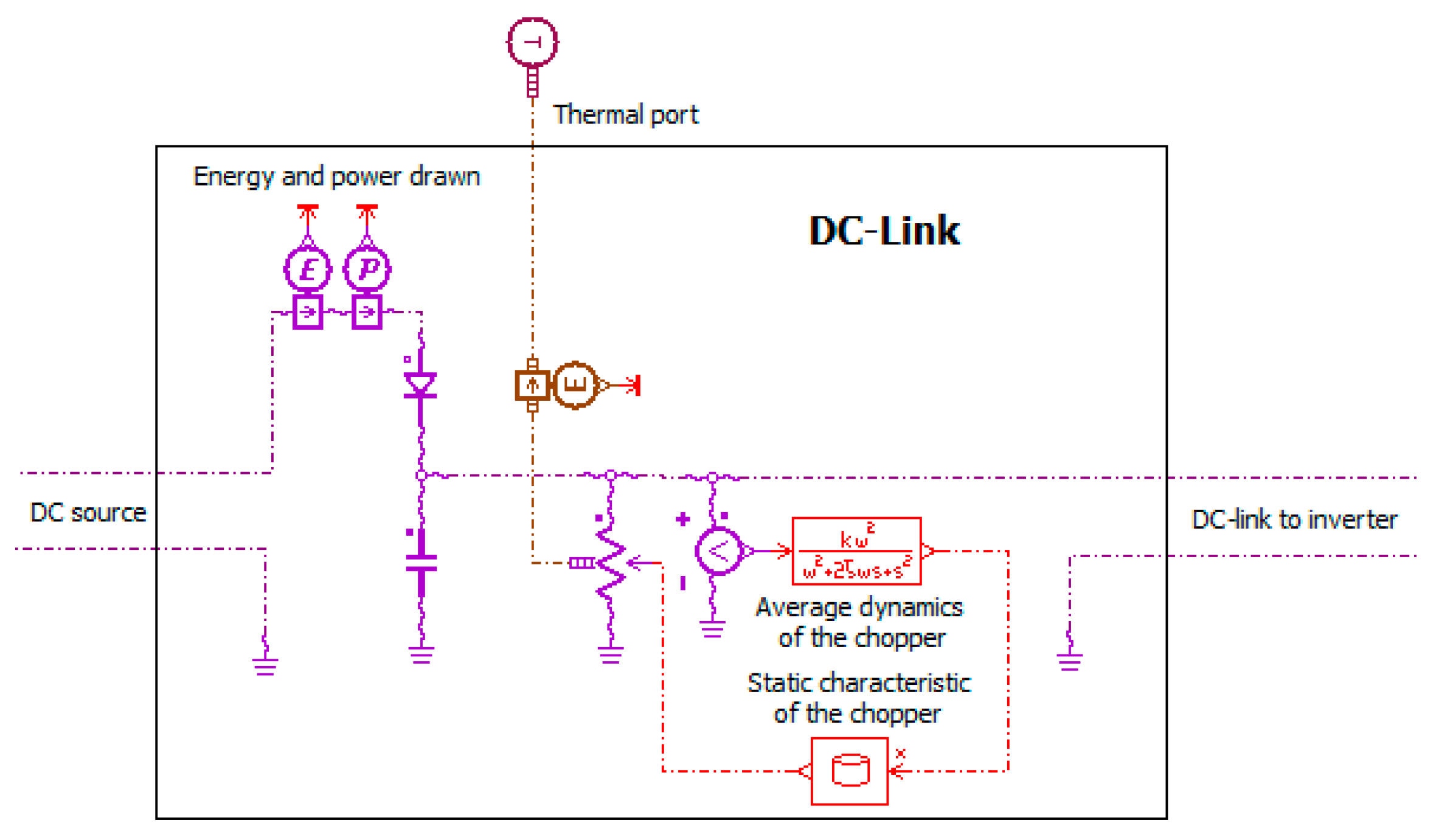
5.1.3. Model of DC-Link
5.2. Friction
5.2.1. Time-Dependent Variables Affecting Friction
5.2.2. Management of Sticking/Sliding Transition
- The hyperbolic tangent model is very simple to implement, involving a single parameter to manage the sticking/sliding transition. It enables each location of friction be modelled independently. The main drawback lies in its inability to produce true stiction, unlike the following models, because the simulated friction force is null at null speed. Moreover, it may generate numerical instability in particular cases. This is due to the huge equivalent viscous effect produced near the null relative speed to smooth the sign function.
- The Dahl and Reset Integrator models, or their generalization as the LuGre model, solve the transition issue by considering the compliance of the asperities of the facing surfaces in sticking conditions. This additional energy storage effect solves the causality issue by introducing a first-order differential model. Unfortunately, the combination of contact stiffness with inertia effect generates high-frequency natural dynamics that significantly increases the computational burden of the integration algorithm. In practice, there is generally no engineering need to model this compliance, except in very specific cases such as mirror positioning for imaging satellites. Nevertheless, this type of model is often used implicitly for its ability to solve the transition issue.
- The “rendez-vous” model is very efficient but requires the numerical solver to be able to accurately locate a state-event between two integration steps (external forces exceeding the breakaway friction force for starting, or speed crossing zero for possible stopping). It also generates a multitude of search functions that significantly increase the computational burden.
- Non-causal simulation languages—e.g., Modelica [30]—and associated solvers enable a particular type of friction modelling that also reproduces true sticking. As an additional advantage, they also allow inverse simulation, which is welcome for sizing. However, non-causal friction models are implemented with assumptions for inverse simulation that are not always explicit. So far, it is the author’s experience that industry sometimes hesitates to switch to these tools because the engineers concerned are not sufficiently experienced and they fear that the tools may be insufficiently mature for use in industrial projects.
- The Karnopp model is efficient to reproduce the true stiction and manage the sticking/sliding transition with a little computational expense. It uses a single parameter, the velocity threshold, below which relative speed is forced to null. Unfortunately, this means that the model is intimately linked to the inertance model (mass for translation, moment of inertia for rotation). Therefore, the friction model cannot be dissociated from the inertance model—with all the consequences for causalities (e.g., difficulty in simulating friction between two moving bodies, or multiple frictions on a single body).
5.2.3. Proposed Generic Friction Model
- Aeproduce true stiction at the lowest computational expense;
- Enable multiple locations of friction to be modelled for a single rigid assembly;
- Enable the load, temperature, and velocity effects to be considered;
- Enable implementation within a wide set of commercial simulation environments, in particular without resort to non-causal simulation languages and associated SW;
- As far as possible, reuse a friction model from the standard library of the simulation SW, which is documented, verified, and numerically robust.
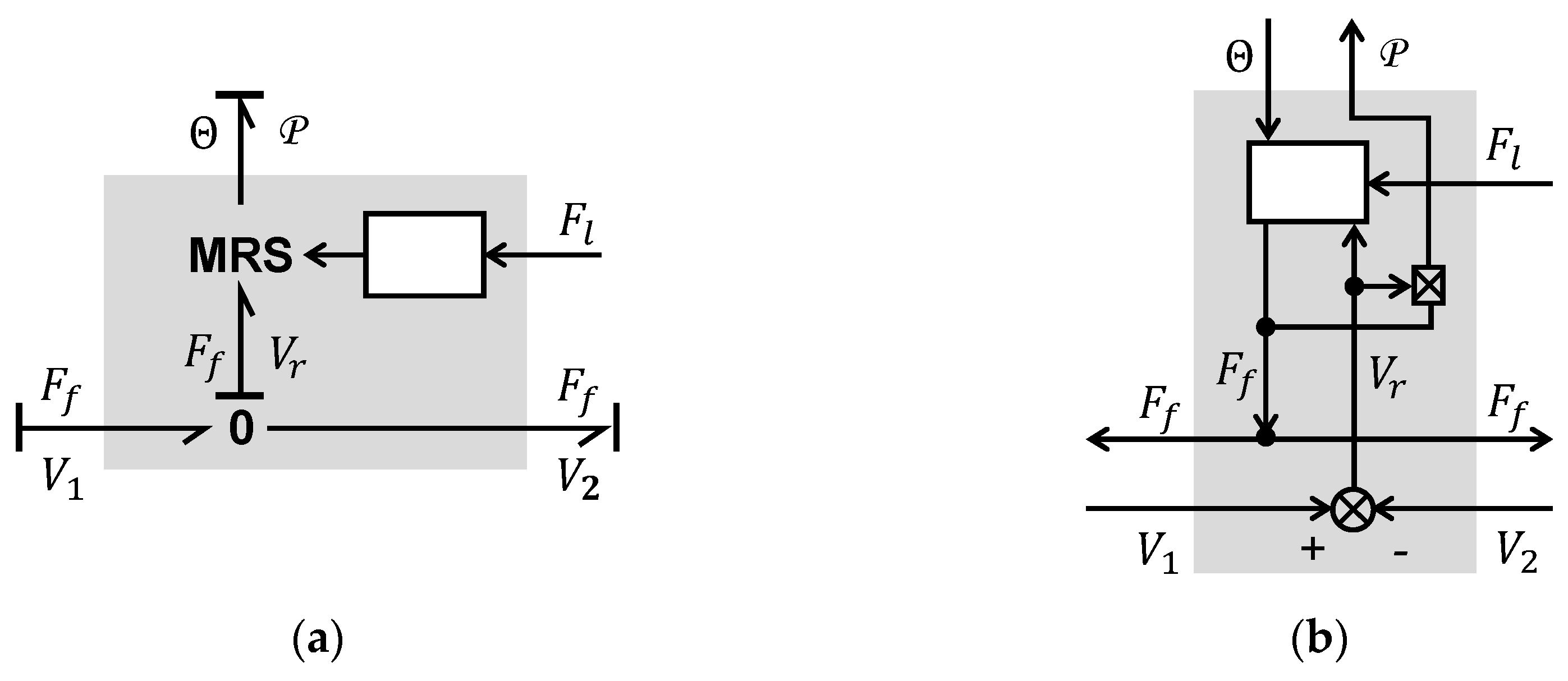
- Independently of the management of the sticking/sliding transition, the proposed friction model architecture is given in Bond-graph and block diagram forms in Figure 12. It involves:
- Two mechanical power ports that feed the model with the linear velocities, and , of each of the facing bodies (or angular velocities and ), and obtains the friction force (or torque ) applied to each facing body from the model.
- A thermal power port that feeds the model with the temperature at the contact interface, and gets the heat power generated by friction from the model.
- A signal port that inputs the transmitted load force, (or torque ), to introduce the effect of the normal force at the contact location.
- A parametric function or a multi-D table that shows the friction force vs. relative speed, temperature, and transmitted load.
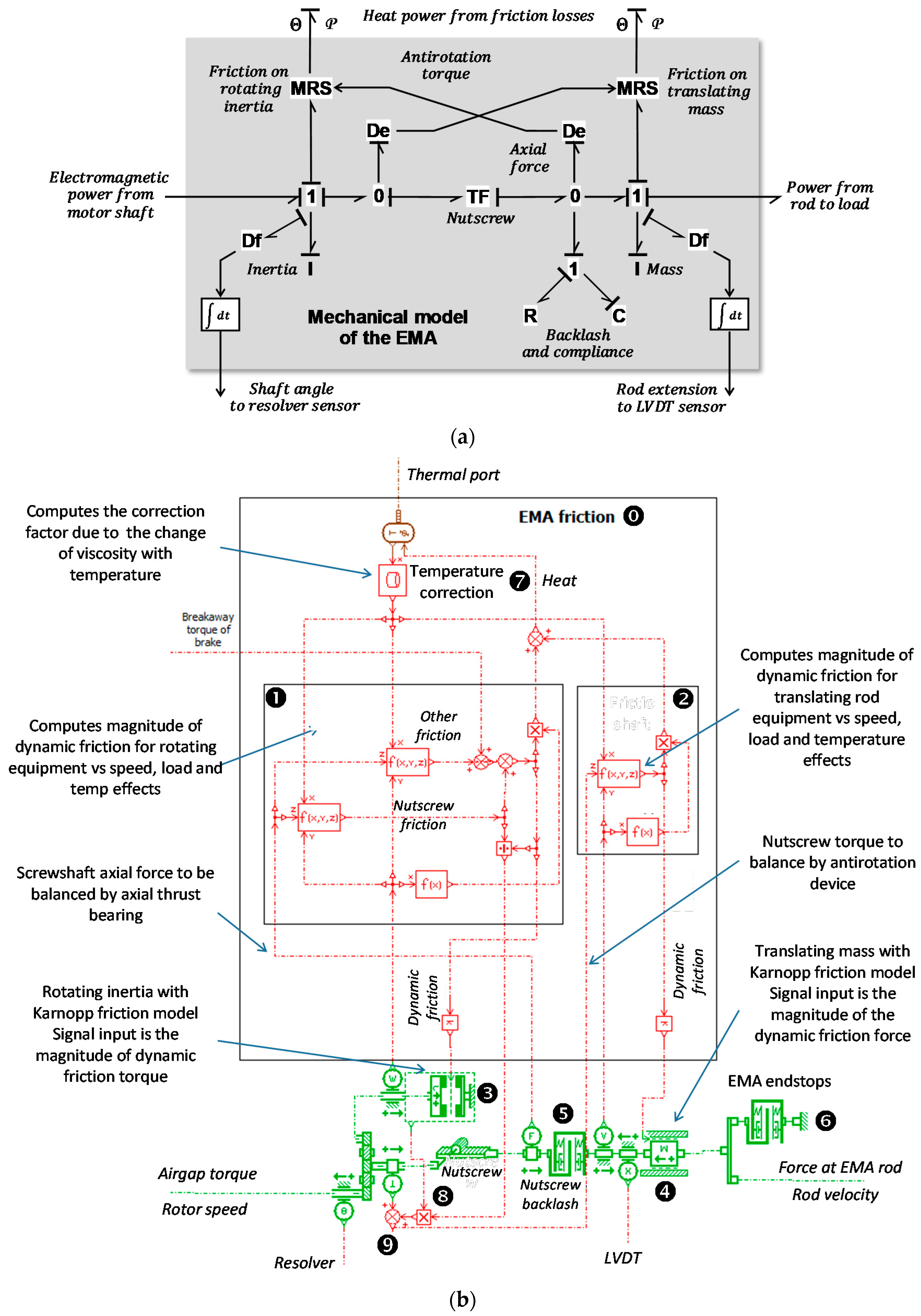
5.2.4. Application to EMA
5.3. Compliance and Backlash
- The viscous damping coefficient at contact can be determined to produce, e.g., a 0.2 dimensionless damping factor when it combines the contact stiffness and attached load inertia to make a second-order dynamic.
- The limit penetration for full damping can be set, e.g., to 1/100th of the backlash, or 1/10th of the elastic deformation of the contact under the rated load.
- The reference speed for the Karnopp friction model can be set, e.g., to 1/10,000th of the rated speed or, e.g., 50% of the resolution of the speed measurement.
6. Detailed Modelling of the Signal and Control Chain
6.1. Control and Digital Implementation
6.1.1. Controller Parameters
- The motor rotor angle and speed and the phase current signals.
- The motor parameters, such as the BEMF constant, winding resistance and inductance, and number of pole pairs.
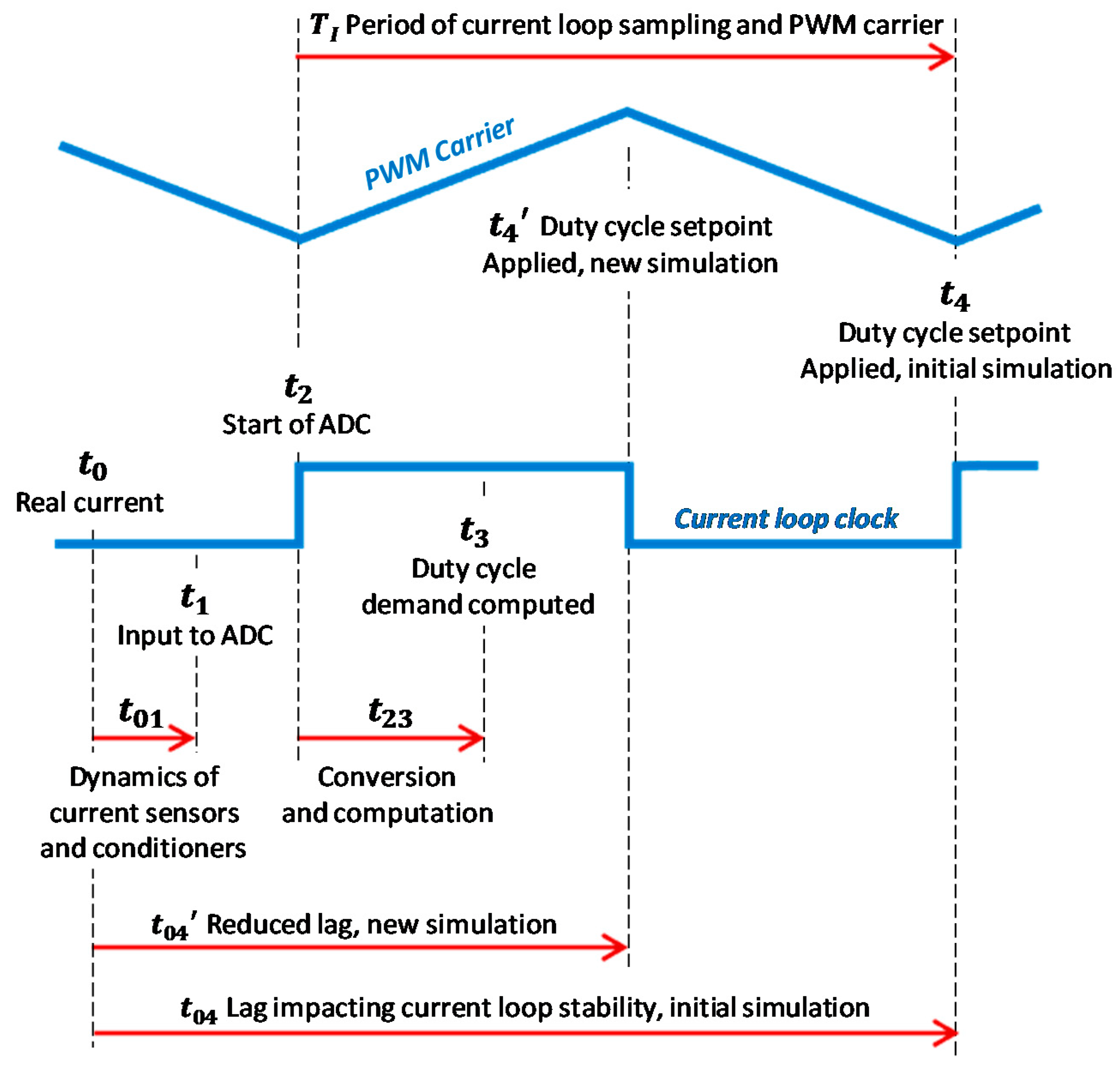
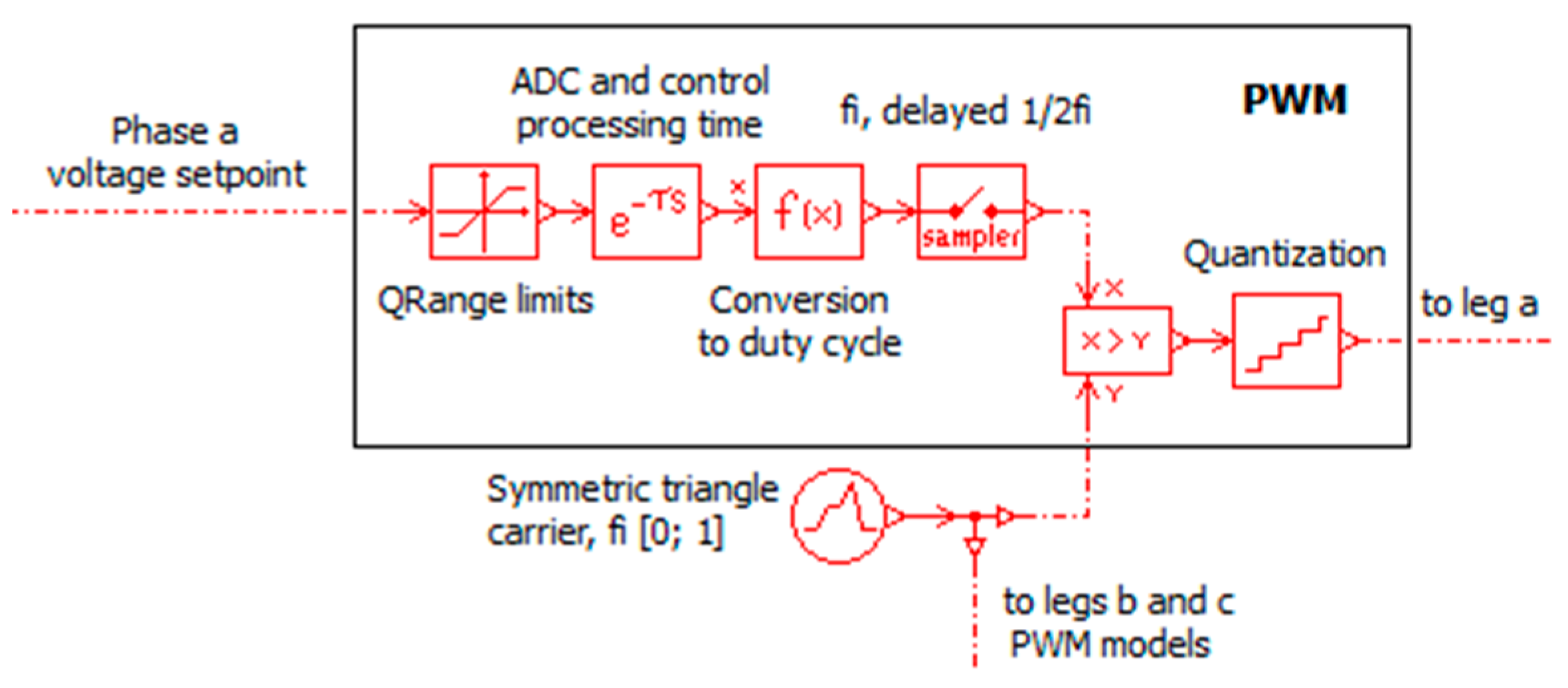
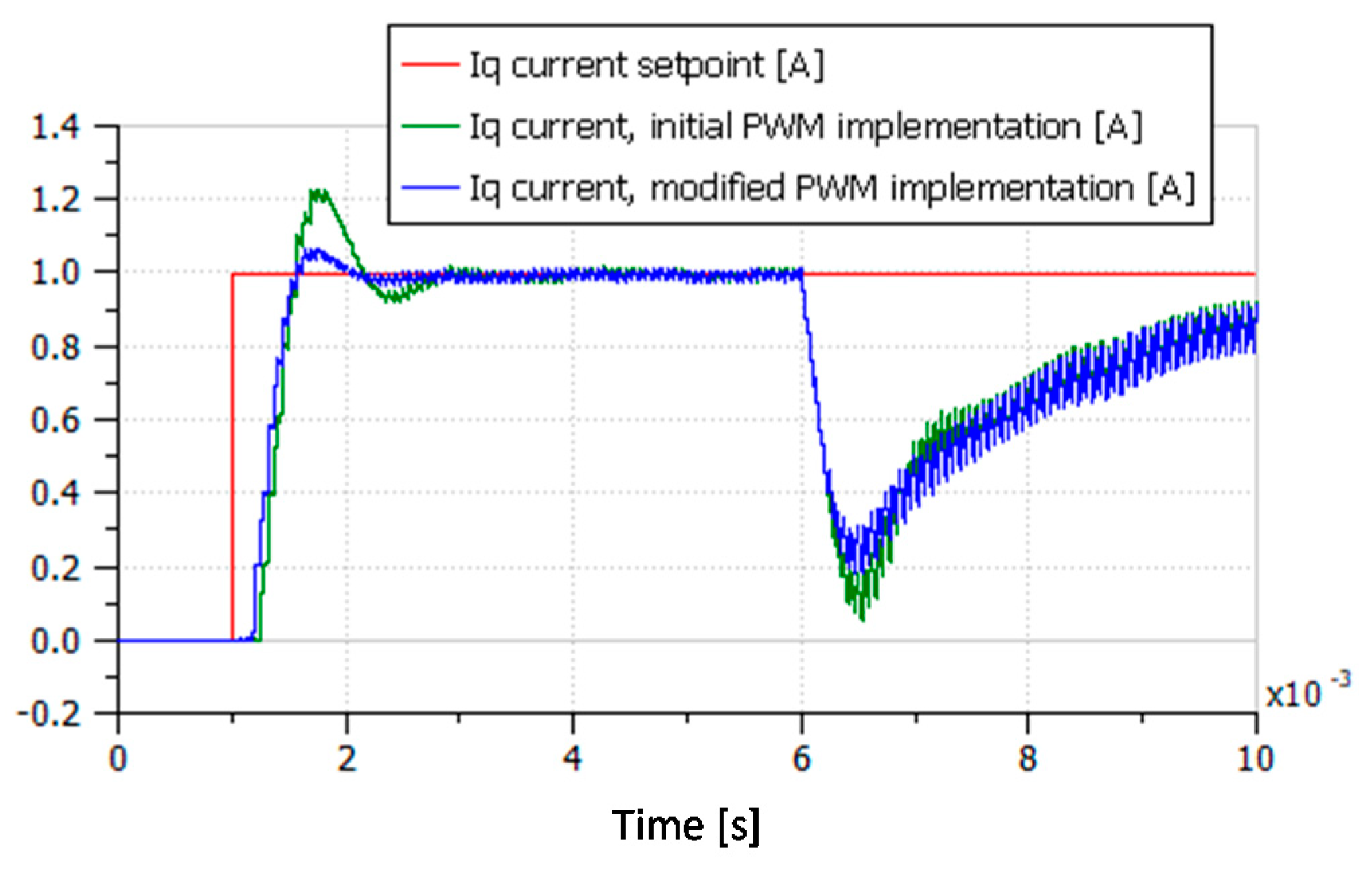
6.1.2. Timing for Digital Implementation
6.2. Sensors and Conditioners
- Electric noise coming from the harsh vibration and electromagnetic environment. For example, it is set to ±2 LSB (Least Significant Bit) of the ADC conversion for the better reproduction of ripple and chattering.
- Offset for the better consideration of the drift of the sensor and its electronic conditioning—e.g., under thermal effects.
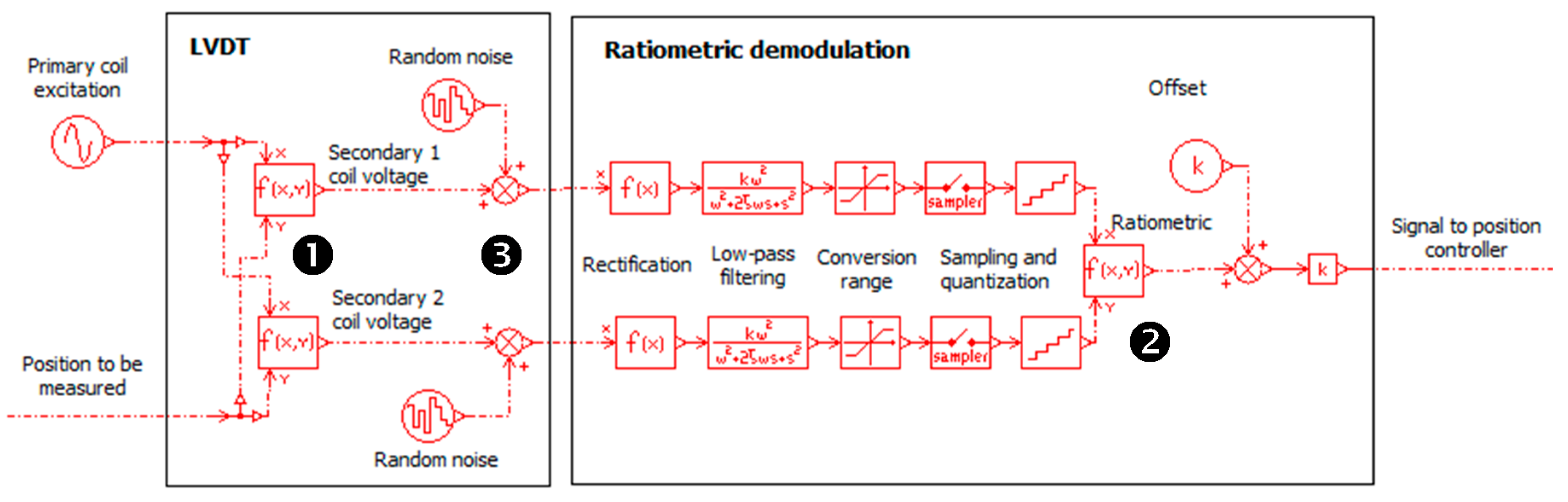
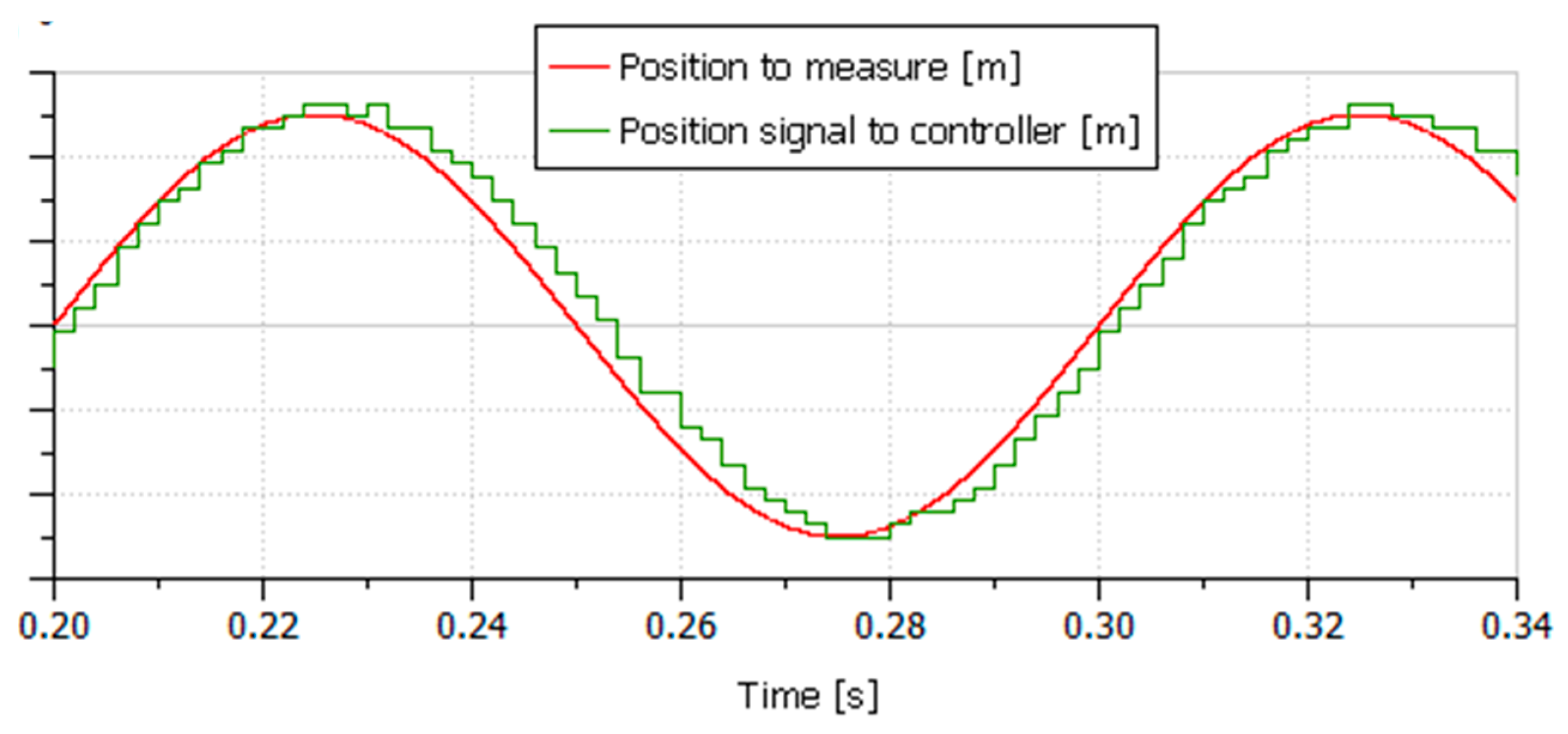
6.2.1. Rod Position Sensor
- Supplying the primary coil with the carrier, a constant magnitude, and a constant frequency sine voltage (a few volts, a few kilohertz).
- For each of the secondary coils, performing the rectification and low-pass filtering of the secondary voltage.
- Sampling the secondary voltages to compute the ratiometric value, the image of the measured position.
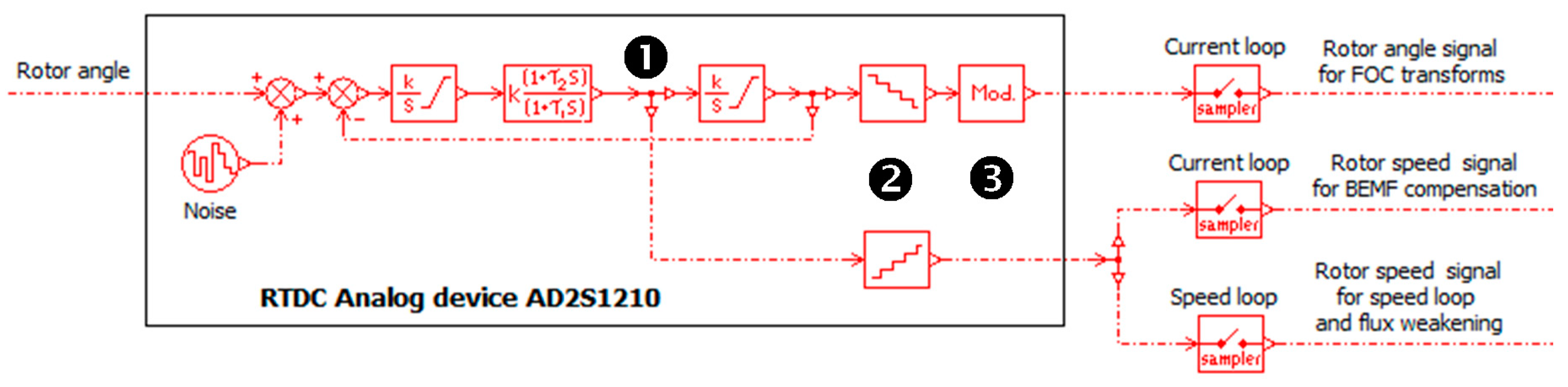
6.2.2. Rotor Position/Speed Measurement
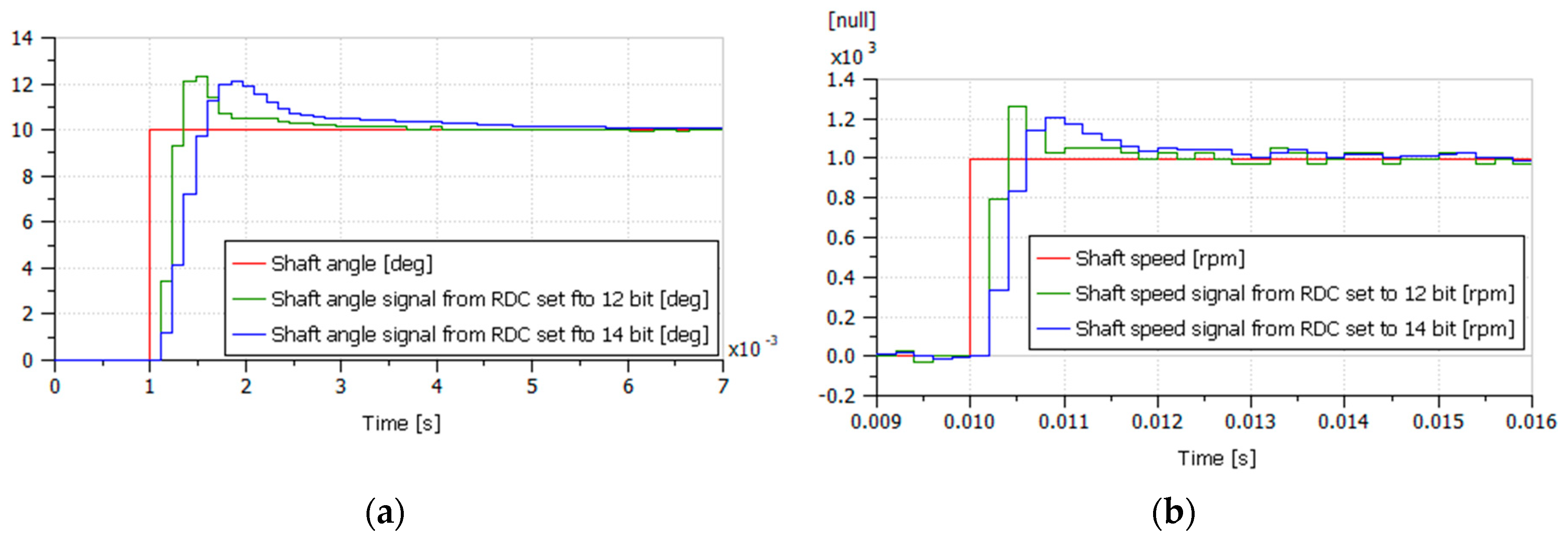
- For 12/14-bit resolutions, the overshoot of the speed measurement chain is 23%/21%, while the ±5% response time is 0.877/2.13 ms. Given these values, the RDC behaves globally as a second order system having a dimensionless damping factor of 0.45 and a natural frequency of 907/373 Hz. If the phase margin of the speed loop is measured at 100 Hz, the parasitic phase lag introduced by the 14-bit RDC at this frequency is 14.5°. This value is not negligible in comparison with the phase lag introduced by the equivalent delay of the speed loop sampling.
- The amount of quantization is verified with respect to the datasheet (0.088° and 176°/s for 12-bit configuration, 0.0217° and 21.6°/s for 14-bit configuration). For angle measurement, the 12-bit resolution could be acceptable for motors having a small number of pole pairs (e.g., the quantization error is 0.44° of the electric angle for five pole pairs). In contrast, the 12-bit resolution provides a very poor speed signal with a resolution of 146 rpm for the electric speed, even for a motor having five pole pairs. When the RDC model is integrated in the full model of the EMA, this poor resolution generates a high magnitude ripple on motor winding currents. This ripple is introduced at the current setpoint computed by the speed controller, the flux weakening function, and the BEMF compensation.
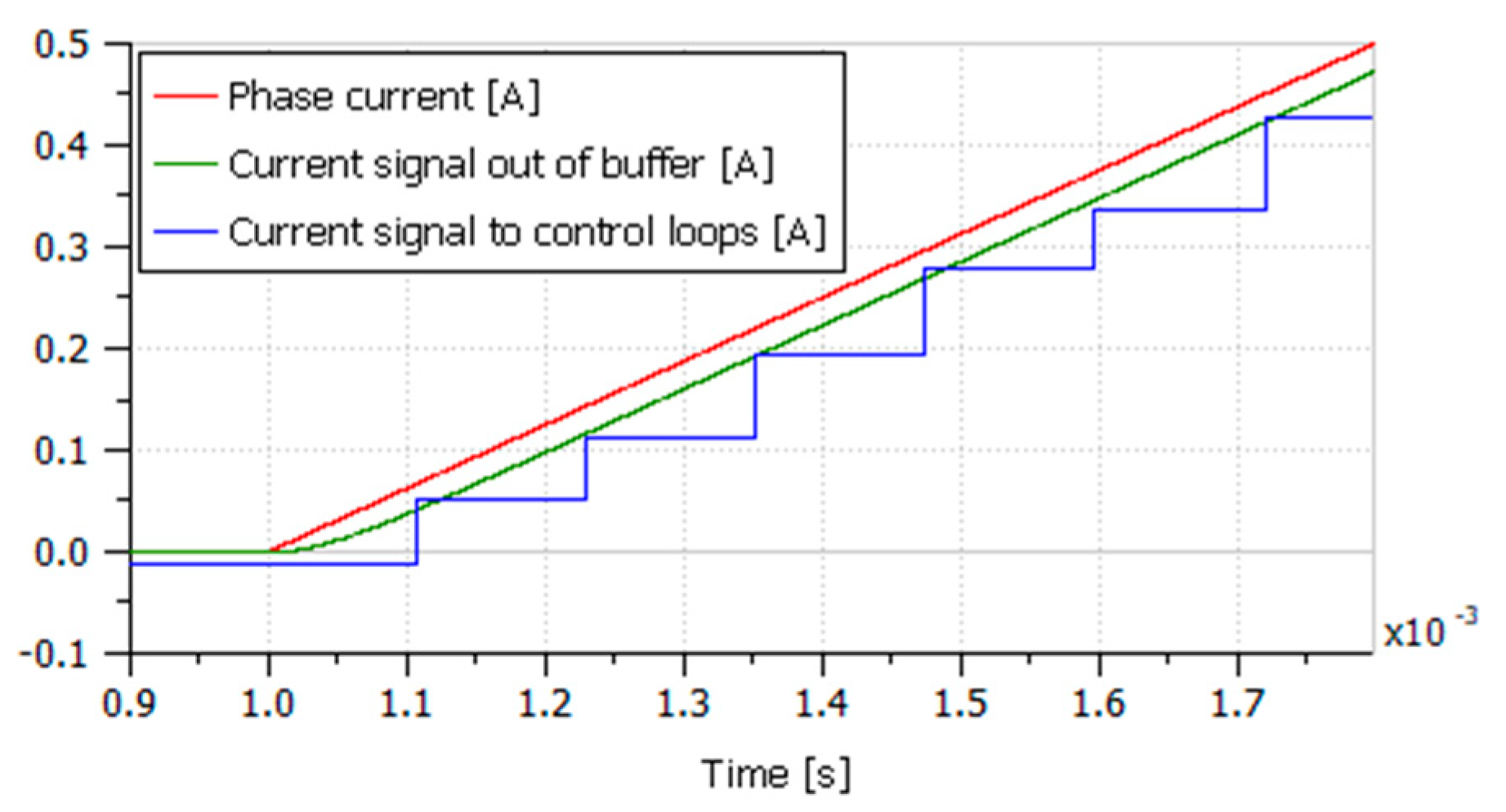
6.2.3. Current Measurement
- A model of the current sensor, identified from the ASC724 data sheet [36], which combines a pure delay of 3.49 μs and a first order lag of time constant 1.25 μs.
- A model of the signal conditioning that combines a buffer (also acting as an antialiasing filter), and the ADC (range limit, sampling, and quantization).
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| ADC | Analog-To-Digital conversion |
| AW | Anti Windup |
| BEMF | Back ElectroMotive Force |
| EMA | ElectroMechanical Actuator |
| FOC | Field Oriented Control |
| IGBT | Insulated Gate Bipolar Transistor |
| LL | Line to Line |
| LN | Line to Neutral |
| LSB | Least Significant Bit |
| LVDT | Linear Variometer Differential Transducer |
| MBD | Model-Based Design |
| M&S | Modelling and Simulation |
| PI | Proportional-Integral |
| PMM | Property Model Methodology |
| PMSM | Permanent Magnet Synchronous Machine |
| PWM | Pulse Width Modulation |
| RDC | Resolver to Digital Converter |
| TRL | Technology Readiness Level |
| Nomenclature | |
| a, b, c | Phase labels (-) |
| f | Frequency (Hz) |
| F | Force (N) |
| I | Current (A) |
| J | Moment of inertia (kg·m2) |
| K | Gain (depends on context) |
| l | Lead (m/revolution) |
| L | Inductance (H) |
| m | Modulation factor (-) |
| p | Number of pole pairs (-) |
| P | Pressure (Pa) |
| P | Heat power (W) |
| R | Resistance (Ohm) |
| s | Laplace variable (s−1) |
| t | Time (s) |
| T | Torque (N.m) |
| V | Velocity (m/s) |
| x | Position (m) |
| X | General variable (depends on context) |
| U | Voltage (V) |
| ψ | Flux linkage (Wb) |
| ξ | Damping factor (-) |
| ω | Angular frequency (rad/s) |
| θ | Angular position (rad) |
| Ω | Angular velocity (rad/s) |
| τ | Time constant (s) |
| Θ | Temperature (°K) |
| ν | Kinematic viscosity (m2/s) |
| Subscript | |
| d | Direct axis, or drive |
| DC | Direct current |
| e | Equivalent |
| E | Electric |
| f | Force |
| i | Integral |
| I | Current |
| l | Limited, load |
| m | Motor |
| n | Natural, nut |
| r | Relative |
| rms | Root mean square |
| q | Quadrature axis |
| t | Transmission |
| T | Torque |
| x | Position |
| Ω | Velocity |
| Superscript | |
| * | Setpoint |
| ~ | Measure |
| ‘ | Maximal value in pseudo linear mode |
References
- SAE AE-7 Committee. Aerospace Information Report AIR6326: Aircraft Electrical Power Systems Modeling and Simulation Definitions; SAE: Warrendale, PA, USA, August 2015. [Google Scholar]
- Rose, L.M. The Application of Mathematical Modelling to Process Development and Design; Applied Science Publishers: London, UK, 1974; ISBN 0-85334-584-8. [Google Scholar]
- Van Der Linden, F.L.; Schlegel, C.; Christmann, M.; Regula, G.; Hill, C.; Giangrande, P.; Maré, J.-C.; Egaña, I. Implementation of a Modelica Library for Simulation of Electromechanical Actuators for Aircraft and Helicopters. In Proceedings of the 10th International Modelica Conference, Lund, Sweden, 10–12 March 2014; pp. 757–766. [Google Scholar]
- Rani, B.L.; Tom, A.M. Dynamic simulation of brushless DC drive considering phase commutation and backemf waveform for electromechanical actuator. In Proceedings of the TENCON 2008—2008 IEEE Region 10 Conference, Hyderabad, India, 19–21 November 2008; pp. 1–6. [Google Scholar]
- Bilyaletdinova, L.; Steblinkin, A. Simulation of Direct Drive Electromechanical Actuator with Ballscrew. Procedia Eng. 2017, 176, 85–95. [Google Scholar] [CrossRef]
- Byington, C.S.; Watson, M.; Edwards, D.; Stoelting, P. A model-based approach to prognostics and health management for flight control actuators. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No.04TH8720), Big Sky, MT, USA, 6–13 March 2004; Volume 6, pp. 3551–3562. [Google Scholar] [CrossRef]
- Hill, C.; Gerada, C.; Giangrande, P.; Bozhko, S. Development of a Modelica Library for Electro-Mechanical, Actuator System Studies Including Fault Scenarios and Losses; SAE Technical Paper 2014-01-2181; SAE: Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Şen, M.; Balabozov, J.; Yatchev, L.; Ivanov, R. Modelling of current sensor based on hall effect. In Proceedings of the 2017 15th International Conference on Electrical Machines, Drives and Power Systems (ELMA), Sofia, Bulgaria, 1–3 June 2017; pp. 457–460. [Google Scholar]
- Qiao, F.; Liu, Z. An Accurate Mathematic Model for PMSM by Taking Total Losses and Saturation into Account. Appl. Mech. Mater. 2015, 742, 505–510. [Google Scholar] [CrossRef]
- Micouin, P.; Fabre, L.; Becquet, R.; Paper, P.; Razafimahefa, T.; Guérin, F. Property Model Methodology: A Landing Gear Operational Use Case. In Proceedings of the INCOSE International Symposium 2018, Washington, DC, USA, 7–12 July 2018. [Google Scholar]
- Budinger, M.; Liscouët, J.; Maré, J.-C. Estimation models for the preliminary design of electromechanical actuators. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 243–259. [Google Scholar] [CrossRef]
- Maré, J.-C. Requirement-based system-level simulation of mechanical transmissions with special consideration of friction, backlash and preload. Simul. Model. Pract. Theory 2016, 63, 58–82. [Google Scholar] [CrossRef]
- Takashi, M. The Effect of Tare Loss on the Efficiency of Mechanical Linear Actuators. Form Rev. N 2018. under revision. [Google Scholar]
- Akitani, S.; Bertolino, A. Increasing the fidelity of EMAs real-time simulation. In Proceedings of the SAE A-6 Symposium, Saint Pete Beach, FL, USA, 8 October 2019; Society of Automotive Engineers: Warrendale, PA, USA, 2019. [Google Scholar]
- Fu, J.; Maré, J.-C.; Yu, L.; Fu, Y. Multi-level virtual prototyping of electromechanical actuation system for more electric aircraft. Chin. J. Aeronaut. 2018, 31, 892–913. [Google Scholar] [CrossRef]
- Krykowski, K.; Hetmańczyk, J. Constant Current Models of Brushless DC Motor. Electr. Control. Commun. Eng. 2013, 3, 19–24. [Google Scholar] [CrossRef]
- Krishnan, R. Electric Motor Drives: Modeling, Analysis, and Control; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Cai, H.; Dakai, H. On PMSM Model Fidelity and its Implementation in Simulation. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE) 2018, Portland, OR, USA, 23–27 September 2018; pp. 1674–1681. [Google Scholar] [CrossRef]
- Park, R.H. Two Reaction Theory of Synchronous Machines. In Transactions of the American Institute of Electrical Engineers. AIEE Trans. 1929, 48, 716–730. [Google Scholar] [CrossRef]
- Clarke, E. Circuit Analysis of A-C Power Systems, Vols. I and II. Stud. Q. J. 1951, 22, 95. [Google Scholar] [CrossRef]
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives; Taylor and Francis Group: Boca Raton, FL, USA, 2010. [Google Scholar]
- Wu, T.; Bozhko, S.; Asher, G.; Wheeler, P.; Thomas, D. Fast Reduced Functional Models of Electromechanical Actuators for More-Electric Aircraft Power System Study; SAE Technical Paper 008-01-2859; SAE: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Maré, J.-C. Friction modelling and simulation at system level—Considerations to load and temperature effects. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2014, 229, 27–48. [Google Scholar] [CrossRef]
- Hersey, M.D. The laws of lubrication of horizontal journal bearings. J. Wash. Acad. Sci. 1914, 4, 542–552. [Google Scholar]
- Aeroshell, Aerospace Grease 7, Technical Datasheet V1.1. 29 November 2014. Available online: https://www.shell.comwww.shell.com (accessed on 20 July 2020).
- The SKF Model for Calculating the Frictional Moment, SKF General Catalog 5000 E. 2003. Available online: https://www.skf.com (accessed on 20 July 2020).
- Olsson, H.; Åström, K.J.; de Wit, C.; Gäfvert, M.; Lischinsky, P. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef]
- Maré, J.-C. Friction modelling and simulation at system level: A practical view for the designer. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2012, 226, 728–741. [Google Scholar] [CrossRef]
- Pennestri, E.; Rossi, V.; Salvini, P.; Valentini, P.P. Review and comparison of dry friction force models. Nonlinear Dyn. 2015, 83. [Google Scholar] [CrossRef]
- Modelica Association. Modelica®—A Unified Object-Oriented Language for Systems Modeling Language Specification; Version 3.4. 10 April 2017. Available online: https://www.modelica.org/documents/ModelicaSpec34.pdf (accessed on 25 September 2020).
- Coïc, C.; Fu, J.; Maré, J.-C. Bond Graphs Aided development of Mechanical Power Transmission for Aerospace Electromechanical Actuators. In Proceedings of the International Conference on Bond Graph Modeling and Simulation, Montreal, QC, Canada, 24–27 July 2016; pp. 221–228. [Google Scholar] [CrossRef]
- Maré, J.-C.; Akitani, S. Foundation for virtual prototyping of mechanical power management functions in electromechanical actuators. In Proceedings of the BATH/ASME FPMC Symposium on Fluid Power and Motion Control, Bath, UK, 12–14 September 2018. [Google Scholar] [CrossRef]
- Maré, J.-C. Aerospace Actuators—Volume 2: Signal-by-Wire and Power-by-Wire; ISTE/Wiley: London, UK, 2017. [Google Scholar]
- Drumea, A.; Svasta, P.; Blejan, M. Modelling and simulation of an inductive displacement sensor for mechatronic systems. In Proceedings of the 33rd International Spring Seminar on Electronics Technology, ISSE 2010, Warsaw, Poland, 12–16 May 2010; pp. 304–307. [Google Scholar] [CrossRef]
- Analog Devices, ADS1210 Datasheet Rev. A. 2010; p. 36. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD2S1210.pdf (accessed on 20 July 2020).
- ACS724LLCTR-20AB Current Sensor Datasheet, Allegro Microsystems ACS724-DS, Rev. 16. 3 April 2020. Available online: https://www.allegromicro.com (accessed on 20 July 2020).




| Phenomenom Considered in the Model | Engineering Needs | Effects on Simulation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Functional | Power Sizing | Thermal Balance | Natural Dynamics | Closed-Loop Performance | Consumed/Regenerated Energy | Mechanical Load Propagation | Mode Switching /Response to Fault | Number of Parameters | Number ofState Variables | Time Scale | ||
| Control | ||||||||||||
| 1—Perfect (continuous, no saturation) | ||||||||||||
| 2—Discrete with saturations | ||||||||||||
| 3—Discrete with timing | ||||||||||||
| Sensors | ||||||||||||
| 1—Perfect (pure gain) | ||||||||||||
| 2—Plus accuracy, noise and dynamics | ||||||||||||
| 3—Plus detailed conditioning | ||||||||||||
| Power electronics | ||||||||||||
| 1—Perfect (modulated power transformer) | ||||||||||||
| 2—Basic (averaged, with efficiency) | ||||||||||||
| 3—Advanced (losses, heat, switched) | ||||||||||||
| Electric motor | ||||||||||||
| 1—Perfect (power transformer) | ||||||||||||
| 2—DC Equivalent (copper losses, inductance, inertia) | ||||||||||||
| 3—D-Q equivalent (copper losses, inductance, inertia) | ||||||||||||
| 4—3-phase, plus iron losses, cogging torque, cyclic L, saturation | ||||||||||||
| Mechanical transmission | ||||||||||||
| 1—Perfect (pure gain) | ||||||||||||
| 2—Plus inertia and simplified friction | ||||||||||||
| 3—Plus detailed friction, compliance and backlash | ||||||||||||
| 4—Plus multiple degrees of freedom | ||||||||||||
| Controller | Practical Limit | Assumption and Comment |
|---|---|---|
| speed setpoint issued by the position controller. | Allowing the PWM to operate in the pseudo linear domain. | |
| and current demands issued by the speed controller and flux weakening function. | must be the max transient value permitted. | |
| and voltage demands issued by the current controllers. | Allowing the PWM to operate in the pseudo linear domain. In the simplest form, each and voltage is limited to . |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maré, J.-C. Practical Considerations in the Modelling and Simulation of Electromechanical Actuators. Actuators 2020, 9, 94. https://doi.org/10.3390/act9040094
Maré J-C. Practical Considerations in the Modelling and Simulation of Electromechanical Actuators. Actuators. 2020; 9(4):94. https://doi.org/10.3390/act9040094
Chicago/Turabian StyleMaré, Jean-Charles. 2020. "Practical Considerations in the Modelling and Simulation of Electromechanical Actuators" Actuators 9, no. 4: 94. https://doi.org/10.3390/act9040094
APA StyleMaré, J.-C. (2020). Practical Considerations in the Modelling and Simulation of Electromechanical Actuators. Actuators, 9(4), 94. https://doi.org/10.3390/act9040094





