Styrenic-Rubber Dielectric Elastomer Actuator with Inherent Stiffness Compensation
Abstract
1. Introduction
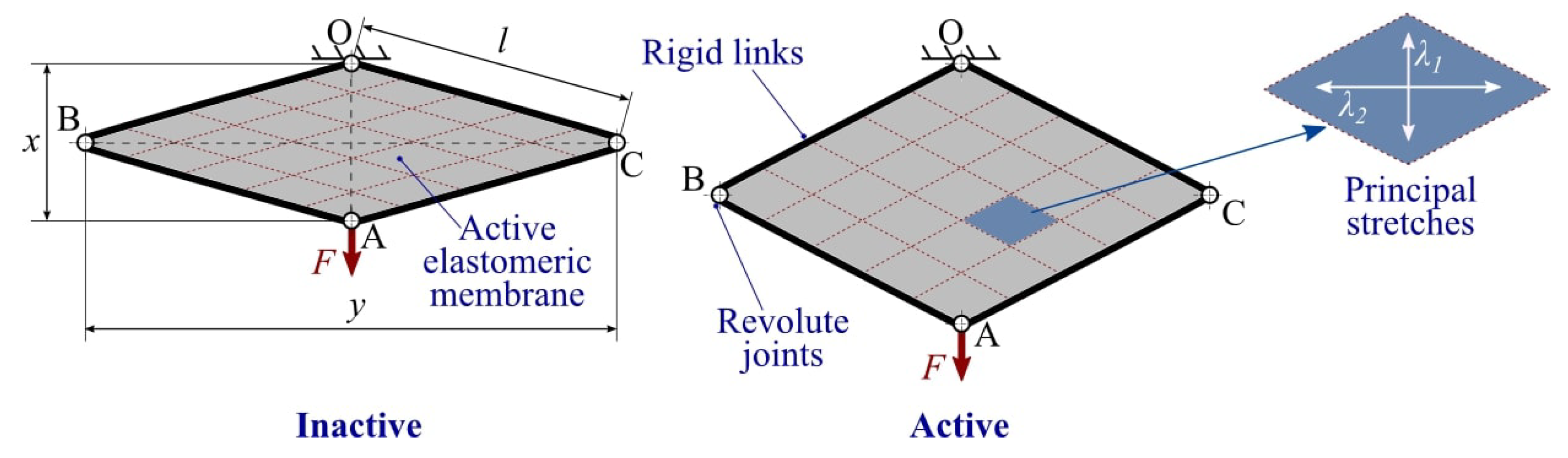
2. Layout and Modeling
3. Design
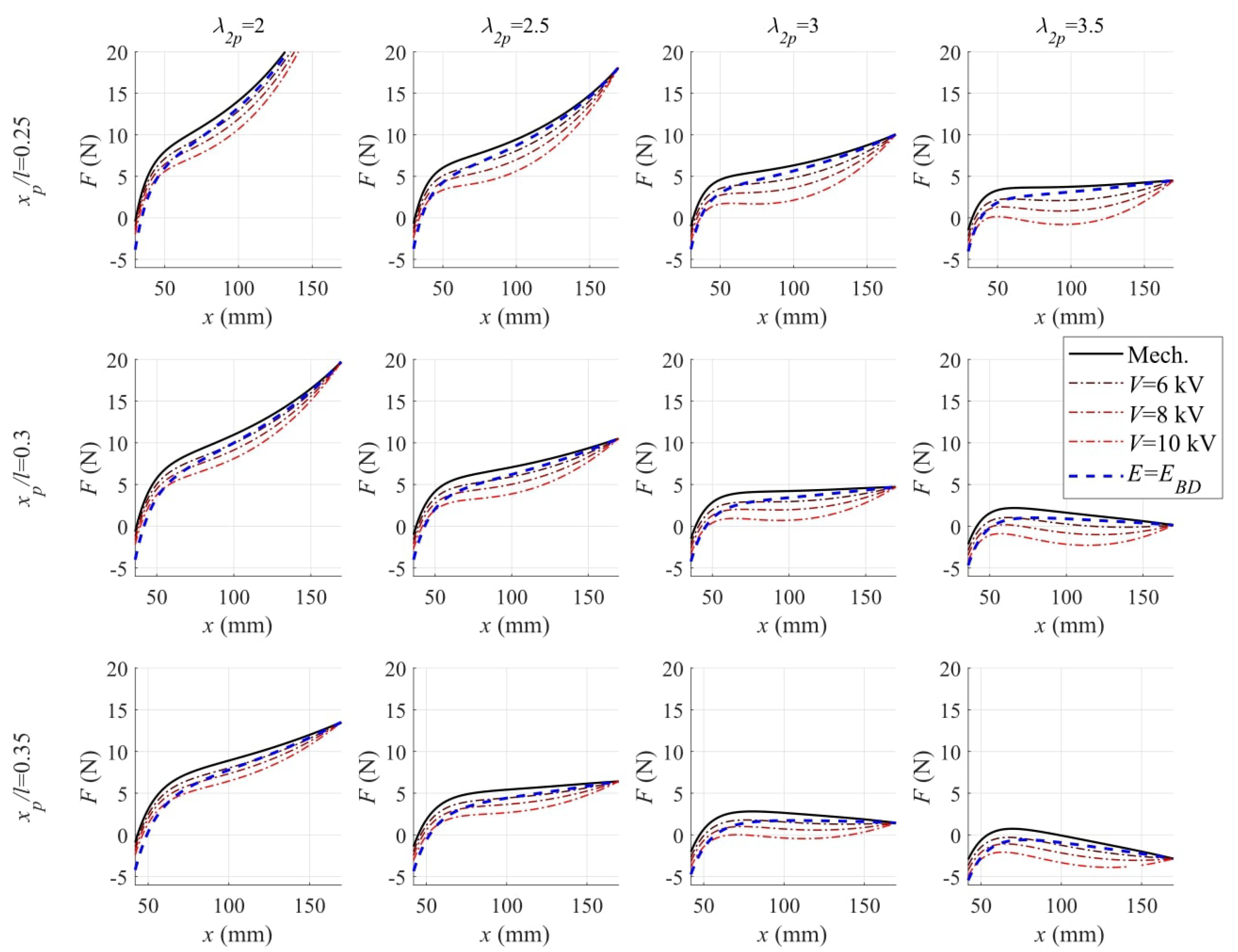
- In correspondence with the low values of and , the LS-DEA has a stiff response (i.e., large slope of the force-displacement curves). As a consequence, the force variation achievable through electric activation in a given configuration x is small compared to the bias mechanical force required to hold the actuator in such a configuration.
- Increasing and provides an increase in the compressive stresses in the y direction and a consequent reduction in the actuator stiffness (in the x direction). As a result, the mechanical response curves assume a nearly-horizontal trend. This leads to an increase in the ratio of the electrostatic force variation over the mechanical biasing force (at fixed x) and in the nominal voltage-induced stroke (at fixed F).
- At large values of and , the characteristic curves have a negative slope over a significant portion of the range, hence potentially suffering from unstable response (unless the DEA is coupled with a positive-stiffness biasing element [14]).
4. Prototype and Characterization Setup
- isopotential tensile tests, aimed at mapping the quasi-static force-displacement characteristic of the prototype actuators at different levels of constant applied voltage.
- isometric tests, aimed at measuring the actuator blocking force in different configurations.
- isotonic tests, aimed at measuring the LS-DEA actuation stroke in the presence of constant applied forces.
4.1. LS-DEA Prototype Manufacturing
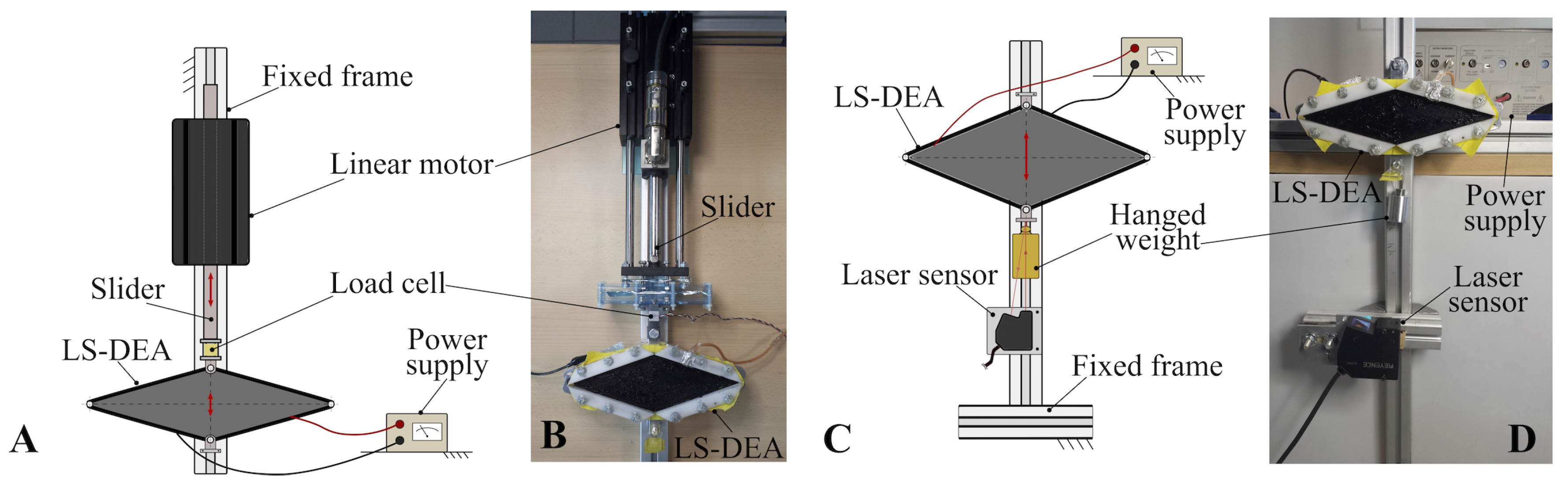
4.2. Experimental Setups and Procedures
5. Experimental Tests and Results
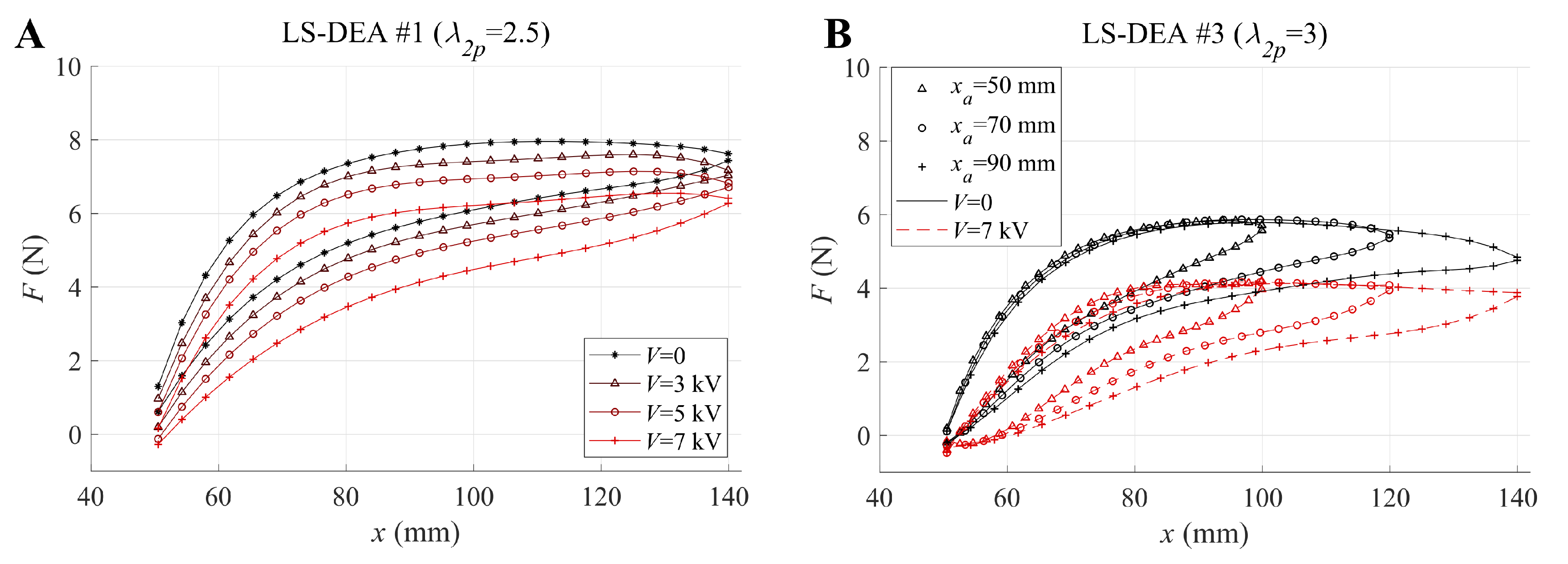
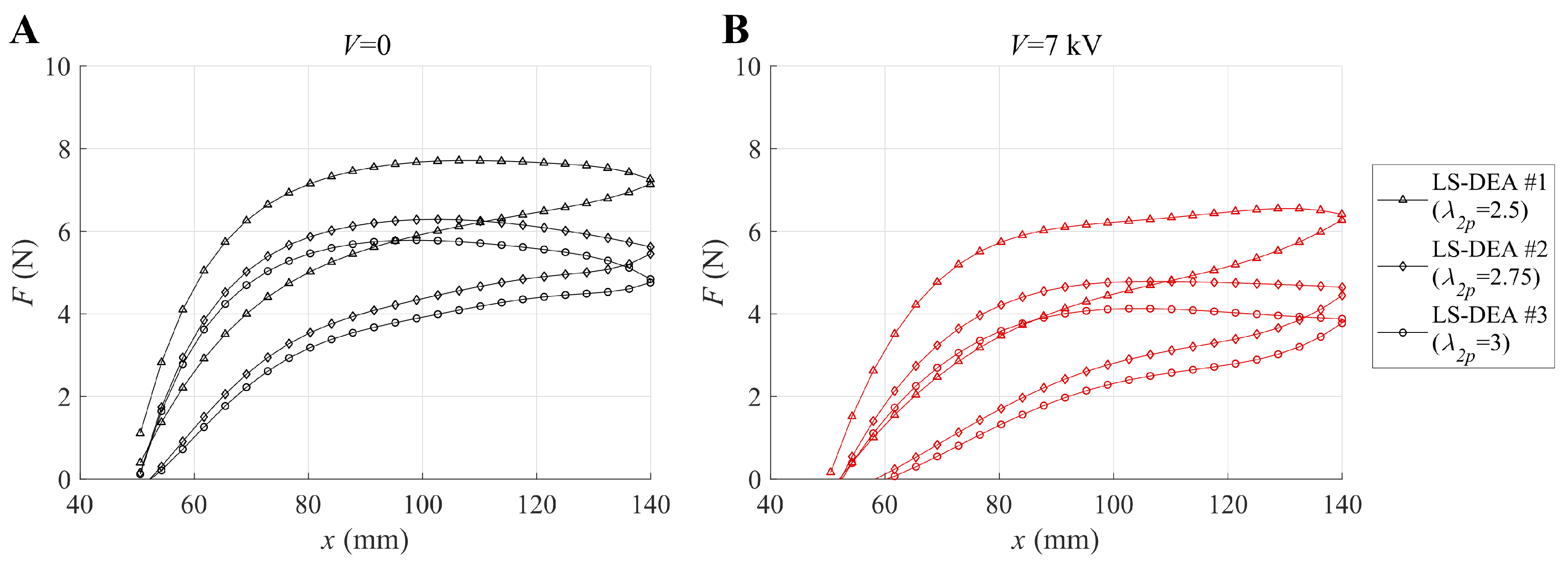
5.1. Isopotential Tests
- Consistent with the design assumptions, the force-displacement responses show a nearly-flat trend (i.e., a low value of the actuator stiffness) over a significant portion of the considered working range.
- Applying voltages within the considered range produces significant variations in the force-displacement response of the actuator. Based on these measurements, electrically-induced force variations of up to 2 N might potentially be obtained, assuming to lock the actuator at intermediate positions within the working range.
- The LS-DEA specimen has an inelastic response, due to the SR viscosity and hysteresis, as observed by [3]. A quantitative analysis of the associated dissipation is presented in the following.
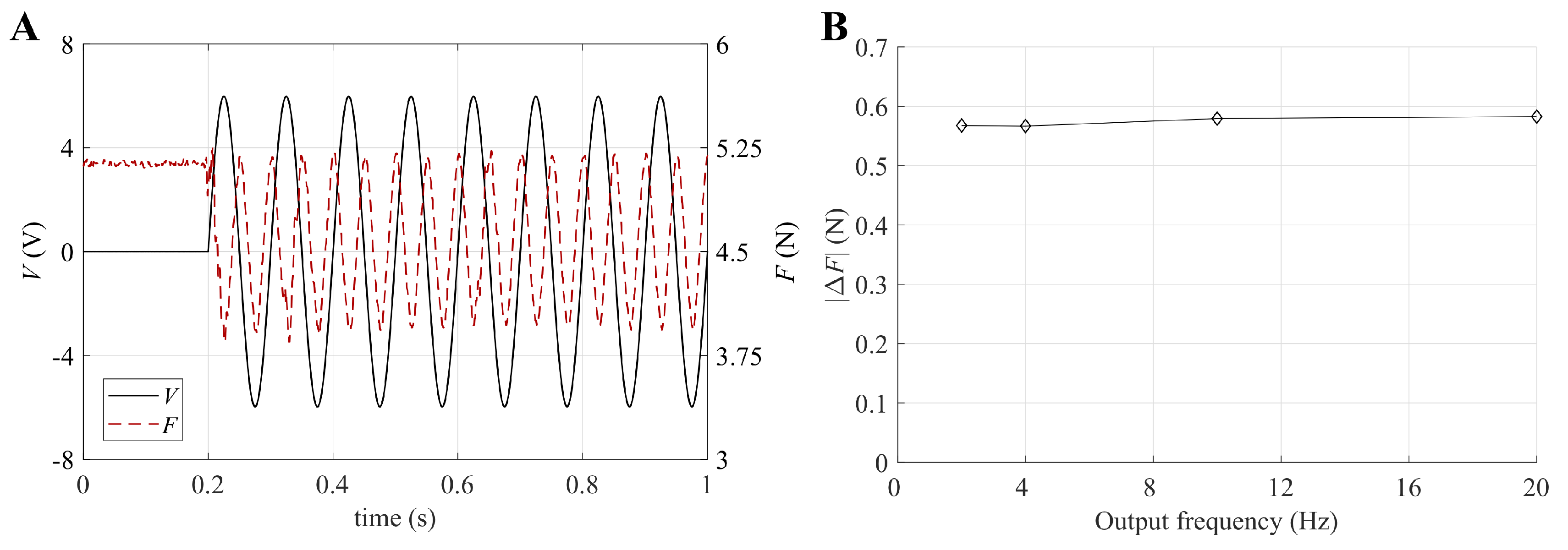
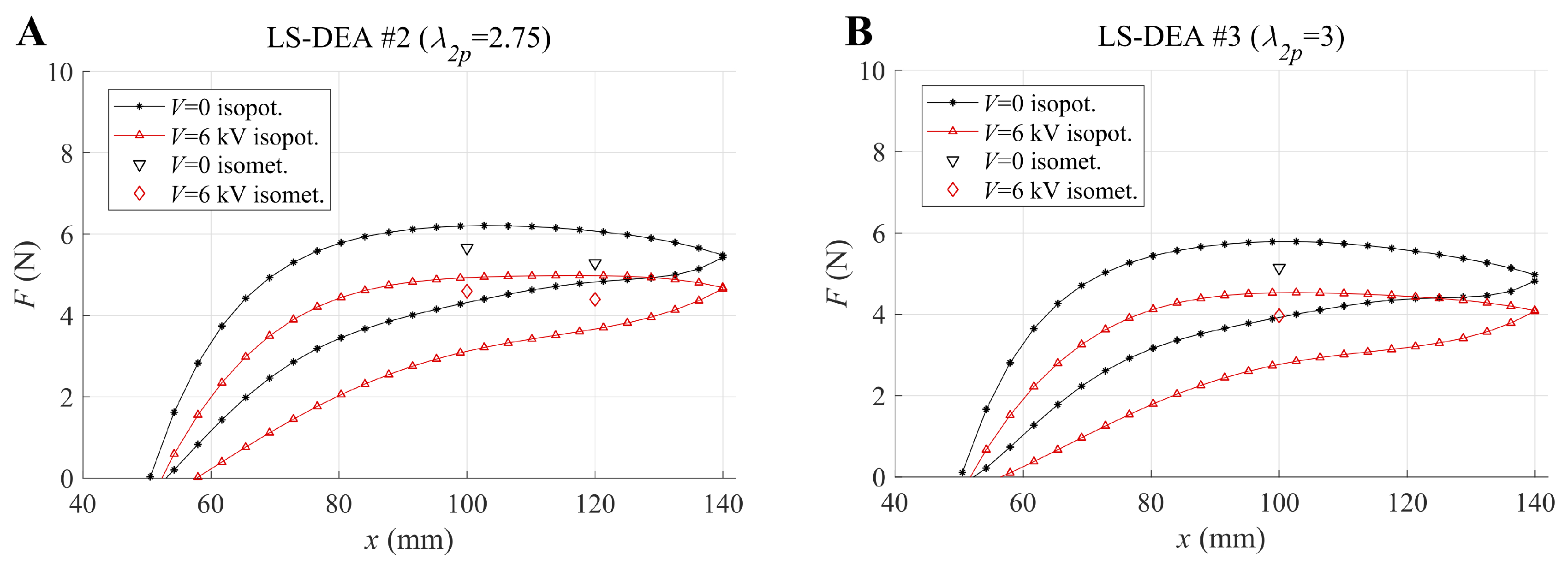
5.2. Isometric Tests
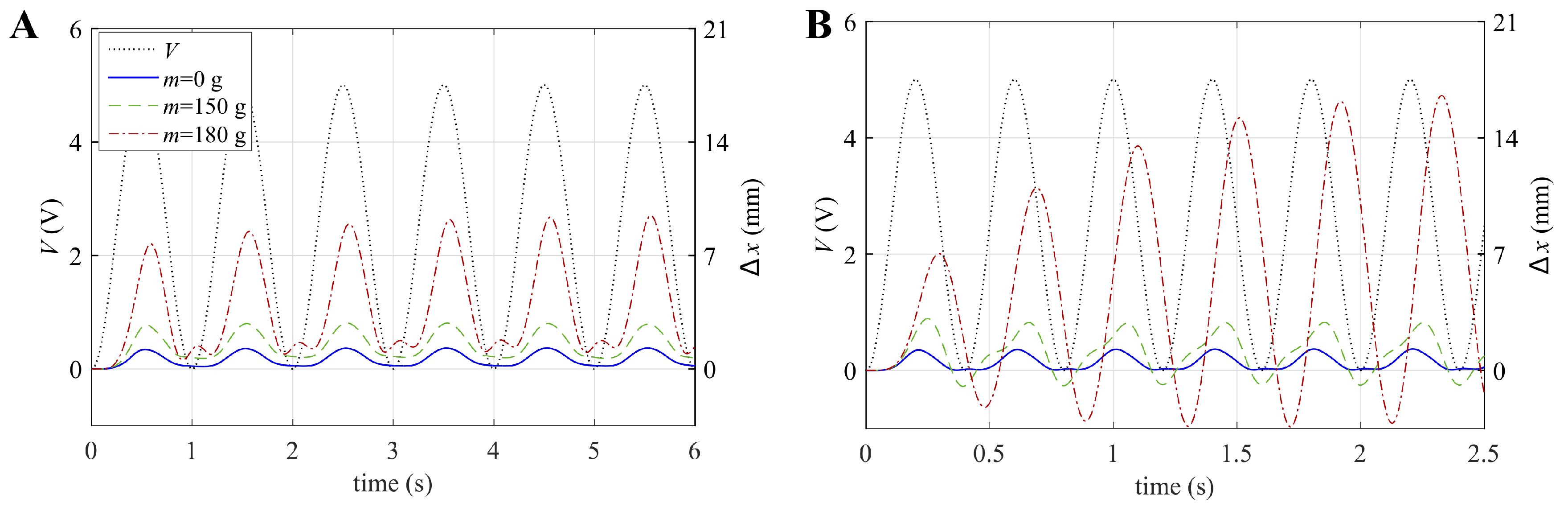
5.3. Isotonic Tests
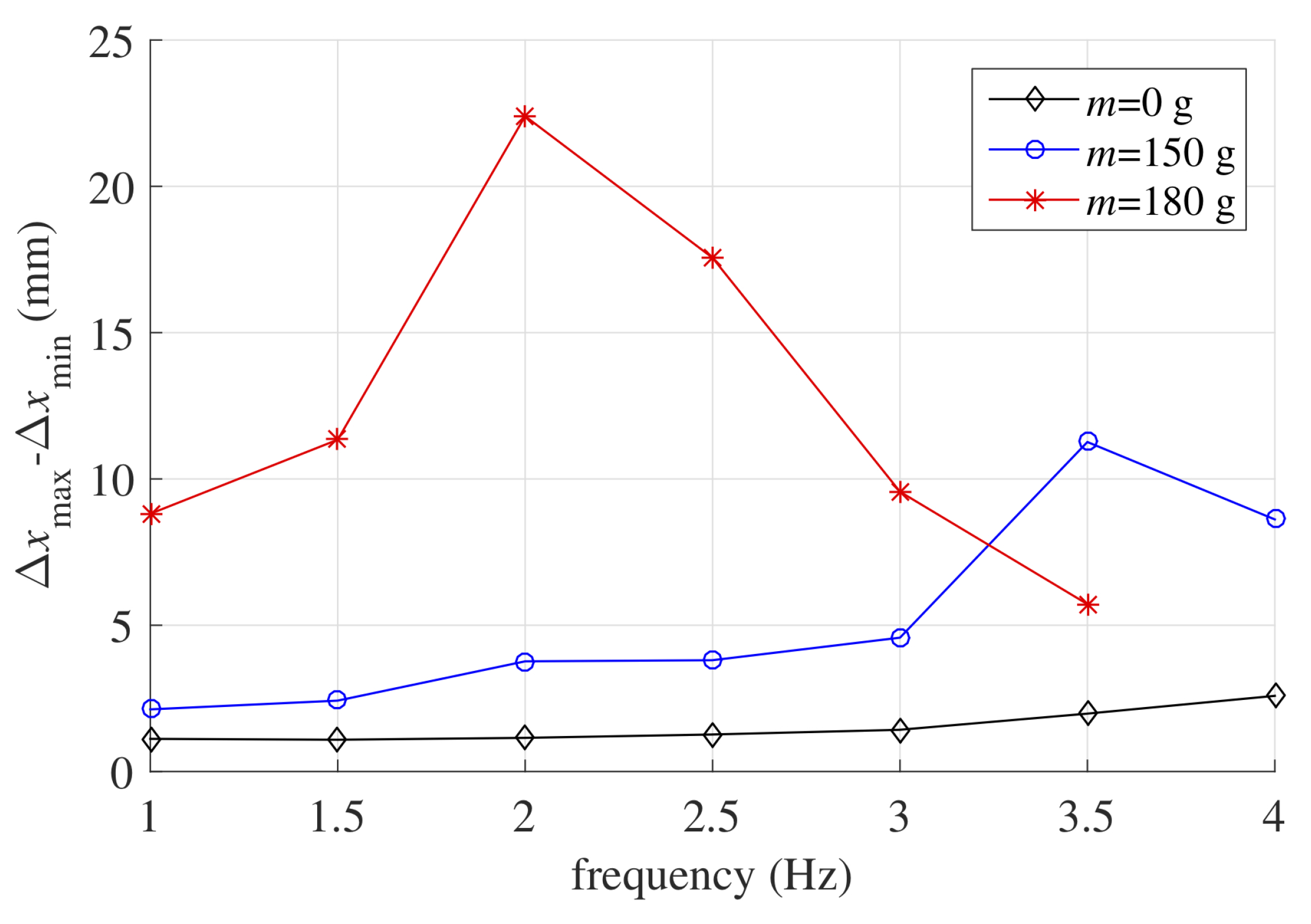
- At the lowest frequency (Figure 9A), the actuator operation can be considered quasi-static. As a consequence, the LS-DEA displacement was in phase with the electrical excitation. At the time instants where the voltage equaled zero, the device reached a position that approximately equaled the initial equilibrium position (i.e., ). The oscillation amplitude increased with the applied load (hung mass), owing to the lower stiffness of the LS-DEA at large applied forces (see the slope of the curves in Figure 6)
- The increase in the oscillation amplitude was maximum in the case 180 g, while it was practically negligible for . This is easily explained in terms of the actuator natural frequency in the different scenarios. The higher the applied weight on the device, the lower the natural frequency is, due to two combined effects: (1) the increase in the actuator inertia; (2) the decrease in the LS-DEA stiffness. In the case , the actuator still behaved in a quasi-static way, whereas in the case g, it showed a nearly-resonant behavior, as demonstrated by the significant phase shift between the excitation signal and the displacement.
- The displacement time series significantly divert from the sinusoidal trend, owing to the highly nonlinear LS-DEA response and to the presence of low-amplitude parasitic oscillation modes (e.g., rotation above the lozenge mechanism fixed hinge), which led to the presence of multiple peaks within the same oscillation.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SR | Synthetic Rubber |
| LS-DEA | Lozenge-Shaped Dielectric Elastomer Actuator |
| DE | Dielectric Elastomer |
| DEA | Dielectric Elastomer Actuator |
References
- Carpi, F.; Anderson, I.; Bauer, S.; Frediani, G.; Gallone, G.; Gei, M.; Graaf, C.; Jean-Mistral, C.; Kaal, W.; Kofod, G.; et al. Standards for dielectric elastomer transducers. Smart Mater. Struct. 2015, 24, 105025. [Google Scholar] [CrossRef]
- Carpi, F. Electromechanically Active Polymers: A Concise Reference, 1st ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Chen, Y.; Agostini, L.; Moretti, G.; Fontana, M.; Vertechy, R. Dielectric elastomer materials for large-strain actuation and energy harvesting: A comparison between styrenic rubber, natural rubber and acrylic elastomer. Smart Mater. Struct. 2019, 28, 114001. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, J.; Zhu, L.M.; Zhu, X. A survey on dielectric elastomer actuators for soft robots. Bioinspir. Biomimetics 2017, 12, 011003. [Google Scholar] [CrossRef] [PubMed]
- Shintake, J.; Rosset, S.; Schubert, B.; Floreano, D.; Shea, H. Versatile soft grippers with intrinsic electroadhesion based on multifunctional polymer actuators. Adv. Mater. 2016, 28, 231–238. [Google Scholar] [CrossRef] [PubMed]
- Babiç, M.; Vertechy, R.; Berselli, G.; Lenarçiç, J.; Parenti Castelli, V.; Vassura, G. An electronic driver for improving the open and closed loop electro-mechanical response of Dielectric Elastomer actuators. Mechatronics 2010, 20, 201–212. [Google Scholar] [CrossRef]
- Lee, B.Y.; Kim, J.; Kim, H.; Kim, C.; Lee, S.D. Low-cost flexible pressure sensor based on dielectric elastomer film with micro-pores. Sens. Actuators A Phys. 2016, 240, 103–109. [Google Scholar] [CrossRef]
- Zhu, Y.; Tairych, A.; Rosset, S.; Anderson, I.A. An approach to validate the design and fabrication of dielectric elastomer tactile sensor. In Electroactive Polymer Actuators and Devices; SPIE: Bellingham, DC, USA, 2019. [Google Scholar]
- Binh, P.C.; Ahn, K.K. Performance optimization of dielectric electro active polymers in wave energy converter application. Int. J. Precis. Eng. Manuf. 2016, 17, 1175–1185. [Google Scholar] [CrossRef]
- Moretti, G.; Herran, M.S.; Forehand, D.; Alves, M.; Jeffrey, H.; Vertechy, R.; Fontana, M. Advances in the development of dielectric elastomer generators for wave energy conversion. Renew. Sustain. Energy Rev. 2020, 117, 109430. [Google Scholar] [CrossRef]
- Kovacs, G.; Düring, L.; Michel, S.; Terrasi, G. Stacked dielectric elastomer actuator for tensile force transmission. Sens. Actuators A Phys. 2009, 155, 299–307. [Google Scholar] [CrossRef]
- Berselli, G.; Vertechy, R.; Vassura, G.; Parenti-Castelli, V. Optimal synthesis of conically shaped dielectric elastomer linear actuators: Design methodology and experimental validation. IEEE/ASME Trans. Mechatron. 2011, 16, 67–79. [Google Scholar] [CrossRef]
- Jean-Mistral, C.; Jacquet-Richardet, G.; Sylvestre, A. Parameters influencing fatigue life prediction of dielectric elastomer generators. Polym. Test. 2020, 81, 106198. [Google Scholar] [CrossRef]
- Hodgins, M.; York, A.; Seelecke, S. Experimental comparison of bias elements for out-of-plane DEAP actuator system. Smart Mater. Struct. 2013, 22, 094016. [Google Scholar] [CrossRef]
- Hau, S.; Bruch, D.; Rizzello, G.; Motzki, P.; Seelecke, S. Silicone based dielectric elastomer strip actuators coupled with nonlinear biasing elements for large actuation strains. Smart Mater. Struct. 2018, 27, 074003. [Google Scholar] [CrossRef]
- Kaltseis, R.; Keplinger, C.; Koh, S.J.A.; Baumgartner, R.; Goh, Y.F.; Ng, W.H.; Kogler, A.; Tröls, A.; Foo, C.C.; Suo, Z.; et al. Natural rubber for sustainable high-power electrical energy generation. RSC Adv. 2014, 4, 27905–27913. [Google Scholar] [CrossRef]
- Moretti, G.; Fontana, M.; Vertechy, R. Parallelogram-shaped dielectric elastomer generators: Analytical model and experimental validation. J. Intell. Mater. Syst. Struct. 2015, 26, 740–751. [Google Scholar] [CrossRef]
- Vertechy, R.; Fontana, M. Electromechanical characterization of a new synthetic rubber membrane for dielectric elastomer transducers. In Electroactive Polymer Actuators and Devices (EAPAD) 2015; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9430, p. 94300K. [Google Scholar]
- Berselli, G.; Guerra, A.; Vassura, G.; Andrisano, A.O. An engineering method for comparing selectively compliant joints in robotic structures. IEEE Trans. Mechatron. 2014, 19, 1882–1895. [Google Scholar] [CrossRef]
- Youn, J.H.; Jeong, S.M.; Choi, Y.S.; Kyung, K.U. A soft tactile display using dielectric elastomer actuator for fingertip interaction. In Haptic Interaction; Kajimoto, H., Lee, D., Kim, S.Y., Konyo, M., Kyung, K.U., Eds.; Springer: Singapore, 2019; pp. 15–17. [Google Scholar]
- Weight, B.L.; Magleby, S.P.; Howell, L.L. Selection of compliant constant-force mechanisms based on stress and force criteria. In ASME IDETC-CIE International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2002; pp. 51–63. [Google Scholar]
- Plante, J.; Dubowsky, S. On the properties of dielectric elastomer actuators and their design implications. Smart Mater. Struct. 2007, 16, S227. [Google Scholar] [CrossRef]
- Plante, J.S.; Dubowsky, S. On the performance mechanisms of dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 137, 96–109. [Google Scholar] [CrossRef]
- Vertechy, R.; Berselli, G.; Parenti Castelli, V.; Vassura, G. Optimal design of lozenge-shaped dielectric elastomer linear actuators: Mathematical procedure and experimental validation. J. Intell. Mater. Syst. Struct. 2010, 21, 503–515. [Google Scholar] [CrossRef]
- Dorfmann, L.; Ogden, R.W. Nonlinear Theory of Electroelastic and Magnetoelastic Interactions; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Moretti, G.; Fontana, M.; Vertechy, R. Model-based design and optimization of a dielectric elastomer power take-off for oscillating wave surge energy converters. Meccanica 2015, 50, 2797–2813. [Google Scholar] [CrossRef]
- Ogden, R.; Saccomandi, G.; Sgura, I. Fitting hyperelastic models to experimental data. Comput. Mech. 2004, 34, 484–502. [Google Scholar] [CrossRef]
- Elastosil Films Catalogue, Wacker. Available online: https://www.wacker.com/h/en-us/silicone-rubber/silicone-films/elastosil-film-2030/p/000038005 (accessed on 27 May 2020).
- Tröls, A.; Kogler, A.; Baumgartner, R.; Kaltseis, R.; Keplinger, C.; Schwödiauer, R.; Graz, I.; Bauer, S. Stretch dependence of the electrical breakdown strength and dielectric constant of dielectric elastomers. Smart Mater. Struct. 2013, 22, 104012. [Google Scholar] [CrossRef]
- Berselli, G.; Vertechy, R.; Fontana, M.; Pellicciari, M. An experimental assessment of the thermo-elastic response in acrylic elastomers and natural rubbers for application on electroactive polymer transducers. In ASME 2014 Conference on Smart Materials, Adaptive Structures and Intelligent Systems; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Harwood, J.; Mullins, L.; Payne, A. Stress softening in natural rubber vulcanizates. Part II. Stress softening effects in pure gum and filler loaded rubbers. J. Appl. Polym. Sci. 1965, 9, 3011–3021. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. Modeling, identification, and control of a dielectric electro-active polymer positioning system. IEEE Trans. Control Syst. Technol. 2014, 23, 632–643. [Google Scholar] [CrossRef]
- Wilson, E.D.; Assaf, T.; Pearson, M.J.; Rossiter, J.M.; Anderson, S.R.; Porrill, J. Bioinspired adaptive control for artificial muscles. In Conference on Biomimetic and Biohybrid Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 311–322. [Google Scholar]
- Pelrine, R.; Kornbluh, R.; Pei, Q.; Joseph, J. High-speed electrically actuated elastomers with strain greater than 100%. Science 2000, 287, 836–839. [Google Scholar] [CrossRef]
- Carpi, F.; Bauer, S.; De Rossi, D. Stretching dielectric elastomer performance. Science 2010, 330, 1759–1761. [Google Scholar] [CrossRef]

| Property | Value |
|---|---|
| Unstretched thickness | m |
| Hyperelastic parameters | kPa, , kPa |
| Dielectric permittivity | F/m |
| Stretch-dependent breakdown electric field | |
| (92% reliability) | MV/m, |
| Identifier | DE Material Mass | ||
|---|---|---|---|
| LS-DEA #1 | 2.5 | 40 mm | 0.78 g |
| LS-DEA #2 | 2.75 | 40 mm | 0.74 g |
| LS-DEA #3 | 3 | 40 mm | 0.71 g |
| Identifier | kV | kV | kV | kV |
|---|---|---|---|---|
| LS-DEA #1 | 23.3% | 24.4% | 26.0% | 29.5% |
| LS-DEA #2 | 31.9% | 33.5% | 37.1% | 43.3% |
| LS-DEA #3 | 33.4% | 35.4% | 39.0% | 45.8% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moretti, G.; Sarina, L.; Agostini, L.; Vertechy, R.; Berselli, G.; Fontana, M. Styrenic-Rubber Dielectric Elastomer Actuator with Inherent Stiffness Compensation. Actuators 2020, 9, 44. https://doi.org/10.3390/act9020044
Moretti G, Sarina L, Agostini L, Vertechy R, Berselli G, Fontana M. Styrenic-Rubber Dielectric Elastomer Actuator with Inherent Stiffness Compensation. Actuators. 2020; 9(2):44. https://doi.org/10.3390/act9020044
Chicago/Turabian StyleMoretti, Giacomo, Luca Sarina, Lorenzo Agostini, Rocco Vertechy, Giovanni Berselli, and Marco Fontana. 2020. "Styrenic-Rubber Dielectric Elastomer Actuator with Inherent Stiffness Compensation" Actuators 9, no. 2: 44. https://doi.org/10.3390/act9020044
APA StyleMoretti, G., Sarina, L., Agostini, L., Vertechy, R., Berselli, G., & Fontana, M. (2020). Styrenic-Rubber Dielectric Elastomer Actuator with Inherent Stiffness Compensation. Actuators, 9(2), 44. https://doi.org/10.3390/act9020044









