Linear-Quadratic Regulator for Control of Multi-Wall Carbon Nanotube/Polydimethylsiloxane Based Conical Dielectric Elastomer Actuators
Abstract
1. Introduction
2. Methods
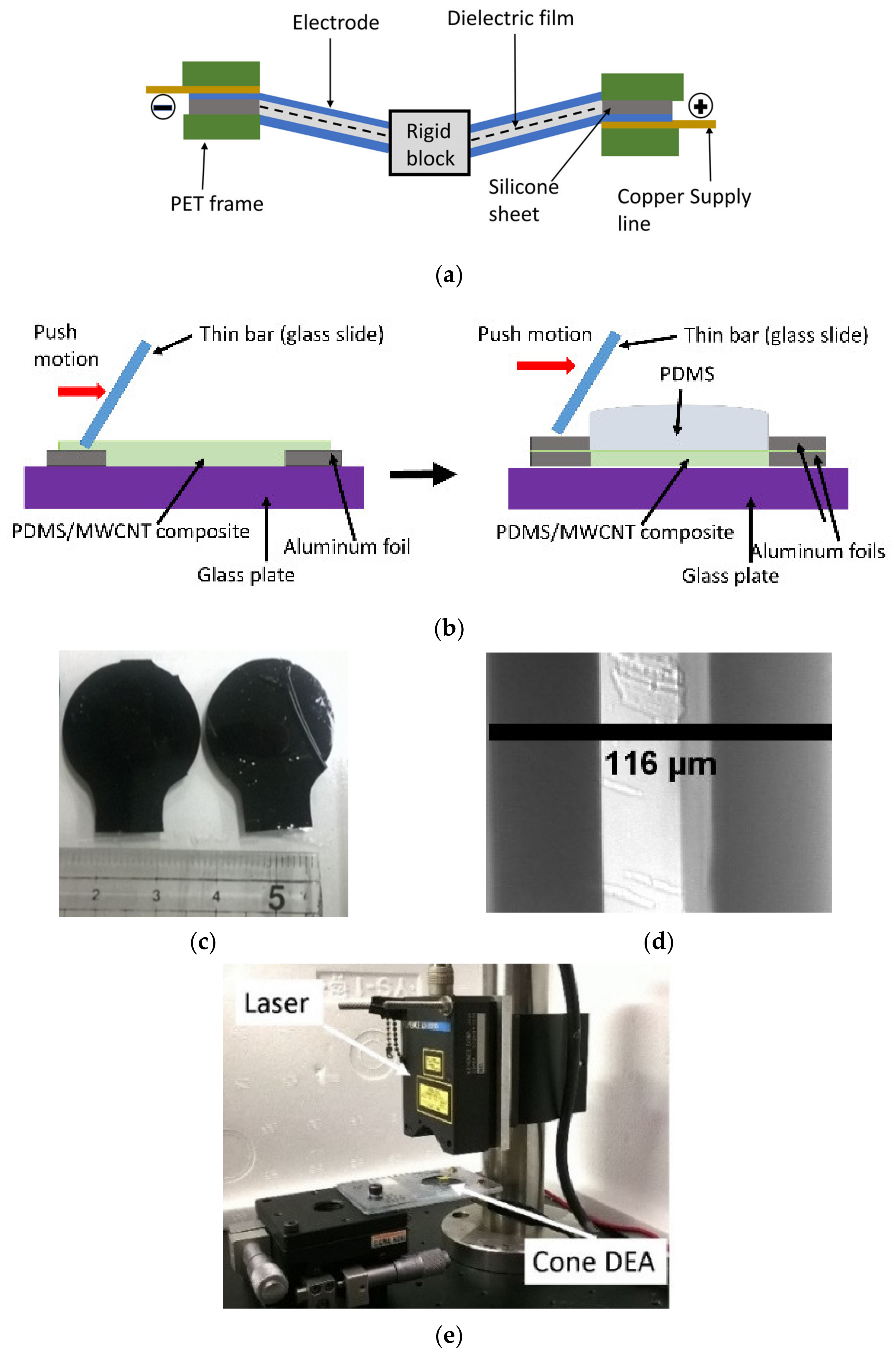
2.1. Development of the Cone DEA
2.1.1. Design of the Cone DEA
2.1.2. Fabrication of Composite for the Electrode
2.1.3. Mold Casting of the Electrode and Dielectric Elastomer Membranes
2.1.4. Assembly of the Cone DEA
2.1.5. Mounting the Cone DEA for Testing and Experimental Phenomenon
2.2. Modeling of the Cone DEA
- Poles: 100 × (−0.1968 + 2.5363i, −0.1968 − 2.5363i, −1.3406 + 0.0000i, −0.0406 + 0.0000i, −0.0023 + 0.0000i)
- Zeros: −266.8760, −4.8979, −0.2762
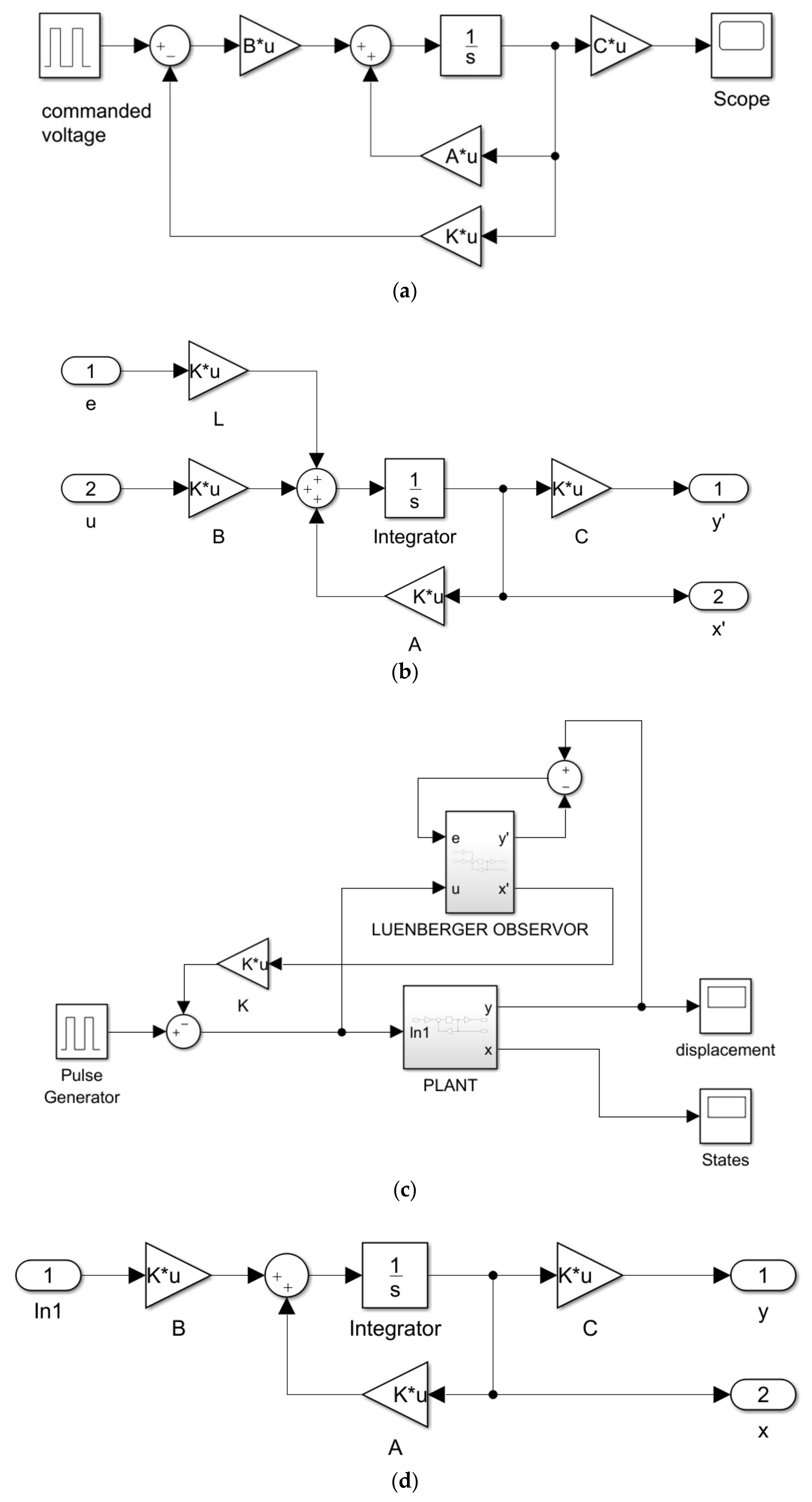
2.3. LQR Controller Design
2.3.1. Basic LQR Controller
2.3.2. Luenberger Observer Design
2.3.3. LQR Controller Augmented with the Luenberger Observer
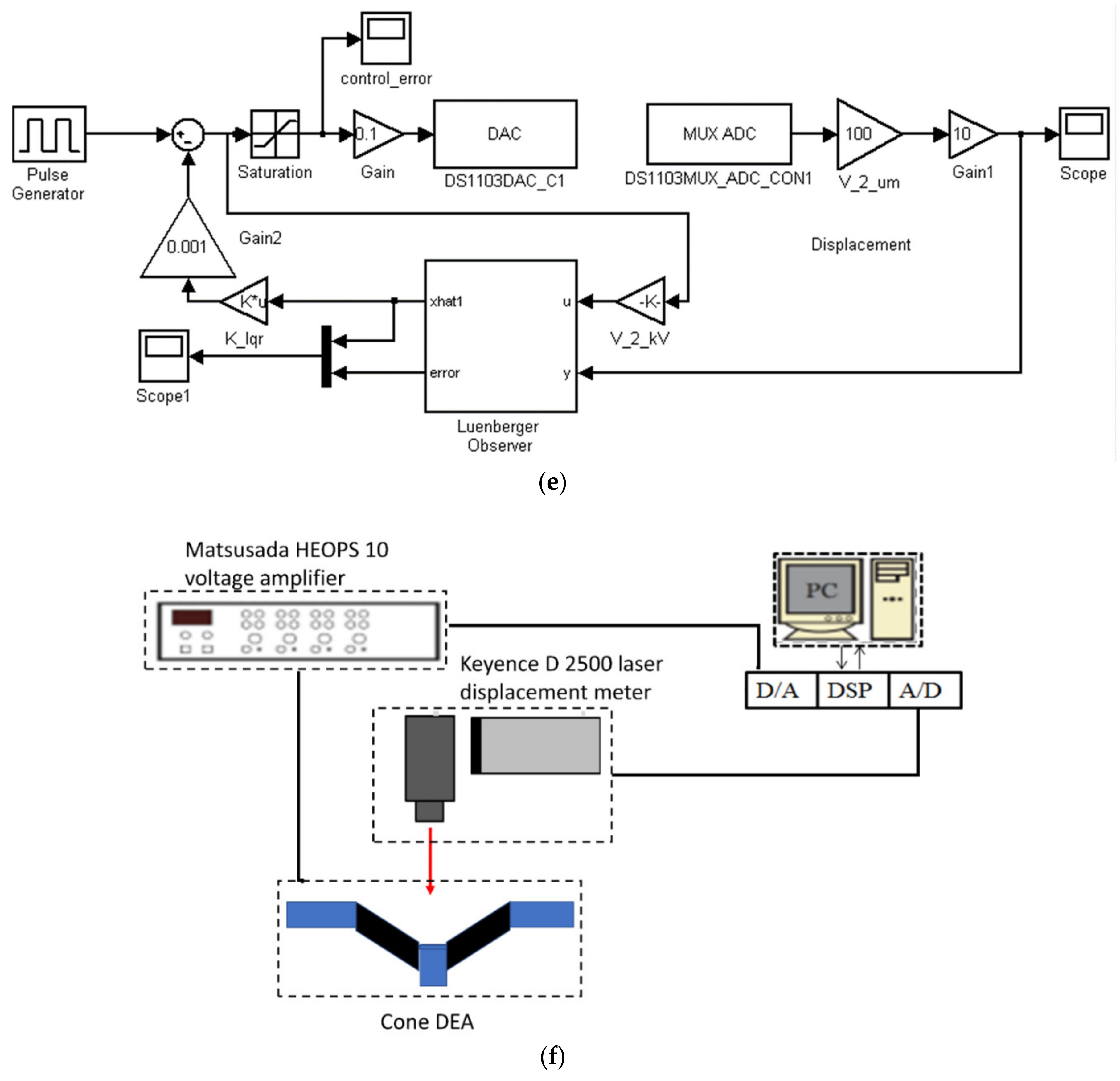
2.3.4. Experimental Implementation of the LQR Controller with Luenberger Observer
3. Results and Discussion
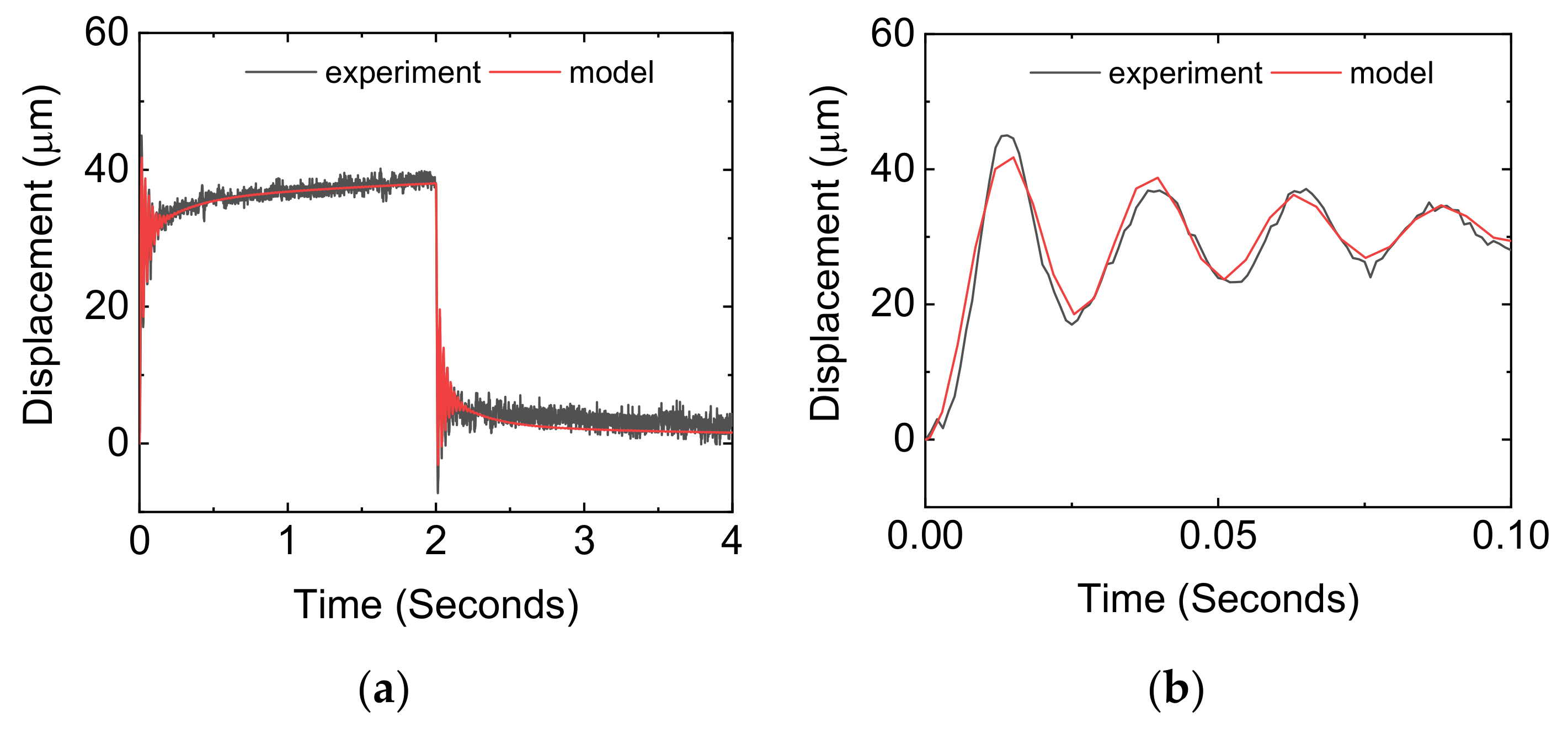
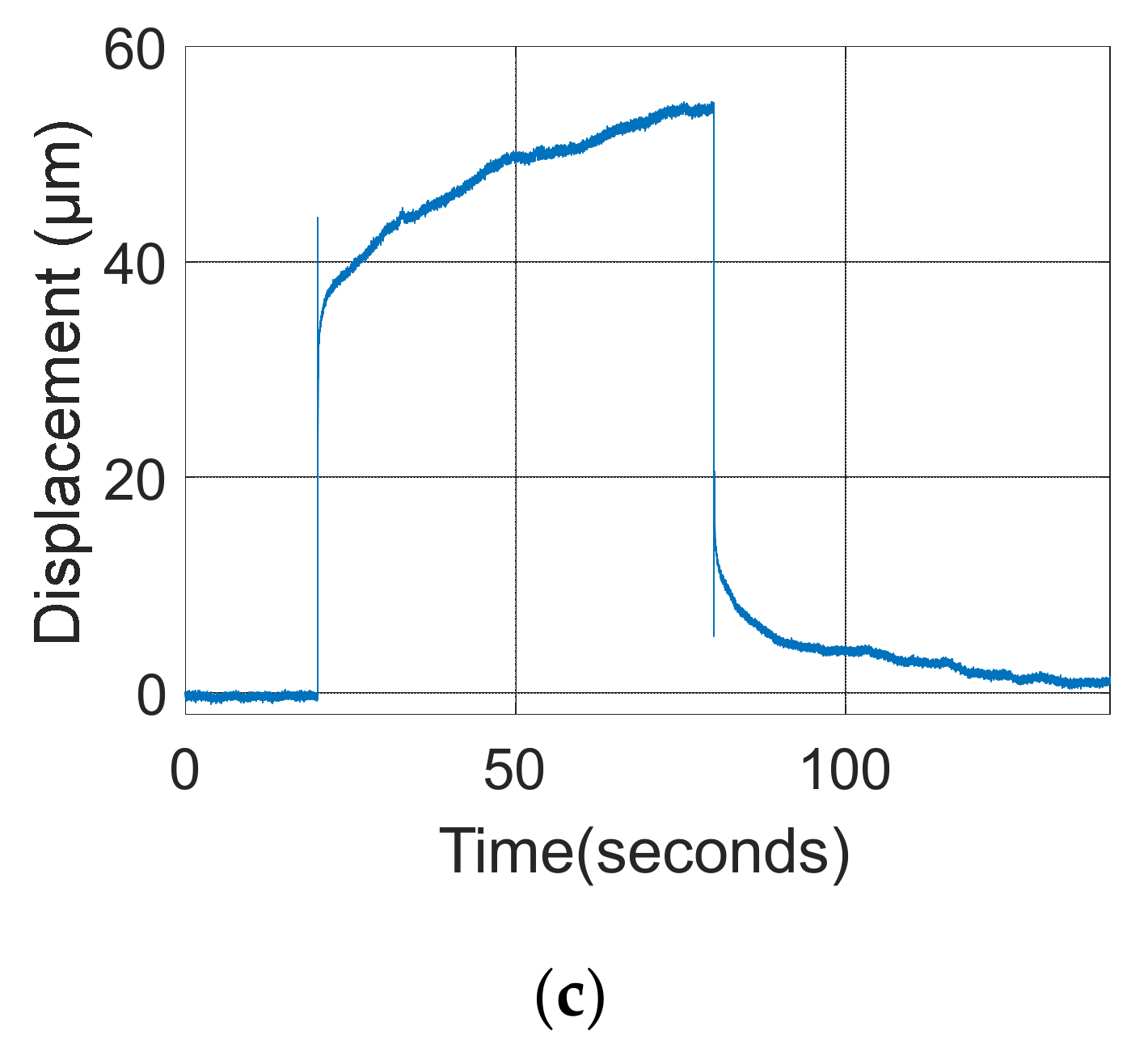
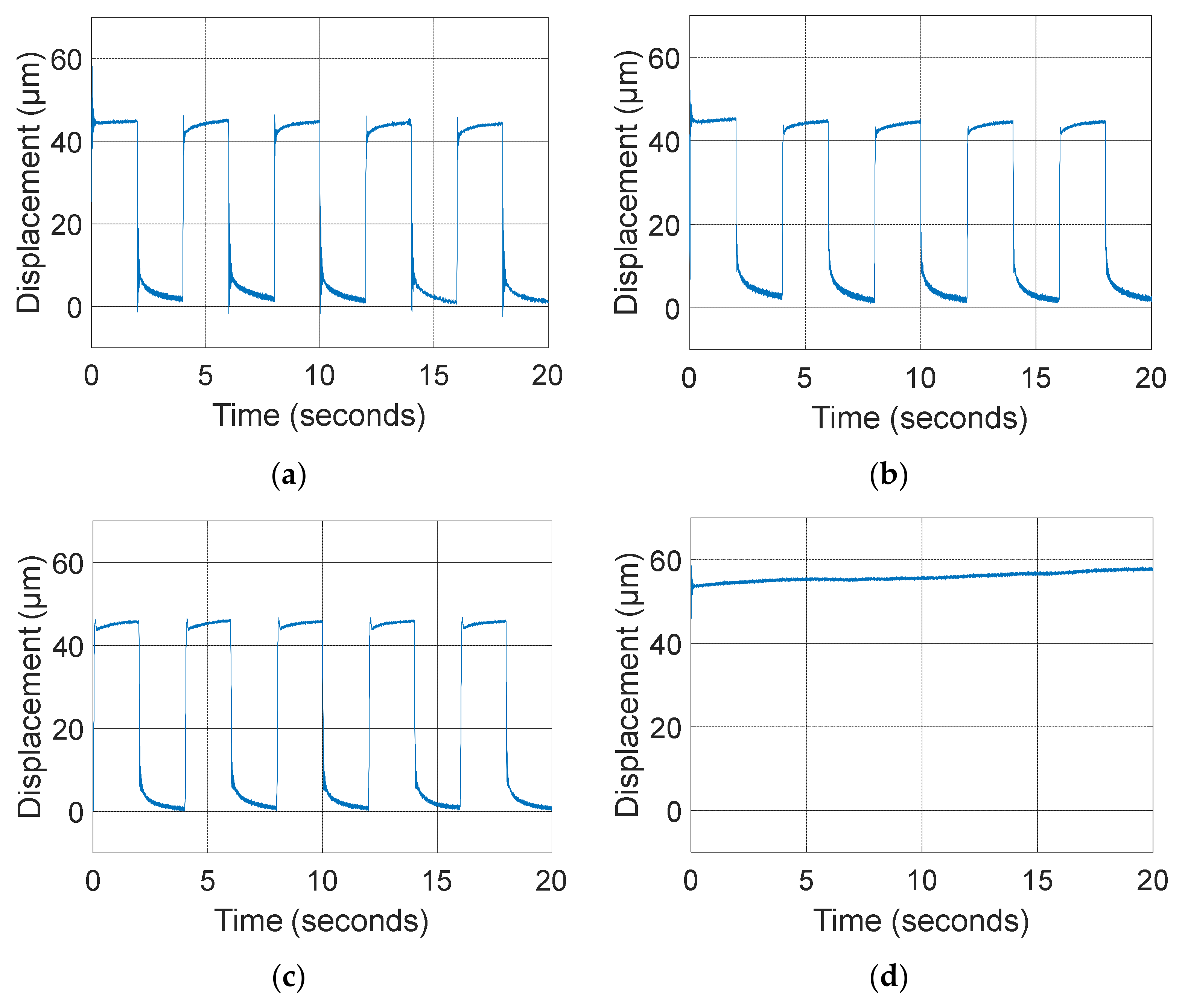
3.1. Model Validation, Overshoot Criteria, and Viscoelastic Phenomenon
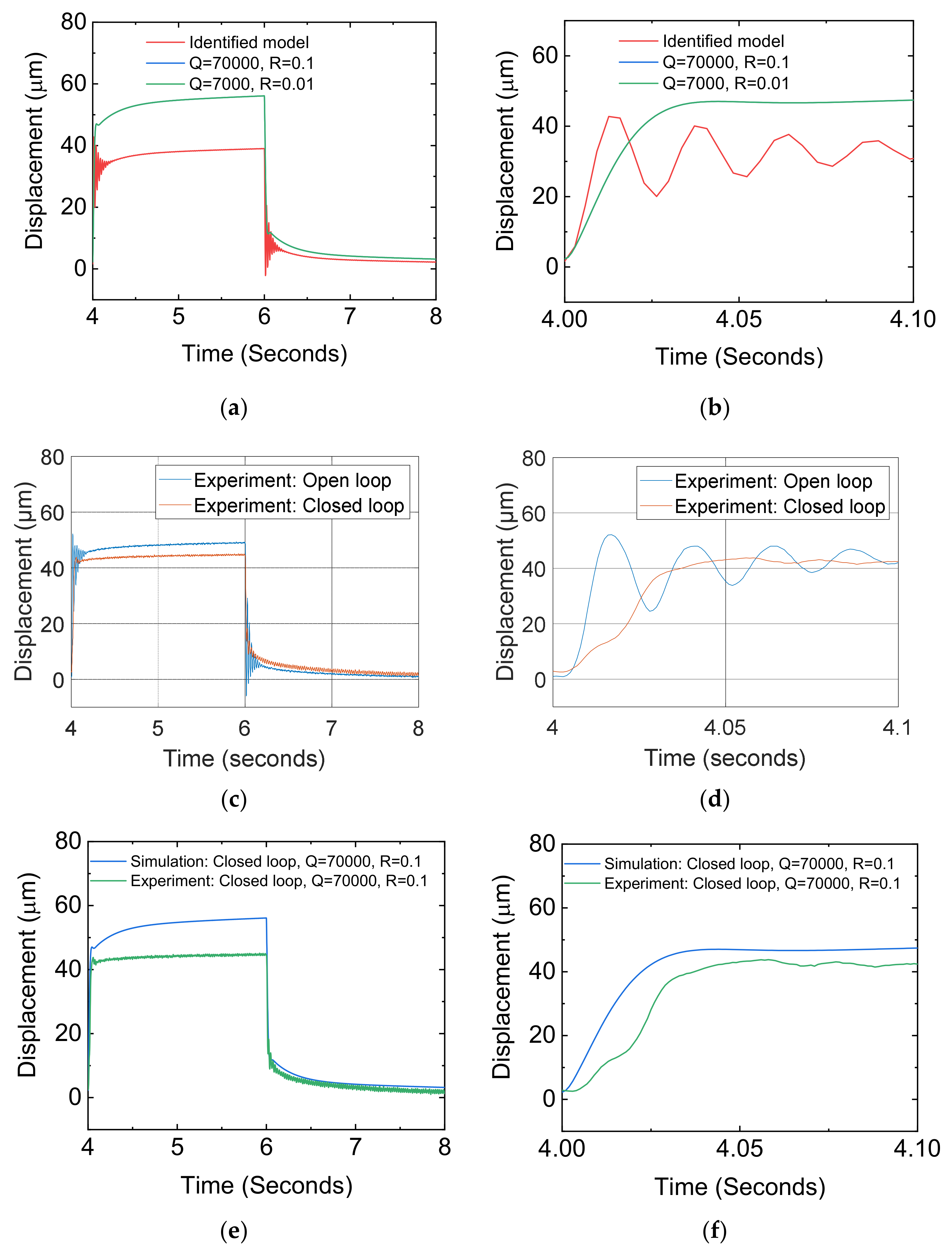
3.2. Simulation Results
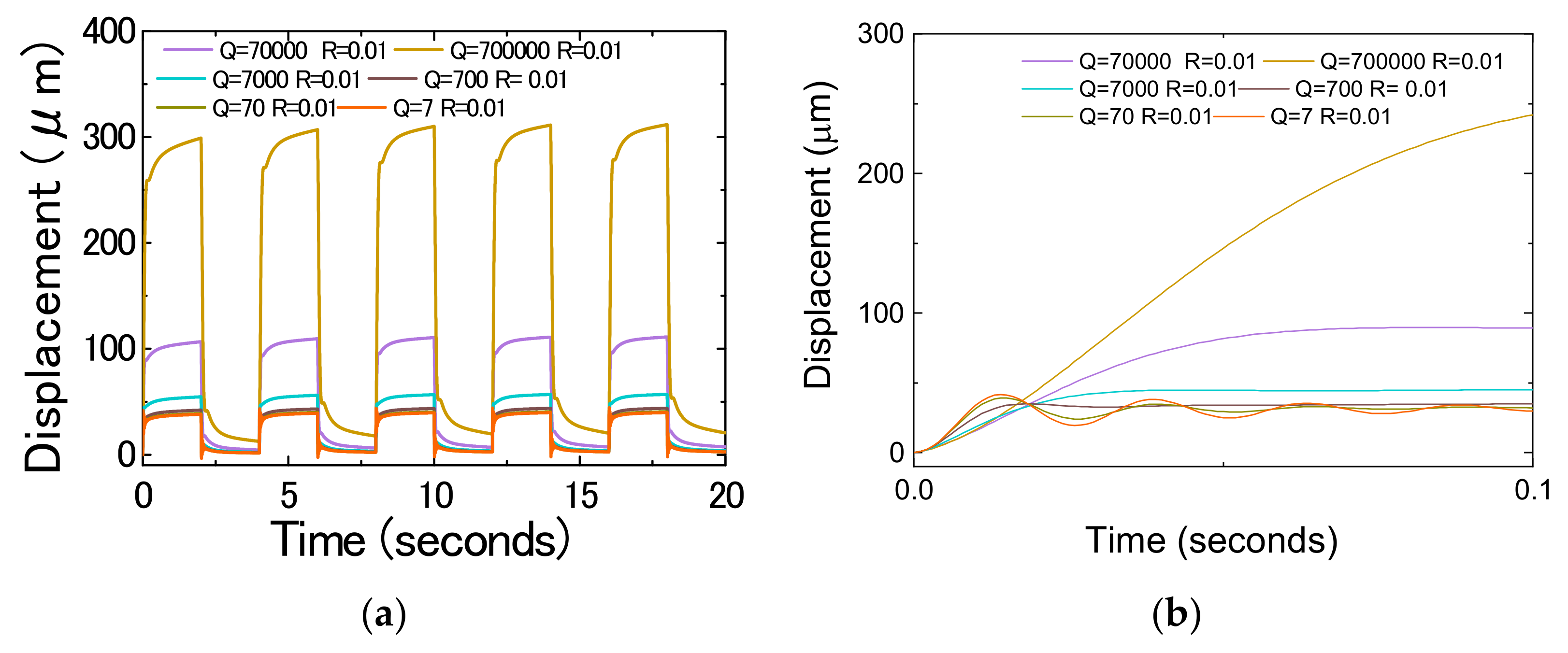
3.2.1. Effect of Varying Q
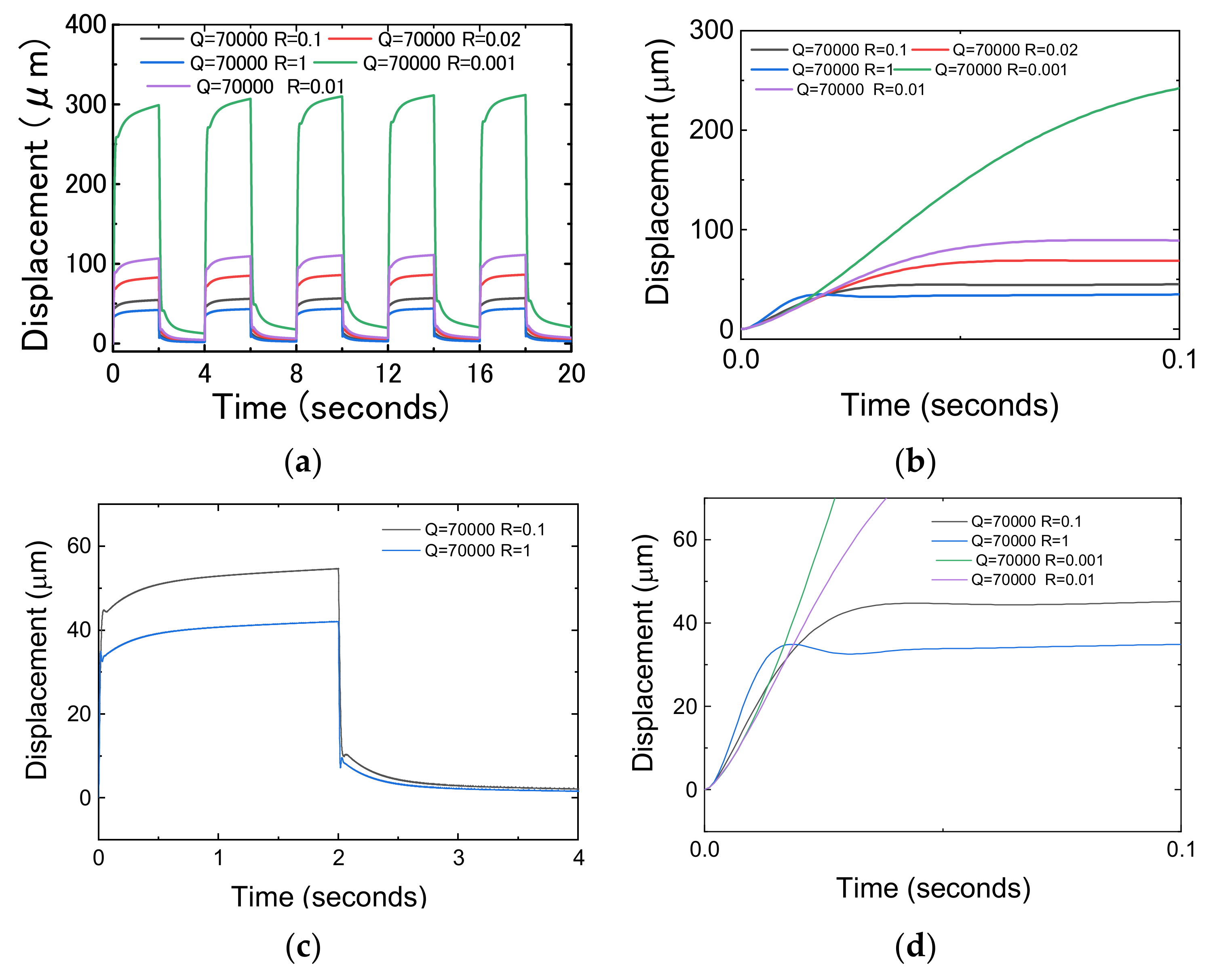
3.2.2. Effect of Varying R
3.3. Experimental Results
3.3.1. Effect of Varying Q
3.3.2. Effect of Varying R
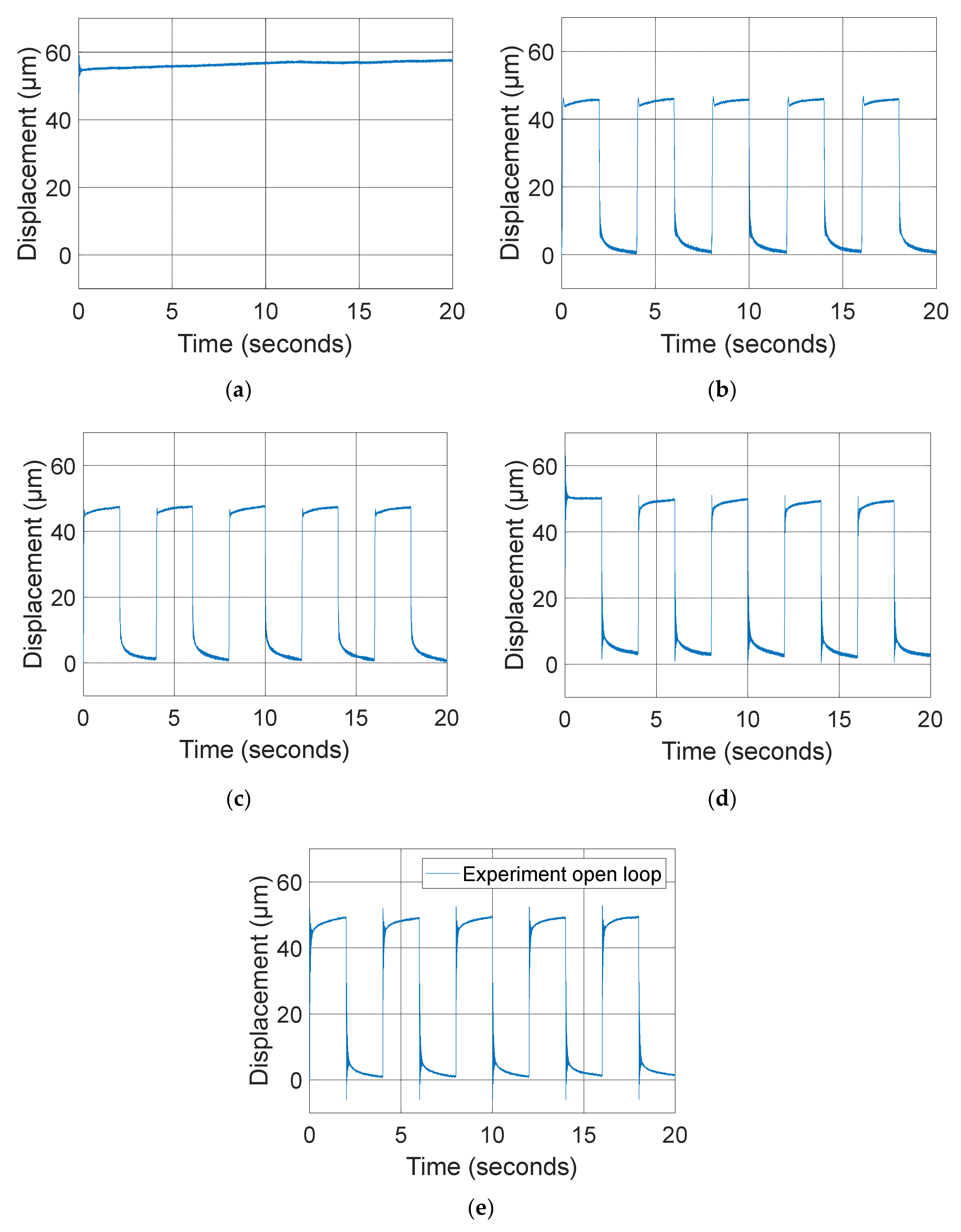
3.4. Comparison of Open-Loop and Closed-Loop Performance
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gu, G.Y.; Zhu, J.; Zhu, L.M.; Zhu, X. A survey on dielectric elastomer actuators for soft robots. Bioinspir. Biomim. 2017, 12, 011003. [Google Scholar] [CrossRef] [PubMed]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Carpi, F.; Anderson, I.; Bauer, S.; Frediani, G.; Gallone, G.; Gei, M.; Graaf, C.; Jean-Mistral, C.; Kaal, W.; Kofod, G.; et al. Standards for dielectric elastomer transducers. Smart Mater. Struct. 2015, 24, 105025. [Google Scholar] [CrossRef]
- Chen, B.; Kollosche, M.; Stewart, M.; Busfield, J.; Carpi, F. Electrical breakdown of dielectric elastomers: Influence of compression, electrode’s curvature and environmental humidity. In Electroactive Polymer Actuators and Devices (EAPAD) 2016; International Society for Optics and Photonics: Washington, DC, USA, 2016; Volume 9798, pp. 1–10. [Google Scholar]
- Carpi, F.; De Rossi, D.; Kornbluh, R.; Pelrine, R.E.; Sommer-Larsen, P. Dielectric Elastomers as Electromechanical Transducers: Fundamentals, Materials, Devices, Models and Applications of an Emerging Electroactive Polymer Technology; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 0080557724. [Google Scholar]
- Poulin, A.; Rosset, S.; Shea, H.R. Printing low-voltage dielectric elastomer actuators. Appl. Phys. Lett. 2015, 107, 244104. [Google Scholar] [CrossRef]
- Rosset, S.; O’Brien, B.M.; Gisby, T.; Xu, D.; Shea, H.R.; Anderson, I.A. Self-sensing dielectric elastomer actuators in closed-loop operation. Smart Mater. Struct. 2013, 22, 104018. [Google Scholar] [CrossRef]
- Brochu, P.; Pei, Q. Advances in dielectric elastomers for actuators and artificial muscles. Macromol. Rapid Commun. 2010, 31, 10–36. [Google Scholar] [CrossRef]
- Rosset, S.; Shea, H.R. Small, fast, and tough: Shrinking down integrated elastomer transducers. Appl. Phys. Rev. 2016, 3, 31105. [Google Scholar] [CrossRef]
- O’Halloran, A.; O’malley, F.; McHugh, P. A review on dielectric elastomer actuators, technology, applications, and challenges. J. Appl. Phys. 2008, 104, 9. [Google Scholar] [CrossRef]
- Hoffstadt, T.; Maas, J. Self-sensing Algorithms for Dielectric Elastomer Multilayer Stack-Transducers. IFAC Pap. 2016, 49, 373–379. [Google Scholar] [CrossRef]
- Kovacs, G.; Düring, L.; Michel, S.; Terrasi, G. Stacked dielectric elastomer actuator for tensile force transmission. Sens. Actuators A Phys. 2009, 155, 299–307. [Google Scholar] [CrossRef]
- Hau, S.; Rizzello, G.; Seelecke, S. A novel dielectric elastomer membrane actuator concept for high-force applications. Extrem. Mech. Lett. 2018, 23, 24–28. [Google Scholar] [CrossRef]
- Hau, S.; Rizzello, G.; Hodgins, M.; York, A.; Seelecke, S. Design and control of a high-speed positioning system based on dielectric elastomer membrane actuators. IEEE/ASME Trans. Mechatron. 2017, 22, 1259–1267. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; Turchiano, B.; Seelecke, S. Robust Position Control of Dielectric Elastomer Actuators Based on LMI Optimization. IEEE Trans. Control. Syst. Technol. 2016, 24, 1909–1921. [Google Scholar] [CrossRef]
- Hodgins, M.; Rizzello, G.; York, A.; Naso, D.; Seelecke, S. A smart experimental technique for the optimization of dielectric elastomer actuator (DEA) systems. Smart Mater. Struct. 2015, 24, 094002. [Google Scholar] [CrossRef]
- Rizzello, G.; Fugaro, F.; Naso, D.; Seelecke, S. Simultaneous Self-Sensing of Displacement and Force for Soft Dielectric Elastomer Actuators. IEEE Robot. Autom. Lett. 2018, 3, 1230–1236. [Google Scholar] [CrossRef]
- Fasolt, B.; Hodgins, M.; Rizzello, G.; Seelecke, S. Effect of screen printing parameters on sensor and actuator performance of dielectric elastomer (DE) membranes. Sens. Actuators A Phys. 2017, 265, 10–19. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; Seelecke, S. A Nonlinear Electro-Mechanical Model for an Annular Dielectric Elastomer Actuator with a Biasing Mass. VDI Tag. Mechatronik 2013, 117–122. [Google Scholar]
- Hodgins, M.; Rizzello, G.; Naso, D.; York, A.; Seelecke, S. An electro-mechanically coupled model for the dynamic behavior of a dielectric electro-active polymer actuator. Smart Mater. Struct. 2014, 23, 104006. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. Model. Based PID Control of a Dielectric Electro-Active Polymer Positioning System; IFAC: Geneva, Switzerland, 2014; Volume 19, ISBN 9783902823625. [Google Scholar]
- Fadel, M.; Carriere, S.; Caux, S. Optimal LQI synthesis for speed control of synchronous actuator under load inertia variations. IFAC Proc. Vol. 2008, 17, 5831–5836. [Google Scholar]
- Mallavarapu, K.; Leo, D.J. Feedback control of resonant modes in bending response of ionic polymer actuators. Am. Soc. Mech. Eng. 2001, 64, 283–292. [Google Scholar]
- Zou, J.; Gu, G.Y.; Zhu, L.M. Open-loop control of creep and vibration in dielectric elastomer actuators with phenomenological models. IEEE/ASME Trans. Mechatron. 2017, 22, 51–58. [Google Scholar] [CrossRef]
- Zou, J.; Gu, G. High-precision tracking control of a soft dielectric elastomer actuator with inverse viscoelastic hysteresis compensation. IEEE/ASME Trans. Mechatron. 2019, 24, 36–44. [Google Scholar] [CrossRef]
- Zou, J.; Gu, G. Modeling the viscoelastic hysteresis of dielectric elastomer actuators with a modified rate-dependent Prandtl-Ishlinskii model. Polymers 2018, 10, 525. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.Y.; Gupta, U.; Zhu, J.; Zhu, L.M.; Zhu, X. Modeling of Viscoelastic Electromechanical Behavior in a Soft Dielectric Elastomer Actuator. IEEE Trans. Robot. 2017, 33, 1263–1271. [Google Scholar] [CrossRef]
- Branz, F.; Francesconi, A. Modelling and control of double-cone dielectric elastomer actuator. Smart Mater. Struct. 2016, 25, 95040. [Google Scholar] [CrossRef]
- Meng, L.; Bao, W.; Li, F.; Li, H. Hysteresis compensation control of a dielectric elastomer vibration isolator. J. Low Freq. Noise Vib. Act. Control. 2019. [Google Scholar] [CrossRef]
- Jones, R.W.; Sarban, R. Model validation and feedback controller design for a dielectric elastomer actuator. J. Intell. Mater. Syst. Struct. 2016, 27, 2078–2090. [Google Scholar] [CrossRef]
- Khosla, A.; Gray, B.L. Preparation, characterization and micromolding of multi-walled carbon nanotube polydimethylsiloxane conducting nanocomposite polymer. Mater. Lett. 2009, 63, 1203–1206. [Google Scholar] [CrossRef]
- Mulembo, T.; Nagai, G.; Tamagawa, H.; Nitta, T.; Sasaki, M. Conductive and flexible multi-walled carbon nanotube/polydimethylsiloxane composites made with naphthalene/toluene mixture. J. Appl. Polym. Sci. 2019, 136, 48167. [Google Scholar] [CrossRef]
- Bauman, J.T.; Bauman, J.T. Fatigue, Stress, and Strain of Rubber Components; Carl Hanser Verlag GmbH Co KG: Munich, Germany, 2012; ISBN 3446433406. [Google Scholar]
| Notation | Full Name |
|---|---|
| PDMS | Polydimethylsiloxane |
| DEA | Dielectric elastomer actuator |
| LQR | Linear quadratic regulator |
| PID | Proportional Integral Derivative |
| DC | Direct current |
| VHB | Very high bond |
| MWCNT | Multi wall carbon nanotube |
| PET | Polyethylene |
| DAC or D/A | Digital to analog converter |
| ADC or A/D | Analog to digital converter |
| Poles | Zeros | Estimation Fit % | Validation Fit % |
|---|---|---|---|
| 1 | 0 | 79.16 | 74.20 |
| 2 | 0 | 89.29 | 87.54 |
| 2 | 1 | 82.65 | 76.76 |
| 3 | 1 | 91.59 | 88.99 |
| 3 | 2 | 91.96 | 89.32 |
| 4 | 0 | −0.37 | 3.97 |
| 4 | 1 | 92.37 | 89.77 |
| 4 | 2 | 93.42 | 91.40 |
| 4 | 3 | 93.70 | 91.86 |
| 5 | 0 | 17.40 | 15.97 |
| 5 | 1 | 66.39 | 66.34 |
| 5 | 2 | 93.82 | 92.48 |
| 5 | 3 | 94.05 | 93.49 |
| 5 | 4 | 94.08 | 93.70 |
| 6 | 0 | −2.96 | −1.46 |
| 6 | 1 | −76.23 | −69.55 |
| 6 | 2 | 28.14 | 28.63 |
| 6 | 3 | 94.09 | 93.92 |
| 6 | 4 | 93.89 | 93.18 |
| 6 | 5 | 94.06 | 93.96 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulembo, T.; Njeri, W.; Nagai, G.; Tamagawa, H.; Naito, K.; Nitta, T.; Sasaki, M. Linear-Quadratic Regulator for Control of Multi-Wall Carbon Nanotube/Polydimethylsiloxane Based Conical Dielectric Elastomer Actuators. Actuators 2020, 9, 18. https://doi.org/10.3390/act9010018
Mulembo T, Njeri W, Nagai G, Tamagawa H, Naito K, Nitta T, Sasaki M. Linear-Quadratic Regulator for Control of Multi-Wall Carbon Nanotube/Polydimethylsiloxane Based Conical Dielectric Elastomer Actuators. Actuators. 2020; 9(1):18. https://doi.org/10.3390/act9010018
Chicago/Turabian StyleMulembo, Titus, Waweru Njeri, Gakuji Nagai, Hirohisa Tamagawa, Keishi Naito, Takahiro Nitta, and Minoru Sasaki. 2020. "Linear-Quadratic Regulator for Control of Multi-Wall Carbon Nanotube/Polydimethylsiloxane Based Conical Dielectric Elastomer Actuators" Actuators 9, no. 1: 18. https://doi.org/10.3390/act9010018
APA StyleMulembo, T., Njeri, W., Nagai, G., Tamagawa, H., Naito, K., Nitta, T., & Sasaki, M. (2020). Linear-Quadratic Regulator for Control of Multi-Wall Carbon Nanotube/Polydimethylsiloxane Based Conical Dielectric Elastomer Actuators. Actuators, 9(1), 18. https://doi.org/10.3390/act9010018





