Interval Analysis of the Eigenvalues of Closed-Loop Control Systems with Uncertain Parameters
Abstract
1. Introduction
2. Fundamental Equations for the Interval Analysis of Intelligent Structures
2.1. Finite Element Equations for Uncertain Systems
2.2. Interval Mass Matrix, Interval Damping Matrix, and Interval Stiffness Matrix
2.3. State Equation of the Uncertain System with/without Feedback Control
3. Optimization of Actuator Position in Vibration Control of Intelligent Structure
3.1. The Measure of the Modal Controllability of Intelligent Structures
3.2. Singular Value Element Sensitivity of Modal Control Matrix
3.3. Control Position Optimization Criteria
4. The Recursive Design Method of Multi-Input Modal Controller
4.1. Required Control Force Calculation Based on the Receptance Method
4.2. Optimal Number and Location of Actuators When the Actual Control Force Is Smaller than the Required Control Force
- If , one actuator can provide the feedback gain required by the controlled structure in excess;
- If , one actuator just provides the feedback gain required by the controlled structure;
- If , the single-input control cannot make the structure fully controllable and multiple actuators are needed to provide sufficient feedback gain to make the structure fully controllable.
5. Interval Analysis of the Robustness of Closed-Loop Systems
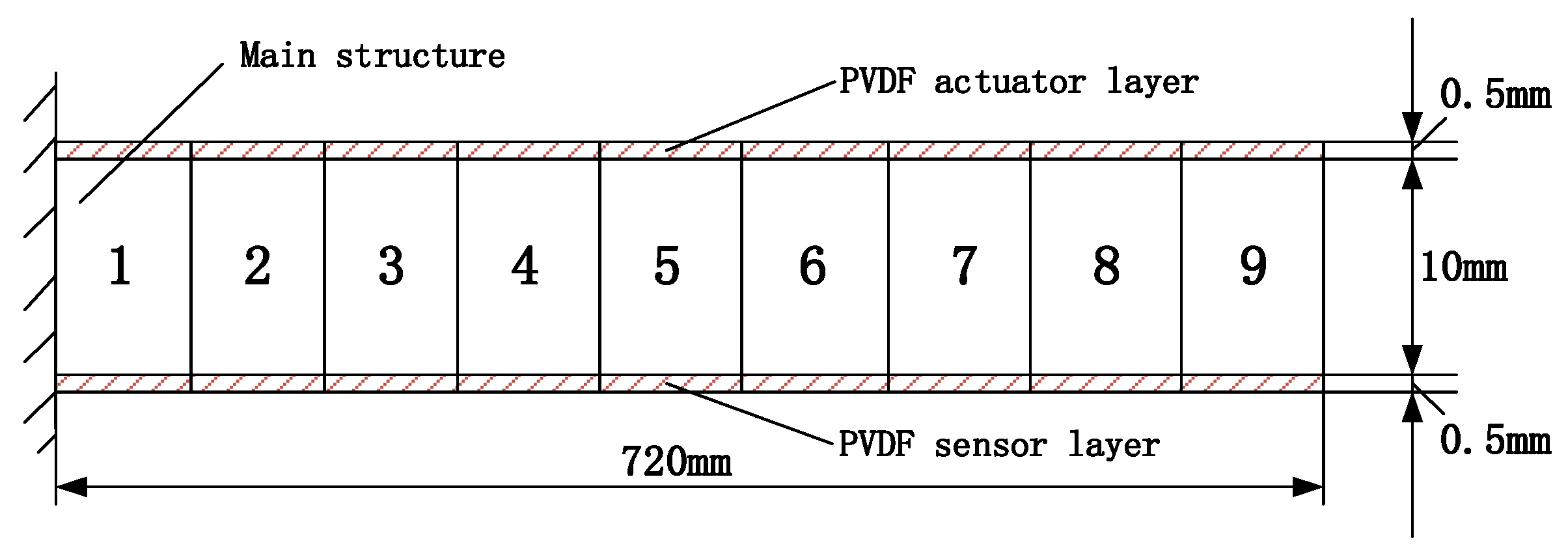
6. Numerical Example
- 1.
- The calculation of the optimal position of the control force that controls the first-order mode under the condition of realizable control.
- 2.
- The optimal number and location of actuators.
- The first step:
- The second step:
- The third step:
- 3.
- The effect of uncertain parameters on eigenvalues of the closed-loop control system.
7. Conclusions
- This paper discusses the measurement of modal controllability of intelligent structures, deduces a control matrix singular value sensitivity formula, and determines the optimal position of piezoelectric actuators for an intelligent structure. In a numerical example, when the sizes of the actuators are exactly the same and the displacement feedback gains are exactly the same, it is very important to select the location of actuators in a structural vibration control;
- When a single actuator is applied, the feedback gain matrix is calculated using the receptance method, and the ideal control force of actuator is calculated. When the control force required for complete controllability of the structure is much higher than the actual force of the actuator, a single-input control cannot fully control the structure, and a multi-input control is needed for the purpose of vibration control. The recursive design method of a modal controller is introduced to study the optimal number and location of the actuators;
- The change rate of eigenvalues of a closed-loop control system increases with the increase in the uncertain parameters. Uncertain parameters are expressed as intervals. A method is proposed to solve the upper and lower bounds of the eigenvalues of a closed-loop control system with uncertain parameters using perturbation theory and interval analysis and is illustrated with a numerical example.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, Y.K. Probabilistic Theory of Structural Dynamics; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Dief, A.S. Sensitivity Analysis in Linear Systems; Springer: Berlin, Germany, 1986. [Google Scholar]
- Lindberg, H.E. Dynamic response and buckling failure measures for structures with bounded and random imperfections. Trans. ASME J. Appl. Mech. 1991, 58, 1092–1094. [Google Scholar] [CrossRef]
- Ganzerli, S.; Pantelides, C.P. Load and resistance convex models for optimum design. Struct. Optim. 1999, 17, 259–268. [Google Scholar] [CrossRef]
- Moore, R.E. Methods and Applications of Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1979. [Google Scholar]
- Dessombz, O.; Thouverez, F.; Laine, J.P.; Jezequal, L. Analysis of mechanical system using interval computations applied to finite element methods. J. Sound Vibr. 2001, 239, 949–968. [Google Scholar] [CrossRef]
- Mori, T.; Kokame, H. Convergence property of interval matrices and interval polynomials. Int. J. Contr. 1987, 45, 481–484. [Google Scholar] [CrossRef]
- Rachid, A. Robustness of discrete systems under structural uncertainties. Int. J. Contr. 1989, 50, 1563–1566. [Google Scholar] [CrossRef]
- Wonham, W.M. On pole assignment in multi-input controllable linear system. IEEE Trans. Autom. Control 1967, 12, 660–665. [Google Scholar] [CrossRef]
- Datta, B.N.; Elhay, S.; Ram, Y.M. Orthogonality and partial pole assignment for the symmetric difinite quadratic pencil. Linear Algebra Its Appl. 1997, 257, 29–48. [Google Scholar] [CrossRef]
- Duan, G.R. Parametric eigenstructure assigment in second-order descriptor linear systems. IEEE Trans. Autom. Control 2004, 49, 1789–1795. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Ram, Y.M. Receptance method in active vibration control. AIAA J. 2007, 3, 562–567. [Google Scholar]
- Ram, Y.M.; Mottershead, J.E. Multiple-input active vibration control by partial pole placement using the method of receptances. Mech. Syst. Signal Process. 2013, 40, 727–735. [Google Scholar] [CrossRef]
- Mokrani, B.; Palazzo, F.; Mottershead, J.E.; Fichera, S. Multiple-input multiple-output experimental aeroelastic control using a receptance-based method. AIAA J. 2019, 7, 3066–3077. [Google Scholar] [CrossRef]
- Tsai, S.H.; Ouyang, H.; Chang, J.Y. Identification of torsional receptances. Mech. Syst. Signal Process. 2019, 126, 116–136. [Google Scholar] [CrossRef]
- Gao, X. Research on Theory and Algorithm of Local Vibration Control of Structure. Ph.D. Thesis, Jilin University, Changchun, China, 2009. [Google Scholar]
- Chen, S.; Cao, Z. A new method for determining locations of the piezoelectric Sensor/Actuator for vibration control of intelligent structures. J. Intell. Mater. Syst. Struct. 2000, 11, 108–115. [Google Scholar] [CrossRef]
- Lim, T.W. Actuator/sensor placement for modal parameter identification of flexible structures. Modal Anal. Int. J. Anal. Exp. Modal Anal. 1993, 1, 1–13. [Google Scholar]
- Schulz, G.; Heimbold, G. Dislocated actuator/sensor positioning and feedback design for flexible Structures. J. Guid. Control. Dyn. 1982, 6, 361–367. [Google Scholar] [CrossRef]
- Rao, S.S.; Pan, T. Optimal placement of actuators in actively controlled structures using genetic algorithm. AIAA J. 1991, 5, 942–943. [Google Scholar] [CrossRef]
- Levine, W.S.; Athans, M. On the determination of the constant output feedback gains for linear multivariable systems. Trans. Autom. Control 1970, 15, 44–48. [Google Scholar] [CrossRef]
- Kang, Y.K.; Park, H.C.; Hwang, W.; Han, K.S. Optimum placement of piezoelectric sensor/actuator for vibration control of laminated beams. AIAA J. 1996, 9, 1921–1926. [Google Scholar] [CrossRef]
- Choe, K.; Baruh, H. Actuator placement in structural control. J. Guid. Control Dyn. 1991, 1, 40–46. [Google Scholar] [CrossRef]
- Baruh, H.; Merovitch, L. On the placement of actuators in the control of distributed-parameter systems. AIAA J. 1981, 611–618. [Google Scholar] [CrossRef]
- Chen, S.H. Matrix Perturbation Theory in Structural Dynamics; Science Press: Beijing, China, 2007. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; Butterwort-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Craig, R.R. Structural Dynamics: An Introduction to Computer Methods; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Rong, B.; Rui, X.; Lu, K.; Tao, L.; Wang, G.; Ni, X. Transfer matrix method for dynamics modeling and independent modal space vibration control design of linear hybrid multibody system. Mech. Syst. Signal Process. 2018, 104, 589–606. [Google Scholar] [CrossRef]
- Neto, M.A.; Ambrósio, J.A.C.; Roseiro, L.M.; Amaro, A.; Vasques, C.M.A. Active vibration control of spatial flexible multibody systems. Multibody Syst. Dyn. 2013, 30, 13–35. [Google Scholar] [CrossRef]
- Tzou, H.S.; Tseng, C.I. Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter system: A piezoelectric finite element approach. J. Sound Vib. 1990, 138, 17–34. [Google Scholar] [CrossRef]
- Preumont, A. Mechatronics Dynamics of Electromechnical and Piezoelectric Systems; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Mokrani, B.; Batou, A. The minimum norm multi-input multi-output receptance method for partial pole placement. J. MSSP 2019, 129, 437–448. [Google Scholar] [CrossRef]
- Yao, G.; Gao, X. Controllability of regular systems and defective systems with repeated eigenvalues. J. Vib. Control. 2010, 17, 1574–1581. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.-Z.; Yao, G.-F.; Liu, R.-Y.; Zhu, Y.-C.; Gao, K.-Y.; Wang, M. Interval Analysis of the Eigenvalues of Closed-Loop Control Systems with Uncertain Parameters. Actuators 2020, 9, 31. https://doi.org/10.3390/act9020031
Zhao J-Z, Yao G-F, Liu R-Y, Zhu Y-C, Gao K-Y, Wang M. Interval Analysis of the Eigenvalues of Closed-Loop Control Systems with Uncertain Parameters. Actuators. 2020; 9(2):31. https://doi.org/10.3390/act9020031
Chicago/Turabian StyleZhao, Jing-Zhou, Guo-Feng Yao, Rui-Yao Liu, Yuan-Cheng Zhu, Kui-Yang Gao, and Min Wang. 2020. "Interval Analysis of the Eigenvalues of Closed-Loop Control Systems with Uncertain Parameters" Actuators 9, no. 2: 31. https://doi.org/10.3390/act9020031
APA StyleZhao, J.-Z., Yao, G.-F., Liu, R.-Y., Zhu, Y.-C., Gao, K.-Y., & Wang, M. (2020). Interval Analysis of the Eigenvalues of Closed-Loop Control Systems with Uncertain Parameters. Actuators, 9(2), 31. https://doi.org/10.3390/act9020031




