1. Introduction
The emergence of semiconductor technology has provided a field for a wide range of research works and industrial practices for the development of Micro Electro Mechanical Systems (MEMS). More sophisticated issues on design, fabrication, simulation, packaging, and testing has appeared since. Since the mid-1970s, MEMS technology has contributed innovative prospects for basic science and engineering studies [
1,
2,
3,
4]. Although MEMS fabrication processes are generally similar to microelectronic Integrated Circuits (ICs), their characterization methods are completely different [
4], because there are various stimuli that affect the functions of MEMS devices such as physio-chemical, biological, optical, etc. During manufacturing processes, generally, MEMS devices are tested in different phases. To ensure the performance of the device and verify the functionalities of some components, a testing process is crucial. ATE (Automatic Test Equipment) [
5,
6,
7] is frequently used for alternative current (AC) and direct current (DC) testing parameters (e.g., accelerometers, microphones, micromirrors, etc.) to get to know the Known Good Die (KGD) under fabrication on a wafer to reduce higher costs of testing at packaging level [
5,
6]. MEMS devices are not entered into the market without being tested and characterized. To do functional testing at the final stage and die level, it is important to design a calibration datasheet for a specific component of the sensor during the product development phase [
8,
9,
10]. During these stages, a known physical or electrical stimulus is applied to the sensor, and the output results are compared with standard safe-mode-working sensor calibration information; therefore, the non-functional sensor will be selected and separated from the rest. The MEMS testing industry is interested in moving the testing procedure from final product packaging state to early wafer level to significantly reduce costs.
From an economic perspective, in MEMS device mass-production procedures, testing is a vital stage that consumes a staggering sum of money. For this reason, many studies have focused on cost prediction and, more importantly, cost reduction. In a recent study [
8,
9] related to micromirrors fabrication (voltage-controllable deflectable MEMS-based tiny mirrors for video projection applications), the overall testing cost for this MEMS device was estimated to be 25–35% of the overall cost. For the cost of wafer-level testing and final packaged micromirrors, a cost of 8% and 14% was reported by Texas Instruments [
10]. Also, in reports from MEPTEC (MicroElectronics Packaging and Testing Engineering Council) and MEMS Industry Group (MIG) on MEMS test cost estimation, a cost of 20–45% and up to 50% was analyzed respectively in general MEMS devices [
11,
12,
13,
14].
Due to the effects of testing methods on the final cost, it is vital to design novel methods and optimize current processes of testing to minimize the corresponding cost as far as possible. To do so, it is necessary to enhance the test efficacy by testing numerous DUTs (device under test) in parallel [
8,
9,
10,
11,
12,
13,
14,
15]. MEMS device testing methods target specific sorts of failures that can occur during the fabrication and packaging processes, or after being released into the market. Some MEMS devices do not have any movable devices, such as gas sensors, DNA sequencers, chemical biosensors, etc., where the main source of failure has been reported to be particle contaminations that cause short circuits associated with mechanical testing methods. There are MEMS devices that do not have movable parts such as microcantilevers, but there are frictions between components such as relays, thermal actuators, etc. Debris is created when MEMS working components slide on each other, which is the main source of device failure [
15]. The only categories of MEMS devices targeted in this study are inertial sensors, pressure sensors, and microcantilever-based sensors, which contain at least one movable and elastic part as sensing element. This sector of MEMS products, according to recent MEMS market analysis, [
16], will have a 20 B
$ market size in 2021. Most of this market will be mechanical sensors such as accelerometers, gyroscopes, pressure sensors, micromirrors, Radio Frequesncy (RF) MEMS, oscillators, etc. This huge market needs formidable manufacturing processes on the one hand, and on the other, needs more economical and high-throughput testing equipment [
15,
16]. MEMS devices are becoming more complex, and instead of bearing one axis, they are relying on three axes to be adapted to multiple applications in a single chip. This situation significantly complicates the testing mechanism and decreases the throughput, which is not appropriate for this huge market in the near future [
15].
MEMS accelerometers, for instance, which work based on comb drive microcantilevers, are attractive in various sectors of industries, from automobiles to healthcare [
17]. Their causes of failure have been reported as fracture, fatigue, mechanical wear, charging, and change in friction forces [
15,
18]. The reliability test for MEMS accelerometers includes lifetime analysis, fatigue and creep, and so on, which are too complex to be tested on the production line. Therefore, these MEMS devices need a specified testing and characterization method. A sophisticated testing line has been established in Sandia National Laboratories (SHiMMeR—Sandia High-Volume Measurement of Micro-Machine Reliability), which is capable of simultaneous control and test of up to 256 MEMS devices, which is a lab test scale [
19]. X-Ray Diffraction (XRD) has been adopted to test the creep of MEMS accelerometers, but is very slow in mass production [
19,
20]. These inefficient methods have motivated more studies in this imperative industry. Along these lines, wafer-level testing has been practiced for reduction of costs [
15], but the problem is that die specification might not be meet by wafer-level testing. Manufacturers and laboratories have become associated with in-house designed testing equipment in the laboratories. For instance, for inertial MEMS characterization, the University of Pisa in Italy has introduced a fully electrical test procedure at the wafer level. The test algorithm runs on a National Instruments PXI-7854R board [
21]. In this testing setup, the electrical stimuli are used for stimulation of sensors and getting feedback [
21].
At the University of Minho in Portugal, a digital platform for wafer-level MEMS testing and characterization, by means of electrical responses, was developed. With electrostatic actuation of the structure’s actuation electrodes, the sensors were tested. After doing actuation, the displacement of the structure was measured by means of variation in capacitance using a charge amplifier [
22]. Electrical stimulation has not always been the case for testers. Sound, light, vibration, fluidics, pressure, and temperature can also be used [
22]. In a different scenario, Freescale Semiconductor Inc. proposed a method for wafer-level tests of MEMS pressure sensors using a pneumatic pressure stimulus applied to the diaphragm via a nozzle outlet [
23]. As we can notice, in all these attempts, the testing platform should be implemented in the sensor itself (such as actuation electrodes).
The last decade has witnessed an admirable surge for the introduction of diverse general characterizing and testing methods for MEMS devices, some of which are shown in
Table 1 [
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41]. These methods are categorized into two main groups: destructive and non-destructive testing approaches. In the test systems, a handler always transfers the stimuli to the die and therefore causes a physical change in the system. All the handler and ATE systems for accelerometers, gyroscopes, flow sensors, and microphones are introduced and discussed precisely in [
15]. Current MEMS test cells include handler, stimulus, tester, contactors, and tri-temp modules [
42]. The three main sections are pick-and-place handlers, stimulus stations, and signal testers [
42]. SPEA has recently introduced an ATE system compatible with a wide range of sensors such as inertial sensors, gas and biochemical sensors, magnetic speed sensors, and Ultraviolet (UV) sensors. The ULTRA P is a high-performance production MEMS testing handler that provides thermal conditioning, full 6 degrees of freedom (DOF) mechanical stimulus, and an electrical ATE signal path for testing MEMS Accelerometers and Gyroscopes made by Focus Test [
43]. This device can do up to 96 DUT at the same time and apply mechanical and thermal stimuli to sensors [
43].
The impact of intensive development in ATE MEMS testing systems was such that the cost axis of testing significantly decreased from
$2700 in 1997 (1 axis) to just below
$30 in 2012 (6 axis) for MEMS accelerometers and gyroscopes during the boom time for the inertial MEMS sensors market during the 2010s [
44]. Specifically, for the characterization and testing of accelerometers, some researchers used the combined methods introduced in
Table 1. Maude [
45] introduced a new methodology for enhancing the performance of the testing handler to evaluate a single domain of die that is an electrostatic evaluation. The main disadvantage of this method was the need for precise testing design for a specific domain. In terms of the optical–electrostatic domain, Schaellel designed a handler for the parallel test. The thermographic imaging method was used as a new method for testing a specific electrostatic microphone [
46]. Kerkhoff introduced a new handler for testing capacitive-based flow sensors and developed a comparatively different method, but the focus was on testing a single domain [
47]. For testing piezoelectric accelerometers, Chen, by using Quad Serial Port Interface (QSPI), introduced a method with a lower time compared with other methods [
45]. Based on Serial Interface Module (SIM), Ciganda demonstrated a handler to increase the parallel processing of an array of accelerometer chips at the same time. Brasca [
48] developed an FPGA ( Field-Programmable Gate Array) methodology for testing accelerometers and gyroscopes. However, this technique was not applicable for testing piezoelectric and electromagnetic devices. There are still various challenges in MEMS testing and characterization both at wafer level and final testing. Applying mechanical stimuli to wafer-level testing is a concern as it is not safe enough to ensure the safety of the parts to prevent failure or cause defects, which may cause malfunctioning after being released into the market. Apart from the physical issues raised from mechanical stimulation, there are other challenges, such as test cost, time to market, scalability, and dual functioning of MEMS devices. MEMS are densely integrated with ICs (Integrated Circuits), which causes concerns for IC testing at the time of MEMS testing in the production line [
15,
47,
48].
In retrospect, the 2000s witnessed a severe lack of universal MEMS standards for all MEMS vendors, while during this time offshoots from IC ATE providers began to emerge. In the middle of the 2000s, some regulations were established for MEMS standardization in design for standard testing. Nevertheless, presently, huge strides have been made by MEMS vendors to provide standardized ATE solutions. The need for providing KGD protocols in final packaging has highlighted the need to establish wafer-level testing of dies. This has opened a new avenue in the MEMS testing community for developing wafer-level testers. In the 2010s, new specialized vendors started to focus solely on MEMS testing and provided that in parallel with ICs testing. This prepared the stage for the emergence of Test Labs that provides local MEMS testing services. The appearance of a myriad of mechanical MEMS sensors with a different mode of functioning (piezoelectric, capacitive, piezoelectric, etc.) demanded a new ATE system that was supposed to be capable of covering all of these sensors for testing and characterizing.
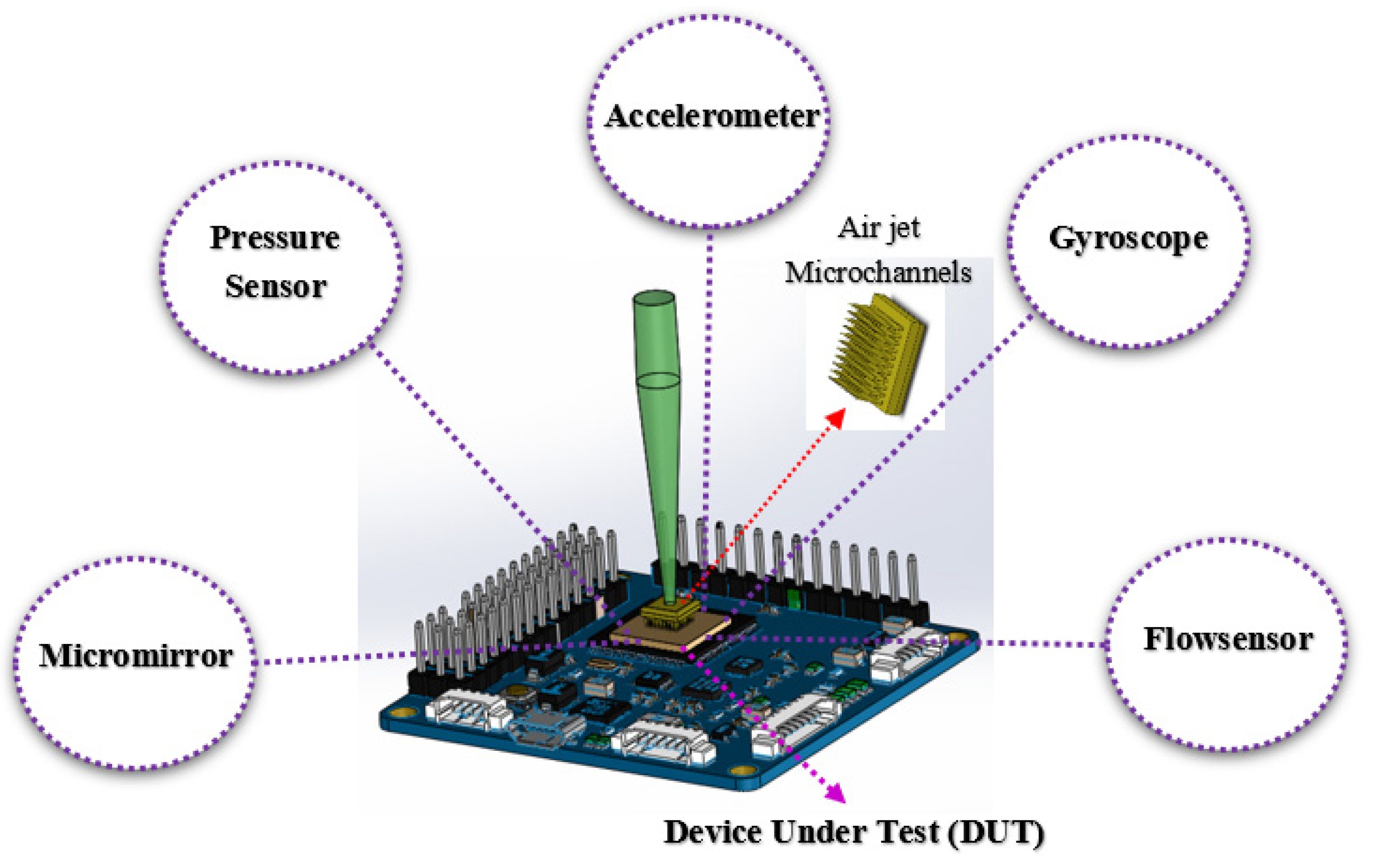
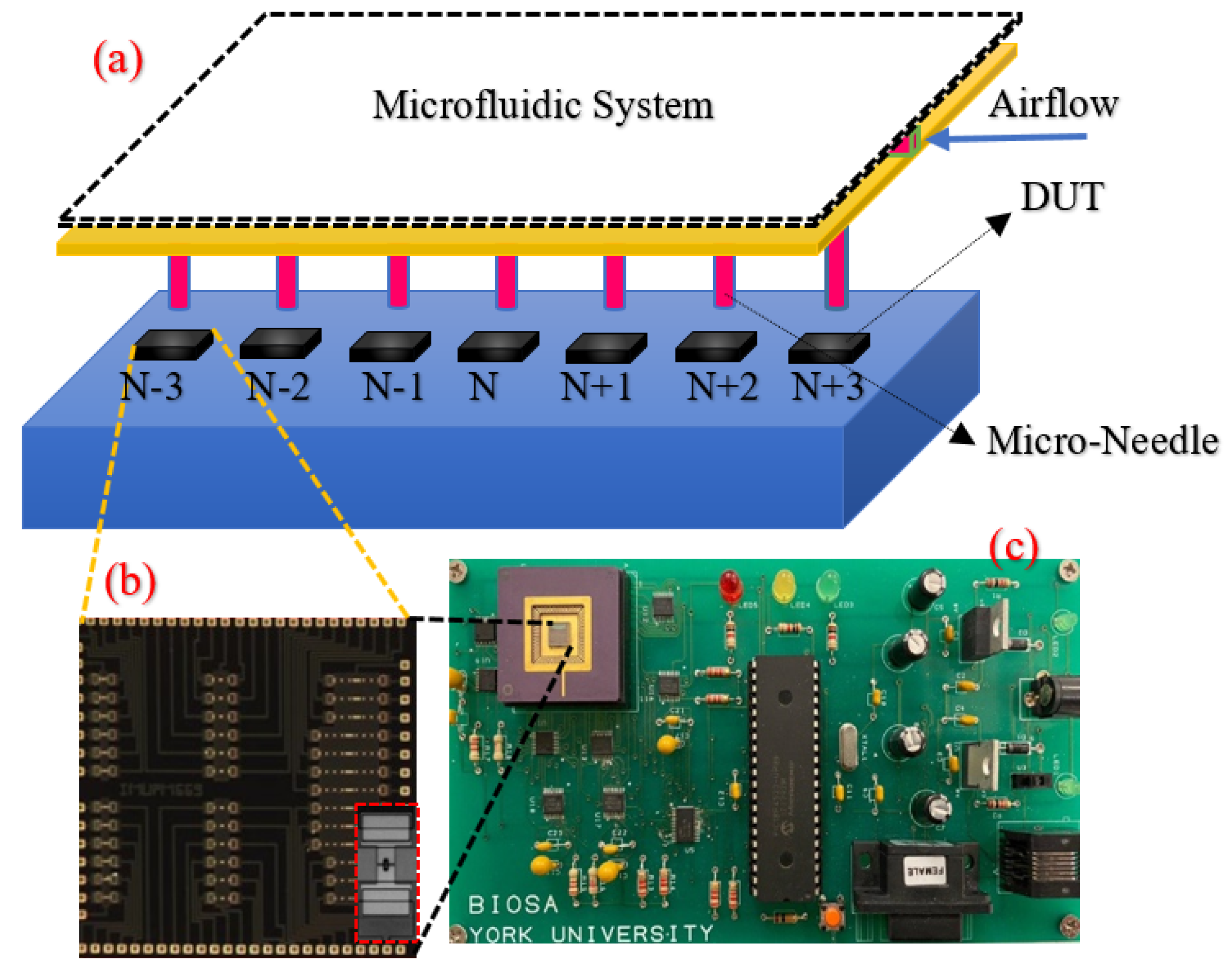
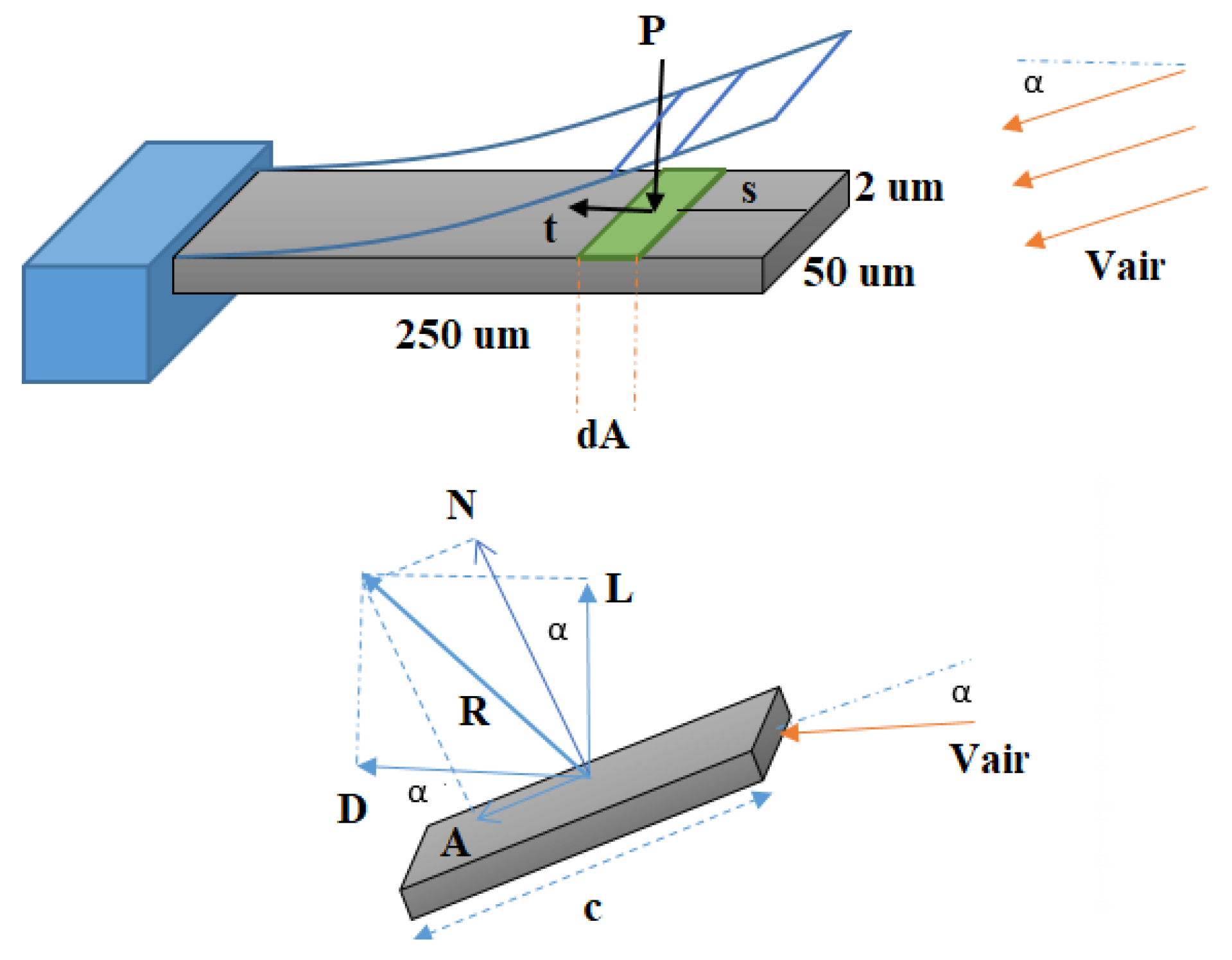
Along these lines, herein, we introduce a comparatively new method for characterizing and testing MEMS sensors based on aerodynamic force on movable components. The principle of this method could be generalized to all families of MEMS sensors such as accelerometers, pressure sensors, micromirrors, etc. that work based on vibration or deflection of an elastic movable mechanical part. Air is cheap and ubiquitous and is expected to be the working fluid in a system of microfluidic channels to flow over the sensor in specific channels (
Figure 1). As it is focused on a defined part of the sensor, airflow can help to test the movement of subcomponents of the device, and generally test the functionality of the device in the final stage of the production line.
Most of the methods mentioned in
Table 1 are non-destructive. The interferometry [
24,
25], which is used for detection of the tilt or deflection of a sample, can be used to test the functionality of mechanical devices and only is used to create a topographical picture of the device that in most cases will not reveal the non-idealities. From this perspective, Airflow-based Force Manipulation (AbFM), the current method, has the potential to manipulate while being non-destructive. With the pull-in method [
27,
28], the device can be tested only in capacitive mode while AbFM can be used for other MEMS modes (e.g., piezoelectric, piezoresistive). To observe running devices within the package, the acoustic emission method has been used [
31]. This method is not for general purpose and has not been used for wafer-level testing; moreover, its applicability for high throughput is not tested yet. AbFM, on the other hand, has the potential to test multi-array sensors and multi-component MEMS sensors in parallel. To measure out-of-plane motion, the laser-Doppler vibrometer has been frequently used while the out-of-plane deflections and vibration can be tracked [
33]. Scanning Electron Microscopy (SEM) is a solution for imaging defects at high magnification, but for internal cracks and non-idealities related to the material this is not a good solution [
35]. Here, we have proved that AbFM is a good option for such analysis and to determine whether there is an internal non-ideality or not. Computed Tomography (CT) is another solution for taking internal photos, but simplicity and high throughput is the main drawback in front of this technology [
36]. Transmission Electron Microscopy (TEM), Energy-Dispersive X-ray Spectroscopy (EDS) [
38], Wavelength-Dispersive X-ray Spectroscopy (WDS) [
39], Infrared Microscopy [
40], and Thermally Induced Voltage Alteration (TIVA) [
41] are some of the methods for MEMS material testing and chemical composition evaluation that are non-destructive. These methods are also not too cheap to be used in highly parallel sensor and actuator testing, while the AbFM is a cheap solution that can be adopted to test MEMS devices at wafer-level scale. Here we have proved the functionality of this air-based method for testing MEMS devices, although there is a long way to go before making this method a perfect and reliable MEMS testing procedure. Generally, there are some common challenges pertaining to the abovementioned destructive and non-destructive methods, which are as follows: (1) the signal for processing is weak when we are dealing with many DUTs; (2) in all cases, noise is a problem due to having numerous sockets; (3) only a specific type of device will be analyzed each run; (4) the positioning of the DUT handler is a difficult task; (5) the coverage number of DUTs is limited and therefore the throughput decreases; (6) for each DUT, a specific algorithm is required; (7) for each design, the testing requirement should be adopted; and (8) when a simultaneous fault is determined in multiple DUTs, there is a need for test redundancy.
2. Materials and Methods
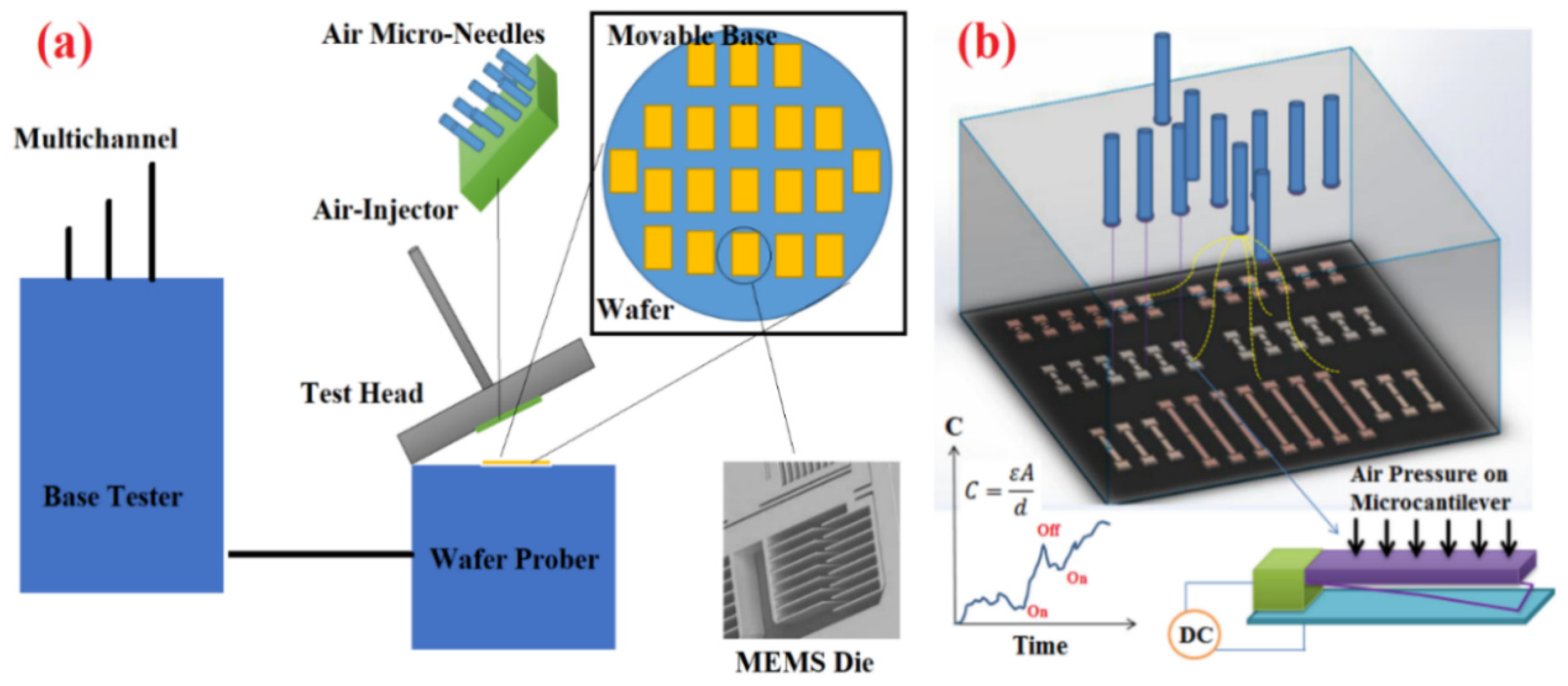
Due to the tremendous progress in microfluidic technology and MEMS fabrication processes, it is now viable to flow air through tiny micro or nanochannels with meticulous precision on the MEMS die and manipulate MEMS sensor subcomponents without contact. The schematic representation of the proposed system is depicted in
Figure 1, in which the air is directed through a microfluidic system toward each DUT while the air is controlled in microfluidic networks in a thin membrane placed on top of the movable plate containing DUTs. We call this method AbFM; see
Figure 2. Due to the usage of air as stimuli of characterization, it can be very cheap and become functional with simple equipment. Based on our simulation results and experimental evidence, we have shown that this method might open a new field for mechanical MEMS device testing and characterization both in the wafer level and final stage of production. The AbFM system can be used to measure the mechanical properties of the MEMS device subcomponent and do functionality analysis because it can manipulate the movable parts both in dynamic and static modes. We have considered the capacitive microcantilever (MCL) chip with 74 MCLs as the MEMS device volunteers, in which MCLs with different lengths but the same thickness and wideness are fabricated [
49,
50,
51]. Microcantilevers are flexible components used in various fields such as biology, chemical detection, monitoring of blood glucose, and screening of disease [
48]; therefore, we have chosen them for the test case of our hypothesis.
To characterize the MCLs, AbFM has been frequently used as the method for measuring mechanical properties and testing the functions of devices under loading. This method is not appropriate for mass production, considering the requirements for low cost and fast procedure of testing [
38]. The main application of AbFM is to generate the force on MCLs and mechanical parts of the sensor. On the other hand, the generation of force is achieved by gas interaction with MEMS components and due to this interaction, a force generates on the component that is controlled by the velocity of gas on a precise location of the device. In this paper, we have shown that the force could be controlled and, more importantly, the exact magnitude of the force, which is experienced by every component in the chip, has been determined for MCL case. According to the output of the device (voltage, charge, etc.) the mechanical properties and functionalities will be analyzed accordingly by comparing the results with an Ideal Good Die (IGD). In AbFM applications, is very important for the IGD to be fabricated as it is the basis for comparison with other dies. If the DUT violates the IGD characteristics, that die would be considered to be a failed die and excluded from the rest of the testing procedure.
In previous studies [
15,
16,
17,
18,
19,
20,
21,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41], the focus was on developing a specific handler for a specific domain for ATE parallel testing. However, in a situation of existing different domains such as electrostatic, piezoelectric, and piezoresistive, a methodology capable of handling all the domains are required. Such a method could minimize the testing time and eventually decrease testing costs. When a gas flow is directed onto a die with precise accuracy, it can scan all parts of the sensor and stimulate all components of interest. The components under test should be movable, regardless of their physical domain. The design of a changeover handler for AbFM is easy and could be fabricated by just designing a porous microfluidic–polymeric membrane or an array of microneedles on top of the system. Applying fluid mechanics simulations, the position of needles on top of the die can be determined with acceptable accuracy. This will open the field to develop an application-specific ATE (AS-ATE) method based on aerodynamic forces. The main objective of this work is to introduce the AbFM technique as a new ATE method for testing and characterization of MEMS devices in parallel using finite element method (FEM) simulation of the system, toward measuring the precise force acting on the chip from the airflow. In other words, AbFM includes a simulation study to design the system handler before manufacturing, and in the next step, extracting the calibration curve of each component of interest (which will be the reference data for analyzing all dies in mass production lines). Software such as COMSOL helps us to develop a FEM model that acts as a reference model to be compared with the test results and decide on the functionality of the DUT.
Here, we have selected the microcantilever as the test case and showed the application of this method on a microcantilever MEMS chip. This procedure has the potential to be generalized for testing and characterizing all mechanical MEMS sensors that include movable and elastic parts. Microcantilevers are widely used in various applications such as biological, chemical detection, monitoring of blood glucose, and disease detection [
49], therefore designing a reliable and easy-to-operate testing system for them is inevitable. In the AbFM, it is assumed that the DUTs include different parts or components that work based on the same physics or varied domains that contain movable elements that could be stimulated with the air force generated from an air-injector handler. The chip will be stationary and the air-injector moves on top of the chip to sweep all components and exert a specific force on each one that is characterized before testing (in the stage of Fluid-Solid Interaction) simulations (FSI). From a general perspective, the AbFM system that consists of some components for generating the airflow on a chip from a specific distance above the chip and moving support for aligning the chip under the precise position for focusing air jet on the MEMS components.
In this method (AbFM) (see
Figure 3), the main assumption is that the MEMS device is already fabricated, and the focus is to design the specific AbFM testing system. Nevertheless, before that stage, it is necessary to analyze the distribution of air pressure (or velocity) throughout the chip and drive the specific relationship between the flow velocity and corresponding force exerted by the airflow on a specific location of MEMS device (here the upper surface of MCLs). There are some influencing parameters such as: (1) the vertical distance between air microjet from the sensor; (2) the diameter of hole (strength of air jet); (3) gas type; and (4) non-idealities that arise from different conditions in designing the system of airflow. In other words, simulation is a preliminary and essential part of the AbFM method that paves the way for the next steps of calibrations of the chip under air pressure and driving the corresponding information for characterizing and validating mechanical properties. When the chip is fabricated, and the general geometries of all components are well defined (through layout design process), the preceding simulations could be done to obtain raw data for evaluating the generated force on a specific component in MEMS. Subsequently, a graph showing the force-airflow velocity will be acquired, then, according to the output of sensors (e.g., capacitance, electrical charge, and current), a calibration curve will be clarified, demonstrating a relationship between airflow velocity and sensor output. During this phase, many different test procedures could be derived that are capable of addressing different concerns regarding the non-idealities which are raised from both generated faults (during fabrication processes) and well-known mechanical defects in MEMS subcomponents. One of these faults is discussed in the following chapters, which shows how one recognizes a crack in a microstructure using airflow by only watching the electrical output of the sensor. In particular, AbFM has the potential to be designed for a testing procedure even in parallel with constructing steps for every individual MEMS sensor. Considering this specific feature, AbFM has the potential to serve the MEMS industry as a non-invasive and reliable Application-Specific MEMS Testing (ASMT) method.
Figure 3 demonstrates the workflow of the AbFM method in which simulation of air-interaction with MEMS components is its inherent feature and necessity. In the AbFM method, analyzing the airflow forces on the flexible components is of paramount importance. To achieve this goal, we have used COMSOL to precisely analyze the system and to validate its results with precise theoretical approaches that consider the side effects of MEMS devices (effects raised from micro size) before starting to design the parameters of the AbFM system. In this work, a commercially available AC/DC power supply or so-called voltage adaptor was used to generate two regulated DC voltages with minimum or no ripples using LM7805 to supply the analog and digital components, individually. This conventionally designed power supply is sufficient to provide the required DC voltage for the proposed MEMS-based sensing system; however, we used another low-complexity technique to enhance the noise immunity of the sensing system. The readout system incorporated with the cantilever chip was placed inside a Faraday cage with a small opening for applying air. This cage can further cancel the electromagnetic noise during the experiment. Based on our experiences, the isolation of voltage adaptors from the rest of the printed circuit board using this Faraday cage has significantly enhanced the accuracy of the cantilever sensor in measuring the changes due to the applied very weak airflows.
In the simulation, the effect of all important parameters has been studied; afterwards, the whole chip with a size of 2.5 mm × 2.5 mm was simulated, in which a group of MCLs (with the length of 250 µm and 400 µm) are modeled which are exactly the same as a fabricated chip. After obtaining the relationship between air velocities, deflection of MCLs, and the resultant capacitance, the results of experiments on MCLs in the same condition of airflow on the chip is discussed. This step is a precursor to design the AbFM specific handler for that specific chip under test before experimental procedures, to calibrate and drive chip AbFM datasheet for future testing in mass production. Next, the graph of output will be compared to the previously designed parameters and experiments; afterwards, a decision is made on whether the device has failed or not. In this approach, it is inevitable to use simulation software for fluid–solid interaction analysis; therefore, here we have approached the COMSOL software as our FEM simulation software and scrutinized its performance in numerical results for further design.
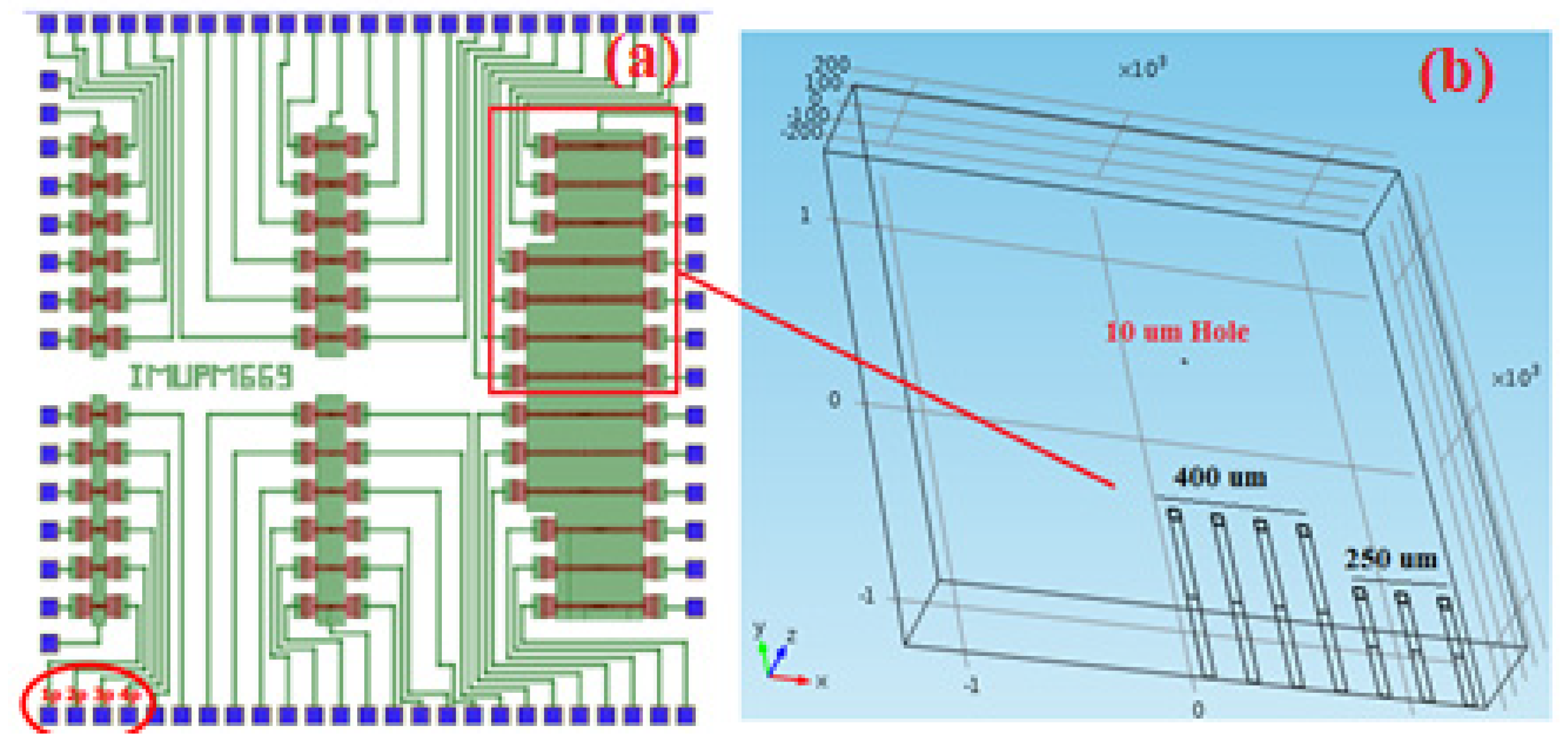
The layout of microcantilevers sensors is demonstrated in
Figure 4. As can be seen, a group of sensors with a length of 250 µm and 400 µm that are positioned in front of each other are simulated. The simulation system is exactly the same as the real chip, but for simplicity and decreasing the cost of simulation time, only two sets of MCLs are analyzed, which are demonstrated in
Figure 4, with a group of 8 tip-to-tip MCLs with 400 µm length and a pack of 6 MCLs with 250 µm length. These components are according to the layout showed in
Figure 4a, which belongs to a fabricated MCLs die.
The chip dimensions (projected area along the z-direction) are 2.5 mm × 2.5 mm, modeled as demonstrated in
Figure 4. The distances between MCLs are the same as the fabricated chip. This simulation exactly demonstrates the deflection of MCLs relative to each other and in response to the airflow simultaneously. Because the experimental results are done on 400 µm, only these cantilevers are simulated, not the rest. However, the 250 µm length MCLs nearby are also considered for more realistic simulation results. The fluid flow in the channel is described by the incompressible Naiver–Stocks equation for the velocity field of
u = (u,v), and the pressure
p, in the spatial deforming and moving coordinates.
In Equations (1) and (2), I denotes unit diagonal matrix and F is the volume force affecting the fluid and with the assumption of no gravitational force affecting the fluid and supposing the coordinate system, velocity is
Referring to
Figure 1, the outflow (surrounding boundaries), and the condition is
p = 0. On the solid (non-deforming) walls which are the underneath substrate (which is the ground contact for MCLs), no-slip conditions are imposed that imply
while on the deforming interfaces of MCLs in contact with the airflow all the velocities are equal to the deformation rate,
and
.
The structural deformations of MCLs are solved for using an elastic formulation, while a nonlinear geometry formulation is solved simultaneously to allow large deformations for MCLs in the narrow air gap. The MCLs are fixed to the wall of the fluid channel that around them, and an open boundary condition is applied for the fluid region. All other object boundaries experience a load from the fluid, given by
where n is the normal vector to the boundary, and u shows the velocity field. This load represents a sum of pressure and viscous forces.
In FSI module of COMSOL 5.3, the above equations are solved in specific boundary conditions. The air is flowing from a hole with the “inlet flow” boundary condition, and underneath the MCLs, the “wall” boundary conditions are used. On other faces on the channel, the boundary condition is set to “open boundary”, because the boundaries are all open to outside space. In terms of material used in the simulation, the air was used in the fluid region and the polysilicon was set for MCLs as their material, the same as the properties used in the fabrication process (Standard PolyMUMPs). The polysilicon density, Young Modules, and Poisson ratio are 2030 kg/m3, 158×109 Pa, and 0.22, respectively. The contributing forces that play an essential role in the system are demonstrated in
Figure 5; as it shows, airflow exerts a tangential and vertical force on the cantilever, which are shear stress and pressure field forces, respectively. The aerodynamic force acting on the sensor is calculated by treating the microcantilever as a uniform plate, as a model of the thin airfoil, and then the overall force of airflow on the MCL is derived.
According to aerodynamics principles, when air is flowing around an object, normal pressure and shear forces act on the airfoil (here MCL) and results in aerodynamic forces and momentums. The air forces on the cantilever will be mathematically calculated as shown in
Figure 5. If we suppose that the incoming airflow is moving with a velocity of V and with an α angle from the horizon (Angle Of Attack (AOA)) there are two vectors, lift force and drag force, resulting from the interaction of those important forces.
After some mathematical simplifications and also ignoring the effects of airflow viscous stresses on MCLs surface, the following relationships will be derived for lift force and drag force coefficient, which are used to calculate the lift and drag force.
In Equations (4) and (5), the C
N and C
A are calculated by knowing the pressure profile distribution along the surface of the microcantilever and, after that, the following forces are calculated which are exerted on the microcantilever.
N means vertical to the flow direction and
A means in direction of flow is demonstrated in
Figure 5. The
α is the AOA.
In the case of the vertical flow of air on the microcantilever, the
CL becomes zero, and the only force will be drag force, which is Equation (7). The interaction between the fluid and solid (FSI) is calculated the same way as proposed in [
49]. Here the main force resulting from airflow is discussed, but in FSI simulations, the force is simultaneously calculated as the solid domain is solved.
To have a precise description of the deformation of MCL, accurate modeling of MCL is undertaken in order to evaluate the performance of COMSOL in predicting the dynamic response of MCL due to the action of aerodynamic forces. It is noteworthy that the accurate mathematical modeling of static and dynamic behaviors of microbeams has been a crucial issue for researchers during recent years. The thickness of beams used in MEMS and Nano Electro-Mechanical System (NEMS) are in the order of microns and sub-microns such that their physical description completely defies classical mechanics theories accepted for large-scale systems. The size-dependent deformation and vibration behaviors in micro-scales are experimentally validated. The classical continuum mechanics theory is not capable of predicting and explaining the size-dependent behaviors of microbeams, which occur in micron- and sub-micron-scale structures. However, non-classical continuum theories (such as the modified couple-stress theory, strain gradient theory, micropolar theory, nonlocal elasticity theory, surface elasticity, etc.) are acceptably capable of interpreting the size-dependence behaviors [
52]. Here, the system is modeled based on the modified couple-stress theory coupled with the Timoshenko beam theory to accurately model the MCL with the aim of evaluating the results of COMSOL [
52].
Timoshenko beam theory (TSBT) is considered to predict the dynamic characteristics of the system. According to the mathematics of couple-stress theory and TSB theory, the overall equation of motion for the beam will be derived as follows:
In TSBT, the displacement field is as follows:
in which
is the displacement field function,
U is displacement field in all directions, and the non-zero strain tensor for the Timoshenko beam model is:
Here
and
are strain tensor in xx and xz plane. To drive the equation of motion for MCL, the beam kinetic energy (
Tc) should be derived and used in the total energy equation. The kinetic energy equation is as follow:
To calculate the potential energy of MCL, the modified couple-stress theory of energies is used, which is in the form of:
In Equation (11), the
and
demonstrate the stress and strain tensor, respectively. Also
is curvature vector and
is a coupled stress coefficient. They could be written as Equations (12) to (15):
For TSBT model, the following requirements for Equations (12) to (15) are:
According to Equations (16), (17), (18), and (12), (13), (14), (15), Equation (11) is written as follows:
Therefore, Equation (19) shows the potential energy of MCL and Equation (10) shows the corresponding kinetic energy. To drive the equations of motion, the Hamiltonian principle is approached. It states that the sum of partial differentiation of kinetic energy, potential energy, and all imaginary works (
from outside is equal zero.
By applying this equation to the abovementioned equations, the equation of motion will be derived. The outcome of such mathematical efforts is seen in Equations (20) and (21).
The equation of motion for MCLs, in general, is demonstrated in Equations (21) and (22), which F(x,t) shows the term for external forces that here are considered electrostatic and aerodynamic forces which are from the underneath electrode and also the airflow, respectively. This equation is solved based on the FEM, which is completely described in [
52] and is based on the Timoshenko beam model.
The forces participating in the static deflection and dynamics vibration of MCLs are aerodynamics and electrostatic forces that are as follows:
For the condition of this problem in which air is directed vertically on the MCLs, the lift force approaches zero and the only force from the air is the drag force which is Equation (7) and also with the assumption of :
The total force exerting on MCL is:
In Equation (22) the CD is drag coefficient, is the density of the fluid, A is the projected area along with the flow, V is the velocity of air, d is the air-gap distance between MCLs and the ground electrode, and z is the displacement of MCL. Equation (24) is the total force in Equation (25) that results in a general equation of motion for MCLs when electrostatic and airflow forces simultaneously exist. The assumptions behind Equation (24) are that the flow is laminar and streamlined along its main direction. With this assumption, the air velocity in the drag force could be the same as the incoming air velocity from the nozzle or air injection on-chip area.
The reason that we have approached such elaborate mathematical formulations is to evaluate the efficiency of COMSOL in estimating the dynamics and also the order of errors in its predictions that could be used for further FSI analysis. For the A
bFM method, approaching fundamental mathematics is not appropriate, and the FEM software in the area is enough due to its user-friendly graphical interface and acceptable accuracy. However, due to its importance in evaluating the performance of this software, it should be verified before any further attempts on other data from simulations. To do so, here we have chosen one of the most accurate models of beam modeling, namely Timoshenko beam theory with couple-stress theory, which considers the effect of micro-sizes in MCLs dimension and also the planar shear stress along the MCLs [
53,
54]. Therefore, the theory that was expanded through Equation (8) to Equation (21) is accurate enough for validating the results of COMSOL software. For this reason, in the next section, the results from the experiment, COMSOL and the TSBT are compared to each other to evaluate the COMSOL results for further simulation on the FSI problems and investigating the main design parameters of AbFM.
To evaluate the accuracy of COMSOL 5.3 (for further simulations) the natural frequency of this microstructure is calculated, and the corresponding modal shapes for the first natural frequency are presented in
Table 1. As can be seen, COMSOL has enough accuracy to be reliable and accurate enough for other analyses and results. The fundamental vibration mode of a cantilever, which generally is considered to have the lowest resonance frequency, always relates to a flexural vibration mode. The natural frequencies related to this vibration mode is measured with the FEM method using COMSOL 5.3. The importance of such a study is having a clear understanding of system vibration to evaluate the system and to design it for the avoidance of resonance phenomena.
3. Results
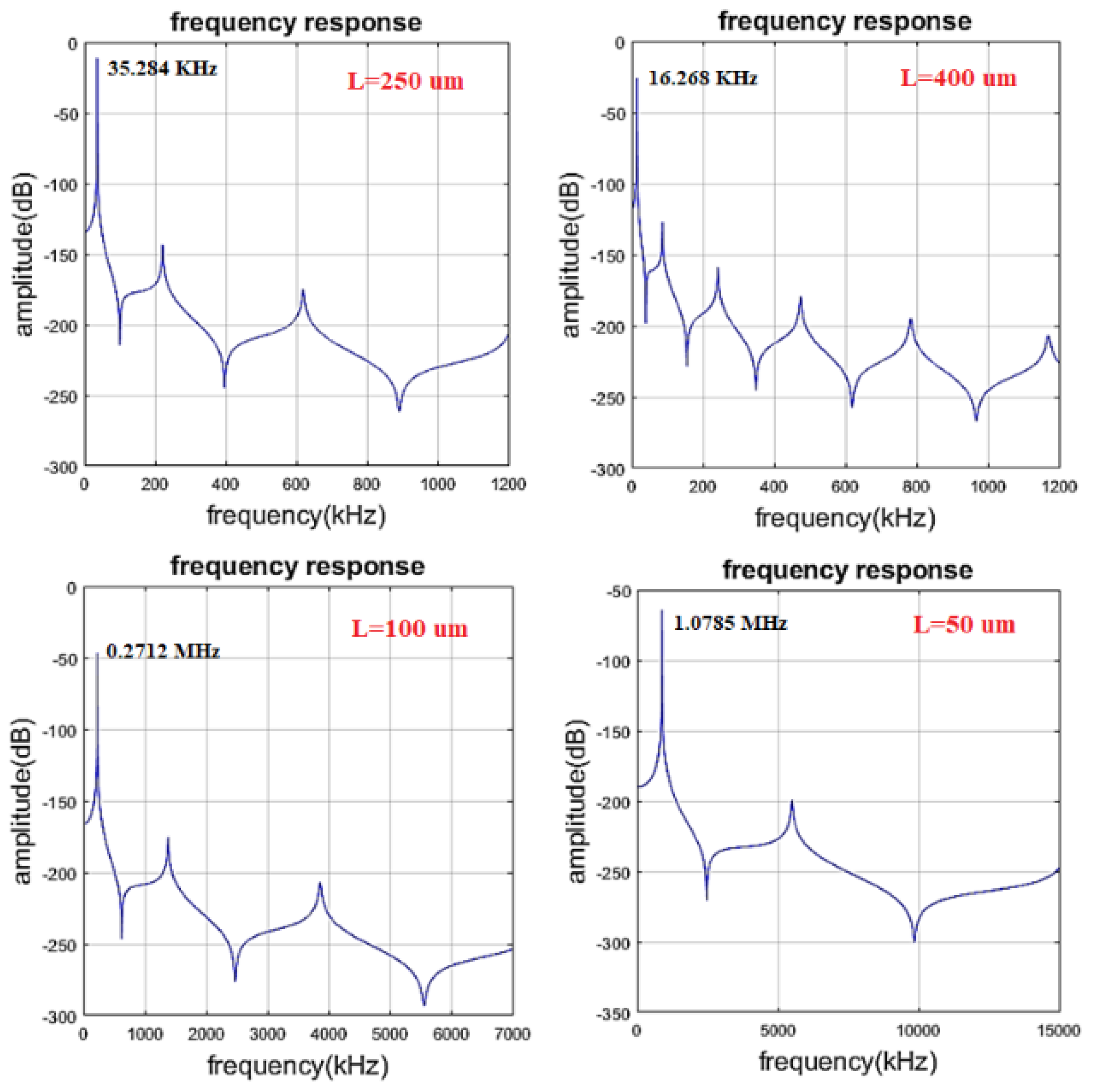
The first resonant frequency of MCLs with different lengths is reported in
Table 1. The frequency responses calculated with TSBT method are also reported for all lengths of MCLs in
Figure 5, in which the first resonant frequency is followed for comparison with COMSOL results in
Table 2. For an MCL with
L=250 µm, all six mode shapes are illustrated in
Figure 6 for better analysis of MCLs vibrational mode in the narrow region above the electrode. These vibrations may cause some errors when evaluating the results of capacitance in experiments. These vibrational modes are responsible for some unwanted vibrations that appeared in experimental results. The errors in
Table 2 have been calculated by subtracting the COMSOL result from experiments and theoretical modeling and then dividing by the COMSOL results (Error = 1– (Experiment&Theory/COMSOL Result)).
The same procedure was carried out for all MCLs in a chip with
L = 400 µm, 250 µm, 100 µm, and 50 µm with all of them having the same thickness (2 µm) and width (50 µm).
Figure 6 demonstrates the possible mode shapes when the frequency of the system approaches the value of the corresponding resonance frequency shown in
Figure 7.
According to the simulation results, analytical data, and considering experimental results, it is evident that COMSOL has enough accuracy to do other analyses and achieve the AbFM parameters. There are important contributory factors in AbFM design such as (1) the vertical distance between the vertical needle and the corresponding movable part on-chi; (2) the diameter of vertical microhole/microneedle; (3) the positioning of microneedle/hole on the die/chip; (4) the relationships between the air inlet pressure/velocity and the electrical output signals of a chip; (5) the deflection and air velocity relationships from a specified hole on the system; (6) the cross-talking between all components of movable parts in the die responding to different stimuli from all other parts in the system and other important design parameters, which should be considered in a more accurate design before construction steps. AbFM generally is the method for microscale manipulation with force resulting from airflow, and its accuracy of operation is very important for the DUT. For this reason, we have simulated the airflow hitting a flat surface to investigate the relationships between parameters such as vertical distances, and the velocity of an air jet on the focusing efficiency of AbFM in simulated working conditions. Based on our futuristic picture of AbFM, as demonstrated in
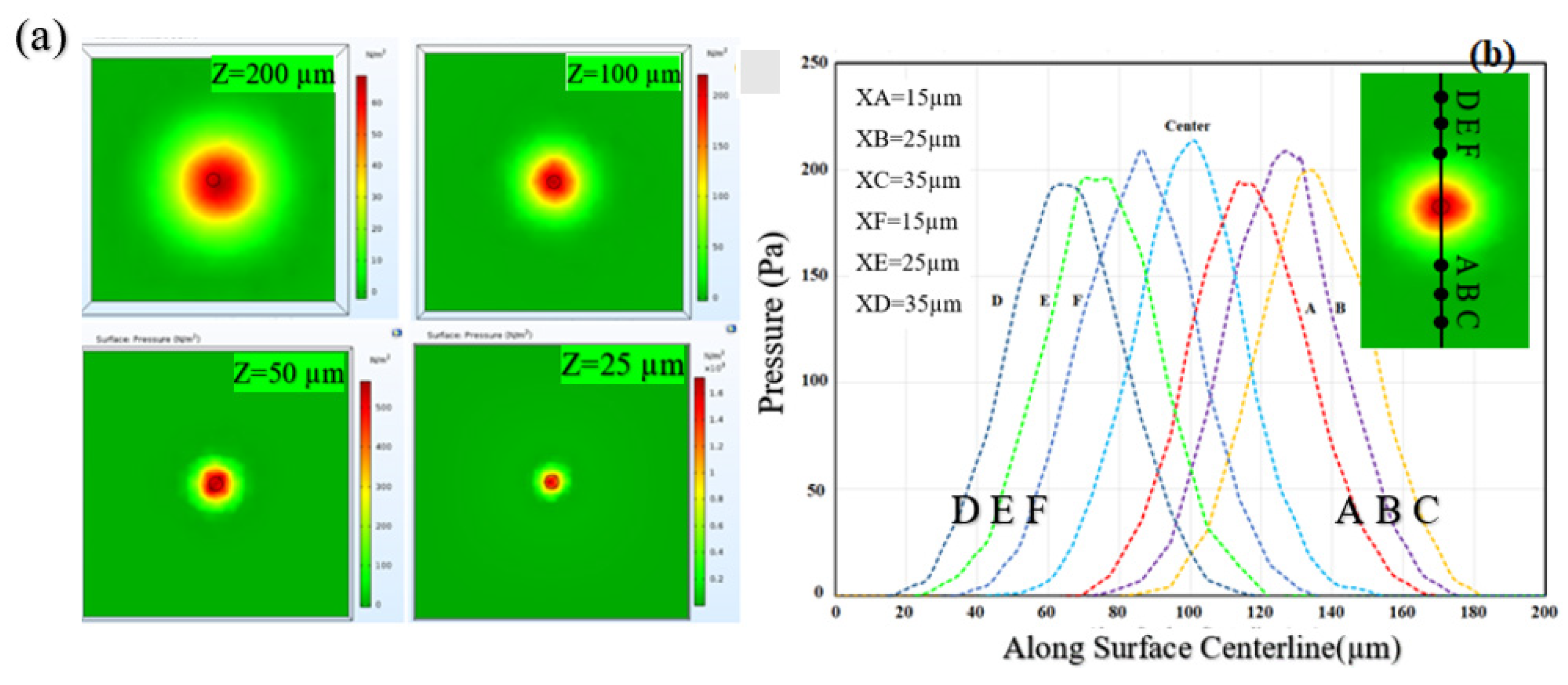
Figure 2, there will be some microholes above every component that can sweep the surface of a die with a nanopositioning handler. To demonstrate the proficiency of those microholes and its capability in generating a small amount of force, a simulation is conducted in which the air is directed from a 5 µm radius microhole positioned at different vertical distances above the surface and also translocated along the centerline (see
Figure 8b) to show the pressure distributions on the focusing area. The surface is considered uniform and flat fixed in the space under the microhole locating vertically on the surface. The surface area is 200 µm × 200 µm and the flow is directed from a hole with
R = 5 µm for different distances.
Figure 8 demonstrates the accuracy of an air jet on the surface, which is an important result. When the air jet vertical distance was 200 µm the flow was splashed on the surface, and there were not enough focusing areas at the center. Due to the effects of fluid dissipation energy, the flow spread out along the surface and does not focus enough on the surface. However, as the vertical distance is reduced from 200 to 25 µm, the focusing area became as small as the inlet injector hole, and this illustrates the importance of microhole vertical distance from the surface as an essential parameter in AbFM system design. The results showed that a force of 15.7 nN could be generated on a circular surface of
R = 5 µm when air velocity is 60 m/s, and the
Z is 25 µm. This phenomenon also was reported by Jungchul Lee et al. [
55,
56], in which they asserted that the effective flow field depends on the separation field, which is the distance between the nozzle exit and the effective area. However, in the same distance of nozzle exit, the liquid jet is focused, and the nitrogen will flow on the surface in a cone-shaped area. However, for nitrogen flow from a microhole with a diameter of 1 µm and a distance of 27 µm, the spray angle is 84°. Based on our simulation results, the flow pressure distribution shows that the pressure at the center is higher, and according to the Bernoulli equation, the velocity will reach the lowest possible. As
Figure 8b shows, the flow pressure at the center is higher, and therefore, we expect that the diagram for velocity track the reverse trend and make a cone of flow.
For every AbFM system, there will be a system for blowing air on the MEMS sensors and components, therefore before construction of the parallel testing setup, it is necessary to drive some parameters from the simulation for the system and specifically design the system to exert a defined force on a component in the chip. Here, for analysis and characterization of MCL chip, the vertical distance between MCLs and the microhole, which is located at the center of the membrane (above the chip) is very important in order to reach enough resolution and sensitivity. To do so, three microcantilevers were designed and a microhole with a diameter of 20 µm was simulated for different air velocity. Then the maximum deflection of MCLs is calculated, which is depicted in
Figure 9.
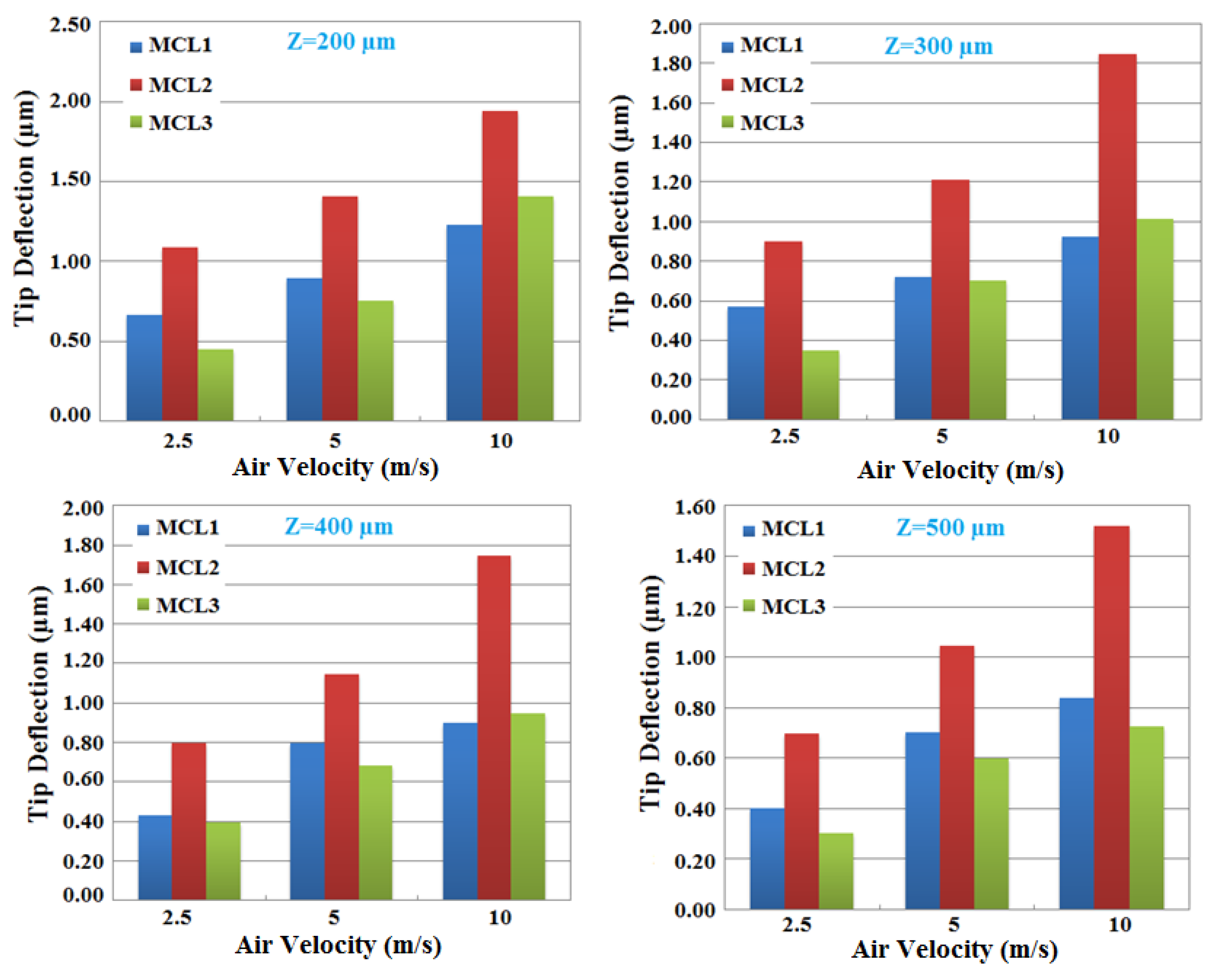
Figure 10 demonstrates the tip deflection of MCLs with
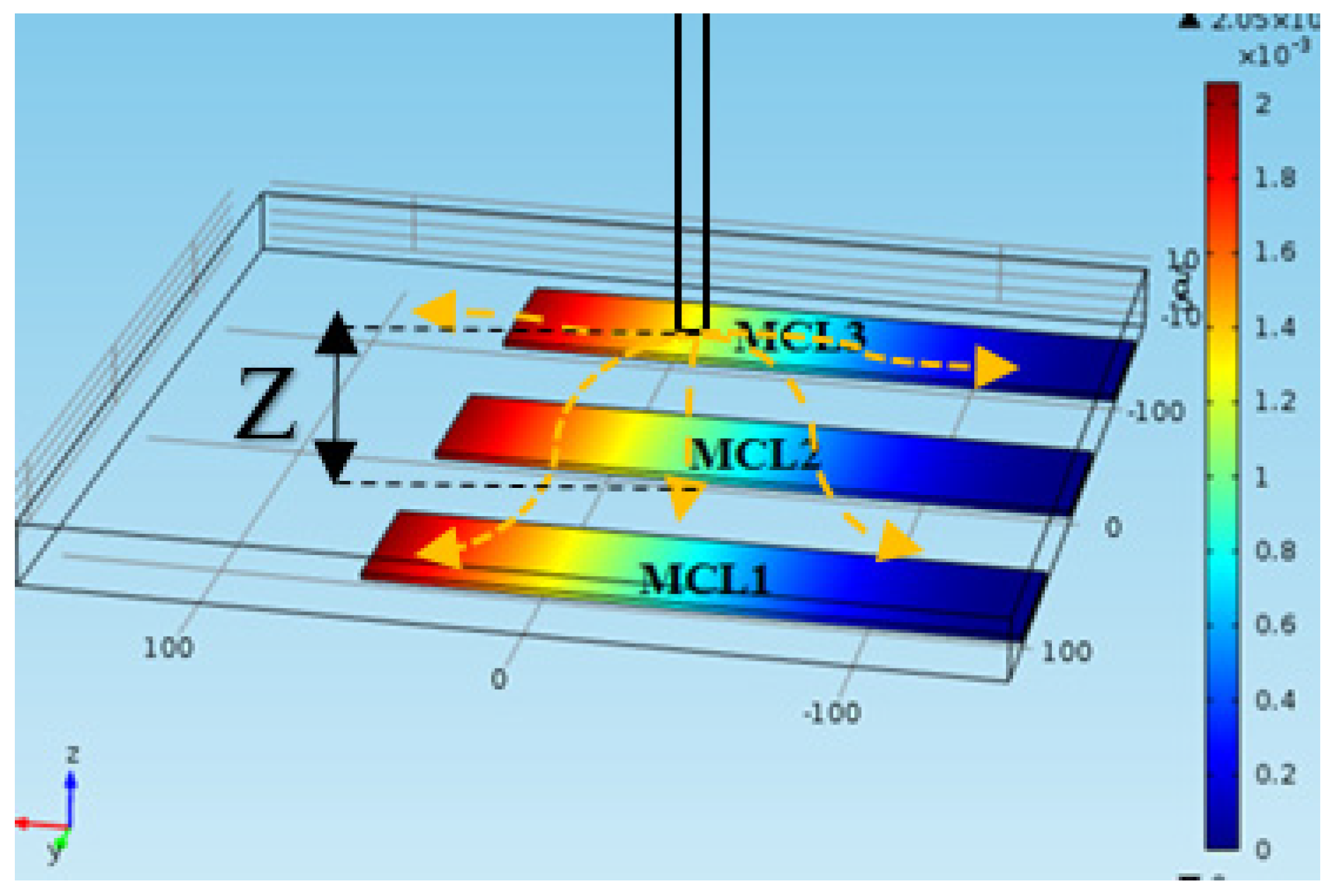
L = 250 µm in the chip for different air velocities and vertical distance between microhole in the membrane to the surface of MCL. The Z distance (see
Figure 8) varied from 200 to 500 µm. All the maximum deflections were under 2 µm, which was the distance between the MCLs with the substrate.
Figure 10 conveys very important results that if a microhole were located along the center of the chip, all MCLs would experience different pressure from airflow and consequently different deflection. The deflection of MCLs increases as the air velocity goes up. However, the difference between the tip deflection of MCL1 and MCL3 decreases as the vertical distance between microhole increases. Therefore, the force on the cantilevers as MEMS components could be controlled with controlling the air velocity. This is a simple step toward demonstrating the fact of how the AbFM works. In the next sections, the forces are calculated in a real chip.
Analysis of airflow force generated on the micro cantilever’s surface is performed. The contributing factors include air velocity, variable microhole, and variable vertical distance, and so forth, that have a considerable effect on the resulting force generated on MCLs surface. The force is very important because this is one of the important steps for the design of AbFM, and by doing so, we precisely derive a relationship between airflow velocity and force exerted on the surface of MEMS components to be used it in an experimental system for characterization.
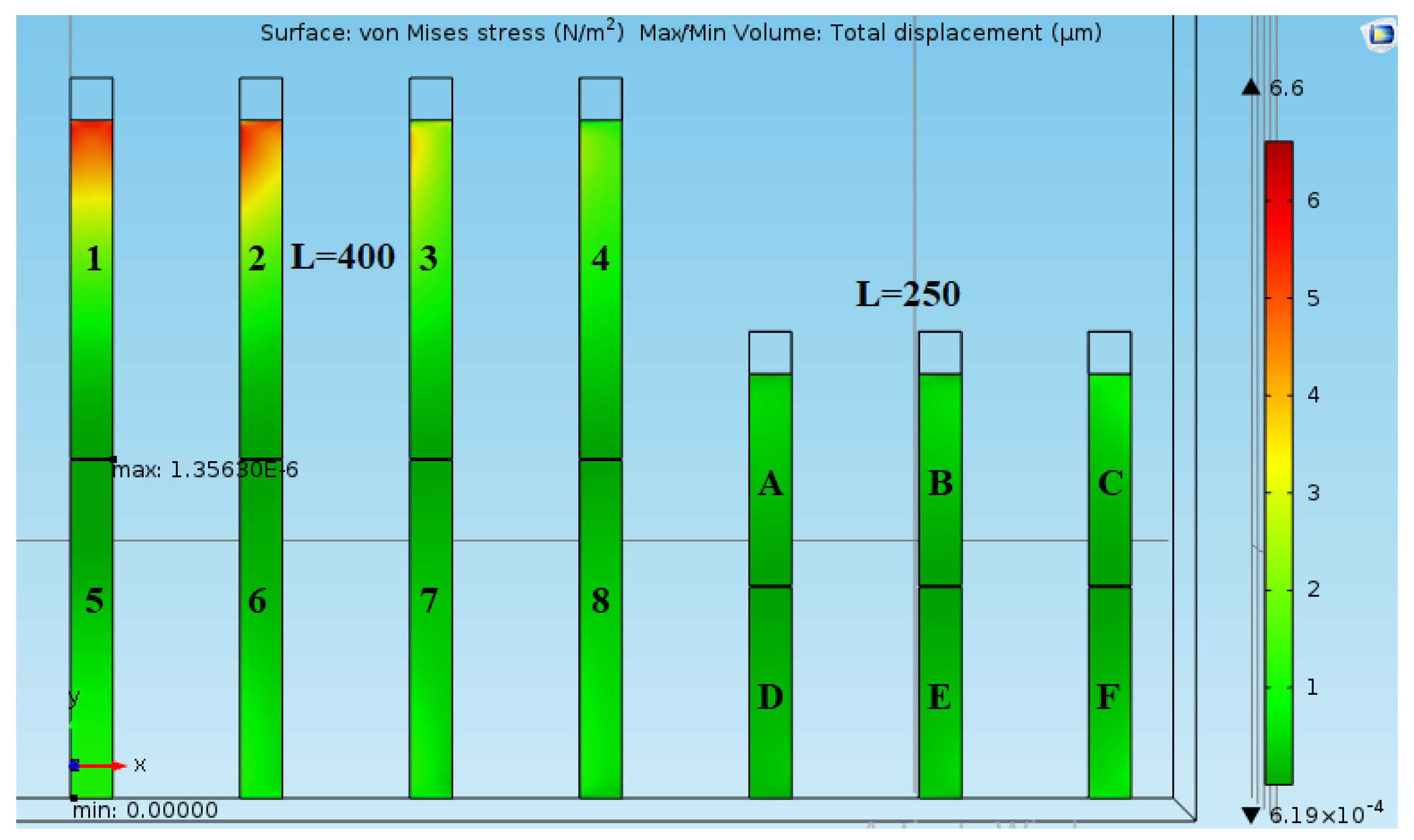
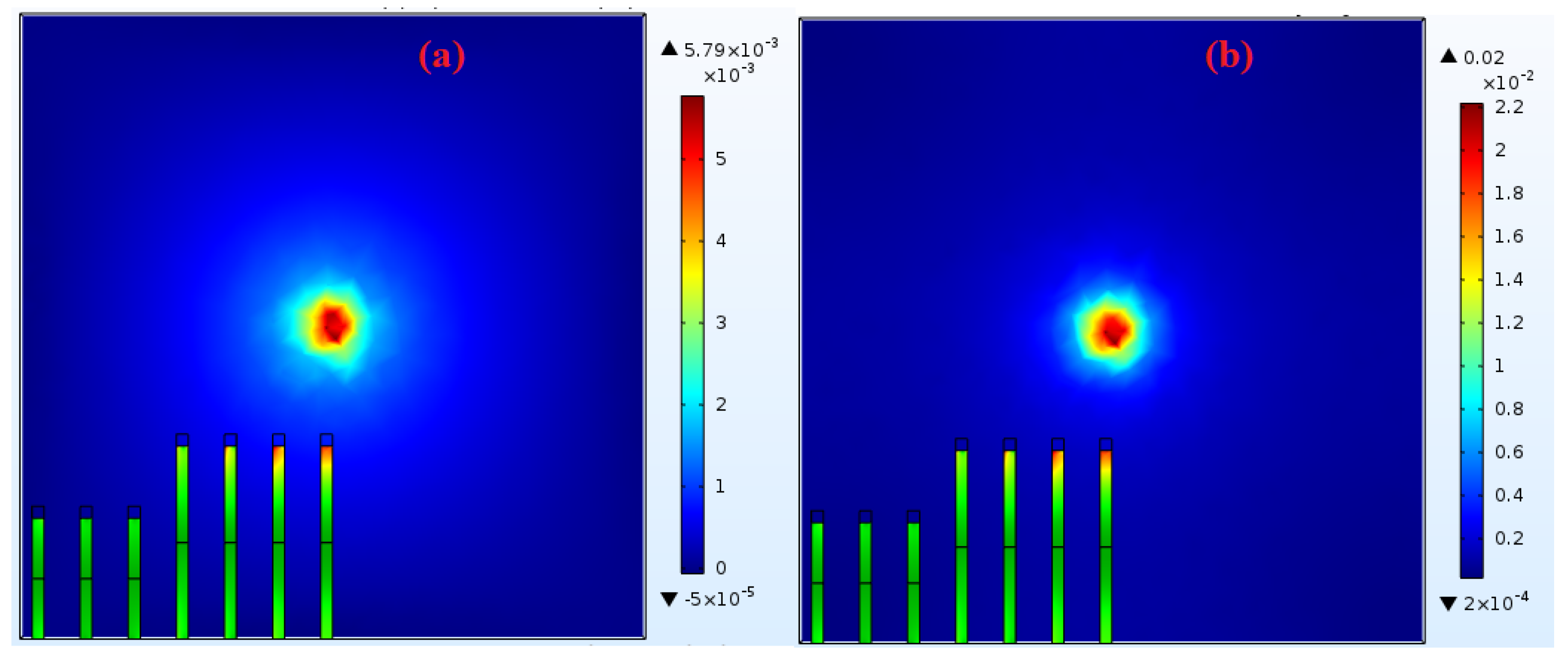
Figure 11 demonstrates the Von Mises stress (N/m2) generated in the microcantilevers due to airflow with a velocity of 5 m/s from a hole of 10 µm (diameter) and about 400 µm above the substrate. As it shows, the maximum deflection happens in MCL-1, which is about 1.35 µm. (See also
Figure 4 for a real chip)
As
Figure 11 represents, by using airflow as a stimulus for functional analysis of the mechanical parts of the MEMS device, the stress generated due to fluid–solid interaction on the MEMS subcomponents will be different based on the location and distance from the microhole. This could result in a different response from all microcantilevers (generally the targeted component). However, the importance of simulation is here that we want to design the system before the test. In the layout design and in the component design process flow of a MEMS device, we generated the 3D sketch of the sensor, and then the fabrication is processed. As with the concept of ASIC (Application-Specific Integrated Circuit), here we proceed with the same workflow for having Application-Specific AbFM, a MEMS ATE system design. In this process of design, the transaction mechanism of sensors and actuators will become clear and the mechanical moving objects in the system, such as microcantilevers, microplates, microneedles, comb fingers, etc., with specific geometry on the die, has gone through an AbFM fluid–solid interaction (FSI) simulation process to evaluate the MEMS components response to air pressure and trying to assess all of the contributing parameters playing a role in AbFM. Here the minimum gas velocity, the direction of focusing, the gas type, and optimization of the distance between microhole and the MEMS components will be defined with highly accurate simulation FEM, BEM software (as proceeded in this study). Then the testing requirements go through the manufacturing process and a specific testing AbFM system will be adapted to the production line of that specific MEMS component.
Figure 11, at first glance, gives a view of the response of the microcantilevers device to an airflow (5 m/s), from a specific vertical distance (here 400 µm). The response of a microcantilever to airflow stimuli from a microhole placed a certain vertical distance is shown in
Figure 12. The whole deflection of the microcantilever is presented.
Figure 13 depicts the deflections of MCL1 for the different conditions of radii of microhole above the chip. The tip deflection for microhole radii of
R = 10, 12, 14, 16 and 18 µm are 0.36, 0.42, 0.61, 0.98, and 1.22 µm, respectively. Therefore, by doing the simulation, we can estimate the flow effects on MCLs with different lengths. This could be generalized for different sensors with different moving parts, for instance, micromirrors, MEMS accelerometers, pressure sensors, etc., in the die-testing stage.
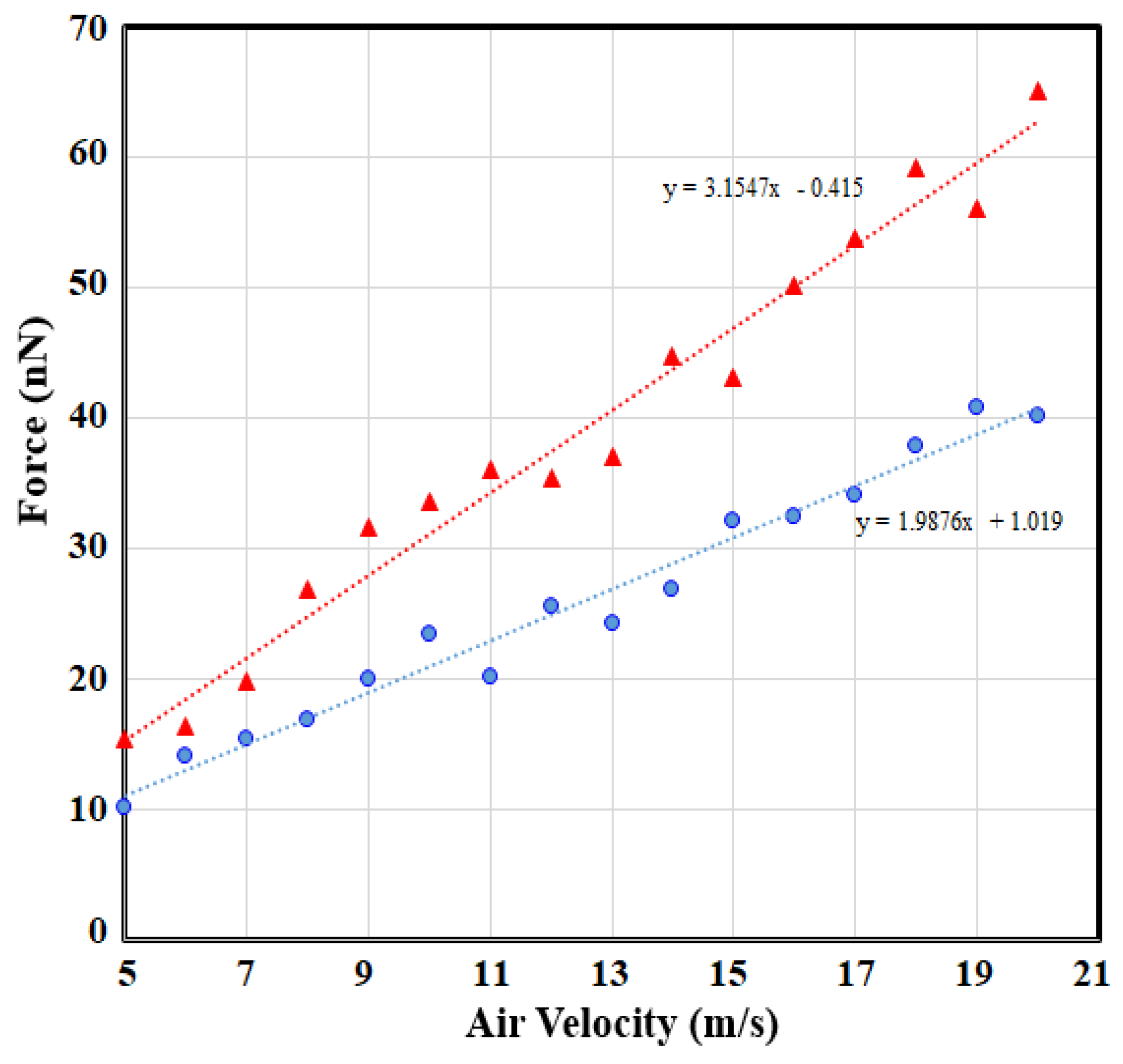
To have a better understanding of the effect of microhole size on the generated force, for different velocity ranges between 5 to 20 m/s, the force was calculated on the top surface of MCL1 (see
Figure 13). The velocities were directed on MCL1 for two microhole radii (
R = 12 and 14 µm). As
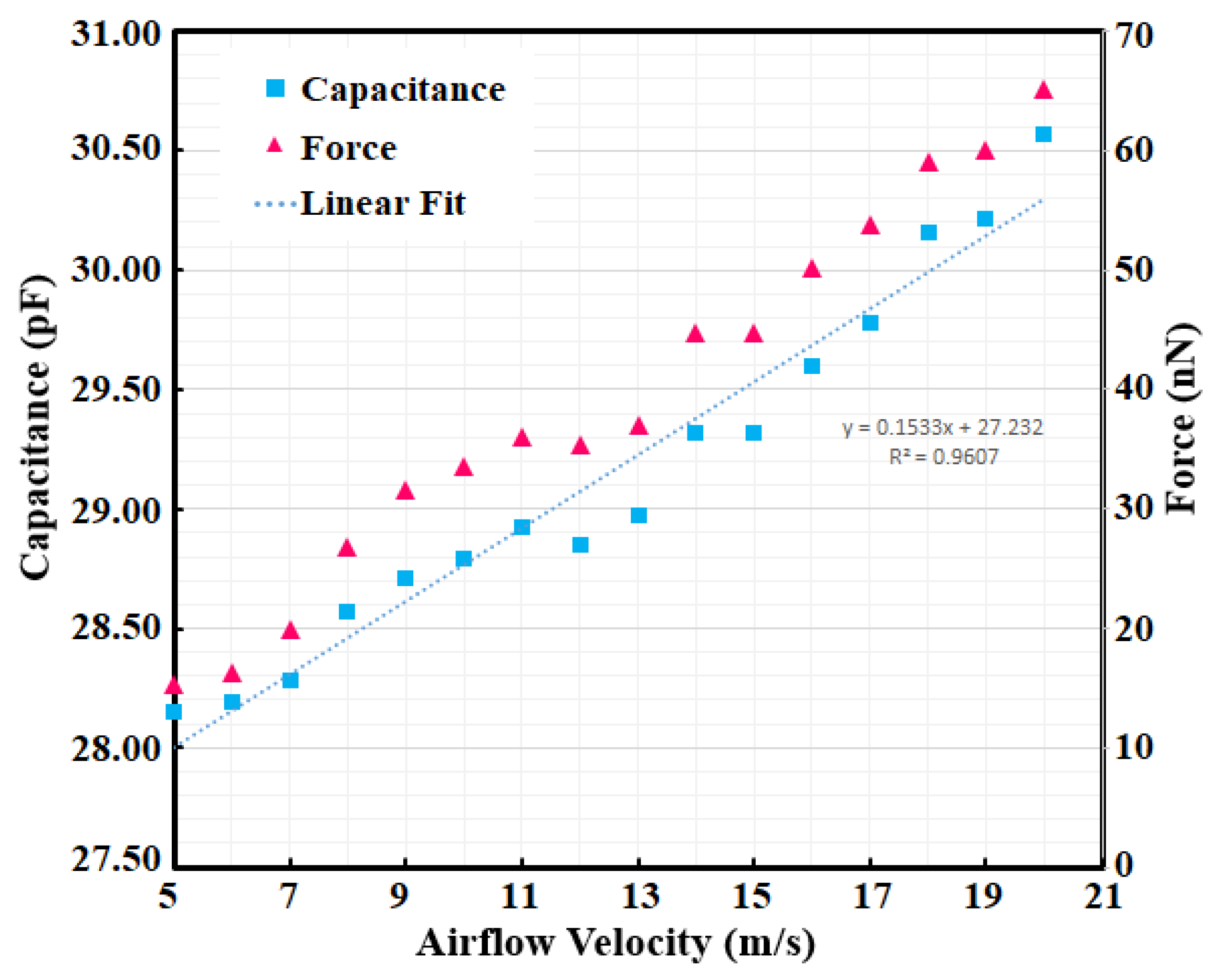
Figure 14 shows, the force generated on a specific surface of the MEMS device (here the upper surface of MCL1) could be related to air velocities, and as shown, the relationship is almost linear. For
R = 14 µm, the approximate relation is
F = 3.1547 V-0.415, and for
R = 12 µm the relation is
F = 1.9876 V + 1.019. The results are derived from simulation, and many factors contribute to the results. Nonetheless, the errors are not high, according to our error analysis explained in
Table 1. The linear-fit equations, which are related to the airflow velocity and force generated on the surface of MCL1, are promising results that reveal this fact that it is possible to control the force on a surface or volume in MEMS components by controlling the airflow velocity, and that is the key feature of the AbFM system. Having a controllable air pressure on a surface could be calculated numerically and then the resulting relationship with the experiment can be calibrated. The airflow velocity and the generated force relations are of high importance if the mechanical characterization is our aim. With this approach, we can drive the equation between flow velocity and force generated and then relate the force to output results (here capacitance) for getting the mechanical properties (e.g., Yonge module of elasticity or torsional module in micromirrors).
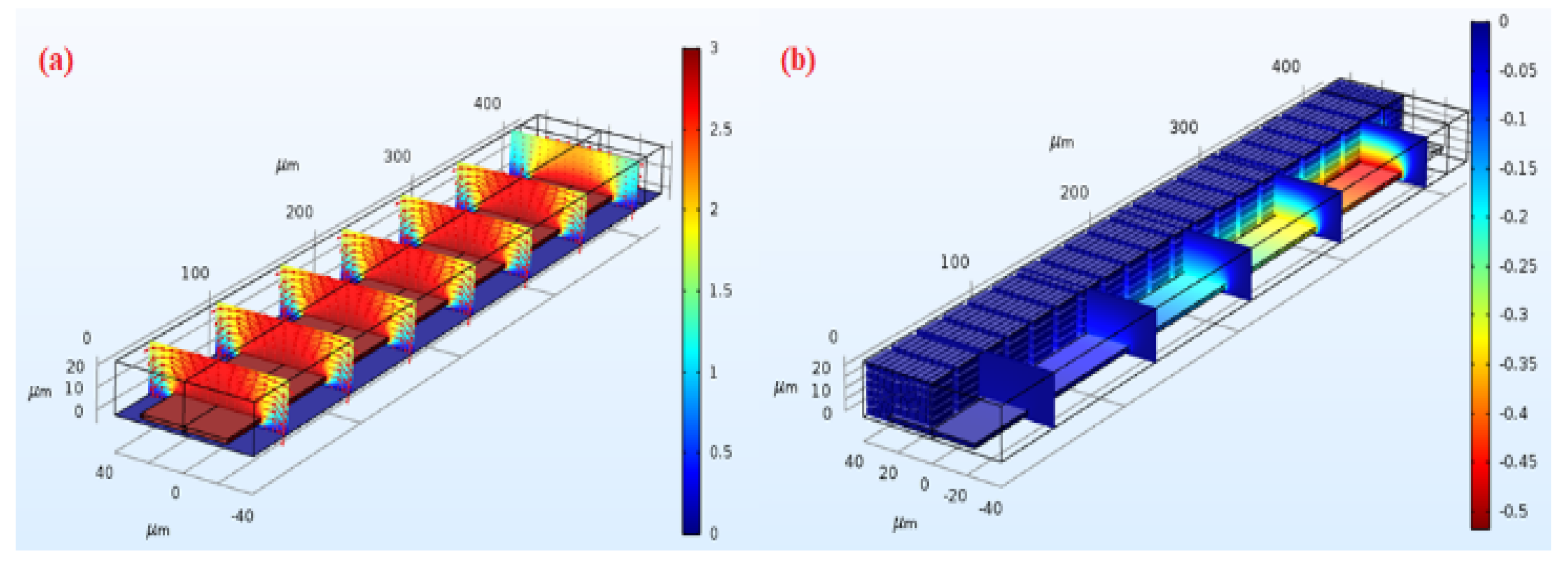
To find out the reason behind the numerical results of force exerted on MCLs with the length of 250 µm and 400 µm, the profile of air velocity and its corresponding pressure at a plane just above the MCLs is depicted in
Figure 15. It shows that each MCL that is closer to the center and microhole senses more pressure and consequently deflects more.
Figure 15 demonstrates why MCL1 deflects more and why MCL D senses low force compared to others. This is the reason that MLCs with
L = 250 µm resulted in considerably lower force compared to MCLs with
L = 400 µm because of their position. However, this force will deflect the mechanical parts, and even nanometer deflections are enough to be recognized in the capacitive sensor and other transaction mechanisms. For this reason, an electrostatic simulation is done for measuring the output capacitance when this force is applied.
When the generated forces on MCLs are determined, the forces were used as a required input for calculation of capacitance in electrostatic simulation by applying the same force for analysis of voltage and electrical field generation in the system. The microcantilevers distance with the substrate was about 2 µm, and the bias voltage was 5 V, which is shown in
Figure 16. The resulting capacitance was derived for each velocity of the air and, therefore a specific uniform force on top of the MCL. The resulted capacitance and velocities are represented in
Figure 16 in which for every fluid velocity, there is a corresponding force and capacitance values.
In the electrostatic simulation, the relationship between the air pressure as the stimuli and the electrical output results is conducted. The results are demonstrated in
Figure 17 in which there is approximately a linear relationship between the input stimuli and the electrical output results. The results shown in
Figure 17 are the core results of the AbFM simulation, which could be derived for each component in a MEMS sensor, according to the specific physics of operation.
Figure 18 shows the relationship between capacitance, force, and airflow velocity for a subcomponent of microcantilever die, which is MCL1 (see
Figure 4). There is nearly a linear dependence between capacitance and air velocity. Once the sensor is fabricated, one can use this diagram if one wants to test one component of the die. Here, if a microneedle were placed at the middle of the die plane and the air velocity changed from 5 to 20 m/s, the certain value of capacitance would be expected with some errors (say, 2%). The corresponding CFV (capacitance, force and velocity) diagram is the main reference for further calibration steps, which we call “CFV calibration curve” for component MCL1. There is no difference and in that component; it might be the comb fingers of an accelerometer or the bridge of micromirrors. However, the main process of the AbFM are: (1) preparing a computer-assisted file (CAD) file of the whole die; (2) running an FSI simulation for the whole chip and designing the main parameters such as the hole diameter, vertical distance, and so forth; (3) getting the CFV diagram for calibration purposes. However, this diagram for capacitance output is called CFV but, e.g., for voltage output, could be VFV (voltage, force, and velocity), which is flexible based on electrical output that the sensor would show according to certain mechanical stimuli.
In the next section, how AbFM can help us to recognize a certain microcrack on the MEMS device is discussed.
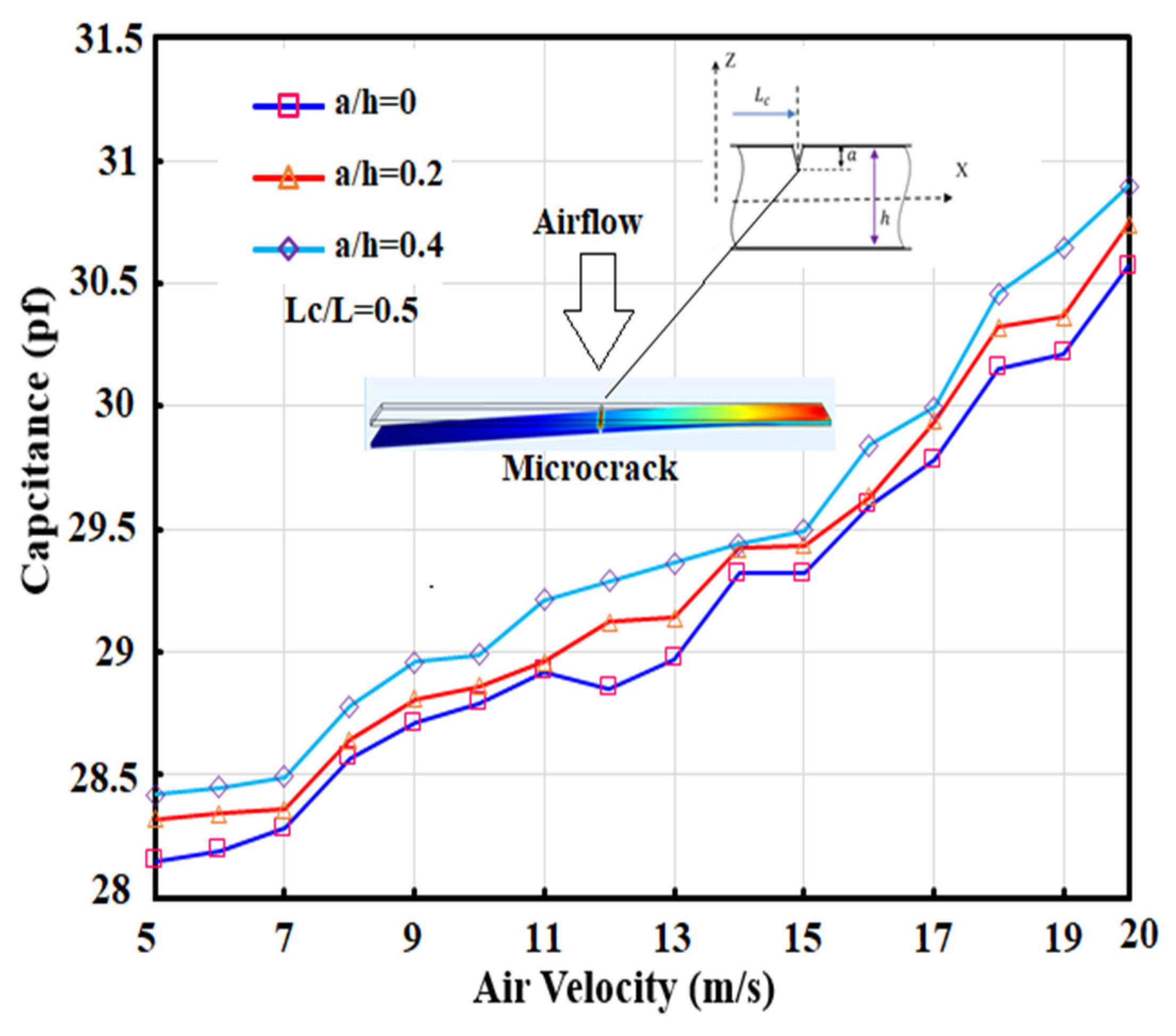
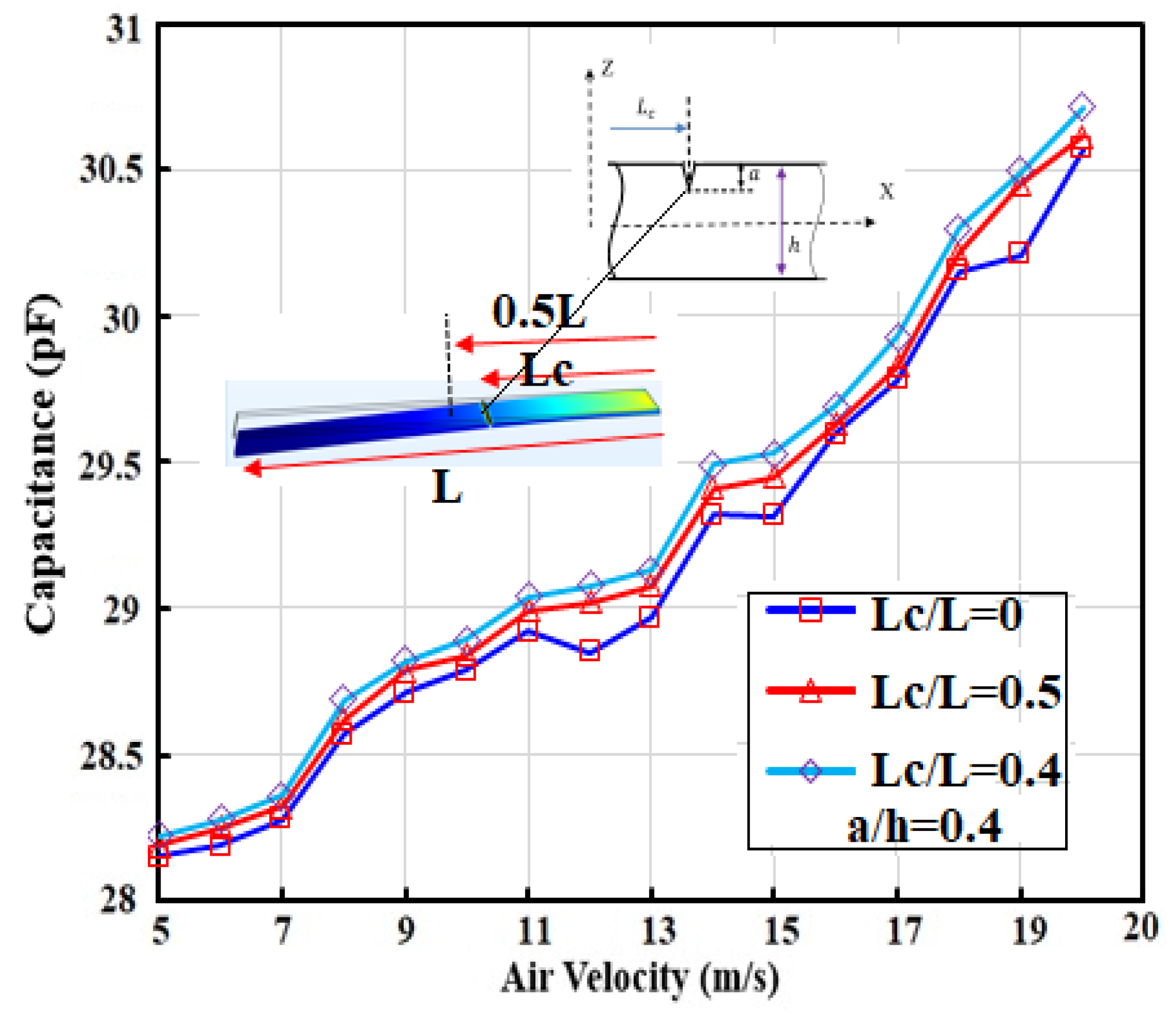
It is supposed that a V-shaped microcrack develops along the width of a microcantilever. This crack has two main characteristics, which are its depth and also its distance relative to the clamped end, which is shown in
Figure 18 and
Figure 19 as Lc/L and a/h in which a is the depth of the micro V-shaped crack.
Figure 18 demonstrates the capacitance output of MCL1 when an airflow with velocity range from 5 m/s to 20 m/s is applied from a microhole with a diameter of 10 µm placed at 400 µm above the center of microcantilever chip (see
Figure 4), the microcrack depth will cause more deflection and results in increasing the overall capacitance between MCL1 and substrate. The same expectations have happened in the resulting diagram for three different conditions: (1) without crack; (2) crack with 0.4 µm depth; (3) crack with 0.8 µm depth, while the crack has been developed exactly at the middle of the microcantilever.
The microcracks would cause more flexibility in the beam when they are located at the longitudinal axis of MCL. There are many forms of microcracks. However, we have treated a simple and too ideal one, though, in reality, the cracks on MEMS devices are far from this ideal shape. These microcracks are a type of non-ideality, which happens due to manufacturing processes and should be recognized in the device before doing more electrical practices and packaging in the testing procedure. It was shown that microcracks with deeper tip length had shown more capacitance compared to the case with smaller size. This is the main take-home message of the functionality of AbFM in testing and fault detection in MEMS devices using airflow. We know by simulation and experiment the functionality and response of a not damaged microcomponent and its response to airflow forces; therefore, it should be considered to be the reference, and the defected MEMS device be compared with it. As
Figure 17 illustrates, there is a good resolution for the recognition of two microcracks with different lengths, which appear in the capacitance results for varying airflow velocity. Another important feature of a microcrack is its exact position on the surface and its depth.
Figure 18 demonstrates the capacitance variation versus airflow velocity for a constant size of microcrack and a different distance from the clamped side.
The location of microcrack as an example of non-ideality could be recognized along the microcantilevers by monitoring the output results which here is capacitance.
Figure 19 shows that there is considerable variation in the output results when the crack position moved from
Lc/L = 0.5 to
Lc/L = 0.4 and also relative to the situation where there is no crack on the surface. There are some common non-idealities in the MEMS industry such as cracks, edge-cutting, and other unexpected mechanical deformation (affects the dynamics and static characteristics of device change) which could be simulated and put into the AbFM simulation for testing and characterizing their availability in the MEMS device.