Piezoelectric Vibration-Based Energy Harvesting Enhancement Exploiting Nonsmoothness
Abstract
1. Introduction
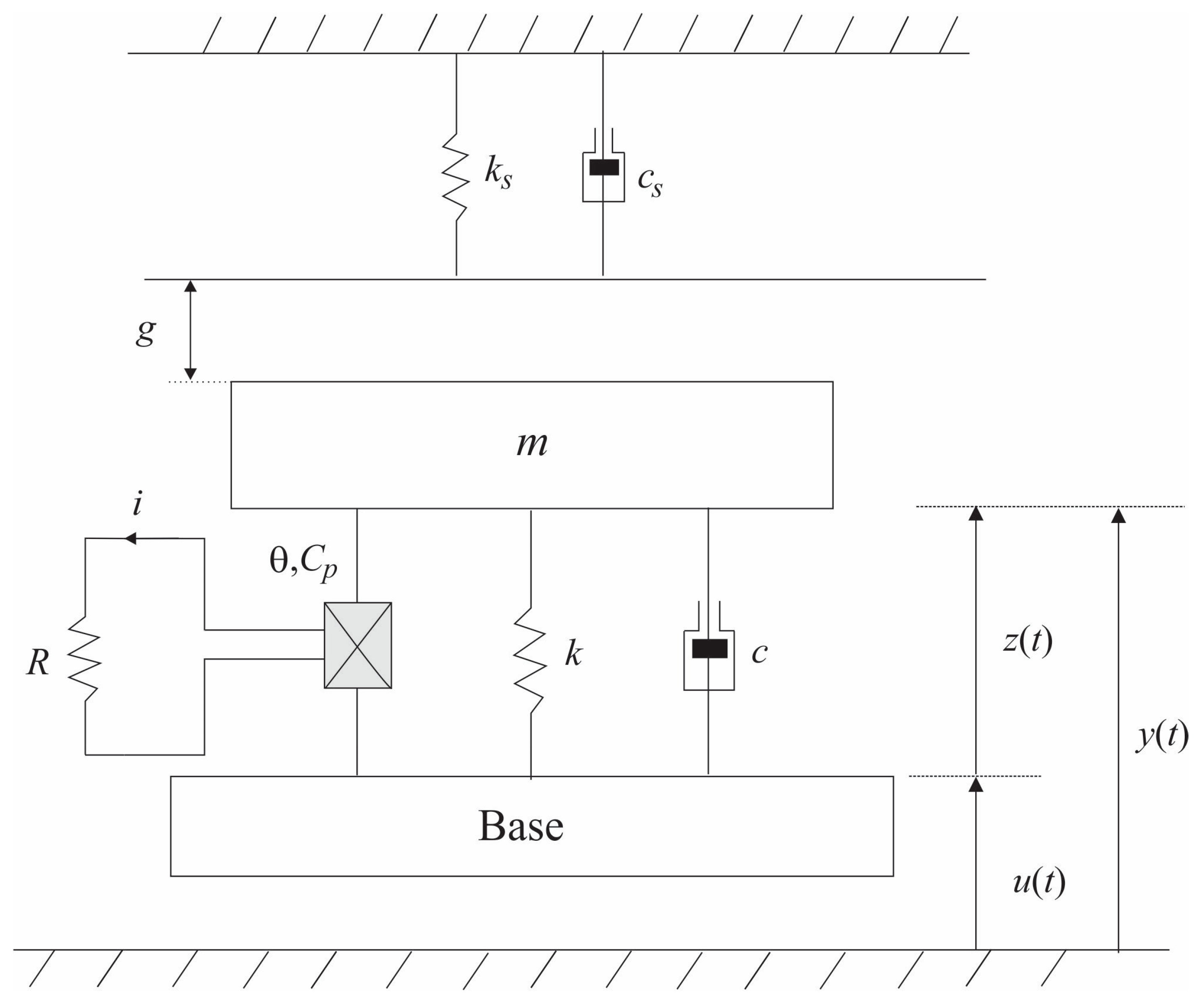
2. The Vibration-Based Energy Harvesting System
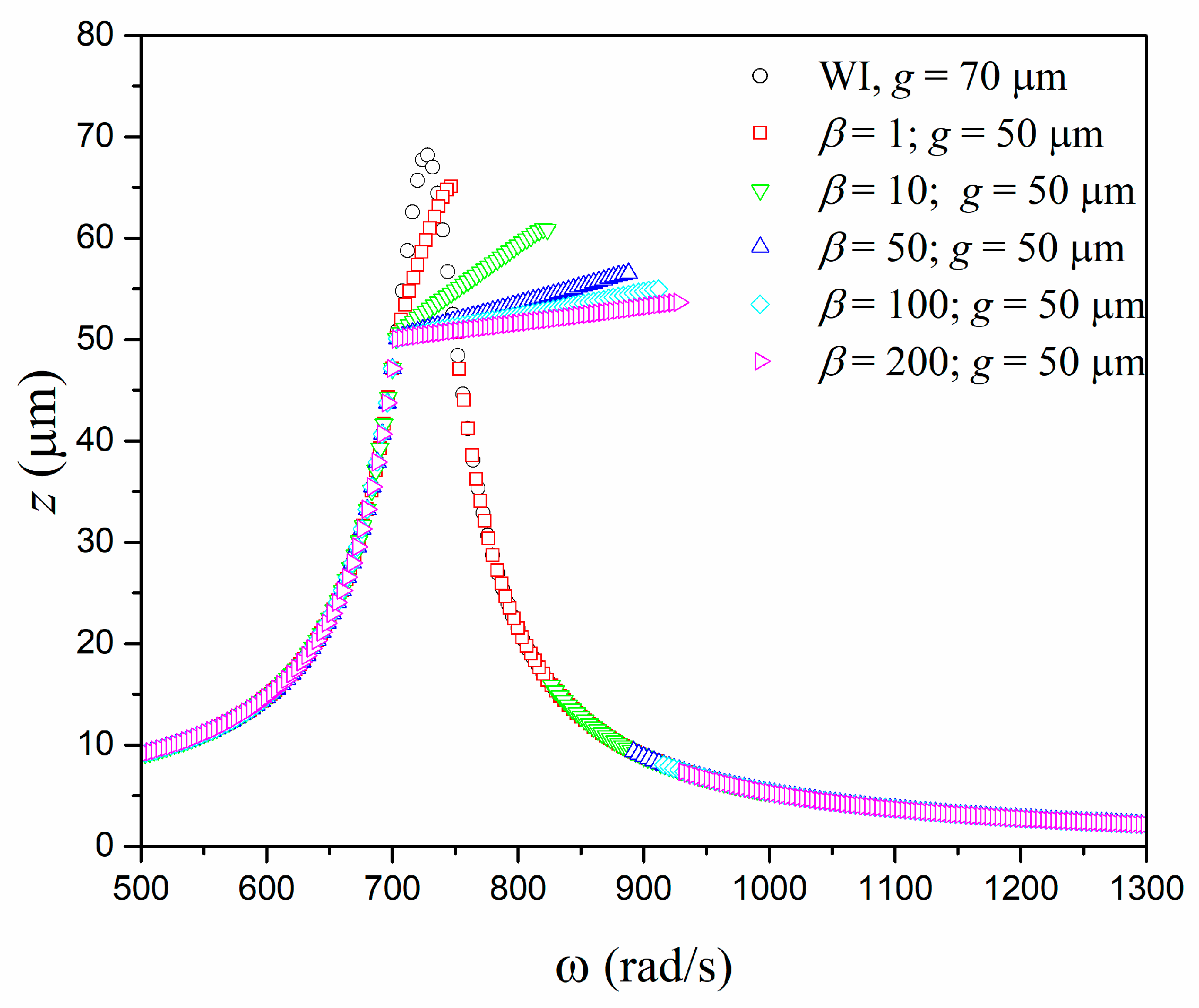
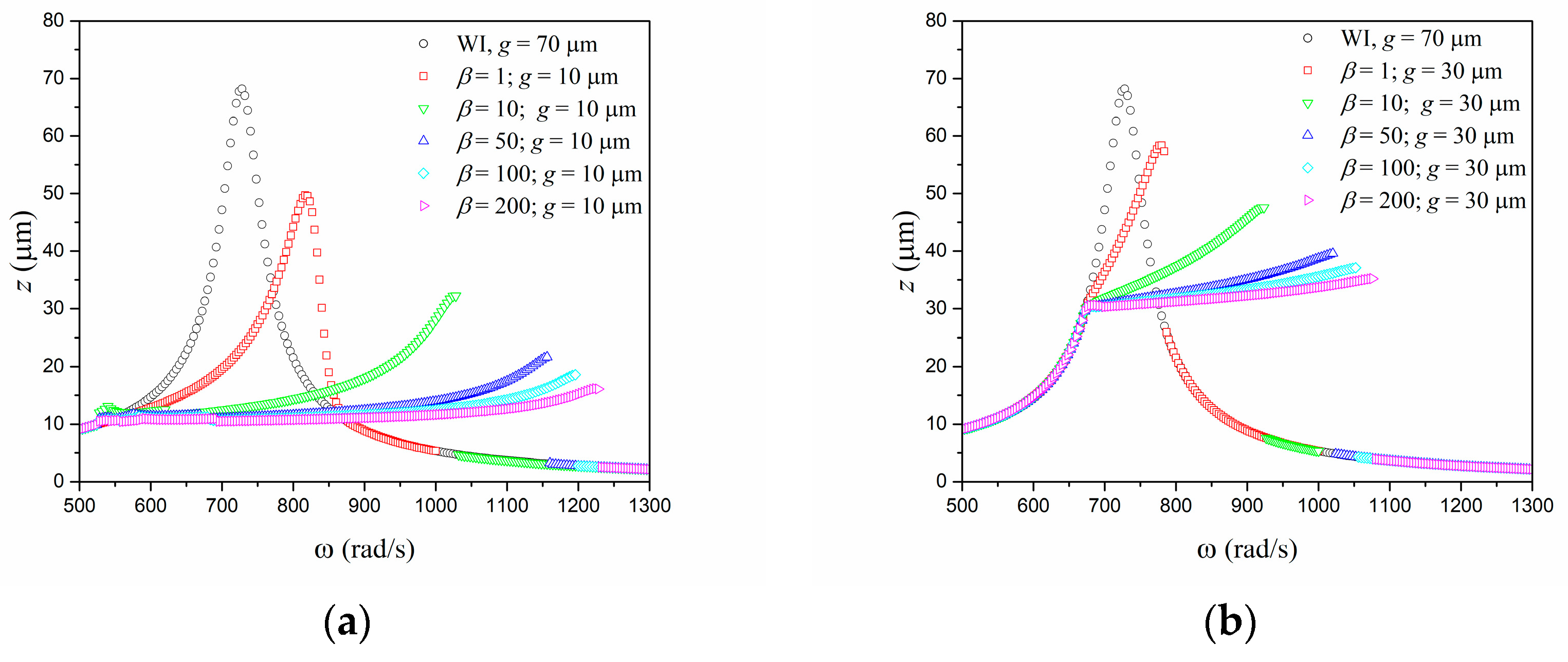
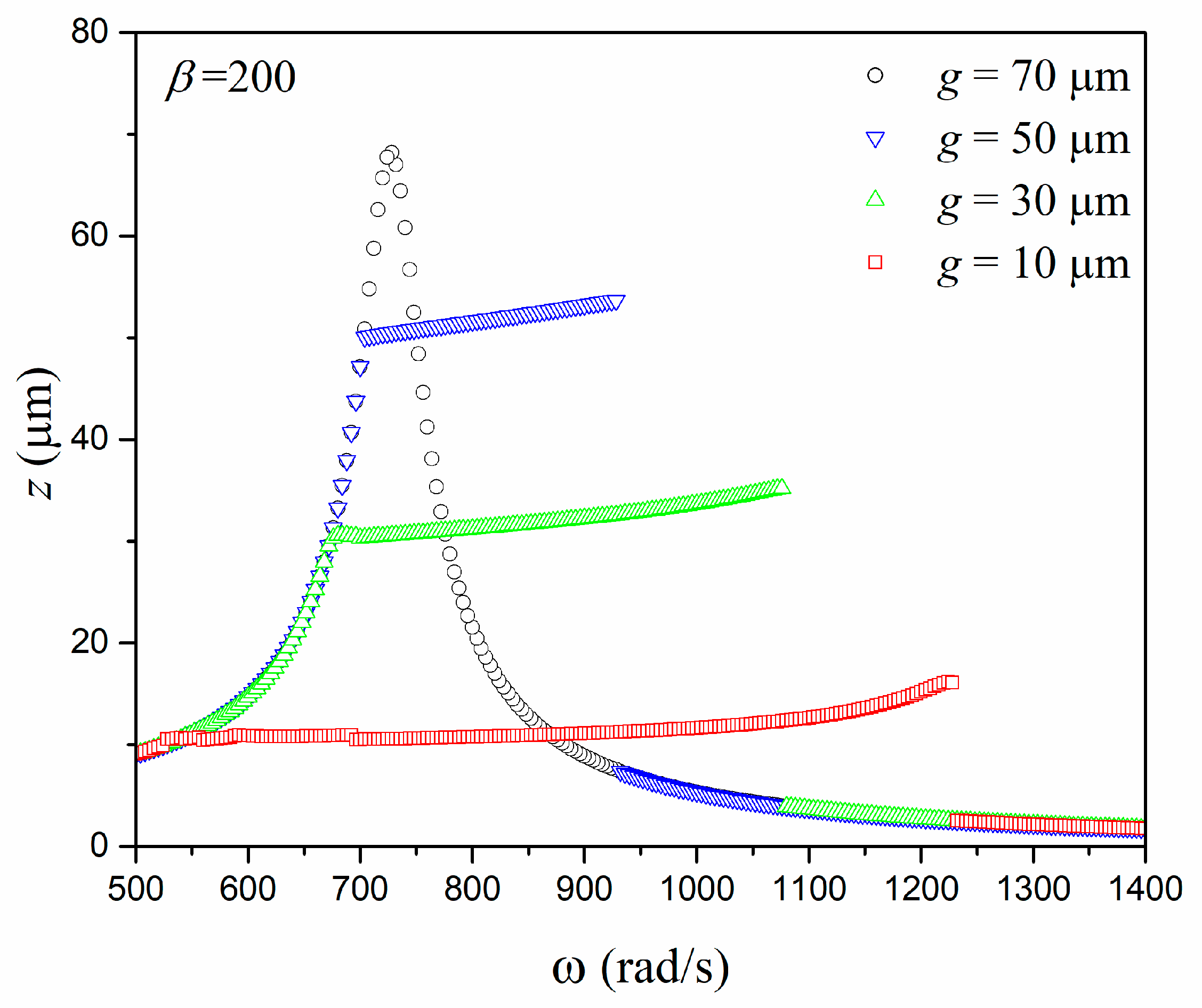
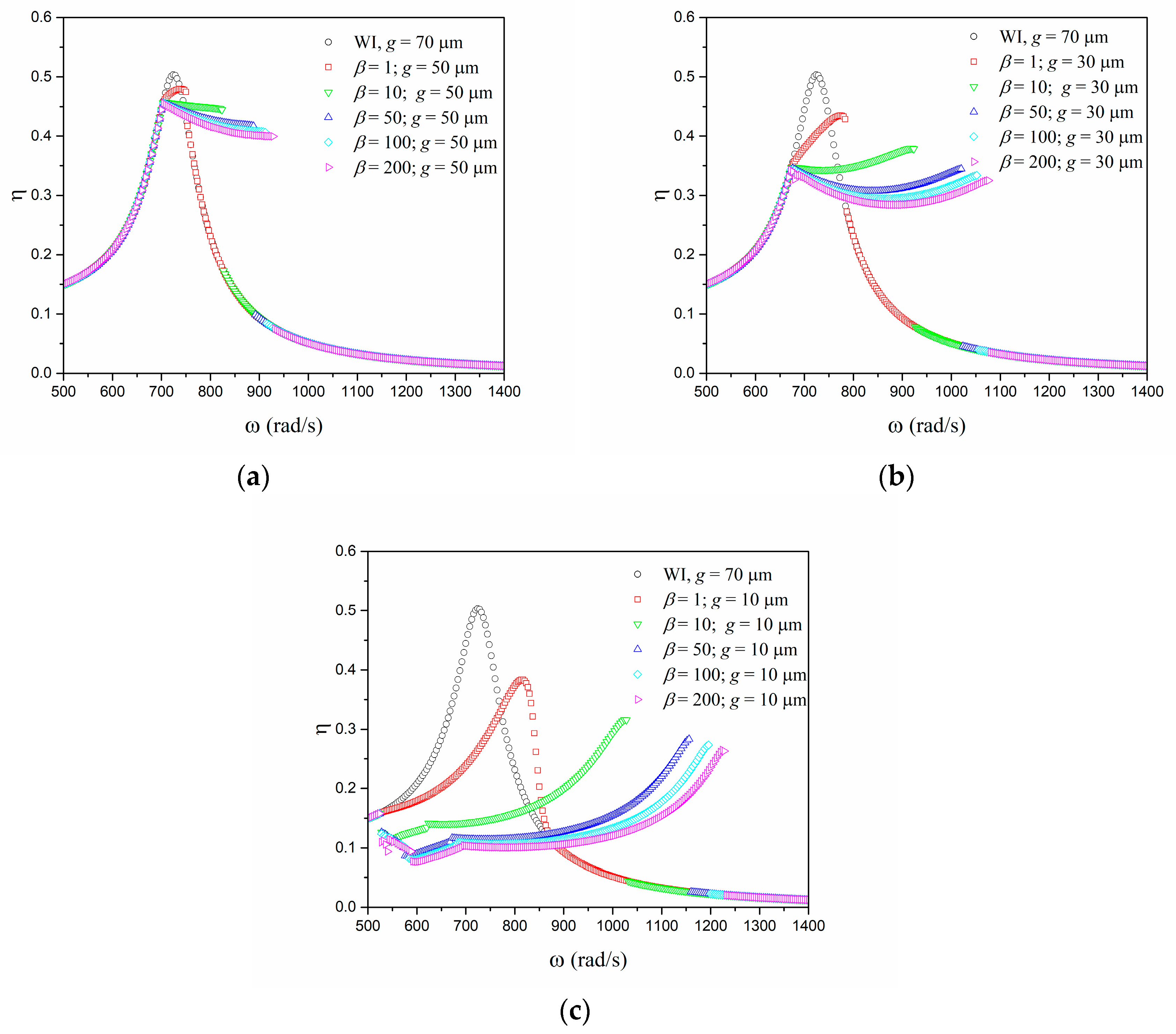
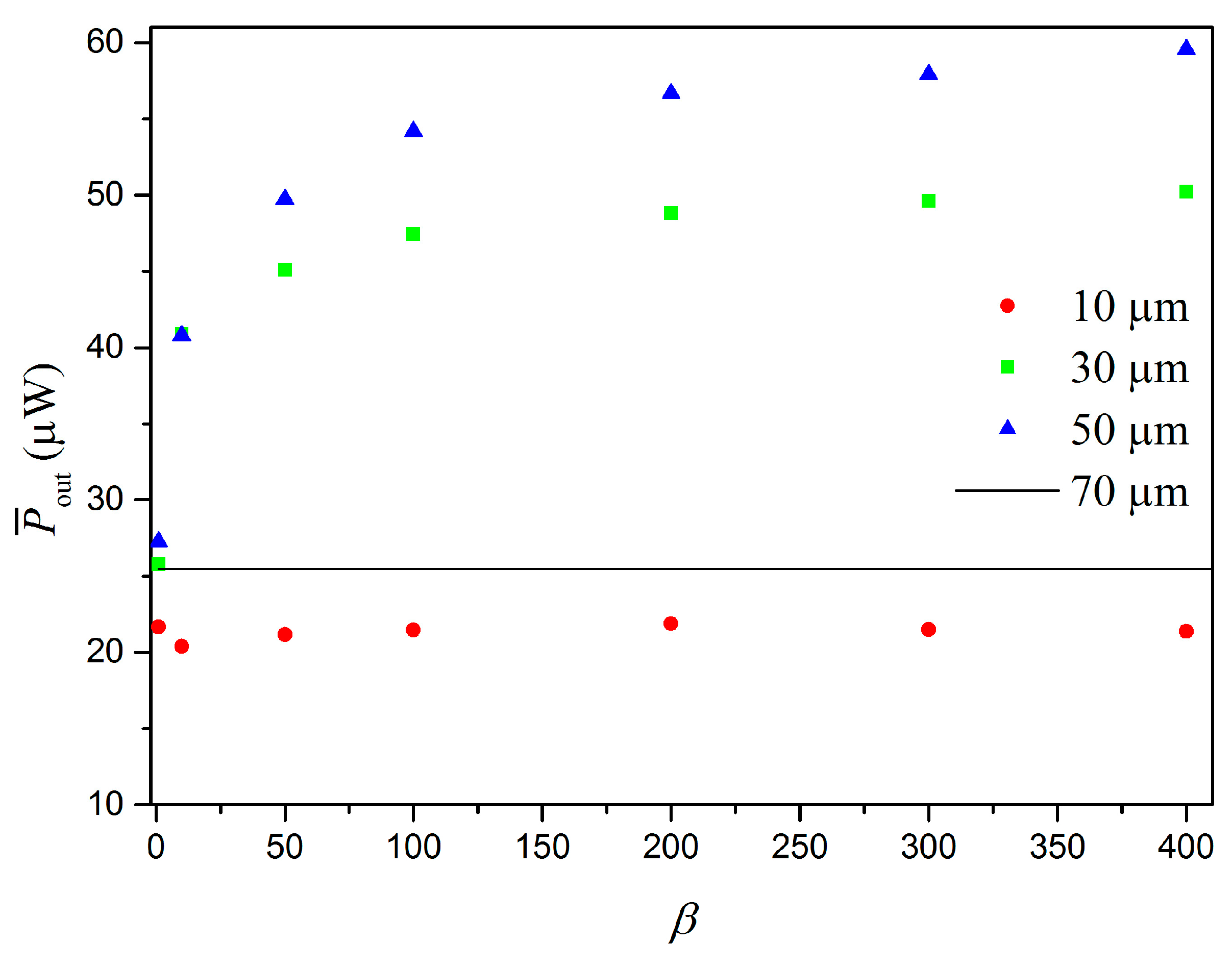
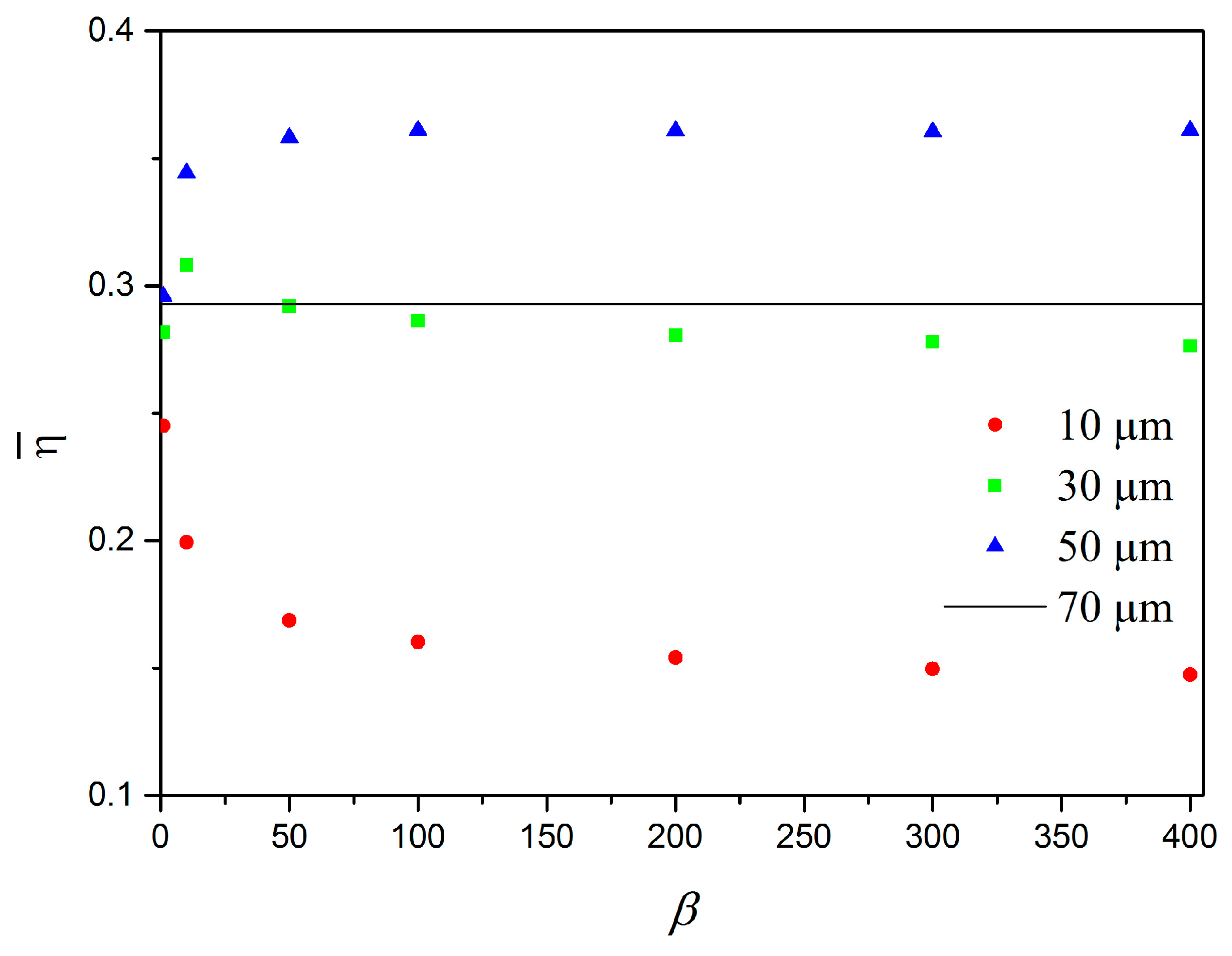
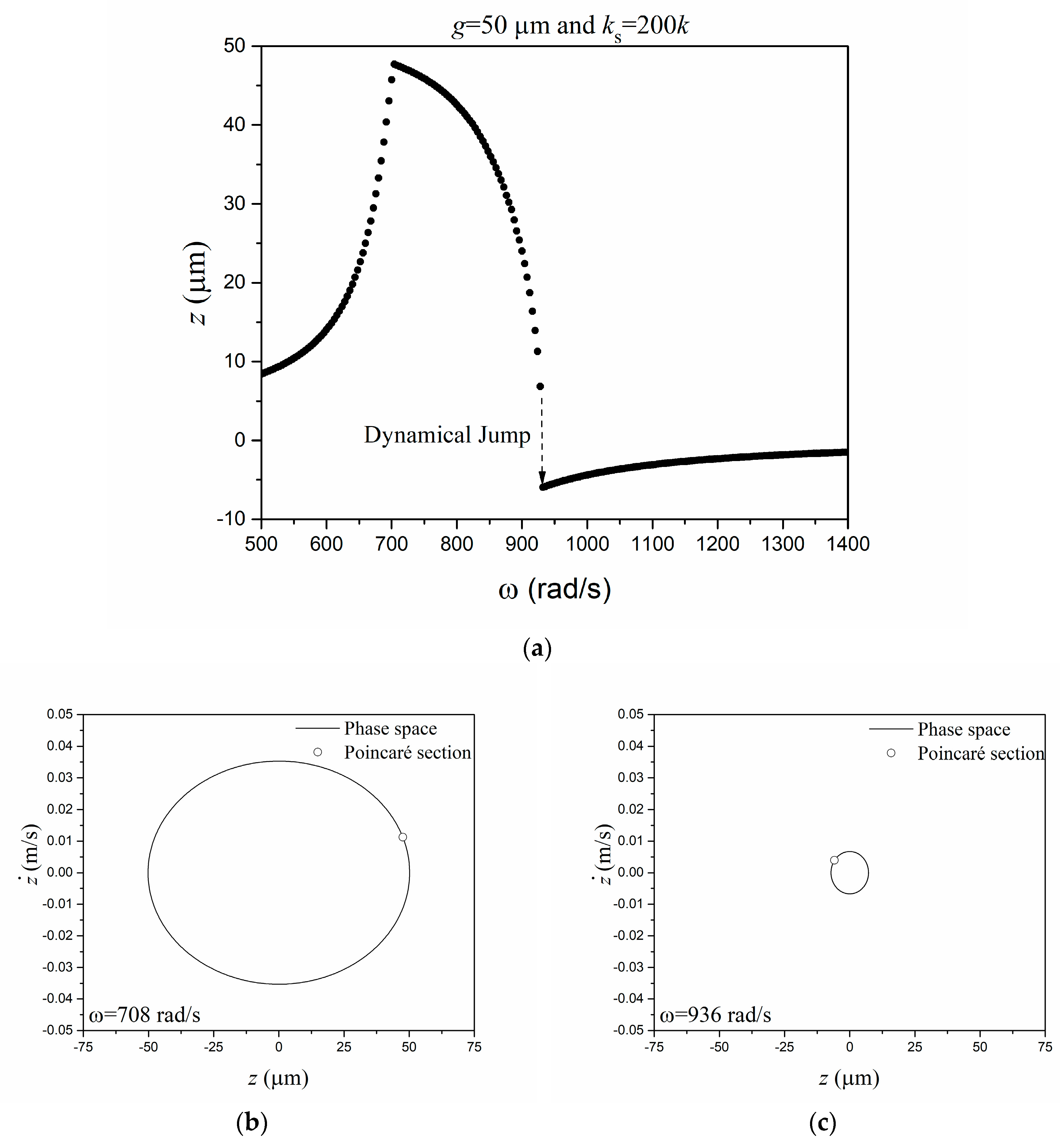
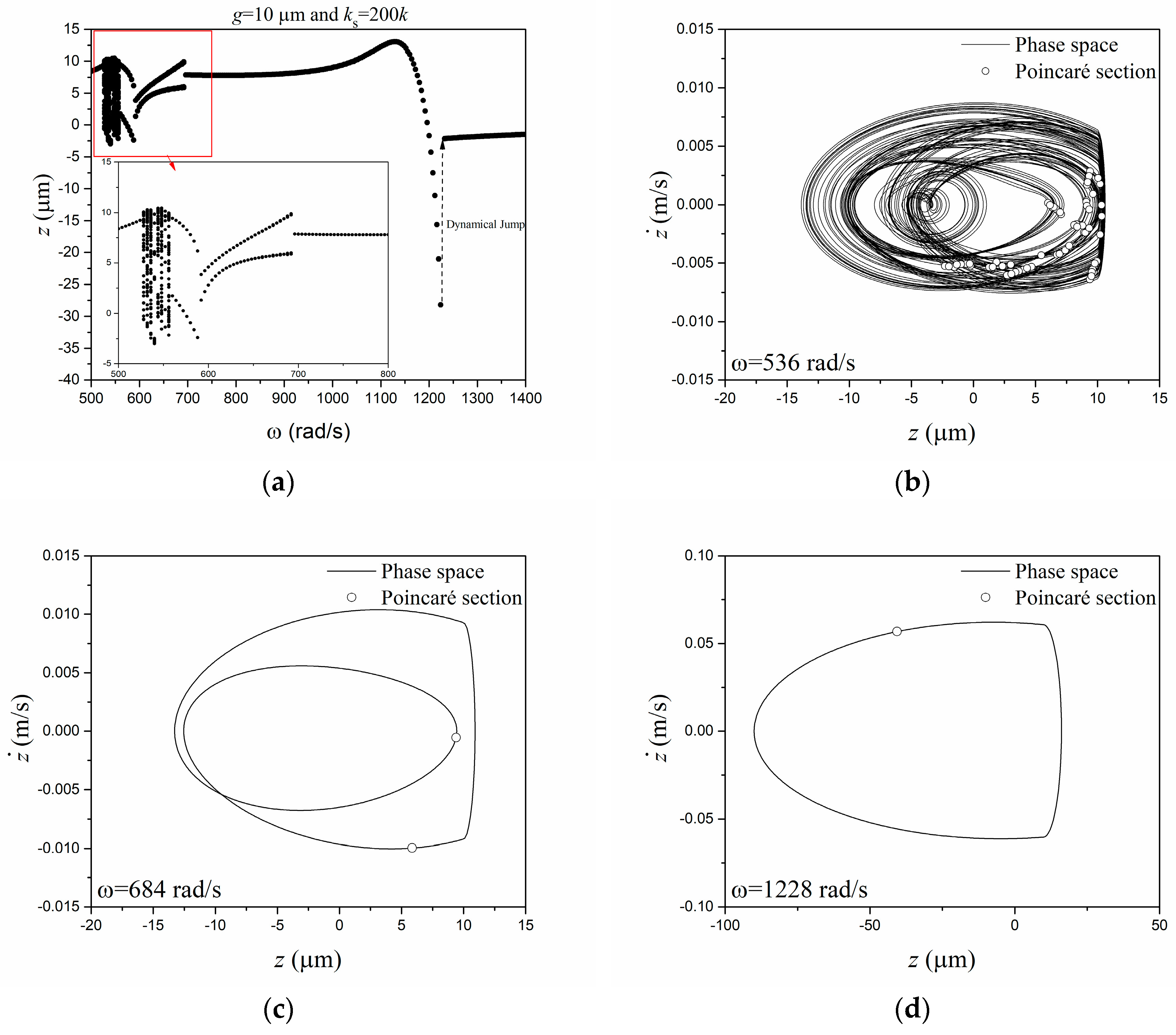
3. Numerical Simulations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hadas, Z.; Vetiska, V.; Huzlik, R.; Singule, V. Model-based design and test of vibration energy harvester for aircraft application. Microsyst. Technol. 2014, 20, 831–843. [Google Scholar] [CrossRef]
- Silva, T.M.P.; De Marqui, C. Self-powered active control of elastic and aeroelastic oscillations using piezoelectric material. J. Intell. Mater. Syst. Struct. 2017, 28, 2023–2035. [Google Scholar] [CrossRef]
- Arsalan, M.J.; Ahmad, T.; Saeed, S.A. Energy Harvesting for Downhole Applications in Open-hole Multilaterals. Soc. Pet. Eng. 2018. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Toward Broadband Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Dane Quinn, D.D. On the Role of Nonlinearities in Vibratory Energy Harvesting: A Critical Review and Discussion. ASME. Appl. Mech. Rev. 2014, 66, 040801–040824. [Google Scholar] [CrossRef]
- Zhang, H.; Corr, L.R.; Ma, T. Issues in vibration energy Harvesting. J. Sound Vib. 2018, 421, 79–90. [Google Scholar] [CrossRef]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. Unified nonlinear electroelastic dynamics of a bimorph piezoelectric cantilever for energy harvesting, sensing, and actuation. Nonlinear Dyn. 2015, 79, 1727–1743. [Google Scholar] [CrossRef]
- De Paula, A.S.; Inman, D.J.; Savi, M.A. Energy harvesting in a nonlinear piezomagnetoelastic beam subjected to random excitation. Mech. Syst. Signal Process. 2015, 54, 405–416. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A Vibration Energy Harvesting Device with Bidirectional Resonance Frequency Tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Reissman, T.; Wolff, E.M.; Garcia, E. Piezoelectric Resonance Shifting Using Tunable Nonlinear Stiffness. In Proceedings of the SPIE Active and Passive Smart Structures and Integrated Systems, San Diego, CA, USA, 9–12 March 2009; Volume 7288, p. 72880G. [Google Scholar]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons Ltd.: Chichester, UK, 2011. [Google Scholar]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Andò, B.; Baglio, S.; Trigona, C. Improved Energy Harvesting from Wideband Vibrations by Nonlinear Piezoelectric Converters. Sens. Actuators A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electroelastic energy harvesters: Modeling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Cammarano, A.; Neild, S.A.; Burrow, S.G.; Inman, D.J. The bandwidth of optimized nonlinear vibration-based energy harvesters. Smart Mater. Struct. 2014, 23, 055019–055028. [Google Scholar] [CrossRef]
- Roundy, S.; Zhang, Y. Toward self-tuning adaptive vibration based micro-generators. In Proceedings of the SPIE Smart Structures, Devices, and Systems II, Singapore, 24–26 October 2005; Volume 5649, pp. 373–384. [Google Scholar]
- Dutoit, N.E.; Wardle, B.L. Performance of microfabricated piezoelectric vibration energy harvesters. Integr. Ferroelectr. 2006, 83, 13–32. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Erturk, A.; Vieira, W.G.R.; De Marqui, C., Jr.; Inman, D.J. On the energy harvesting potential of piezoaeroelastic systems. Appl. Phys. Lett. 2010, 96, 184103. [Google Scholar] [CrossRef]
- Kim, M.; Hoegen, M.; Dugundji, J.; Wardle, B.L. Modeling and experimental verification of proof mass effects on vibration energy harvester performance. Smart Mater. Struct. 2010, 19, 045023. [Google Scholar] [CrossRef]
- Crawley, E.F.; Anderson, E.H. Detailed models of piezoceramic actuation of beams. J. Intell. Mater. Syst. Struct. 1990, 1, 4–25. [Google Scholar] [CrossRef]
- Triplett, A.; Quinn, D.D. The Effect of Non-linear Piezoelectric Coupling on Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2009, 20, 1959–1967. [Google Scholar] [CrossRef]
- Silva, L.L.; Monteiro, P.C.; Savi, M.A.; Netto, T.A. Effect of the piezoelectric hysteretic behavior on the vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2013, 24, 1285. [Google Scholar] [CrossRef]
- Silva, L.L.; Monteiro, P.C.; Savi, M.A.; Netto, T.A. On the Nonlinear Behavior of the Piezoelectric Coupling on Vibration-Based Energy Harvesters. Shock Vib. 2015, 2015, 739381. [Google Scholar] [CrossRef]
- Avirovik, D.; Kumar, A.; Bodnar, R.J.; Priya, S. Remote light energy harvesting and actuation using shape memory alloy-piezoelectric hybrid transducer. Smart Mater. Struct. 2013, 22, 052001–052007. [Google Scholar] [CrossRef]
- Silva, L.L.; Oliveira, S.A.; Pacheco, P.M.C.L.; Savi, M.A. Synergistic Use of Smart Materials for Vibration-Based Energy Harvesting. Eur. Phys. J. Spec. Top. 2015, 224, 3005–3012. [Google Scholar] [CrossRef]
- Le, C.P.; Halvorsen, E.; Sørasen, O.; Yeatman, E.M. Wideband excitation of an electrostatic vibration energy harvester with power-extracting end-stops. Smart Mater. Struct. 2013, 22, 075020–075029. [Google Scholar] [CrossRef]
- Bai, Y.; Carl, M.; Button, T.W. Investigation of using free-standing thick-film piezoelectric energy harvesters to develop wideband devices. Int. J. Struct. Stab. Dyn. 2014, 14, 1440016. [Google Scholar] [CrossRef]
- Hu, H.P.; Cui, Z.J.; Cao, J.G. Performance of a piezoelectric bimorph harvester with variable width. J. Mech. 2007, 23, 197–202. [Google Scholar] [CrossRef]
- Friswell, M.I.; Ali, S.F.; Adhikari, S.; Lees, A.W.; Bilgen, O.; Litak, G. Nonlinear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Davis, C.L. Can a coupling coefficient of a piezoelectric actuator be higher than those of its active material? J. Intell. Mater. Syst. Struct. 1997, 8, 859–867. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K. Resonance Tuning of Piezoelectric Vibration Energy Scavenging Generators Using Compressive Axial Preload. Smart Mater. Struct. 2006, 15, 14131420. [Google Scholar] [CrossRef]
- Betts, D.N.; Kim, H.A.; Bowen, C.R.; Inman, D.J. Optimal configurations of bistable piezo-composites for energy harvesting. Appl. Phys. Lett. 2012, 100, 114104. [Google Scholar] [CrossRef]
- Soliman, M.S.M.; Abdel-Rahman, E.M.; El-Saadany, E.F.; Mansour, R.R. A wideband vibration-based energy harvester. J. Micromech. Microeng. 2008, 18, 115021. [Google Scholar] [CrossRef]
- Kaur, S.; Halvorsen, E. Parameter sensitivity of an in-plane gap closing electrostatic energy harvester with end-stop impacts. J. Intell. Mater. Syst. Struct. 2016, 1, 11. [Google Scholar] [CrossRef]
- Blystad, L.C.J.; Halvorsen, E. A piezoelectric energy harvester with a mechanical end stop on one side. Microsyst. Technol. 2011, 17, 505–551. [Google Scholar] [CrossRef]
- Vijayan, K.; Friswell, M.I.; Khodaparast, H.H.; Adhikari, S. Energy harvesting in a coupled system using nonlinear impact. Struct. Health Monit. 2014, 5, 255–261. [Google Scholar]
- Basset, P.; Galayko, D.; Cottone, F.; Guillemet, R.; Blokhina, E.; Marty, F.; Bourouina, T. Electrostatic vibration energy harvester with combined effect of electrical nonlinearities and Mechanical impact. J. Micromech. Microeng. 2014, 24, 035001. [Google Scholar] [CrossRef]
- Rysak, A.; Müller, M.; Borowiec, M.; Zubrzycki, J.; Litak, G.; Godlewska-Lach, A.; Wittstock, V. Broadband Concept of Energy Harvesting in Beam Vibrating Systems for Powering Sensors. Adv. Sci. Technol. Res. J. 2014, 8, 62–67. [Google Scholar]
- Savi, M.A.; Divenyi, S.; Franca, L.F.P.; Weber, H.I. Numerical and experimental investigations of the on linear dynamics and chaos in non-smooth systems. J. Sound Vib. 2007, 30, 59–73. [Google Scholar] [CrossRef]
- Divenyi, S.; Savi, M.A.; Franca, L.F.P.; Weber, H.I. Nonlinear dynamics and chaos in systems with discontinuous support. Shock Vib. 2006, 13, 315–326. [Google Scholar] [CrossRef]
- Divenyi, S.; Savi, M.A.; Weber, H.I.; Franca, L.F.P. Experimental investigation of an oscillator with discontinuous support considering different system aspects. Chaos Solitons Fractals 2008, 38, 685–695. [Google Scholar] [CrossRef]
- Jacquelin, E.; Adhikari, S.; Friswell, M.I. A piezoelectric device for impact energy harvesting. Smart Mater. Struct. 2011, 20, 105008–105020. [Google Scholar] [CrossRef]
- Vijayan, K.; Friswell, M.I.; Khodaparast, H.H.; Adhikari, S. Non-linear energy harvesting from coupled impacting beams. Int. J. Mech. Sci. 2015, 96, 101–109. [Google Scholar] [CrossRef]
- Kaur, S.; Halvorsen, E.; Søråsen, O.; Yeatman, E.M. Numerical Analysis of Nonlinearities due to Rigid End-Stops in Energy Harvesters. In Proceedings of the Conference: Power MEMS Technical Digest Poster Sessions, Leuven, Belgium, 1–3 December 2010. [Google Scholar]
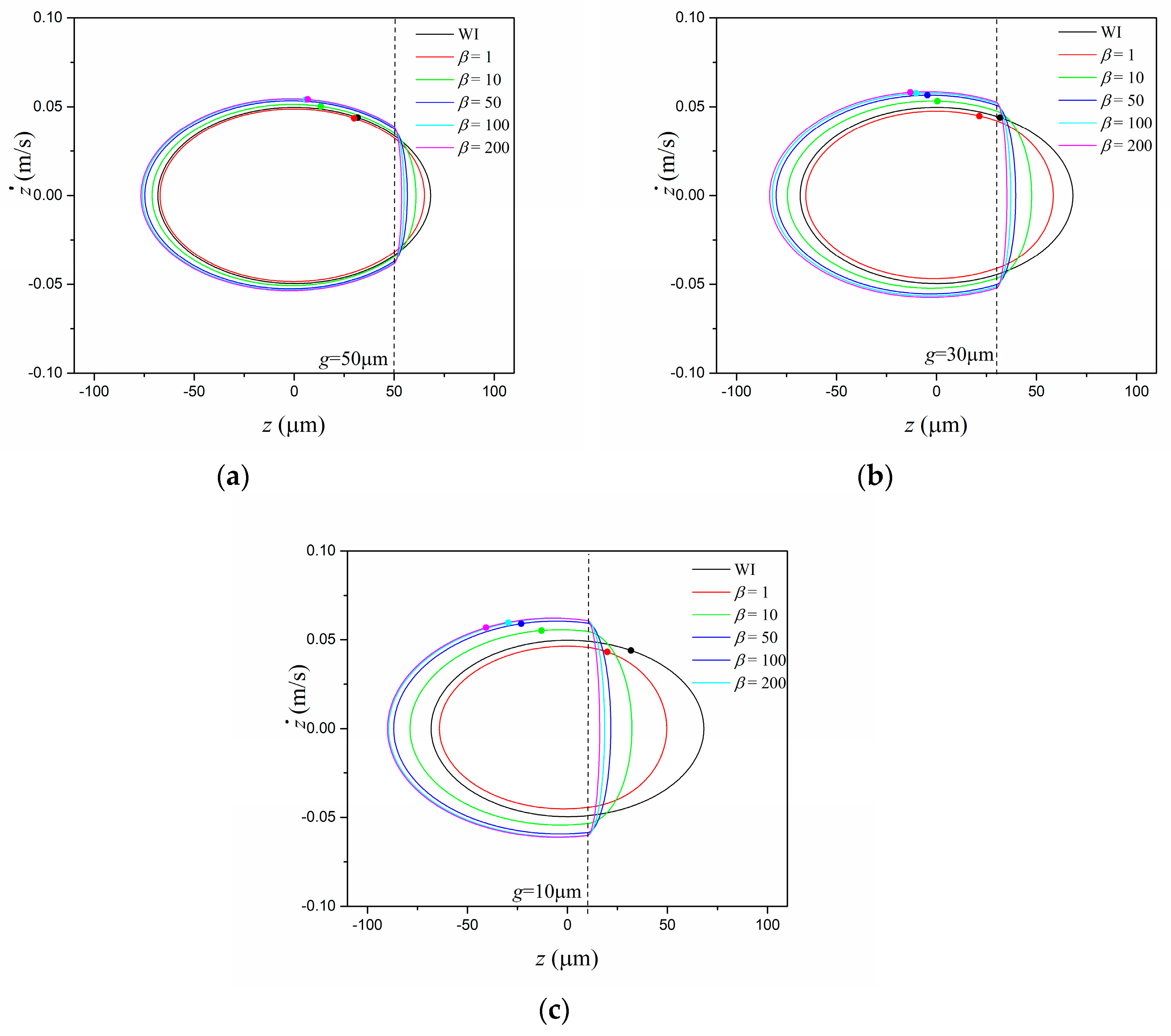
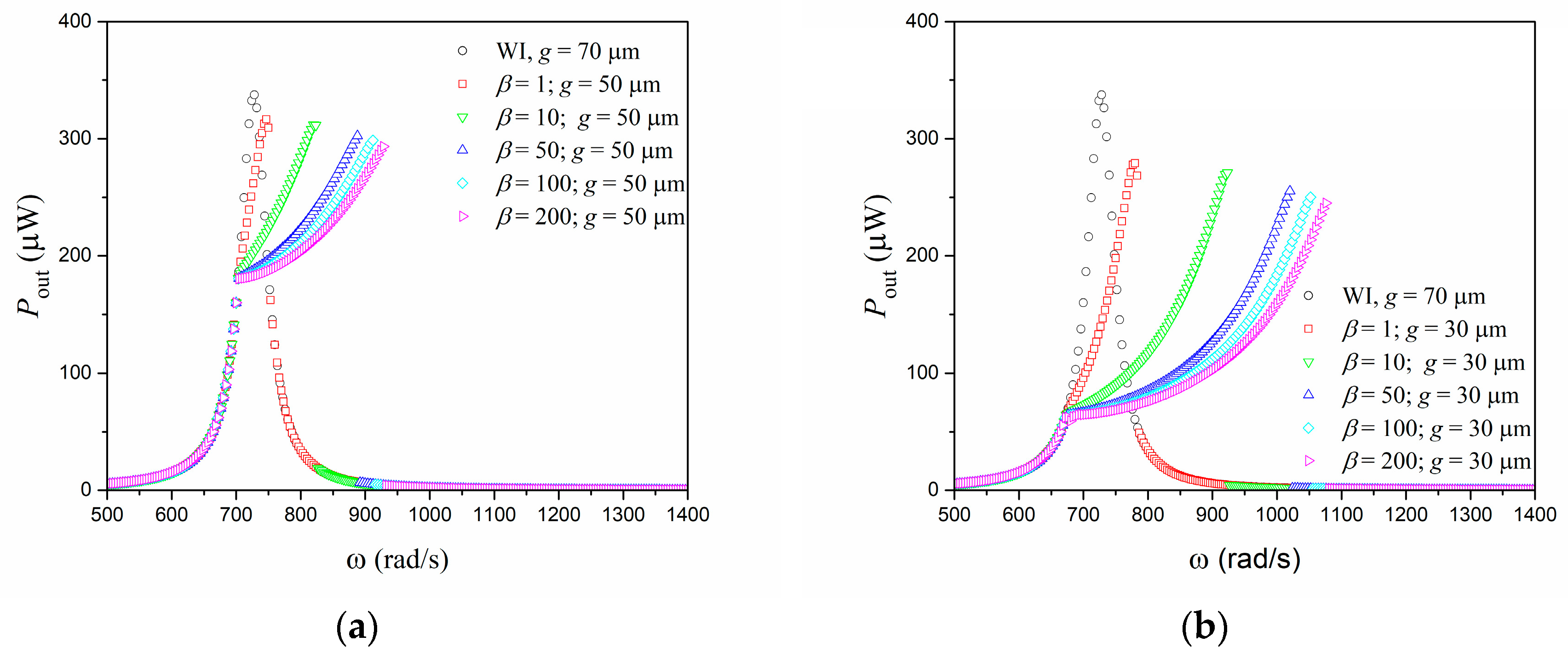
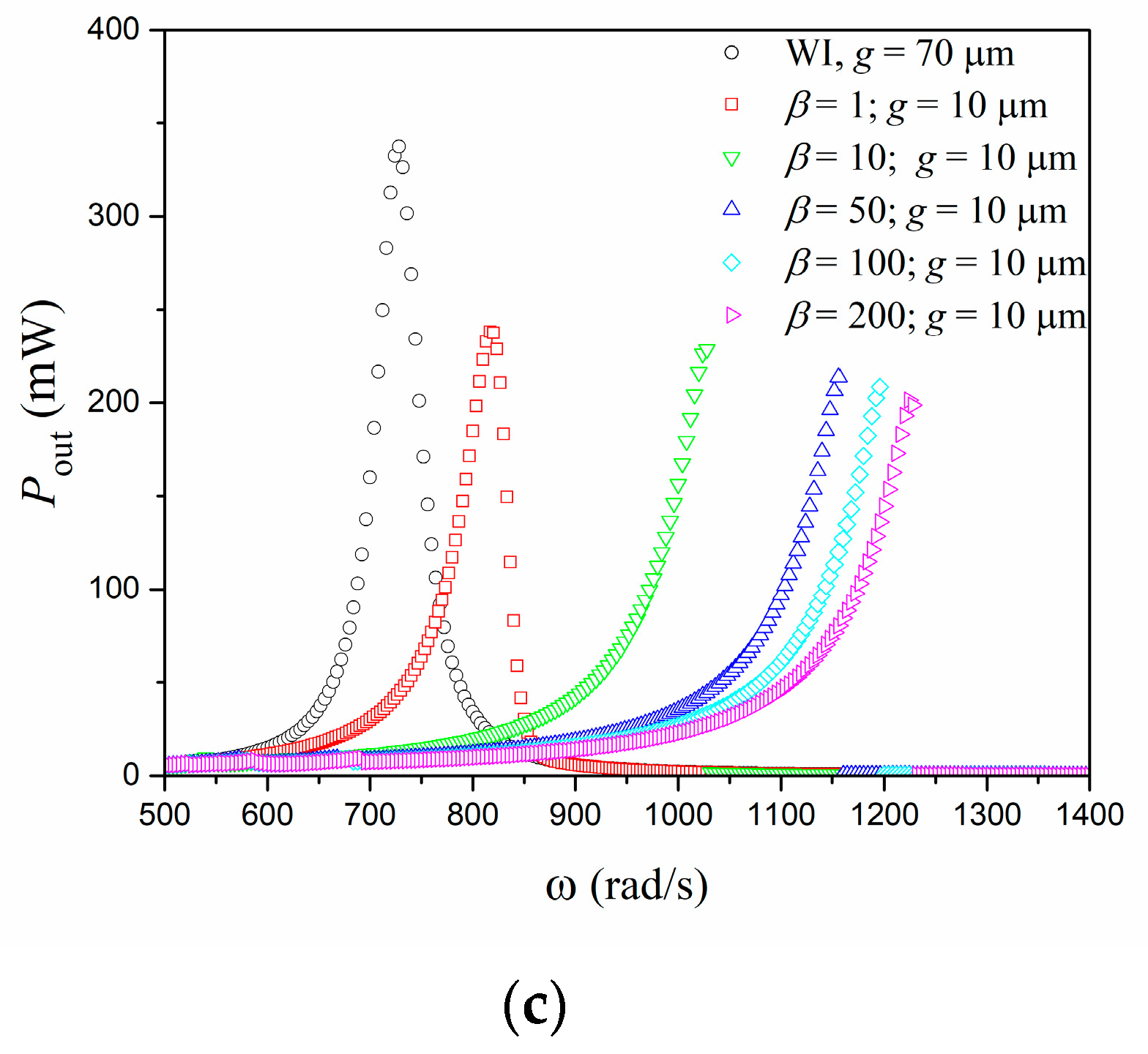
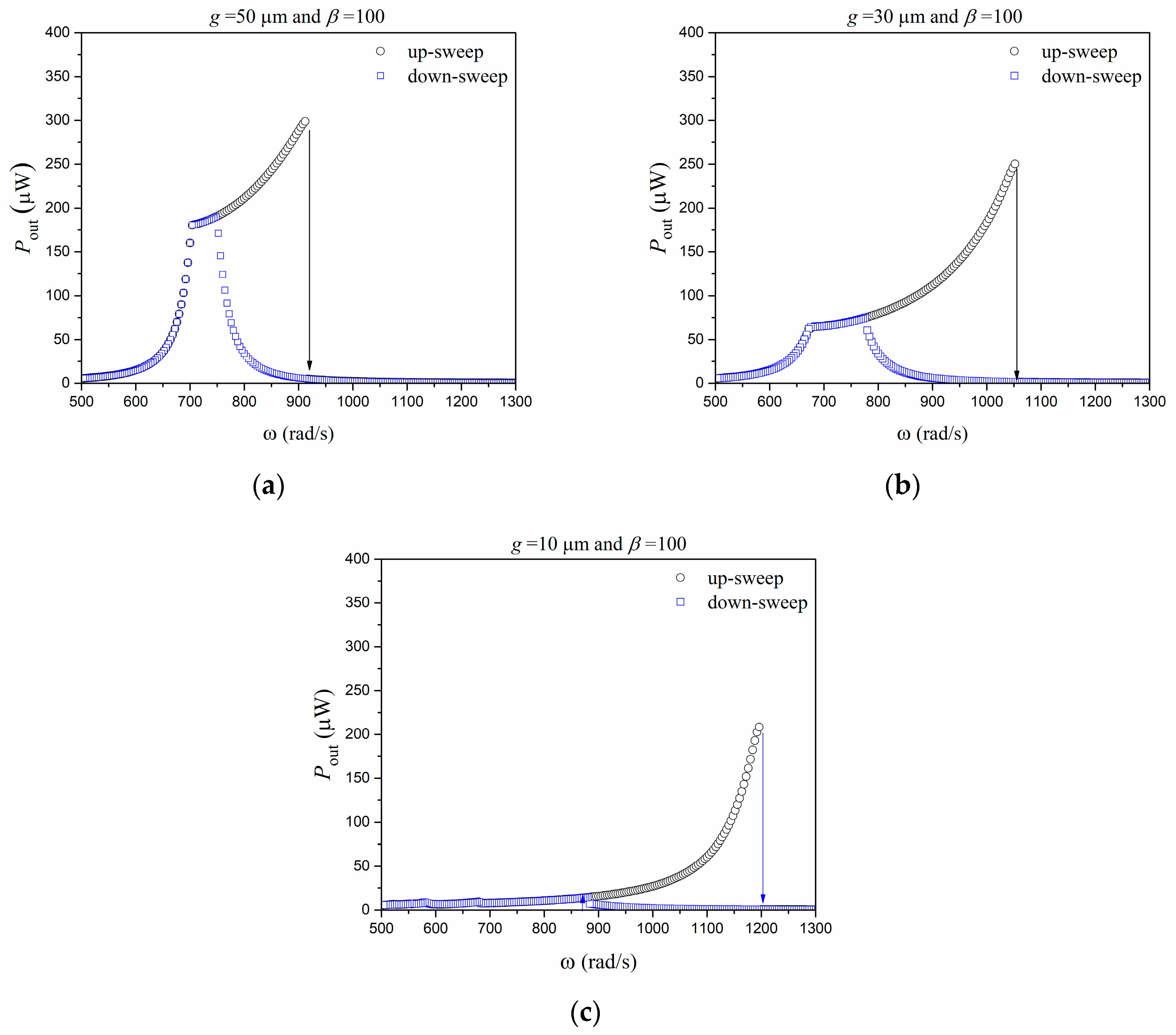
| (kg) | ||||||
|---|---|---|---|---|---|---|
| 0.00878 | 4150 | 2.5 | −0.004688 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, R.; Monteiro, L.L.S.; Monteiro, P.C.C., Jr.; Pacheco, P.M.C.L.; Savi, M.A. Piezoelectric Vibration-Based Energy Harvesting Enhancement Exploiting Nonsmoothness. Actuators 2019, 8, 25. https://doi.org/10.3390/act8010025
Ai R, Monteiro LLS, Monteiro PCC Jr., Pacheco PMCL, Savi MA. Piezoelectric Vibration-Based Energy Harvesting Enhancement Exploiting Nonsmoothness. Actuators. 2019; 8(1):25. https://doi.org/10.3390/act8010025
Chicago/Turabian StyleAi, Rodrigo, Luciana L. S. Monteiro, Paulo Cesar. C. Monteiro, Jr., Pedro M. C. L. Pacheco, and Marcelo A. Savi. 2019. "Piezoelectric Vibration-Based Energy Harvesting Enhancement Exploiting Nonsmoothness" Actuators 8, no. 1: 25. https://doi.org/10.3390/act8010025
APA StyleAi, R., Monteiro, L. L. S., Monteiro, P. C. C., Jr., Pacheco, P. M. C. L., & Savi, M. A. (2019). Piezoelectric Vibration-Based Energy Harvesting Enhancement Exploiting Nonsmoothness. Actuators, 8(1), 25. https://doi.org/10.3390/act8010025







