Coevolution of the Features of the Dynamics of the Accelerator Pedal and Hyperparameters of the Classifier for Emergency Braking Detection
Abstract
1. Introduction
2. Methods
2.1. Cooperative Coevolution
- Step 0:
- Creating the initial population of randomly generated individuals;
- Step 1:
- Evaluating the fitness of the individuals in the population;
- Step 2:
- Checking the termination criteria: good enough fitness value (of the best individual in the population), too long runtime, or too many generations. The evolutionary algorithm (EA) terminates if one of the criteria is satisfied;
- Step 3:
- Selection: selecting the mating pool of individuals. The size of the mating pool is a fraction (i.e., 10%) of the overall size of the population, and the selection of the forests in the mating pool is fitness-proportional (roulette-wheel, tournament, elitism, etc.);
- Step 4:
- Reproduction: implementing crossover by swapping random nodes (genes) of trees (chromosomes) of randomly selected pairs (parents) of individuals from the mating pool. Crossover produces pairs of offspring forests (chromosomes) that are inserted into the newly growing population;
- Step 5:
- Mutation: individuals’ random node(s) (gene(s)) of newly generated individuals (offspring) are randomly modified with a given probability.
2.2. Cross Validation
2.3. Quality Metrics
2.4. Extreme Gradient Boosting
2.5. Wilcoxon Signed Rank Test
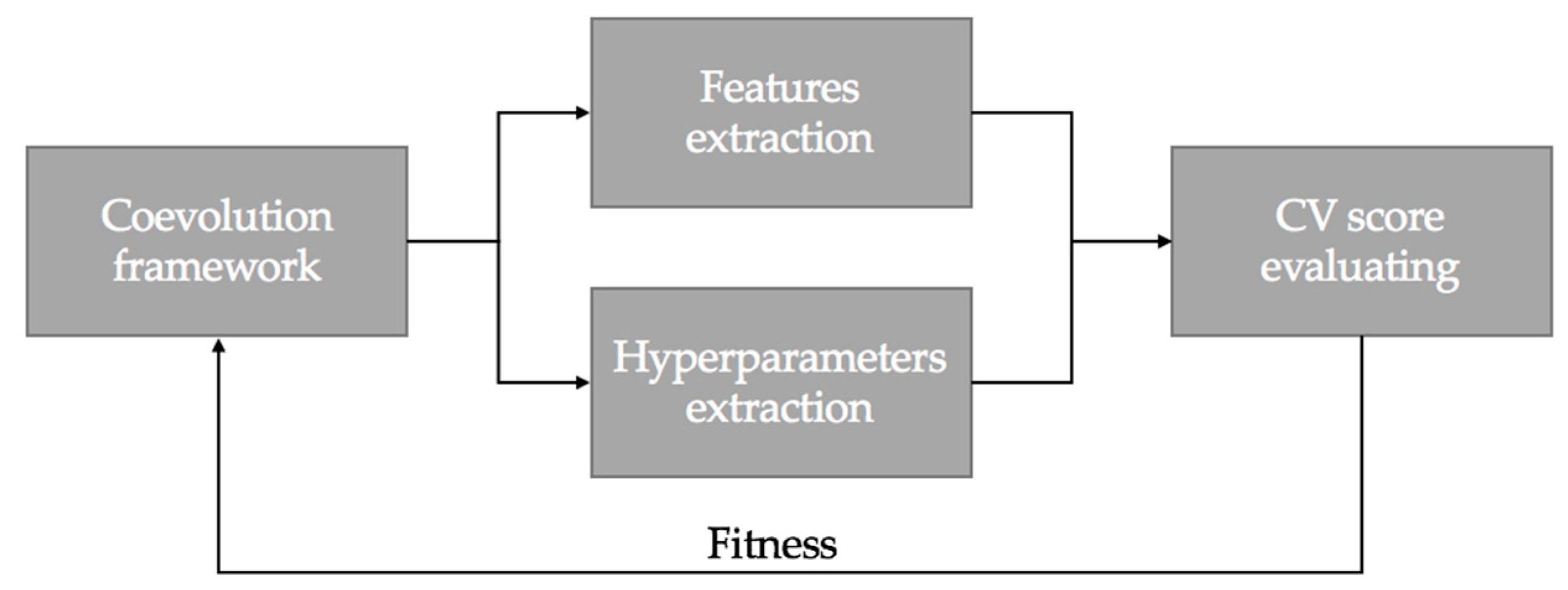
3. Proposed Approach
4. Methodology
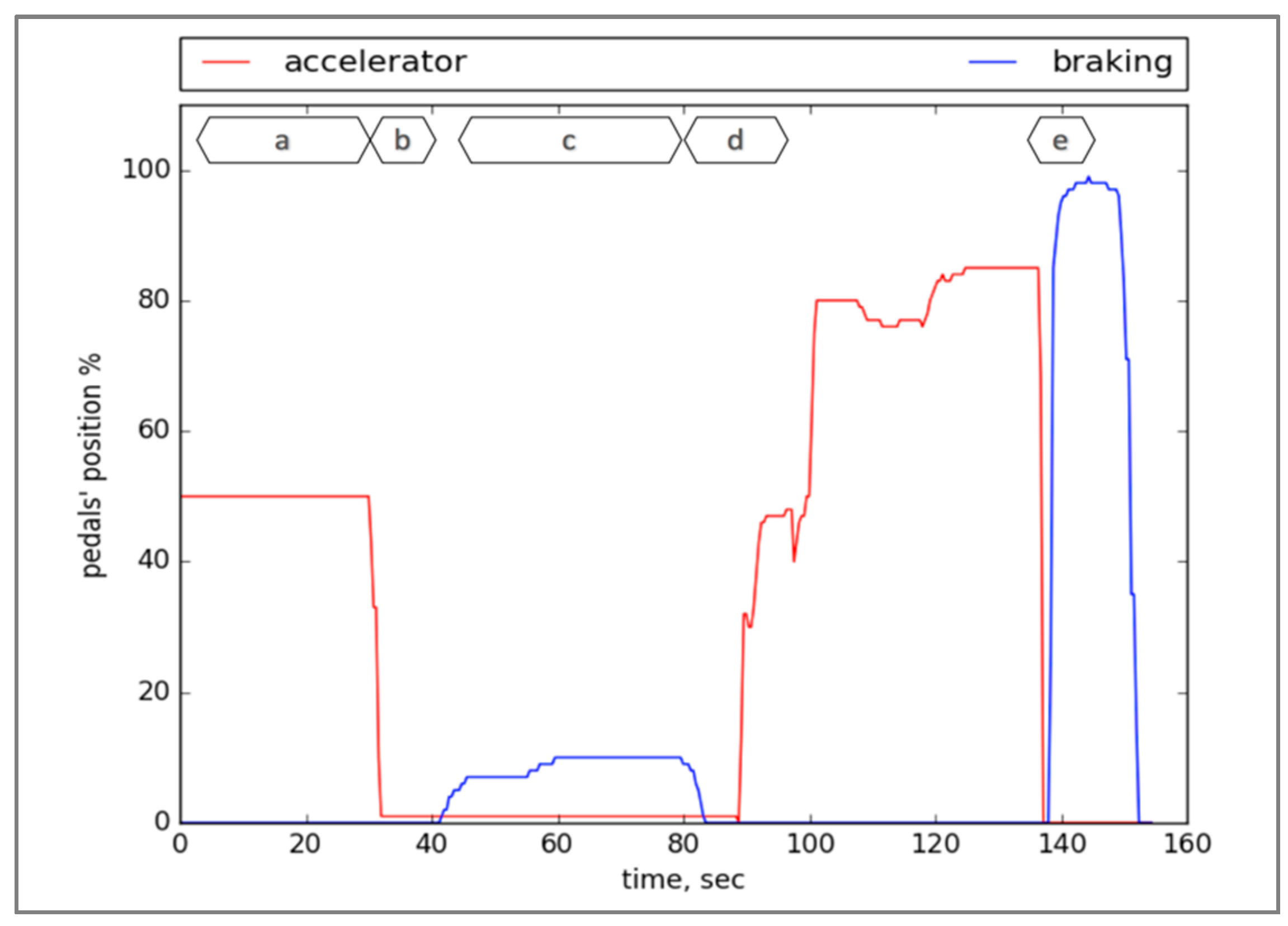
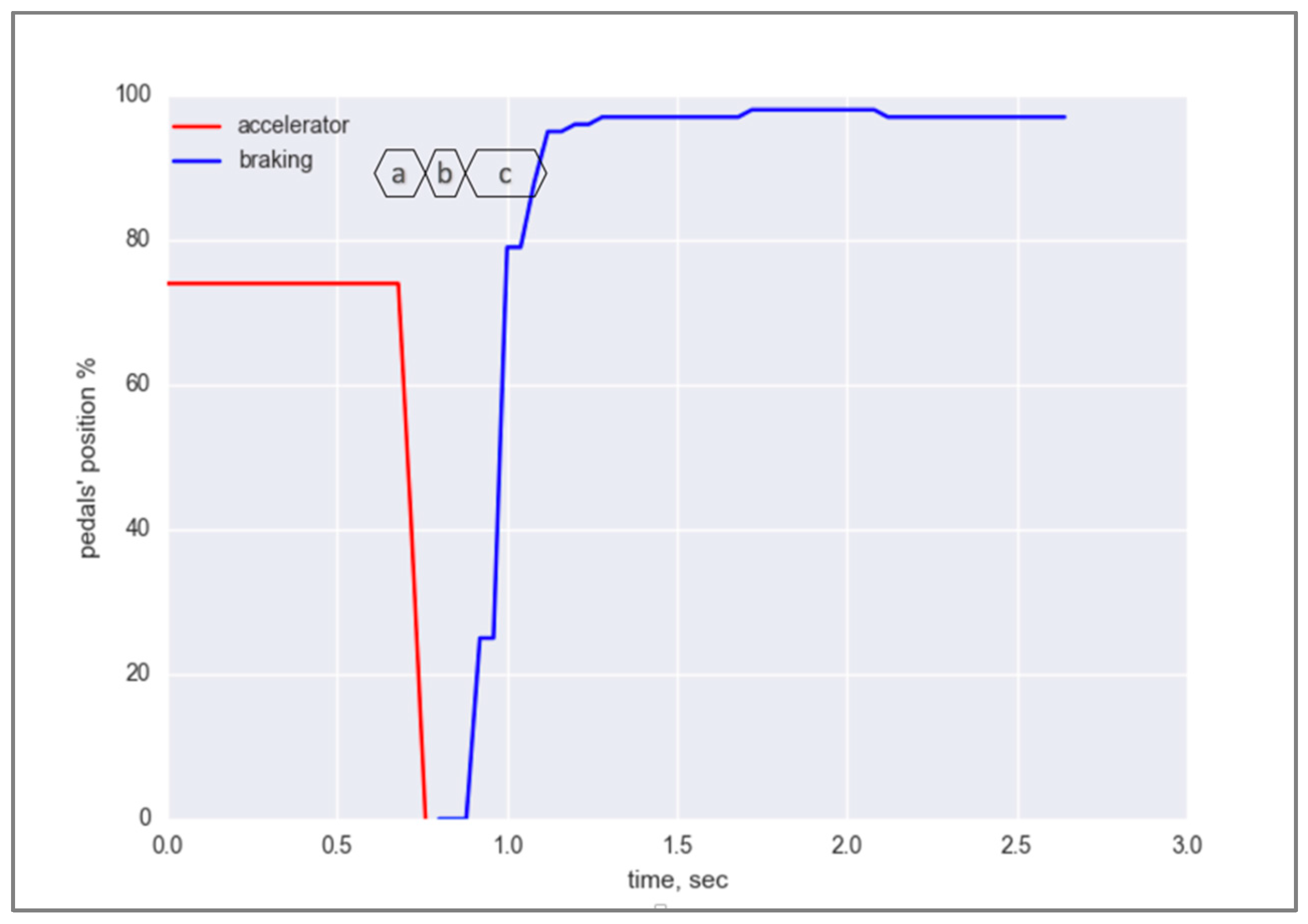
4.1. Data Collection and Analysis
4.2. Implementation of the Cooperative Coevolution
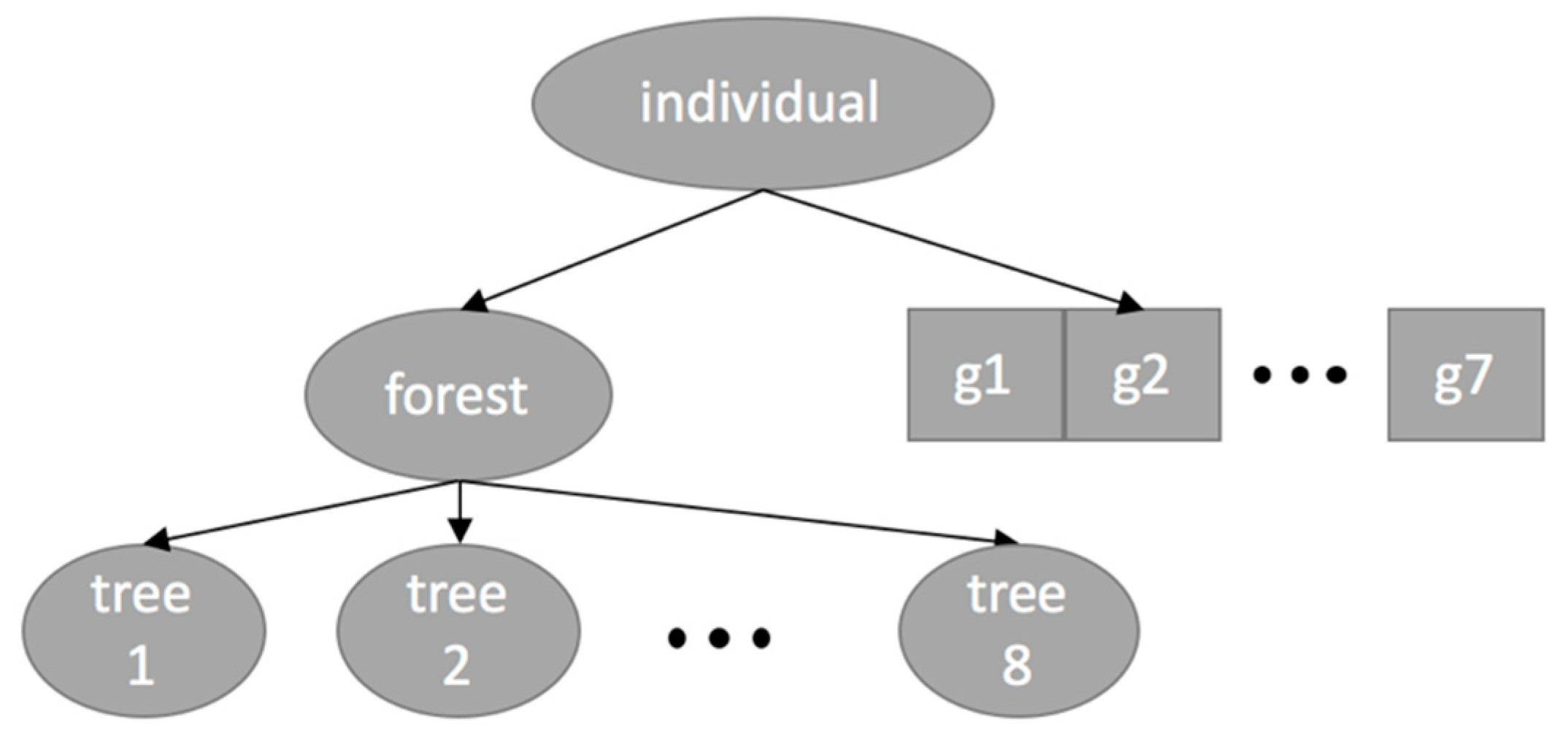
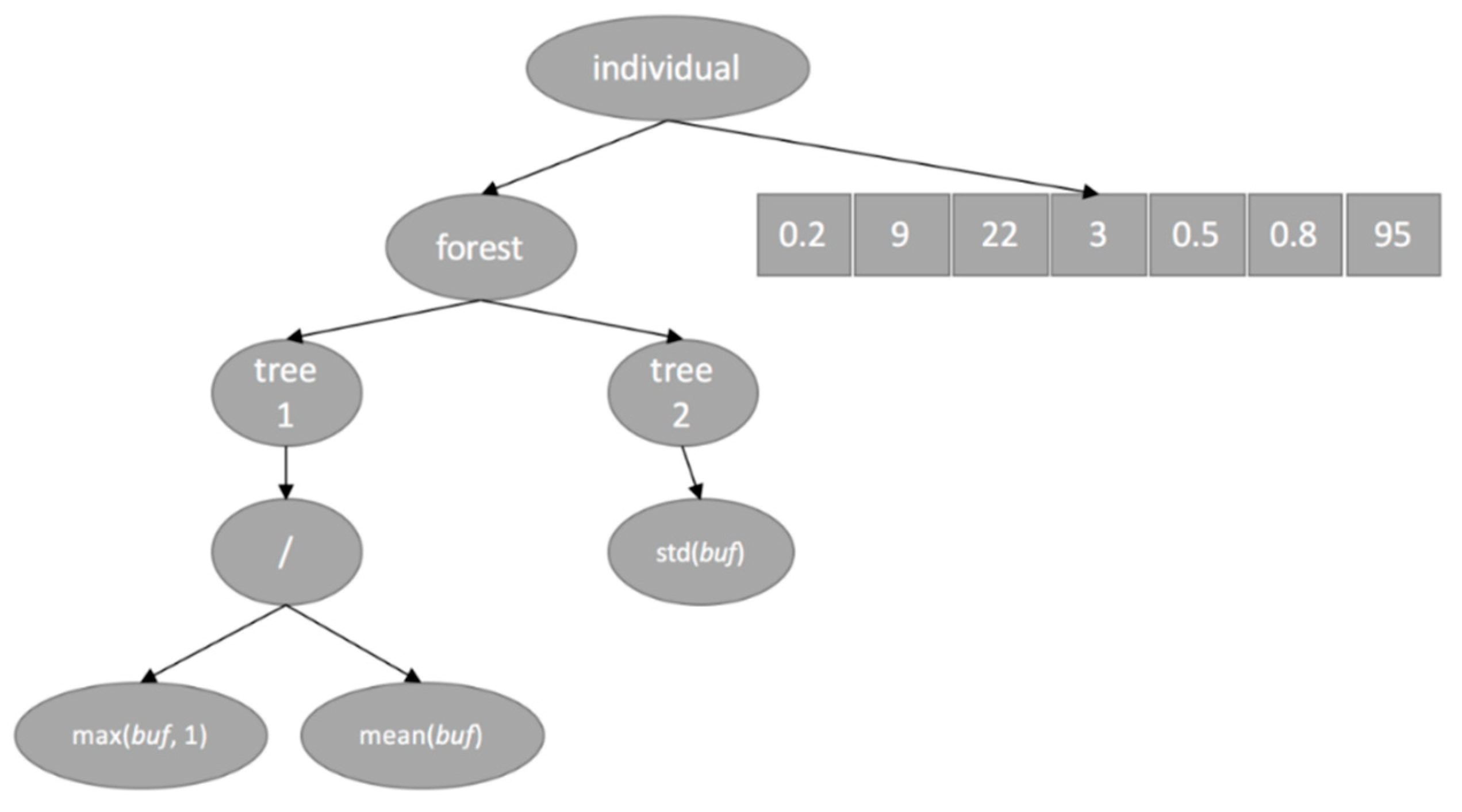
4.2.1. Set of Terminals in the Trees of the Forest
4.2.2. Set of Function in the Trees of the Forest
4.2.3. Evolving the Features
4.2.4. Evolving the Hyperparameters
4.2.5. Fitness Function
- These metrics describe different aspects of the classifier. It is not evident which metric is more preferable for building the emergency braking system, and
- The consideration of only precision or recall as fitness function can lead to the phenomenon known as “evolutionary cheating”. For instance, evolution will choose the features that decrease the number of FP, without any respect to FN. Consequently, the precision might even become 1.0, however the recall will be significantly lower.
4.2.6. Main Parameters of Coevolution
4.2.7. The Entire System
- Initialization: Generating the random initial population of 200 individuals. Each individual is a conjunction of forest and chromosome. The forest can contain up to eight trees (features), while the number of genes (hyperparameters) is fixed and equal to 7.
- Fitness evaluation, phase A: Obtaining the sets of features and hyperparameters for each individual by parsing the trees in the forest and the linear chromosome.
- Fitness evaluation, phase B: Extracting the values of each of the features from the raw time series of accelerator pedal.
- Fitness evaluation, phase C: Calculating the fitness value of each individual (set of features) as a CV f-score of XGBoost classifier that uses the obtained hyperparameters and calculated features.
- Checking the termination criteria. Terminating if any of them has been satisfied.
- Selection: based on the obtained fitness values of all individuals, selecting the mating pool of 24 individuals via binary tournament and elitism.
- Reproduction: Reproducing the population via crossover of individuals in the mating pool and mutation of offspring.
- Continuing with step 2.
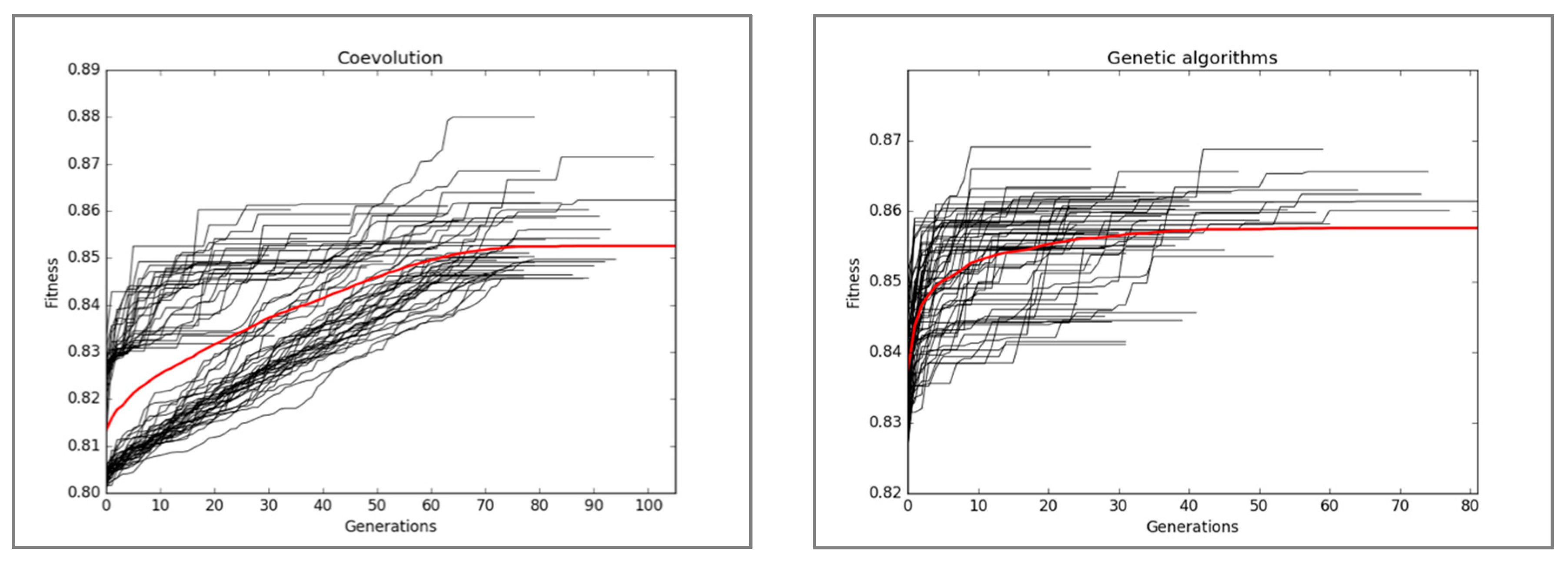
5. Experimental Results
5.1. Statistical Significance Test
5.2. Best Solutions Comparison
6. Discussion
- Mislabelled (by a human expert) samples in the whole dataset,
- Lack of a sufficient number of samples featuring a similar trend,
- Personal traits of the drivers that result in contradictory data for the classifier, and
- XGBoost could not capture the underlying trends of the data.
- sample1 = {0, 7, 7, 7, 21, 35, 37, 37, 38, 38, 39, 41, 43, 45, 46, 47, 48, 48, 49, 49, 50, 50, 52, 53, 54, 54, 54, 54, 54, 54, 54, 54, 54, 54, 54, 54, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 54, 54, 54, 54, 53, 54, 54, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 20, 20, 1}
- sample2 = {0, 17, 17, 31, 31, 34, 34, 35, 36, 36, 37, 39, 40, 41, 41, 41, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 41, 42, 44, 44, 45, 45, 45, 45, 45, 46, 46, 47, 47, 48, 48, 49, 49, 49, 49, 49, 49, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 51, 51, 51, 51, 51, 51, 51, 52, 52, 52, 52, 53, 53, 53, 53, 35, 2, 1}
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- 13 Advanced Driver Assistance Systems. Available online: https://www.lifewire.com/advanced-driver-assistance-systems-534859 (accessed on 20 June 2018).
- Wikipedia. List of Countries by Traffic-Related Death Rate. 2018. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_traffic-related_death_rate (accessed on 20 June 2018).
- Coelingh, E.; Eidehall, A.; Bengtsson, M. Collision Warning with Full Auto Brake and Pedestrian Detection—A practical example of Automatic Emergency Braking. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 155–160. [Google Scholar]
- Coelingh, E.; Jakobsson, L.; Lind, H.; Lindman, M. Collision Warning with Auto Brake—A Real-Life Safety Perspective. In Proceedings of the 20th International Technical Conference on the Enhanced Safety of Vehicles (ESV), Lyon, France, 18–21 July 2007. [Google Scholar]
- Kusano, K.D.; Gabler, H.C. Safety Benefits of Forward Collision Warning, Brake Assist, and Autonomous Braking Systems in Rear-End Collisions. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1546–1555. [Google Scholar] [CrossRef]
- Fancher, P.; Bareket, Z.; Ervin, R. Human-Centered Design of an Acc—With Braking and Forward-Crash-Warning System. Int. J. Veh. Mech. Mobil. 2001, 36, 203–223. [Google Scholar] [CrossRef]
- Wilde, G.J.S. The theory of risk homeostasis: Implications for safety and health. Risk Anal. 1982, 2, 209–225. [Google Scholar] [CrossRef]
- Podusenko, A.; Nikulin, V.; Tanev, I.; Shimohara, K. Cause and Effect Relationship between the Dynamics of Accelerator and Brake Pedals during Emergency Braking. In Proceedings of the FAST-Zero’17, Nara, Japan, 18–22 September 2017. [Google Scholar]
- Kiesewetter, W.; Klinkner, W.; Reichelt, W.; Steiner, M. Der neue Brake-Assist von Mercedes-Benz. Automobiltechnische Zeitschrift 1997, 6, 330–339. [Google Scholar]
- Haufe, S.; Kim, J.; Kim, I.H.; Treder, M.S.; Sonnleitner, A.; Schrauf, M.; Curio, G.; Blankertz, B. Electrophysiology-based detection of emergency braking intention in real-world driving. J. Neural Eng. 2014, 11, 056011. [Google Scholar] [CrossRef] [PubMed]
- Podusenko, A.; Nikulin, V.; Tanev, I.; Shimohara, K. Emergency Braking based on the Pattern of Lifting Motion of Accelerator Pedal. In Proceedings of the SICE 2017, Kanazawa, Japan, 19–22 September 2017. [Google Scholar]
- Forum-8 Drive Simulator. Available online: http://www.forum8.co.jp/english/uc-win/road-drive-e.htm (accessed on 20 June 2018).
- Podusenko, A.; Nikulin, V.; Tanev, I.; Shimohara, K. Comparative Analysis of Classifiers for Classification of Emergency Braking of Road Motor Vehicles. Algorithms. Algorithms 2017, 10, 129. [Google Scholar] [CrossRef]
- Guo, L.; Rivero, D.; Dorado, J.; Munteanu, C.R.; Pazos, A. Automatic feature extraction using genetic programming: An application to epileptic EEG classification. Expert Syst. Appl. 2011, 38, 10425–10436. [Google Scholar] [CrossRef]
- Zhang, Y.; Rockett, P.I. Multiobjective Genetic Programming Feature Extraction with Optimized Dimensionality. Soft Comput. Ind. Appl. 2017, 39, 159–168. [Google Scholar] [CrossRef]
- Oechsle, O.; Clark, A.F. Feature Extraction and Classification by Genetic Programming. Computer Vision Systems. Lect. Notes Comput. Sci. 2008, 5008, 131–140. [Google Scholar] [CrossRef]
- Di Francescomarino, C.; Dumas, D.; Federici, M.; Ghidini, C.; Maggi, F.M.; Rizzi, W.; Simonetto, L. Genetic algorithms for hyperparameter optimization in predictive business process monitoring. Inf. Syst. 2018, 74, 67–83. [Google Scholar] [CrossRef]
- Ahmad, F.K.; Al-Qammaz, A.Y.A.; Yusof, Y. Optimization of Least Squares Support Vector Machine Technique using Genetic Algorithm for Electroencephalogram Multi-Dimensional Signals. J. Teknologi 2016, 78, 107–115. [Google Scholar] [CrossRef]
- Potter, M.A.; Jong, K.A.D. A cooperative coevolutionary approach to function optimization. In Proceedings of the International Conference on Parallel Problem Solving from Nature, London, UK, 9–14 October 1994; pp. 249–257. [Google Scholar]
- Yang, Z.; Tang, K.; Yao, X. Large scale evolutionary optimization using cooperative coevolution. Inf. Sci. 2008, 178, 2985–2999. [Google Scholar] [CrossRef]
- Kohavi, F. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Measure to ROC. Inf. Mark. Correl. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Kaggle. Available online: http://blog.kaggle.com/2016/11/03/red-hat-business-value-competition-1st-place-winners-interview-darius-barusauskas/ (accessed on 20 June 2018).
- Kaggle. Available online: http://blog.kaggle.com/2017/02/22/santander-product-recommendation-competition-3rd-place-winners-interview-ryuji-sakata/ (accessed on 20 June 2018).
- Lewis, R.J. An Introduction to Classification and Regression Tree (CART) Analysis. In Proceedings of the Annual Meeting of the Society for Academic Emergency Medicine, San Francisco, CA, USA, 22–25 May 2000. [Google Scholar]
- Demsar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–13. [Google Scholar]
- Podusenko, A. Implementation of CC and GA for Emergency Braking Classifier in Python. Available online: http://isd-si.doshisha.ac.jp/a.podusenko/research/ (accessed on 15 July 2018).
- Goldberg, E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- XGBoost Package. Available online: https://github.com/dmlc/xgboost (accessed on 20 June 2018).


| Actual Condition | |||
|---|---|---|---|
| Positive | Negative | ||
| Predicted Condition | Positive | True positive (TP) | False positive (FP) |
| Negative | True negative (TN) | False negative (FN) | |
| Track | Road Conditions | Traffic Conditions |
|---|---|---|
| Highway | Dry, wet | Moderate, high-speed traffic |
| City road | Dry | Empty road (no traffic) |
| Country side | Both dry and wet | Dense, low-speed traffic |
| Experiment | Requirements | Number of Samples |
|---|---|---|
| Normal driving | Emergency braking is not allowed | 1659 |
| Emergency braking | Audible signal prompts the drivers to apply emergency braking | 714 |
| Fragment of the Time Series | Corresponding Class |
|---|---|
| {0, 20, 22, 20, 15, 9, 3, 2, 1} | “0” (Normal driving) |
| {0, 10, 20, 19, 23, 2, 1} | “1” (Emergency braking) |
| {0, 50, 74, 72, 67, 58, 45, 24, 4, 1} | “0” (Normal driving) |
| {0, 13, 30, 40, 30, 45, 72, 68, 68, 65, 61, 22, 1} | “1” (Emergency braking) |
| Function | Meaning | Example |
|---|---|---|
| mean (buf) | mean of the last decreasing subsequent | mean ({0, 10, 50, 2, 0}) = 17.3 |
| std (buf) | standard deviation of the last decreasing subsequence | std ({0, 10, 50, 2, 0}) = 23.1 |
| max (buf, i) | i-th maximum element of the buffer | max ({0, 10, 50, 2, 0}, 0) = 50 max ({0, 10, 50, 2, 0}, 1) = 2 |
| mdelta (buf, i) | i-th maximum delta of the buffer | mdelta ({0, 10, 50, 2, 0}, 0) = 48 mdelta ({0, 10, 50, 2, 0}, 0) = 2 |
| suminc (buf) sumdec (buf) | average sum of all increasing/decreasing subsequences | suminc ({0, 10, 50, 2, 0}) = 20 sumdec ({0, 10, 50, 2, 0}) = 17.3 |
| auf (buf) | area under the buffer, dx = 1 | suminc ({0, 10, 50, 2, 0}) = 20 |
| aud (buf) | area under the last decreasing subsequence, dx = 1 | aud ({0, 10, 50, 2, 0}) = 27 |
| maxinc (buf) mininc (buf) | maximum/minimum between all averages of increasing subsequences | maxinc ({0, 10, 50, 2, 0}) = 20 mininc ({0, 10, 50, 2, 0}) = 20 |
| maxdec (buf) mindec (buf) | maximum/minimum between all averages of decreasing subsequences | maxdec ({0, 10, 50, 2, 0}) = 17.3 mindec ({0, 10, 50, 2, 0}) = 17.3 |
| fullmean (buf) | average value of the buffer | fullmean ({0, 10, 50, 2, 0}) = 12.4 |
| fullstd (buf) | standard deviation value of the buffer | fullstd ({0, 10, 50, 2, 0}) = 19.6 |
| dlen (buf) | length of last decreasing subsequent | dlen ({0, 10, 50, 2, 0}) = 3 |
| Hyperparameter | Interval of Discretization | Range | Meaning |
|---|---|---|---|
| eta | 0.002 | [0, 1] | Step size shrinkage. Controls the learning rate in update and prevents overfitting |
| gamma | 0.1 | [0, 100] | Minimum loss reduction required to make a node split. The split happens when the resulting split gives a positive reduction in the loss function. |
| max depth | 1 | [1, 20] | The maximum depth of a tree |
| min child weight | 1 | [1, 100] | Minimum sum of weights of all observations required in a child |
| subsample | 0.002 | [0.001, 1] | Subsample ratio of the training instance |
| colsample by tree | 0.001 | [0.5, 1] | Subsample ratio of columns when constructing each tree |
| n estimators | 1 | [100, 500] | The number of boosting stages to perform |
| Parameter | Value |
|---|---|
| Genotype | Conjunction of forest and chromosome |
| Population size | 200 individuals |
| Selection | Binary tournament |
| Selection ratio | 10% |
| Elite | Best 4 individuals |
| Crossover | Single-point |
| Mutation | Single-point |
| Mutation ratio | 5% |
| Fitness value | Cross validation (CV) f-score, with 1% subtraction penalty |
| Termination criteria | (# Generations > 200) or (Fitness value = 100%) |
| Parameter | Value |
|---|---|
| Genotype | Set of parameters shown in Table 6 and fixed combination of features (pertinent to the last decreasing subsequence of the buffer). Among them are the highest position of the accelerator pedal before starting the deceleration (mP), the maximum and average rate of lifting the accelerator (mR and aR respectively) |
| Population size | 40 individuals |
| Selection | Binary tournament |
| Selection ratio | 10% |
| Elite | Best two individuals |
| Crossover | Single-point |
| Mutation | Single-point |
| Mutation ratio | 5% |
| Fitness value | CV f-score |
| Termination criteria | (# Generations > 100) or (Fitness value = 100%) |
| Metric | xgbga | xgbcc | ||
|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | |
| Accuracy | 0.9052959 | 0.9036458 | 0.9850467 | 0.9466146 |
| Precision | 0.8609022 | 0.7988506 | 0.9776119 | 0.9254658 |
| Recall | 0.8544776 | 0.7808989 | 0.9776119 | 0.8370789 |
| f-score | 0.8576779 | 0.7897727 | 0.9776119 | 0.8790560 |
| Classifier | TP | TN | FP | FN |
|---|---|---|---|---|
| xgbga | 139 | 555 | 35 | 39 |
| xgbcc | 149 | 578 | 12 | 29 |
| # | xgbga Features | xgbga Features Importance | xgbcc Features | xgbcc Features Importance |
|---|---|---|---|---|
| 1 | mP | 0.17105263 | 0.14775977 | |
| 2 | mR | 0.30263159 | 0.15157293 | |
| 3 | aR | 0.30263159 | 0.16301239 | |
| 4 | mPaR | 0.22368421 | 0.1749285 | |
| 5 | | | 0.08674929 | |
| 6 | | | 0.0729266 | |
| 7 | | | 0.20305052 |
| Hyperparameter | xgbga | xgbcc |
|---|---|---|
| eta | 0.1840816 | 0.080092 |
| gamma | 8.1 | 1.6 |
| max depth | 18 | 14 |
| min child weight | 2 | 1 |
| subsample | 0.4660533 (9) | 0.70003 |
| colsample by tree | 0.7 (3) | 0.71 (8) |
| n estimators | 145 | 144 |
| Stage | Mean Overhead, ms | Maximum Overhead, ms |
|---|---|---|
| Stage 1: Feature calculation | 0.323 | 2.005 |
| Stage 2: Classification | 0.252 | 0.515 |
| Overall | 0.575 | 2.520 |
| Classifier | Sample | Extracted | Output | Real Class |
|---|---|---|---|---|
| xgbga | 1 | [53, 825, 433.3, 22,966.6] | 1 | 1 |
| 2 | [53, 825, 433.3, 22,966.6] | 1 | 0 | |
| xgbcc | 1 | [5,981,896.76, 49.98, 11.31, 33, 3, 1, 38] | 1 | 1 |
| 2 | [4,625,878.23, 45.21, 8.76, 33, 3, 0.99, 4] | 0 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podusenko, A.; Nikulin, V.; Tanev, I.; Shimohara, K. Coevolution of the Features of the Dynamics of the Accelerator Pedal and Hyperparameters of the Classifier for Emergency Braking Detection. Actuators 2018, 7, 39. https://doi.org/10.3390/act7030039
Podusenko A, Nikulin V, Tanev I, Shimohara K. Coevolution of the Features of the Dynamics of the Accelerator Pedal and Hyperparameters of the Classifier for Emergency Braking Detection. Actuators. 2018; 7(3):39. https://doi.org/10.3390/act7030039
Chicago/Turabian StylePodusenko, Albert, Vsevolod Nikulin, Ivan Tanev, and Katsunori Shimohara. 2018. "Coevolution of the Features of the Dynamics of the Accelerator Pedal and Hyperparameters of the Classifier for Emergency Braking Detection" Actuators 7, no. 3: 39. https://doi.org/10.3390/act7030039
APA StylePodusenko, A., Nikulin, V., Tanev, I., & Shimohara, K. (2018). Coevolution of the Features of the Dynamics of the Accelerator Pedal and Hyperparameters of the Classifier for Emergency Braking Detection. Actuators, 7(3), 39. https://doi.org/10.3390/act7030039





