Modelling and Operator-Based Nonlinear Control for a Miniature Pneumatic Bending Rubber Actuator Considering Bellows
Abstract
1. Introduction
2. Materials and Methods
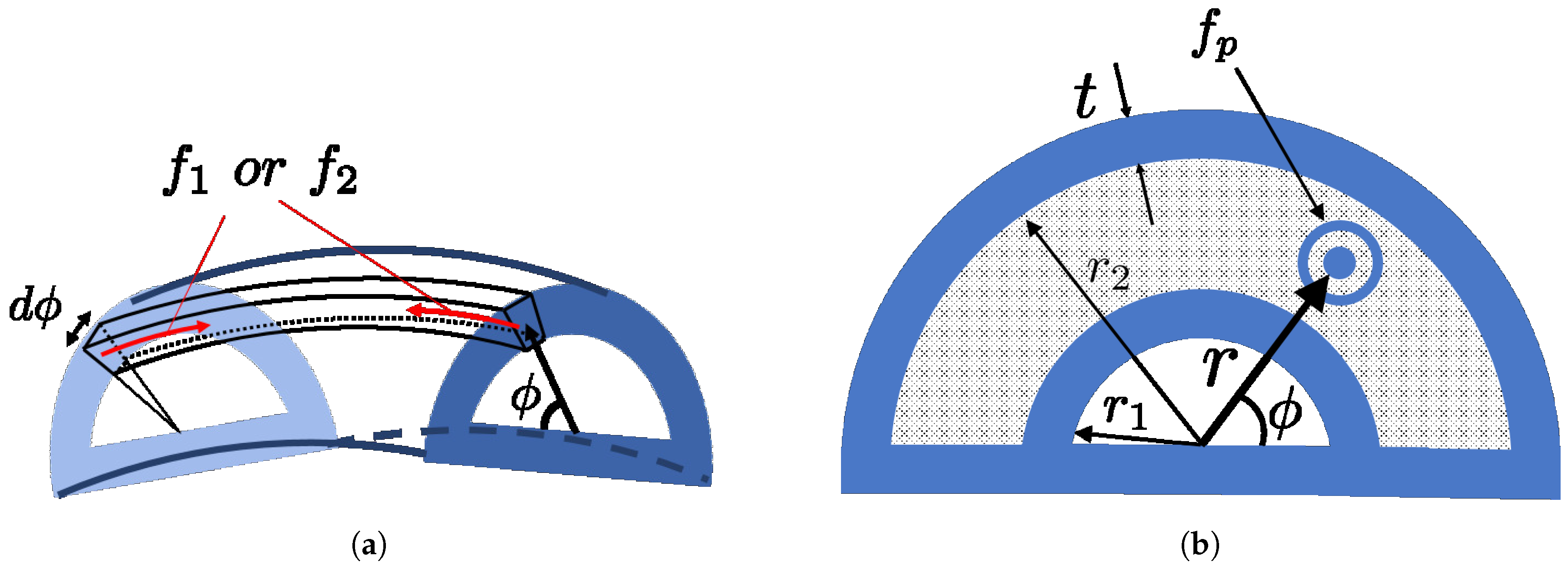
2.1. The Structure of the Miniature Pneumatic Bending Rubber Actuator
2.2. Modelling
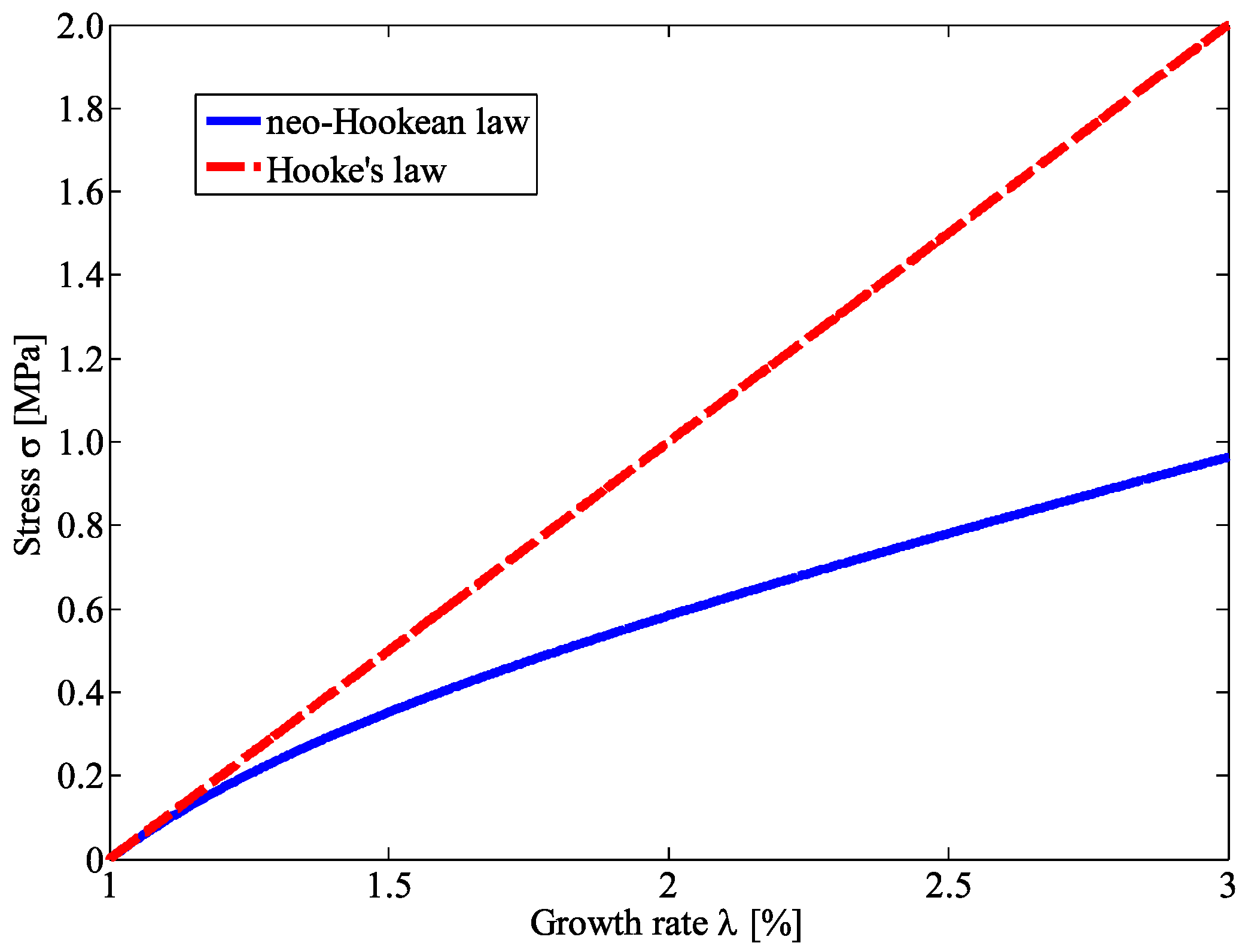
2.2.1. Neo-Hookean Model
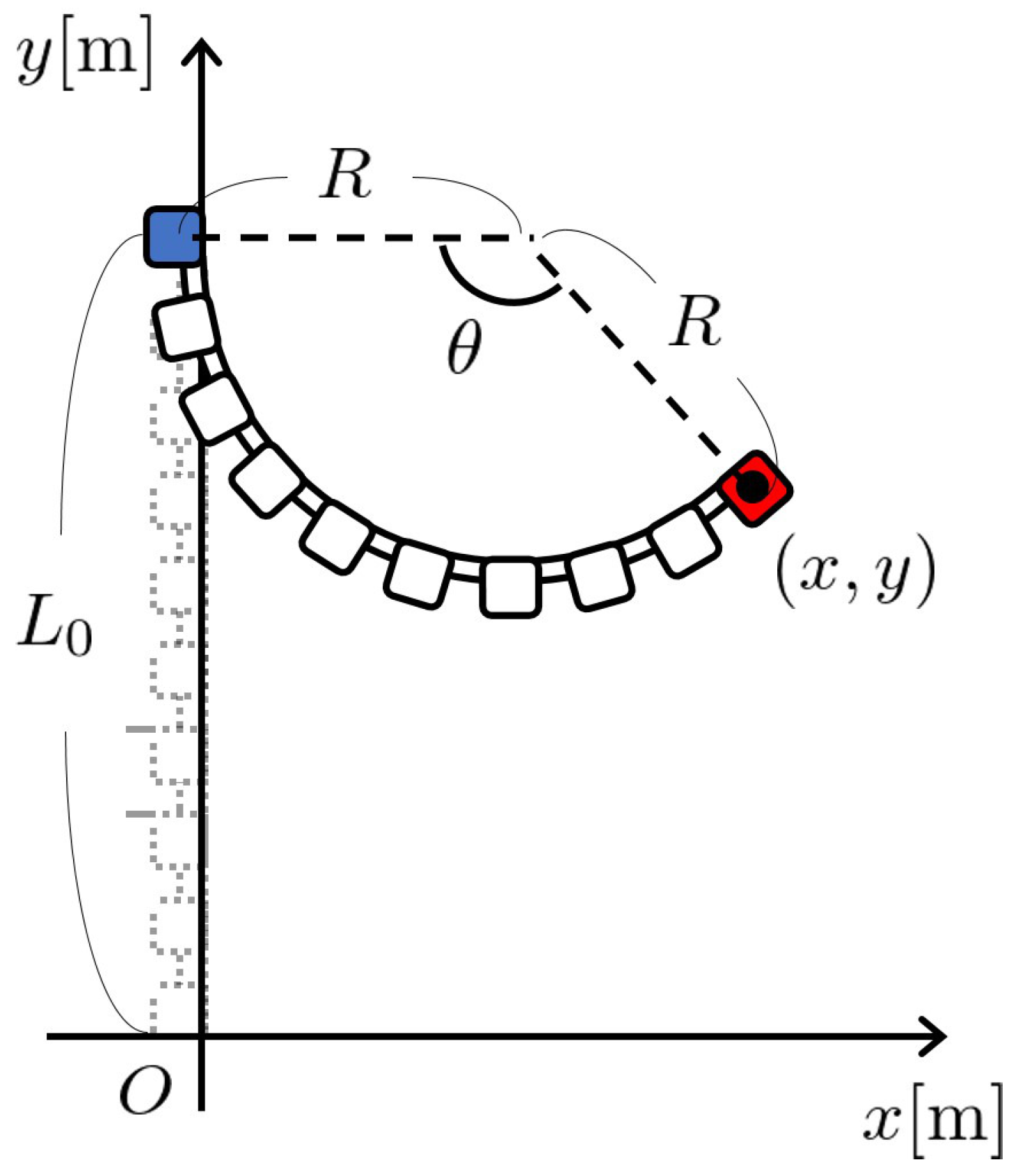
2.2.2. Relation between Input Pressure and Output Angle
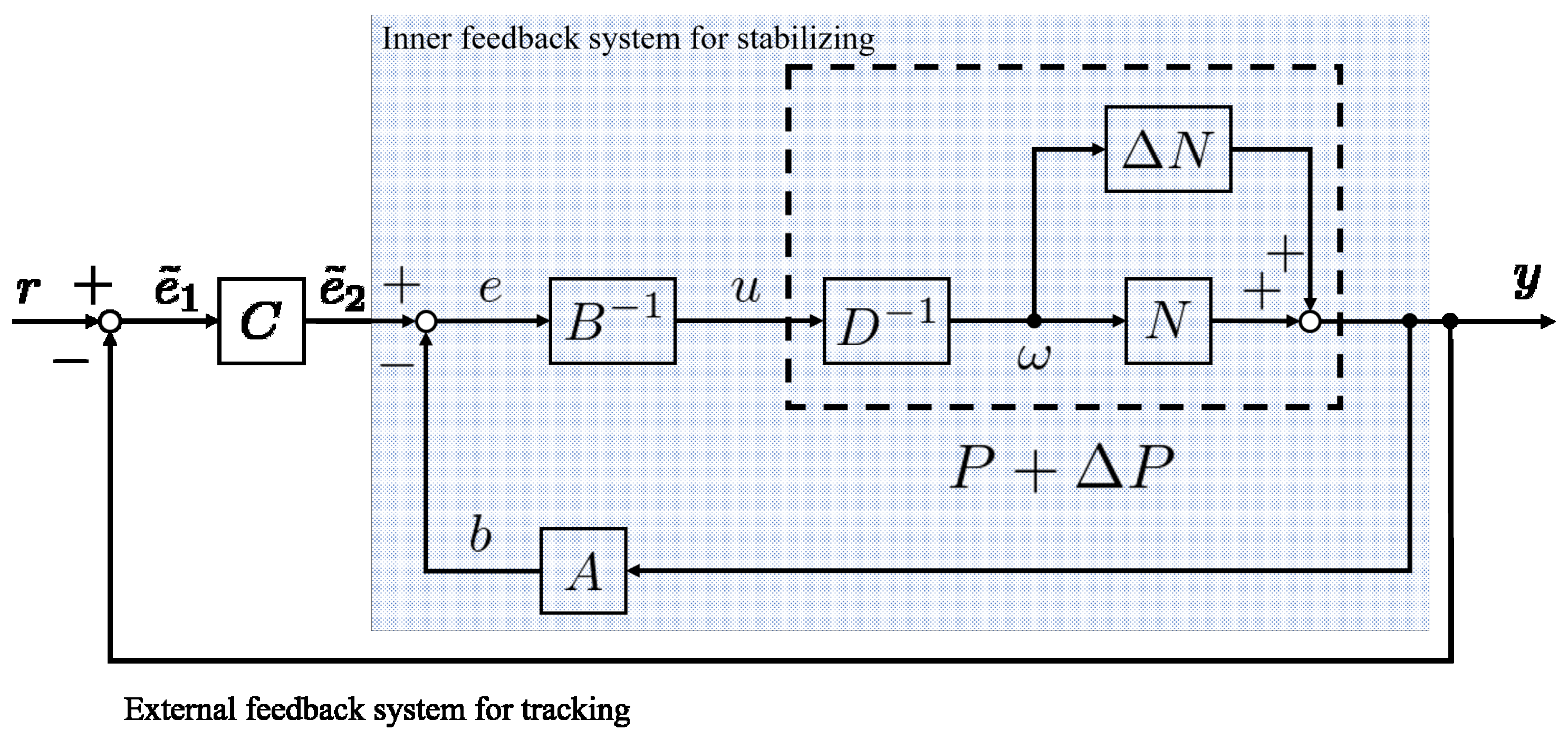
2.3. Operator-Based Nonlinear Control Feedback System Design
2.3.1. Right Coprime Factorization
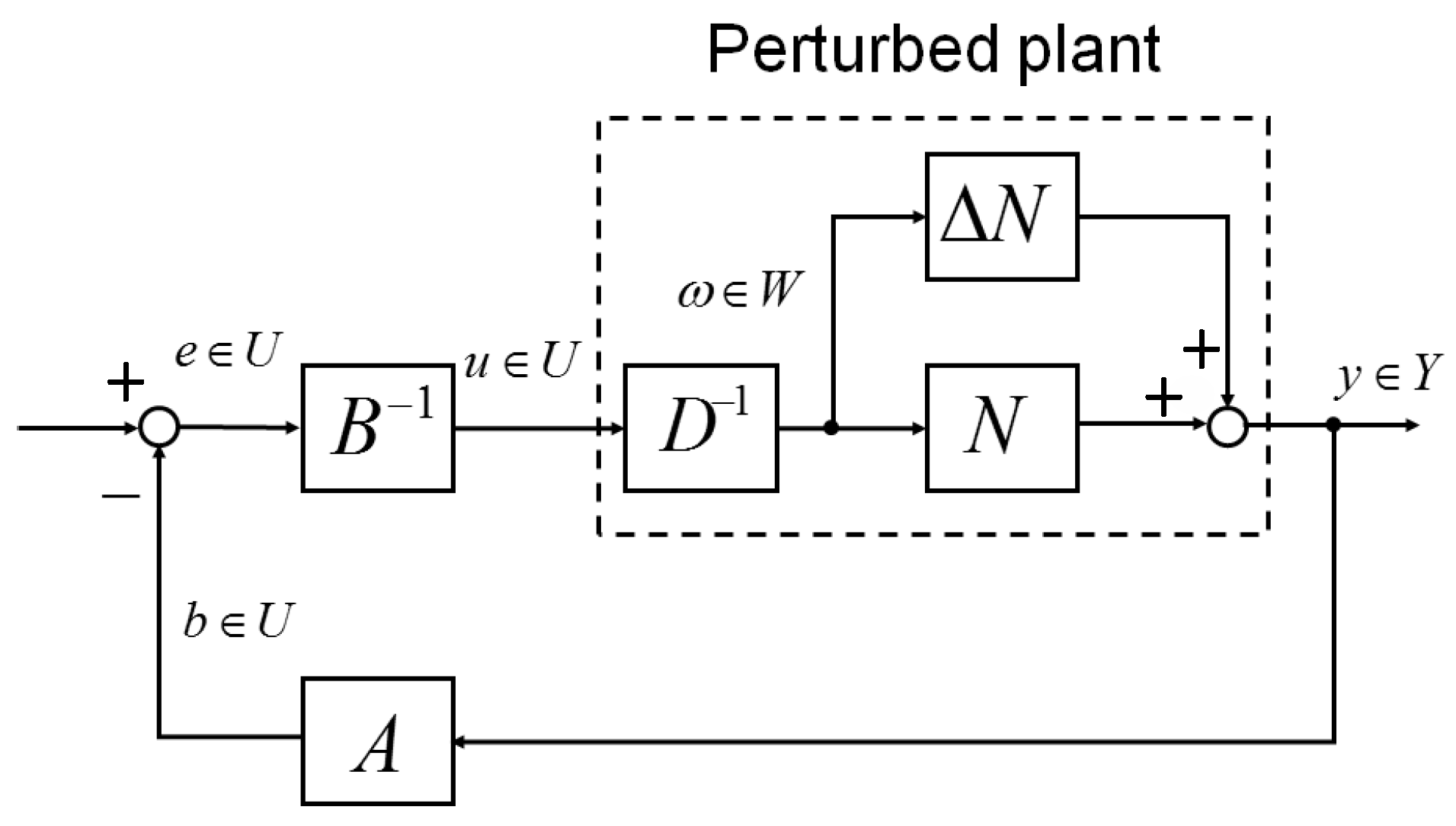
2.3.2. Robust Stability
2.3.3. Designing Operators
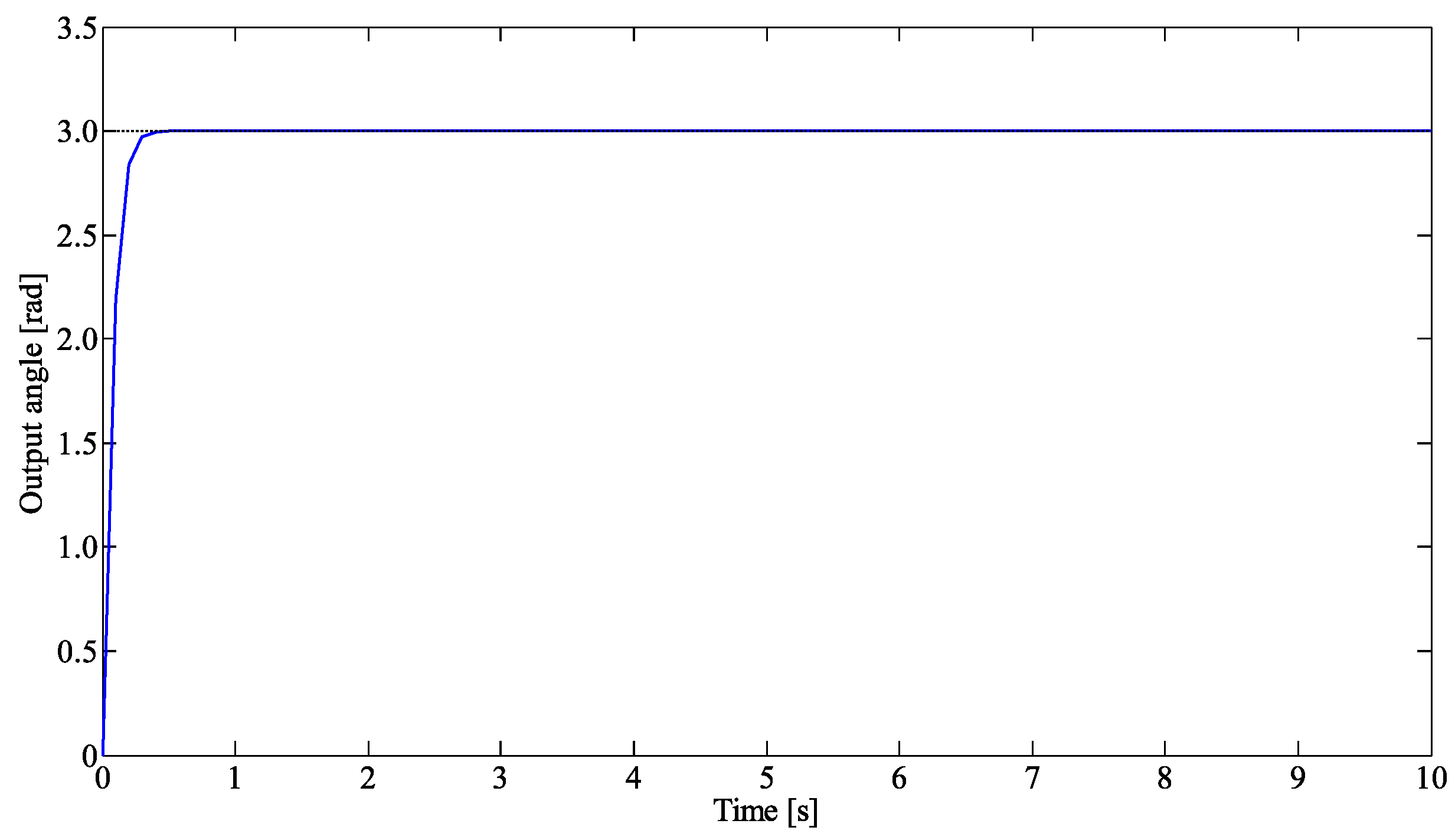
3. Results
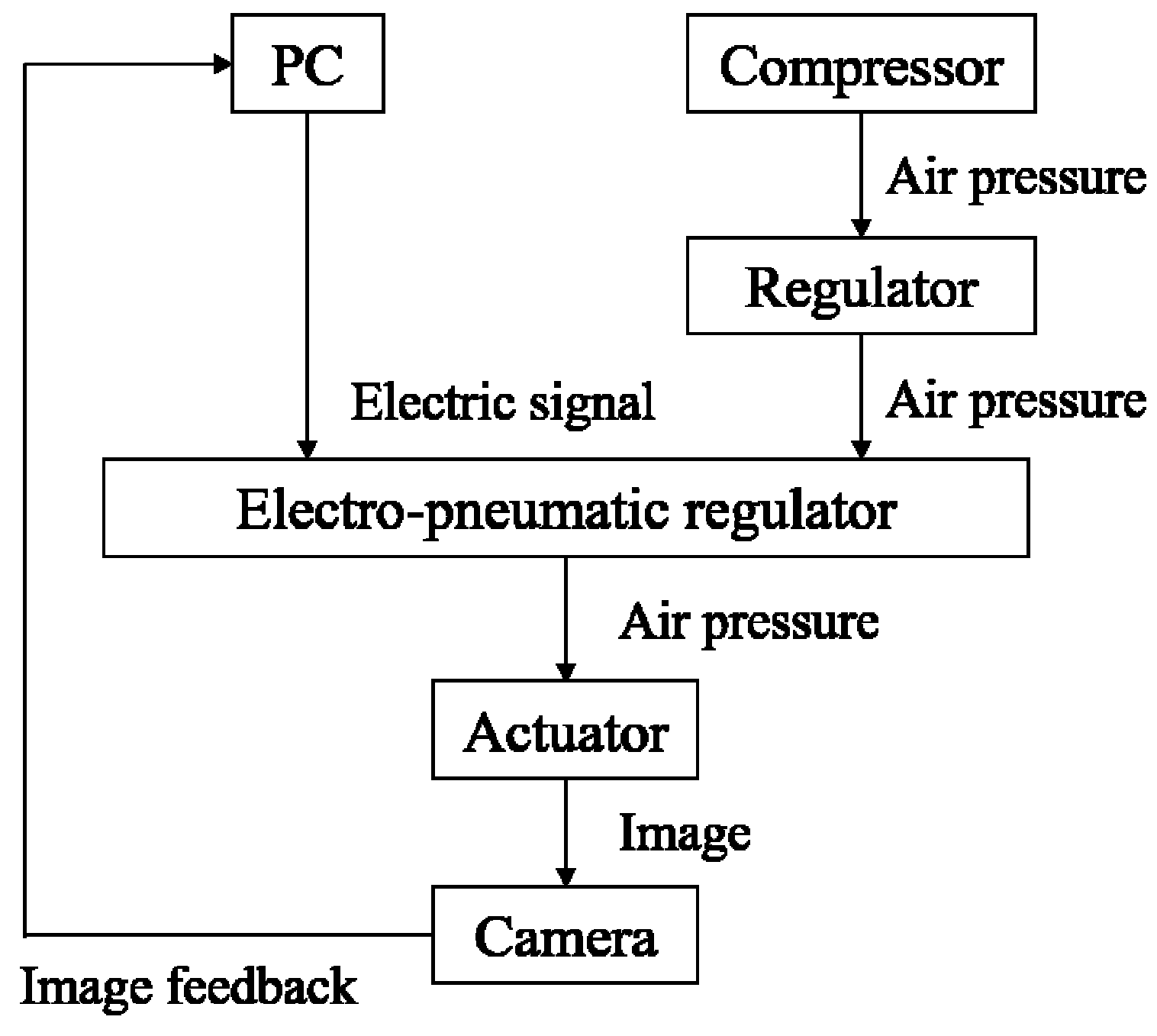
3.1. Experiment
- Convert captured color image to a gray scale.
- Dissolve the image into three pixel numbers; R, B, G.
- Extract only R pixels from the image in comparison with a gray scale.
- Find the center coordinate from extracted R pixel area.
- Do the same process as 4 and 5 to B pixels.
- Calculate bending angle from center coordinate of R and B area.
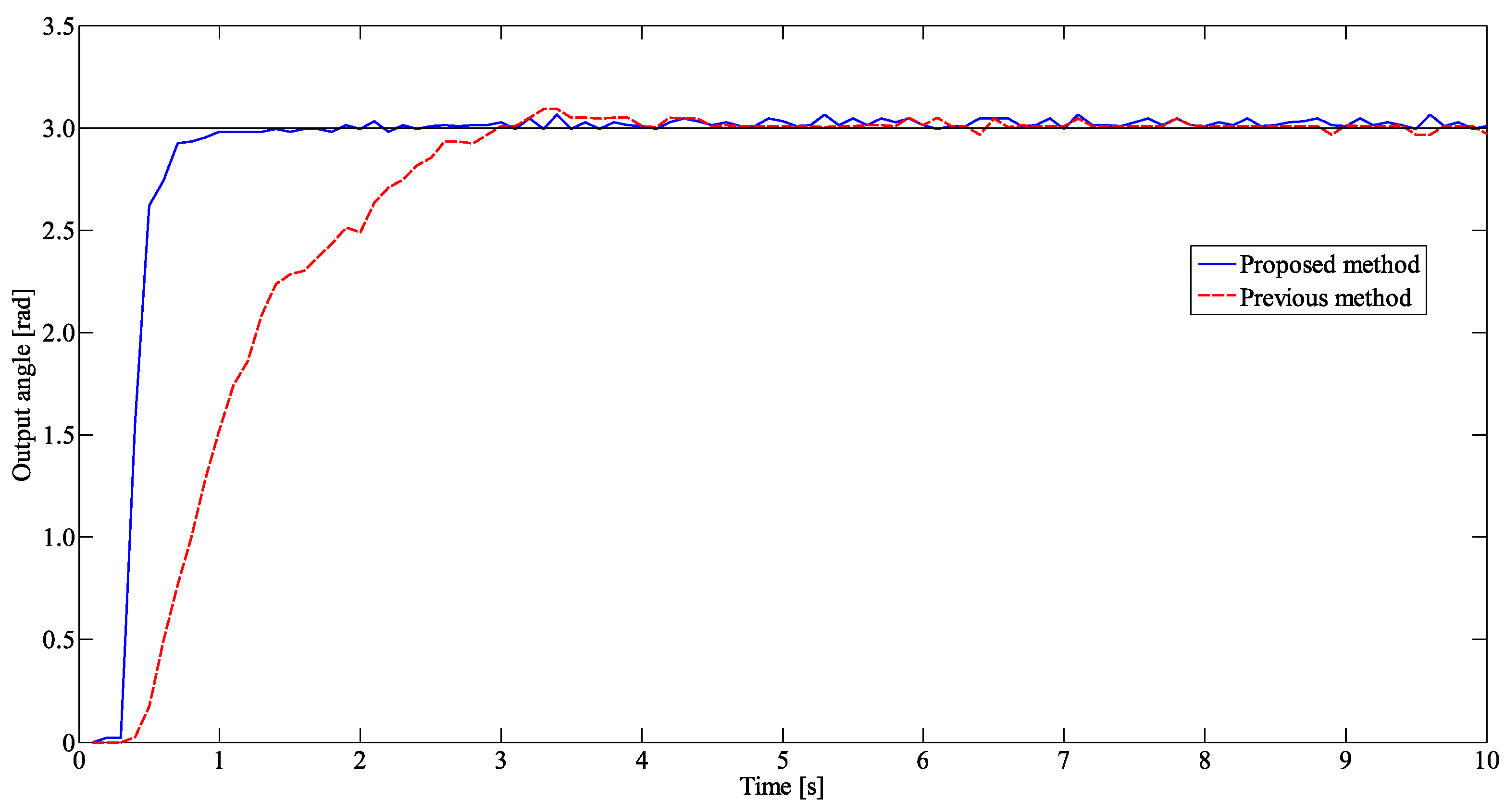
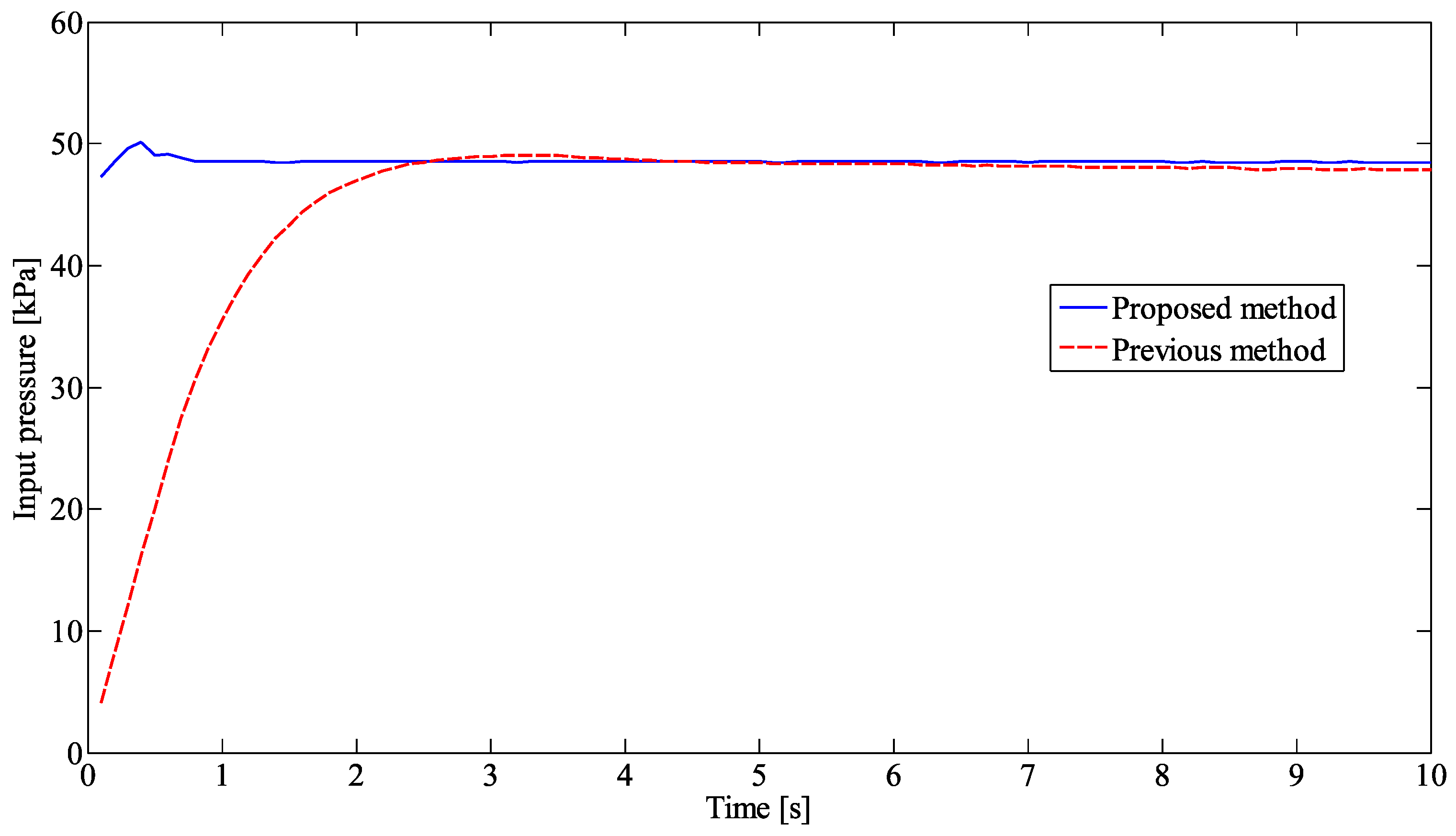
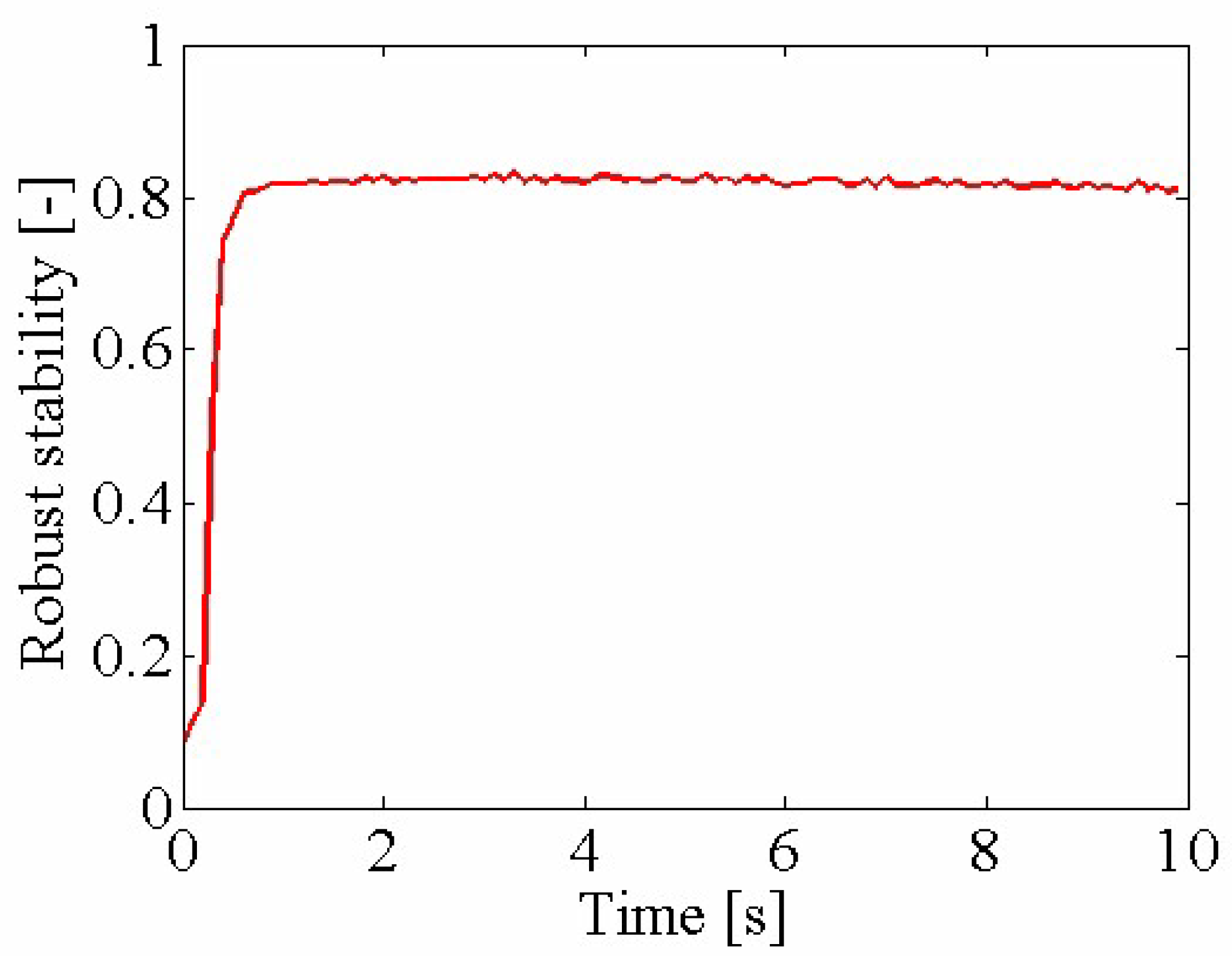
3.2. Experimental Result
4. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| FMA | Flexible micro actuator |
References
- Chen, X.; Su, C.Y. Adaptive Control for Ionic Polymer-Metal Composite Actuators. In Proceedings of the 2016 IEEE Transactions on Systems, Man, and Cybernetics: Systems, Sacramento, CA, USA, 1 October 2016; Volume 46, pp. 1468–1477. [Google Scholar] [CrossRef]
- Suzumori, K.; Iikura, S.; Tanaka, H. Development of flexible microactutor and its applications to robotic mechanisms. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 4, pp. 1622–1627. [Google Scholar] [CrossRef]
- Wakimoto, S.; Suzumori, K.; Ogura, K. Miniature pneumatic curling rubber actuator generating bidirectional motion with one air-supply tube. Adv. Robot. 2011, 25, 1311–1330. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Adv. Funct. Mater 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Yoshioka, R.; Wakimoto, S.; Yamamoto, Y.; Suzumori, K. Development of a micro pneumatic actuator realizing bidirectional bending motions. In Proceedings of the 2013 JSME Conference on Robotics and Mechatronics, Tsukuba, Japan, 22–25 May 2013; Volume 5, pp. 2A1-D06(1)–2A1-D06(3). [Google Scholar] [CrossRef]
- Deng, M. Operator-Based Bonlinear Control Systems Design and Applications; Willy-IEEE Press: Piscataway, NJ, USA, 2014. [Google Scholar]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback control design using robust right coprime factorization. IEEE Trans. Autom. Control 2006, 51, 645–648. [Google Scholar] [CrossRef]
- Chen, G.; Han, Z. Robust right coprime factorization and robust stabilization of nonlinear feedback control system. IEEE Trans. Autom. Control 1998, 43, 645–648. [Google Scholar] [CrossRef]
- Deng, M.; Bu, N.; Inoue, A. Output tracking of nonlinear feedback systems with perturbation based on robust right coprime factorization. Int. J. Innov. Comput. Inf. Control 2009, 5, 3359–3366. [Google Scholar]
- Wang, A.; Deng, M. Robust nonlinear multivariable tracking control design to a manipulator with unknown uncertainties using operator-based robust right coprime factorization. Trans. Inst. Meas. Control 2013, 35, 788–797. [Google Scholar] [CrossRef]
- Deng, M.; Bu, N. Robust control for nonlinear systems with unknown perturbations using simplified robust right coprime factorization. Int. J. Control 2012, 85, 842–850. [Google Scholar] [CrossRef]
- Deng, M.; Kawashima, T. Adaptive nonlinear sensorless control for an uncertain miniature pneumatic curling rubber actuator using passivity and robust right coprime factorization. IEEE Trans. Control Syst. Technol. 2016, 24, 318–324. [Google Scholar] [CrossRef]
- Miyagawa, T.; Toya, K.; Kubota, Y. Static characteristics of pneumatic soft actuator using fiber reinforced rubber. In Proceedings of the JSME Conference on Robotics and Mechatronics, Akita, Japan, 10–12 May 2007; pp. 1A2–A01(1)–1A2–A01(4). [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.B.; Lee, J.; Cho, S.; Park, H.; Yeom, S.; Park, S.H. A comparison among neo-hookean model, mooney-rivlin model, and ogden model for chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012, 13, 759–764. [Google Scholar] [CrossRef]
- Editorial Board. Nyumonkouza yasashigomunobutsururi daisankou gomudanseitonendanseinokiso. [Introductory course of simple physics of rubber: No. 3 Basics of rubber elasticity and viscoelasticity]. J. SRI. Jpn. 2007, 80, 404–407. (In Japanese) [Google Scholar]
- Fujita, K.; Deng, M.; Wakimoto, S. A Miniature bending rubber controlled by using the PSO-SVR-based motion estimation method with the generalized gaussian kernel. Actuators 2017, 6. [Google Scholar] [CrossRef]




| Parameter | Definition | Value |
|---|---|---|
| l | Initial length of the actuator | m |
| t | Thickness of the rubber | m |
| Internal radius of small chambers | m | |
| Representative radius of small chambers | m | |
| Internal radius of large chambers | m | |
| Representative radius of large chambers | m | |
| n | Number of the bellows | 11 |
| E | Young’s modulus | Pa |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sudani, M.; Deng, M.; Wakimoto, S. Modelling and Operator-Based Nonlinear Control for a Miniature Pneumatic Bending Rubber Actuator Considering Bellows. Actuators 2018, 7, 26. https://doi.org/10.3390/act7020026
Sudani M, Deng M, Wakimoto S. Modelling and Operator-Based Nonlinear Control for a Miniature Pneumatic Bending Rubber Actuator Considering Bellows. Actuators. 2018; 7(2):26. https://doi.org/10.3390/act7020026
Chicago/Turabian StyleSudani, Mizuki, Mingcong Deng, and Shuichi Wakimoto. 2018. "Modelling and Operator-Based Nonlinear Control for a Miniature Pneumatic Bending Rubber Actuator Considering Bellows" Actuators 7, no. 2: 26. https://doi.org/10.3390/act7020026
APA StyleSudani, M., Deng, M., & Wakimoto, S. (2018). Modelling and Operator-Based Nonlinear Control for a Miniature Pneumatic Bending Rubber Actuator Considering Bellows. Actuators, 7(2), 26. https://doi.org/10.3390/act7020026






