Piezoelectric Plates Distribution for Active Control of Torsional Vibrations
Abstract
:1. Introduction
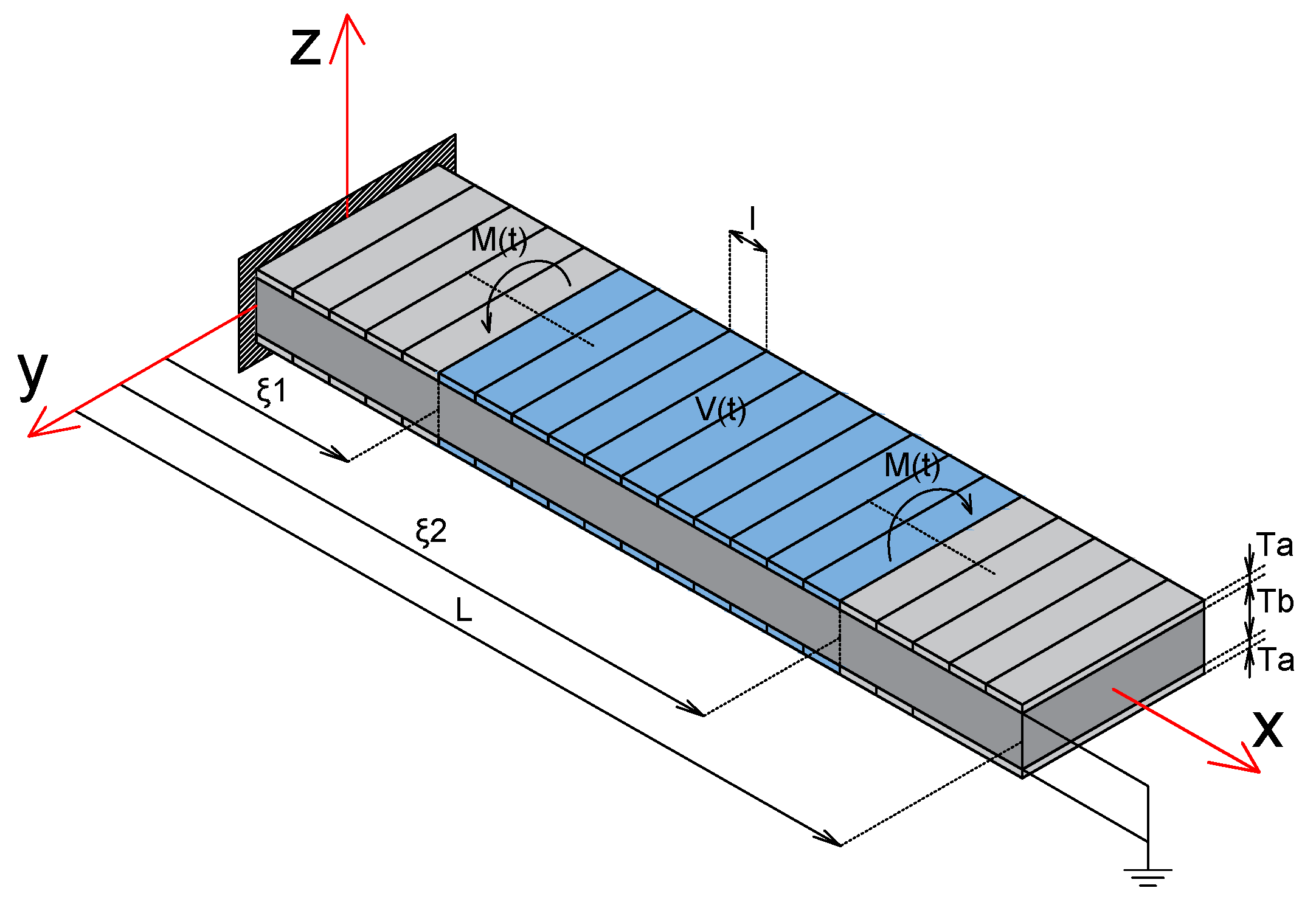
2. Governing Equations for Piezoelectric Coupled Torsional Beam
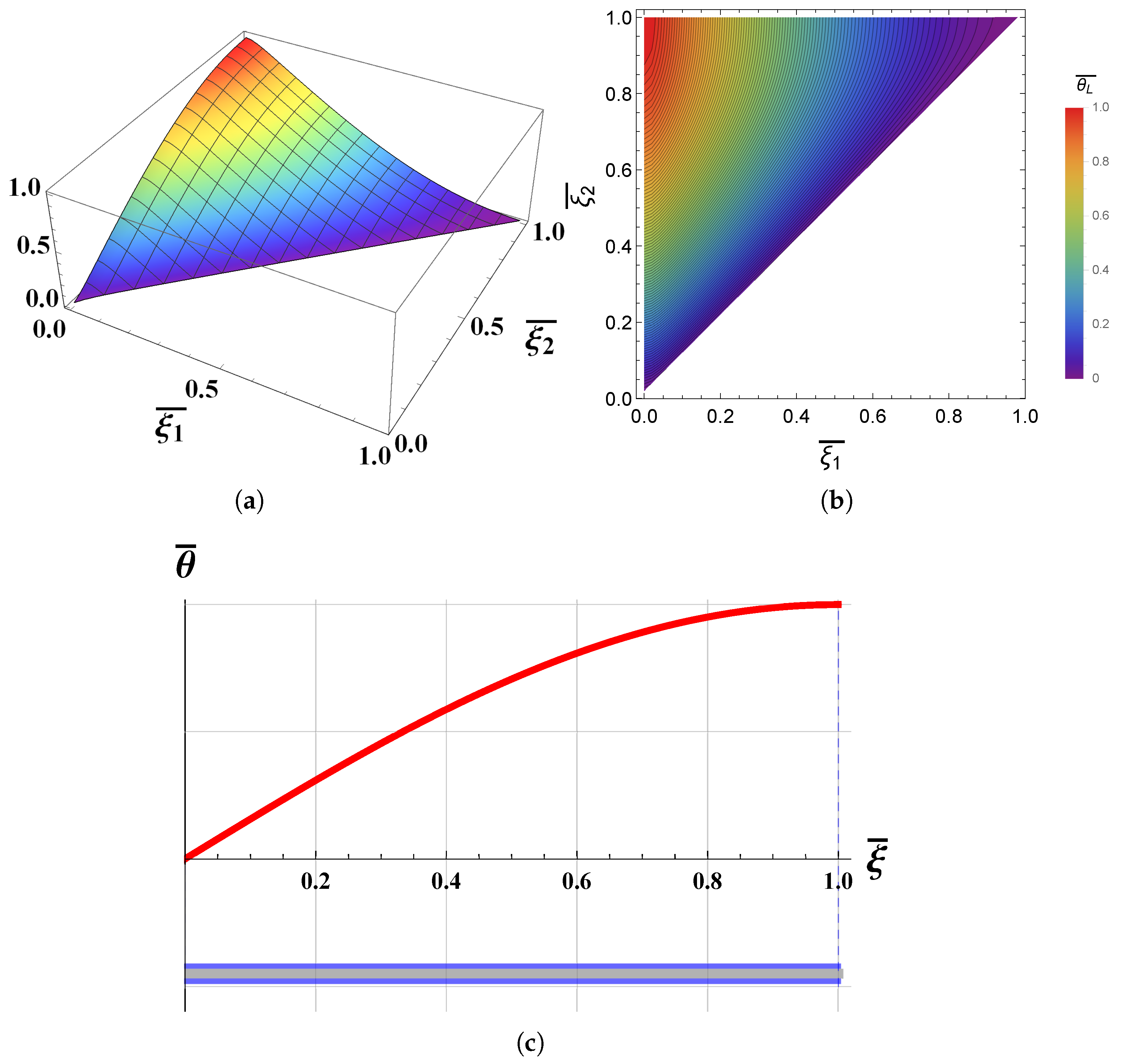
2.1. Damping of One Mode
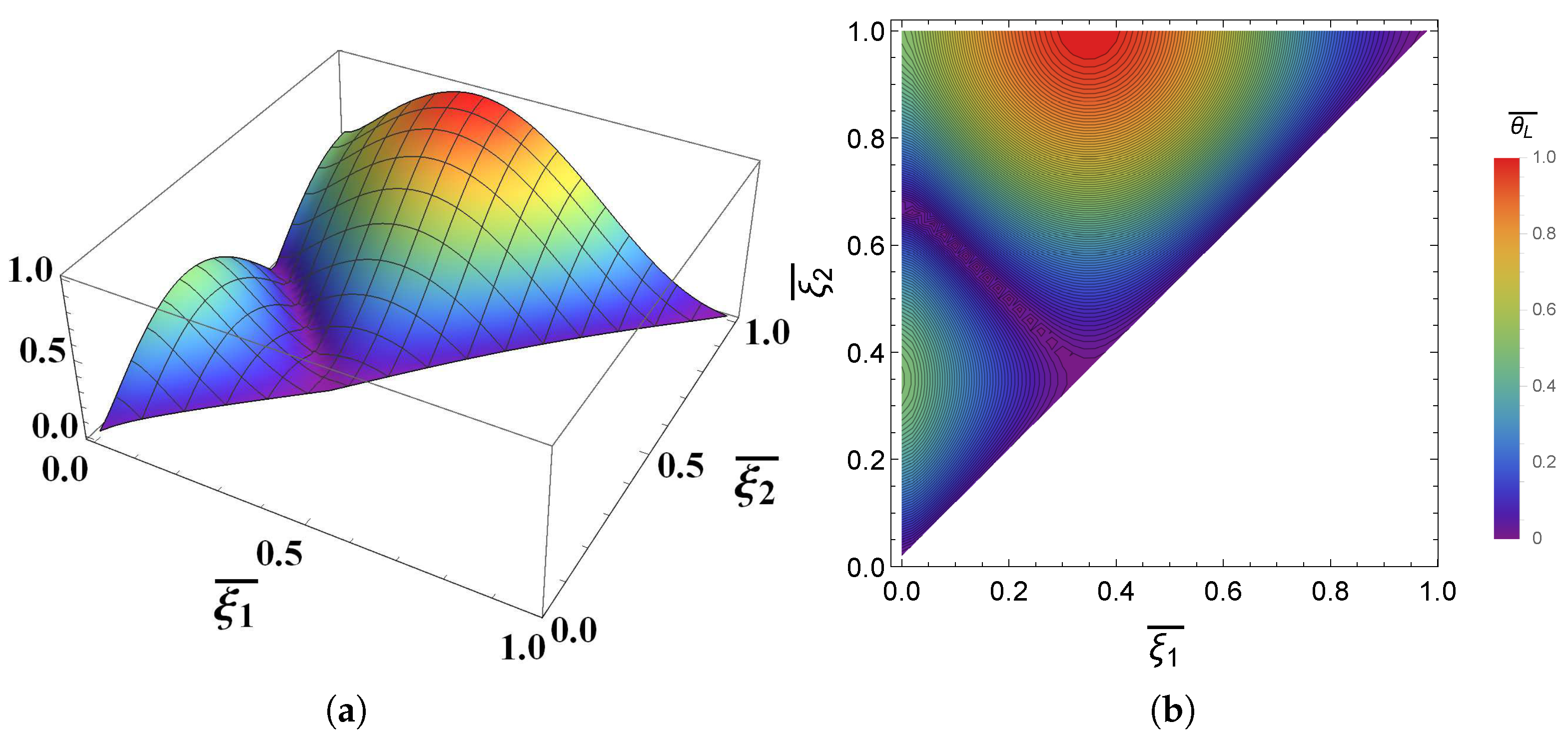
2.2. Damping of Two Combined Modes
3. Results and Discussions
4. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| B | control vector |
| damping matrices | |
| piezoelectric coefficient | |
| j | polar moment of inertia per unit length |
| J | St Venant torsion constant |
| stiffness matrices | |
| G | shear modulus |
| L | beam length |
| m | applied moment per unit length |
| piezoelectric torsional moment | |
| mass matrices | |
| applied moment vector | |
| r | ratio of the j-th component of the tension |
| V | voltage applied to the piezoelectric plates |
| damping coefficient | |
| damping coefficient | |
| angle of twist | |
| virtual angle of twist | |
| non dimensional length | |
| warping function | |
| adimensional length of the beam: | |
| modal amplitude | |
| torsional modes | |
| natural frequency | |
| Superscripts | |
| virtual quantity | |
| non dimensional length |
References
- Alkhatib, R.; Golnaraghi, M.F. Active structural vibration control: A review. Shock Vib. Dig. 2003, 35, 367–383. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H.; Fischer, S.; Braun, C. MR damper controlled vibration absorber for enhanced mitigation of harmonic vibrations. Actuators 2016, 54, 27. [Google Scholar] [CrossRef]
- Yang, S.-Y.; Han, C.; Shin, S.-U.; Choi, S.-B. Design and Evaluation of a Semi-Active Magneto-Rheological Mount for a Wheel Loader Cabin. Actuators 2017, 62, 16. [Google Scholar]
- Botta, F.; Dini, D.; Schwingshackl, C.; di Mare, L.; Cerri, G. Optimal placement of piezoelectric plates to control multimodal vibrations of a beam. Adv. Acoust. Vib. 2013, 2013, 10:1–10:8. [Google Scholar]
- Baz, A.; Poh, S. Performance of an active control system with piezoelectric actuators. J. Sound Vib. 1988, 126, 327–343. [Google Scholar] [CrossRef]
- Chopra, I. Review of state of art of smart structures and integrated system. AIAA J. 2002, 40, 2145–2187. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Hu, Z.; Wu, C.; Zhang, X. Shunt Damping Vibration Control Technology: A Review. Appl. Sci. 2017, 7, 494. [Google Scholar] [CrossRef]
- Herold, S.; Mayer, D. Adaptive Piezoelectric Absorber for Active Vibration Control. Actuators 2016, 5, 7. [Google Scholar] [CrossRef]
- Al Hamidi, Y.; Rakotondrabe, M. Multi-Mode Vibration Suppression in MIMO Systems by Extending the Zero Placement Input Shaping Technique: Applications to a 3-DOF Piezoelectric Tube Actuatorl. Actuators 2016, 5, 13. [Google Scholar] [CrossRef]
- Alvarez, N.; Cardoni, A.; Cerisola, N.; Riera, E.; Andrade, M.A.B.; Adamowski, J.C. Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers. Actuators 2015, 4, 255–266. [Google Scholar] [CrossRef]
- Guo, K.; Xu, Y. Random Vibration Suppression of a Truss Core Sandwich Panel Using Independent Modal Resonant Shunt and Modal Criterion. Appl. Sci. 2017, 7, 496. [Google Scholar] [CrossRef]
- Botta, F.; Cerri, G. Wave propagation in Reissner-Mindlin piezoelectric coupled cylinder with non-constant electric field through the thickness. Int. J. Solids Struct. 2007, 44, 6201–6219. [Google Scholar] [CrossRef]
- Wang, S.Y.; Tai, K.; Quek, S.T. Topology optimization of piezoelectric sensor/actuators for torsional vibration control of composite plates. Smart Mater. Struct. 2006, 15, 253–269. [Google Scholar] [CrossRef]
- Crawley, E.F.; de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA J. 1987, 25, 1373–1385. [Google Scholar] [CrossRef]
- Botta, F.; Scorza, A.; Rossi, A. Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations. Appl. Sci. 2018, 8, 551. [Google Scholar] [CrossRef]
- Botta, F.; Marx, N.; Schwingshackl, C.W.; Cerri, G.; Dini, D. A wireless vibration control technique for gas turbine blades using piezoelectric plates and contactless energy transfer. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; GT2013-95666. p. V07AT32A006. [Google Scholar]
- Botta, F.; Marx, N.; Gentili, S.; Schwingshackl, C.W.; Di Mare, L.; Cerri, G.; Dini, D. Optimal placement of piezoelectric plates for active vibration control of gas turbine blades: Experimental results. Proc. SPIE Int. Soc. Opt. Eng. 2012, 8345, 83452H. [Google Scholar]
- Park, C.; Walz, C.; Chopra, I. Bending and torsion models of beams with induced-strain actuators. Smart Mater. Struct. 1996, 5, 98–113. [Google Scholar]
- Park, C.; Chopra, I. Modeling piezoceramic actuation of beams in torsion. AIAA J. 1996, 34, 2582–2589. [Google Scholar] [CrossRef]
- Aldraihem, O.J.; Wetherhold, R.C. Mechanics and control of coupled bending and twisting vibration of laminated beams. Smart Mater. Struct. 1997, 6, 123. [Google Scholar] [CrossRef]
- Spearritt, D.J.; Asokanthan, S.F. Torsional vibration control of a flexible beam using laminated PVDF actuators. J. Sound Vib. 1996, 193, 941–956. [Google Scholar] [CrossRef]
- Zehetner, C. Compensation of torsion in rods by piezoelectric actuation. Arch. Appl. Mech. 2008, 78, 921–933. [Google Scholar] [CrossRef]
- Zehetner, C. Compensation of torsional vibrations in rods by piezoelectric shear actuators. Acta Mech. 2009, 207, 121–133. [Google Scholar] [CrossRef]
- Sunar, M.; Rao, S.S. Distribuited Modeling and Actuator Location for Piezoelectric Control System. AIAA J. 1996, 34, 2209–2221. [Google Scholar] [CrossRef]
- Demetriou, M.A. A Numerical Algorithm for the Optimal Placement of Actuators and Sensors for Flexible Structures. In Proceedings of the American Control Conference, Chicago, IL, USA, 28–30 June 2000; pp. 2290–2294. [Google Scholar]
- Barboni, R.; Mannini, A.; Fantini, E.; Gaudenzi, P. Optimal placement of PZT actuators for the control of beam dynamics. Smart Mater. Struct. 2000, 9, 110–120. [Google Scholar] [CrossRef]
- Aldraihem, O.J.; Singh, T.; Wetherhold, R.C. Optimal Size and Location of Piezoelectric Actuator/Sensors: Practical Considerations. J. Guid. Control Dyn. 2000, 23, 509–515. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.M. Optimal placement and size of piezoelectric patches on beams from the controllability perspective. Smart Mater. Struct. 2000, 9, 558–567. [Google Scholar] [CrossRef]
- Bruant, I.; Coffignal, G.; Lene, F.; Verge, M. A methodology for determination of piezoelectric actuator and sensor location on beam structures. J. Sound Vib. 2001, 245, 861–882. [Google Scholar] [CrossRef]
- Frecker, M.I. Recent Advances in Optimization of Smart Structures and Actuators. J. Intell. Mater. Syst. Sruct. 2003, 14, 207–216. [Google Scholar] [CrossRef]
- Yang, Y.; Jin, Z.; Soh, C.K. Integrated optimal design of vibration control system for smart beams using genetic algorithms. J. Sound Vib. 2005, 119, 487–508. [Google Scholar] [CrossRef]
- Dhuri, K.D.; Seshu, P. Piezo actuator placement and sizing for good control effectiveness and minimal change in original system dynamics. Smart Mater. Struct. 2006, 15, 1661–1672. [Google Scholar] [CrossRef]
- Kumar, K.R.; Narayanan, S. Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs. Smart Mater. Struct. 2008, 17, 1–15. [Google Scholar]
- Gupta, V.; Sharma, M.; Nagesh, T. Optimization Criteria for Optimal Placement of Piezoelectric Sensors and Actuators on a Smart Structure: A Technical Review. J. Intell. Mater. Syst. Struct. 2010, 21, 1227–1243. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botta, F.; Toccaceli, F. Piezoelectric Plates Distribution for Active Control of Torsional Vibrations. Actuators 2018, 7, 23. https://doi.org/10.3390/act7020023
Botta F, Toccaceli F. Piezoelectric Plates Distribution for Active Control of Torsional Vibrations. Actuators. 2018; 7(2):23. https://doi.org/10.3390/act7020023
Chicago/Turabian StyleBotta, Fabio, and Federico Toccaceli. 2018. "Piezoelectric Plates Distribution for Active Control of Torsional Vibrations" Actuators 7, no. 2: 23. https://doi.org/10.3390/act7020023
APA StyleBotta, F., & Toccaceli, F. (2018). Piezoelectric Plates Distribution for Active Control of Torsional Vibrations. Actuators, 7(2), 23. https://doi.org/10.3390/act7020023



