Design and Stiffness Evaluation of a Compliant Joint with Parallel Architecture Realizing an Approximately Spherical Motion
Abstract
:1. Introduction
- Analytical computation of the SJ compliance matrix and its subsequent diagonalization via Euclidean transformations;
- Validation of the analytical model via Finite Element Analysis (FEA) within the small deflection hypothesis;
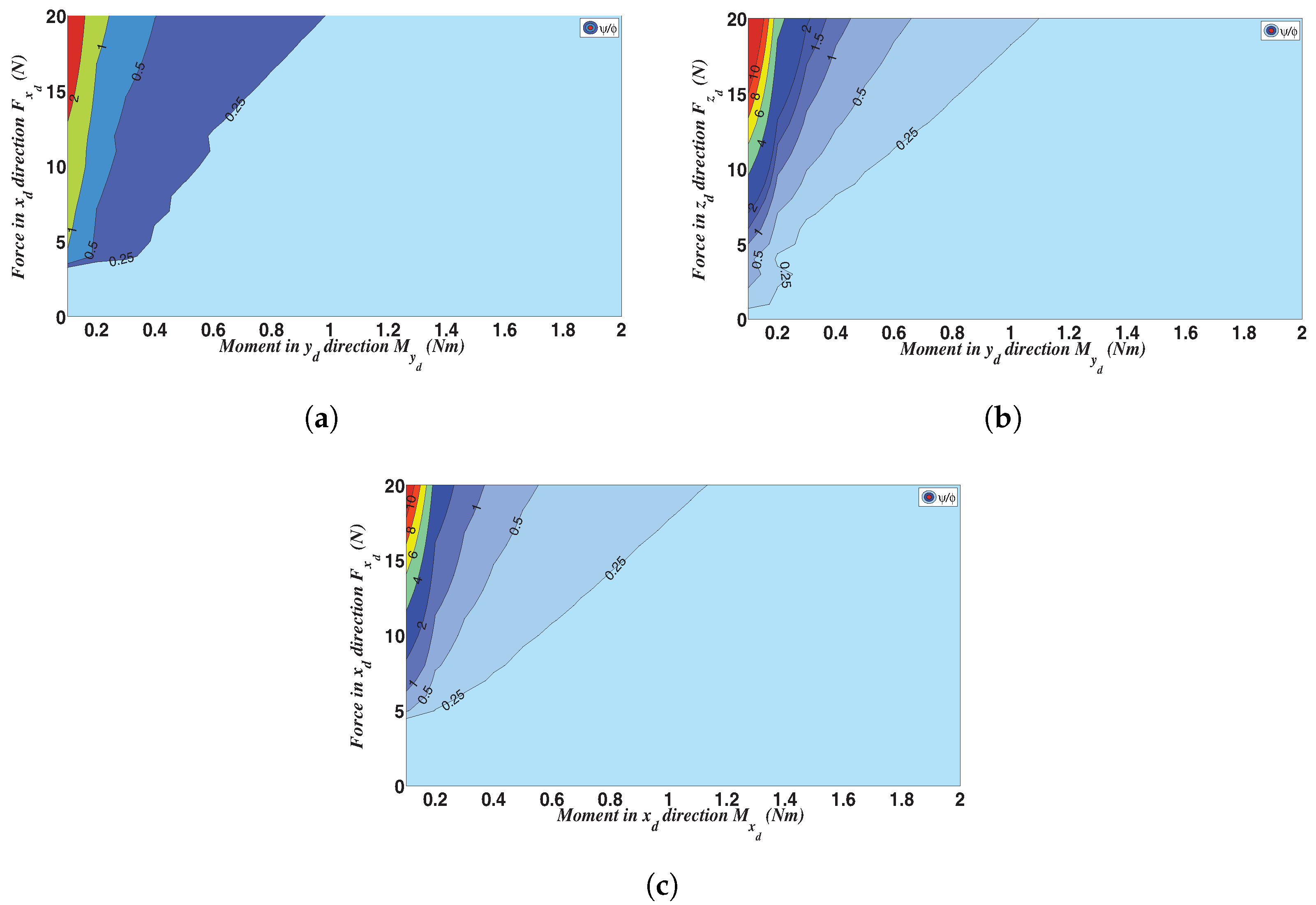
- Extension of the numerical results in the large deflection range, results being provided via a set of normalized design graphs that allow to clearly spot the optimal CFB geometric parameter for a reduced SJ parasitic behavior.
2. Analytical Design of Flexible Beam-Based Systems: Background Theory
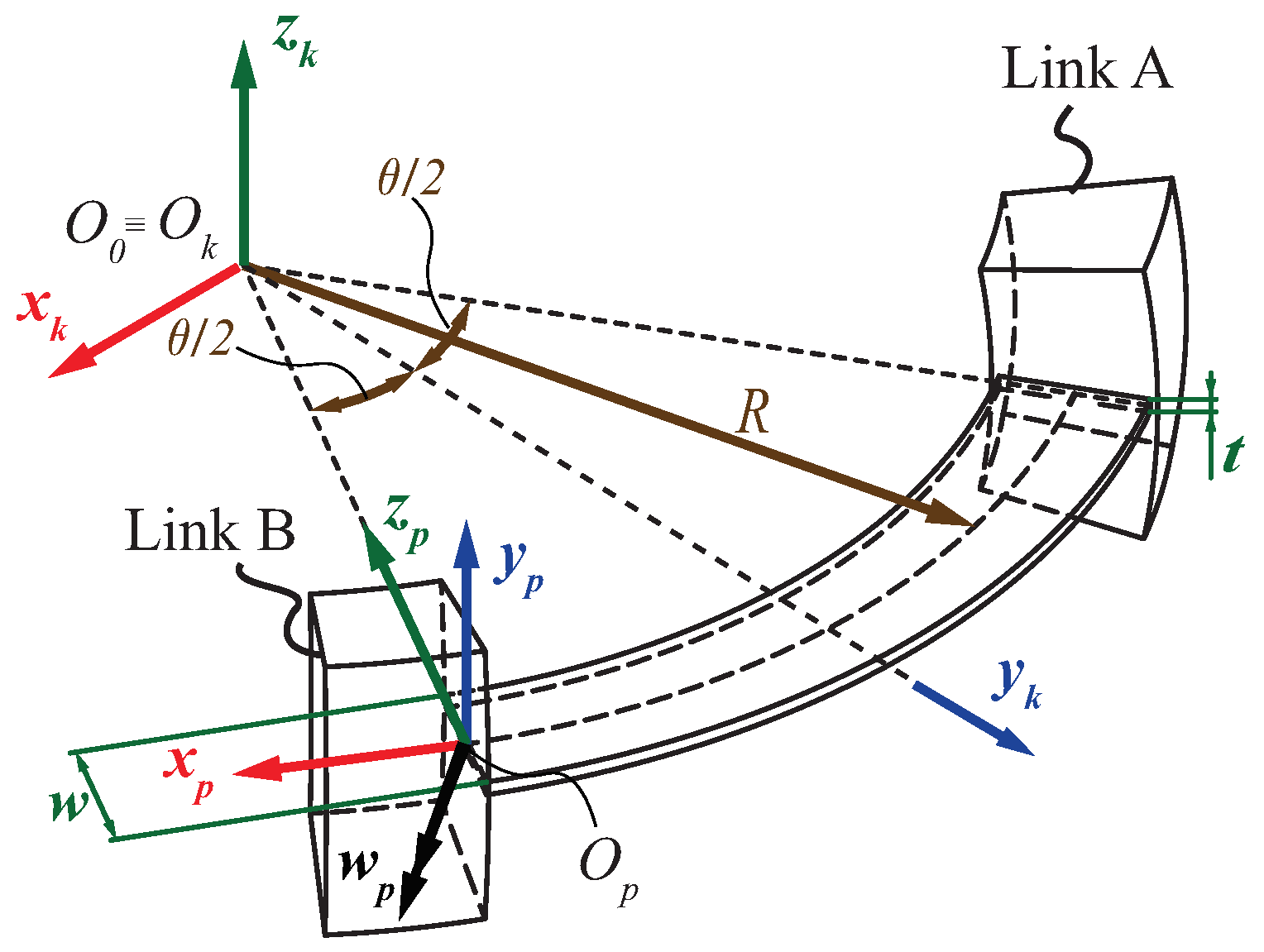
Compliance Matrix of a Single CFB
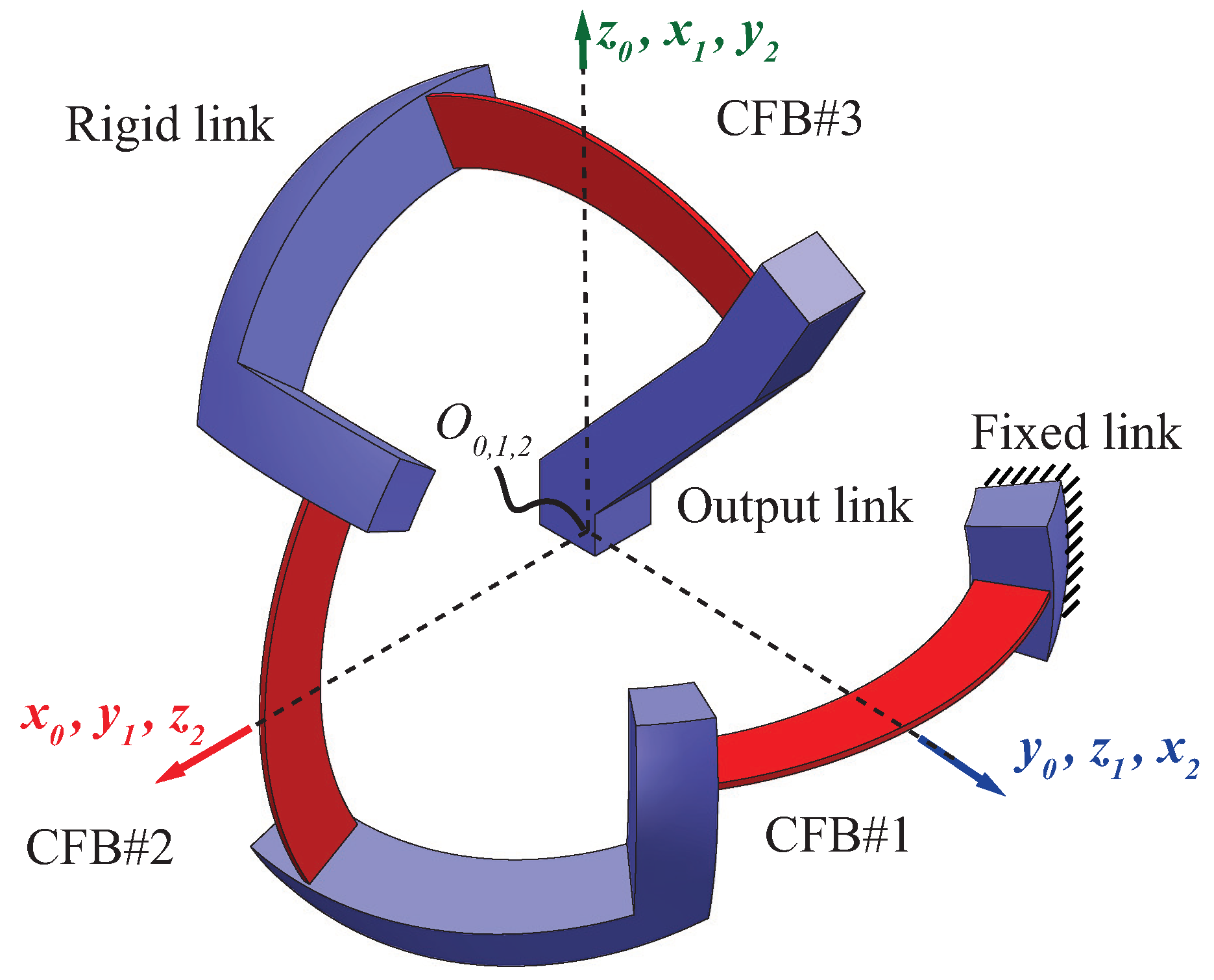
3. Compliance Matrix of the Compliant Spherical Joint
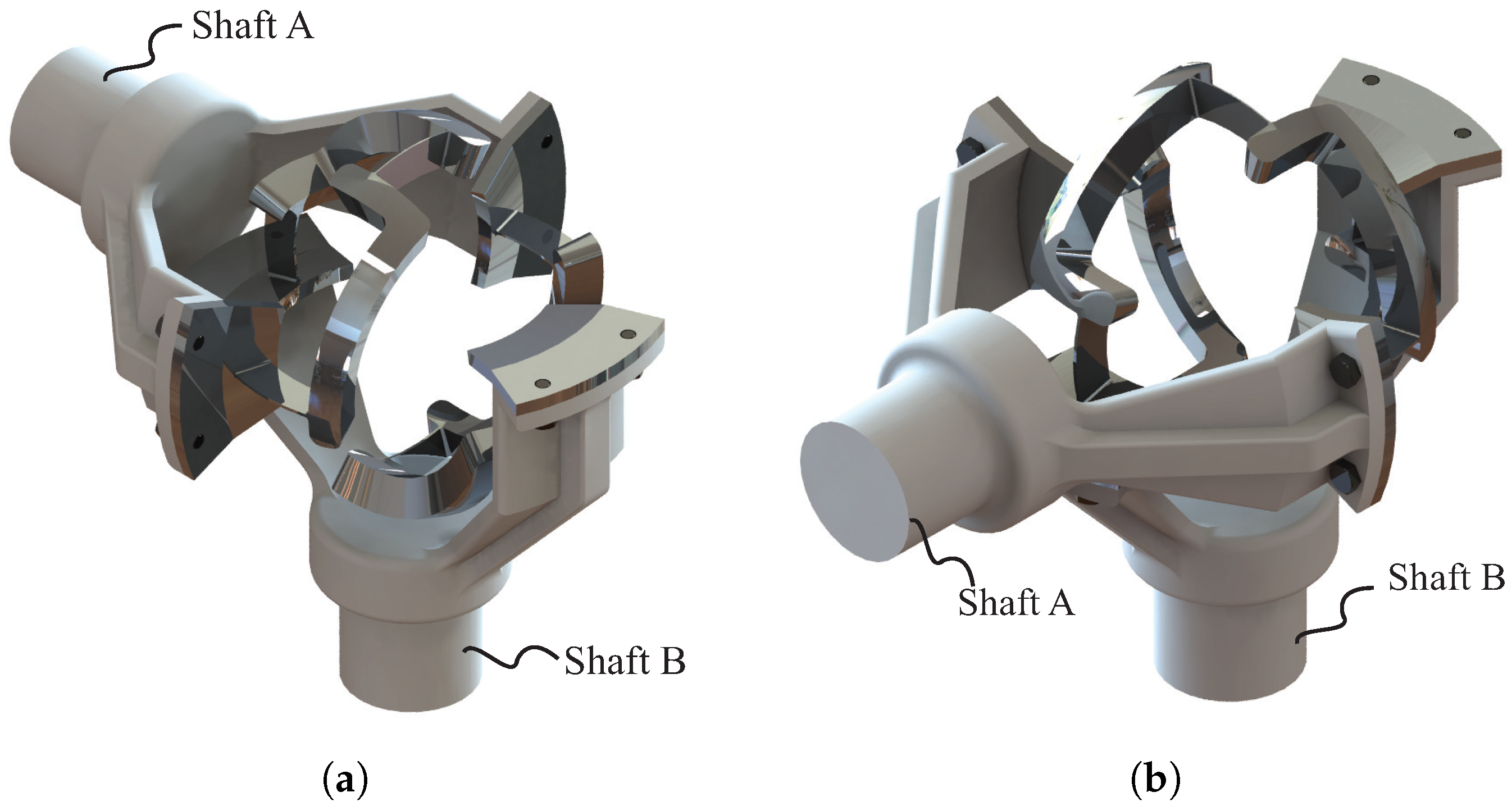
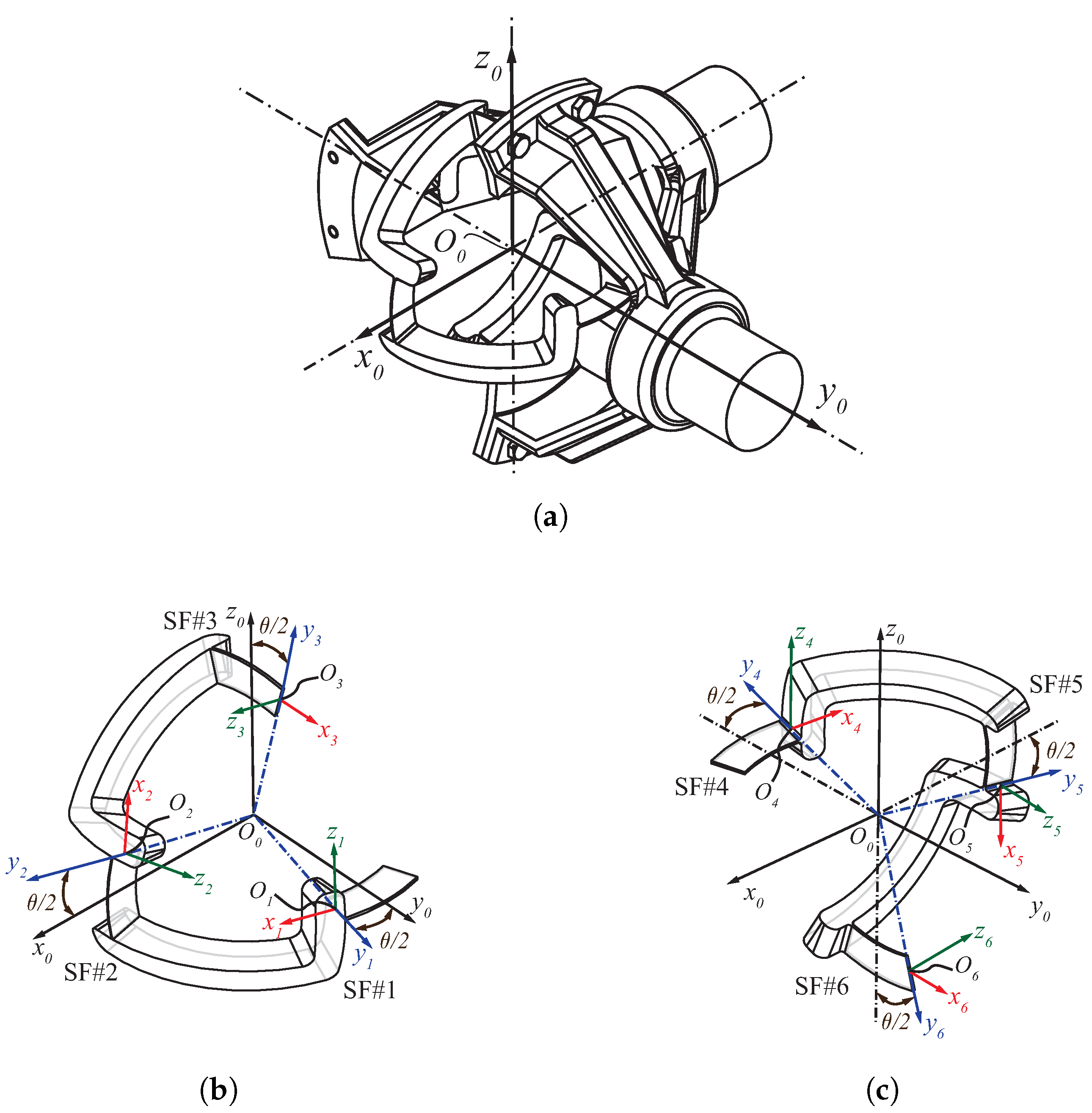
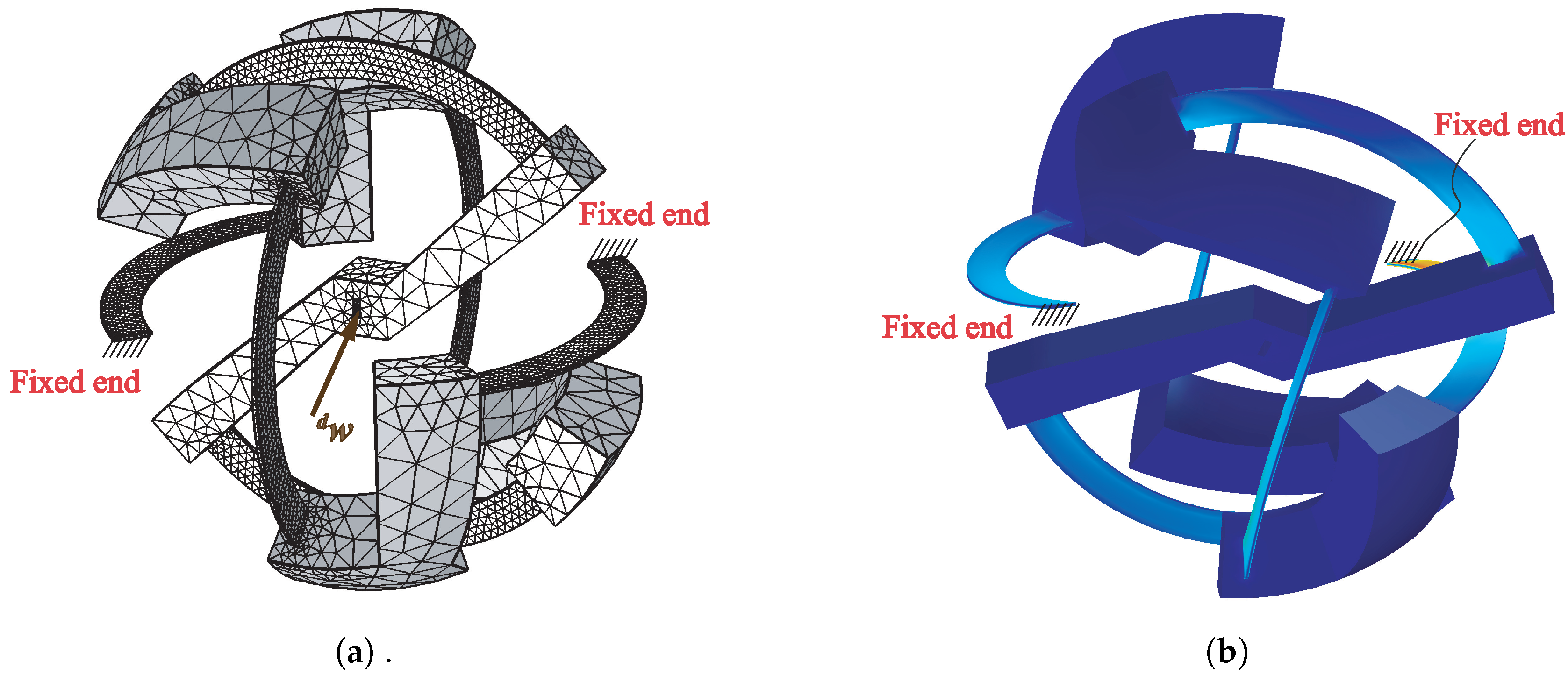
4. Numerical Example and Model Validation
4.1. Finite Element Analysis with a Small Deflection Hypothesis
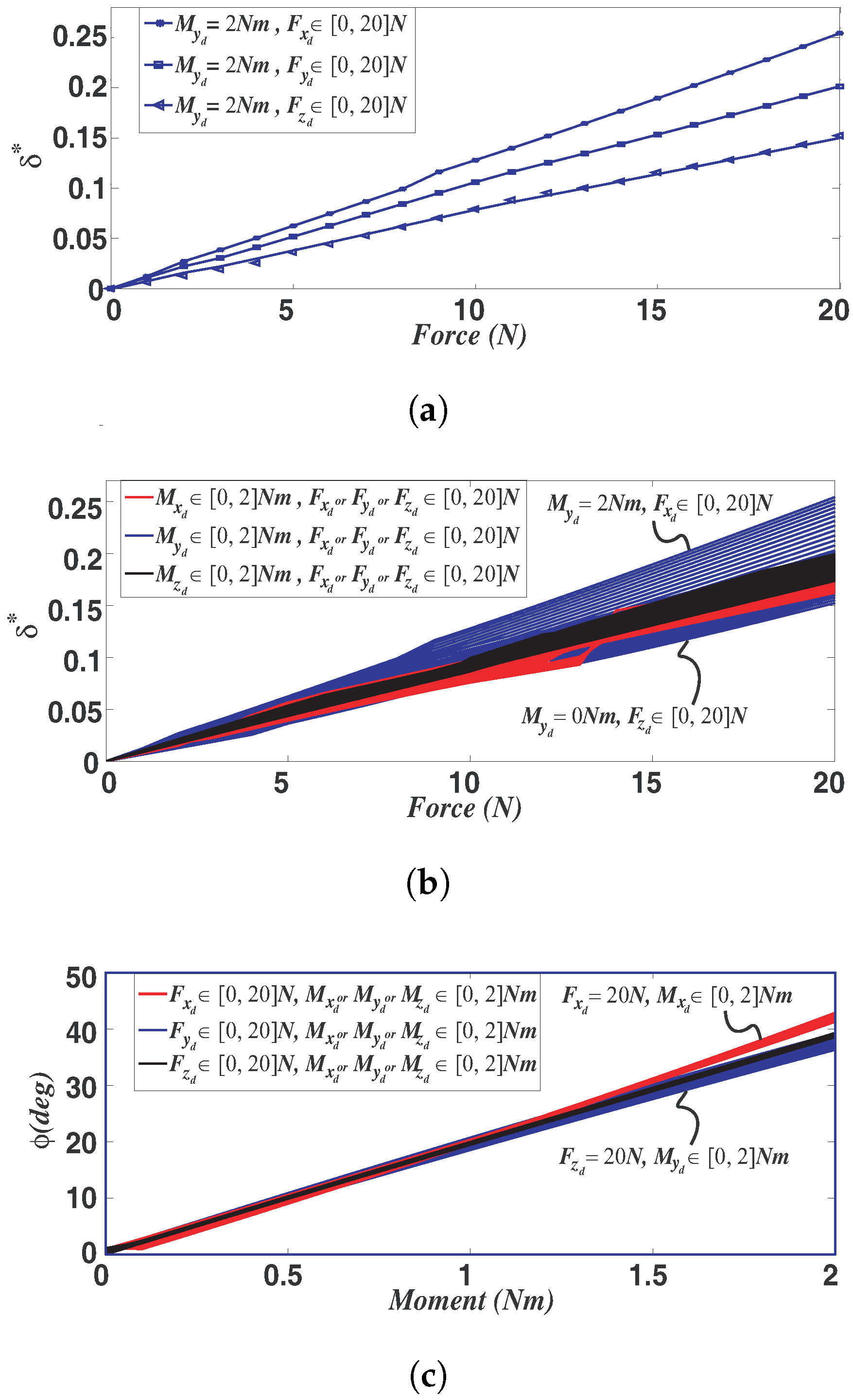
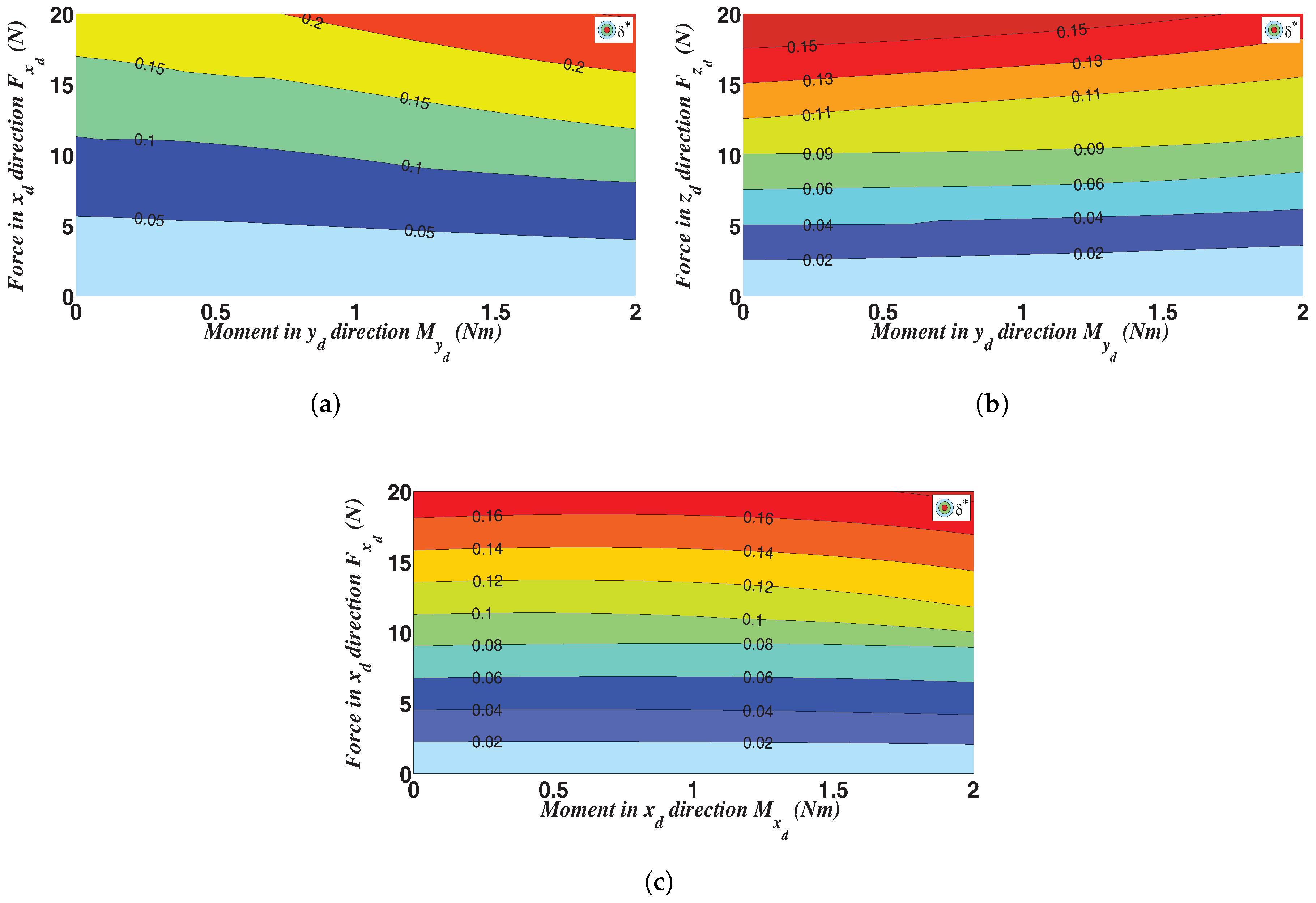
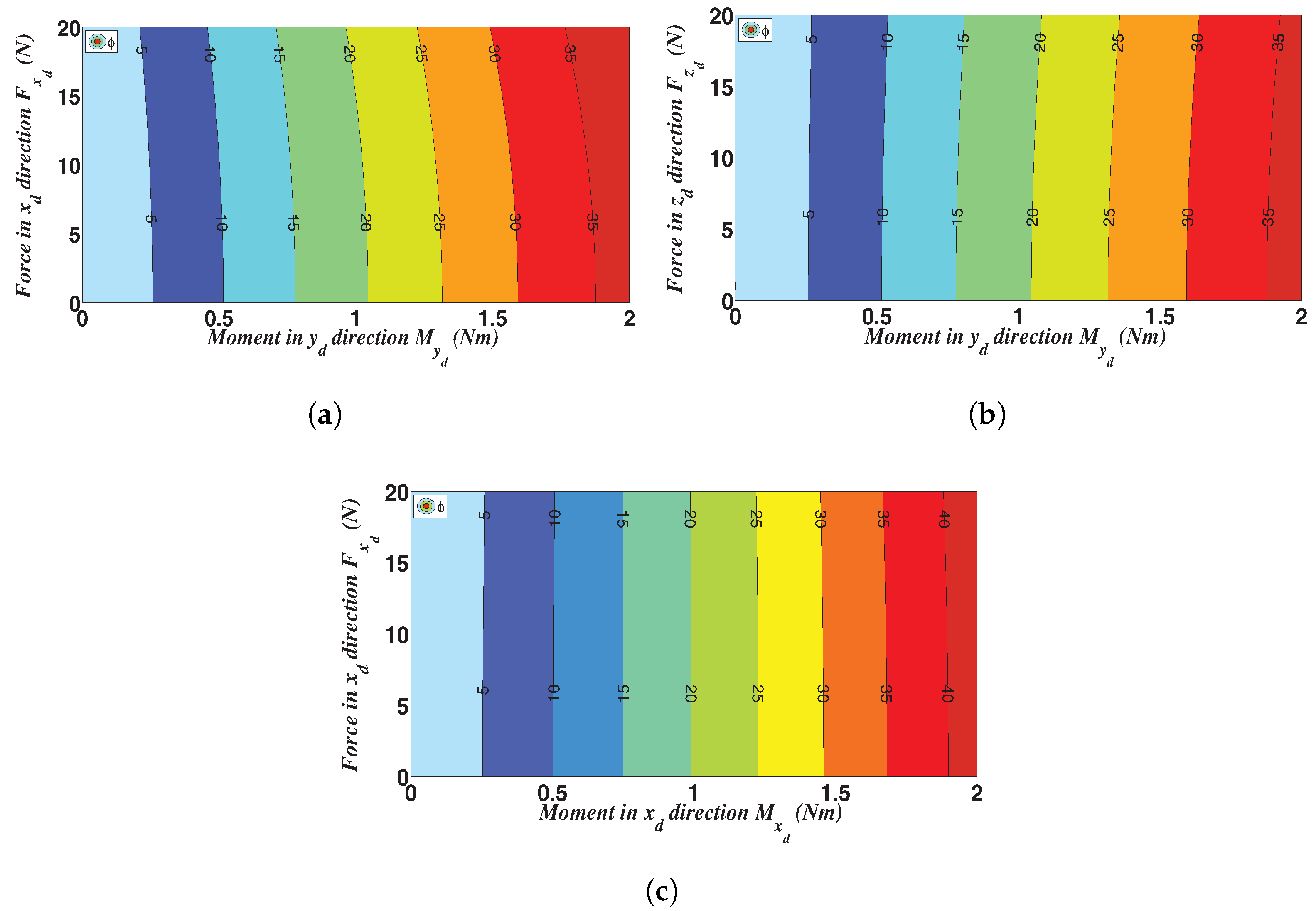
4.2. Finite Element Analysis with Large Deformation Hypothesis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Plots
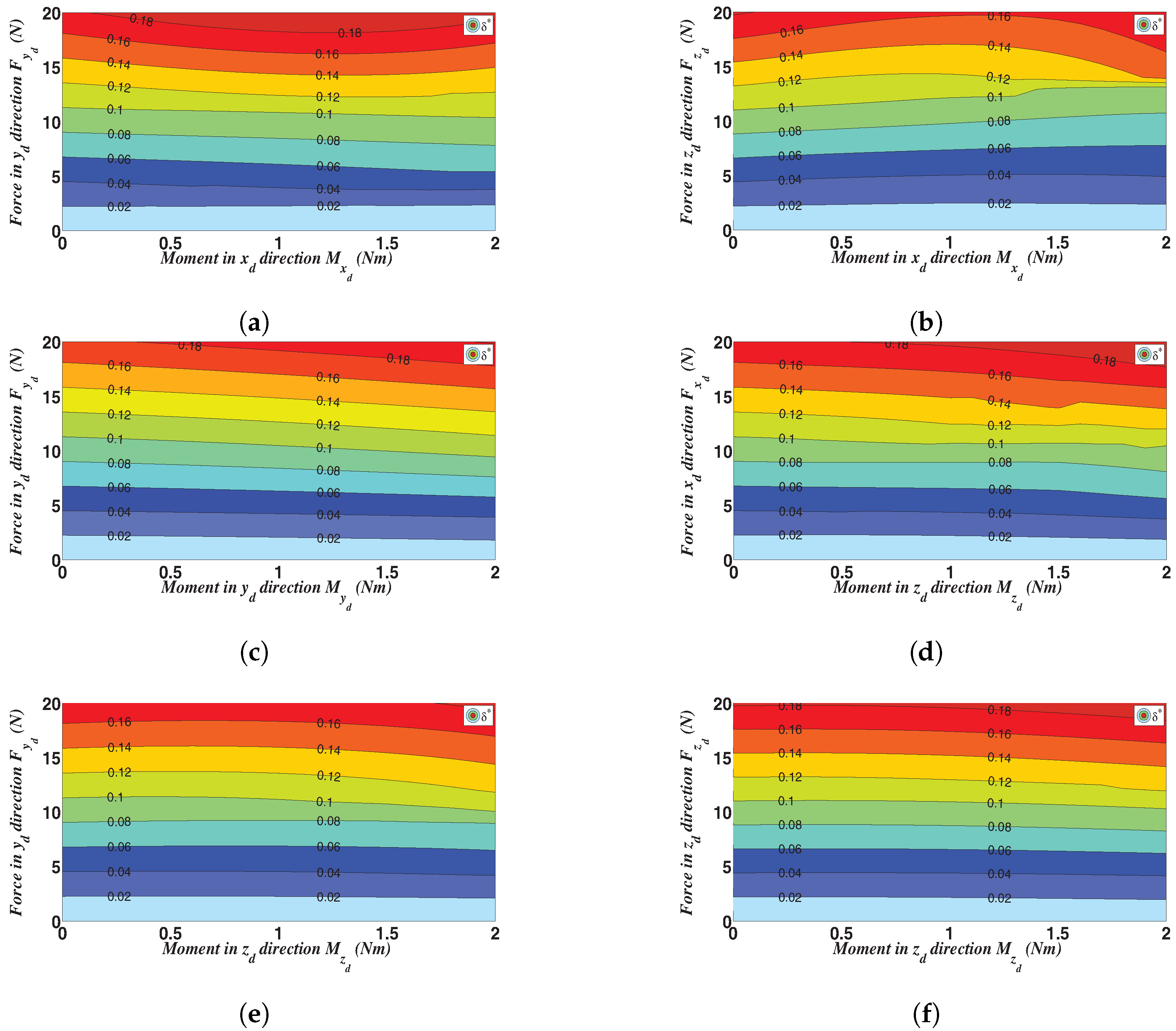
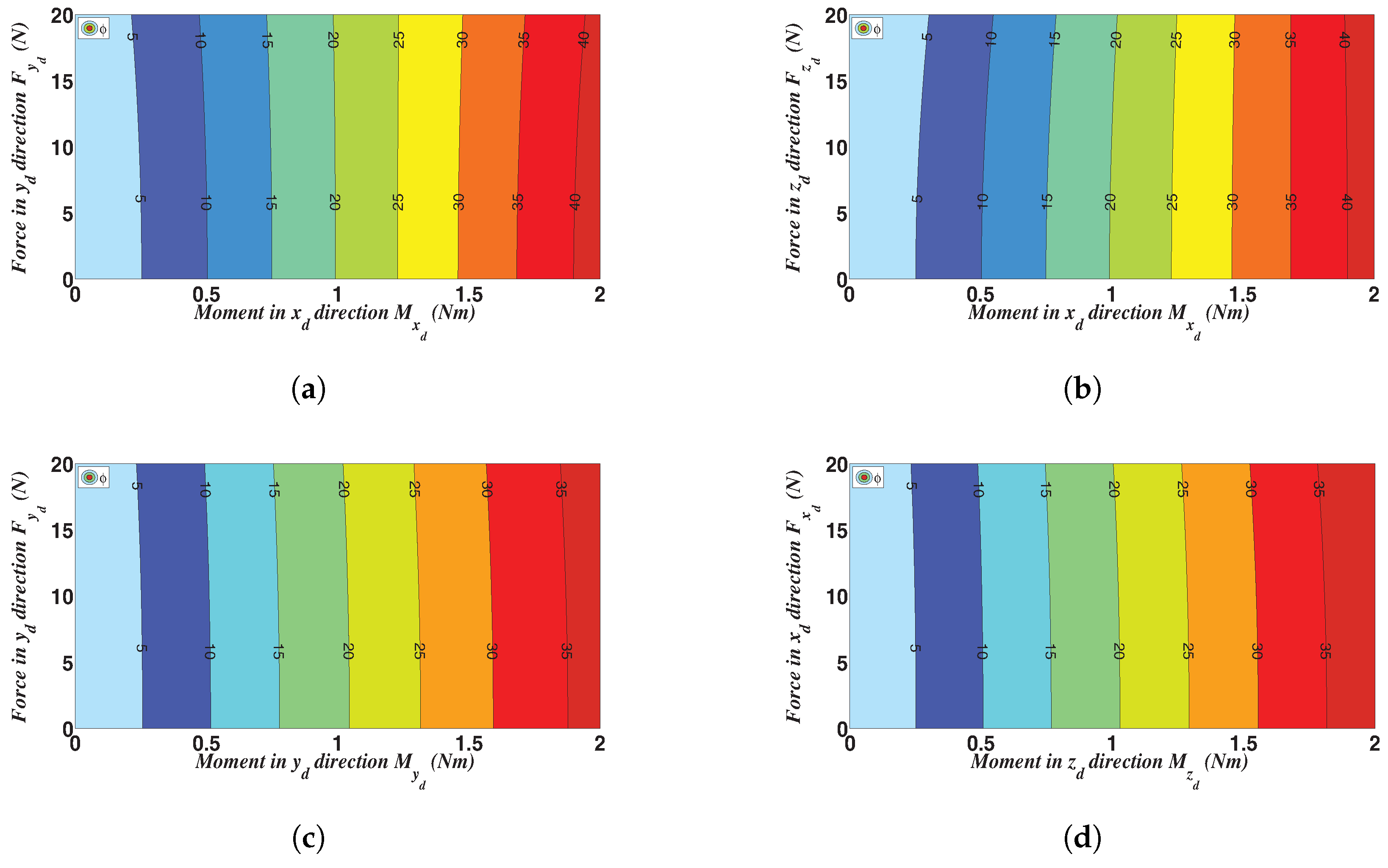
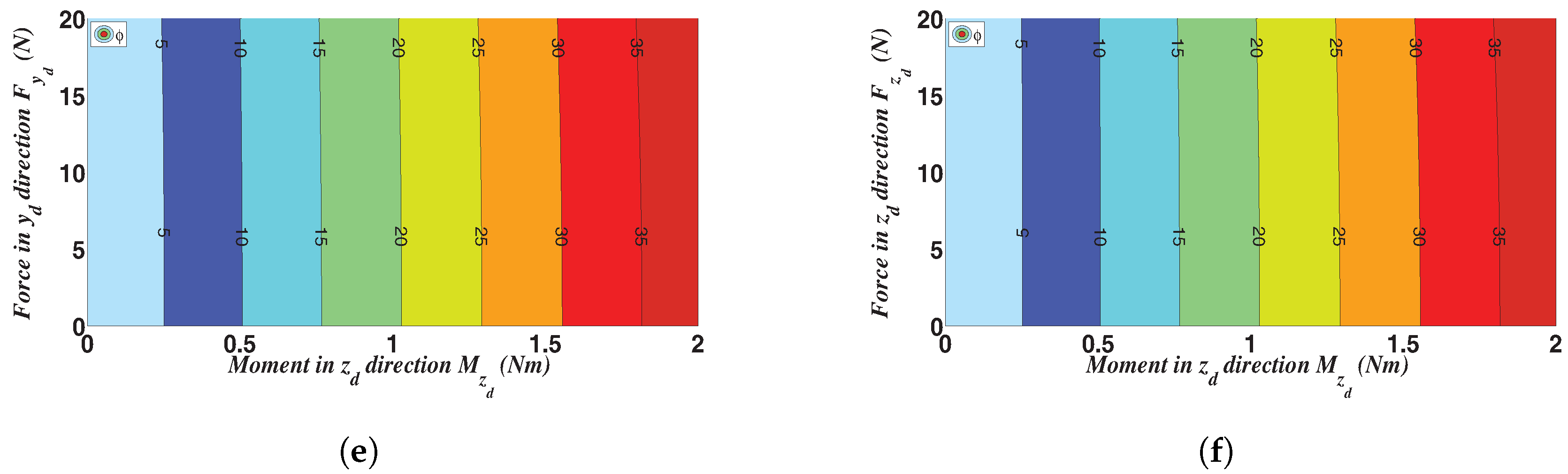
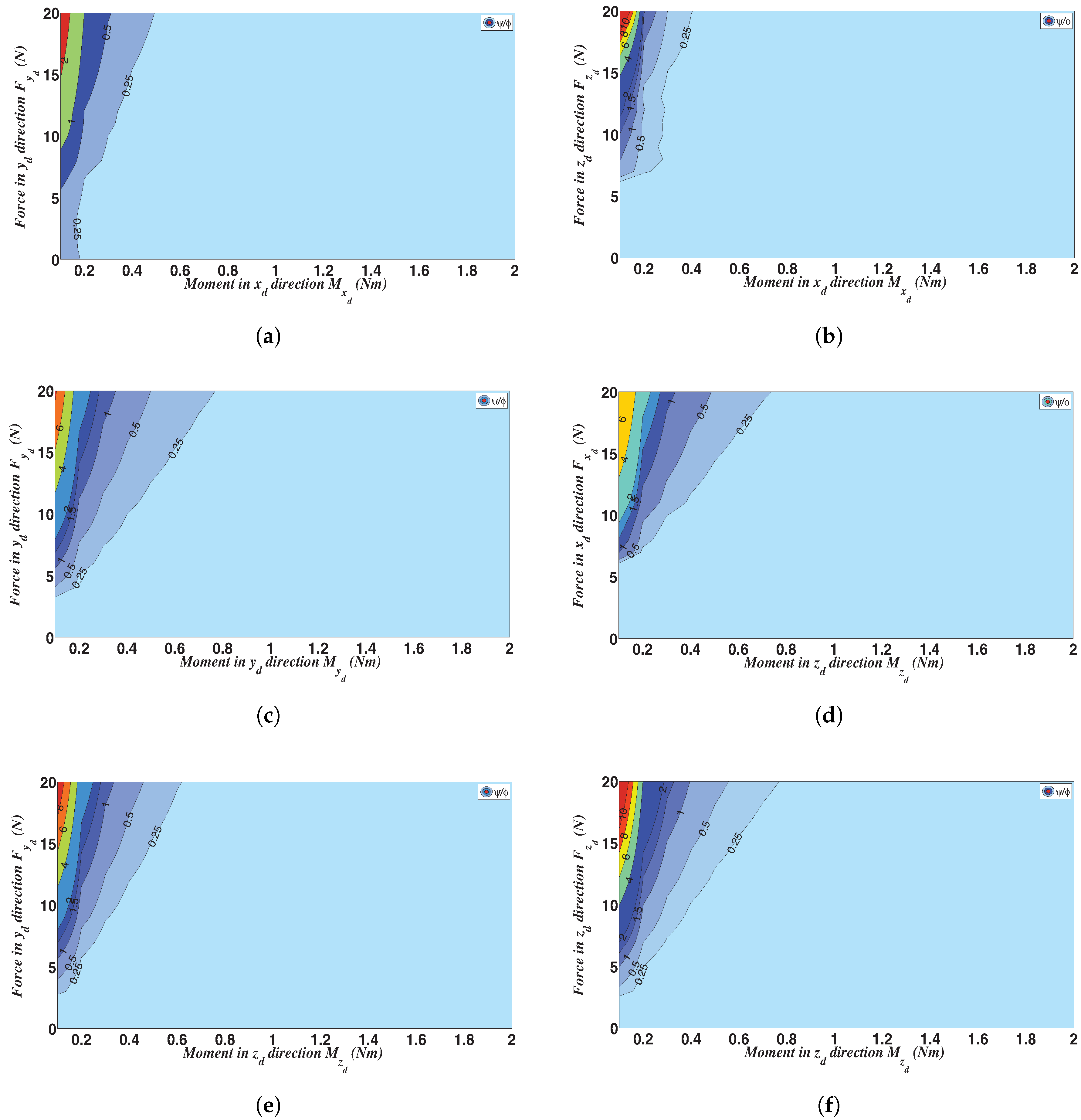
References
- Howell, L.L. Compliant Mechanisms; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lu, K.-J. Syntheis of Shape Morphing Compliant Mechanisms. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2004. [Google Scholar]
- Hesselbach, J.; Wrege, J.; Raatz, A.; Becker, O. Aspects on design of high precision parallel robots. Assem. Autom. 2004, 24, 49–57. [Google Scholar] [CrossRef]
- Erkaya, S.; Doğan, S.; Ulus, S. Effects of joint clearance on the dynamics of a partly compliant mechanism: Numerical and experimental studies. Mech. Mach. Theory 2015, 88, 125–140. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Tjiptoprodjo, R.C.; Zhang, W.J.; Yang, G.S. Micro-motion devices technology: The state of arts review. Int. J. Adv. Manuf. Technol. 2008, 38, 463–478. [Google Scholar] [CrossRef]
- Soemers, H. Design Principles for Precision Mechanisms; T-Pointprint: Enschede, The Netherlands, 2010. [Google Scholar]
- Palli, G.; Melchiorri, C.; Berselli, G.; Vassura, G. Design and modeling of variable stiffness joints based on compliant flexures. In Proceedings of the 34th Annual Mechanisms and Robotics Conference, Montreal, QC, Canada, 15–18 August 2010; Volume 2, pp. 1069–1078. [Google Scholar]
- Borboni, A.; Faglia, R.; Mor, M. Compliant device for hand rehabilitation of stroke patient. In Proceedings of the ASME 12th Biennial Conference on Engineering Systems Design and Analysis, Copenhagen, Denmark, 25–27 July 2014; Volume 1, p. V001T03A001. [Google Scholar]
- Borboni, A.; Faglia, R. Robust design of a shape memory actuator with slider and slot layout and passive cooling control. Microsyst. Technol. 2018, 24, 1379–1389. [Google Scholar] [CrossRef]
- Scarfogliero, U.; Stefanini, C.; Dario, P. The use of compliant joints and elastic energy storage in bio-inspired legged robots. Mech. Mach. Theory 2009, 44, 580–590. [Google Scholar] [CrossRef]
- Ham, R.V.; Sugar, T.G.; Vanderborght, B.; Hollander, K.W.; Lefeber, D. Compliant actuator designs. IEEE Robot. Autom. Mag. 2009, 16, 81–94. [Google Scholar] [CrossRef]
- Wang, D.H.; Yang, Q.; Dong, H.M. A monolithic compliant piezoelectric-driven microgripper: Design, modeling, and testing. IEEE/ASME Trans. Mechatron. 2013, 18, 138–147. [Google Scholar] [CrossRef]
- Reddy, B.N.; Naik, S.; Saxena, A. Systematic synthesis of large displacement contact-aided monolithic compliant mechanisms. ASME J. Mech. Des. 2012, 134, 011007. [Google Scholar] [CrossRef]
- Teo, T.J.; Yang, G.; Chen, I. Compliant manipulators. In Handbook of Manufacturing Engineering and Technology; Springer: London, UK, 2014; pp. 1–63. [Google Scholar]
- Gao, Z.; Zhang, D. Workspace representation and optimization of a novel parallel mechanism with three-degrees-of-freedom. Sustainability 2011, 3, 2217–2228. [Google Scholar] [CrossRef]
- Guo, K.; Ni, M.; Chen, H.; Sui, Y. A monolithic adjusting mechanism for optical element based on modified 6-pss parallel mechanism. Sens. Actuators A Phys. 2016, 251, 1–9. [Google Scholar] [CrossRef]
- Palmieri, G.; Palpacelli, M.C.; Callegari, M.M. Study of a fully compliant u-joint designed for minirobotics applications. ASME J. Mech. Des. 2012, 134, 111003. [Google Scholar] [CrossRef]
- Berselli, G.; Guerra, A.; Vassura, G.; Andrisano, A. An engineering method for comparing selectively compliant joints in robotic structures. IEEE/ASME Trans. Mechatron. 2014, 19, 1882–1895. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J. Design of circular cross-section corner-filleted flexure hinges for three-dimensional compliant mechanisms. J. Mech. Des. Trans. ASME 2002, 124, 479–484. [Google Scholar] [CrossRef]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Borboni, A.; Faglia, R. Parasitic Phenomena in the Dynamics of Industrial Devices; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Coiffet, P. Les Robots: Modelisation et Commande; Hermes Publishing: Hunt Valley, MD, USA, 1981. [Google Scholar]
- Berselli, G.; Parvari Rad, F.; Vertechy, R.; Parenti-Castelli, V. Comparative evaluation of straight and curved beam flexures for selectively compliant mechanisms. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Wollongong, NSW, Australia, 9–12 July 2013; pp. 1761–1766. [Google Scholar]
- Hasse, A.; Campanile, L.F. Design of compliant mechanisms with selective Compliance. Smart Mater. Struct. 2009, 18, 115016. [Google Scholar] [CrossRef]
- Yin, L.; Ananthasuresh, G.K. Design of distributed compliant mechanisms. Mech. Based Des. Struct. Mach. 2003, 31, 151–179. [Google Scholar] [CrossRef]
- Meng, Q.; Li, Y.; Xu, J. New empirical stiffness equations for corner-filleted flexure hinges. Mech. Sci. 2013, 4, 345–356. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.; Garcia, E.; Goldfarb, M. Design of symmetric conic-section flexure hinges based on closed-form compliance equations. Mech. Mach. Theory 2002, 37, 477–498. [Google Scholar] [CrossRef]
- Berselli, G.; Meng, Q.; Vertechy, R.; Parenti-Castelli, V. An improved design method for the dimensional synthesis of flexure-based compliant mechanisms: Optimization procedure and experimental validation. Meccanica 2016, 51, 1209–1225. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Du, Y. Elliptical-arc-fillet flexure hinges: Toward a generalized model for commonly used flexure hinges. J. Mech. Des. 2011, 133, 081002. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Design and analysis of a high-accuracy flexure Hinge. Rev. Sci. Instrum. 2016, 87, 055106. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Zhang, X.; Fatikow, S. Design of single-axis flexure hinges using continuum topology optimization method. Sci. China Technol. Sci. 2014, 57, 560–567. [Google Scholar] [CrossRef]
- Meirovitch, L. Elements of Vibration Analysis; McGraw Hill: New York, NY, USA, 1986. [Google Scholar]
- Parvari Rad, F.; Vertechy, R.; Berselli, G.; Parenti-Castelli, V. Compliant serial 3R chain with spherical flexures. Adv. Robot Kinemat. 2018, 2016, 11–21. [Google Scholar]
- Smith, C.; Lusk, C. Modeling and parameter study of bistable spherical compliant Mechanisms. In Proceedings of the ASME Design Engineering Technical Conference, Washington, DC, USA, 28–31 August 2011; Volume 6, pp. 51–58. [Google Scholar]
- Wilding, S.E.; Howell, L.L.; Magleby, S.P. Spherical lamina emergent mechanisms. Mech. Mach. Theory 2012, 49, 187–197. [Google Scholar] [CrossRef]
- Tanık, Ç.M.; Parlaktaş, V.; Tanık, E.; Kadıoğlu, S. Steel compliant cardan universal joint. Mech. Mach. Theory 2015, 92, 171–183. [Google Scholar] [CrossRef]
- Farhadi Machekposhti, D.; Tolou, N.; Herder, J.L. The scope for a compliant homokinetic coupling based on review of compliant joints and rigid-body constant velocity universal joints. In Proceedings of the ASME IDETC International Design Engineering Technical Conferences, Chicago, IL, USA, 12–15 August 2012; Volume 4, pp. 379–392. [Google Scholar]
- Parvari Rad, F.; Vertechy, R.; Berselli, G.; Parenti-Castelli, V. Analytical compliance analysis and finite element verification of spherical flexure hinges for spatial compliant mechanisms. Mech. Mach. Theory 2016, 101, 168–180. [Google Scholar] [CrossRef]
- Parvari Rad, F.; Berselli, G.; Vertechy, R.; Parenti-Castelli, V. Design and stiffness analysis of a compliant spherical chain with three degrees of freedom. Precis. Eng. 2017, 47, 1–9. [Google Scholar] [CrossRef]
- Berselli, G.; Vassura, G.; Piccinini, M. Comparative evaluation of the selective compliance in elastic joints for robotic structures. In Proceedings of the IEEE ICRA International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 759–764. [Google Scholar]
- Mankame, N.D.; Ananthasuresh, G.K. Contact aided compliant mechanisms: Concept and preliminaries. In Proceedings of the ASME IDETC, International Design Engineering Technical Conferences, Montreal, QC, Canada, 29 September–2 October 2002; Volume 5, pp. 109–121. [Google Scholar]
- Cannon, J.R.; Howell, L.L. A compliant contact-aided revolute joint. Mech. Mach. Theory 2005, 40, 1273–1293. [Google Scholar] [CrossRef]
- Carter Hale, L. Principles and Techniques for Designing Precision Machines. Ph.D. Thesis, Department of Mechanical Engineering, MIT, Cambridge, MA, USA, 1999. [Google Scholar]
- Loncaric, J. Normal forms of stiffness and compliance matrices. IEEE J. Robot. Autom. 1987, 3, 567–572. [Google Scholar] [CrossRef]
- Howard, S.; Zefran, M.; Kumar, V. On the 6x6 cartesian stiffness matrix for three-dimensional motions. Mech. Mach. Theory 1998, 33, 389–408. [Google Scholar] [CrossRef]
- Zhang, S.; Fasse, E.D. A finite-element-based method to determine the spatial stiffness properties of a notch hinge. ASME J. Mech. Des. 2001, 123, 141–147. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J. Theory of Elasticity, Vol. 412; McGraw Hill: New York, NY, USA, 1951. [Google Scholar]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer: New York, NY, USA, 2010. [Google Scholar]

| Compliance factors | ||||
| Analytic | 6.1980 × | 6.3279 × | 0.3505 | 0.3579 |
| FEA | 5.7876 × | 5.8937 × | 0.3428 | 0.3504 |
| Percentage error (%) | 6.6 | 6.8 | 2.2 | 2.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parvari Rad, F.; Vertechy, R.; Berselli, G.; Parenti-Castelli, V. Design and Stiffness Evaluation of a Compliant Joint with Parallel Architecture Realizing an Approximately Spherical Motion. Actuators 2018, 7, 20. https://doi.org/10.3390/act7020020
Parvari Rad F, Vertechy R, Berselli G, Parenti-Castelli V. Design and Stiffness Evaluation of a Compliant Joint with Parallel Architecture Realizing an Approximately Spherical Motion. Actuators. 2018; 7(2):20. https://doi.org/10.3390/act7020020
Chicago/Turabian StyleParvari Rad, Farid, Rocco Vertechy, Giovanni Berselli, and Vincenzo Parenti-Castelli. 2018. "Design and Stiffness Evaluation of a Compliant Joint with Parallel Architecture Realizing an Approximately Spherical Motion" Actuators 7, no. 2: 20. https://doi.org/10.3390/act7020020
APA StyleParvari Rad, F., Vertechy, R., Berselli, G., & Parenti-Castelli, V. (2018). Design and Stiffness Evaluation of a Compliant Joint with Parallel Architecture Realizing an Approximately Spherical Motion. Actuators, 7(2), 20. https://doi.org/10.3390/act7020020







