Abstract
Since fine powders tend strongly to adhesion and agglomeration, their processing with conventional methods is difficult or impossible. Typically, in order to enable the handling of fine powders, chemicals are added to increase the flowability and reduce adhesion. This contribution shows that instead of additives also vibrations can be used to increase the flowability, to reduce adhesion and cohesion, and thus to enable or improve processes such as precision dosing, mixing, and transport of very fine powders. The methods for manipulating powder properties are described in detail and prototypes for experimental studies are presented. It is shown that the handling of fine powders can be improved by using low-frequency, high-frequency or a combination of low- and high-frequency vibration.
Keywords:
powder handling; flowability; dosing; transport; mixing; dispersion; piezoelectric actuators; vibrations 1. Introduction
In the field of biotechnology, the pharmaceutical industry, production of plastics, and additive manufacturing, raw materials are increasingly provided as fine powders in order to optimize the process quality or duration.
Due to specific adhesive and cohesive material behavior that leads to agglomeration and permanent adhesion to surfaces, the handling—in particular the exact dosing, the transport, and the production of uniform powder mixtures and the dispersion of fine powders—is challenging and has not yet been satisfactorily solved. While commercialized solutions with conventional knocking, vibrating, stirring or shaking technologies work well with coarser powders, they have reached their technical limits with fine powders.
In order to enable dosing, transportation, dispersion and mixing of fine powders, new techniques have to be found. There are several ways to improve the handling of fine powders. While chemists prefer to use additives [1] to reduce adhesion and cohesion in order to improve the flowability and avoid agglomeration, physicists prefer to use air flow [2] or mechanical vibration [3] to achieve the same effect. The use of additives leads to a permanent altering of powder characteristics. Thus, the application of additives may have a negative effect on the subsequent process steps. The application of vibrations, on the other hand, does not cause a permanent change in the powder characteristics. The effect is reversible, and when used correctly does not affect the following process steps. Hereafter, new methods are described that contribute to improving the handling of fine powders.
The following experiments were all done with standard flour (Type 405). With particle sizes between 2 and 200 μm, it exhibits all the characteristic features of fine powders, such as poor flowability, strong agglomeration and strong adhesion.
2. Flowability and Powder Dosing
Poor flowability makes dosing a difficult task. When handling coarse, free-flowing powders, gravity is in most cases sufficient to remove powder from a conical container (for example a silo or funnel). Fine powders, however, tend to bridging at conical outlets. The powder sets and interrupts any gravity-driven flow. If bridging occurs unexpectedly during a process, the most common solutions to enable the flow are hammer beats or inflowing air. As shown in [4], the correct use of mechanical vibrations can reduce the shear strength of cohesive powders and thus improve the flow behavior.
A simple method for determining the flowability of powders is the measurement of the angle of repose on a powder heap [5]. To investigate the effect of vertical vibrations on the flowability of cohesive powders, a heap of flour was placed on a circular vibratory surface with a diameter of 30 mm. Figure 1 shows the described setup. Figure 1a was taken at a static state and shows an angle of repose of 55°. With increasing vibration amplitude, see Figure 1b,c, the angle of repose decreases. At a critical vibration amplitude, the whole powder heap is dispersed and shaken off.

Figure 1.
Characterization of the flow of flour (Type 405) at vertical vibration; (a) without vibration, , (b) , , , (c) , , .
The same experiment was carried out at different frequencies and vibration amplitudes. Figure 2 shows a set of individual measurements at frequencies of 30, 50 and 100 Hz. There is a linear relationship between the angle of repose and the acceleration amplitude; frequency doesn’t seem to have an impact.
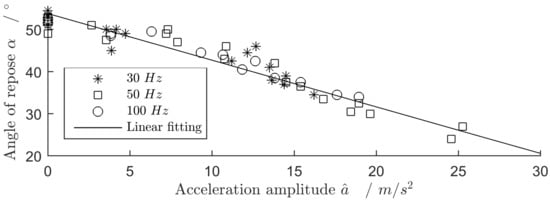
Figure 2.
Angle of repose over acceleration amplitude for flour (Type 405).
However, for higher frequencies, this relationship becomes increasingly non-linear. At frequencies above 100 Hz, especially in the ultrasonic range, the vibration is highly damped by interparticular friction. The vibration does not penetrate far enough into the powder heap and therefore has less influence on the flowability. However, ultrasonic vibrations can still be used to reduce flowability, but are limited to very small amounts of dry fine powders, as shown by [6,7,8] on the microfeeding of dry fine powders.
For dosing powders, sufficient flowability is a basic requirement. By means of a coordinated increase of the flowability, the powder flow in a dosing system can be controlled. Figure 3 shows systems for fine and coarse dosing of fine powders. For fine dosing, a glass pipette with a knocking device is used, as shown in Figure 3a. Fine powders like flour build bridges, and thus block up the conical outlet of the pipette. When knocking at the pipette, the powder is fluidized and flows out. For the shown system with an outlet diameter of 2 mm, the knocking frequency was chosen within the range between 100 and 300 Hz. By varying frequency and amplitude of the excitation signal, the powder flow could be controlled between 1 and 70 mg/s.
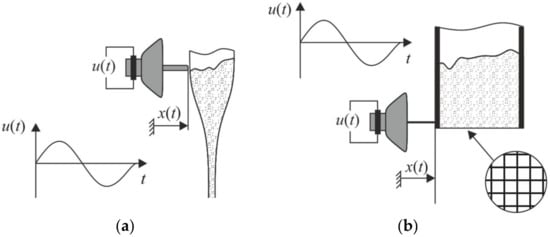
Figure 3.
Dosing systems that use vibrations to enable powder flow; (a) glass pipette with knocking device, (b) cylindrical vessel with vibrating sieve at the outlet.
A similar system, consisting of a cylindrical pipe with a sieve at the outlet, as shown in Figure 3b, is used to reach higher flow rates. Due to bridging and agglomeration, fine powder clogs over the sieve. When the powder is excited to vibrations, it flows through the sieve. A system was built up with a pipe diameter of 20 mm and a mesh size of 1 mm. At excitation frequencies of up to 100 Hz and amplitudes below 1 mm, flow rates between 120 mg/s and 3 g/s could be set.
The two systems show that coarse dosing of fine powders can be made possible by the use of vibrations as well as fine dosing. To achieve an uninterrupted powder flow at low flow rates, the two systems can easily be combined, so that the system for fine dosing is filled at certain intervals by the system for coarse dosing. In both systems, powder flows can be controlled by adjusting the vibration amplitude using a characteristic diagram of powder flow and vibration amplitude. A measurement of the powder flow during operation with conventional methods like a load cell is difficult due to the strong vibrations. To regulate the powder flow in a feedback control, complex signal processing must be handled or special sensors must be used.
3. Manipulation of Friction Forces and Powder Transport
The fact that friction forces can be manipulated by vibrations has been proven by different scientists [9,10,11,12,13]. Depending on the direction of the vibration, different mechanisms lead to apparent friction reduction. All mechanisms can be explained using a mass on an inclined plane, see Figure 4.
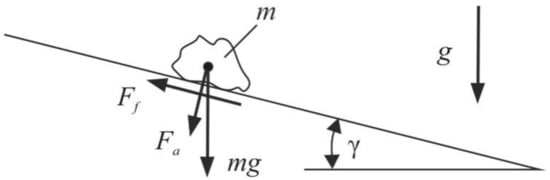
Figure 4.
Resulting forces acting on a powder particle on an inclined plane.
When the surface below the mass is excited to vibrate in sliding direction, the friction force has an accelerating effect for short phases instead of only acting as a brake, which leads to a lower time-average of friction force, and thus to an apparently reduced coefficient of friction. A transverse vibration in the sliding plane causes a similar effect [9,10]. When exciting the surface to orthogonal vibration there is indeed friction reduction possible if the mass temporary loses contact as well as if the contact persists permanently [13]. In all cases, the vibration causes only a reduction of the time-averaged, effective frictional force. In detail, the frictional force oscillates. To simplify the modeling, the described effects can be summarized in a reduced time-averaged, effective friction coefficient . For simplification, it is also assumed that the coefficients of static and sliding friction are identical. So far, literature covers experiments on metallic solids only. Thus, similar experiments were carried out on dry fine powders.
A common method for the determination of friction coefficients is to measure the minimum inclination angle at which a mass starts to slide. According to Figure 4 the powder mass will slide down when the part of the weight force parallel to the contact surface is higher than the frictional force
The normal force between plane and powder particle consists of a partial weight force and the adhesion force . If the adhesion force is negligible, the static friction coefficient can be calculated based on the inclination angle :
Although neglecting the adhesion force might cause larger errors, this method is well suited to studying the influence of vibration on the effective friction. In a simple test rig, the coefficient of effective friction for flour was determined under the influence of ultrasonic vibrations. Figure 5 shows the experimental setup consisting of an ultrasonic bolted Langevine transducer with a magnifying sonotrode with a cuboid tip. The transducer is operated at its resonance frequency of about 20 kHz. The powder is placed on top of the sonotrode tip. With the shown setup, the influence of longitudinal vibrations (i.e., parallel to the sliding direction) on the effective friction coefficient could be studied. The transducer can be tilted along all three axes so that vibrations in the transversal (i.e., perpendicular to sliding direction, in sliding plane) and orthogonal (i.e., perpendicular to sliding plane) directions can be examined as well.

Figure 5.
Experimental Setup for measuring coefficients of effective friction at ultrasonic vibration parallel to the sliding direction.
In an experimental series, the effective friction coefficient of flour on aluminum alloy (polished surface) at vibration excitation in longitudinal, transversal, and orthogonal direction with different vibration amplitudes was determined. A thin layer of powder was spread on the vibrating surface. While the inclination angle was fixed, the vibration amplitude was slowly increased until the particles moved into a sliding state. Since the sliding does not start at the same amplitude for all particles, average displacement amplitudes were recorded.
As shown in Figure 6, all the vibrational directions show a significant reduction in the effective friction coefficient with increasing vibration amplitude. As lower friction coefficients are achieved at the same displacement amplitudes, the excitations in transversal and orthogonal directions are much more efficient than in the longitudinal direction.
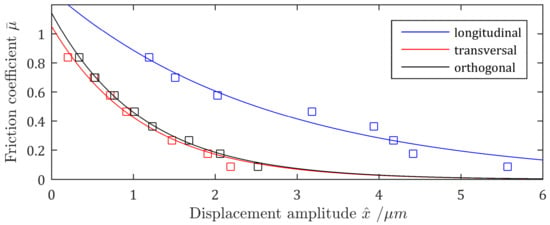
Figure 6.
Effective friction coefficient of flour (Type 405) on aluminum alloy for vibration of the surface in longitudinal, transversal and orthogonal direction.
Knowing that the friction of powders can be apparently reduced by ultrasonic vibration, many chute-like transport processes for powders could be optimized. Additionally, conventional transport mechanisms like vibratory conveyors using the principle of inertia, which have increasingly problems with finer powders, can be optimized using “friction reduction” by ultrasound. As an example, the setup of a powder transport principle that is based on a harmoniously vibrating pipe and coordinated friction manipulation is described in the following [14,15,16].
Schematically, the powder-carrying substrate vibrates harmoniously in an axial direction with frequency and amplitude as shown in Figure 7 and Equation (3). Under negative relative velocity , a vibration in orthogonal direction is superimposed, as shown in Equation (4), so that the effective coefficient of friction between powder mass and pipe is reduced. The powder mass is therefore highly accelerated during time periods of positive relative velocity and slightly decelerated during periods of negative relative velocity due to lower friction and thus moves in one direction.

Figure 7.
Schematic of the powder transport by coordinated manipulation of friction forces.
According to the described principle, a transport system was built, as shown in Figure 8 [14,15]. The conveying part consists of a pipe which is excited to harmonious axial vibration by a voice-coil actuator (12 , 75 W, Sony, Tokyo, Japan). The friction reduction is achieved by a radial vibration of the pipe, which corresponds to an orthogonal vibration of the substrate. This radial vibration is excited by an annular piezoelectric actuator (similar to Sonox P8, Ceramtec, Plochingen, Germany), which is adhered around the pipe wall and excites the pipe at the radial resonance frequency.

Figure 8.
System using coordinated manipulation of friction forces for the transportation of dry flour.
In order to ensure reliable transport, the excitation signals of the voice-coil actuator and the piezoelectric actuator have to be synchronized exactly. The excitation signal of the piezoelectric actuator, which generates the radial vibration, has to be activated depending on the relative velocity, which presupposes the knowledge of the powder velocity . Since the online measurement of the powder velocity requires significant effort, the piezoelectric actuator is turned on only at negative velocities of the conveying pipe . This is much easier, as the stroke of the pipe is directly proportional to the excitation voltage of the voice-coil actuator. However, this simplification comes along with a lower maximum of the powder velocity. The excitation signals for the voice-call actuator, as well as the piezoelectric actuator, were generated by a signal generator (Model 195, Wavetek, San Diego, CA, USA) which can output and synchronize several signals. Figure 9 displays the axial and radial displacement of the pipe for an exemplary excitation. The axial vibration, shown as a blue line with vertical axis on the left side is a sinusoidal curve with a frequency of 50 Hz and an amplitude of 0.5 mm. The radial vibration is shown as an orange curve with vertical axis on the right side. The pulsed signal has a frequency of about 35 kHz, which is a radial resonance frequency of the system and an amplitude of about 0.25 µm. Due to the high radial resonance frequency of the aluminum pipe, the transient phases of the radial vibration are extremely short. Therefore, the transportation is possible even at much higher frequencies of the axial vibration.
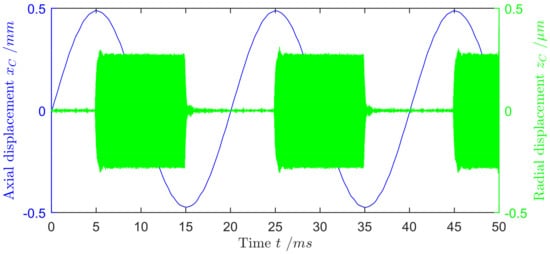
Figure 9.
Axial and radial displacement of the pipe vibration in the powder transportation system; pipe material: aluminum alloy.
Figure 10 shows the mean powder velocity for different excitation amplitudes of both axial and radial vibration. This was determined as an average of the time that particles needed to travel along the pipe (20 cm).
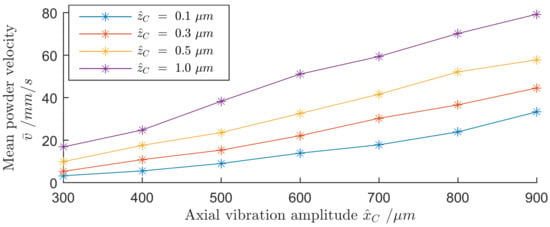
Figure 10.
Mean powder velocity for variation of amplitudes of axial and radial excitation of the pipe; test powder: flour; frequencies .
Powder velocity and mass-flow can be adjusted by changing the amplitudes of either the low-frequency axial vibration or the high-frequency radial vibration of the pipe as well as the pulse width of the radial vibration. The powder flow is reversed by shifting the phase between axial and radial excitation by 180°. The built transport system was able to transport dry fine powders at a tilt angle of more than 10° upwards. Due to the ultrasonic vibration of the pipe surface, which overcomes the strong adhesion of fine powders, only minimal residues of powder remain inside the pipe. The shown powder transportation principle can be used for very small, as well as for large, powder flows using the same pipe diameter. Experiments showed that the finest powders, with particle sizes of less than one micrometer, could be transported, as well as coarser powders.
4. Deagglomeration, Dispersion, and Mixing
There are a variety of principles for the deagglomeration and dispersion of powders using ultrasound. The easiest might be just putting powder on a vibrating surface. This principle is shown in Figure 11a. When touching the vibrating sonotrode surface, agglomerates receive an extremely high acceleration and are deagglomerated and dispersed. To achieve similar results without contact with the vibration surface, an intensive airborne ultrasonic field is needed. This can be generated by the vibrating surface of a sonotrode and a passive reflector (see Figure 11b) or with two opposite vibrating sonotrodes. In both cases, the distance should be adjusted to achieve a resonant tuned standing wave field for maximizing sound pressure. Loose particles, as well as agglomerates, are trapped at pressure nodes, and due to the extreme pressure fluctuations over time, powders are deagglomerated and dispersed [17]. The disadvantages of this principle include the fact that the powder is dispersed in all directions and might touch the reflector, where it sticks or is dispersed as described above. In order to get a reliable powder flow, an additional airflow is advisable. A third option for achieving high sound pressure is shaping the vibrating surface so that the sound is focused. At this focus, the acoustic waves veer away from the sonotrode surface. When powder is dosed into the focus, it is deagglomerated and dispersed in a preferred direction. Figure 11c shows such a setup, consisting of a transducer with specially shaped sonotrode and dosing apparatus.

Figure 11.
Principles for deagglomeration and dispersion of dry fine powders: (a) flour on vibrating sonotrode, ; (b) flour in a standing ultrasonic wave, ; (c) flour in a focused ultrasonic wave, .
To show the effectiveness of ultrasonic deagglomeration and dispersion, flour was dosed using the dosing apparatus described in Figure 3a with an outlet diameter of 2 mm. Thus, the agglomerates have a size of up to 2 mm, see Figure 12a. When ultrasound is applied as shown in Figure 11c, the agglomerates are dissolved, and a fine powder dust is generated, see Figure 12b.

Figure 12.
Comparison of the particle size at dispersing flour with the system shown in Figure 11c (outlet diameter of dosing module: 2 mm) with and without using ultrasound; (a) flour being dosed without dispersion; (b) flour after dispersion.
The diagram in Figure 13 shows the relative frequency of agglomerates or particles over their diameter. Agglomerates with diameters of up to 2 mm occur when the flour is dosed without using ultrasound. When ultrasound is applied, the maximum size of the agglomerates is at about 200 μm, which corresponds to the maximum particle size of flour and thus allows for the assumption that all agglomerates are dissolved.
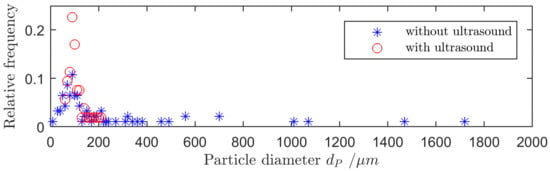
Figure 13.
Comparison of the particle size distribution of dispersing flour with the system shown in Figure 11c with and without ultrasound.
A homogeneous mixture of fine powders can be achieved dosing two powders into the ultrasonic acoustic field inside a mixing chamber, see Figure 14. The powders are deagglomerated, dispersed, and a fine powder dust is formed. Due to turbulences in the mixing chamber, caused by the same acoustic field, the dust of the two powders is mixed.

Figure 14.
Setup for homogeneous mixing of two dry fine powders using a focused ultrasonic wave.
At the outlet of the mixing chamber, a homogeneously distributed powder mixture is obtained. Figure 15 shows the results of mixing flour and cocoa. Without using ultrasound, large agglomerates occur, see Figure 15a. When ultrasound is applied, a homogeneously distributed powder mixture is achieved, see Figure 15b.

Figure 15.
Comparison of mixing flour and cocoa without (a) and with (b) using focused ultrasound.
5. Conclusions
It was shown that the use of vibrations enhances the handling of dry fine powders. Vibrations can be used to fluidize powders, prevent deposits, reduce effective friction, deagglomerate, disperse and mix powders. Depending on the application, low-frequency or high-frequency vibrations are required to achieve optimum effects in increasing flowability, reducing friction forces and separation of agglomerates. Thus, the application of vibration is a powerful technique to improve dosing, transport, deagglomeration, dispersion and mixing of fine powders.
The dosing systems shown in Figure 3a,b are able to generate powder flows in the range of a few mg/s up to a few g/s. The shown transportation principle is able to transport powders with flow rates of a few g/s but also single particles. The mixing principle achieves best results with low powder flows at low speeds. Thus, the principles shown are well suited for use in laboratory equipment or in other processes with small powder flows.
Acknowledgments
This work was supported by Zentrales Innovationsprogramm Mittelstand (ZIM), (No. KF 2363847WO4).
Author Contributions
W.S. and T.H. organized and supervised the project. P.B. worked on vibration-assisted Deagglomeration, Dispersion and Mixing of Powders and developed the ultrasonic mixing chamber. P.D. investigated how flowability and friction is influenced by vibrations. He developed the dosing modules and the transport module. P.D. wrote the paper under supervision of the other authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, J.; Sliva, A.; Banerjee, A.; Dave, R.N.; Pfeffer, R. Dry particle coating for improving the flowability of cohesive powders. Powder Technol. 2005, 158, 21–33. [Google Scholar] [CrossRef]
- Turki, D.; Fatah, N. Behaviour and fluidization of the cohesive powders: Agglomerates sizes approach. Braz. J. Chem. Eng. 2008, 25, 697–711. [Google Scholar] [CrossRef]
- Kollmann, T.; Tomas, J. Effect of Applied Vibration on Silo Hopper Design. Part. Sci. Technol. 2002, 20, 15–31. [Google Scholar] [CrossRef]
- Kache, G. Verbesserung des Schwerkraftflusses Kohäsiver Pulver durch Schwingungseintrag. Dissertation, Fakultät für Verfahrens- und Systemtechnik der Otto-von-Guericke-Universität Magdeburg, Magdeburg, Germany, 2009. [Google Scholar]
- Lumay, G.; Boschini, F.; Traina, K.; Bontempi, S.; Remy, J.-C.; Cloots, R.; Vandewalle, N. Measuring the flowing properties of powders and grains. Powder Technol. 2012, 224, 19–27. [Google Scholar] [CrossRef]
- Lu, X.; Yang, S.; Evans, J.R.G. Studies on ultrasonic microfeeding of fine powders. J. Phys. D Appl. Phys. 2006, 39, 2444–2453. [Google Scholar] [CrossRef]
- Lu, X.; Yang, S.; Evans, J.R.G. Ultrasound-assisted microfeeding of fine powders. Particuology 2008, 6, 2–8. [Google Scholar] [CrossRef]
- Lu, X.; Yang, S.; Evans, J.R.G. Microfeeding with different ultrasonic nozzle designs. Ultrasonics 2009, 49, 514–521. [Google Scholar] [CrossRef] [PubMed]
- Littmann, W.; Storck, H.; Wallascheck, J. Reibung bei Ultraschallschwingungen. VDI Berichte 2002, 1736, 231–238. [Google Scholar]
- Storck, H.; Littmann, W.; Wallascheck, J.; Mracek, M. The effect of friction reduction in presence of ultrasonic vibrations and its relevance to travelling wave ultrasonic motors. Ultrasonics 2002, 40, 379–383. [Google Scholar] [CrossRef]
- Popov, V.L. Friction under the Influence of Ultrasonic Vibrations. In Contact Mechanics and Friction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-662-53080-1. [Google Scholar]
- Kache, G.; Kollmann, T.; Tomas, J. Wandreibungsverhalten Hochdisperser, Kohäsiver Pulver unter Schwingungseinwirkung; Kunze, G., Ed.; Wissensportal baumaschine.de: Dresden, Germany, 2005. [Google Scholar]
- Teidelt, E.; Starcevic, J.; Popov, V. Influence of Ultrasonic Oscillation on Static and Sliding Friction. Tribol. Lett. 2012, 48, 51–62. [Google Scholar] [CrossRef]
- Dunst, P.; Bornmann, P.; Hemsel, T.; Littmann, W.; Sextro, W. Transportation of dry fine powders by coordinated friction manipulation. Proc. Appl. Math. Mech. 2016, 16, 635–636. [Google Scholar] [CrossRef][Green Version]
- Dunst, P.; Hemsel, T.; Sextro, W. Analysis of pipe vibration in an ultrasonic powder transportation system. Sens. Actuators A Phys. 2017, 263, 733–736. [Google Scholar] [CrossRef]
- Chitic, R.; Giraud, F.; Lemaire-Semail, B.; Béarée, R.; Favre, M.; Tierce, P.; Jehanno, J. Modeling of an Ultrasonic Powder Transportation System. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013. [Google Scholar]
- Knoop, C.; Todorova, Z.; Tomas, J.; Fritsching, U. Agglomerate fragmentation in high-intensity acoustic standing wave fields. Powder Technol. 2016, 291, 214–222. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).