Levitating Micro-Actuators: A Review
Abstract
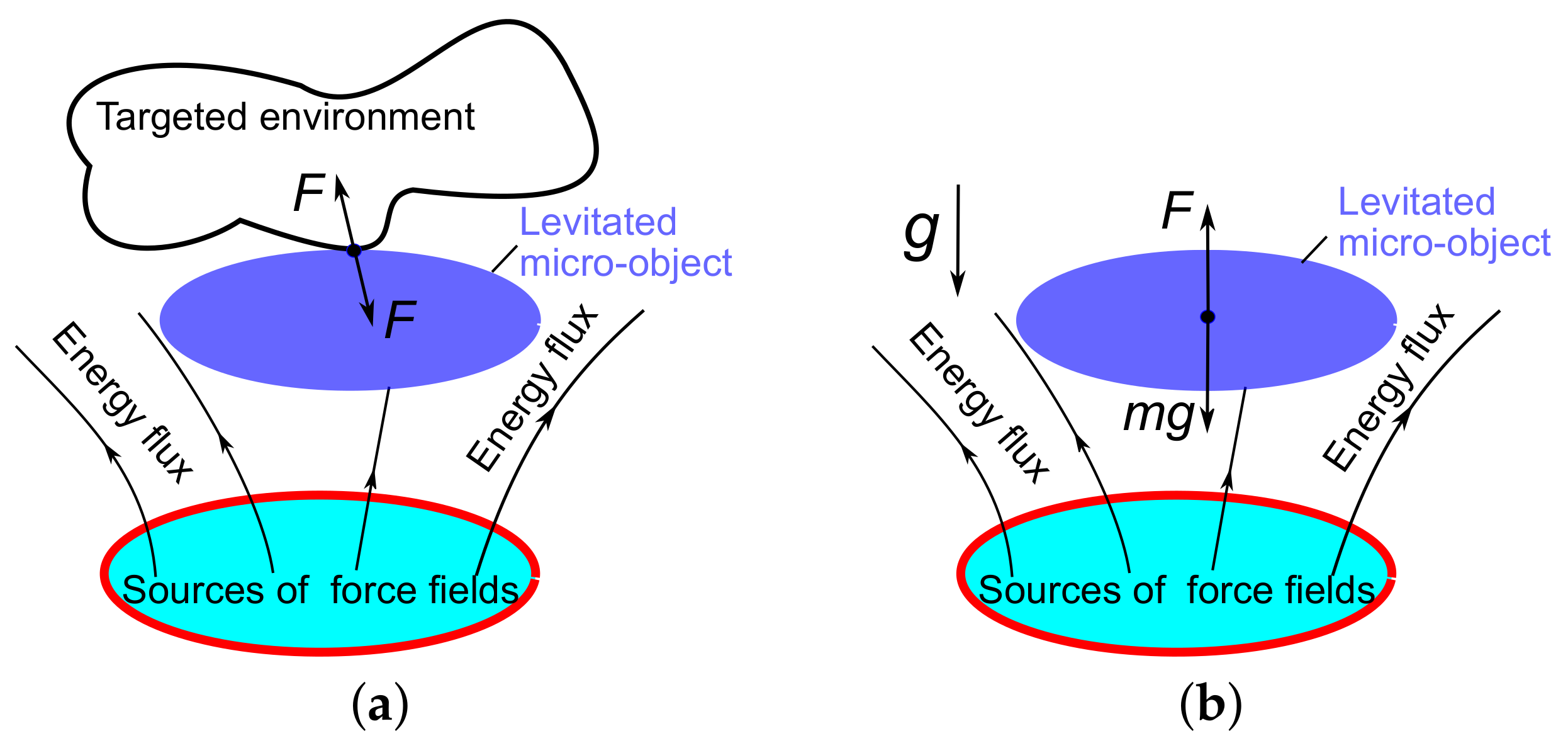
1. Introduction
2. Levitating Micro-Actuators
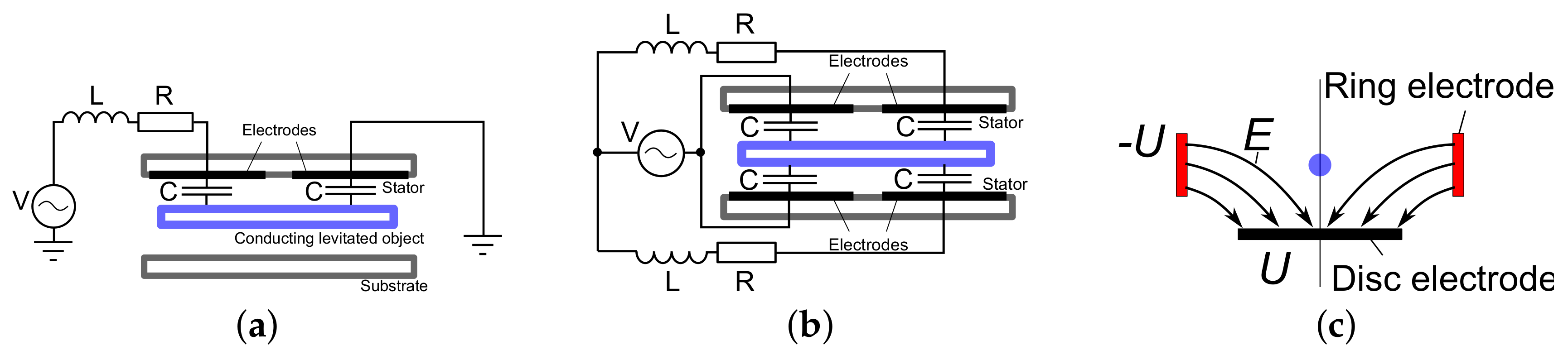
3. Electric Levitation Micro-Actuators
4. Magnetic Levitation Micro-Actuators
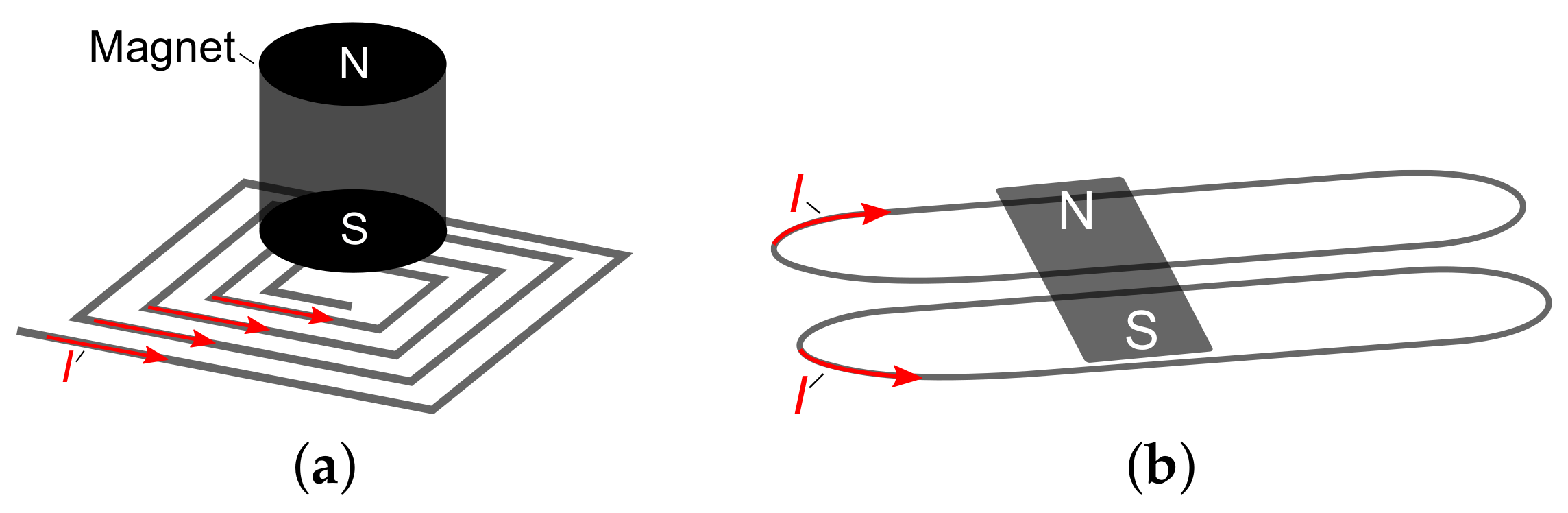
5. Inductive Levitation Micro-Actuators
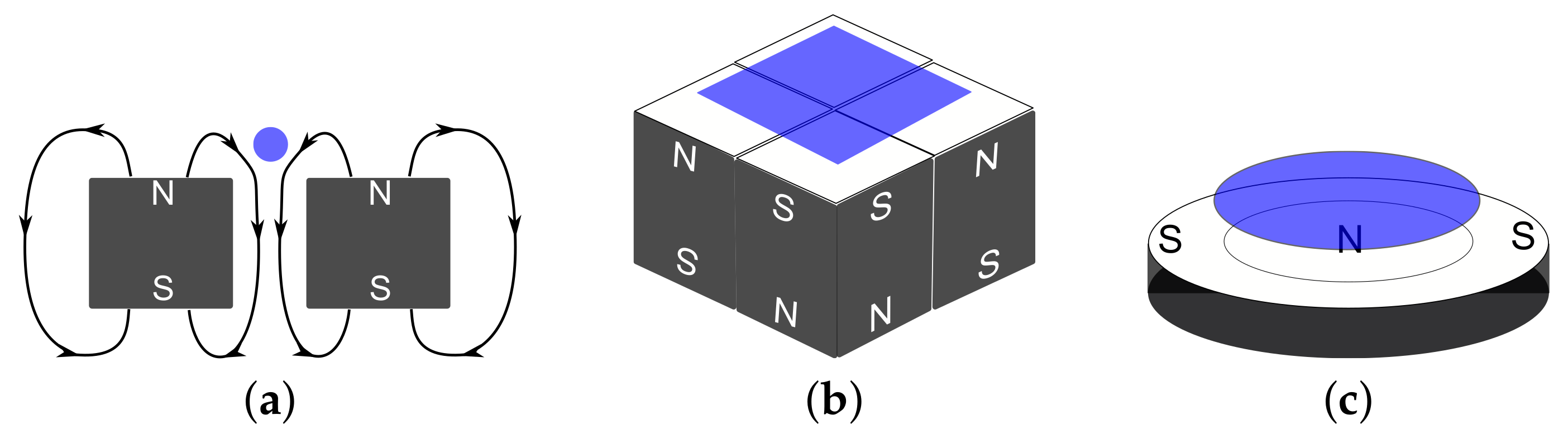
6. Diamagnetic Levitation Micro-Actuators
7. Superconducting Levitation Micro-Actuators
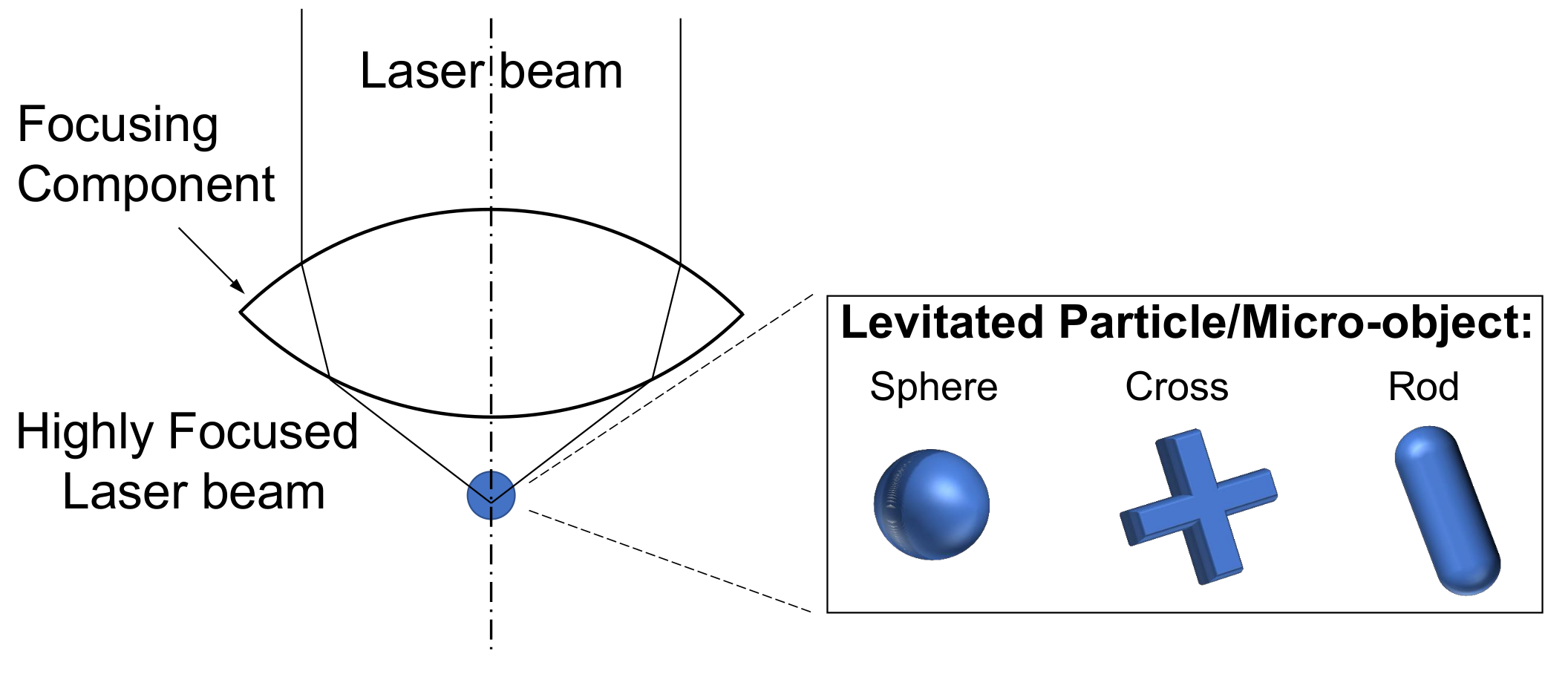
8. Optical Levitation Micro-Actuators
9. Hybrid Levitation Micro-Actuators
10. Summary and Future Trends
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternate current |
| c | Stiffness, N/m |
| DC | Direct current |
| DLMA | Diamagnetic levitation micro-actuators |
| ELMA | Electric levitation micro-actuators |
| HLMA | Hybrid levitation micro-actuators |
| ILMA | Inductive levitation micro-actuators |
| Boltzmann constant, JK | |
| LMA | Levitating micro-actuators |
| MLMA | Magnetic levitation micro-actuators |
| MEMS | Micro-Electro-Mechanical Systems |
| NA | numerical aperture |
| OLMA | Optical levitation micro-actuators |
| OT | Optical Trapping |
| revolution per minute | |
| SLMA | Superconducting levitation micro-actuators |
| T | Absolute temperature, K |
| Frequency band, Hz |
References
- Petersen, K.E. Silicon as a mechanical material. Proc. IEEE 1982, 70, 420–457. [Google Scholar] [CrossRef]
- Boxenhorn, B.; Greiff, P. Monolithic silicon accelerometer. Sens. Actuators A Phys. 1990, 21, 273–277. [Google Scholar] [CrossRef]
- Polla, D.L.; Erdman, A.G.; Robbins, W.P.; Markus, D.T.; Diaz-Diaz, J.; Rizq, R.; Nam, Y.; Brickner, H.T.; Wang, A.; Krulevitch, P. Microdevices in medicine. Annu. Rev. Biomed. Eng. 2000, 2, 551–576. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P. There’s plenty of room at the bottom. Eng. Sci. 1960, 23, 22–36. [Google Scholar]
- Thielicke, E.; Obermeier, E. Microactuators and their technologies. Mechatronics 2000, 10, 431–455. [Google Scholar] [CrossRef]
- Fujita, H. Microactuators and micromachines. Proc. IEEE 1998, 86, 1721–1732. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Korvink, J.G.; Badilita, V. Mechanical Thermal Noise in Micro-Machined Levitated Two-Axis Rate Gyroscopes. IEEE Sens. J. 2018, 18, 1390–1402. [Google Scholar] [CrossRef]
- Arnold, D.P.; Wang, N. Permanent magnets for MEMS. J. Microelectromech. Syst. 2009, 18, 1255–1266. [Google Scholar] [CrossRef]
- Kratt, K.; Badilita, V.; Burger, T.; Korvink, J.; Wallrabe, U. A fully MEMS-compatible process for 3D high aspect ratio micro coils obtained with an automatic wire bonder. J. Micromech. Microeng. 2010, 20, 015021. [Google Scholar] [CrossRef]
- Fischer, A.C.; Korvink, J.G.; Roxhed, N.; Stemme, G.; Wallrabe, U.; Niklaus, F. Unconventional applications of wire bonding create opportunities for microsystem integration. J. Micromech. Microeng. 2013, 23, 083001. [Google Scholar] [CrossRef]
- Neuman, K.C.; Block, S.M. Optical trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.J.; Block, S.M. Resource Letter: LBOT-1: Laser-based optical tweezers. Am. J. Phys. 2003, 71, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Moffitt, J.R.; Chemla, Y.R.; Smith, S.B.; Bustamante, C. Recent advances in optical tweezers. Annu. Rev. Biochem. 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Verdeny, I.; Farré, A.; Mas Soler, J.; López Quesada, C.; Martín Badosa, E.; Montes Usategui, M. Optical trapping: A review of essential concepts. In Óptica Pura y Aplicada; SEDO—Sociedad Española de Óptica: Madrid, Spain, 2011; Volume 44, pp. 527–551. [Google Scholar]
- Baldacchini, T. Three-Dimensional Microfabrication Using Two-Photon Polymerization: Fundamentals, Technology, and Applications; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]
- Mariappan, S.G.; Moazenzadeh, A.; Wallrabe, U. Polymer magnetic composite core based microcoils and microtransformers for very high frequency power applications. Micromachines 2016, 7, 60. [Google Scholar] [CrossRef]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Korvink, J.; Badilita, V. Stable dynamics of micro-machined inductive contactless suspensions. Int. J. Mech. Sci. 2017, 131-132, 753–766. [Google Scholar] [CrossRef]
- Earnshaw, S. On the nature of the molecular forces which regulate the constitution of the luminiferous ether. Trans. Camb. Phil. Soc. 1842, 7, 97–112. [Google Scholar]
- Kumar, S.; Cho, D.; Carr, W. A proposal for electrically levitating micromotors. Sens. Actuators. A Phys. 1990, 24, 141–149. [Google Scholar] [CrossRef]
- Paul, W. Electromagnetic traps for charged and neutral particles. Rev. Mod. Phys. 1990, 62, 531–540. [Google Scholar] [CrossRef]
- Kumar, S.; Cho, D.; Carr, W.N. Experimental study of electric suspension for microbearings. J. Microelectromech. Syst. 1992, 1, 23–30. [Google Scholar] [CrossRef]
- Jin, L.; Higuchi, T.; Kanemoto, M. Electrostatic levitator for hard disk media. IEEE Trans. Ind. Electron. 1995, 42, 467–473. [Google Scholar] [CrossRef]
- Jeon, J.U.; Higuchi, T. Electrostatic suspension of dielectrics. IEEE Trans. Ind. Electron. 1998, 45, 938–946. [Google Scholar] [CrossRef]
- Jin, J.; Yih, T.C.; Higuchi, T.; Jeon, J.U. Direct electrostatic levitation and propulsion of silicon wafer. IEEE Trans. Ind. Appl. 1998, 34, 975–984. [Google Scholar] [CrossRef]
- Jeon, J.U.; Woo, S.J.; Higuchi, T. Variable-capacitance motors with electrostatic suspension. Sens. Actuators A Phys. 1999, 75, 289–297. [Google Scholar] [CrossRef]
- Torti, R.P.; Gondhalekar, V.; Tran, H.; Selfors, B.; Bart, S.; Maxwell, B. Electrostatically suspended and sensed micromechanical rate gyroscope. In Proceedings of the SPIE’s International Symposium on Optical Engineering and Photonics in Aerospace Sensing, Orlando, FL, USA, 13 June 1994; Volume 2220. [Google Scholar]
- Han, F.; Fu, Z.; Dong, J. Design and simulation of an active electrostatic bearing for MEMS micromotors. In Proceedings of the 2009 4th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Shenzhen, China, 5–8 January 2009; pp. 80–85. [Google Scholar]
- Han, F.T.; Wu, Q.P.; Wang, L. Experimental study of a variable-capacitance micromotor with electrostatic suspension. J. Micromech. Microeng. 2010, 20, 115034. [Google Scholar] [CrossRef]
- Han, F.T.; Wang, L.; Wu, Q.P.; Liu, Y.F. Performance of an active electric bearing for rotary micromotors. J. Micromech. Microeng. 2011, 21, 085027. [Google Scholar] [CrossRef]
- Damrongsak, B.; Kraft, M. A micromachined electrostatically suspended gyroscope with digital force feedback. In Proceedings of the 2005 IEEE Sensors, Irvine, CA, USA, 30 October–3 November 2005. [Google Scholar]
- Damrongsak, B.; Kraft, M.; Rajgopal, S.; Mehregany, M. Design and fabrication of a micromachined electrostatically suspended gyroscope. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 53–63. [Google Scholar] [CrossRef]
- Han, F.T.; Liu, Y.F.; Wang, L.; Ma, G.Y. Micromachined electrostatically suspended gyroscope with a spinning ring-shaped rotor. J. Micromech. Microeng. 2012, 22, 105032. [Google Scholar] [CrossRef]
- Sun, B.; Han, F.; Li, L.; Wu, Q. Rotation Control and Characterization of High-Speed Variable-Capacitance Micromotor Supported on Electrostatic Bearing. IEEE Trans. Ind. Electron. 2016, 63, 4336–4345. [Google Scholar] [CrossRef]
- Murakoshi, T.; Endo, Y.; Fukatsu, K.; Nakamura, S.; Esashi, M. Electrostatically levitated ring-shaped rotational gyro/accelerometer. Jpn. J. Appl. Phys 2003, 42, 2468–2472. [Google Scholar] [CrossRef]
- Nakamura, S. MEMS inertial sensor toward higher accuracy & multi-axis sensing. In Proceedings of the 4th IEEE Conference on 2005 IEEE Sensors, Irvine, CA, USA, 30 October–3 November 2005; pp. 939–942. [Google Scholar]
- Toda, R.; Takeda, N.; Murakoshi, T.; Nakamura, S.; Esashi, M. Electrostatically levitated spherical 3-axis accelerometer. In Proceedings of the Fifteenth IEEE International Conference on Micro Electro Mechanical Systems, (Cat. No. 02CH37266), Las Vegas, NV, USA, 24 January 2002; pp. 710–713. [Google Scholar]
- Han, F.; Gao, Z.; Li, D.; Wang, Y. Nonlinear compensation of active electrostatic bearings supporting a spherical rotor. Sens. Actuators A Phys. 2005, 119, 177–186. [Google Scholar] [CrossRef]
- Cui, F.; Liu, W.; Chen, W.; Zhang, W.; Wu, X. Design, Fabrication and Levitation Experiments of a Micromachined Electrostatically Suspended Six-Axis Accelerometer. Sensors 2011, 11, 11206–11234. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Sun, B.; Li, L.; Wu, Q. Performance of a Sensitive Micromachined Accelerometer With an Electrostatically Suspended Proof Mass. IEEE Sens. J. 2015, 15, 209–217. [Google Scholar]
- Post, E.R.; Popescu, G.A.; Gershenfeld, N. Inertial measurement with trapped particles: A microdynamical system. Appl. Phys. Lett. 2010, 96, 143501. [Google Scholar] [CrossRef]
- Rhim, W.; Chung, S.K.; Barber, D.; Man, K.F.; Gutt, G.; Rulison, A.; Spjut, R.E. An electrostatic levitator for high-temperature containerless materials processing in 1-g. Rev. Sci. Instrum. 1993, 64, 2961–2970. [Google Scholar] [CrossRef]
- Ye, X.Y.; Huang, Y.; Zhou, Z.Y.; Li, Q.C.; Gong, Q.L. A magnetic levitation actuator for micro-assembly. In Proceedings of the TRANSDUCERS ’97 Chicago International Conference on Solid State Sensors and Actuators, Chicago, IL, USA, 19 June 1997; Volume 2, pp. 797–799. [Google Scholar]
- Dieppedale, C.; Desloges, B.; Rostaing, H.; Delamare, J.; Cugat, O.; Meunier-Carus, J. Magnetic bistable micro-actuator with integrated permanent magnets. In Proceedings of the IEEE Sensors, Vienna, Austria, 24–27 October 2004; Volume 1, pp. 493–496. [Google Scholar]
- Ruffert, C.; Gehrking, R.; Ponick, B.; Gatzen, H.H. Magnetic Levitation Assisted Guide for a Linear Micro-Actuator. IEEE Trans. Magn. 2006, 42, 3785–3787. [Google Scholar] [CrossRef]
- Ruffert, C.; Li, J.; Denkena, B.; Gatzen, H.H. Development and Evaluation of an Active Magnetic Guide for Microsystems With an Integrated Air Gap Measurement System. IEEE Trans. Magn. 2007, 43, 2716–2718. [Google Scholar] [CrossRef]
- Dauwalter, C.R.; Ha, J.C. Magnetically suspended MEMS spinning wheel gyro. IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 21–26. [Google Scholar] [CrossRef]
- Shearwood, C.; Williams, C.; Mellor, P.; Yates, R.; Gibbs, M.; Mattingley, A. Levitation of a micromachined rotor for application in a rotating gyroscope. Electron. Lett. 1995, 31, 1845–1846. [Google Scholar] [CrossRef]
- Williams, C.; Shearwood, C.; Mellor, P.; Mattingley, A.; Gibbs, M.; Yates, R. Initial fabrication of a micro-induction gyroscope. Microelectron. Eng. 1996, 30, 531–534. [Google Scholar] [CrossRef]
- Shearwood, C.; Williams, C.B.; Mellor, P.H.; Chang, K.Y.; Woodhead, J. Electro-magnetically levitated micro-discs. In Proceedings of the IEE Colloquium on Microengineering Applications in Optoelectronics, London, UK, 27 February 1996. [Google Scholar]
- Shearwood, C.; Ho, K.; Williams, C.; Gong, H. Development of a levitated micromotor for application as a gyroscope. Sens. Actuators A Phys. 2000, 83, 85–92. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, W.; Zhao, X.; Wu, X.; Liu, W.; Huang, X.; Shao, S. The study of an electromagnetic levitating micromotor for application in a rotating gyroscope. Sens. Actuators A Phys. 2006, 132, 651–657. [Google Scholar] [CrossRef]
- Tsai, N.C.; Huan, W.M.; Chiang, C.W. Magnetic actuator design for single-axis micro-gyroscopes. Microsyst. Technol. 2009, 15, 493–503. [Google Scholar] [CrossRef]
- Badilita, V.; Rzesnik, S.; Kratt, K.; Wallrabe, U. Characterization of the 2nd generation magnetic microbearing with integrated stabilization for frictionless devices. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1456–1459. [Google Scholar]
- Lu, Z.; Jia, F.; Korvink, J.; Wallrabe, U.; Badilita, V. Design optimization of an electromagnetic microlevitation System based on copper wirebonded coils. In Proceedings of the 2012 Power MEMS, Atlanta, GA, USA, 2–5 December 2012; pp. 363–366. [Google Scholar]
- Lu, Z.; Poletkin, K.; den Hartogh, B.; Wallrabe, U.; Badilita, V. 3D micro-machined inductive contactless suspension: Testing and modeling. Sens. Actuators A Phys. 2014, 220, 134–143. [Google Scholar] [CrossRef]
- Lu, Z.; Poletkin, K.; Wallrabe, U.; Badilita, V. Performance Characterization of Micromachined Inductive Suspensions Based on 3D Wire-Bonded Microcoils. Micromachines 2014, 5, 1469–1484. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. A qualitative technique to study stability and dynamics of micro-machined inductive contactless suspensions. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 528–531. [Google Scholar]
- Poletkin, K.V.; Lu, Z.; Moazenzadeh, A.; Mariappan, S.G.; Korvink, J.G.; Wallrabe, U.; Badilita, V. Polymer Magnetic Composite Core Boosts Performance of Three-Dimensional Micromachined Inductive Contactless Suspension. IEEE Magn. Lett. 2016, 7, 1–3. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Lu, Z.; Maozenzadeh, A.; Mariappan, S.G.; Korvink, J.; Wallrabe, U.; Badilita, V. 3D Micro-machined Inductive Suspensions with the Lowest Energy Consumption. In MikroSystemTechnik Kongress 2017; VDE Verlag: München, Germany, 2017; pp. 500–502. [Google Scholar]
- Poletkin, K.V.; Lu, Z.; Moazenzadeh, A.; Mariappan, S.G.; Korvink, J.G.; Wallrabe, U.; Badilita, V. Energy aware 3D micro-machined inductive suspensions with polymer magnetic composite core. In Proceedings of the 17th International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications Power MEMS 2017, Kanazawa, Japan, 14–17 November 2017; pp. 219–222. [Google Scholar]
- Lyuksyutov, I.F.; Naugle, D.G.; Rathnayaka, K.D.D. On-chip manipulation of levitated femtodroplets. Appl. Phys. Lett. 2004, 85, 1817–1819. [Google Scholar] [CrossRef]
- Chetouani, H.; Jeandey, C.; Haguet, V.; Rostaing, H.; Dieppedale, C.; Reyne, G. Diamagnetic Levitation With Permanent Magnets for Contactless Guiding and Trapping of Microdroplets and Particles in Air and Liquids. IEEE Trans. Magn. 2006, 42, 3557–3559. [Google Scholar] [CrossRef]
- Haguet, V.; Jeandey, C.; Chetouani, H.; Reyne, G.; Chatelain, F. Magnetic levitation of microdroplets in air. In Proceedings of the 10th International Conference on Miniaturized Systems for Chemistry and Life Sciences (MicroTAS), Tokyo, Japan, 5–9 November 2006; Volume 1, pp. 110–112. [Google Scholar]
- Jeandey, C.; Chetouani, H.; Haguet, V.; Chatelain, F.; Reyne, G. Diamagnetic levitation based digital microfluidics. In Proceedings of the MicroTAS, Paris, France, 7–11 October 2007; Volume 2, pp. 922–924. [Google Scholar]
- Pigot, C.; Chetouani, H.; Poulin, G.; Reyne, G. Diamagnetic Levitation of Solids at Microscale. IEEE Trans. Magn. 2008, 44, 4521–4524. [Google Scholar] [CrossRef]
- Kauffmann, P.; Pham, P.; Masse, A.; Kustov, M.; Honegger, T.; Peyrade, D.; Haguet, V.; Reyne, G. Contactless Dielectrophoretic Handling of Diamagnetic Levitating Water Droplets in Air. IEEE Trans. Magn. 2010, 46, 3293–3296. [Google Scholar] [CrossRef]
- Garmire, D.; Choo, H.; Kant, R.; Govindjee, S.; Sequin, C.H.; Muller, R.S.; Demmel, J. Diamagnetically Levitated MEMS Accelerometers. In Proceedings of the 2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 1203–1206. [Google Scholar]
- Ando, B.; Baglio, S.; Marletta, V.; Valastro, A. A Short-Range Inertial Sensor Exploiting Magnetic Levitation and an Inductive Readout Strategy. IEEE Trans. Instrum. Meas. 2018, PP, 1–8. [Google Scholar] [CrossRef]
- Su, Y.; Xiao, Z.; Ye, Z.; Takahata, K. Micromachined Graphite Rotor Based on Diamagnetic Levitation. IEEE Electron Device Lett. 2015, 36, 393–395. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, K.; Ye, Z.; Xiao, Z.; Takahata, K. Exploration of micro-diamagnetic levitation rotor. Jpn. J. Appl. Phys. 2017, 56, 126702. [Google Scholar] [CrossRef]
- Abadie, J.; Piat, E.; Oster, S.; Boukallel, M. Modeling and experimentation of a passive low frequency nanoforce sensor based on diamagnetic levitation. Sens. Actuators A Phys. 2012, 173, 227–237. [Google Scholar] [CrossRef]
- Kim, Y.; Katsurai, M.; Fujita, H. A proposal for a superconducting actuator using Meissner effect. In Proceedings of the an Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Micro Electro Mechanical Systems, Salt Lake City, UT, USA, 20–22 February 1989; pp. 107–112. [Google Scholar]
- Kim, Y.K.; Katsurai, M.; Fujita, H. A superconducting actuator using the Meissner effect. Sens. Actuators 1989, 20, 33–40. [Google Scholar] [CrossRef]
- Coombs, T.A.; Samad, I.; Ruiz-Alonso, D.; Tadinada, K. Superconducting micro-bearings. IEEE Trans. Appl. Supercond. 2005, 15, 2312–2315. [Google Scholar] [CrossRef]
- Lin, C.L.; Li, Y.H.; Lin, C.T.; Chiang, C.C.; Liu, Y.J.; Chung, T.T.; Baldeck, P.L. Preliminary study of lever-based optical driven micro-actuator. In Proceedings of the Third International Conference on Smart Materials and Nanotechnology in Engineering, Shenzhen, China, 11–13 November 2011; Volume 8409, p. 840920. [Google Scholar]
- Tabib-Azar, M. Optically controlled silicon microactuators. Nanotechnology 1990, 1, 81–92. [Google Scholar] [CrossRef]
- Svoboda, K.; Block, S.M. Biological applications of optical forces. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 247–285. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Abedin, K.S.; Kerbage, C.; Fernandez-Nieves, A.; Weitz, D.A. Optical manipulation and rotation of liquid crystal drops using high-index fiber-optic tweezers. Appl. Phys. Lett. 2007, 91, 091119. [Google Scholar] [CrossRef]
- Decombe, J.B.; Huant, S.; Fick, J. Single and dual fiber nano-tip optical tweezers: Trapping and analysis. Opt. Express 2013, 21, 30521–30531. [Google Scholar] [CrossRef] [PubMed]
- Bragheri, F.; Minzioni, P.; Liberale, C.; Fabrizio, E.D.; Cristiani, I. Design and optimization of a reflection-based fiber-optic tweezers. Opt. Express 2008, 16, 17647–17653. [Google Scholar] [CrossRef] [PubMed]
- Cabrini, S.; Liberale, C.; Cojoc, D.; Carpentiero, A.; Prasciolu, M.; Mora, S.; Degiorgio, V.; Angelis, F.D.; Fabrizio, E.D. Axicon lens on optical fiber forming optical tweezers, made by focused ion beam milling. Microelectron. Eng. 2006, 83, 804–807. [Google Scholar] [CrossRef]
- Liberale, C.; Cojoc, G.; Bragheri, F.; Minzioni, P.; Perozziello, G.; La Rocca, R.; Ferrara, L.; Rajamanickam, V.; Di Fabrizio, E.; Cristiani, I. Integrated microfluidic device for single-cell trapping and spectroscopy. Sci. Rep. 2013, 3, 1258. [Google Scholar] [CrossRef] [PubMed]
- Van Leest, T.; Caro, J. Cavity-enhanced optical trapping of bacteria using a silicon photonic crystal. Lab Chip 2013, 13, 4358–4365. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, A.; Huang, N.; Wu, S.H.; Martínez, L.J.; Povinelli, M.L. Enhanced and selective optical trapping in a slot-graphite photonic crystal. Opt. Express 2016, 24, 23271–23279. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef] [PubMed]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic holographic optical tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Fournier, J.M.R.; Burns, M.M.; Golovchenko, J.A. Writing diffractive structures by optical trapping. In Proceedings of the Practical Holography IX. International Society for Optics and Photonics, San Jose, CA, USA, 5–10 February 1995; Volume 2406, pp. 101–112. [Google Scholar]
- He, H.; Friese, M.; Heckenberg, N.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826. [Google Scholar] [CrossRef] [PubMed]
- Bellini, N.; Vishnubhatla, K.C.; Bragheri, F.; Ferrara, L.; Minzioni, P.; Ramponi, R.; Cristiani, I.; Osellame, R. Femtosecond laser fabricated monolithic chip for optical trapping and stretching of single cells. Opt. Express 2010, 18, 4679–4688. [Google Scholar] [CrossRef] [PubMed]
- Ganic, D.; Gan, X.; Gu, M. Optical trapping force with annular and doughnut laser beams based on vectorial diffraction. Opt. Express 2005, 13, 1260–1265. [Google Scholar] [CrossRef] [PubMed]
- Gu, M.; Morrish, D.; Ke, P.C. Enhancement of transverse trapping efficiency for a metallic particle using an obstructed laser beam. Appl. Phys. Lett. 2000, 77, 34–36. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef] [PubMed]
- Kampmann, R.; Chall, A.; Kleindienst, R.; Sinzinger, S. Optical system for trapping particles in air. Appl. Opt. 2014, 53, 777–784. [Google Scholar] [CrossRef] [PubMed]
- JPK; JPK Instruments AG: Berlin, Germany, 2018.
- MMI; Molecular Machines and Industries GmbH: Eching, Germany, 2018.
- Thorlabs; Thorlabs Inc.: Newton, NJ, USA, 2018.
- Dholakia, K.; MacDonald, M.; Spalding, G. Optical tweezers: The next generation. Phys. World 2002, 15, 31. [Google Scholar] [CrossRef]
- Friese, M.; Enger, J.; Rubinsztein-Dunlop, H.; Heckenberg, N.R. Optical angular-momentum transfer to trapped absorbing particles. Phys. Rev. A 1996, 54, 1593. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343. [Google Scholar] [CrossRef]
- Bayoudh, S.; Nieminen, T.; Heckenberg, N.; Rubinsztein-Dunlop, H. Orientation of biological cells using plane-polarized Gaussian beam optical tweezers. J. Mod. Opt. 2003, 50, 1581–1590. [Google Scholar] [CrossRef][Green Version]
- Dharmadhikari, J.; Roy, S.; Dharmadhikari, A.; Sharma, S.; Mathur, D. Torque-generating malaria-infected red blood cells in an optical trap. Opt. Express 2004, 12, 1179–1184. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Medina, B.; Andreasson, J.O.; Greenleaf, W.J.; LaPorta, A.; Block, S.M. An optical apparatus for rotation and trapping. In Methods in Enzymology; Elsevier: New York, NY, USA, 2010; Volume 475, pp. 377–404. [Google Scholar]
- Arita, Y.; Mazilu, M.; Dholakia, K. Laser-induced rotation and cooling of a trapped microgyroscope in vacuum. Nat. Commun. 2013, 4, 2374. [Google Scholar] [CrossRef] [PubMed]
- Galajda, P.; Ormos, P. Rotors produced and driven in laser tweezers with reversed direction of rotation. Appl. Phys. Lett. 2002, 80, 4653–4655. [Google Scholar] [CrossRef]
- La Porta, A.; Wang, M.D. Optical torque wrench: Angular trapping, rotation, and torque detection of quartz microparticles. Phys. Rev. Lett. 2004, 92, 190801. [Google Scholar] [CrossRef] [PubMed]
- O’Neil, A.T.; Padgett, M.J. Rotational control within optical tweezers by use of a rotating aperture. Opt. Lett. 2002, 27, 743–745. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, M.; Volke-Sepulveda, K.; Paterson, L.; Arlt, J.; Sibbett, W.; Dholakia, K. Revolving interference patterns for the rotation of optically trapped particles. Opt. Commun. 2002, 201, 21–28. [Google Scholar] [CrossRef]
- Paterson, L.; MacDonald, M.; Arlt, J.; Sibbett, W.; Bryant, P.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Higurashi, E.; Ohguchi, O.; Tamamura, T.; Ukita, H.; Sawada, R. Optically induced rotation of dissymmetrically shaped fluorinated polyimide micro-objects in optical traps. J. Appl. Phys. 1997, 82, 2773–2779. [Google Scholar] [CrossRef]
- Higurashi, E.; Ukita, H.; Tanaka, H.; Ohguchi, O. Optically induced rotation of anisotropic micro-objects fabricated by surface micromachining. Appl. Phys. Lett. 1994, 64, 2209–2210. [Google Scholar] [CrossRef]
- Galajda, P.; Ormos, P. Complex micromachines produced and driven by light. Appl. Phys. Lett. 2001, 78, 249–251. [Google Scholar] [CrossRef]
- Neale, S.L.; MacDonald, M.P.; Dholakia, K.; Krauss, T.F. All-optical control of microfluidic components using form birefringence. Nat. Mater. 2005, 4, 530. [Google Scholar] [CrossRef] [PubMed]
- Terray, A.; Oakey, J.; Marr, D.W.M. Fabrication of linear colloidal structures for microfluidic applications. Appl. Phys. Lett. 2002, 81, 1555–1557. [Google Scholar] [CrossRef]
- Terray, A.; Oakey, J.; Marr, D.W.M. Microfluidic Control Using Colloidal Devices. Science 2002, 296, 1841–1844. [Google Scholar] [CrossRef] [PubMed]
- Leach, J.; Mushfique, H.; di Leonardo, R.; Padgett, M.; Cooper, J. An optically driven pump for microfluidics. Lab Chip 2006, 6, 735–739. [Google Scholar] [CrossRef] [PubMed]
- Maruo, S.; Takaura, A.; Saito, Y. Optically driven micropump with a twin spiral microrotor. Opt. Express 2009, 17, 18525–18532. [Google Scholar] [CrossRef] [PubMed]
- Maruo, S.; Inoue, H. Optically driven micropump produced by three-dimensional two-photon microfabrication. Appl. Phys. Lett. 2006, 89, 144101. [Google Scholar] [CrossRef]
- Maruo, S.; Hiratsuka, Y. Optically driven micromanipulators with rotating arms. J. Robot. Mechatron. 2007, 19, 565. [Google Scholar] [CrossRef]
- Maruo, S.; Ikuta, K.; Korogi, H. Submicron manipulation tools driven by light in a liquid. Appl. Phys. Lett. 2003, 82, 133–135. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Chernomorsky, A.I.; Shearwood, C. A Proposal for Micromachined Accelerometer, base on a Contactless Suspension with Zero Spring Constant. IEEE Sens. J. 2012, 12, 2407–2413. [Google Scholar] [CrossRef]
- Poletkin, K.V. A novel hybrid Contactless Suspension with adjustable spring constant. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 934–937. [Google Scholar]
- Poletkin, K.V.; Korvink, J.G. Modeling a Pull-In Instability in Micro-Machined Hybrid Contactless Suspension. Actuators 2018, 7, 11. [Google Scholar] [CrossRef]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Badilita, V. A New Hybrid Micromachined Contactless Suspension With Linear and Angular Positioning and Adjustable Dynamics. J. Microelectromech. Syst. 2015, 24, 1248–1250. [Google Scholar] [CrossRef]
- Sari, I.; Kraft, M. A MEMS Linear Accelerator for Levitated Micro-objects. Sens. Actuators A Phys. 2015, 222, 15–23. [Google Scholar] [CrossRef]
- Kampmann, R.; Sinzinger, S. Optical tweezers affected by monochromatic aberrations. Appl. Opt. 2017, 56, 1317–1326. [Google Scholar] [CrossRef]
- Kauffmann, P.; Nussbaumer, J.; Masse, A.; Jeandey, C.; Grateau, H.; Pham, P.; Reyne, G.; Haguet, V. Self-Arraying of Charged Levitating Droplets. Anal. Chem. 2011, 83, 4126–4131. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, W.Y.; Zhang, W.P.; Huang, X.G.; Zhang, Z.R. Variable-capacitance micromotor with levitated diamagnetic rotor. Electron. Lett. 2008, 44, 681–683. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, Q.; Kan, R.; Bleuler, H.; Zhou, J. Realization of a Diamagnetically Levitating Rotor Driven by Electrostatic Field. IEEE/ASME Trans. Mechatron. 2017, 22, 2387–2391. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, W.; Liu, W.; Chen, W.; Li, K.; Cui, F.; Li, S. An innovative micro-diamagnetic levitation system with coils applied in micro-gyroscope. Microsys. Technol. 2009, 16, 431. [Google Scholar] [CrossRef]
- Sari, I.; Kraft, M. A micro electrostatic linear accelerator based on electromagnetic levitation. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1729–1732. [Google Scholar]

| Types of Actuator | Sources of Force Field | Materials of Levitated Mass/Rotor | Applications | Technologies | Ref. |
|---|---|---|---|---|---|
| Active | |||||
| Electric | Electrical | Dielectric, | Suspension | Bulk | [22,23,24,41] |
| field | Semiconductors | Accelerometer | Exotic Ball- | ||
| and conductive | micromaching | [36,37] | |||
| material | Motor | Bulk- | [25,27,28,29] | ||
| Gyroscope | micromaching | [26,30,31,32,33] | |||
| Multi-sensor | [34,35] | ||||
| Acelerometer | [38,39] | ||||
| Magnetic | DC current | Magnet | Actuator | Surface- | |
| micromaching | [42,43,44,45] | ||||
| Iron | Motor | Milli-machining | [46] | ||
| Passive | |||||
| Electric | Electrical | Conductive | Suspension | Surface- | |
| field | material | micromaching | [21] | ||
| Particles | Trapping | Mix of micromaching | |||
| and Bulk | [40] | ||||
| Inductive | Actuator | [47,52] | |||
| Gyroscope | Surface- | ||||
| AC current | Conductive | Motor | micromaching | [50,51] | |
| material | Suspension | [48,49] | |||
| 3D-micro-coil | [53,54,55,56,58,59,60] | ||||
| Diamagnetic | Trapping, Digital | Mix of Surface- | [61,62,65] | ||
| micro-fluidic | micromaching | [63,64,66] | |||
| Magnet | Diamagnetic | Accelerometer | and Bulk | [67,68] | |
| Gyroscope | [69,70] | ||||
| Force-sensor | [71] | ||||
| Supercon- | Magnet | Superconductor | Micro-bearing | Surface- | |
| ducting | micromaching | [73,74] | |||
| Optical | Light | Dielectric | Trapping, Rotation, | Precision mechanics | |
| Microfluidics, | Two Photon | [106,114,115,116,117,118,119,120,121,127] | |||
| Biochips, | Lithography | ||||
| Lab-on-Chip | |||||
| Hybrid | |||||
| Diamagnetic- | Magnet- | Diamagnetic | Trapping | Mix of Surface- | [128] |
| Electrostatic | electric field | Motor | micromaching | [129,130] | |
| Gyroscope | and Bulk | ||||
| Diamagnetic- | Magnet- | Diamagnetic- | |||
| Inductive | AC current | Conductive | [131] | ||
| material | |||||
| Electrostatic- | Electric | Conductive | Suspension, | Mix of Surface- | |
| Inductive | field- | material | Transporter | micromaching | [125] |
| AC current | and 3D-micro-coil | [17,123,124] | |||
| Accelerator | Surface- | ||||
| Accelerator | micromaching | [126,132] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poletkin, K.V.; Asadollahbaik, A.; Kampmann, R.; Korvink, J.G. Levitating Micro-Actuators: A Review. Actuators 2018, 7, 17. https://doi.org/10.3390/act7020017
Poletkin KV, Asadollahbaik A, Kampmann R, Korvink JG. Levitating Micro-Actuators: A Review. Actuators. 2018; 7(2):17. https://doi.org/10.3390/act7020017
Chicago/Turabian StylePoletkin, Kirill V., Asa Asadollahbaik, Ronald Kampmann, and Jan G. Korvink. 2018. "Levitating Micro-Actuators: A Review" Actuators 7, no. 2: 17. https://doi.org/10.3390/act7020017
APA StylePoletkin, K. V., Asadollahbaik, A., Kampmann, R., & Korvink, J. G. (2018). Levitating Micro-Actuators: A Review. Actuators, 7(2), 17. https://doi.org/10.3390/act7020017






